Solitons in the Heimburg–Jackson model of sound propagation in lipid bilayers are enabled by dispersion of a stiff membrane

Abstract

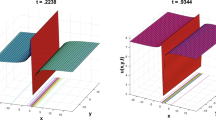
Experiments show that elastic constants of lipid bilayers vary greatly during the liquid-to-gel phase transition. This fact forms the cornerstone of the Heimburg–Jackson model of soliton propagation along membranes of axons, in which the action potential is accompanied by a traveling phase transition. However, the dispersion term, which is crucial for the existence of solitons, is added to the Heimburg–Jackson model ad hoc and set to fit experimental observations. In the present paper, we aim to consolidate this view with continuous membrane mechanics. Using literature data, we show that the compression modulus of a DPPC membrane is smaller by approximately an order of magnitude during phase transition. With a series expansion of the compression modulus, we write the action of a membrane and solve the corresponding wave equation analytically using an Exp-function method. We confirm that membrane solitons with speeds around 200 m/s are possible with amplitudes inversely proportional to their speed. We conclude that dispersion necessary for existence of solitons is directly related to a membrane’s bending properties, offering a possible explanation for h. Our findings are in general agreement with existing literature and give insight into a general mechanism of wave propagation in membranes close to transition.

Graphical abstract

Appendix A - Peakons

The solitary wave solutions are assumed to be of the form u(z), $z=x-vt$ where v is the speed of propagation. Since we are looking for localized wave packets, our solutions have to obey u(z), $u'(z)$, $u''(z) \rightarrow 0$ as $z \rightarrow \pm \infty$. The primes denote derivatives with respect to z. After substitution and chain rule, Eq. (2) becomes

$$\begin{aligned} v^2\left( \frac{\partial ^2 u}{\partial z^2}\right) =c^2\left( \frac{\partial ^2 u}{\partial z^2}\right) -h\left( \frac{\partial ^4 u}{\partial z^4}\right) . \end{aligned}$$

(22)

Here, $c^2=k_{a}/\mu$ and $h=k_{b}/\mu$. Rearranging, we get

$$\begin{aligned} 0=\frac{\partial ^2}{\partial z^2}\left[ u(c^2-v^2) -h \frac{\partial ^2 u}{\partial z^2}\right] . \end{aligned}$$

(23)

Following the assumption that solitons are localized and vanish for $z \rightarrow \pm \infty$, we can perform double integration immediately. After multiplying both sides by $2(\partial u/\partial z)$ and considering the identity $2(\partial u/\partial z)(\partial ^2 u/\partial z^2)=\partial /\partial z(\partial u/\partial z)^2$, we get

$$\begin{aligned} \left( \frac{\partial u}{\partial z}\right) ^2=\frac{(c^2-v^2)}{h}u^2. \end{aligned}$$

(24)

We see that solitons are possible only for the cases where $|v|<c$, otherwise the solutions do not decay to zero at infinity. The solution is

$$\begin{aligned} u(x,t)=c_{1}e^{-|x-vt|\sqrt{(c^2-v^2)/h}}, \end{aligned}$$

(25)

where $c_{1}$ is given by the initial conditions. The solution is smooth apart from the peak at its crest leading to a finite jump in the first derivative of the solution. Such solutions are sometimes called peaked solitary wave solutions or peakons in short [13].

1.1 Appendix B - Coefficient list

Coefficients from Eq. (14) are

$$\begin{aligned}&c_1 = a_{-1}^2 a_0 b_{-1}^2 \gamma ^2-a_{-1}^3 b_0 b_{-1} \gamma ^2-2 a_{-1} a_0 b_{-1}^3 \gamma \\&\qquad +2 a_{-1}^2 b_0 b_{-1}^2 \gamma -a_0 b_{-1}^4+a_{-1} b_0 b_{-1}^3, \\&c_2 = 3 a_{-1} a_0^2 b_{-1}^2 \gamma ^2+4 a_{-1}^2 a_1 b_{-1}^2 \gamma ^2\\&\qquad -5 a_{-1}^2 a_0 b_0 b_{-1} \gamma ^2-4 a_{-1}^3 b_1 b_{-1} \gamma ^2\\&\qquad +2 a_{-1}^3 b_0^2 \gamma ^2-3 a_0^2 b_{-1}^3 \gamma -8 a_{-1} a_1 b_{-1}^3 \gamma \\&\qquad +4 a_{-1} a_0 b_0 b_{-1}^2 \gamma \\&\qquad +8 a_{-1}^2 b_1 b_{-1}^2 \gamma -a_{-1}^2 b_0^2 b_{-1} \gamma -16 a_1 b_{-1}^4\\&\qquad +11 a_0 b_0 b_{-1}^3+16 a_{-1} b_1 b_{-1}^3-11 a_{-1} b_0^2 b_{-1}^2, \\&c_3 = 7 a_{-1}^3 b_0 b_1 \gamma ^2+3 a_0 a_{-1}^2 b_0^2 \gamma ^2\\&\qquad -3 a_1 a_{-1}^2 b_{-1} b_0 \gamma ^2\\&\qquad -18 a_0 a_{-1}^2 b_{-1} b_1 \gamma ^2+14 a_0 a_1 a_{-1} b_{-1}^2 \gamma ^2\\&\qquad -5 a_0^2 a_{-1} b_{-1}b_0 \gamma ^2\\&\qquad +2 a_0^3 b_{-1}^2 \gamma ^2-3 a_{-1}^2 b_0^3 \gamma +4 a_0 a_{-1} b_{-1} b_0^2 \gamma \\&\qquad -8 a_1 a_{-1} b_{-1}^2 b_0 \gamma +22 a_0 a_{-1} b_{-1}^2 b_1 \gamma \\&\qquad -14 a_0 a_1 b_{-1}^3 \gamma -a_0^2 b_{-1}^2 b_0 \gamma \\&\qquad +11 a_{-1} b_{-1} b_0^3-77 a_{-1} b_{-1}^2 b_0 b-11 a_0 b_{-1}^2 b_0^2\\&\qquad +a_1 b_{-1}^3 b_0+76 a_0 b_{-1}^3 b_1, \\&c_4 = a_{-1} a_0^2 b_0^2 \gamma ^2+2 a_{-1}^2 a_1 b_0^2 \gamma ^2\\&\qquad -a_0^3 b_{-1} b_0 \gamma ^2-2 a_{-1} a_0 a_1 b_{-1} b_0 \gamma ^2+11 a_{-1}^2 a_0 b_1 b_0 \gamma ^2\\&\qquad +12 a_{-1} a_1^2 b_{-1}^2 \gamma ^2+11 a_0^2 a_1 b_{-1}^2 \gamma ^2\\&\qquad +8 a_{-1}^3 b_1^2 \gamma ^2-22 a_{-1} a_0^2 b_{-1} b_1 \gamma ^2-20 a_{-1}^2 a_1 b_{-1} b_1 \gamma ^2\\&\qquad -2 a_{-1} a_0 b_0^3 \gamma \\&\qquad +2 a_0^2 b_{-1} b_0^2 \gamma -2 a_{-1} a_1 b_{-1} b_0^2 \gamma \\&\qquad -13 a_{-1}^2 b_1 b_0^2 \gamma -20 a_0 a_1 b_{-1}^2 b_0 \gamma \\&\qquad +24 a_{-1} a_0 b_{-1} b_1 b_0 \gamma -12 a_1^2 b_{-1}^3 \gamma -4 a_{-1}^2 b_{-1} b_1^2 \gamma \\&\qquad +11 a_0^2 b_{-1}^2 b_1 \gamma +16 a_{-1} a_1 b_{-1}^2 b_1 \gamma \\&\qquad -a_{-1} b_0^4+a_0 b_{-1} b_0^3-11 a_1 b_{-1}^2 b_0^2 +58 a_{-1} b_{-1} b_1 b_0^2\\&\qquad -47 a_0 b_{-1}^2 b_1 b_0-176 a_{-1} b_{-1}^2 b_1^2+176 a_1 b_{-1}^3 b_1, \\&c_5 = -8 a_0^3 b_{-1} b_1 \gamma ^2+3 a_1 a_0^2 b_{-1} b_0 \gamma ^2+3 a_{-1} a_0^2 b_0 b_1 \gamma ^2\\&\qquad +17 a_1^2 a_0 b_{-1}^2 \gamma ^2+2 a_{-1} a_1 a_0 b_0^2 \gamma ^2\\&\qquad +17 a_{-1}^2 a_0 b_1^2 \gamma ^2-44 a_{-1} a_1 a_0 b_{-1} b_1 \gamma ^2+5 a_{-1} a_1^2 b_{-1} b_0 \gamma ^2\\&\qquad +5 a_{-1}^2 a_1 b_0 b_1 \gamma ^2\\&\qquad +18 a_0^2 b_{-1} b_0 b_1 \gamma -8 a_1 a_0 b_{-1} b_0^2 \gamma \\&\qquad +10 a_{-1} a_0 b_{-1} b_1^2 \gamma +10 a_1 a_0 b_{-1}^2 b_1 \gamma \\&\qquad -8 a_{-1} a_0 b_0^2 b_1 \gamma -2 a_{-1} a_1 b_0^3 \gamma -22 a_{-1}^2 b_0 b_1^2 \gamma \\&\qquad -22 a_1^2 b_{-1}^2 b_0 \gamma +24 a_{-1} a_1 b_{-1} b_0 b_1 \gamma -230 a_0 b_{-1}^2 b_1^2\\&\qquad +10 a_0 b_{-1} b_0^2 b_1-5 a_1 b_{-1} b_0^3\\&\qquad +115 a_{-1} b_{-1} b_0 b_1^2-5 a_{-1} b_0^3 b_1+115 a_1 b_{-1}^2 b_0 b_1, \\&c_6 = 2 a_{-1} a_1^2 b_0^2 \gamma ^2+a_0^2 a_1 b_0^2 \gamma ^2+11 a_0 a_1^2 b_{-1} b_0 \gamma ^2\\&\qquad -a_0^3 b_1 b_0 \gamma ^2-2 a_{-1} a_0 a_1 b_1 b_0 \gamma ^2\\&\qquad +8 a_1^3 b_{-1}^2 \gamma ^2+11 a_{-1} a_0^2 b_1^2 \gamma ^2+12 a_{-1}^2 a_1 b_1^2 \gamma ^2\\&\qquad -20 a_{-1} a_1^2 b_{-1} b_1 \gamma ^2\\&\qquad -22 a_0^2 a_1 b_{-1} b_1 \gamma ^2-2 a_0 a_1 b_0^3 \gamma -13 a_1^2 b_{-1} b_0^2 \gamma \\&\qquad +2 a_0^2 b_1 b_0^2 \gamma -2 a_{-1} a_1 b_1 b_0^2 \gamma -20 a_{-1} a_0 b_1^2 b_0 \gamma \\&\qquad +24 a_0 a_1 b_{-1} b_1 b_0 \gamma -12 a_{-1}^2 b_1^3 \gamma +11 a_0^2 b_{-1} b_1^2 \gamma \\&\qquad +16 a_{-1} a_1 b_{-1} b_1^2 \gamma -4 a_1^2 b_{-1}^2 b_1 \gamma -a_1 b_0^4+a_0 b_1 b_0^3\\&\qquad -11 a_{-1} b_1^2 b_0^2+58 a_1 b_{-1} b_1 b_0^2-47 a_0 b_{-1} b_1^2 b_0\\&\qquad +176 a_{-1} b_{-1} b_1^3-176 a_1 b_{-1}^2 b_1^2, \\&c_7 = 2 a_0^3 b_1^2 \gamma ^2-5 a_1 a_0^2 b_0 b_1 \gamma ^2+3 a_1^2 a_0 b_0^2 \gamma ^2\\&\qquad +14 a_{-1} a_1 a_0 b_1^2 \gamma ^2-18 a_1^2 a_0 b_{-1} b_1 \gamma ^2\\&\qquad +7 a_1^3 b_{-1} b_0 \gamma ^2-3 a_{-1} a_1^2 b_0 b_1 \gamma ^2-a_0^2 b_0 b_1^2 \gamma \\&\qquad -14 a_{-1} a_0 b_1^3 \gamma +22 a_1 a_0 b_{-1} b_1^2 \gamma \\&\qquad +4 a_1 a_0 b_0^2 b_1 \gamma -3 a_1^2 b_0^3 \gamma -8 a_{-1} a_1 b_0 b_1^2 \gamma \\&\qquad +76 a_0 b_{-1} b_1^3-11 a_0 b_0^2 b_1^2\\&\qquad +a_{-1} b_0 b_1^3-77 a_1 b_{-1} b_0 b_1^2+11 a_1 b_0^3 b_1, \\&c_8 = 4 a_{-1} a_1^2 b_1^2 \gamma ^2+3 a_0^2 a_1 b_1^2 \gamma ^2-4 a_1^3 b_{-1} b_1 \gamma ^2\\&\qquad -5 a_0 a_1^2 b_0 b_1 \gamma ^2+2 a_1^3 b_0^2 \gamma ^2-3 a_0^2 b_1^3 \gamma \\&\qquad -8 a_{-1} a_1 b_1^3 \gamma +8 a_1^2 b_{-1} b_1^2 \gamma +4 a_0 a_1 b_0 b_1^2 \gamma \\&\qquad -a_1^2 b_0^2 b_1 \gamma -16 a_{-1} b_1^4\\&\qquad +16 a_1 b_{-1} b_1^3+11 a_0 b_0 b_1^3-11 a_1 b_0^2 b_1^2, \\&c_9 = a_0 a_1^2 b_1^2 \gamma ^2-a_1^3 b_0 b_1 \gamma ^2-2 a_0 a_1 b_1^3 \gamma \\&\quad +2 a_1^2 b_0 b_1^2 \gamma -a_0 b_1^4+a_1 b_0 b_1^3. \end{aligned}$$