Diseased Social Predators

Abstract

Social predators benefit from cooperation in the form of increased hunting success, but may be at higher risk of disease infection due to living in groups. Here, we use mathematical modeling to investigate the impact of disease transmission on the population dynamics benefits provided by group hunting. We consider a predator–prey model with foraging facilitation that can induce strong Allee effects in the predators. We extend this model by an infectious disease spreading horizontally and vertically in the predator population. The model is a system of three nonlinear differential equations. We analyze the equilibrium points and their stability as well as one- and two-parameter bifurcations. Our results show that weakly cooperating predators go unconditionally extinct for highly transmissible diseases. By contrast, if cooperation is strong enough, the social behavior mediates conditional predator persistence. The system is bistable, such that small predator populations are driven extinct by the disease or a lack of prey, and large predator populations survive because of their cooperation even though they would be doomed to extinction in the absence of group hunting. We identify a critical cooperation level that is needed to avoid the possibility of unconditional predator extinction. We also investigate how transmissibility and cooperation affect the stability of predator–prey dynamics. The introduction of parasites may be fatal for small populations of social predators that decline for other reasons. For invasive predators that cooperate strongly, biocontrol by releasing parasites alone may not be sufficient.

Appendices

Appendix A: Isocline Analysis in the Endemic Predator–Prey Phase Plane

We perform an isocline analysis of the three-dimensional model (5)–(7), which will lead us to a reduced model in the two-dimensional phase plane. Any nontrivial equilibrium satisfies the following zero-growth conditions

$$\begin{aligned} \text {prey nullcline:}\,n= & {} k\left[ 1-\frac{1+\alpha p}{r}p\right] , \end{aligned}$$

(10)

$$\begin{aligned} \text {predator nullcline:}\,n= & {} \frac{1+\mu i}{1+\alpha p}, \end{aligned}$$

(11)

$$\begin{aligned} \text {prevalence nullcline:}\,i= & {} 1-\frac{(1+ \alpha p)(1- \theta )}{\beta -\mu }n. \end{aligned}$$

(12)

Substituting the value of n from equation (11) into equation (12), we find the nontrivial prevalence value at any equilibrium with $p^*>0$

$$\begin{aligned} i^*= \frac{\beta -\mu -(1-\theta )}{\beta -\mu \theta }, \end{aligned}$$

which is exactly expression (9) shown in the main text.

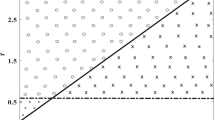
We can now intersect the three-dimensional state space with the prevalence nullplane $i=i^*$ and work on the (p, n) plane, where $p>0$ and $n>0$. This simplifies the analysis because it allows us to find the intersection of curves (10) and (11) with $i=i^*$ constant (see Fig. 1).

The parabola (10) intersects the n–axis at the point (0, k), while the hyperbola (11) intersects the n–axis at the point $(0, 1+ \mu i^*)$. That is, if the vertical intercept of the parabola (solid red dashed curve in Fig. 1) is higher than the vertical intercept of the hyperbola (dashed blue curve in Fig. 1), then there is a unique intersection of the parabola and hyperbola (Fig. 1b, d). This condition can be expressed as $k>1+\mu i^*$ or equivalently as ${\mathcal R}_p(i^*)>1$. If ${\mathcal R}_p(i^*)<1$, there can be 0, 1, or 2 intersections (Fig. 1a, c).

Appendix B: Existence and Stability of the Stationary States

To analyze the equilibrium point, we consider the Jacobian of system (5)–(7):

$$\begin{aligned} J= \left( \begin{array}{ccc} r\left( 1-\frac{2n}{k}\right) -p\alpha ' &{} -p'n &{} 0 \\ \alpha ' p &{} -(1+ \mu i )+p' n &{} -\mu p \\ -\alpha ' \theta ' i &{} -\alpha \theta ' ni &{} b '(1-2i)-\alpha ' \theta ' n \end{array} \right) , \end{aligned}$$

where $b'= \beta -\mu$, $\theta ' = 1-\theta$, $\alpha ' =1+\alpha p$, and $p'=1+2\alpha p$. The system has the following possible equilibria:

• 1. $E_{0} = (0,0,0)$. The trivial extinction state always exists and is always unstable, since the eigenvalues of the Jacobian evaluated at this equilibrium are

  $$\begin{aligned} \lambda _{1} = r > 0 , \quad \lambda _{2}= -1+k, \quad \lambda _{3}= \beta - \mu -(1 -\theta ) k. \end{aligned}$$

• 2. $E_\mathrm{n} = (k,0,0)$. This represents the disease- and predator-free equilibrium with the prey being at carrying capacity. It always exists and its eigenvalues are

  $$\begin{aligned} \lambda _{1}=-r < 0,\quad \lambda _{2}= -1+k, \quad \lambda _{3}= \beta - \mu -(1 -\theta ) k. \end{aligned}$$

  Hence, $E_\mathrm{n}$ is stable if

  $$\begin{aligned} k<1, \quad {\mathcal R}_i=\frac{\beta +\theta k}{\mu +k}<1. \end{aligned}$$

• 3. $E_{i}= (0,0,1)$. This is the disease-induced extinction state with both predators and prey being absent. It always exists, but it is always unstable because its eigenvalues are:

  $$\begin{aligned} \lambda _{1}=r > 0,\quad \lambda _{2}= -1+\mu ,\quad \lambda _{3}= \beta - \mu -(1 -\theta ) k. \end{aligned}$$

• 4. $E_\mathrm{ni}= (k,0,i^{\dagger })$, where $i^{\dagger } = 1-\frac{(1-\theta )k}{\beta -\mu }$. This is the state corresponding to disease-induced predator extinction, with the prey reaching carrying capacity. It exists if

  $$\begin{aligned} {\mathcal R}_i=\frac{\beta +\theta k}{\mu +k}>1. \end{aligned}$$

  The eigenvalues are

  $$\begin{aligned} \lambda _{1}=-r,\quad \lambda _{2}= k-(1+ \mu i^{\dagger }), \quad \lambda _{3}= (\beta - \mu )(1- 2i^{\dagger }) -(1 -\theta ) k. \end{aligned}$$

  That is, $E_\mathrm{ni}$ is stable if $k<1+\mu i^{\dagger }$, which translates into ${\mathcal R}_p(i^*)<1$.

• 5. $E_\mathrm{np}= (n^{\circ },p^{\circ },0)$ is the disease-free coexistence state of predators and prey. The values of $n^{\circ }$ and $p^{\circ }$ are cumbersome to obtain. If $k>1$, $E_\mathrm{np}$ is unique. If $k<1$, there can be up to two equilibria $E_\mathrm{np}$ which (dis-)appear in a saddle–node bifurcation in the disease-free plane (see Teixeira Alves and Hilker 2017). The stability of $E_\mathrm{np}$ is investigated numerically and discussed in the main text.

• 6. $E_\mathrm{npi}= (n^*,p^*,i^*)$, with $i^*= [\beta -\mu -(1-\theta )](\beta -\mu \theta )^{-1}$ as shown in Appendix A. This equilibrium is the endemic coexistence state where all three species (prey, predators and disease) coexist. As for the disease-free coexistence equilibrium, we cannot find the explicit values of the prey and predator values. From $i^*>0$, we obtain that a necessary existence condition for $E_\mathrm{npi}$ is

  $$\begin{aligned} {\mathcal R}_0(0,1)=\frac{\beta +\theta }{1+\mu }>1. \end{aligned}$$

  In Sect. 3, we find that if ${\mathcal R}_p(i^*)>1$ the equilibrium exists and is unique and stable. If ${\mathcal R}_p(i^*)<1$, there can be two, one or no equilibrium point $E_\mathrm{npi}$. We study the existence and stability of $E_\mathrm{npi}$ numerically in the main text and show that there is a saddle–node bifurcation when varying $\alpha$.