Skip to main content
SpringerLink
Log in

Bifurcation Analysis of Reaction Diffusion Systems on Arbitrary Surfaces

  • Original Article
  • Published:
Bulletin of Mathematical Biology Aims and scope Submit manuscript

Abstract

In this paper, we present computational techniques to investigate the effect of surface geometry on biological pattern formation. In particular, we study two-component, nonlinear reaction–diffusion (RD) systems on arbitrary surfaces. We build on standard techniques for linear and nonlinear analysis of RD systems and extend them to operate on large-scale meshes for arbitrary surfaces. In particular, we use spectral techniques for a linear stability analysis to characterise and directly compose patterns emerging from homogeneities. We develop an implementation using surface finite element methods and a numerical eigenanalysis of the Laplace–Beltrami operator on surface meshes. In addition, we describe a technique to explore solutions of the nonlinear RD equations using numerical continuation. Here, we present a multiresolution approach that allows us to trace solution branches of the nonlinear equations efficiently even for large-scale meshes. Finally, we demonstrate the working of our framework for two RD systems with applications in biological pattern formation: a Brusselator model that has been used to model pattern development on growing plant tips, and a chemotactic model for the formation of skin pigmentation patterns. While these models have been used previously on simple geometries, our framework allows us to study the impact of arbitrary geometries on emerging patterns.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18

Similar content being viewed by others

Notes

  1. Throughout this paper, we deal with cases with only one parameter of interest, at a time, to study bifurcations. Thus, we use terms ‘bifurcation parameter’ and ‘continuation parameter’ interchangeably to refer to the same system parameter and denote it by \(\alpha \). We refer to \(\alpha \) as a bifurcation parameter when the context pertains to pattern emergence. Similarly, we refer to \(\alpha \) as the continuation parameter when the context relates to branch tracing and continuation algorithms. We always perform continuation with the same parameter as that was used to locate the bifurcation at the first instance. However, this is not a strict requirement and our framework can be used for branch tracing with a different continuation parameter.

  2. i.e, Characterising the zero crossings of a circumferential profile of a radially symmetric soliton.

  3. Strictly speaking, a and b are functions of time as well and one must express \(a:\Omega \times t \mapsto {\mathbb {R}}\) and \(b:\Omega \times t \mapsto {\mathbb {R}}\). However, we are concerned only with steady-state solutions and they do not change with time. To avoid the confusion which may arise with equations from spectral decomposition during linear stability analysis, we do not express the time dimension explicitly.

  4. We refer to a two-dimensional, connected manifold with or without boundaries as a ‘surface’. We discuss relevant boundary conditions in Sect. 3.2. Throughout this paper, we use terms ‘surface’ and ‘domain’ interchangeably.

  5. Often, the Laplace–Beltrami operator for surface functions is denoted as \(\nabla ^2_{S}\). We omit the subscript ‘S’ for the simplicity of expressions.

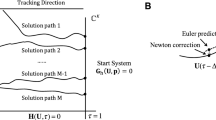
  6. Note that, in our framework, the bifurcation parameter is also the continuation parameter.

  7. Note that the growth rates for the amplitudes of the eigenmodes, as discussed here, do not refer to the scale or growth of the domain \(\Omega \) itself.

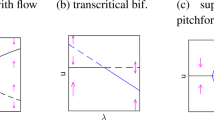
  8. While Chien and Liao (2001) label all bifurcations made of two or more eigenmodes as mixed-mode, we reserve this term only for the bifurcations that involve eigenmodes with different eigenvalues.

  9. Note that Eq. 8 is homogeneous and the terms \(u_i\) and \(v_i\) can only be solved up to a common scale factor, say \(s_i = v_i/u_i\).

  10. See our supplemental material (SM01.D4) for detailed derivation for these coefficients and Eq. 15.

  11. We refrain from introducing an additional notation such as \(\Omega _d\) for the discrete surface.

  12. In practice, when the parameters \({}^uD_u, {}^uD_v, {}^vD_v, {}^vD_u, {}^uK_u, {}^uK_v, {}^vK_u\) and \({}^vK_v\) are themselves expressed in terms of a set of some other (real) system parameters, then \({\mathbf {p}}\) is the set of these real parameters and \(\alpha \) is one of them.

  13. The units for the parameters and the domain size are same as those assumed by Nagata et al. (2013).

  14. We label the branches as low, mid or high frequency branches based on the range of the eigenspectrum which is explored.

  15. In this example as well, we apply nonlinear soft-thresholding to aid visualisation of the patterns. We use the same nonlinear mapping for each pattern which is first scaled and off-setted to the range [0, 1].

References

  • Banerjee M, Banerjee S (2012) Turing instabilities and spatio-temporal chaos in ratio-dependent Holling–Tanner model. Math Biosci 236(1):64–76

    Article  MathSciNet  MATH  Google Scholar 

  • Bangerth W, Hartmann R, Kanschat G (2007) Deal.II—a general purpose object oriented finite element library. ACM Trans Math Softw 33(4):24/1–24/27

    Article  MathSciNet  Google Scholar 

  • Bauer HF (1986) Tables of the roots of the associated Legendre function with respect to the degree. Math Comput 46(174):601–602

    Article  MathSciNet  MATH  Google Scholar 

  • Bolstad JH, Keller HB (1986) A multigrid continuation method for elliptic problems with folds. SIAM J Sci Stat Comput 7(4):1081–1104

    Article  MathSciNet  MATH  Google Scholar 

  • Bonito A, Pauletti S, Bangerth W (2013) The step-38 tutorial program, Reference documentation for Deal.II version 8.4.0. https://dealii.org/8.4.0/doxygen/deal.II/step_38.html, Accessed 11 May 2016

  • Chien CS, Liao Y (2001) Multiple bifurcations generated by mode interactions in a reaction–diffusion problem. J Comput Appl Math 130(1):345–368

    Article  MathSciNet  MATH  Google Scholar 

  • Cignoni P, Callieri M, Corsini M, Dellepiane M, Ganovelli F, Ranzuglia G (2008) MeshLab: an open-source mesh processing tool. In: Scarano V, Chiara RD, Erra U (eds) Sixth Eurographics Italian Chapter Conference, The Eurographics Association, pp 129–136

  • Crampin EJ, Gaffney EA, Maini PK (1999) Reaction and diffusion on growing domains: scenarios for robust pattern formation. Bull Math Biol 61(6):1093–1120

    Article  MATH  Google Scholar 

  • Demlow A (2009) Higher-order finite element methods and pointwise error estimates for elliptic problems on surfaces. SIAM J Numer Anal 47(2):805–827

    Article  MathSciNet  MATH  Google Scholar 

  • Draelants D, Broeckhove J, Beemster GT, Vanroose W (2013) Numerical bifurcation analysis of the pattern formation in a cell based auxin transport model. J Math Biol 67(5):1279–1305

    Article  MathSciNet  MATH  Google Scholar 

  • Dziuk G (1988) Finite elements for the Beltrami operator on arbitrary surfaces. In: Hildebrandt S, Leis R (eds) Partial differential equations and calculus of variations. Springer, Berlin, pp 142–155

    Chapter  Google Scholar 

  • Dziuk G, Elliott CM (2013) Finite element methods for surface PDEs. Acta Numer 22:289–396

    Article  MathSciNet  MATH  Google Scholar 

  • Gafiychuk V, Datsko B, Meleshko V, Blackmore D (2009) Analysis of the solutions of coupled nonlinear fractional reaction–diffusion equations. Chaos Solitons Fractals 41(3):1095–1104

    Article  MathSciNet  MATH  Google Scholar 

  • Gambino G, Lombardo M, Sammartino M (2012) Turing instability and traveling fronts for a nonlinear reaction–diffusion system with cross-diffusion. Math Comput Simul 82(6):1112–1132

    Article  MathSciNet  MATH  Google Scholar 

  • Gambino G, Lombardo M, Sammartino M (2013a) Pattern formation driven by cross-diffusion in a 2D domain. Nonlinear Anal Real World Appl 14(3):1755–1779

    Article  MathSciNet  MATH  Google Scholar 

  • Gambino G, Lombardo MC, Sammartino M, Sciacca V (2013b) Turing pattern formation in the Brusselator system with nonlinear diffusion. Phys Rev E 88:042925

    Article  Google Scholar 

  • Garland M, Heckbert PS (1997) Surface simplification using quadric error metrics. Proceedings of the 24th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH ’97). ACM Press, New York, pp 209–216

  • Gary, Julia (2013) [photograph] A Gecko lizard with small spots. Retrieved from http://www.westcoastleopardgecko.com/images/00451.JPG, Accessed 07 July 2015

  • Harrison LG, Von Aderkas P (2004) Spatially quantitative control of the number of cotyledons in a clonal population of somatic embryos of hybrid larch larix \(\times \) leptoeuropaea. Ann Bot 93(4):423–434

    Article  Google Scholar 

  • Heroux MA, Bartlett RA, Howle VE, Hoekstra RJ, Hu JJ, Kolda TG, Lehoucq RB, Long KR, Pawlowski RP, Phipps ET et al (2005) An overview of the Trilinos project. ACM Trans Math Softw 31(3):397–423

    Article  MathSciNet  MATH  Google Scholar 

  • Jiang Z, Duan P, Guo X, Hua D (2010) Improvement of FEM’s dynamic property. Appl Math Mech 31:1337–1346

    Article  MathSciNet  MATH  Google Scholar 

  • Kealy BJ, Wollkind DJ (2012) A nonlinear stability analysis of vegetative Turing pattern formation for an interaction–diffusion plant-surface water model system in an arid flat environment. Bull Math Biol 74(4):803–833

    Article  MathSciNet  MATH  Google Scholar 

  • Kondo S, Miura T (2010) Reaction–diffusion model as a framework for understanding biological pattern formation. Science 329(5999):1616–1620

    Article  MathSciNet  MATH  Google Scholar 

  • Lévy B, Zhang HR (2010) Spectral mesh processing. In: ACM SIGGRAPH 2010 Courses, ACM Press, New York, pp 8:1–8:312. doi:10.1145/1837101.1837109

  • Lo WC, Chen L, Wang M, Nie Q (2012) A robust and efficient method for steady state patterns in reaction–diffusion systems. J Comput Phys 231(15):5062–5077

    Article  MathSciNet  MATH  Google Scholar 

  • Locke T (2007) [photograph] A Gecko lizard with an aligned spot pattern. Retrieved from http://www.geckotime.com/breeding-leopard-geckos-on-a-small-scale/, Accessed 07 July 2015

  • Lou Y, Ni WM (1996) Diffusion, self-diffusion and cross-diffusion. J Differ Equ 131(1):79–131

    Article  MathSciNet  MATH  Google Scholar 

  • Ma M, Hu J (2014) Bifurcation and stability analysis of steady states to a Brusselator model. Appl Math Comput 236:580–592

    MathSciNet  MATH  Google Scholar 

  • Madzvamuse A (2008) Stability analysis of reaction–diffusion systems with constant coefficients on growing domains. Int J Dyn Syst Differ Equ 1(4):250–262

    MathSciNet  MATH  Google Scholar 

  • Madzvamuse A, Zenas George U (2013) The moving grid finite element method applied to cell movement and deformation. Finite Elements Anal Des 74:76–92

    Article  MathSciNet  MATH  Google Scholar 

  • Madzvamuse A, Gaffney EA, Maini PK (2010) Stability analysis of non-autonomous reaction–diffusion systems: the effects of growing domains. J Math Biol 61(1):133–164

    Article  MathSciNet  MATH  Google Scholar 

  • Maini P, Myerscough M, Winter K, Murray J (1991) Bifurcating spatially heterogeneous solutions in a chemotaxis model for biological pattern generation. Bull Math Biol 53(5):701–719

    Article  MATH  Google Scholar 

  • Méndez V, Campos D (2008) Population extinction and survival in a hostile environment. Phys Rev E 77(2):022901

    Article  MathSciNet  Google Scholar 

  • Murray J (2003) Mathematical biology II: spatial models and biomedical applications, 3rd edn. Springer, New York

    MATH  Google Scholar 

  • Murray J, Myerscough M (1991) Pigmentation pattern formation on snakes. J Theor Biol 149(3):339–360

    Article  Google Scholar 

  • Nagata W, Harrison LG, Wehner S (2003) Reaction–diffusion models of growing plant tips: bifurcations on hemispheres. Bull Math Biol 65(4):571–607

    Article  MATH  Google Scholar 

  • Nagata W, Zangeneh HR, Holloway DM (2013) Reaction–diffusion patterns in plant tip morphogenesis: bifurcations on spherical caps. Bull Math Biol 75(12):2346–2371

    Article  MathSciNet  MATH  Google Scholar 

  • Paulau P (2014) Fundamental-and first-order localized states in a cubic-quintic reaction–diffusion system. Phys Rev E 89(3):032910

    Article  Google Scholar 

  • Psyon (2009) [photograph] A Gecko lizard with bands on its back. Retrieved from https://commons.wikimedia.org/wiki/File:Juvenile-leopard-gecko-2.jpg, Accessed 07 July 2015

  • Qian H, Murray JD (2001) A simple method of parameter space determination for diffusion-driven instability with three species. Appl Math Lett 14(4):405–411

    Article  MathSciNet  MATH  Google Scholar 

  • Qiao L, Kevrekidis I, Punckt C, Rotermund H (2006) Geometry-induced pulse instability in microdesigned catalysts: the effect of boundary curvature. Phys Rev E 73(3):036217

    Article  Google Scholar 

  • Raven (2009) [photograph] An Eublepharis macularius Gecko lizard with irregular spots. Retrieved from https://plus.google.com/communities/107069611951806704428, Accessed 07 July 2015

  • Reuter M, Biasotti S, Giorgi D, Patanè G, Spagnuolo M (2009) Discrete Laplace–Beltrami operators for shape analysis and segmentation. Comput Graph 33(3):381–390

    Article  Google Scholar 

  • Rooster (2009) [photograph] A juvenile Gecko lizard with a stripe pattern. Retrieved from http://www.captivebredreptileforums.co.uk/members/rooster/albums/rooster-s-geckos/4223-jungle-leopard-gecko-baby-pic-hes-bigger-now/, Accessed 07 July 2015

  • Rozada I, Ruuth SJ, Ward M (2014) The stability of localized spot patterns for the Brusselator on the sphere. SIAM J Appl Dyn Syst 13(1):564–627

    Article  MathSciNet  MATH  Google Scholar 

  • Salinger AG, Bou-Rabee NM, Pawlowski RP, Wilkes ED, Burroughs EA, Lehoucq RB, Romero LA (2002) LOCA 1.0 Library of continuation algorithms: theory and implementation manual. Sandia National Laboratories, Albuquerque, NM, Technical Report No SAND2002-0396

  • Satnoianu RA, Maini PK, Menzinger M (2001) Parameter space analysis, pattern sensitivity and model comparison for Turing and stationary flow-distributed waves (FDS). Phys D Nonlinear Phenom 160(1):79–102

    Article  MathSciNet  MATH  Google Scholar 

  • Seydel R (2010) Practical bifurcation and stability analysis, 3rd edn. Springer, New York

    Book  MATH  Google Scholar 

  • Tuncer N, Madzvamuse A, Meir A (2015) Projected finite elements for reaction–diffusion systems on stationary closed surfaces. Appl Numer Math 96:45–71

    Article  MathSciNet  MATH  Google Scholar 

  • Turing AM (1952) The chemical basis of morphogenesis. Phil Trans R Soc Lond Ser B Biol Sci 237(641):37–72

    Article  MathSciNet  Google Scholar 

  • Vasquez DA (2013) Pattern formation induced by a differential shear flow. Phys Rev E 87(2):024902

    Article  MathSciNet  Google Scholar 

  • Winters K, Myerscough M, Maini PK, Murray JD (1990) Tracking bifurcating solutions of a model biological pattern generator. IMPACT Comput Sci Eng 2(4):355–371

    Article  MATH  Google Scholar 

  • Wyller J, Blomquist P, Einevoll GT (2007) Turing instability and pattern formation in a two-population neuronal network model. Phys D Nonlinear Phenom 225(1):75–93

    Article  MathSciNet  MATH  Google Scholar 

  • Yang L, Dolnik M, Zhabotinsky AM, Epstein IR (2002) Spatial resonances and superposition patterns in a reaction–diffusion model with interacting Turing modes. Phys Rev Lett 88(20):208303

    Article  Google Scholar 

  • Yochelis A, Tintut Y, Demer L, Garfinkel A (2008) The formation of labyrinths, spots and stripe patterns in a biochemical approach to cardiovascular calcification. New J Phys 10(5):055002

    Article  Google Scholar 

  • Zamora-Sillero E, Hafner M, Ibig A, Stelling J, Wagner A (2011) Efficient characterization of high-dimensional parameter spaces for systems biology. BMC Syst Biol 5(1):142

    Article  Google Scholar 

Download references

Acknowledgements

MCM was supported by grants from the Swiss National Science Foundation (FNSNF, grants 31003A_140785 and SINERGIA CRSII3_132430), and the SystemsX.ch initiative (project EpiPhysX) for this work. We thank Liana Manukyan from LANE, University of Geneva for 3D scanning a gecko surface and providing us with the point-cloud data. We used Meshlab software for surface reconstruction with this point-cloud. DSD was also supported by the FNSNF grant SINERGIA CRSII3_132430 for this work. He is thankful to his colleague Shihao Wu at CGG, Univ. of Bern for uniform re-sampling of the gecko surface mesh, for level \(L_2\) in Fig. 17. DSD thanks Prof. Dr. T. Wihler at Mathematical Institute, Univ. of Bern for suggesting Deal.II library.

Author information

Author notes

  1. Daljit Singh J. Dhillon

    Present address: Department of Computing, Imperial College London, London, UK

Authors and Affiliations

  1. Institute of Computer Science, University of Bern, Bern, Switzerland

    Daljit Singh J. Dhillon & Matthias Zwicker

  2. Laboratory of Artificial & Natural Evolution (LANE), Department of Genetics and Evolution, University of Geneva, Geneva, Switzerland

    Michel C. Milinkovitch

  3. SIB Swiss Institute of Bioinformatics, Geneva, Switzerland

    Michel C. Milinkovitch

Authors
  1. Daljit Singh J. Dhillon
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michel C. Milinkovitch
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Matthias Zwicker
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Daljit Singh J. Dhillon.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dhillon, D.S.J., Milinkovitch, M.C. & Zwicker, M. Bifurcation Analysis of Reaction Diffusion Systems on Arbitrary Surfaces. Bull Math Biol 79, 788–827 (2017). https://doi.org/10.1007/s11538-017-0255-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11538-017-0255-8

Keywords

Search

Navigation