Bifurcation Analysis of Reaction Diffusion Systems on Arbitrary Surfaces

Abstract

In this paper, we present computational techniques to investigate the effect of surface geometry on biological pattern formation. In particular, we study two-component, nonlinear reaction–diffusion (RD) systems on arbitrary surfaces. We build on standard techniques for linear and nonlinear analysis of RD systems and extend them to operate on large-scale meshes for arbitrary surfaces. In particular, we use spectral techniques for a linear stability analysis to characterise and directly compose patterns emerging from homogeneities. We develop an implementation using surface finite element methods and a numerical eigenanalysis of the Laplace–Beltrami operator on surface meshes. In addition, we describe a technique to explore solutions of the nonlinear RD equations using numerical continuation. Here, we present a multiresolution approach that allows us to trace solution branches of the nonlinear equations efficiently even for large-scale meshes. Finally, we demonstrate the working of our framework for two RD systems with applications in biological pattern formation: a Brusselator model that has been used to model pattern development on growing plant tips, and a chemotactic model for the formation of skin pigmentation patterns. While these models have been used previously on simple geometries, our framework allows us to study the impact of arbitrary geometries on emerging patterns.

1 Introduction

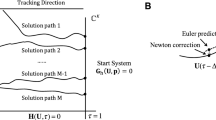
Reaction–diffusion (RD) is often used to model the development of biological systems, most prominently in the study of biological pattern formation (Kondo and Miura 2010). The mathematical representation of these models results in systems of nonlinear partial differential equations (PDEs) (Turing 1952). The analysis of these systems of PDEs aim at answering two fundamental questions: (i) what are the possible solutions that satisfy the given system of PDEs, and how can these solutions be discovered systematically; and (ii) which of these solutions are stable against minor perturbations. Two strategies are commonly used to perform this analysis. First, linear stability analysis can predict the emergence of new patterns near trivial, homogeneous solutions (homogeneities) of the PDEs (Murray 2003). This happens with small changes in one or more critical parameters in the system, called bifurcation parameters. The emergent patterns correspond to sudden qualitative changes to the state of an RD system and, hence, constitute bifurcations from the homogeneity. Second, nonlinear analysis provides solutions of the nonlinear RD equations far away from the homogeneous steady states. To construct these solutions, numerical continuation techniques are used to follow continuous branches of solutions starting from initial bifurcation patterns constructed using the linear analysis (Seydel 2010). Solutions vary gradually with one of the system parameters, called the continuation parameter,¹ along each branch.

Several existing tools allow to delineate solutions for an RD system through linear and nonlinear bifurcation analyses. However, many of them are constrained to work with only simple surface geometries such as rectangles or hemispheres, and at low resolutions. These are serious limitations given that surface geometry plays an important role in pattern formation (Murray 2003, page 108) and most of the interesting biological domains for RD systems have rather arbitrary shapes. In addition, corresponding patterns are too complex to be resolved with low-resolution meshes.

In this paper, we develop a framework to perform bifurcation analysis for generic RD systems with two components, with or without cross-diffusion, acting on arbitrary surfaces. Unlike standard detection-based approaches that iteratively step along a trivial branch of patternless homogeneous solutions to detect bifurcation points (Seydel 2010, Chapter 5), our proposed framework uses an analysis–synthesis approach to directly determine bifurcation points and construct emerging patterns along the trivial branch. In our approach, we exploit the Hermitian nature of the Laplace–Beltrami (LB) operator acting on a given arbitrary surface (Lévy and Zhang 2010), which enables the computation of a spectral basis for emerging patterns. This, in turn, allows us to derive formulae to directly compose emergent bifurcation patterns from eigenfunctions (also called eigenmodes or wavemodes) of the LB operator. Similarly, given a bifurcation pattern in terms of its eigenvectors and eigenvalues, we can directly compute the corresponding bifurcation point. We elaborate on our analysis–synthesis approach in Sect. 3 along with several boundary conditions for our framework that are common for biological systems and ensure that the LB operator is Hermitian. Unlike detection-based approaches, our analysis–synthesis approach avoids missing out on bifurcations due to potential failures of a test function (Refer to Seydel (2010, Sect. 5.2) for details on test functions). In addition, our approach allows for tracing multiple and mixed-mode bifurcations apart from simple bifurcations.

For accurate branch tracing with complex bifurcation patterns, we require higher resolution meshes to triangulate surfaces. This increases computational complexities. We propose a multiresolution approach that decouples branch tracing complexity from the complexity of dealing with a large-scale system at a higher resolution.

We demonstrate the working of our framework for a Brusselator system with zero Dirichlet boundary conditions to study the emergent patterns of cotyledons on a conifer tip (Nagata et al. 2003). We also demonstrate its working with Murray’s chemotactic model for pattern formation of skin pigmentation (Murray and Myerscough 1991), subject to zero Neumann boundary conditions. In both cases, we illustrate the influence of surface shape on pattern formation using several example geometries. Finally, we evaluate the computational performance of our multiresolution branch tracing approach. In summary, our contributions include:

• A framework for analysing two-component RD systems with or without cross-diffusion that supports arbitrary triangulated surface domains.

• A direct analysis–synthesis approach for computing emergent patterns and locating bifurcation points along the trivial branch based on spectral analysis of the Laplace–Beltrami operator on arbitrary triangulated surface domains.

• A progressive geometric multigrid approach supporting high-resolution FEM discretisation to determine patterns along nonlinear branches.

• Two case studies illustrating the effect of arbitrary geometries on pattern formation.

2 Related Work

2.1 Emergent Patterns Near Homogeneity

Linear stability analysis with two-component RD systems is often employed to study the emergence of new patterns from near homogeneous patternless initial conditions. Nagata et al. (2003, 2013) study the relation between the shape and size of a conifer embryo and the emergent cotyledon patterns. They use a Brusselator RD system acting on a parametric family of spherical caps while imposing zero Dirichlet boundary conditions near homogeneity. With this, they explain how the number of emergent cotyledons is simply the selection of a spherical cap harmonic based on the radius of the conifer and its curvature (Nagata et al. 2013). Winters et al. (1990) explain emergence of heterogeneous snake skin colour patterns with a chemotactic RD model with cross-diffusion (i.e. where the flux of one component is driven by gradients in the concentration of the second component). They perform numerical simulations on flat rectangular domains and illustrate the similarity of emergent patterns to the patterns observed in nature, for different snake species. Winters et al. use zero Neumann boundary conditions for their RD system. Similarly, Gambino et al. (2013) discuss pattern formation due to cross-diffusion for Lotka–Volterra kinetics between two components in a 2D rectangular domain, commonly used to model predator–prey populations. Kealy and Wollkind (2012) use linear stability analysis to study onset of various spatial Turing patterns for vegetation in an arid flat land using a two-component RD system. They also apply a weak nonlinear stability analysis to predict the long-term behaviour of these emerging vegetation patterns. Murray (2003, Chapter 3) demonstrates the effect of both geometry and scale on the emergence of patterns under a two-component RD system and discusses the relevance of these parameters for explaining animal coat patterns. He derives an analytical form for the stripe and spot patterns that emerge on a tapering cylinder representing an animal tail. Also, he presents the selection of different stripe or patchy patterns (modes) with changes in the size of a planar 2D shape representing an animal coat. Most studies on the emergence of patterns, such as those discussed above, are limited to simple, well-defined surface geometries with analytically defined emergent patterns. Recently, Tuncer et al. (2015) have introduced a projected Finite Elements Method for studying pattern formation by RD systems on surfaces that can be approximated analytically and later mapped with Lipschitz continuity onto a sphere. They note that studying RD systems on arbitrary surfaces is rather a “young and emerging research area”— (Tuncer et al. 2015) and that surface geometry is crucial for such studies. Our framework extends studies of RD systems with or without cross-diffusion to arbitrary surface domains without any geometric constraints by directly (numerically) computing emergent patterns on them. Also, it supports several common boundary conditions that arise in biological problems such as homogeneous Dirichlet, Neumann and Robin boundary conditions. As noted earlier, (arbitrary) surface geometry plays an important role in pattern formation. Thus our framework serves as an important tool for studying emergent patterns on ‘real’ geometries.

2.2 Marginal Stability Analysis

Marginal stability analysis is often used to study the interaction and mutual-exclusivity of two or more emergent wavemodes. It is also used to demarcate and characterise the parameter space of an RD system. Kealy and Wollkind (2012) use analytically defined marginal stability curves to demarcate regions in the parameter space with subjectively different vegetation patterns on arid flat lands (represented as 2D rectangles). Nagata et al. (2013) define marginal stability curves for emergent wavemodes in terms of their corresponding eigenvalues and investigate the influence of the spherical cap surface geometry on the pattern of cotyledons development. In particular, they note that changes in the curvature or size of a plant tip may cause a change in the number of cotyledons that develop despite that the concentrations of chemical precursors are fixed. Our framework generalises such marginal stability analysis to arbitrary domains. It numerically computes the eigenvalues for the wavemodes that constitute emergent patterns. These eigenvalues can then be used to plot corresponding marginal stability curves. In general, our framework supports case studies with arbitrarily shaped surface domains at different scales for marginal stability analyses, as demonstrated later.

2.3 Bifurcations and Branch Tracing

Analytical solutions for branch tracing are only possible for simple surface domains. Ma and Hu (2014) express branches and patterns for a two-component Brusselator model acting on a 1D straight line domain in analytical forms. They prove that, except for the first branch along the continuation parameter dimension, all other branches are unstable. Méndez and Campos (2008) derive analytical expressions for tracing a branch with a single component RD system to predict the survival of an isolated 1D patch of a population in its surrounding 1D hostile environment. Using stability predictions along the branch, they establish that the survival of a population at a very low or negative growth rate depends on its initial density. Instead, we support branch tracing with numerical methods in our framework. Winters et al. (1990) and Maini et al. (1991) perform branch tracing numerically for their two-component RD system with cross-diffusion acting on simple 2D rectangular domains. They simulate a diverse range of complex patterns with significant amplitudes for studying snakeskin pigmentations. Yochelis et al. (2008) perform numerical branch tracing for a two-component Gierer–Meinhardt RD system on a simplified periodic 1D domain to study cardiovascular calcification patterns. They use the insights gained from branch tracing to characterise the parameter space for further experiments with 2D domains. Chien and Liao (2001) investigate multiple modes bifurcating at a given bifurcation point for a two-component Brusselator system subject to Robin boundary conditions. They demonstrate numerical continuation of multiple branches due to mode interactions for a 2D square domain. Paulau (2014) performs numerical branch tracing for a two-component FitzHugh–Nagumo (FHN) RD system on a 2D planar domain to study the properties of its localised solutions, i.e. solitons. With this, he establishes the existence and stability of certain first higher order radially symmetric solitons with non-zero azimuthal quantum number ² which require the third and fifth order nonlinear reaction terms to produce them. Our framework generalises such studies with two-component RD systems to arbitrary surfaces.

2.4 Other Cases

In general, studies with emergent patterns, marginal stability or bifurcation analysis may deal with more than two-components (Qian and Murray 2001), coupled layers (Yang et al. 2002; Vasquez 2013), quasi equilibrium (Rozada et al. 2014), advection (Vasquez 2013; Satnoianu et al. 2001; Madzvamuse and Zenas George 2013), a very large number (Zamora-Sillero et al. 2011) or range (Lo et al. 2012) of control parameters, shear-induced instability (Vasquez 2013), growth-induced instability (Madzvamuse 2008), nonlinear diffusion (Gambino et al. 2013), fractional RD (Gafiychuk et al. 2009) or even non-steady state (oscillatory) or travelling wave solutions (Draelants et al. 2013; Banerjee and Banerjee 2012; Wyller et al. 2007; Qiao et al. 2006; Gambino et al. 2012). While our framework may be used directly or with simple modifications for only a few of these general cases, they serve as directions for future work on our framework.

3 Analysis–Synthesis of Bifurcation Patterns Using Laplacian Eigenbasis

In this section, we formulate our analysis–synthesis approach to compute bifurcation patterns using eigenfunctions of the Laplace–Beltrami operator. We derive a general form for an emergent pattern near homogeneity for a generic two-component RD system acting on arbitrary surfaces, with or without cross-diffusion. This specifies how a bifurcation pattern can be composed from eigenvectors of the Laplace–Beltrami operator. As a key feature, given a bifurcation pattern in terms of its eigenvectors and eigenvalues, our approach allows us to directly compute the constraints to be satisfied by the bifurcation parameter.

We first perform a simplification of the generic RD system equations near homogeneity into a linear form, to be satisfied by an emergent pattern (Sect. 3.1). Next, we present a spectral decomposition of potential patterns and the boundary conditions that allow expressing these patterns with orthogonal basis functions (Sect. 3.2). Then, we substitute a spectrally decomposed potential pattern into the linearised system equations to obtain an explicit general form for an emergent pattern along with expressions and conditions for its spectral coefficients (Sect. 3.3). This allows us to define the bifurcation point in terms of spectral eigenvalues and system parameters. Next, we discuss three cases of simple, multiple and mixed-mode bifurcations and the constraints that they impose on our general derivations (Sect. 3.4), and finally, we describe our analysis–synthesis approach to directly compose bifurcation patterns for these cases (Sect. 3.5).

3.1 Linearising Generic Two-Component RD Systems

Let us consider a two-component general RD system with cross diffusion, defined over an arbitrary surface. Irrespective of its dimensional or non-dimensional characteristic, such a system can be expressed mathematically, in a general form, as

$$\begin{aligned} \frac{\partial a}{\partial t}&= \nabla ^2\left[ \left( {}^aD_a + {}^aD_\alpha a + {}^aD_\beta b \right) a \right] + f(a,b) \,,\nonumber \\ \frac{\partial b}{\partial t}&= \nabla ^2\left[ \left( {}^bD_b + {}^bD_\alpha a + {}^bD_\beta b \right) b \right] + g(a,b) \,. \end{aligned}$$

(1)

Here, $a:\Omega \mapsto {\mathbb {R}}$ and $b:\Omega \mapsto {\mathbb {R}}$ ³ are the concentrations of two components over the surface domain⁴ $\Omega$, diffusion is represented with the Laplace–Beltrami operator⁵ $\nabla ^2$, and functions f and g represent nonlinear reaction terms. The scalar coefficients ${}^aD_a$ and ${}^bD_b$ are positive diffusion rates, ${}^aD_\alpha$ and ${}^bD_\upbeta$ are non-negative self-diffusion factors, and ${}^aD_\upbeta$ and ${}^bD_\alpha$ are non-negative cross-diffusion factors for the system (Lou and Ni 1996). We discuss the boundary conditions for the system of PDEs in Eq. 1 in Sect. 3.2. Throughout this paper, we consider only steady-state solutions of RD systems. For Eq. 1, this implies that we are interested in solutions with ${}{\partial a}\!/{\partial t} = {}{\partial b}\!/{\partial t} = 0$.

To linearise the RD system defined in Eq. 1, we first define its homogeneous steady state $(a_0,b_0)$ as a solution to the simultaneous equations $f(a_0,b_0) = 0$ and $g(a_0,b_0) = 0$. Note that depending on the complexity of f and g (say polynomial order), there may be multiple choices for the homogeneous steady state $(a_0,b_0)$. Given a steady state $(a_0,b_0)$, we now perform a Taylor series expansion for the nonlinear reaction terms f and g for infinitesimal deviations $u = \left. \Delta a\right| _{a_0}$ and $v = \left. \Delta b\right| _{b_0}$,

$$\begin{aligned} f(a_0 + u, b_0 + v)&= f(a_0,b_0) + u \left. \frac{\partial f}{\partial a}\right| _{(a_0,b_0)} + v \left. \frac{\partial f}{\partial b}\right| _{(a_0, b_0)} + n_f(u,v), \nonumber \\ g(a_0 + u, b_0 + v)&= g(a_0,b_0) + u \left. \frac{\partial g}{\partial a}\right| _{(a_0,b_0)} + v \left. \frac{\partial g}{\partial b}\right| _{(a_0, b_0)} + n_g(u,v), \end{aligned}$$

(2)

where $n_f$ and $n_g$ are polynomial functions containing the second and higher order terms in u and v for their respective Taylor series expansions. In other words, $n_f$ and $n_g$ represent the nonlinear part of the reaction terms for the system defined by Eq. 1 near the homogeneous steady state $(a_0, b_0)$. Now substituting $a=a_0 + u$, $b=a_0 + v$, $f(a_0 + u, b_0 + v)$, and $g(a_0 + u, b_0 + v)$ from Eq. 2 into Eq. 1 and ignoring the nonlinear terms yields

$$\begin{aligned} \frac{\partial u}{\partial t}&= {}^uD_u \nabla ^2 u \,\,+\,{}^uD_v \nabla ^2 v \,\,+\,\, f_l(u,v) \, , \nonumber \\ \frac{\partial v}{\partial t}&= {}^vD_v \nabla ^2 v \,\,+\,{}^vD_u \nabla ^2 u \,\,+\,\, g_l(u,v) \, ,\quad \end{aligned}$$

(3)

$$\begin{aligned} \text {with }\quad \quad&\nonumber \\ f_l(u,v)&= \,\, {}^uK_u\, u \,\,+\,\, {}^uK_v\, v \, , \nonumber \\ g_l(u,v)&= \,\, {}^vK_u\, u \,\,+\,\, {}^vK_v\, v \, , \end{aligned}$$

(4)

for $u:\Omega \mapsto {\mathbb {R}}$ and $v:\Omega \mapsto {\mathbb {R}}$. Here, new diffusion coefficients $\lbrace {}^uD_u,{}^uD_v, {}^vD_u, {}^vD_v\rbrace$ and reaction coefficients $\lbrace {}^uK_u,{}^uK_v, {}^vK_u, {}^vK_v\rbrace$ are defined in terms of old coefficients in Eq. 1, $a_0, b_0$, and partial derivatives ${}{\partial f}\!/{\partial a}$, ${}{\partial f}\!/{\partial b}$, ${}{\partial g}\!/{\partial a}$ and ${}{\partial g}\!/{\partial b}$ evaluated at $(a_0,b_0)$. See the supplemental material (SM01.D1) for the definition of these new coefficients along with necessary derivations. We emphasise that for the above linearisation, all nonlinear terms with factors u, v, $\nabla u$, $\nabla v$, $\nabla ^2 u$ and $\nabla ^2 v$ become negligible and can be ignored. To understand this, reconsider that u and v are infinitesimal deviations. We may restate this fact as $u = \varepsilon u^{*}, v = \varepsilon v^{*}$ and $\varepsilon \rightarrow 0$. Here $u^{*}$, $v^{*}$ represent the deviations on a relative scale and $\varepsilon$ represents the absolute scale for deviations. Thus, while the $\varepsilon$ term gets factored out from linear terms on both sides of PDEs, all second and higher order terms tend to zero as $\varepsilon \rightarrow 0$.

3.2 Spectral Decomposition and Boundary Conditions

Our framework performs bifurcation analysis near homogeneity using spectral analysis of the Laplace–Beltrami operator $\nabla ^2$. If a second-order linear operator such as $\nabla ^2$ is Hermitian, then its eigenmodes form a set of orthonormal basis functions that can express any surface function such as u and v. Using an orthonormal spectral decomposition, we derive the conditions for an emergent pattern directly in terms of the eigenmodes and eigenvalues for the Laplace–Beltrami operator.

To ensure the orthonormality of the basis functions, we need to consider the boundary conditions for u and v on the surface domain $\Omega$. Most biological problems expressed as RD systems are subject to either periodic boundary conditions or zero Dirichlet, Neumann, or Robin boundary conditions near homogeneity, or they deal with closed surfaces without boundaries. We show in the supplemental material (SM01.D2) that all these cases satisfy the Hermitian property of the Laplace–Beltrami operator, thus implying that the following derivations are valid for all such cases.

3.2.1 Spectral Decomposition

To generate a set $\lbrace {\upphi }_k\rbrace$ of orthonormal basis functions ${\upphi }_k:\Omega \mapsto {\mathbb {R}}$ using the Laplace–Beltrami operator $\nabla ^2$, we must solve the corresponding eigenvalue problem

$$\begin{aligned} \nabla ^2 {\upphi }_k = - \lambda _k {\upphi }_{k}\,,\quad \forall k\,. \end{aligned}$$

(5)

Note that each basis function ${\upphi }_k$ is subject to the same boundary conditions as those for the RD system under investigation. We discuss a few working examples of how to compute ${\upphi }_k$ with different boundary conditions in Sect. 6. Here, all the eigenvalues $\lambda _k$ are real and non-negative since $\nabla ^2$ is Hermitian. We thus assume that the basis functions form an ordered set, where the ordering index k satisfies $\lambda _k \le \lambda _{k+1}$. Using the basis functions $\lbrace {\upphi }_k\rbrace$ we can express a smooth surface function $f:\Omega \mapsto {\mathbb {R}}$ as

$$\begin{aligned} f = \sum _{k} {f_k\,{\upphi }_k}\, , \quad \text {where}\quad f_k = \langle f, {\upphi }_k \rangle \,\quad \forall k\,, \end{aligned}$$

(6)

and $f_k$ are called spectral coefficients. Next, we leverage the spectral decomposition in Eq. 6 to express a pattern emergent near homogeneity for a generic RD system defined in Eq. 1.

3.3 Bifurcation Patterns Near Homogeneity

While the spectral decomposition suggests that potential patterns could in general contain any superposition of eigenmodes, the conditions near homogeneity impose additional constraints on actual emergent patterns. We now derive an as–general–as–possible form for emergent steady-state patterns, expressed in the spectral basis, that respects these constraints.

Consider a steady-state bifurcation pattern $(u^b, v^b)$, where the superscript b denotes that this emergent pattern is a bifurcation from the trivial homogeneous solution. Substituting its spectral decomposition from Eq. 6 into Eq. 3, and setting the temporal derivatives to zero to obtain a steady-state solution, gives us

$$\begin{aligned} \quad \frac{\partial u^b}{\partial t}&= {}^uD_u \nabla ^2 \sum _k{u_k {\upphi }_k} \,\,+\,\, {}^uD_v \nabla ^2 \sum _k{v_k {\upphi }_k} \,\,+\,\, {}^uK_u\, \sum _k{u_k {\upphi }_k} \,\,\nonumber \\&\quad +\,\, {}^uK_v\, \sum _k{v_k {\upphi }_k} \,\, = \,\,0\, , \nonumber \\ \quad \frac{\partial v^b}{\partial t}&= {}^vD_v \nabla ^2 \sum _k{v_k {\upphi }_k} \,\,+\,\,{}^vD_u \nabla ^2 \sum _k{u_k {\upphi }_k} \,\,+\,\, {}^vK_u\, \sum _k{u_k {\upphi }_k} \,\,\nonumber \\&\quad +\,\, {}^vK_v\, \sum _k{v_k {\upphi }_k} \,\, = \,\,0\, . \end{aligned}$$

(7)

For simplicity, we dropped the superscript b from the spectral coefficients $u_k$ and $v_k$.

Simplifying Eq. 7 using substitutions $\nabla ^2{\upphi }_k=-\lambda _k {\upphi }_k$, $\forall k$, and imposing linear independence of orthonormal basis functions ${\upphi }_k$ yields the following relations between the spectral coefficients $u_k$, $v_k$, and eigenvalues $\lambda _k$, $\forall k$ (see supplemental material (SM01.D3) for a detailed derivation),

$$\begin{aligned} ({}^uK_u\,-\, {}^uD_u \lambda _k)\, u_k \,\,+\,\, ({}^uK_v\, - {}^uD_v \lambda _k) \, v_k \,\,&= \,\,0\, , \nonumber \\ ({}^vK_v\,-\, {}^vD_v \lambda _k)\, v_k \,\,+\,\, ({}^vK_u\, - {}^vD_u \lambda _k) \, u_k \,\,&= \,\,0\,. \end{aligned}$$

(8)

For each non-zero pair of $u_k$ and $v_k$, we derive the following constraint on the corresponding eigenvalue $\lambda _k$ from the above equation,

$$\begin{aligned}&({}^uD_u {}^vD_v \,\,-\,\, {}^uD_v {}^vD_u) \lambda _k^2 \,\,-\,\, \text {{}} \nonumber \\&\quad ({}^uD_u {}^vK_v \,\,+\,\, {}^vD_v {}^uK_u \,\,-\,\,{}^uD_v {}^vK_u\,\,-\,\,{}^vD_u {}^uK_v ) \lambda _k \,\,\nonumber \\&\qquad + \,\, {}^uK_u {}^vK_v - {}^uK_v {}^v K_u \,\, = \,\,0 \,. \end{aligned}$$

(9)

Eq. 9 is quadratic in $\lambda _k$ and it admits at most two real valued roots for $\lambda _k$, say $\Lambda _m$ and $\Lambda _n$.

This implies,

$$\begin{aligned} u^b = \sum _{\lbrace i \rbrace } {u_i {\upphi }_i} \,\, + \,\,\sum _{\lbrace j \rbrace } {u_j {\upphi }_j}\,,\quad \quad v^b = \sum _{\lbrace i \rbrace } {v_i {\upphi }_i} \,\,+\,\, \sum _{\lbrace j \rbrace } {v_j {\upphi }_j}\,,\, \nonumber \\ \text {with}\quad \lbrace i \rbrace \,=\, \lbrace k \,|\,\lambda _k=\Lambda _m\rbrace \, \quad \text {and}\quad \lbrace j \rbrace \,=\, \lbrace k \,|\,\lambda _k=\Lambda _n\rbrace \,. \end{aligned}$$

(10)

This means that at most two sets of eigenfunctions with two distinct eigenvalues $\Lambda _m$ and $\Lambda _n$, i.e. $\lbrace {\upphi }_i \rbrace = \lbrace {\upphi }_k \,|\, \lambda _k = \Lambda _m \rbrace$ and $\lbrace {\upphi }_j \rbrace = \lbrace {\upphi }_k \,|\, \lambda _k = \Lambda _n \rbrace$ may be combined linearly to form an emergent pattern. Thus, Eq. 10 expresses the most general form for a bifurcation pattern $(u^b,v^b)$, emergent near homogeneity for an RD system as in Eq. 3.

3.4 Classifying Diffusion-Driven Instabilities

An important requirement for patterns given by Eq. 10 to emerge due to diffusion-driven instabilities is that the RD systems must be linearly stable in absence of diffusion. Murray expresses this requirement in terms of the differentials of the reaction terms in an RD system equation Murray (see 2003, Equation 2.19). For RD systems given by Eq. 1, near homogeneity, the stability constraints are expressed in terms of system parameters as (refer to Eq. 4):

$$\begin{aligned} \frac{\partial f_l}{\partial u} \,+\, \frac{\partial g_l}{\partial v} \,&= \, {}^uK_u \,+\,{}^vK_v \, < 0\,, \text { and}\quad \frac{\partial f_l}{\partial u} \, \frac{\partial g_l}{\partial v} \,-\, \frac{\partial f_l}{\partial v} \, \frac{\partial g_l}{\partial u}\,\nonumber \\&= \, {}^uK_u \,{}^vK_v \,-\, {}^uK_v \,{}^vK_u \, > 0\,. \end{aligned}$$

(11)

In absence of diffusion, a bifurcation pattern emerges when one of the system parameters called the bifurcation parameter⁶ $\alpha$, undergoes a change to invalidate the above inequalities. A bifurcation parameter may be any function of the parameters ${}^uK_u,{}^uK_v,{}^vK_u,$ and ${}^vK_v$ in Eq. 11. In contrast, a diffusion-driven bifurcation occurs whenever Eq. 9 is brought to satisfaction for some $\lambda _k$ with a change in the bifurcation parameter $\alpha$ without violating Eq. 11.

To facilitate direct composition of emergent patterns, we classify them based on two criteria. First, we classify patterns as (i) exclusive mode selections or (ii) non-exclusive mode selections based on certain conditions for the diffusion induced instability. Diffusion-driven instabilities may activate multiple eigenmodes ${\upphi }_k$ to grow or emerge simultaneously under a fixed set of system parameters. This is captured by the dispersion relation (Murray 2003, page 86), which indicates the range of eigenvalues that are unstable for the fixed system parameters. The dispersion relation provides a temporal growth rate ⁷ $\xi _k$ for each potential eigenvalue $\lambda _k$. The growth rate $\xi _k$ indicates the rate at which the amplitude of the corresponding eigenmode ${\upphi }_k$ would increase with time, under a given set of system parameters. Only eigenmodes with non-negative growth rates are unstable and may participate in pattern formation.

Fig. 1

Dispersion relation curves for the first three bifurcations for Murray’s chemotactic RD system (Winters et al. 1990) with $\alpha$ as a bifurcation parameter. Potential eigenvalues are represented along the $\lambda$-axis and the rates at which the amplitude of the corresponding eigenfunctions may grow with time are represented along the $\xi$-axis. For a two-component RD system, the dispersion relation is an implicit equation with second-order polynomial terms in $\xi$ and $\lambda$. Actual eigenvalues of the LB operator are shown as circles. As we move along the trivial branch by increasing the value of the bifurcation parameter $\alpha$, different eigenmodes (represented by bigger brown circles) become unstable to branch out new bifurcations. For mathematical details refer to Eq. 22 in Sect. 6.2. RD system parameters other than $\alpha$ are set to default values as specified in that section (Color figure online)

Figure 1 plots dispersion relations as curves of growth rates $\xi$ over potential eigenvalues $\lambda$ for an example. The shapes of the curves are determined by the given system parameters, and varying a free continuation parameter $\alpha$ leads to a family of curves. We show three such curves for three different values of $\alpha$, increasing from left to right. Circles along the $\lambda$-axis indicate actual eigenvalues $\lambda _k$ from the spectral analysis (Sect. 3.2). In exclusive mode selection (left image), eigenmodes corresponding to exactly one eigenvalue, say $\Lambda _n$, become unstable (they have a non-negative growth rate) at the bifurcation point. In non-exclusive mode selection (middle image), the system becomes unstable to a new set of eigenmodes with eigenvalue $\Lambda _n$, while it remains unstable to other eigenmodes with positive growth rates (red dot on the $\lambda$-axis).

Further, similar to Chien and Liao (2001),⁸ we classify bifurcations as: (a) simple if only a single wavemode constitutes the emergent pattern, (b) multiple if more than one wavemode constitutes the emergent pattern but all such wavemodes have the same eigenvalue, and (c) mixed-mode for the bifurcations with constituent wavemodes of more than one eigenfrequency, say $\Lambda _n$ and $\Lambda _m$. Figure 1 on the right illustrates the dispersion relation for a mixed-mode pattern at its bifurcation point. Next, we derive different formulae to compose bifurcation patterns directly for these cases.

3.5 Composing Bifurcation Patterns for Continuation

Building on the derivations from Sects. 3.1, 3.2 and 3.3, we now derive equations to directly compose bifurcation patterns using an analysis–synthesis approach. We discuss simple, multiple, and mixed-mode bifurcations for the RD system in Eq. 1 (near homogeneity), both under exclusive and non-exclusive mode selection. At this point, we assume that the eigenvalues $\lambda _k$ and eigenmodes ${\upphi }_k$ for the Laplace–Beltrami operator (the “analysis”) are given and discuss their numerical computation later in Sect. 4. Our composition algorithm (the “synthesis”) allows: (a) selecting one of the system (reaction) parameters as the bifurcation parameter $\alpha$, (b) setting values for all other system parameters arbitrarily without violating preconditions like those in Eq. 11, and (c) setting scale factors $u_k, \forall k$ in Eq. 10 for a desired linear combination of eigenmodes ${\upphi }_k$ in $u^b$, i.e. a desired emergent pattern in one system component. It then outputs: (a) the value of the (free) bifurcation parameter at the bifurcation point for the emergent pattern with desired $u^b$, and (b) the complete (discretised) emergent pattern $(u^b,v^b)$ with appropriately scaled $v_k, \forall k$ for eigenmodes ${\upphi }_k$ in $v^b$, i.e. the second system component concentration. We present the method details in the following.

3.5.1 Simple Bifurcations

Simple bifurcation patterns are composed of a single wave ${\upphi }_i$ such that the algebraic multiplicity of its corresponding eigenvalue $\lambda _i = \Lambda$ is 1. Let for some i, $(u^b = u_i {\upphi }_i\,,\,v^b = v_i {\upphi }_i)$ be the steady-state bifurcation pattern of interest. We now investigate the conditions that the bifurcation parameter must satisfy to branch out a steady-state pattern $(u^b,\,v^b)$.

Exclusive Mode Selection For simple bifurcations in exclusive mode selection problems, the system is driven into instability by one single eigenmode, while it remains linearly stable against all other eigenmodes. Thus, the quadratic Eq. 9 must admit only one real root for $\lambda _k = \Lambda$ corresponding to the eigenmode under investigation, at the bifurcation point. In this case, chosen $\Lambda$ satisfies

$$\begin{aligned} 2\,\Lambda \,({}^uD_u {}^vD_v \,\,-\,\, {}^uD_v {}^vD_u) \,\,=\,\,{}^uD_u {}^vK_v \,\,+\,\, {}^vD_v {}^uK_u \,\,-\,\,{}^uD_v {}^vK_u\,\,-\,\,{}^vD_u {}^uK_v. \end{aligned}$$

(12)

For RD systems without cross-diffusion, ${}^uD_v = {}^vD_u =0$ and the above relation becomes $2\,\Lambda \,{}^uD_u {}^vD_v \,\,=\,\,{}^uD_u {}^vK_v \,\,+\,\, {}^vD_v {}^uK_u\,$. Thus for studying exclusive mode selection for RD systems without cross-diffusion, the bifurcation parameter must be associated with ${}^uK_u$ or ${}^vK_v$ if the bifurcation is attributed to reaction kinetics.

An interesting class of problems deals with domains of a fixed shape and their size or scale as the mode selection criterion (Murray 2003, page 117 and Figure 3.6 on page 151) and thus the bifurcation parameter in these cases. These problems correspond to the simple cases of isotropic growth with the rates for changes in the component concentrations owing to growth being far too slow as compared to the rates at which these concentrations change due to reaction or diffusion effects, refer to Crampin et al. (1999) for quasi-steady-state problems. Our framework does not address the dynamics of domain growth, however, even for these simplest of the cases of isotropic growth, as formalised by Madzvamuse et al. (2010). For such cases, let us introduce a common scale factor $\gamma > 0$ for all the parameters to represent isotropic growth, i.e. ${}^uK_u =\gamma \,\,\,{}^uG_u$, ${}^uK_v =\gamma \,\,\,{}^uG_v$, ${}^vK_u =\gamma \,\,\,{}^vG_u$ and ${}^vK_v =\gamma \,\,\,{}^vG_v$. Substituting these terms in Eq. 12 gives us $\gamma$ at the bifurcation point directly in terms of the system parameters as

$$\begin{aligned} \gamma \,\,=\,\,{}{2\,\Lambda \,({}^uD_u {}^vD_v \,\,-\,\, {}^uD_v {}^vD_u)\,\,}\!/{\,\left( {}^uD_u {}^vG_v + {}^vD_v {}^uG_u -{}^uD_v {}^vG_u\,\,-\,\,{}^vD_u {}^uG_v \right) }\,. \end{aligned}$$

(13)

Non-Exclusive Mode Selection For simple bifurcations that emerge non-exclusively, the $\lambda _i = \Lambda$ for a given wavemode ${\upphi }_i$ may not be a unique root for Eq. 9. Nevertheless, for detecting bifurcations near homogeneity with all but one unknown system parameter, we can use Eq. 9 with $\lambda _i = \Lambda$ to directly compute the free (bifurcation) parameter.

Thus, for all simple bifurcations along the trivial branch, we can directly compute a bifurcation parameter to locate the bifurcation point for a given wavemode ${\upphi }_i$ by substituting $\Lambda =\lambda _i$ in either Eq. 12 (exclusive mode selection), Eq. 13 (exclusive mode selection under domain growth) or Eq. 9 (non-exclusive mode selection). Finally, with all system parameters known, we can obtain the spectral coefficients $u_i$ and $v_i$ by solving the simultaneous Eqs. 8. This yields the desired bifurcation pattern $(u^b,v^b)$, and we can switch to the new branch for tracing (see Sect. 4.6).⁹

3.5.2 Multiple Bifurcations

For an eigenvalue $\lambda _i = \Lambda$ with algebraic multiplicity $> 1$, we have multiple candidate wavemodes ${\upphi }_i$ that satisfy the conditions and equations that we derived for simple bifurcations. Thus, for such cases, every linear combination of these wavemodes is a bifurcation pattern emergent at the same bifurcation point located using the results from Sect. 3.5.1. We discuss branch switching and continuation for such multiple bifurcations in more detail in Sect. 4.

3.5.3 Mixed-Mode Bifurcations

Let us now consider an as–general–as–possible emergent steady-state bifurcation pattern as given in Eq. 10. This means there are eigenmodes of two different eigenvalues $\Lambda _m$ and $\Lambda _n$, and we assume that $\Lambda _{m} < \Lambda _{n}$. Let us define $s_i = v_i/u_i$ and $s_j = v_j/u_j$, where $u_{i,j}$ and $v_{i,j}$ are the spectral coefficients as given in Eq. 10. Since $\lambda _i = \Lambda _m$, $\forall i$, Eq. 8 implies that all $s_i$ are equal, say $s_i = s_m$, $\forall i$. Similarly, $s_j = s_n$ (say), $\forall j$. Substituting these scale factors with their respective eigenvalues in Eq. 8 yields¹⁰

$$\begin{aligned} {}^u K_u&= {}{\left[ \,{}^uD_u (s_n \Lambda _{m} - s_m \Lambda _{n})\,\,+\,\, {}^uD_v s_m s_n (\Lambda _{m} - \Lambda _{n})\,\right] \,\,}\!/{\,(s_n - s_m)} \,,\nonumber \\ {}^u K_v&= {}{\left[ \, {}^uD_u (\Lambda _{n} - \Lambda _{m})\,\,+\,\, {}^uD_v (s_n \Lambda _{n} - s_m \Lambda _{m})\,\right] \,\,}\!/{\,(s_n - s_m)} \,,\nonumber \\ {}^v K_u&= {}{\left[ \,{}^vD_v s_m s_n (\Lambda _{m} - \Lambda _{n})\,\,+\,\, {}^vD_u (s_n\Lambda _{m} - s_m\Lambda _{n}) \,\right] \,\,}\!/{\,(s_n - s_m)} \,,\nonumber \\ {}^v K_v&= {}{\left[ \, {}^vD_v (s_n \Lambda _{n} - s_m \Lambda _{m})\,\,+\,\, {}^vD_u (\Lambda _{n} - \Lambda _{m})\,\right] \,\,}\!/{\,(s_n - s_m)} \,. \end{aligned}$$

(14)

Now, one of the linear stability requirements in absence of diffusion is that ${}^uK_u \,{}^vK_v \,> \, {}^uK_v \,{}^vK_u$ (Eq. 11). Expanding this inequality with substitutions from Eq. 14 gives us a constraint on the diffusion parameters,

$$\begin{aligned} {}^uD_u {}^vD_v > {}^uD_v {}^vD_u\,, \end{aligned}$$

(15)

which needs to be satisfied, as a pre-condition, to obtain a mixed mode bifurcation. Next, using the fact that $\Lambda _n$ and $\Lambda _m$ are solutions for $\lambda _k$ in Eq. 9, we can solve for the bifurcation parameter which is the only unknown in the following equation,

$$\begin{aligned}&({}^uD_u {}^vD_v \,\,-\,\, {}^uD_v {}^vD_u)^2(\Lambda _n - \Lambda _m)^2 \,\nonumber \\&\quad +\,4\,({}^uD_u {}^vD_v \,\,-\,\, {}^uD_v {}^vD_u)\,({}^uK_u {}^vK_v - {}^uK_v {}^v K_u) \,\nonumber \\&\quad -({}^uD_u {}^vK_v \,\,+\,\, {}^vD_v {}^uK_u \,\,-\,\,{}^uD_v {}^vK_u\,\,-\,\,{}^vD_u {}^uK_v )^2 = 0\,. \end{aligned}$$

(16)

Finally, with all system parameters determined, we can compute $s_m$ and $s_n$ as

$$\begin{aligned} s_m\,&=\,{}{({}^uD_u\Lambda _m -{}^uK_u)}\!/{({}^uK_v - {}^uD_v\Lambda _m)}\,,\nonumber \\ s_n\,&=\,{}{({}^vD_u\Lambda _n -{}^vK_u)}\!/{({}^vK_v - {}^vD_v\Lambda _n)}\,. \end{aligned}$$

(17)

In summary, to study a mixed-mode bifurcation, we start composing a desired emergent pattern by selecting two eigenvalues, $\Lambda _m$ and $\Lambda _n$, and the corresponding sets of eigenmodes $\lbrace {\upphi }_i \,|\, \lambda _i = \Lambda _m\rbrace$ and $\lbrace {\upphi }_j \,|\, \lambda _j = \Lambda _n\rbrace$. In addition, we freely choose desired spectral coefficients $u_i$ and $u_j$.

We choose any one of the (reaction) system parameter as the unknown/free bifurcation parameter and arbitrarily fix all other system parameters as suitable for the case under investigation, while satisfying Eq. 15. Then, we compute the unknown bifurcation parameter by solving the (quadratic) Eq. 16. In order to continue with branch tracing, the solved bifurcation parameter must be real valued and satisfy preconditions in Eq. 11. Else, our framework reports an error. Finally, we compute $s_m$ and $s_n$ using Eq. 17, and the spectral coefficients $v_i$ and $v_j$ using $u_i$, $u_j$, $s_m$ and $s_n$. Now, all terms are determined to compose the bifurcation pattern $(u^b,v^b)$ using Eq. 10.

4 Numerical Method

In this section, we describe the numerical implementation of our framework in more detail. We explain the basics of the FEM discretisation in Sect. 4.1, which supports the following operations for bifurcation analysis and branch tracing: approximating eigenfunctions of the Laplace–Beltrami operator (Sect. 4.2), resolving bifurcations (Sect. 4.3), and branch tracing (Sect. 4.6). In addition, we will describe a strategy for resolving patterns at higher resolutions in Sect. 5. Our framework also includes a generic, indirect reference method for branch detection using a test function (see Seydel 2010, Sect. 5.3). We use it for various comparisons during the evaluation of our framework.

4.1 FEM Discretisation

Our framework builds on the surface finite element method (SFEM) as supported in the Deal.II software library (Bangerth et al. 2007). With SFEM in Deal.II, $\Omega$ represents a piecewise linear surface that approximates the original continuous surface¹¹ with quadrilateral finite elements (Q-FEs). The Laplace–Beltrami operator on $\Omega$ is defined as the divergence of the tangential gradients, i.e. $\nabla ^2 f = \nabla \cdot \nabla f$ for $f:\Omega \mapsto {\mathbb {R}}$ and $\nabla f = \nabla _{{\mathbb {R}}^3}f - (\nabla _{{\mathbb {R}}^3 }f\cdot {\widehat{n}}){\widehat{n}}$. Here, $\nabla _{{\mathbb {R}}^3}$ is the standard Laplacian operator in the embedding 3D-Euclidean space ${\mathbb {R}}^3$ with the assumption that the function f is extended in the immediate surface neighbourhood along the surface normal ${\widehat{n}}$ at each surface point.  Dziuk (1988) was the first to formulate this definition for piecewise linear FE basis functions on a piecewise linear surface approximation, and it was extended to piecewise polynomial FE basis functions of arbitrary degree on piecewise polynomial (arbitrary degree) surface approximations by Demlow (2009). Our framework supports configuring the order of the FEs (i.e. the degree of the piecewise polynomial basis functions) up to three. We numerically compute the Laplace–Beltrami operator and surface gradients of surface functions using Gauss quadrature rules for integration over FEs. Details of these computations can be found in the tutorials for Deal.II, for example (Bonito et al. 2013, Step-38). For a more comprehensive understanding of SFEMs, we refer the reader to Dziuk and Elliott (2013, Sect. 4.4).

4.2 Approximating Laplacian Eigenfunctions

We saw in Sect. 3.3 that the eigenfunctions ${\upphi }_k$ of the Laplace–Beltrami operator are the building blocks for composing bifurcation patterns. Interestingly, the eigenfunctions depend only on the shape of the surface domain $\Omega$ and the boundary conditions. They are independent, however, of the RD system formulation and its parameters. We use an FEM discretisation of the domain $\Omega$ and apply a Galerkin method to discretise the eigenvalue problem in Eq. 5 as

$$\begin{aligned} {\mathbf {L}} {\mathbf {b}}_k =\,\,-\lambda _k {\mathbf {M}} {\mathbf {b}}_k\,. \end{aligned}$$

(18)

Here, ${\mathbf {b}}_k$ is a discrete vector representation of the eigenfunction ${\upphi }_k$. We obtain the stiffness matrix ${\mathbf {L}}$ and the mass matrix ${\mathbf {M}}$ by applying a weak formulation integration to the Laplace–Beltrami operator $\nabla ^2$ and the eigenfunction ${\upphi }_k$, respectively. As before, $\lambda _k$ is the eigenvalue corresponding to the eigenfunction ${\upphi }_k$. Equation 18 is a generalised eigenvalue problem, and in our case we obtain a large-scale system of sparse matrices. We use the Anasazi eigensolver package from the Trilinos library (Heroux et al. 2005) for finding the eigenvectors ${\mathbf {b}}_k$. For large-scale general eigenvalue problems, a shift-invert approach is commonly used to solve for a band of eigenvectors as recommended by Lévy and Zhang (2010). However, for RD systems with zero Neumann boundary conditions, ${\mathbf {L}}$ is singular and the shift-invert method cannot be used to compute the lowest frequency band of eigenvectors. To keep things simple, we apply ${\mathbf {M}}^{-1}$ as a preconditioner to both sides and solve the resulting standard eigenvalue problem. We avoid explicit computation of the possibly non-sparse, large matrix ${\mathbf {M}}^{-1}$ with the use of the AztecOO package from the Trilinos library. AztecOO provides an inner loop implementation for each application of matrix ${\mathbf {M}}^{-1}$ to a vector (say) ${\mathbf {y}}$ for computing ${\mathbf {k}} = {\mathbf {M}}^{-1}{\mathbf {y}}$ by solving the linear system ${\mathbf {M}} {\mathbf {k}} = {\mathbf {y}}$ instead of matrix inversion.

4.3 Resolving Bifurcations

Given the eigenvectors $\lbrace {\mathbf {b}}_k\rbrace$ and their respective eigenvalues $\lbrace \lambda _k\rbrace$, we can now compose bifurcation patterns and locate their point of emergence on the trivial branch. Section 3.5 explains how a bifurcation pattern may be categorised as a simple, multiple or mixed-mode bifurcation. For simple bifurcations, each basis vector ${\mathbf {b}}_k$ defines a bifurcation pattern, which we denote as ${\mathbf {x}}_b$. We first locate the bifurcation point corresponding to ${\mathbf {x}}_b$ as follows. Let ${\mathbf {p}} = \{ {}^uD_u, {}^uD_v, {}^vD_v, {}^vD_u, {}^uK_u, {}^uK_v, {}^vK_u, {}^vK_v \}$ be the set of system parameters.¹² We choose any one $\alpha \in {\mathbf {p}}$ as the ‘unknown’ bifurcation parameter for an investigation and set the rest, i.e. ${\mathbf {p}} \setminus \alpha$ as fixed. Depending on the problem, we use one of the Eqs. 9, 12 or 13 to compute $\alpha$ by substituting values from ${\mathbf {p}} \setminus \alpha$ and $\lambda _k$ (or $\Lambda = \lambda _k$) in it. Then, without loss of generality, we set $u_k = 1$ and solve for $v_k$ using Eq. 8 to compute ${\mathbf {x}}_b = (u_k{\mathbf {b}}_k,\,v_k{\mathbf {b}}_k)$. For multiple bifurcations, to compose a bifurcation pattern ${\mathbf {x}}_b$, we first select a set of eigenvectors $\lbrace {\mathbf {b}}_i\rbrace = \lbrace {\mathbf {b}}_k\,|\,\lambda _k = \Lambda _m\rbrace$. We then use $\Lambda _m$ as $\lambda _k$ in the case of simple bifurcations to compute $\alpha$ for the corresponding bifurcation point. Next we select an arbitrary set of spectral coefficients $u_i$ to define a desired linear combination of ${\mathbf {b}}_i$ as an emergent pattern and compute the $v_i$, $\forall i$ using Eq. 8. Thus we compute the multiple bifurcation pattern ${\mathbf {x}}_b=(\sum _i{u_i {\mathbf {b}}_i},\, \sum _i{v_i {\mathbf {b}}_i})$. For a mixed mode bifurcation, we pick two sets $\lbrace {\mathbf {b}}_i \rbrace = \lbrace {\mathbf {b}}_k \,|\, \lambda _k = \Lambda _m \rbrace$ and $\lbrace {\mathbf {b}}_j \rbrace = \lbrace {\mathbf {b}}_k \,|\, \lambda _k = \Lambda _n \rbrace$ and compose an arbitrary linear combination of eigenvectors ${\mathbf {b}}_k \in \lbrace {\mathbf {b}}_i \rbrace \cup \lbrace {\mathbf {b}}_j \rbrace$ to define a desired emergent pattern. We then solve for the bifurcation point $\alpha$ by substituting all parameters from ${\mathbf {p}} \setminus \alpha$, and $\Lambda _m$ and $\Lambda _n$ in Eq. 16. With the known bifurcation point and $\Lambda _m$ and $\Lambda _n$, we compute $s_m$ and $s_n$ using Eq. 17. Next, with the previously defined arbitrary values of $u_i$ and $u_j$ for the desired emergent pattern, we compute $v_i = s_m u_i$ and $v_j = s_n u_j$ $\forall i, j$. Finally, we compose the mixed mode bifurcation pattern ${\mathbf {x}}_b=(\sum _i{u_i {\mathbf {x}}_i} + \sum _j{u_j {\mathbf {b}}_j} ,\, \sum _i{v_i {\mathbf {b}}_i}+ \sum _j{v_j {\mathbf {b}}_j})$.

4.4 Reference Method

For evaluation purposes, we also implemented a standard approach for detecting bifurcation points (Seydel 2010, Chapter 5). We call this the reference method since it uses common techniques for different tasks in detecting bifurcation points and computing bifurcation patterns. To detect a bifurcation point, we use a test function $\tau$ which is evaluated at (${\mathbf {x}}$,$\alpha$) as, $\tau = {\mathbf {e}}_k^T{\mathbf {J}}\,{\mathbf {v}}$, where vector ${\mathbf {v}}$ satisfies equation ${\mathbf {J}}_k\,{\mathbf {v}} = {\mathbf {e}}_k$, with ${\mathbf {J}}_k\, = ( {\mathbf {I}} - {\mathbf {e}}_k {\mathbf {e}}_k^T ){\mathbf {J}}\, + {\mathbf {e}}_k {\mathbf {e}}_k^T$. Here, ${\mathbf {e}}_k$ is a unit vector with all but the kth element set to zero and ${\mathbf {J}}$ is the Jacobian matrix for function ${\mathbf {f}}$ as discussed for branch tracing in Sect. 4.6. A bifurcation is detected each time $\tau$ changes its sign from − to $+$ in an interval, say $(\alpha _l,\,\alpha _u)$. Next we perform a mid-point search to locate the 0-crossing for $\tau$ by iteratively evaluating it at $\alpha _\mathrm{{mid}} = {}{(\alpha _l + \alpha _u)}\!/{2}$ and then setting $\alpha _l = \alpha _\mathrm{{mid}}$ if $\tau < 0$ at $\alpha _\mathrm{{mid}}$ or otherwise setting $\alpha _u = \alpha _\mathrm{{mid}}$. Upon convergence $|\tau | \approx 0$. This implies that vector ${\mathbf {v}}$ lies in the null space of the Jacobian matrix ${\mathbf {J}}$ at $\alpha _\mathrm{{mid}}$ and it is a good approximation to the bifurcation pattern ${\mathbf {x}}_s$. We thus output ${\mathbf {x}}_s = {\mathbf {v}}$ and $\alpha _0 = \alpha _\mathrm{{mid}}$ as the next detected bifurcation pattern which may be used for branch tracing in a manner similar to the previous methods. Note that this method is not capable of resolving multiple bifurcations.

4.5 Advantages and Limitations of the Proposed Approach

The main advantage of our proposed approach is that finding bifurcation points and patterns is not dependent on the goodness of the tracing test function described in Sect. 4.4. Using a test function poses two issues: first, the potential presence of more than one bifurcation in an interval, and second, the lack of a guarantee for any test function to detect the presence of each bifurcation. While there are several strategies to address these two issues, often incompletely, our proposed direct approach completely avoids them. Furthermore, we do not need to perform repeated evaluations of the test function along the trivial branch. As a further advantage, depending on the complexity of the test function and the interval size, our approach reduces computational overheads. We tabulate performance gains due to our approach in Sect. 6. A third, important advantage of our approach is that it allows the direct composition of infinite multiple and mixed-mode bifurcation patterns. This adds considerable possibilities to bifurcation analysis by supporting the exploration of multiple co-located branches.

At present, the main limitation of our proposed approach is that it can only be used to analyse primary branches emerging from the trivial branch.

4.6 Branch Tracing for Nonlinear Analysis

Our framework also supports nonlinear analysis with branch tracing in the far-off nonlinear region for the PDEs. The first task in branch tracing is to switch over to the new branch of patterns characterised by a given bifurcation pattern ${\mathbf {x}}_b = ({\mathbf {u}}_b, {\mathbf {v}}_b)$. While the linear stability analysis gives us ${\mathbf {x}}_b$, we are interested in a non-trivial solution ${\mathbf {x}}_s$ that fully satisfies the actual nonlinear PDE given in Eq. 1, near the bifurcation point ${\mathbf {p}}$ (with $\alpha = \alpha _0$) on the trivial branch. With ${\mathbf {x}}_h \equiv (a_0, b_0)$ as the homogeneous solution at the bifurcation point ${\mathbf {p}}$, estimating a good starting point ${\mathbf {x}}_s = {\mathbf {x}}_h + \Delta {\mathbf {x}}$ with $\alpha \approx \alpha _0$ on the new branch is a non-trivial task. The nonlinear solution ${\mathbf {x}}_s$ must be qualitatively similar to the bifurcation pattern ${\mathbf {x}}_b$; yet far-enough away from the trivial branch to allow continuation without falling back. To achieve this, we propose two improvements over a standard method of parallel computation approach for branch switching (see Seydel 2010, Sect. 5.6.3).

For the first improvement, we suggest using a bordering algorithm (Salinger et al. 2002) to iteratively compute the jump $\Delta {\mathbf {x}}$ until a successful switch is made. Our key idea is to select a pattern dependent pivot (a discrete FEM node) for fixing the jump size and the direction of parallel computation. As a second improvement which helps multiple and mixed mode bifurcations, we propose to apply a strong guidance to the jump $\Delta {\mathbf {x}}$ at each intermediate step of our iterative switching algorithm. The bifurcation pattern ${\mathbf {x}}_b$ serves as a good guidance for the jump $\Delta {\mathbf {x}}$. The details for our proposed improvements are presented in the supplemental material (SM02.A1).

Once we switch over to a new branch by jumping from the trivial solution ${\mathbf {x}}_h$ to the nonlinear solution ${\mathbf {x}}_s$, we follow it by means of continuation. Our framework uses the LOCA and NOX packages from the Trilinos library to perform pseudo arc-length continuation. We use an adaptive approach that updates the step size after each continuation step and impose a tangent scale factor to manoeuvre the direction of the continuation curve as supported by the Trilinos library. In particular, we propose to establish an initial tangent direction which is strongly orthogonal to the trivial branch by attempting a jump from the nonlinear solution ${\mathbf {x}}_s$ to its antithetic solution $\widehat{{\mathbf {x}}}_s = {\mathbf {x}}_h - \Delta {\mathbf {x}}$, instead of jumping from the trivial solution ${\mathbf {x}}_h$ to the nonlinear solution ${\mathbf {x}}_s$. Again, we present the details of our proposed improvement for branch tracing with other implementation details in the supplemental material (SM02.A1). Also, we provide further details about the configurability of our framework in the supplemental material (SM02.A2).

5 Multiresolution Adaptation

Unlike simple spot and stripe patterns, most interesting biological surface patterns exhibit high shape contour irregularities. The complexity of these patterns is attributed to the surface geometry and the (mid or high) frequency of the constituent eigenmodes (of the LB operator $\nabla ^2$). For accurate computation of such complex patterns, the surface geometry must be represented with a high-resolution FEM discretisation. We thus propose a simple multilevel approach in which branch tracing is performed at the base-level of discretisation and the resultant patterns are upsampled and resolved at higher levels progressively. With this, we decouple the computations at different levels to gain in performance, scalability and parallelisability.

Our framework uses a simplified geometric multigrid approach where the surface domain $\Omega$ is organised in multiple levels $L_l$, with $l= 0, \ldots , N$, where $L_0$ is the lowest resolution representation and $L_N = \Omega$. We begin with the highest level mesh $L_N = \Omega$ and generate each lower level mesh $L_{l-1}$ from mesh $L_{l}$ by applying a quadric-based edge collapse decimation algorithm (Garland and Heckbert 1997; Cignoni et al. 2008). We perform branch tracing at the lowest resolution $L_0$ and progressively upsample resulting patterns up to the highest resolution $L_N$. Unlike most of the multigrid approaches where all the mesh levels are used simultaneously in a V-cycle or a W-cycle (for the full multigrid approach), we perform complete upsampling of a solution using only two levels at a time. We thus call our approach a progressive geometric multigrid approach.

We propose a two-step approach for upsampling the results between two levels $l-1$ and l. For the first step, we increase the mesh resolution for $L_{l-1}$ without changing its geometry. We perform an in-plane subdivision of each existing (quad) finite element into four to give a new mesh, say $R_{l-1}$. In the second step, we map the geometry of the mesh $R_{l-1}$ to $L_{l}$. For each solution vector ${\mathbf {x}}_b^{l-1}$ defined over $L_{l-1}$ with continuation parameter $\alpha = \alpha _b$, we first interpolate it linearly to the higher resolution mesh $R_{l-1}$ and then solve the nonlinear system ${\mathbf {f}}({\mathbf {r}}_b^{l-1}, \alpha _b) = 0$ over $R_{l-1}$. In general, we use a Newton method with backtracking to solve for ${\mathbf {r}}_b^{l-1}$. We compute the direction vector for the Newton method using a biconjugate gradient method with stabilisation as implemented in the AztecOO package. For difficult cases, we use a trust region method for solving the above nonlinear system with a GMRES approach for establishing the search direction. Next we perform a similar interpolation from $R_{l-1}$ to $L_{l}$ and then solve for ${\mathbf {x}}_b^{l}$ with ${\mathbf {f}}({\mathbf {x}}_b^{l}, \alpha _b) = 0$.

For linear interpolation of a solution across two meshes (say, from $L_{l-1}$ to $R_{l-1}$ or from $R_{l-1}$ to $L_{l}$), we use a projection-based mapping scheme between meshes. We project each node from a target mesh (say $R_{l-1}$) onto the nearest face of the source mesh ($L_{l-1}$) and use the barycentric coordinates of the projected node to compute linear interpolation weights. A naive implementation of this mapping scheme has a computational complexity ${\mathcal {O}}(MN)$ with M and N as the number of nodes for the source and target meshes respectively. Computational complexity can be reduced to ${\mathcal {O}}(M\log {}N)$ with the use of a kd-tree for the nearest face search. Note that we compute the multilevel meshes and the mappings for linear interpolation of solutions only once as a preprocessing step for a given surface domain $\Omega$.

Our two-step approach separates the complexity of resolution improvements from the complexity of geometry improvements for an upsampling task. The results for our progressive geometric multigrid approach are presented in Sect. 6.

6 Experiments and Results

In this section, we describe our experimental setup, discuss case studies and present results. We use a 64-bit Ubuntu 14.04 LTS platform running on an Intel Xeon E5-2630 CPU with 6 Cores @2.3Ghz with 16GB RAM for all performance evaluations and most other experiments. We demonstrate our framework with two RD system case studies, a Brusselator system for the cotyledon patterning of conifer embryos (Sect. 6.1) and Murray’s chemotactic model for snakeskin pattern formation (Sect. 6.2).

6.1 Case Study I: A Brusselator Model

Nagata et al. (2013) present a study of emergent cotyledon patterns on a plant tip. They model observed patterns as bifurcations for a two-component Brusselator RD system. They represent the plant tip with a simple geometric shape, a spherical cap. This spherical cap domain $\Omega$ is parametrised by its size factor R and a curvature factor $\upzeta$ as shown in Fig. 2. Nagata et al. (2013) perform marginal stability analysis to study the relation between the number of emergent cotyledons and the size factor R or the curvature factor $\upzeta$ for a cap. With $a: \Omega \mapsto {\mathbb {R}}$ and $b: \Omega \mapsto {\mathbb {R}}$ as time-dependent concentrations of two Turing morphogens, their model is defined mathematically in a dimensional form as,

$$\begin{aligned} \frac{\partial a}{\partial t}&= D_1 \nabla ^2 a \,+\, A \, - \,(D + B) a\, + \,C a^2 b\,, \quad \quad \quad \frac{\partial b}{\partial t}\,\,=\,\, D_2 \nabla ^2 b \,+\, B a \, - \,C a^2 b\,, \nonumber \\&\text {with b.c.}\quad a(\Gamma ) = \frac{A}{D},\quad b(\Gamma ) = \frac{B D}{A C},\quad \text {at } \Gamma \in \partial \Omega \,. \end{aligned}$$

(19)

Here, A, B, C and D are positive rate constants, $D_1$ and $D_2$ are positive diffusion rates and $\Gamma$ is a surface point on the domain boundary $\partial \Omega$. These boundary conditions imply that the concentrations are fixed at levels corresponding to a non-zero, homogeneous steady state. Nagata et al. linearise Eq. 19 near homogeneity with $(a_0 = {}{A}\!/{D},\, b_0 = {}{B D}\!/{A C})$ by substituting $a =a_0 +u$ and $b =b_0 +v$ to derive an analytical expression for their continuation parameter (represented by A here) at a simple bifurcation point. This also results in zero Dirichlet boundary conditions for the linearised problem in u and v, i.e. $u(\Gamma ) = v(\Gamma ) = 0$ at $\Gamma \in \Omega$. The continuation parameter A is determined by the other system parameters and the eigenvalue $\Lambda = \lambda _i$ of a spherical cap harmonic ${\upphi }_i$, which constitutes the emergent pattern. Note that $\lambda _i$, in turn, depends on the shape $\upzeta$ and size R of the cap, and it can be computed by evaluating an associated Legendre function. This makes it possible to study the marginal stability of emergent patterns with respect to A, R and $\upzeta$.

Fig. 2

A spherical cap (Color figure online)

In our framework, the spherical cap harmonics are just a special case of eigenfunctions $\lbrace {\upphi }_i\rbrace$ satisfying Eq. 5 for a specific, simple domain. The benefit of our approach, however, is that we can easily generalise the analysis to arbitrarily shaped domains. This could facilitate the discovery of shape-induced anomalies in emergent patterns, as we discuss in an example later. Further, we simplify the analysis by incorporating the size factor R directly into the RD model. To do this, we introduce a factor $\gamma$ that represents the relative scale of an arbitrary domain with respect to its canonic unit size. We then relate $\gamma$ to the R and numerically compute the emergent patterns and corresponding $\Lambda$ values, as explained next.

We first modify Eq. 19 to include the scale factor $\gamma$ in all the reaction terms, that is, in all coefficients except the diffusion rates $D_1$ and $D_2$. Scaling the reaction relative to the diffusion coefficients has a similar effect as scaling the domain (Murray 2003, page 78). We use the notation $A = \gamma A_*$, where $*$ indicates corresponding rates at unit scale, and similarly for the other coefficients. This yields new linearisation parameters

$$\begin{aligned} \quad {}^uK_u = \gamma \,(B_* - D_*),\quad {}^uK_v = \gamma \,\frac{A_*^2C_*}{D_*^2}&,\quad {}^vK_u = - \gamma \,B_*,\quad {}^vK_v = - \gamma \,\frac{A_*^2C_*}{D_*^2}\,. \end{aligned}$$

(20)

Substituting these parameters along with ${}^uD_u=D_1$, ${}^uD_v=0$, ${}^vD_v=D_2$, ${}^vD_u=0$ and $\lambda _i=\Lambda$ in Eq. 9 gives us the new continuation parameter $A_*$ as

$$\begin{aligned} A_*\,\,&=\,\, D_* \left( \frac{ D_2 ( B_* - D_*) \Lambda _* \,-\,D_1 D_2 \Lambda _*^2}{C_* \left( D_1 \Lambda _*\,+\, D_* \right) }\right) ^{{}{1}\!/{2}} \,,\, \text {with}\quad \Lambda _* \,\,=\,\,\frac{\Lambda }{\gamma }\,\,. \end{aligned}$$

(21)

Here $\Lambda$ denotes the eigenvalue for a pattern ${\upphi }_i$ at unit scale of the domain $\Omega$. It can be shown that under uniform scaling of a surface domain $\Omega$ by a factor R, the eigenvalue for a given eigenfunction is inversely proportional to $R^2$. For spherical cap harmonics, for example, eigenvalues are analytically defined as $\lambda _i = {}{\Psi ({\upphi }_i,\,\upzeta )}\!/{R^2}$, where $\Psi$ is defined in terms of an associated Legendre function dependent on the wavemode ${\upphi }_i$ and the curvature factor $\upzeta$ (see Nagata et al. 2013, Eq. 11). Thus substituting $\gamma =R^2$ in our modified Brusselator model allows us to incorporate the size factor R for studying marginal stability with arbitrary domains. We compute each eigenmode ${\upphi }_i$ and its respective eigenvalue $\Lambda$ numerically only for a representative arbitrary shape $\Omega$ at a unit scale. Our modified Brusselator model then enables us to plot marginal stability curves for different bifurcation patterns on this arbitrarily shaped plant tip against the size factor R, similar to the plots for spherical caps as presented by Nagata et al. (2013) in Fig. 3 of their paper.

Fig. 3

Spherical cap harmonics in order of their emergence along the trivial branch with $(a_0 = {}{A_*}\!/{D_*},\,b_0 = {}{B_* D_*}\!/{A_* C_*})$ for a spherical cap (Color figure online)

Table 1 Errors in locating bifurcation points $A_*$ for the Brusselator model acting on a spherical cap domain

6.1.1 Experiments

First we validate our framework against analytically derived results from Nagata et al. (2013). We use the same parameter values as given by Nagata et al. for their Fig. 3 (i.e. $D_1 = 0.005$, $D_2 = 0.1$, $B_* = 1.5$, $C_* = 1.8$, $D_* = 0.375$)¹³ and a spherical cap with radius $R=1$ and curvature factor $\upzeta = 0.5$. For all quantitative evaluations in this section, we compute seven different emergent patterns as shown in Fig. 3 and their corresponding bifurcation points $A_*$ using both our proposed method, and the reference method, as explained in Sect. 4. We begin by examining errors in computing $A_*$ with an FEM mesh of order one, i.e. piecewise linear basis functions, with about 4300 nodes. Table 1 provides a numerical comparison of relative errors for both methods against the analytically derived values. For all emergent patterns, our proposed method has a low relative error on the order of $10^{-3}$ when compared with the expected analytical results, and the errors are quantitatively similar to those for the reference method. This implies that our direct approach works well and most of the errors can be explained as approximation errors due to FEM discretisation.

Fig. 4

Error in computing bifurcation points $A_*$ for seven emergent wavemodes ${\upphi }_i$ using different mesh resolutions. The plot shows relative errors in comparison with analytically derived values for different wavemodes in order of their corresponding eigenvalues (Color figure online)

Fig. 5

Relative mean error in computing the wavemode pattern ${\upphi }_i$. a Different resolutions, b Different FEM order with  5K mesh (Color figure online)

Figure 4 shows relative errors for locating all seven bifurcation points at five mesh resolutions ranging from 1–20K vertices. The bifurcation points are ordered according to increasing eigenvalues along the horizontal axis. We found the relative error to fall quickly as a power-law function of the mesh resolution for each pattern. Mode (5, 1) is closest to the exclusive mode selection criterion in Eq. 12 and it has the lowest relative error. We observe that the errors increase with the distance from this reference mode (5, 1) in the eigenspectrum and expect larger relative errors in locating bifurcation points for higher frequency patterns. Thus for applications requiring high accuracy for studying emergent patterns with arbitrary domains, our multiresolution approach presented in Sect. 5 is beneficial.

Next, we examine numerical errors in computing bifurcation patterns for our proposed method in comparison with analytically defined spherical cap harmonics (i.e. the ground truths). We denote differences in numerically computed values for eigenfunctions at FEM nodes and the respective ground truth values as errors. Figure 5a shows relative root-mean-square (RMS) errors in emergent patterns with different mesh resolutions. For comparison we normalise all spherical cap harmonics to have unit amplitude. Again we see that the accuracy improves with the discretisation resolution with some power-law function. We also include the errors for the reference method for a mesh with 4300 nodes in Fig. 5a, which indicates that our proposed method is quantitatively consistent with the reference method.

We also studied the impact of the FEM order, i.e. the degree of the piecewise polynomial basis functions, on RMS errors with about 5000 nodes in each case, see Fig. 5b. We denote surface geometries that are approximated with finite elements of order 1, 2 and 3, each with about 5000 nodes, by G1, G2, and G3. Since FEM of increasing order has an increasing number of nodes per planar finite element, the spherical surface geometry is approximated with a decreasing number of planar elements for higher orders. Comparing the solutions of order 1 FEM on G1, order 2 on G2, and order 3 on G3, we see that FEM order 1 outperforms higher orders for all emergent patterns. At the given resolution of 5K FEM nodes, the increase in error due to the geometric approximation in G2 and G3 apparently outweighs the error reduction due to higher order polynomials. In addition, we also report the error of order 1 FEM on the lower resolution geometries G2 and G3. As expected this increases the error due to the use of lower order polynomials, but only marginally.

Next, we illustrate the key advantage of our approach, that is, the ability to study the effects of arbitrary shape distortions on emergent patterns. Figure 6 shows one such distorted shape in its second row, which we generate by deforming the circular boundary of the cap and propagating the distortions smoothly over the entire surface. We visualise the effects of these shape distortions on three emergent patterns using a nonlinear colour mapping, as illustrated in the figure. Clearly, new patterns show marked deviations from the respective spherical cap harmonics shown at the top row. Deviations from normal emergent patterns often lead to developmental anomalies, which are studied extensively in mathematical biology, refer to Harrison and Aderkas (2004) for an example. While our illustration here does not explain any specific anomaly, our framework can certainly be used to study the role of domain shape deviations on actual observed cases.

Fig. 6

Effects of shape distortion on emergent patterns. Images show numerically computed eigenmodes for Eq. 18 with different geometries for two rows. These eigenmodes emerge as simple bifurcation patterns for bifurcation parameter $A_*$, at values as indicated ($A=100A_*$ above). The normal cap was modelled with about 20K FEM nodes while the distorted cap was modelled with about 12K FEM nodes (Color figure online)

Finally, we present marginal stability curves for mode (5, 1) in Fig. 7. Here we consider three cases: (a) a spherical cap with different domain sizes (greenish colour), (b) a distorted cap with different domain sizes (brownish colour), and (c) a cap with different shapes and sizes. Its shape is fixed as a spherical cap for its size $R \le 1$. Thereafter, its shape is progressively changed to that for the cap in case (b) until $R \le 1.2$. (blue-grey colour). We first computed eigenvalues $\Lambda$ for the spherical cap with $R=1$, corresponding to a boundary perimeter $P=2{\uppi } R$, and $\upzeta = 0.5$, and for the distorted cap with boundary perimeter $P = 2{\uppi }$. Using these eigenvalues we plot solid curves in Fig. 7 for $A_*$–vs.–R (or P) with $\gamma = {}{P^2}\!/{4{\uppi }^2}$ for Eq. . Our numerically computed marginal stability curve for the spherical cap domain conforms well with expected theoretical values shown using greenish circles (Nagata et al. 2013). The brown solid curve in Fig. 7 shows that our framework can perform a similar study for an arbitrary shape domain. Last but not least, we demonstrate our capability to study marginal stability with a cap with different shapes and sizes. We progressively morph the spherical cap into a distorted cap as in case (b) with a shape-blending factor $\alpha$ that varies from 0 to 1 for $P= 1\times 2{\uppi }$ to $P= 1.2\times 2{\uppi }$. The blue-grey solid curve in Fig. 7 shows the respective stability curve.

Fig. 7

Marginal stability for mode (5, 1) in $A_*$ -vs- P (cap boundary perimeter in $2{\uppi }$ units) parameter slice. Analytically derived values as in Fig. 3 by Nagata et al. (2013) for an isotropically growing spherical cap are indicated with circular markers. Solid lines indicate results for our proposed method (Color figure online)

6.2 Case Study II: Murray’s Model

Winters et al. (1990) present bifurcation analysis of a two-component RD system with nonlinear reaction terms to model snakeskin pigmentation. They consider the role of chemotaxis, which is expressed in terms of surface gradients of the components. The non-dimensional form of their system is given as

$$\begin{aligned} \frac{\partial a}{\partial t}&= \, D \nabla ^2 a \,-\,\alpha \nabla \cdot \left( a \nabla b\right) \,+\, S \,C\, a (N - a)\,,\quad \frac{\partial b}{\partial t} \, = \, \nabla ^2 b \,+\,S\left( \frac{a}{1+a} \,-\,b\right) \,, \nonumber \\&\text {with b.c. }\quad {\widehat{n}}\cdot \nabla b (\Gamma )\,=\, {\widehat{n}}\cdot \nabla a (\Gamma )\,=\,0\,,\quad \Gamma \in \partial \Omega \,. \end{aligned}$$

(22)

Here, at any given time, $a:\Omega \mapsto {\mathbb {R}}$ represents the melanophore cell density and $b:\Omega \mapsto {\mathbb {R}}$ the concentration of a chemoattractant that attracts the melanophores, D is the cell diffusion rate within the cell matrix over the surface, $\alpha$ is the strength of chemoattraction, C represents the cell mitotic rate, S is a positive scale factor, and N is the maximum cell concentration capacity for the growth model. All these parameters are positive and uniform over the entire snakeskin. Finally, $\Gamma$ is a surface point on the domain boundary $\partial \Omega$, ${\widehat{n}}$ is the outward surface normal at the same point, $\nabla a$ is the surface gradient of a (same applies to $\nabla b$), and the model uses zero Neumann boundary conditions.

Winters et al. (1990) perform bifurcation detection and branch tracing to discover the steady-state solutions of the system in Eq. 22 for 2D rectangular domains. They employ a second-order FEM approximation to represent the system state with a vector ${\mathbf {x}} = ({\mathbf {a}},\,{\mathbf {b}})$, where ${\mathbf {a}}$ and ${\mathbf {b}}$ discretise a and b, respectively, at FEM nodes. With a standard Galerkin weak formulation for FEM discretisation of the problem in Eq. 22, Winter et al. formulate a vector ${\mathbf {f}}({\mathbf {x}}, {\mathbf {p}}, \alpha ) = - {\mathbf {M}} ({}{\partial {\mathbf {x}}}\!/{\partial t})$ with ${\mathbf {M}}$ as the mass matrix arising in the eigenproblem in Eq. 18. Here, ${\mathbf {p}} = \left\{ C,\,D,\,N,\,S \right\}$ is the set of fixed parameters and $\alpha$, the chemoattraction strength, is the free continuation parameter. Loosely speaking, vector ${\mathbf {f}}$ represents the temporal derivatives, and it is obtained via standard Galerkin FEM discretisation.

Winters et al. (1990) determine the next bifurcation point and its corresponding bifurcation pattern as follows. They first initialise the system with the only none-zero homogeneous steady-state solution $\mathbf {x_0}\equiv (a_0 = N,\,b_0 = {}{N}\!/{1+N})$ and $\alpha = \alpha _0$ as a guess for the next bifurcation point. Next, using a Newton method, they solve an extended system of equations ${\mathbf {f}}({\mathbf {x}}, {\mathbf {p}}, \alpha ) = 0,$ and ${\mathbf {J}} \Delta {\mathbf {x}} = 0$ with ${\mathbf {x}} = \mathbf {x_0} + \Delta {\mathbf {x}}$ and $\alpha = \alpha _0 + \Delta \alpha$ as the unknowns, and ${\mathbf {J}}$ as the Jacobian of ${\mathbf {f}}$ at $({\mathbf {x}}_0, {\mathbf {p}}, \alpha _0)$. The equation extension solves for a non-trivial $\Delta {\mathbf {x}}$ that lies in the nullspace of the Jacobian matrix and thus represents a pattern that may grow without affecting the system steadiness. From a solution of this extended system, $(u^b,\,v^b) = \Delta {\mathbf {x}}$ represents the emergent bifurcation pattern and $\alpha ^b = \alpha _0 + \Delta \alpha$ defines the corresponding bifurcation point along the trivial branch. Then, they use a pseudo-arclength continuation approach to follow the new branch and to determine the family of steady-state solutions along it.

Our framework avoids the repetitive complexity of solving an extended system by directly locating each bifurcation point. Also, more importantly, our approach works on arbitrary surfaces and not just on rectangles. Consider linearising Eq. 22 near the homogeneous solution $a_0 = N,\, b_0 = N/(1+N)$. We find the terms in the generic linearised PDE from Eq. 3 as

$$\begin{aligned} {}^uD_u&=D,\quad {}^uD_v= -\alpha N,\quad {}^vD_u=0,\quad {}^vD_v=1,\nonumber \\ {}^uK_u&= - C N S,\,\,^uK_v=0,\,\,^vK_u= {}{S}\!/{(1+N)^2}\,\text { and }\,^vK_v= - S\,. \end{aligned}$$

(23)

We substitute these parameters in Eq. 9 for a given mode ${\upphi }_i$ with eigenvalue $\lambda _i = \Lambda$ to express the continuation parameter $\alpha$ at the bifurcation point as

$$\begin{aligned} {\alpha }^{b}\,\,=\,\,(1 + N)^2 \left[ \,\, C\,\left( 1 + \frac{S}{\Lambda }\right) \,\,+ \frac{D}{N}\,\left( 1 + \frac{\Lambda }{S}\right) \,\,\right] \,. \end{aligned}$$

(24)

Making similar substitutions in Eq. 8 gives us the scale factor $s_\Lambda = v_i/u_i$ as

$$\begin{aligned} s_\Lambda \,\,=\,\,\frac{ D \Lambda \,+\, C N S}{ \alpha ^b N \Lambda }\,. \end{aligned}$$

(25)

In our framework, we directly compute an eigenvector ${\mathbf {b}}_k$ of the discrete Laplacian using Eq. 18, corresponding to a continuous eigenfunction ${\upphi }_k$, and its respective eigenvalue $\Lambda$. Then, using Eqs. 24 and 25, we immediately locate the bifurcation point $\alpha = \alpha ^b$ and compute the bifurcation pattern ${\mathbf {x}}_b =({\mathbf {u}}_b = {\mathbf {b}}_k,\, {\mathbf {v}}_b = s_\Lambda {\mathbf {b}}_k)$ by setting $u_k=1$, without loss of generality. For all experiments with Murray’s model, we set $D=0.25$, $C = 1.522$, $N=1$, and $S=1$.

6.2.1 Emergent Patterns

Again, we first validate our framework with analytically known emergent patterns on a simple geometry. We provide a general description of our experiments here and provide detailed numerical results in the supplemental material (SM02.A3).

For the rectangular domain $\Omega$ that we use in this case study, eigenvalues of the LB operator may have geometric multiplicity (independent eigenmodes) greater than one. In such cases, the uniqueness of numerically computed eigenvectors is not guaranteed. Thus, to analyse the accuracy of a numerically computed emergent pattern ${\mathbf {x}}_b = ({\mathbf {u}}_b, {\mathbf {v}}_b)$, we need to first determine an analytically defined vector $\widehat{{\mathbf {u}}}_b$ which is nearest to ${\mathbf {u}}_b$. We do this with an approach similar to that of Reuter et al. (2009), i.e. by projecting the normalised vector ${\mathbf {u}}_b$ onto a space with analytically defined basis vectors $\lbrace {\mathbf {b}}_i\rbrace$, which represent the ground truth patterns. This yields the closest analytically defined pattern $\widehat{{\mathbf {u}}}_b$. We then use the root-mean-square error $\varepsilon _\mathrm{{RMS}} = {}{||{\mathbf {u}}_b -\widehat{{\mathbf {u}}}_b||}\!/{\sqrt{n}}$, with n FEM nodes, as our error measure for the numerically determined bifurcation pattern. We obtain each basis vector ${\mathbf {b}}_i$ by discretising its corresponding continuous eigenfunction ${\upphi }_i$ at the FEM node positions. The analytical eigenfunctions on a rectangular domain are

$$\begin{aligned}&{\upphi }_{i} \,\,= \,\,\cos {({}{p{\uppi } x}\!/{W})}\cos {({}{q{\uppi } y}\!/{H})}\,,\text { and} \quad \quad \lambda _{i} \,\,= \,\,\left( \frac{p{\uppi }}{W}\right) ^2 + \left( \frac{q{\uppi }}{H}\right) ^2 \,,\nonumber \\&\text { for } \quad \Omega \,\,= \,\,\lbrace \left( x,y,0\right) \,\,| \,\,0 \le x \le W = 1,\, 0 \le y \le H=4\rbrace \,, \end{aligned}$$

(26)

where W and H are the width and height of the rectangle, respectively. The index i denotes a wavemode with p sinusoidal extrema (crust/trough) along the x-axis and q extrema along the y-axis.

In the supplemental material, we evaluate RMS errors $\varepsilon _\mathrm{{RMS}}$ for 100 emergent patterns with our proposed method and the reference method. We assign each emergent pattern an index based on its nearest analytically determined eigenvector ${\mathbf {b}}_i$. We solve for the eigenvectors with a convergence limit on the order of $10^{-12}$, and this results in low RMS errors in general (on the order of $10^{-4}$–$10^{-6}$). In general, the emergent patterns ${\mathbf {u}}_i$ found with our method and their projections $\widehat{{\mathbf {u}}}_i$ onto the analytical solutions are visually indistinguishable. In addition, while the reference method misses out on some emergent patterns due to multiple bifurcations or failures of the chosen test function, we discover all emergent patterns. We also analyse the relative error in locating a bifurcation point $\alpha ^b$ corresponding to ${\mathbf {x}}_b$ by comparing it with an analytically defined $\alpha _\mathrm{{ref}}$. We compute $\alpha _\mathrm{{ref}}$ from Eq. 24 using analytically defined $\lambda _i$ corresponding to basis vector ${\mathbf {b}}_i$ closest to ${\mathbf {u}}_b$.

We further investigated the impact of the FEM order on the accuracy of the discovered patterns, and we obtained similar conclusions as for the Brusselator model. Notably we observe that for FEM of order one, the error in locating a bifurcation point grows with the magnitude of the eigenvalue for the respective pattern. However, using higher order FEMs improves results considerably, albeit at the cost of some increase in relative errors for the emergent patterns. See supplemental material (SM02.A2) for details. It also includes an evaluation of the impact of mesh triangulation on the accuracy of our proposed method.

Table 2 Performance measures for Murray’s model on a rectangular domain. We used first-order FEM with about 4400 nodes. Graphs on the left show statistics for test function evaluations for the reference method

Table 2 shows a performance comparison between our proposed method and the reference method. We measured average time for different tasks while computing emergent patterns for Murray’s model acting on a rectangular domain. We used about 4400 (first order) FEM nodes for this evaluation with convergence limit set to $10^{-11}$ in each case. The graph on the left indicates that the required number of test function evaluations and thus the computational cost for the reference method decreases with the wavemode frequency. This happens because the distance between the wavemodes decreases with the eigenfrequency. However, it also implies that after some point the step size for evaluating the test function along the trivial branch would not be small enough to detect all emergent modes. Also note that the complexity of evaluating a test function increases with the wavemode frequency. This complexity is somehow artificially limited to 1000 iterations since we limit the BiCG Stab solver for computing the test function to 1000 iterations. Overall, Table 2 indicates that our proposed method is about $25\times$ faster than the reference method in this case.

Next, we evaluate the impact of different domain shapes on emergent patterns found with our framework. Figure 8a shows three different developable deformations of a $1 \times 4$ rectangular domain $\Omega$. This includes a cylindrical surface with constant curvature, a half-bent surface composed of two parts with constant curvatures and curvature discontinuity between them, and a spiral surface with a continuously varying curvature profile. For comparison, we also used the original $1\times 4$ rectangular domain $\Omega$. We used a regular grid of about 4400 vertices in each case. With developable deformations, we do not expect that the non-planarity of the domains has an influence on emergent patterns. Figure 8b shows error statistics for all three deformed surfaces along with the rectangular surface as a reference. The differences in errors for different curvature profiles appear to be well within general variations in error statistics. We found a similar trend in relative errors for computing the bifurcation points and conclude that, as expected, the influence of developable deformations is negligible.

Fig. 8

RMS projection error in computing the wave mode pattern ${\upphi }_i$ using our method on developable surfaces with different curvature profiles for Murray’s model. a Different developable deformations of the $1 \times 4$ rectangular domain $\Omega$ of equal size (Illustrations are not on the same scale), b Error plots on a semi-log scale (Color figure online)

Fig. 9

Changes in emergent patterns for Murray’s model due to a surface bump. a Bump at the centre: Simple bifurcation patterns emerge for different values of the parameter $\alpha$, b Bump at the edge: Simple bifurcation patterns emerge for different values of the parameter $\alpha$. r is a measure of correlation between emergent patterns on the distorted rectangle domain in comparison with the best linear combination of eigenmodes for the regular rectangle domain, under projection (Color figure online)

To study the influence of local non-developable surface deformations on emergent patterns, we use surfaces with bump deformations at different locations or size to the reference rectangular domain $\Omega$, see Fig. 9. These bumps are akin to the emergence of animal limbs or appendices. We observed that even small local non-developable deformations bring out well-defined global deviations in emergent patterns as shown in the figure. To obtain an intuition about these new emergent patterns, we map them back onto the flat rectangular domain and project the mapped patterns onto the eigenvectors of the flat domain, as illustrated in Fig. 9b. A main observation is that we can accurately represent many of the new patterns emerging on the deformed shape with only a few eigenvectors of the flat domain, where we measure accuracy as the correlation between a new pattern and its representation using a few eigenvectors. We indicate the few dominant wavemodes of the flat domain along with the correlation factor r below the emergent patterns in Fig. 9b. This leads to the intuition that surface deformation leads to changes of the eigenfunctions and the eigenspectrum, such that many new, complex patterns emerging on deformed surfaces can be understood as linear combinations of simpler patterns on an original, undeformed domain.

Fig. 10

Emergent patterns on a paraboloid surface (Color figure online)

We also examined the influence of global non-developable deformations on emergent patterns. Figure 10 shows one such distortion comprised of a sliced paraboloid with a perimeter equal to that of the reference rectangular domain. Such a surface is representative of the region on a snake body which is undergoing morphogenesis for skin pattern formation. Again, we see interesting changes in emergent patterns which appear as deformations and mixing of eigenfunctions for the reference domain. Thus, we conclude that non-developability in surface geometry plays an important role on pattern formation and must be taken into consideration while studying such emergent patterns.

Finally, we applied Murray’s model to a 3D reconstruction of a real gecko lizard body. In this hypothetical case, the eyes, the paws and the ventral side of the body are pruned since these regions do not participate in pattern formation. We used first-order FEM with about 4600 nodes. Figure 11 illustrates a subjective comparison of several patterns observed on juvenile geckos and our simulations. For visualisation, we perform a nonlinear soft-thresholding on the emergent patterns. Our simulation results give a good impression of the variety of patterns observed in nature and make a good case for using actual surface geometry in studying pattern formation.

Fig. 11

Emergent patterns on a Gecko lizard body surface. Images in (a) are from (Rooster 2009), (Psyon 2009), (Raven 2009), (Locke 2007) and (Gary and Julia 2013). a Patterns on real lizards, b Simulated patterns (Color figure online)

Fig. 12

Branch tracing results for rectangular domain $\Omega$ of size $4 \times 1$ sq. units (Color figure online)

6.2.2 Branch Tracing

We present results for branch tracing as explained in Sect. 4.6 with Murray’s chemotactic model. We use first-order FEM in all experiments with $\alpha$ as the continuation parameter and other parameters fixed as before. In general, for computing the eigenvectors we use a convergence limit $\varepsilon \in [ 10^{-8},\,\, 10^{-11}]$ on the root-mean-square residual error for solving Eq. 18. Also, we set the tolerance limit to $10^{-12}$ for the AztecOO inner loop GMRES solver. We perform branch switching with the parallel programming distance $\varepsilon _0 \in [ 10^{-3}, 0.07 ]$ for Equation 3 in the supplemental material (SM02). Also, the divergence limit $\alpha _\varepsilon$ discussed in the supplemental material (SM02.A1) is set in the range $[ 10^{-4}, 10^{-2}]\times \alpha _0$. For an arclength continuation step, we set the convergence limit in the range $[ 10^{-8},\,\, 10^{-11}]$ for the RMS residual error.

Fig. 13

Branch J–K for various developable deformed domains and corresponding patterns in sections J and K for the branches (Color figure online)

Figure 12 shows the branches traced for a rectangular domain $\Omega$ using our proposed direct approach. We first compute the eigenvectors for the domain with about 4400 FEM nodes. We then directly compose bifurcation patterns, compute the respective bifurcation points and perform branch tracing as explained in Sect. 4. Our results for branches and segments A–K in Fig. 12 are qualitatively similar to those presented by Winters et al. (1990). Unlike Murray and Myerscough (1991) who change the underlying geometry for the rectangular domain to separate out multiple branches H–I and F–G, we trace these branches using our cosine factor method for branch switching (Refer the second approach in Sect. 4.6) without changing $\Omega$. Next, we repeat the branch tracing experiment for developable surfaces with different curvatures to obtain qualitatively similar results. For comparison, we present branch J–K for all four domains and resolved patterns in sections J and K of the branch, in Fig. 13.

Fig. 14

Tracing branches on an arbitrary surface representing a Gecko lizard. Each row presents progressive changes in the emergent pattern as we move along its respective branch (Color figure online)

After validating our framework with known results for simple geometries, we trace branches for an arbitrary surface geometry representing the Gecko lizard surface with about 900 FEM nodes. We trace branches for the first seventy eigenvectors of this shape. Figure 14 shows some of the interesting branches across the explored spectra. The leftmost column in Fig. 14 plots the branches and each row shows the evolution of a pattern along its respective branch. We perform a nonlinear soft-thresholding again to visualise each pattern. For qualitative comparison, we use the same nonlinear colour mapping for all the solutions along a branch after normalising the pattern range to $\left[ 0,1\right]$ (as shown in the rightmost column of the figure). The first row in the figure shows one of the low frequency branches (branch 7). We notice clear qualitative changes that occur progressively as we move along the branch. The same is true for other branches such as two mid-frequency branches (branch 32 and 50) and one high-frequency branch (branch 69) shown here.¹⁴ Many interesting patterns such as C, G, H, L and P, which are qualitatively quite different from the emergent patterns, are discovered with branch tracing. Thus, we can say that branch tracing contributes significantly to the exploration of the solution space of a nonlinear system of PDEs and it is an important tool to study such biological systems.

Fig. 15

An upsampled branch for the rectangular domain $\Omega$ and plots for performance analysis of this upsampling. a Branch, b Performance plot on a log-log scale (Color figure online)

6.2.3 Results for Multiresolution Adaptation

Our progressive geometric multigrid approach (Sect. 5) allows us to perform branch tracing at high resolutions of up to one million FEM nodes. We proceed in two steps, namely (a) resolution improvements and (b) geometric improvements through multiple levels. We first demonstrate the upsampling of patterns on a branch for the rectangular domain in Fig. 15. Since this domain is planar, we only need to perform step (a) for our multiresolution approach in this case. Figure 15a shows the upsampling of a branch originating at $\alpha = 13.736$ (branch D–E in Fig. 12) from level $L_0 \approx 4400$ FEM nodes to level $L_4 \approx 1.1$M FEM nodes. From one lower level to the next, we divide each quad finite element into four quad elements. For first-order FEM this increases the number of FEM nodes by about $4\times$. Thus, with four levels of higher resolution, we go from about 4400 to 1.1 million FEM nodes.

The flexibility of upsampling only a selective subset of solutions can help to reduce computational load of such studies, and it allows the user to prioritise the upsampling of selected solutions. In Fig. 15a we upsampled only about one third of the solution patterns from each level to the next. The figure shows that the solution patterns at each level lie close to the original branch at the lowest level. We found that the upsampled patterns resolved well in a few iterations and appeared subjectively very similar across all levels (not shown here for brevity). We also profiled the performance of our framework for this example. Table 3 shows the average number of iterations required to achieve convergence at each level along with the time taken. Figure 15b shows a log-log plot of average time taken for each iteration and total time for convergence of a pattern over the number of FEM nodes. Both plots are near linear in nature as illustrated by the line fit. Both fitted lines have a slope of 1.281, indicating the computational complexity of upsampling a given solution as ${\mathcal {O}}(N^{1.281})$ with N FEM nodes. In contrast to our method, we found that a multilevel algebraic grid based preconditioner from the Trilinos library to directly trace a branch for the rectangular domain with about 100K FEM nodes failed to converge.

Speaking of parallelisability, for the above case, we estimate that the overhead of the repeated task of reading mesh files and populating the internal data structures is less than $13\%$ of the time taken to resolve a pattern at the highest level ($L_4$). Thus the theoretical limit on the utility of a parallel processor is set high at ${}{1}\!/{1.13} \times 100 = 88.5\%$.

Table 3 Performance profile for upsampling patterns on a branch for Murray’s model acting on the rectangular domain $\Omega$

Fig. 16

Upsampling a branch with low-frequency patterns on an arbitrary surface, $\Omega$. We see results for both, resolution improvement from $L_0$ to $R_0$ and geometry improvement $R_0$ to $L_1$ in this example (Color figure online)

We next demonstrate upsampling of a branch on the Gecko surface. In this case, we need to perform both (a) resolution improvement as well as (b) geometric improvement in our multiresolution approach. Figure 16 illustrates these two steps for upsampling patterns up by one level. We trace a branch at the lowest level $L_{0}$ (green-coloured branch in the figure) and show qualitatively different patterns along the branch as $A_1$–$D_1$.¹⁵ We first upsample the patterns to level $R_0$, which has a higher resolution but the same geometry as $L_0$. We plot the branch at level $R_{0}$ (orange branch in the figure) and notice that it drifts slightly from the original branch. However, we find patterns $A_2$–$D_2$ to be qualitatively similar to the corresponding patterns on the branch for level $L_0$. Finally, we upsample the patterns to the improved geometry at level $L_1$. Here again, we find considerable changes in the plot for the branch, while the patterns do not change much qualitatively, except for $C_3$ (see patterns $A_3$–$D_3$.). The qualitative changes are limited across the levels mostly because of the low-frequency nature of the patterns. At the same time, changes in the branch contours indicate that the resolution and geometry of the surface domain can influence the results. Particularly, $C_3$ changes considerably because there is a branch-jump from $C_1$ to $D_1$ at the lowest level which gets corrected with our upsampling. We discuss branch-jumping and other issues in detail in Sect. 6.3.

Fig. 17

Upsampling a pattern on a mid-frequency branch for the Gecko surface in a far-off nonlinear region for the solution space of the underlying PDEs. We upsample results over two levels until patterns are fixed qualitatively. Note the pattern in the bottom-right corner with no geometric improvements is qualitatively different from the pattern in the top right with geometric improvements while upsampling (Color figure online)

Next, we present an example of upsampling a pattern on a mid frequency branch (branch 50 in Fig. 14), up by two levels. Figure 17 shows the results for levels $L_0$–$L_2$. For qualitative comparisons across different geometries, we map the values of each pattern into the range [0, 1]. Level $L_0$ has about 900 FEM nodes, and the pattern looks unresolved even with a low RMS error of $1.61\times 10^{-14}$ units. We first improve its resolution to level $R_0$ with about 3400 nodes. Adding more nodes changes the pattern qualitatively in several regions like the tail and the right forelimb. Next, we improve the geometry and resolve the pattern at level $L_1$ with about 4400 nodes. Again we observe qualitative differences from level $R_0$ in several regions like the right limbs. We further upsample the pattern to levels $R_1$ and finally $L_2$ and find that the pattern at level $L_2$ with about 18900 FEM nodes is qualitatively very similar to that at level $L_1$. We thus conclude that the pattern is well resolved, we do not need to further upsample it and the geometry at level $L_1$ sufficed to resolve the pattern.

For comparison, we also continue to sub-divide the quad elements from level $R_0$ for one more step, while keeping the geometry from $L_0$, to resolve the pattern with about 13500 nodes. We show the result in the bottom-right corner and observe that the resolved pattern is qualitatively different from those for the improved geometries $L_1$ and $L_2$. This illustrates the effect that small changes in geometry can have on the resulting patterns.

Fig. 18

Upsampling an emergent pattern on a Gecko surface for a resolution up to 1M FEM nodes. We begin with a relatively good surface geometry of about 4600 FEM nodes, which we do not refine during upsampling in this example (Color figure online)

Finally, Fig. 18 shows our upsampling results for a very high frequency emergent pattern (eigenvector 250). Starting from a geometry with about 4600 nodes, we upsample by only increasing the mesh resolution, but without changing the geometry. We show the results after two and four steps of upsampling in the middle and on the right, respectively. All the patterns were resolved with an RMS residual error ${\mathcal {O}}(10^{-8})$. We observe that as the resolution increases, the pattern contours between the red and blue colour regions become more discernible.

6.3 Challenges, Limitations, and Future Work

Our framework is capable of determining all bifurcations along the trivial branch and works well to study emergent patterns and trace branches in general. However, there are certain aspects with room for improvement. Another limitation for our framework is related to the sampling theorem and FEM discretisation. While, in theory, we can solve for N eigenvectors for a domain $\Omega$ with N FEM nodes, not all of them are usable. For a simple case of a square planar domain, the sampling theorem dictates that there must be at least twice as many nodes along a dimension as the number of cycles for a wavemode along that dimension to model the continuous wave accurately. Zr et al. (2010) discuss this specific limitation in detail in context of their problem relating to inertia moment analysis. Thus, while our framework is able to solve for a larger number of eigenvectors, only a fraction of it can be used for branch tracing. The simplest way out is to solve the eigenproblem by increasing the resolution at the lowest level $\Omega _0$. However, this increase cannot be arbitrarily high since we can trace branches at the lowest level $\Omega _0$ only with domain-size ${\mathcal {O}}(10^4)$ or lower. Another limitation of our framework is that while tracing a branch at a higher resolution with the use of our progressive geometric multigrid approach, we only solve for a solution at a higher resolution for the continuation parameter value given by the respective solution at the lowest resolution. Thus for cases where the branch contour may change with upsampling, the parts of a (higher resolution) branch that lie beyond the continuation parameter range given by the lowest level branch become untraceable. This problem could possibly be addressed by either increasing the order of finite elements to reduce the change in the branch contour with upsampling or by allowing/forcing the continuation parameter to drift while upsampling the solutions at the twists and turns of a branch (Bolstad and Keller 1986).

7 Conclusions

We have presented a framework to perform bifurcation analysis for reaction diffusion systems on arbitrary surfaces. Our framework uses a compositional approach instead of traditional detection approach to discover new emergent patterns along the trivial branch with a homogeneous pattern. We derive formulae to directly compose bifurcation patterns for two-component RD systems and to compute their respective bifurcation points. Our derivations substitute a spectral decomposition of the solution into a generalised system of PDEs linearised near homogeneity. Our framework first computes (FEM) discretised eigenvectors for the Laplace–Beltrami operator acting on a given surface. It then composes bifurcation patterns and computes their respective bifurcation points using our derivations. In addition, our framework supports a multiresolution branch tracing algorithm. We propose a progressive geometric multigrid based approach with multiple levels for branch tracing.

We demonstrate the working of our framework for two different RD systems (a Brusselator and a chemotactic model) with two different boundary conditions (zero Dirichlet and zero Neumann boundary conditions respectively). We validated our framework for these systems against known results in the literature and experimented with the geometry of the underlying domains to obtain new results. In particular for Murray’s chemotactic model, we perform experiments with developable and non-developable distortions of the reference rectangular domain. Our experiments show interesting variations in the emergent patterns due to non-developable distortions. We also apply Murray’s model to study emergent patterns and branches for an arbitrary surface representing a gecko lizard. We upsample results to several higher levels with resolution up to one million FEM nodes, depending on the complexity of the pattern. We conclude that our framework can be used effectively to study emergent patterns and pattern branches for RD systems with or without cross-diffusion, acting on arbitrary surfaces, with up to a few million FEM nodes. Our framework is flexible, highly parallelisable and can be configured to use higher-order FEMs as well.