Malaria Drug Resistance: The Impact of Human Movement and Spatial Heterogeneity

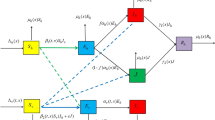
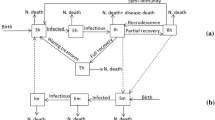
Abstract

Human habitat connectivity, movement rates, and spatial heterogeneity have tremendous impact on malaria transmission. In this paper, a deterministic system of differential equations for malaria transmission incorporating human movements and the development of drug resistance malaria in an $n$ patch system is presented. The disease-free equilibrium of the model is globally asymptotically stable when the associated reproduction number is less than unity. For a two patch case, the boundary equilibria (drug sensitive-only and drug resistance-only boundary equilibria) when there is no movement between the patches are shown to be locally asymptotically stable when they exist; the co-existence equilibrium is locally asymptotically stable whenever the reproduction number for the drug sensitive malaria is greater than the reproduction number for the resistance malaria. Furthermore, numerical simulations of the connected two patch model (when there is movement between the patches) suggest that co-existence or competitive exclusion of the two strains can occur when the respective reproduction numbers of the two strains exceed unity. With slow movement (or low migration) between the patches, the drug sensitive strain dominates the drug resistance strain. However, with fast movement (or high migration) between the patches, the drug resistance strain dominates the drug sensitive strain.

Appendices

Appendix 1: Proof of Theorem 4

Proof

To prove Theorem 4, we follow the method given in Prosper et al. (2012). Assume $\mathcal {R}^2_{0_{_{DR_1}}} >\mathcal {R}^2_{0_{_{DR_2}}}$, by this assumption and from Eq. (16) it follows that $p_1k_4> p_2k_2$. Evaluating the reproduction number $\mathcal {R}^2_{0_{_{DR}}}$ at the boundary of the domain $(\psi _{_{12}},\psi _{_{21}}) \in [0,\infty ) \times [0,\infty )$. We have,

$$\begin{aligned} \mathcal {R}^2_{0_{_{DR}}}(\psi _{_{12}}, 0) = \frac{1}{2k_2q_2}(p_1q_2 + p_2k_2 + |p_1q_2 - p_2k_2|) . \end{aligned}$$

(26)

Since by assumption $p_1k_4 > p_2k_2$, and because $q_2 = k_4 + \psi _{_{12}} \ge k_4$, we know that $p_1q_2 - p_2k_2 > 0$, and so $|p_1q_2 - p_2k_2| = p_1q_2 - p_2k_2$. Thus, Eq. (26) simplifies to $\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{12}}, 0) = \mathcal {R}^2_{0_{_{DR_1}}}(0,0)$ for all $\psi _{_{12}} \in [0,\infty )$. Similarly,

$$\begin{aligned} \mathcal {R}^2_{0_{_{DR}}}(0, \psi _{_{21}})&= \frac{1}{2k_4q_1}(p_1k_4 + p_2q_1 + |p_1k_4 - p_2q_1|)\\&= \frac{1}{k_4q_1} \max \{p_1k_4, p_2q_1\} \\&= \max \bigg \{\frac{p_1}{q_1},\frac{p_2}{k_4}\bigg \}\\&= \max \bigg ( \frac{\mathcal {R}^2_{0_{_{DR_1}}}}{1 + \frac{\psi _{_{21}}}{k_2}},\mathcal {R}^2_{0_{_{DR_2}}}\bigg ). \end{aligned}$$

Hence, $\mathcal {R}^2_{0_{_{DR_2}}}(0,0) \le \mathcal {R}^2_{0_{_{DR}}}(0, \psi _{_{21}}) \le \mathcal {R}^2_{0_{_{DR_1}}}(0,0)$, for all $\psi _{_{21}} \in [0,\infty )$.

Now, evaluating the reproduction number $\mathcal {R}^2_{0_{_{DR}}}$ in the interior of the domain $(\psi _{_{12}},\psi _{_{21}}) \in [0,\infty ) \times [0,\infty )$. Consider the function

$$\begin{aligned} f(x) = \sigma _2y^2 - (p_1q_2 + p_2q_1)y + p_1p_2. \end{aligned}$$

(27)

$f$ is the characteristic polynomial of the next-generation matrix used to derive $\mathcal {R}^2_{0_{_{DR}}}(\psi _{_{12}}, \psi _{_{21}})$ in Eq. (15). $\mathcal {R}^2_{0_{_{DR}}}$ is the larger of the two roots of $f(x)$. Consequently, $f(\mathcal {R}^2_{0_{_{DR}}}) = 0$ and $f^\prime (\mathcal {R}^2_{0_{_{DR}}}) > 0$. Thus, for any real number $y$ for which the inequality $f(y) < 0$ holds, implies that $y<\mathcal {R}^2_{0_{_{DR}}}$. However, if $f(y) > 0$ and $f^\prime (y) > 0$, then $y>\mathcal {R}^2_{0_{_{DR}}}$. Now, suppose $\psi _{_{12}}$ and $\psi _{_{21}}$ are positive, then it follows that

$$\begin{aligned} f\bigg (\mathcal {R}^2_{0_{_{DR_1}}}\bigg )&= f \bigg (\frac{p_1}{k_2}\bigg ) = \sigma _2 \bigg (\frac{p_1}{k_2}\bigg )^2 - (p_1q_2 + p_2q_1)\frac{p_1}{k_2} + p_1p_2\\&= \frac{p_1}{k_2} \bigg [(\psi _{_{21}}k_2 + \psi _{_{21}}k_4 + k_2k_4)\frac{p_1}{k_2} - (p_1q_2 + p_2q_1) + p_2k_2\bigg ]\\&= \frac{p_1}{k_2} \big [p_1\psi _{_{21}} + p_1 \frac{\psi _{_{21}}k_4}{k_2} + p_1k_4 - (p_1q_2 + p_2q_1) + p_2k_2\bigg ]\\&= \frac{p_1}{k_2} \bigg [p_1q_2 + p_1 \frac{\psi _{_{21}}k_4}{k_2} - (p_1q_2 + p_2q_1) + p_2k_2\bigg ]\\&= \frac{p_1}{k_2} \bigg (\frac{p_1k_4}{k_2} \psi _{_{21}} - p_2\psi _{_{21}}\bigg ) \\&= \frac{p_1\psi _{_{21}}}{k^2_2} (p_1k_4 - p_2k_2). \end{aligned}$$

We can similarly show that

$$\begin{aligned} f\bigg (\mathcal {R}^2_{0_{_{DR_2}}}\bigg )&= f \bigg (\frac{p_2}{k_4}\bigg ) = \frac{p_2\psi _{_{12}}}{k^4_2} (p_2k_2 - p_1k_4)\\ f\bigg (\frac{\mathcal {R}^2_{0_{_{DR_1}}}}{1 + \frac{\psi _{_{21}}}{k_2}}\bigg )&= -\bigg (\frac{p_1}{k_2+\psi _{_{21}}}\bigg )^2 \psi _{_{12}}\psi _{_{21}}. \end{aligned}$$

Thus, since $(p_1k_4 - p_2k_2)>0$ by assumption, we have that $f(\mathcal {R}^2_{0_{_{DR_1}}}) > 0$, $f(\mathcal {R}^2_{0_{_{DR_2}}}) <0$ and $f\bigg (\frac{\mathcal {R}^2_{0_{_{DR_1}}}}{1 + \frac{\psi _{_{21}}}{k_2}}\bigg )<0$.

Differentiating $f(y)$ we have $f^\prime (y) = 2\sigma _2y - (p_1q_2 + p_2q_1)$. Thus,

$$\begin{aligned} f^\prime \bigg (\mathcal {R}^2_{0_{_{DR_1}}}\bigg )&= f ^\prime \bigg (\frac{p_1}{k_2}\bigg ) = 2\sigma \bigg (\frac{p_1}{k_2}\bigg ) - (p_1q_2 + p_2q_1)\\&= 2(\psi _{_{21}}k_2 + \psi _{_{21}}k_4 + k_2k_4)\frac{p_1}{k_2} - p_1k_4 - p_1\psi _{_{12}} - p_2k_2 - p_2\psi _{_{21}}\\&= (p_1k_4 - p_2k_2) + \frac{(k_2\psi _{_{12}}+k_4\psi _{_{21}} )p_1}{k_2}+ \frac{(p_1k_4 - p_2k_2)\psi _{_{21}}}{k_2}. \end{aligned}$$

Since $(p_1k_4 - p_2k_2)>0$, it follows that $f^\prime (\mathcal {R}^2_{0_{_{DR_1}}})>0$. Hence, it follows that, for $\psi _{_{12}}$ and $\psi _{_{21}}$ positive, $f(\mathcal {R}^2_{0_{_{DR_2}}})<0$ and $f\bigg (\frac{\mathcal {R}^2_{0_{_{DR_1}}}}{1 + \frac{\psi _{_{21}}}{k_2}}\bigg )<0$ implies that $\mathcal {R}^2_{0_{_{DR}}} > \max \bigg \{\frac{\mathcal {R}^2_{0_{_{DR_1}}}}{1 + \frac{\psi _{_{21}}}{k_2}},\mathcal {R}^2_{0_{_{DR_2}}}\bigg \}.$ Since $f(\mathcal {R}^2_{0_{_{DS_1}}})>0$ and $f^\prime (\mathcal {R}^2_{0_{_{DS_1}}})>0$ we have that $\mathcal {R}^2_{0_{_{DR}}}<\mathcal {R}^2_{0_{_{DS_1}}}$.

Hence, for all $\psi _{_{12}}$ and $\psi _{_{21}}$ positive, $\max \bigg \{\frac{\mathcal {R}^2_{0_{_{DR_1}}}(0,0)}{1 + \frac{\psi _{_{21}}}{k_2}},\mathcal {R}^2_{0_{_{DS_2}}}(0,0)\bigg \} < \mathcal {R}^2_{0_{_{DS}}}(\psi _{_{12}},\psi _{_{21}})<\mathcal {R}^2_{0_{_{DR_1}}}(0,0).$ $\square$

Appendix 2: Proof of Theorem 6

Proof

In the proof of Theorem 4 we have that $\mathcal {R}_{0_{_{DR}}}(0,\psi ) = \max \bigg \{\frac{\mathcal {R}_{0_{_{DR_1}}}(0,0)}{1 + \frac{\psi _{_{21}}}{k_2}},\mathcal {R}_{0_{_{DR_2}}}(0,0)\bigg \}$ and $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi ) >\max \bigg \{\frac{\mathcal {R}_{0_{_{DR_1}}}(0,0)}{1 + \frac{\psi _{_{21}}}{k_2}}, \mathcal {R}_{0_{_{DR_2}}}(0,0)\bigg \}$ for $\psi _{_{12}} > 0$. Thus $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi )\ge \mathcal {R}_{0_{_{DR}}}(0,\psi )$ for all $\psi _{_{12}}\ge 0$. Thus, for $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi )$ to be an increasing function in $\psi _{_{12}}$ we need to show that $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi )$ is monotone in $\psi _{_{12}}$.

Also, from Theorem 4 we also know that $\mathcal {R}_{0_{_{DR}}}(\psi ,0) = \mathcal {R}_{0_{_{DR_1}}}(0,0,) \ge \mathcal {R}_{0_{_{DR}}}(\psi ,\psi _{_{21}})$ for all non-negative $\psi _{_{21}}$. Again, we only need to show that $\mathcal {R}_{0_{_{DR}}}(\psi ,\psi _{_{21}})$ is monotone in $\psi _{_{21}}$ in order to show that it is a decreasing function in $\psi _{_{12}}$.

To show that $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi _{_{21}})$ is monotone, we first show that $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi )$ is monotone in $\psi _{_{12}}$. Since $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi )$ is continuous in $\psi _{_{12}}$, it is monotone with respect to $\psi _{_{12}}$ if for every $B \in (0,\infty )$ such that $\mathcal {R}_{0_{_{DR}}}(\psi _{{12}},\psi ) = B$ has a non-negative solution $\psi _{{12}} \in [0,\infty )$, then this solution is unique. Suppose $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi ) = B$. The reproduction number $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi )$ can be written as

$$\begin{aligned} \frac{1}{2\sigma _2} \bigg (s +\sqrt{s^2 - 4p_1p_2\sigma _2}\bigg ), \end{aligned}$$

where $s = p_1q_2 + p_2q_1 = p_1(k_4 + \psi _{_{12}}) + p_2(k_2 + \psi )$ and $\sigma _2 = k_2k_2 + k_2\psi _{_{12}} + \tau _2\psi .$

Hence,

$$\begin{aligned} \frac{1}{2\sigma _2} \bigg (s +\sqrt{s^2 - 4p_1p_2\sigma _2}\bigg ) = B, \end{aligned}$$

(28)

Equation (28) implies that

$$\begin{aligned} \sigma _2B^2 - sB + p_1p_2 = 0. \end{aligned}$$

(29)

Note that both $\sigma _2$ and $s$ are linear in $\psi _{_{12}}$. Thus, Eq. (29) is linear in $\psi _{_{12}}$, implying that if there exists a $\psi _{_{12}} \in [0,\infty )$ that is, a solution to Eq. (29), then this solution is unique. Hence, $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi )$ is monotone for each $\psi \in [0,\infty )$. By the same argument, $\mathcal {R}_{0_{_{DR}}}(\psi ,\psi _{_{21}})$ is monotone for each $\psi \in [0,\infty ))$. Since $\mathcal {R}_{0_{_{DR}}}(\psi _{_{12}},\psi )$ is monotone for non-negative $\psi _{_{12}}$ and $\mathcal {R}_{0_{_{DR}}}(0,\psi ) \le \mathcal {R}_{0_{_{DR}}}(\psi _{{12}},\psi )$, for each fixed $\psi _{_{21}} = \psi \in [0,\infty )$, $\mathcal {R}_{0_{_{DR}}}(\psi _{{12}},\psi _{{21}})$ is an increasing function of $\psi _{{12}}$. Likewise, since $\mathcal {R}_{0_{_{DR}}}(\psi ,0) \ge \mathcal {R}_{0_{_{DR}}}(\psi ,\psi _{{21}})$ for non-negative $\psi _{_{21}}$, for each fixed $\psi _{{12}} = \psi \in [0,\infty )$, $\mathcal {R}_{0_{_{DS}}}(\psi _{{12}},\psi _{{21}})$ is a decreasing function of $\psi _{{21}}$. $\square$

Appendix 3: Proof of Theorem 8

Proof

The stability of the drug sensitive-only boundary equilibrium is explored by evaluating the Jacobian of system (19) at the boundary equilibrium ${\mathcal E}_{1S}$, taking the following order of the coordinates $I_1,I_{v1},J_1,J_{v1}$.

The Jacobian is given as

$$\begin{aligned} J_S({{\mathcal E}_{1S}})= \begin{pmatrix} J_{S_{1}} &{}\quad \! J_{S_{2}} \\ \\ 0 &{}\quad \! J_{S_{4}} \end{pmatrix} \end{aligned}$$

where

$$\begin{aligned} J_{S_{1}} = \begin{pmatrix} \displaystyle -\frac{\alpha _{h1}\beta _{h1}I^{**}_{v1}}{N^{**}_{h1}}-k_1 &{}\quad \! \displaystyle \frac{\alpha _{h1}\beta _{h1}(N^{**}_{h1}-I^{**}_1)}{N^{**}_{h1}} \\ \\ \displaystyle \frac{\alpha _{v1}\beta _{v1}(N^{**}_{v1}-I^{**}_{v1})}{N^{**}_{h1}} &{}\quad \! \displaystyle -\frac{\alpha _{v1}\beta _{v1}I^{**}_1}{N^{**}_{h1}}-\mu _v \\ \\ \end{pmatrix}, \end{aligned}$$

$$\begin{aligned} J_{S_{2}} = \begin{pmatrix} \displaystyle -\frac{\alpha _{h1}\beta _{h1}I^{**}_{v1}}{N^{**}_{h1}} &{} \displaystyle 0 \\ \\ \displaystyle 0 &{} \displaystyle -\frac{\alpha _{v1}\beta _{v1}I^{**}_1}{N^{**}_{h1}} \\ \\ \end{pmatrix} \end{aligned}$$

$$\begin{aligned} J_{S_{4}} = \begin{pmatrix} \displaystyle -k_2 &{}\quad \! \displaystyle \frac{\theta _{h1}\alpha _{h1}(N^{**}_{h1}-I^{**}_1)}{N^{**}_{h1}} \\ \\ \displaystyle \frac{\theta _{v1}\alpha _{v1}(N^{**}_{v1}-I^{**}_{v1})}{N^{**}_{h1}} &{}\quad \! \displaystyle -\mu _v \\ \\ \end{pmatrix}. \end{aligned}$$

The eigenvalues of $\displaystyle J_S({{\mathcal E}_{1S}})$ are given by the eigenvalues of $J_{S_{1}}$ and $J_{S_{4}}$. The eigenvalues of $J_{S_{1}}$ are determined from the roots of the characteristics equations obtained by substituting in $J_{S_{1}}$, $I^{**}_1,~I^{**}_{v1}$

$$\begin{aligned} P_{S_{11}}&= \lambda ^2 + \bigg [ \frac{N^{**}_{v1}(\alpha _{v1}\beta _{v1}+\mu _v)\beta _{h1}\alpha _{h1}}{N^{**}_{v1}\alpha _{h1}\beta _{h1}+k_1N^{**}_{h1}} +\,\frac{\alpha _{v1}\beta _{v1}(N^{**}_{v1}\alpha _{h1}\beta _{h1}+k_1N^{**}_{h1})}{(\alpha _{v1}\beta _{v1}+\mu _v)N^{**}_{h1}}\bigg ] \lambda \nonumber \\&+\, \mu _vk_1(\mathcal {R}^2_{0_{_{DS_1}}}-1) =0. \end{aligned}$$

(30)

It follows that for $\mathcal {R}^2_{0_{_{DS_1}}} > 1$, the coefficients of the characteristics equation $P_{S_{11}}$ is positive. And thus, satisfies the Routh–Hurwitz criteria, for stability.

For the matrix $J_{S_{4}}$, the eigenvalues are given by the roots of the characteristics equations obtained by substituting in $J_{S_{4},}$ $I^{**}_1,~I^{**}_{v1}$

$$\begin{aligned} P_{S_{41}} = \lambda ^2 + (\mu _v+k_2)\lambda + \mu _v k_2 \bigg (1 -\frac{\mathcal {R}^2_{0_{_{DR_1}}}}{\mathcal {R}^2_{0_{_{DS_1}}}}\bigg ) =0. \end{aligned}$$

(31)

The roots of the characteristics equation $P_{S_{41}}$ have negative real parts if and only if $\mathcal {R}^2_{0_{_{DS_1}}} > \mathcal {R}^2_{0_{_{DR_1}}}$. $\square$

Appendix 4: Proof of Theorem 9

Proof

The stability of the drug resistance-only boundary equilibrium is explored by evaluating the Jacobian of system (20) at the boundary equilibrium ${\mathcal E}_{1R}$, using the following order of coordinates, $I_1,I_{v1},$ $J_1,J_{v1}$.

The Jacobian is given as

$$\begin{aligned} J_R({{\mathcal E}_{1R}})= \begin{pmatrix} J_{R_{1}} &{}\quad \! 0\\ \\ J_{R_{3}} &{}\quad \! J_{R_{4}} \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} J_{R_{1}} = \begin{pmatrix} \displaystyle -k_1 &{} \displaystyle \frac{ \alpha _{h1}\beta _{h1}(N^{**}_{h1}-J^{**}_1)}{N^{**}_{h1}} \\ \\ \displaystyle \frac{ \alpha _{v1}\beta _{v1}(N_{v1}^{**}-J^{**}_{v1})}{N^{**}_{h1}} &{} \displaystyle -\mu _v \\ \\ \end{pmatrix}, \end{aligned}$$

$$\begin{aligned} J_{R_{3}} = \begin{pmatrix} \displaystyle -\frac{\theta _{h1}\alpha _{h1}J^{**}_{v1}}{N^{**}_{h1}} &{} \displaystyle 0 \\ \\ \displaystyle 0 &{} \displaystyle -\frac{\theta _{v1}\alpha _{v1}J^{**}_1}{N^{**}_{h1}} \\ \\ \end{pmatrix}. \end{aligned}$$

and

$$\begin{aligned} J_{R_{4}} = \begin{pmatrix} \displaystyle -\frac{\theta _{h1}\alpha _{h1}J^{**}_{v1}}{N^{**}_{h1}}-k_2 &{} \displaystyle \frac{\theta _{h1}\alpha _{h1}(N^{**}_{h1}-J^{**}_1)}{N^{**}_{h1}} \\ \\ \displaystyle \frac{\theta _{v1}\alpha _{v1}(N^{**}_{v1}-J^{**}_{v1})}{N^{**}_{h1}} &{} \displaystyle -\frac{\theta _{v1}\alpha _{v1}J^{**}_1}{N^{**}_{h1}}-\mu _v \\ \\ \end{pmatrix}. \end{aligned}$$

substituting $J^{**}_1$ and $J^{**}_{v1}$ into $J_{R_{1}}$ and $J_{R_{4}}$ gives the following characteristics equations,

$$\begin{aligned} P_{R_{11}} = \lambda ^2 + (\mu _v+k_1)\lambda + \mu _v k_1 \bigg (1 -\frac{\mathcal {R}^2_{0_{_{DS_1}}}}{\mathcal {R}^2_{0_{_{DR_1}}}}\bigg ) =0. \end{aligned}$$

(32)

and

$$\begin{aligned} P_{R_{41}}&= \lambda ^2 + \bigg [ \frac{N^{**}_{v1}(\theta _{v1}\alpha _{v1}+\mu _v)\theta _{h1}\alpha _{h1}}{N^{**}_{v1}\theta _{h1}\alpha _{h1}+k_2N^{**}_{h1}} +\frac{\theta _{v1}\alpha _{v1}(N^{**}_{v1}\theta _{h1}\alpha _{h1}+k_2N^{**}_{h1})}{(\theta _{v1}\alpha _{v1}+\mu _v)N^{**}_{h1}}\bigg ] \lambda \nonumber \\&\quad +\,\mu _vk_1(\mathcal {R}^2_{0_{_{DR_1}}}-1) =0. \end{aligned}$$

(33)

By Routh–Hurwitz criteria for stability, it follows that the roots of the characteristics equations $P_{R_{1}}$ and $P_{R_{4}}$ have negative real parts if and only if $\mathcal {R}^2_{0_{_{DR_1}}} > \mathcal {R}^2_{0_{_{DS_1}}}$. $\square$

Appendix 5: Proof of Theorem 10

Proof

To prove Theorem 10, we follow the method given in Esteva and Gumel (2009) and Esteva and Vargas (2000). The method essentially entails proving that the linearization of the model system (14), around the co-existence equilibrium ${\mathcal E}_{1}$, has no solutions of the form

$$\begin{aligned} \tilde{Z}(t) = \tilde{Z}_0e^{\omega t}, \end{aligned}$$

(34)

with $\tilde{Z}= \{Z_1, Z_2, Z_3, Z_4\}, ~~Z_i \in C, \omega \in C$, and Re $\omega \ge 0$ (the implication of this is that the eigenvalues of the characteristic polynomial associated with the linearized model will have negative real part; in which case, the equilibrium ${\mathcal E}_{1}$ is LAS).

Let $I^{**}_1,J^{**}_1,I^{**}_{v1},J^{**}_{v1}$ denote the coordinates of the co-existence equilibrium, ${\mathcal E}_{1}$. Substituting a solution of the form (34) into the linearized system of (17) around ${\mathcal E}_{1}$ gives the following system of linear equations

$$\begin{aligned} \begin{array}{lll} \displaystyle \omega Z_1 &{}=&{} \displaystyle -\bigg (\frac{\alpha _{h1}\beta _{h1}I^{**}_{v1}}{N^{**}_{h1}}+p_1\bigg ) Z_1 - \frac{\alpha _{h1}\beta _{h1}I^{**}_{v1}}{N^{**}_{h1}} Z_2 + \frac{\alpha _{h1}\beta _{h1}}{N^{**}_{h1}} (N^{**}_{h1}-I^{**}_1-J^{**}_1)Z_3\\ \\ \displaystyle \omega Z_2 &{}\!=\!&{} \displaystyle \!-\! \frac{\alpha _{h1}\theta _{h1}J^{**}_{v1}}{N^{**}_{h1}} Z_1 \!+\! \xi _1 Z_1 \! -\!\bigg ( \frac{\alpha _{h1}\theta _{h1}J^{**}_{v1}}{N^{**}_{h2}} \!+\!p_2\bigg )Z_2 \!+\! \frac{\alpha _{h1}\theta _{h1}}{N^{**}_{h1}} (N^{**}_{h1}-I^{**}_1\!-\!J^{**}_1)Z_4 \\ \\ \displaystyle \omega Z_3 &{}=&{} \displaystyle \frac{\alpha _{v1}\beta _{v1}}{N^{**}_{h1}} (N^{**}_{v1}-I^{**}_{v1}-J^{**}_{v1})Z_1 -\bigg (\frac{\alpha _{v1}\beta _{v1}I^{**}_1}{N^{**}_{h1}} + \mu _v \bigg )Z_3 - \frac{\alpha _{v1}\beta _{v1}I^{**}_1}{N^{**}_{h1}} Z_4 \\ \\ \displaystyle \omega Z_4 &{}=&{} \displaystyle \frac{\alpha _{v1}\theta _{v1}}{N^{**}_{h1}} (N^{**}_{v1}-I^{**}_{v1}-J^{**}_{v1})Z_2 - \frac{\alpha _{v1}\theta _{v1}J^{**}_1}{N^{**}_{h1}} Z_3 -\bigg (\frac{\alpha _{v1}\theta _{v1}J^{**}_1}{N^{**}_{h1}}+ \mu _v\bigg )Z_4, \end{array} \end{aligned}$$

(35)

where $p_1=\gamma _1 + \xi _1+\mu _h + \delta _{I_1}, ~p_2=\tau _1 + \mu _h + \delta _{J_1}$. Simplifying (35), gives the equivalent system

$$\begin{aligned} \displaystyle \bigg [ 1 + \frac{1}{p_1}\bigg (\omega +\frac{\alpha _{h1}\beta _{h1}I^{**}_{v1}}{N^{**}_{h1}}\bigg )\bigg ] Z_1&= \displaystyle \!-\! \frac{\alpha _{h1}\beta _{h1}I^{**}_{v1}}{p_1N^{**}_{h1}} Z_2 \!+\! \frac{\alpha _{h1}\beta _{h1}}{p_1N^{**}_{h1}} (N^{**}_{h1}\!-\!I^{**}_1\!-\!J^{**}_1)Z_3 \end{aligned}$$

(36)

$$\begin{aligned} \displaystyle \bigg [ 1 + \frac{1}{ p_2}\bigg (\omega +\!\frac{\alpha _{h1}\theta _{h1}J^{**}_{v1}}{N^{**}_{h1}}\bigg )\bigg ]Z_2 \!&= \! \displaystyle \!-\! \frac{\alpha _{h1}\theta _{h1}J^{**}_{v1}}{p_2N^{**}_{h1}} Z_1 \!+\! \frac{\xi _1 Z_1}{p_2} \!+\! \frac{\alpha _{h1}\theta _{h1}}{p_2N^{**}_{h1}} (N^{**}_{h1}-I^{**}_1\!-\!J^{**}_1)Z_4 \end{aligned}$$

(37)

$$\begin{aligned} \displaystyle \bigg [ 1 + \frac{1}{ \mu _v}\bigg (\omega + \frac{\alpha _{v1}\beta _{v1}I^{**}_1}{N^{**}_{h1}} \bigg )\bigg ]Z_3&= \displaystyle \frac{\alpha _{v1}\beta _{v1}}{\mu _vN^{**}_{h1}} (N^{**}_{v1}-I^{**}_{v1}-J^{**}_{v1})Z_1 - \frac{\alpha _{v1}\beta _{v1}I^{**}_1}{\mu _vN^{**}_{h1}} Z_4 \end{aligned}$$

(38)

$$\begin{aligned} \displaystyle \bigg [ 1 + \frac{1}{\mu _v}\bigg ( \omega + \frac{\alpha _{v1}\theta _{v1}J^{**}_1}{N^{**}_{h1}}\bigg )\bigg ]Z_4&= \displaystyle \frac{\alpha _{v1}\theta _{v1}}{\mu _vN^{**}_{h1}} (N^{**}_{v1}-I^{**}_{v1}-J^{**}_{v1})Z_2 - \frac{\alpha _{v1}\theta _{v1}J^{**}_1}{\mu _vN^{**}_{h1}} Z_3 \end{aligned}$$

(39)

Adding Eqs. (36) and (37), (38) and (39) gives the system

$$\begin{aligned} \begin{array}{lll} (1+G_1(\omega ))Z_1 + [1+G_2(\omega )]Z_2 &{}=&{} (H\tilde{Z})_1 + (H\tilde{Z})_2\\ (1+G_3(\omega ))Z_3 + [1+G_4(\omega )]Z_4 &{}=&{} (H\tilde{Z})_3 + (H\tilde{Z})_4\\ \end{array} \end{aligned}$$

(40)

where

$$\begin{aligned} \begin{array}{lll} \displaystyle G_1(\omega ) &{}=&{} \displaystyle \bigg [ 1 + \frac{1}{p_1}\bigg (\omega +\frac{\alpha _{h1}\beta _{h1}I^{**}_{v1}}{N^{**}_{h1}} + \frac{p_1\alpha _{h1}\theta _{h1}J^{**}_{v1}}{N^{**}_{h1}} \bigg )\bigg ] Z_1 \\ \\ \displaystyle G_2(\omega ) &{}=&{} \displaystyle \bigg [ 1 + \frac{1}{ p_2}\bigg (\omega +\frac{\alpha _{h1}\theta _{h1}J^{**}_{v1}}{N^{**}_{h1}} + \frac{p_2\alpha _{h1}\beta _{h1}I^{**}_{v1}}{N^{**}_{h1}} \bigg )\bigg ]Z_2 \\ \\ \displaystyle G_3(\omega ) &{}=&{} \displaystyle \bigg [ 1 + \frac{1}{ \mu _v}\bigg (\omega + \frac{\alpha _{v1}\beta _{v1}I^{**}_1}{N^{**}_{h1}} + \frac{\alpha _{v1}\theta _{v1}J^{**}_1}{N^{**}_{h1}} \bigg )\bigg ]Z_3 \\ \\ \displaystyle G_4(\omega ) &{}=&{} \displaystyle \bigg [ 1 + \frac{1}{\mu _v}\bigg ( \omega + \frac{\alpha _{v1}\theta _{v1}J^{**}_1}{N^{**}_{h1}} + \frac{\alpha _{v1}\beta _{v1}I^{**}_1}{N^{**}_{h1}} \bigg )\bigg ]Z_4 \\ \end{array} \end{aligned}$$

and

$$\begin{aligned} H = \begin{pmatrix} \displaystyle 0 &{} 0&{} \displaystyle \frac{\alpha _{h1}\beta _{h1} S^{**}_1}{p_1N^{**}_{h1}} &{}0&{} \\ \\ \displaystyle \frac{\xi _1}{p_2}&{} 0 &{} 0&{} \displaystyle \frac{\alpha _{h1}\theta _{h1}S^{**}_{1}}{p_2N^{**}_{h1}} \\ \\ \displaystyle \frac{\alpha _{v1}\beta _{v1}S^{**}_{v1}}{\mu _vN^{**}_{h1}} &{} 0&{} 0 &{} 0\\ \\ 0&{} \displaystyle \frac{\alpha _{v1}\theta _{v1}S^{**}_{v1}}{\mu _vN^{**}_{h1}} &{} 0 &{} 0 \\ \\ \end{pmatrix}. \end{aligned}$$

Note that $S^{**}_1 = (N^{**}_{h1}-I^{**}_{1}-J^{**}_{1}),~~S^{**}_{v1} = (N^{**}_{v1}-I^{**}_{v1}-J^{**}_{v1})$ above. It should further be noted that the matrix $H$ has non-negative entries, and the equilibrium ${\mathcal E}_{1} = (I^{**}_1,J^{**}_1,I^{**}_{v1},J^{**}_{v1})$ satisfies ${\mathcal E}_{1} = H {\mathcal E}_{1}$. Furthermore, since the coordinates of ${\mathcal E}_{1}$ are all positive, it follows then that if $\tilde{Z}$ is a solution of (34), then it is possible to find a minimal positive real number $r$ such that

$$\begin{aligned} \left| \tilde{Z}\right| \le r {\mathcal E}_{1}. \end{aligned}$$

(41)

Observe that $r$ is also the minimal positive $r$ such that $|Z_1|+|Z_2| \le r(I^{**}_1+J^{**}_1)$ and $|Z_3|+|Z_4| \le r(I^{**}_{v1}+J^{**}_{v1})$. We want to show that Re $\omega < 0$. Assume the contrary (i.e., Re $\omega \ge 0$), we consider two cases: $\omega = 0$ and $\omega \ne 0$. Assume the first case $\omega = 0$. Then, (35) is a homogeneous linear system in the variables $Z_i ~(i = 1,\ldots ,4)$. The determinant of this system corresponds to that of the Jacobian of system (17) evaluated at $\mathcal {E}_{1}$, which is given by

$$\begin{aligned} \Delta&= \displaystyle \bigg (p_2\mu _v-\frac{\theta _{h1}\alpha _{h1}S^{**}_1}{N^{**}_{h1}}\frac{\theta _{v1}\alpha _{v1}S^{**}_{v1}}{N^{**}_{h1}}\bigg ) \bigg (p_1\mu _v-\frac{\alpha _{v1}\beta _{v1}S^{**}_{v1}}{N^{**}_{h1}}\frac{\alpha _{h1}\beta _{h1}S^{**}_1}{N^{**}_{h1}}\bigg )> 0. \end{aligned}$$

Consequently, the system (35) can only have the trivial solution $\tilde{Z} = \bar{0}$.

The case $\omega \ne 0$, is considered next. In this case, Re $G_i(\omega )\ge 0,~~i=1,\ldots ,4$, since, by assumption, Re $\omega >0$. It is easy to see that this implies $|1+G(\omega )| > 1$ for all $i$. Now, define $G(\omega ) = \min |1+G_i(\omega )|, ~~i = 1,\ldots , 4$. Then, $G(\omega ) > 1$, and therefore $\frac{r}{G(\omega )} < r$. The minimality of $r$ implies that $|\tilde{Z}| > \frac{r}{G(\omega )} \mathcal {E}_{1}$. But, on the other hand, taking norms on both sides of the second equation of (40), and using the fact that $H$ is non-negative, we obtain

$$\begin{aligned} G(\omega )|Z|\le H |Z| \le r\mathcal {E}_{1}. \end{aligned}$$

(42)

Then, it follows from the above inequality that $|Z|\le \frac{r}{G(\omega )} \mathcal {E}_{1}$ which is a contradiction. Hence, Re $\omega < 0$, which implies that $\mathcal {E}_{1}$ is locally asymptotically stable. $\square$