Elastic Material with Systems of Growing or Closing Cracks: Tangential Stiffness

Abstract

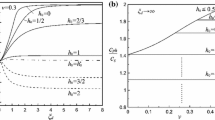
The problem of calculating the overall elastic moduli of a microcracked material is now understood relatively well, however, only under the assumption that the cracks are fixed, that is, neither grow nor shorten during loading. Such a calculation yields the secant moduli for the response stress-strain curves of microcracked materials. The present paper shows how this existing knowledge can be extended to calculate the tangential moduli for incremental deformations of the material during which the cracks are allowed to grow and remain critical, or shorten. For this purpose, the conditions that the energy release rate of several families of cracks in the material must on the average be in balance with the energy dissipation rate characterized by the fracture energy of the material are formulated. The results of preliminary numerical studies still in progress are reported. It is found that the self-consistent scheme for the calculation of elastic constants of a microcracked material does not give realistic results except for deformations up to shortly after the peak load. On the other hand, the differential scheme yields realistic stress-strain curves and it also gives a ratio of uniaxial tensile to compression strengths that is approximately correct for initially highly microcracked materials such as concrete. A comprehensive report on the computation of tangent moduli will be given in a separate paper.