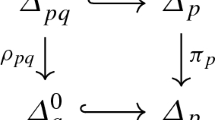Abstract
One purpose of this note is to sketch the generalization of the cohomological interpretation of the Kazhdan-Lusztig polynomials ([KL]) to the case of arbitrary crystallographic groups W. This generalization of the argument in [KL] requires a study of the intersections BwB ∩ B_yB of Bruhat and Birkhoff cosets of the corresponding Kac-Moody group, and unions of such, from a combinatorial as well as a geometric point of view; one of the main tools for this is a systematic use of W. Specific examples are included at the end.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Preview
Unable to display preview. Download preview PDF.
Similar content being viewed by others
References
V. Deodhar, On some geometric aspects of Bruhat ordering I; Indiana U., 1982.
A. Joseph, On the Demazure character formula; Preprint.
D. Kazhdan and G. Lusztig, Schubert varieties and Poincare duality; Proc. Symp. Pure Math. 36, AMS, 1980.
D. Peterson and V. Kac, Infinite flag varieties and conjugacy theorems; Proc. Nat. Acad. Sc., 1983.
C. S. Seshadri, Normality of Schubert varieties; Preprint.
R. Steinberg, Lectures on Chevalley groups; Yale U., 1967.
J. Tits, Théorie des groupes; Res. Cours, Coll. Fr., 1981.
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 1985 Springer Science+Business Media New York
About this paper
Cite this paper
Haddad, Z. (1985). A Coxeter Group Approach to Schubert Varieties. In: Kac, V. (eds) Infinite Dimensional Groups with Applications. Mathematical Sciences Research Institute Publications, vol 4. Springer, New York, NY. https://doi.org/10.1007/978-1-4612-1104-4_6
Download citation
DOI: https://doi.org/10.1007/978-1-4612-1104-4_6
Publisher Name: Springer, New York, NY
Print ISBN: 978-1-4612-7012-6
Online ISBN: 978-1-4612-1104-4
eBook Packages: Springer Book Archive