Introduction

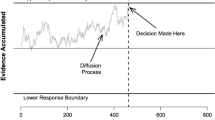
Quantitative models of decision-making have led to important advances in several fields of research. The most common form of these models, known as evidence accumulation models, have had a long history of success in accounting for decision-making data, ranging from simple perceptual tasks, to complex discrete choice data (Hawkins et al. 2014), stop-signal paradigms (Matzke et al. 2013), go/no-go tasks (Gomez et al. 2007), absolute identification data (Brown et al. 2008), and extensions to more complex neural data (Forstmann et al. 2011), and clinical psychological populations (Ho et al. 2014). These models propose that people accumulate evidence from the environment at a rate called the “drift rate”, until this accumulated evidence reaches some set criterion (the “threshold”) which results in a decision. Evidence accumulation models also assume some starting amount of evidence, which can represent differences in bias between responses (the “start point”), and some amount of time taken by non-decision related processes (the “non-decision time”). Figure 1 illustrates these processes using the linear ballistic accumulator model (LBA: Brown and Heathcote, 2008).

Fig. 1
figure 1

The linear ballistic accumulator (LBA) model of decision-making represents a choice as a race between two accumulators. The accumulators gather evidence until one of them reaches a threshold, which triggers a decision response. The time taken to make the decision is just the time taken to reach threshold, plus a constant offset amount for processes unrelated to the decision itself. Variability arises from two sources: both the starting point of the evidence accumulation process and the speed of the accumulation process (the drift rate) vary randomly from trial-to-trial and independently in each accumulator

Full size image

Although there are many evidence accumulation models, two of the most common versions are the diffusion model (Ratcliff 1978; Ratcliff and Rouder 1998; Ratcliff et al. 2004), and the LBA (Brown and Heathcote 2008); both of which have been applied to many different kinds of decision tasks, and different populations of decision-makers. The key difference between the LBA and diffusion model is that the LBA proposes an independent race between multiple response options, whereas the diffusion proposes a mutual competition between two response options – a single evidence accumulator that gathers evidence for and against two different options.

Applied uses of evidence accumulation models have become more common as increasing computing power has made their analysis more accessible, with this popularity driven by several key advantages of model-based analyses. Firstly, evidence accumulation models allow for reaction time and accuracy data to be analyzed together, which addresses the inherent trade-offs between speed and accuracy (Donkin et al. 2009; Ratcliff and Rouder 1998; Wagenmakers et al. 2007). Secondly, the models account for the entire reaction time distribution, using information beyond just the mean or median (Donkin et al. 2009; Brown and Heathcote 2008). Thirdly, evidence accumulation models provide a way to quantitatively compare psychological theories, by relating hypotheses to model parameters. This approach has proven powerful, and underpins many of the most influential findings using evidence accumulation models. For example, an important and popular theory of the cognitive slowdown observed during aging was proven wrong, and overturned, by examination of diffusion model parameter estimates from older and younger adults (Ratcliff et al., 2011, 2010, 2007; Forstmann et al., 2011).

The problem of model inference

The canonical question when testing psychological hypotheses using evidence accumulation models is whether a phenomenon of interest is better explained by changes in one model parameter or another, where those model parameters represent different psychological processes that might underlie the effect. For example, one might be interested to know whether the slower response times of older adults are best explained by a change in drift rate, which represents decreased mental processing speed, or a change in response threshold, which represents increased caution (Ratcliff et al., 2011, 2010, 2007). Answering this question means drawing inferences about which version of the model is best supported by the data. This inference problem is commonly called “model selection”, and it requires finding a balance between the goodness-of-fit, which is how well the model is able to describe observed data, and model complexity, which is the flexibility of the model to fit many different patterns of data. A good model of the underlying process needs to be able to fit the trends in the data successfully. However, this goodness-of-fit must be weighed against the complexity of the model, as more flexible models will also fit noise in the data, producing a better fit that is not necessarily reflective of the underlying process. Accounting for model complexity has proven difficult, especially for more complex models of cognition. As these complex cognitive models explore inter-related cognitive processes, they usually also have statistically correlated parameters. These correlations in model parameters can cause some methods of model selection to perform poorly.

The Akaike Information Criterion (AIC, Burman and Anderson, 2002) and Bayesian Information Criterion (BIC, Schwarz, 1978) are two commonly-used model selection metrics which are easy to calculate following maximum likelihood parameter estimation. Both measure a model’s complexity by counting its free parameters, which fails to account for way the functional form of the model influences its flexibility. Counting parameters treats all parameters as equal, in terms of complexity, which is a very coarse approximation, and problematic when model parameters are correlated. In addition, some types of parameter additions can further constrain a model, such as a hierarchical framework where each participant’s parameters are constrained to follow some group-level parameter distribution, making a model with these parameters less flexible than a model without these parameters. Another popular option is the Deviance Information Criterion (DIC; Spiegelhalter et al., 1998), which is easily calculated after Bayesian model estimation via Markov chain Monte-Carlo. DIC accounts for model complexity including functional form, by examination of the posterior distribution over parameters. While DIC performs well in model selection problems involving relatively simple models (e.g. Gaussian errors and few parameters), it can perform much more poorly with the complex kinds of models typically used to describe cognition, including evidence accumulation models.

A different approach to model selection is via cross validation. Cross validation involves separating the data set into two parts. Data from the “calibration” part are used to estimate the model’s parameters, and then these parameters are fixed while the model’s goodness-of-fit is evaluated against data from the “validation” part. The process is typically repeated several times, known as “folds”, using different separations of the data into calibration and validation parts. Cross validation accounts for model complexity in a sophisticated way, and it can perform well even with complex models. However, the most important disadvantage of cross validation is its computational cost, as the model must be repeatedly fit to each different calibration set, typically implying a ten- or twenty-fold increase in cost compared to the approaches above. Another practical limitation involves the chosen size of the validation data set sizes. Validation data set sizes that are too large will favour more complex models, due to the reduced unique noise in the data, and sizes that are too small will give a poor reflection of the entire data set (when using a reasonable number of folds). Attempting to find the right validation data set size may require rigourous testing, which only increases the computational issues listed above. For these reasons, cross validation has not proven very popular with evidence accumulation models to date.

Another method of model comparison which has been used with evidence accumulation models is based on the examination of parameter estimates. This approach has been particularly popular with the diffusion model (Ratcliff 1978). The method involves estimating the parameters of an overly-complex model, in which many different parameters are allowed to vary with different experimental manipulations. The selection task of deciding which parameters are influenced by which manipulations is then accomplished via investigation of the estimated parameters. For example, if drift rate estimates were found to vary across older and younger adults, then one would conclude that age influences drift rate. However, this method is reliant on the accuracy of the parameter estimation process, as poor or biased estimation will be directly reflected in the resulting inferences. This is particularly problematic when considering complex psychological models, such as evidence accumulation models, in which the parameters are correlated. In that case, and especially when fitting a complex model with many parameters as used in this approach, there can be systematic biases in parameter estimates.

Bayes factors

All the previously mentioned model selection methods rely on an initial estimation of parameters, which are then used for inference, whether this estimation be a single most likely set of parameter values (e.g., maximum likelihood), or a distribution of values (e.g., Bayesian posterior parameter distribution). Since there can be problems with parameter estimation in complex psychological models which have highly correlated parameters, we suggest the use of Bayes factors (Kass and Raftery 1995). Bayes factors are popular with simpler statistical models, and do not separate the stages of parameter estimation and inference, instead integrating the likelihood over the entire prior distribution of the parameters. By integrating over the prior parameter space Bayes factors provide a natural penalty for complexity, as more complex models will occupy a greater volume of parameter space, and usually have lower average likelihood as a result (because the data occupy only a small section of parameter space). By using Bayes factors one is able to avoid problems due to practical difficulties in parameter estimation seen for complex models with highly correlated parameters, such as the LBA.

Bayes factors have not been used for model selection with evidence accumulation models so far, due to computational intractability. Bayes factors require integration over the prior distribution, which is potentially large and high-dimensional in a complex cognitive model. For very simple models, such as general linear models, this integration is possible via analytic methods. For most cognitive models, this integration problem is theoretically easy, using Monte-Carlo methods, but practically difficult, as the the integrals very quickly become too much for even the fastest available computers.

Although computing the multi-dimensional integrals for Bayes factors is computationally intractable in many circumstances, alternative ways to estimate Bayes Factors have been developed. One such method is the Savage-Dickey ratio, which provides a Bayes factor to test a hypothesis about nested models, in the case where one model is defined as a particular point value of a parameter in another model (typically a zero value on an effect size parameter). The Bayes factor for the test of this hypothesis can be approximated by using the ratio of the posterior and prior density at the point value (Wagenmakers et al. 2010; Wetzels et al. 2010). The Savage-Dickey ratio appears, at face value, to be a plausible solution for obtaining Bayes Factors for evidence accumulation models. For example, to test whether drift rate differs between older and younger adults, one could estimate an effect size parameter for the difference in drift rate between groups. The Savage-Dickey ratio could be calculated on the effect size parameter, against a value of zero. Although this seems promising, the Savage-Dickey ratio shares the inference through estimation based properties of the previously mentioned model selection methods, and in our experience has performed poorly for the LBA and diffusion models, due to practical problems still present within model parameter estimation techniques.

Bayes factors can also be calculated by directly estimating the integral over the prior distribution using Monte-Carlo integration. Monte-Carlo integration is just the process of integrating a function over a distribution by taking a large number of samples from the distribution, and averaging the function’s value over these samples. When applied to Bayes factors, Monte-Carlo integration involves drawing a large number of samples from the prior distribution over parameters, assessing the likelihood of the data under each of these sampled parameters, and then averaging over these likelihoods. This gives an estimate of the marginal probability of the data given the model. Taking a ratio of two of these marginal probabilities, for two different models, yields the Bayes factor for that model comparison.

Although this process is tenable for simple models, the process of Monte-Carlo integration over the prior can be computationally intractable for evidence accumulation models, using standard computing approaches. However, the recent development of general purpose graphical processing units (GP-GPUs) offers the potential for a huge increase in speed. GPUs are ideal for problems with the “same instructions multiple data”, including Monte-Carlo integration, in which the same function (likelihood) must be applied to a large number of different inputs (parameter samples from the prior). This works particularly well for the LBA model, as it has a simple, closed-form likelihood expression which is easy to implement in GPU-compatible code, and which takes a mostly predictable amount of time to compute.

The increase in processing speed offered by GPUs makes obtaining Bayes factors for the LBA via Monte-Carlo integration feasible. We implemented the LBA density function and associated code using NVIDIA’s proprietary extension to the C-language, called CUDA. In addition, we provide R code to perform the entire Monte-Carlo integration process, which can be used to estimate marginal probabilities for any standard LBA model, for any number of conditions of a two-accumulator (i.e., two-choice) experiment, with minimal changes required by the user. Although greater efficiency is possible by moving more of the algorithm from the CPU to the GPU (e.g. sampling parameters from the prior distribution), we have chosen to leave everything except the likelihood function within R, computed on the CPU. This choice makes the software more flexible, allowing users to modify the model structure easily. Our code is available for free download from https://osf.io/7cbh7/#. This code requires a computer with a CUDA-compatible GPU, a C compiler, and the NVIDA CUDA compiler, NVCC.

In the three sections that follow, we firstly explore simulated examples for the analysis of individual subjects. This is important to investigate the stability of the Monte-Carlo approximation method for the marginal probability. Next, we will explore the hierarchical analysis method in simulated data, again investigating the stability of the estimated marginal probability, as well as investigating how inferences drawn from finite samples of data are likely to compare with the data-generating model. We finish by providing a description of the code and its components, which explains how to use the code for both individual subjects and for a hierarchical analysis.

Analysis of an individual subject

In this section we analyze simulated data with two purposes: firstly, as a sanity check to illustrate that the method works as expected with sufficiently large samples of data; and secondly to investigate the stability of the Monte-Carlo approximation. We simulated data from a single participant in a two-alternative forced choice task, analyzed those data with two LBA model variants, and varied three elements of the analyses: the number of Monte-Carlo samples; the number of data, and the number of experimental conditions.

Methods

We investigated two data-generating models: a simple model with no variation in parameters over condition, and a more complex model in which the threshold, non-decision time, and the drift rate of the accumulator corresponding to the correct response were all assumed to vary over condition. Each data set was analyzed using each of the two models. We chose these two models in order to engender a large difference in complexity between the theoretical alternatives, as a first step in establishing the properties of the Bayes factor for LBA models.

In all simulations (both individual in this section, and hierarchical in the next section), the finishing time distribution for each LBA accumulator is determined by five basic parameters: mean and standard deviation of the drift rate distribution (d, s); threshold (b); width of the start point distribution (A), and the non-decision time (t 0). We forced all parameters to be equal across the two accumulators corresponding to the two responses, except for means and standard deviations of the drift rate distributions. We constrained one standard deviation (of the accumulator corresponding to the correct response) to be arbitrarily set at s correct = 1, to resolve a scaling property of the model (Donkin et al. 2009).

The more complex LBA model allowed the mean of the distribution of drift rates on the accumulator corresponding to the correct response to vary with condition, as well as the threshold value, and the non-decision time value. The full model was therefore:

$$\begin{array}{@{}rcl@{}} Data \hspace{5pt} level: & & \\ (RT,resp) & \sim & LBA(A,b_{j},t_{0,j},d_{j} \\ & & \hspace{20pt} d_{incorrect},s_{incorrect}) \\ Prior \hspace{5pt} distributions: & & \\ A, d_{incorrect}, s_{incorrect} & \sim & N_{+}(1,1) \\ t_{0,j} & \sim & N_{+}(.3,.3) \\ d_{j} & \sim & N_{+}(3,3) \\ b_{j} - A & \sim & N_{+}(0.4,0.4) \end{array} $$

Here, and below, j indexes the condition, N + refers to a normal distribution truncated to the positive real half-line. The data level distribution was an LBA model with three parameters constant across conditions and three different parameters for each condition, and the data to which this was applied consisted of two response time distributions for each condition (correct and incorrect responses), and the associated response probabilities. For consistency with typical analysis methods, both models contained a contamination process for the analysis, where the probability density was a mixture of the actual probability density (98%), and a contamination distribution (2%), distributed uniformly on the interval 0sec - 5sec, with random choice probability. However, the data were generated without any contamination in order to reduce the noise in the process.

The simple model that included no differences between conditions used the same parameters in all conditions:

$$\begin{array}{@{}rcl@{}} Data \hspace{5pt} level: & & \\ (RT,resp) & \sim & LBA(A,b,t_{0},d \\ & & \hspace{20pt} d_{incorrect},s_{incorrect}) \\ Prior \hspace{5pt} distributions: & & \\ A, d_{incorrect}, s_{incorrect} & \sim & N_{+}(1,1) \\ t_{0} & \sim & N_{+}(.3,.3) \\ d & \sim & N_{+}(3,3) \\ b - A & \sim & N_{+}(0.4,0.4) \end{array} $$

We investigated the stability of the Monte-Carlo approximation to the integral over the prior distribution by varying the number of Monte-carlo samples (102, 103, 104, 105, 106, 107, 108). We investigated the behavior of the Bayes factor for the above LBA models by varying the number of data per condition (50, 175, 300, 600), and the number of conditions (2, 3, 4, 5). We did not vary these three elements factorially, due to computational limitations. For all investigations in which a parameter was not being varied, it was set at a default value of 107 (number of samples), 600 (data), and 2 (conditions). For each simulated data set, which there were one of each per cell (except for the number of Monte-carlo samples investigation, which used a single data set for all cells), the integration process was run 10 times to assess the integral consistency. On an NVIDIA Tesla K20c GPU, we found that there were no noticeable differences in timing caused by the number of trials, with all analyses taking approximately 5.5 minutes on average. Although the timing increased with the number of conditions for the complex model (approximately 6, 8, 10, and 12 minutes for the 2, 3, 4 and 5 number of condition simulations, respectively), no change was seen when using the simple model for the analysis (all approximately 5 minutes), suggesting that this timing difference was purely caused by the increasing number of parameters that the complex model gained for each condition.

We used the following parameter settings to generate data:

$$\begin{array}{@{}rcl@{}} Complex \hspace{5pt} model: & & \\ A &=& 1\\ b_{\{1,2,3,4,5\}} &=& \{1.3,1.7,1.5,2,2.8\}\\ t_{0,\{1,2,3,4,5\}} &=& \{0.6,0.3,0.45,0.15,0.35\}\\ d_{\{1,2,3,4,5\}} &=& \{4,3,3.5,2.5,4.2\}\\ d_{incorrect} &=& 1 \\ s_{incorrect} &=& 1 \\ Simple \hspace{5pt} model: & & \\ A &=& 1\\ b &=& 1.4\\ t_{0} &=& 0.3\\ d &=& 3.5\\ d_{incorrect} &=& 1\\ s_{incorrect} &=& 1 \end{array} $$

Results

The results for the simulation using differing numbers of samples are illustrated in Fig. 2, and the simulations that manipulated the number of trials and experimental conditions can be seen in Table 1. The x-axis shows the number of Monte-Carlo samples, and the y-axis the log of the marginal probability for the two models, separately for the two different data-generating models. The points give the mean of the natural logarithm of the marginal likelihood, and the error bars the standard deviation. Passing the sanity check, the marginal probability is substantially larger for the data-generating model when the number of Monte-Carlo samples is very large. The stability of the Monte-Carlo integral appears quite high in this case: at all Monte-Carlo sample sizes from 1,000 upwards, the error bars of the marginal probabilities (across repeated sampling) do not overlap.

Fig. 2
figure 2

Estimated marginal log-likelihoods for our Monte-Carlo integration method for a single synthetic subject with two experimental conditions and 600 trials per condition. The lines give the mean of the estimated marginal likelihood across 10 sampling runs, with the black lines showing the simple model, the gray lines showing the complex model, the solid lines showing data generated by the simple model, and the broken lines showing the data generated by the complex model. The error bars show the standard deviation of the estimated marginal likelihoods over the 10 sampling runs

Full size image
Table 1 Changes in Bayes factor (always expressed in favor of the data-generating model) with changes in number of data and number of experimental conditions
Full size table

In addition, towards the higher number of samples the marginal probability estimates appear to asymptote, displayed by a stability in log-likelihood values as the number of samples continue to increase, which is consistent with the the notion that the estimated integral is close to the true integral. However, this seems to take a greater number of samples for the complex model (gray lines) than the simple model (black lines), and a greater standard deviation is also seen across all numbers of samples for the complex model, suggesting that model size is a key factor in determining the appropriate number of samples required.

Table 1 shows how the Bayes factor changes with the number of simulated data. As expected, the Bayes factors become increasingly decisive in favor of the data-generating model as the number of data increase. Although the standard deviation in the Bayes factors also increase with sample size, this change is much smaller than the change in mean Bayes factor.

The changes in the Bayes factor with number of conditions (while holding constant data-per-condition) depend on which model generated the data. When the data were generated from the simple model, the Bayes factors become more decisive as the number of conditions increases. However, when the data were generated by the complex model, the Bayes factors don’t change much with number of conditions, but do become less stable (increasing standard deviation across repeated sampling runs). This reflects the increasing model size (number of parameters) with increasing number of conditions. Nevertheless, in all cases the mean Bayes factor is much larger than the standard deviation across sampling runs.

Hierarchical performance

The above simulations provided a sanity check for our methods, and investigated the stability of the Monte-Carlo integral. They also showed that the inference one would draw from the Bayes factor (i.e., which model had the higher marginal probability given the data) matched the identity of the data-generating model. This demonstrates that, at least for these two particular LBA models, the model-based inference supported by the Bayes factor also supports model inversion. That is, the process of deciding which model is best supported by the data at hand (inference) matched the identity of the model which did actually generate those data. Such a match is not trivial, and is not always desirable: for example, if there data were noisy enough, of few enough, the correct inference will always be the simpler model, even if that did not generate the data for a detailed discussion of these important issues, which we and other have frequently gotten wrong, see Lee (in press).

We now extend the investigation of the properties of the Bayes factor for LBA models to hierarchical cases. Hierarchical (or multi-level) analyses are becoming standard in cognitive science, including for the LBA, because they sensibly pool data from different participants. We report two simulation studies that address commonly-investigated analyses using evidence accumulation models, including the LBA. We first simulate the problem of comparing a model that allows an effect on drift rate across condition condition vs. a model that assumes an effect on threshold across conditions. This simulation mirrors the example with aging described above. The second study simulated selecting between a model that assumes an effect on drift over condition vs. a model that assumes no effect of condition (a null model). Each simulation study was repeated with multiple simulated data sets. We compared the inference supported by the Bayes factors against the ground truth of which model generated the data, to illustrate the properties of the Bayes factor for the LBA. In addition, we assessed the stability of the Monte-Carlo integral, conditional on a single simulated data set. This was done by drawing multiple Monte-Carlo samples from the prior for some data sets.

Hierarchical simulation: Drift vs. Threshold

Methods

For this simulation, we investigated the inferences drawn by Bayes factors that compared LBA models assuming changes in drift rate vs. changes in threshold across conditions. These two parameter manipulations were chosen as they are common assumptions in all evidence accumulation models, and can be difficult to tease apart in data, even though they are very different at a psychological level. We simulated data corresponding to an experiment with multiple participants each of whom contributed data from two experimental conditions.

The LBA model that allowed different drift rates across conditions allowed only the mean of the distribution of drift rates on the accumulator corresponding to the correct response to vary with condition:

$$\begin{array}{@{}rcl@{}} Data \hspace{5pt} level: & & \\ (RT_{i},resp_{i}) & \sim & LBA(A_{i},b_{i},t_{0,i},d_{condition1,i} \\ & & \hspace{20pt} d_{condition2,i},d_{incorrect,i},\\ &&\qquad\,\, s_{incorrect,i}) \\ Group \hspace{5pt} level: & & \\ A_{i} & \sim & N_{+}(\mu_{A},\sigma_{A})\\ b_{i}-A_{i} & \sim & N_{+}(\mu_{b},\sigma_{b})\\ t_{0,i} & \sim & N_{+}(\mu_{t0},\sigma_{t0})\\ d_{condition1,i} & \sim & N_{+}(\mu_{d,condition1},\sigma_{d,condition1})\\ d_{condition2,i} & \sim & N_{+}(\mu_{d,condition2},\sigma_{d,condition2})\\ d_{incorrect,i} & \sim & N_{+}(\mu_{d,incorrect},\sigma_{d,incorrect})\\ s_{incorrect,i} & \sim & N_{+}(\mu_{s,incorrect},\sigma_{s,incorrect}) \\ Prior \hspace{5pt} distributions: & & \\ \mu_{A}, \sigma_{A}, \hspace{20pt} & & \\ \mu_{d,incorrect}, \sigma_{d,incorrect}, \hspace{10pt} & & \\ \mu_{s,incorrect}, \sigma_{s,incorrect} & \sim & N_{+}(1,1) \\ \mu_{t0}, \sigma_{t0} & \sim & N_{+}(.3,.3) \\ \mu_{d,condition1}, \sigma_{d,condition1}, \hspace{10pt} & & \\ \mu_{d,condition2}, \sigma_{d,condition2} & \sim & N_{+}(3,3) \\ \mu_{b}, \sigma_{b} & \sim & N_{+}(0.4,0.4) \end{array} $$

Here, and below, i indexes participants. The data level distribution was an LBA model with seven parameters, and the data to which this was applied consisted of four response time distributions (correct and incorrect responses in each condition) and two response probabilities (the proportions of correct responses in each condition). Again, to be consistent with standard fitting methods, both models contained a contamination process, where the probability density was a mixture of the actual probability density (98%), and a contamination distribution (2%), distributed uniformly on the interval 0sec - 5sec, with random choice probability. Also, as before, to reduce the potential noise in the process the data were generated without contamination.

The model that included differences in threshold between conditions was:

$$\begin{array}{@{}rcl@{}} Data \hspace{5pt} level: & & \\ (RT_{i},resp_{i}) & \sim & LBA(A_{i},b_{condition1,i},b_{condition2,i}, \\ & & \hspace{20pt} t_{0,i},d_{i},d_{incorrect,i},s_{incorrect,i}) \\ Group \hspace{5pt} level: & & \\ A_{i} & \sim & N_{+}(\mu_{A},\sigma_{A})\\ b_{condition1,i}-A_{i} & \sim & N_{+}(\mu_{b,condition1},\sigma_{b,condition1})\\ b_{condition2,i}-A_{i} & \sim & N_{+}(\mu_{b,condition2},\sigma_{b,condition2})\\ t_{0,i} & \sim & N_{+}(\mu_{t0},\sigma_{t0})\\ d_{i} & \sim & N_{+}(\mu_{d},\sigma_{d})\\ d_{incorrect,i} & \sim & N_{+}(\mu_{d,incorrect},\sigma_{d,incorrect})\\ s_{incorrect,i} & \sim & N_{+}(\mu_{s,incorrect},\sigma_{s,incorrect}) \\ Prior \hspace{5pt} distributions: & & \\ \mu_{A}, \sigma_{A}, \hspace{20pt} & & \\ \mu_{d,incorrect}, \sigma_{d,incorrect}, \hspace{10pt} & & \\ \mu_{s,incorrect}, \sigma_{s,incorrect} & \sim & N_{+}(1,1) \\ \mu_{t0}, \sigma_{t0} & \sim & N_{+}(.3,.3) \\ \mu_{b,condition1}, \sigma_{b,condition1}, \hspace{10pt} & & \\ \mu_{b,condition2}, \sigma_{b,condition2} & \sim & N_{+}(0.4,0.4) \\ \mu_{d}, \sigma_{d} & \sim & N_{+}(3,3) \end{array} $$

We investigated the Bayes factors in a range of different simulated sample sizes: simulating either 10, 25, or 40 participants, and simulating either 100, 350, or 600 trials per participant. Data were generated for each simulated subject using parameters that were randomly sampled from the following group-level distributions:

$$\begin{array}{@{}rcl@{}} Drift \hspace{5pt} model: & & \\ A_{i} & \sim & N_{+}(1,0.1)\\ b_{i}-A_{i} & \sim & N_{+}(0.4,0.04)\\ t_{0,i} & \sim & N_{+}(0.3,0.03)\\ d_{condition1,i} & \sim & N_{+}(4,0.4)\\ d_{condition2,i} & \sim & N_{+}(3,0.3)\\ d_{incorrect,i} & \sim & N_{+}(1,0.1)\\ s_{incorrect,i} & \sim & N_{+}(1,0.1) \\ Threshold \hspace{5pt} model: & & \\ A_{i} & \sim & N_{+}(1,0.1)\\ b_{condition1,i}-A_{i} & \sim & N_{+}(0.3,0.03)\\ b_{condition2,i}-A_{i} & \sim & N_{+}(0.7,0.07)\\ t_{0,i} & \sim & N_{+}(0.3,0.03)\\ d_{i} & \sim & N_{+}(3.5,0.35)\\ d_{incorrect,i} & \sim & N_{+}(1,0.1)\\ s_{incorrect,i} & \sim & N_{+}(1,0.1) \end{array} $$

For practical reasons, the number of subjects and the number of data per subject were not manipulated factorially. All subject-varying data sets had 600 trials per subject, and all trial-varying data sets had 40 subjects, creating five different cells. For each cell, we generated 30 synthetic data sets. For a randomly-chosen five of these 30, we repeated the Monte-Carlo integration process five times, to examine consistency of the integration.

Each Monte-Carlo integration began with 1,000 samples of the group level parameters, drawn from the prior distributions, and 10,000 individual level parameter samples from each group-level distribution sample. The processing time for each simulated data set increased approximately linearly with the number of simulated subjects, but was almost unaffected by the number of simulated trials, up to very large numbers (more than 10,000 trials per subject). This arises because our code optimized the use of the GPU memory to provide fast access to data from nearby trials, rather than nearby subjects. On an NVIDIA Tesla K20c GPU, a data set with 10 subjects and 600 trials per subject required about 30 minutes analysis, 25 subjects took approximately 65 minutes, and 40 subjects took approximately 105 minutes.

Results

Inference supported by the Bayes factor matched the data-generating model very often; even for very few subjects and small numbers of trials per subject (see Table 2). In the cell with the greatest number of subjects (40) and trials (600), the Bayes factors identified 96% of data sets correctly, and there appeared to be no apparent bias towards either model within the inversion framework. In addition, as the number of trials decrease, there appears to be very gradual decline in performance of the method.

Table 2 Percentage of estimates in which the inference from the Bayes factor matched the data-generating model, during a comparison of drift vs. threshold models, for different numbers of simulated subjects and simulated trials per subject
Full size table

We next examined the stability of the Bayes factor estimate over repeated Monte-Carlo samples from the prior, using the same simulated data set. The first column of Table 3 shows the mean log Bayes factor between the drift and threshold models, averaged over all data sets and manipulations of sample size (manipulations of number of subjects and number of data per subject did not make large differences here). The first row gives this value for when the data were generated by the model that includes a drift rate effect, and the second row when the data were generated by a model that includes a threshold effect. The third and fourth rows of the table give the standard deviation of the log marginal model probabilities for each model, across repeated Monte-Carlo samples. The variation between Monte-Carlo samples is much smaller (< 1) than the difference between the models (> 10).

Table 3 Stability of the Monte-Carlo estimate in hierarchical simulation of Drift vs. Threshold
Full size table

To highlight the performance of the Bayes factor method for the problem of inversion, we compared it against the deviance information criterion (DIC), which is a common model selection methods for hierarchical Bayesian applications. We used the same model specification as above, and estimated posterior distributions over the parameters in a manner that has become standard: we differential evolution Markov chain Monte-Carlo (Turner et al. 2013), with 3 × k chains (where k is equal to the number of free parameters per individual), 3,000 burn-in iterations, and 1,000 iterations after convergence. The bottom two rows of Table 2 show that inferences supported by DIC mis-match the data-generating model in surprising and unpredictable ways. On average, the DIC-based inference matched the data-generating model at about chance rates (51.5%), and also showed a very strong bias in favor of the model that included an effect of threshold – this model was selected in 92.5% of cases, even though it generated the data in only 50% of cases. DIC performed poorly in our example, which was likely due to the complex nature of the model, with its highly correlated parameter estimates. DIC can be prone to erratic behavior because it is based on point estimates rather than the full posterior distribution (Gelman et al. 2014; Vehtari and Gelman 2014). This issue was likely exasperated by the practical problems in parameter estimation for complex models highlighted earlier. Importantly though, these effects appear to suggest that the Bayes factor provides inferences which agree better with the asymptotic truth, in large-sample cases, and behave more predictably in small-sample cases.

Hierarchical simulation: Drift vs. Null

Methods

For the next simulation, we investigated the properties of the LBA Bayes factor in a hierarchical setting comparing a model that allowed variation in drift rate (both correct and error) between conditions against a model that allowed no variation in any parameters between conditions. This can be a difficult model inference task for some statistical approaches, because the null model can never fit any data set better than the alternative model, even when the null model actually generated the data, because it is nested within the more complex model. This makes considerations of model complexity paramount.

The model that allowed drift rate differences between conditions allowed different mean parameters for the drift rate distributions in the accumulators corresponding to both correct and incorrect responses, implying eight parameters per subject at the individual-subject level:

$$\begin{array}{@{}rcl@{}} Data \hspace{5pt} level: & & \\ (RT_{i},resp_{i}) & \sim & LBA(A_{i},b_{i},t_{0,i},v_{condition1,i} \\ & & \hspace{20pt} v_{condition2,i},v_{condition1,incorrect,i} \\ & & \hspace{40pt} v_{condition2,incorrect,i}, s_{incorrect,i}) \\ Group \hspace{5pt} level: & & \\ A_{i} & \sim & N_{+}(\mu_{A},\sigma_{A})\\ b_{i}-A_{i} & \sim & N_{+}(\mu_{b},\sigma_{b})\\ t_{0,i} & \sim & N_{+}(\mu_{t0},\sigma_{t0})\\ v_{condition1,i} & \sim & N_{+}(\mu_{v,condition1},\sigma_{v,condition1})\\ v_{condition2,i} & \sim & N_{+}(\mu_{v,condition2},\sigma_{v,condition2})\\ v_{condition1,incorrect,i} & \sim & N_{+}(\mu_{v,condition1,incorrect},\sigma_{v,condition1,incorrect})\\ v_{condition2,incorrect,i} & \sim & N_{+}(\mu_{v,condition2,incorrect},\sigma_{v,condition2,incorrect})\\ s_{incorrect,i} & \sim & N_{+}(\mu_{s,incorrect},\sigma_{s,incorrect}) \\ Prior \hspace{5pt} distributions: & & \\ \mu_{A}, \sigma_{A}, \hspace{30pt} & & \\ \mu_{v,condition1,incorrect}, \sigma_{v,condition1,incorrect}, \hspace{20pt} & & \\ \mu_{v,condition2,incorrect}, \sigma_{v,condition2,incorrect}, \hspace{10pt} & & \\ \mu_{s,incorrect}, \sigma_{s,incorrect} & \sim & N_{+}(1,1) \\ \mu_{t0}, \sigma_{t0} & \sim & N_{+}(.3,.3) \\ \mu_{v,condition1}, \sigma_{v,condition1}, \hspace{10pt} & & \\ \mu_{v,condition2}, \sigma_{v,condition2} & \sim & N_{+}(3,3) \\ \mu_{b}, \sigma_{b} & \sim & N_{+}(0.4,0.4) \end{array} $$

The null model forced all parameters to be identical across conditions, implying six parameters per participant:

$$\begin{array}{@{}rcl@{}} {\kern43pt} Data \hspace{5pt} level: & & \\ (RT_{i},resp_{i}) & \sim & LBA(A_{i},b_{i},t_{0,i}, \\ & & \hspace{20pt} v_{i},v_{incorrect,i},s_{incorrect,i}) \\ Group \hspace{5pt} level: & & \\ A_{i} & \sim & N_{+}(\mu_{A},\sigma_{A})\\ b_{i}-A_{i} & \sim & N_{+}(\mu_{b},\sigma_{b})\\ t_{0,i} & \sim & N_{+}(\mu_{t0},\sigma_{t0})\\ \end{array} $$
$$\begin{array}{@{}rcl@{}} v_{i} & \sim & N_{+}(\mu_{v},\sigma_{v})\\ v_{incorrect,i} & \sim & N_{+}(\mu_{v,incorrect},\sigma_{v,incorrect})\\ s_{incorrect,i} & \sim & N_{+}(\mu_{s,incorrect},\sigma_{s,incorrect}) \\ Prior \hspace{5pt} distributions: & & \\ \mu_{A}, \sigma_{A}, \hspace{20pt} & & \\ \mu_{v,incorrect}, \sigma_{v,incorrect}, \hspace{10pt} & & \\ \mu_{s,incorrect}, \sigma_{s,incorrect} & \sim & N_{+}(1,1) \\ \mu_{t0}, \sigma_{t0} & \sim & N_{+}(.3,.3) \\ \mu_{v}, \sigma_{v} & \sim & N_{+}(3,3) \\ \mu_{b}, \sigma_{b} & \sim & N_{+}(0.4,0.4) \end{array} $$

All other simulation details were identical to that of the first simulation. Data were generated for each simulated subject using parameters that were randomly sampled from the following group-level distributions:

$$\begin{array}{@{}rcl@{}} Drift \hspace{5pt} model: & & \\ A_{i} & \sim & N_{+}(1,0.1)\\ b_{i}-A_{i} & \sim & N_{+}(0.4,0.04)\\ t_{0,i} & \sim & N_{+}(0.3,0.03)\\ v_{condition1,i} & \sim & N_{+}(4,0.4)\\ v_{condition2,i} & \sim & N_{+}(3,0.3)\\ v_{condition1,incorrect,i} & \sim & N_{+}(1,0.1)\\ v_{condition2,incorrect,i} & \sim & N_{+}(2,0.2)\\ s_{incorrect,i} & \sim & N_{+}(1,0.1) \\ Null \hspace{5pt} model: & & \\ A_{i} & \sim & N_{+}(1,0.1)\\ b_{i}-A_{i} & \sim & N_{+}(0.4,0.04)\\ t_{0,i} & \sim & N_{+}(0.3,0.03)\\ v_{i} & \sim & N_{+}(3.5,0.35)\\ v_{incorrect,i} & \sim & N_{+}(1,0.1)\\ s_{incorrect,i} & \sim & N_{+}(1,0.1) \end{array} $$

Results

The inference supported by the Bayes factor matched the data-generating model less often in this simulation than in the previous simulation. This is consistent with the notion that nested model comparisons can present difficulties for model inversion. Nevertheless, on average the inference supported by the Bayes factor still matched the data-generating model 80% of the time (see Table 4). The Bayes factor preferred the more complex model, identifying it as the correct inference in 97% of data sets which were generated by the more complex model vs. 65% of data sets that were generated by the null model. Once again, inferences supported by DIC were difficult to make sense of.

Table 4 Percentage of runs in which the inference supported by the Bayes factor matched the data-generating model, for a comparison of drift-varying vs. null models
Full size table

As with the Drift vs. Threshold simulation, the estimated marginal probabilities were quite stable against Monte-Carlo noise. The second column of Table 3 shows that the average log Bayes factor was very large when the data were generated by the complex model, but close to zero when the data were generated by the null model. The sampling variability due to Monte-Carlo integration was small compared with this difference, but not so small when compared with the distance from the log Bayes factor to zero (the model selection criterion point). These results suggest that increased amounts of Monte-Carlo integration may be required when comparing nested models, or perhaps the use of more efficient integration methods. One such method is known as importance sampling, which involves defining a distribution to sample from that more efficiently samples from the peak of the likelihood function than the prior, resulting in less samples being required, and therefore, less computational time. As the focus of this paper is not on importance sampling we do not wish to go into too much depth on the topic, but it should be noted that defining an “importance distribution” is not a trivial process, and if done poorly can end up being less efficient than sampling from the prior.

Real data

Lastly, we illustrate how our method and code can be used with experimental data, to make model-based inferences that are relevant to real theoretical questions. However, this single example is only a first step, and ongoing use and experience with the Bayes factor for the LBA is necessary. In addition, improvements to the method such as importance sampling may turn out to be practically necessary, in order to deal with the real-world problems presented by empirical data.

Method

We chose to analyze data reported as Experiment 1 by Rae et al. (2014), which had participants perform a basic perceptual discrimination task, under separate speed- and accuracy-emphasis for different blocks. For precise details on the method, see Rae et al.. Four-fifths of the trials in this experiment were regular decision trials, which we analyzed. The remaining fifth were response signal trials, which we excluded. Using the same data exclusion criteria as the original authors resulted in data from 35 participants with an average of 1705 trials each.

The key theoretical question investigated by Rae et al. (2014) regarded the changes in evidence accumulation model parameters induced by changes in caution (speed vs. accuracy). Rae et al. asked whether caution emphasis uniquely influenced the decision threshold, as has been conventionally assumed, or whether caution emphasis also influenced drift rates. Rae et al. concluded that changing between accuracy and speed emphasis influenced both thresholds and drift rates. Under speed emphasis, participants set lower thresholds, but also had faster drift rates (drift rates increased for accumulators corresponding to both responses, which does not cause an accuracy change).

Therefore, to re-assess the findings of Rae et al. (2014), we used the Bayes factor to compare a model that allowed threshold to vary over conditions, against a model that allowed threshold and drift rate to vary over conditions. The threshold-only model was defined exactly the same as for the hierarchical simulations above. The threshold-and-drift rate model allowed threshold and drift rates (for both accumulators) to vary over conditions:

$$\begin{array}{@{}rcl@{}} Data \hspace{5pt} level: & & \\ (RT_{i},resp_{i}) & \sim & LBA(A_{i},b_{S,i},b_{A,i},t_{0,i},v_{S,i} \\ & & \hspace{20pt} v_{A,i},v_{S,incorrect,i} \\ & & \hspace{40pt} v_{A,incorrect,i}, s_{incorrect,i}) \\ Group \hspace{5pt} level: & & \\ A_{i} & \sim & N_{+}(\mu_{A},\sigma_{A})\\ b_{\{S,A\},i}-A_{i} & \sim & N_{+}(\mu_{b,\{S,A\}},\sigma_{b,\{S,A\}})\\ t_{0,i} & \sim &N_{+}(\mu_{t0},\sigma_{t0})\\ v_{\{S,A\},i} & \sim & N_{+}(\mu_{v,\{S,A\}},\sigma_{v,\{S,A\}})\\ v_{\{S,A\},incorrect,i} & \sim & N_{+}(\mu_{v,\{S,A\},incorrect},\sigma_{v,\{S,A\},incorrect})\\ s_{incorrect,i} & \sim & N_{+}(\mu_{s,incorrect},\sigma_{s,incorrect}) \end{array} $$

Here, the subscripts S and A represent parameters for the speed and accuracy conditions, respectively. We used identical prior distributions as in the simulations for hierarchical models above, with 5,000 samples from the group-level parameters, and 10,000 samples from the individual-level parameters for each group-level sample. In order to assess the variability in the estimate, we split the group-level Monte-Carlo samples randomly into five separate estimates, each based on 1,000 group-level samples and 10,000 individual-level samples.

Results

In all cases below, we report values in terms of the natural logarithm of the marginal likelihood. Differently from Rae et al. (2014), we found the model that only included variation in threshold had a higher marginal likelihood (2075.7) than the model that included variation in both threshold and drift rate (2074). Thus, the Bayes factor was in favor of the conventional assumption (that only threshold varies across speed/accuracy emphasis) to a moderate degree (natural logarithm of the Bayes factor = 1.717).

However, we found a large amount of variation in the estimates for both models across Monte-Carlo samples, with the standard deviation of the more complex threshold and drift rate model (18.1) being larger than in the simpler threshold only model (8.89). This trend was also seen within the range of the estimates, with the threshold and drift rate model (2028.8 - 2075.6) having more than double the range of the threshold model (2055.0 - 2077.1). This again supports our findings from both the individual and hierarchical simulated data, where the estimates for more complex models were much more unable than for simpler models. In addition, the variation in this real data was much greater than for the simulated data, where the simulated data threshold model had a standard deviation of 0.894.

As shown above, the amount of variation (i.e., standard deviation and range of the marginal likelihood estimates) appears to be quite large, especially when compared to the Bayes factor, suggesting that our results may have been effected by unstable estimates. Therefore, in terms of the research question of (Rae et al. 2014), our findings should be interpreted with reservations. In order to be confident about the conclusion of our method, the variation in the estimates should be smaller than the Bayes factor, meaning that a conclusive analysis for this data set would require either a greater number of group and/or individual level samples, or smart sampling techniques such as importance sampling. However, as the goal of this section of the paper was to display how the method could be applied to real data, and the potential differences between simulated data and real data, we will not pursue this avenue within the current paper, and leave such a question for future research.

Discussion

The aim of this paper was to show that through GPU computing, the estimation of Bayes factors by Monte-Carlo integration has become feasible for the LBA, which is a complex psychological model with difficult parameter estimation properties. We investigated the properties of our method through simulations in both the individual-subject case, where we assessed the stability of our method over a different number of samples, and the hierarchical case, where we used two examples inspired by experimental psychology to compare inferences from the Bayes factor with knowledge of the data-generating model. We provided freely available code for download by interested researchers, as well as explanations both within this paper and the code download package on how it can be used, so that others are able to implement our methods easily.

At least in simulated data sets, the Monte-Carlo stability of our method was quite high. Estimates of marginal probabilities were stable for a reasonable number of samples (corresponding to minutes of computer time), reaction times, and conditions. Estimates for both the complex and simple models appeared to stabilize by 107 samples, depending on model complexity. Model discrimination improved with increased data sample size, and this comes at very little cost in terms of computation time, if the number of participants is constant.

For hierarchical models, the method was also stable in the Monte-Carlo sense. Inferences supported by the Bayes factor in hierarchical data also identified the data generating model for large samples, providing an asymptotic sanity check. This was most clearly established in a comparison of models with an effect exclusively on drift rates or on thresholds, which is an important question in psychological research (Rae et al. 2014; Ratcliff et al. 2011, 2010, 2007; Forstmann et al. 2010; Forstmann et al. 2008). For the more difficult comparison between a nested pair of models, the Bayes factor also passed an asymptotic sanity check, and made easily interpreted and plausible inferences with smaller samples. These model inference properties were not shared by inferences based on the deviance information criterion (DIC), which is a currently-popular method of model selection.

Lastly, we applied our hierarchical method to real experimental data, reported by (Rae et al. 2014). This afforded opportunities to compare an inference based on a Bayes factor to an accepted inference in the literature, and also to investigate the Monte-Carlo consistency of our estimates in real data. The inference based on the Bayes factor differed from that drawn by Rae et al.. This is an intriguing result which requires further investigation, both analytically and empirically, in order to establish which approach most suits the scientific interests of the field around these hypotheses. Importantly, the large amount of variability seen within our estimates suggests that a more comprehensive and computationally taxing analysis should be run, involving either a vastly greater number of group and individual level samples, or smarter sampling techniques such as importance sampling. Extensive further investigation will also be required to investigate the properties of all relevant inference methods for the LBA (in this case, Bayes factors and DIC) for robustness against data contamination and outliers.

Another important avenue for future research is the investigation of methods to improve the efficiency of the Monte-Carlo integration. While the GPU approach makes this integration practical in many cases, there will be some cases for which the computation time is prohibitive – for example, when the number of parameters per subject grows large, or the number of subjects is very large. It is also possible that prohibitively many samples are required for numerical stability of the marginal probability estimates when data are particularly noisy, highly contaminated, or just in pathological regions of the model’s parameter space. Approaches such as importance sampling and sequential Monte-Carlo should be investigated as potential solutions to these problems. Nevertheless, we hope that the algorithms and computer code reported here provide a launching point for an important new advance in the way that model-based inference is conducted for the LBA, and potentially other evidence accumulation models in the future.

Description of code

Our CUDA likelihood function and R implementation of the Monte-Carlo integration method are freely available at the listed webpage. It is also important to note that we plan to update this code as we make additional progress, and will continue to make this available, which may result in sections of this description becoming outdated. However, we will try and keep the core of the code as close to the current version as possible, and future developments and changes will always be explained in the respective README.txt files. The current zip file contains eight files: lba-math.cu, hierarchical-BFcode_AUTOMATIC.R, individual-BFcode_AUTOMATIC.R, exampleDataset-hierarchical.Rdata, exampleDataset-individual.Rdata, simulateLBA-hierarchical.R, simulateLBA-individual.R, and README.txt. We would highly recommend any potential user to look through the README.txt file, which contains a lot of important information about using the code, and also make note of the comments within the code, as these will likely prove very useful to any potential user.

The file lba-math.cu contains the CUDA LBA analytic density calculation, and requires no interaction from the user, other than compiling the code (the commands required to do this are listed in the README.txt file). The files with names containing individual refer to the code for analyzing individual subjects, and those which contain the term hierarchical refer to the code for hierarchical analysis. Our focus here will be on the main files that run the Monte-Carlo integration, (BFcode_AUTOMATIC), with the other two files for individual and hierarchical analyses being an example data set (exampleDataset), and some R code to simulate data from the LBA (simulateLBA).

Table 5 describes the different variables within both the individual subjects and hierarchical code, what type they must be, and a brief description of what the variable is for. Additional explanations can be found in both the README.txt file as well as in comments within the BFcode_AUTOMATIC file. Generally, these variables can be grouped into two different classes: those which specify the sampling, and those which specify the model. The sampling specification firstly includes the number of samples used in the Monte-carlo integral (“n.samples”), which is the number of parameter vector samples taken from the joint prior (assuming no co-variance). Importantly, the more samples that are included, the more accurate the estimate of the integral. However, this must be carefully balanced with the amount of time taken, as increasing the samples can rapidly become computationally intractable. For the hierarchical code, both the number of samples from the group level priors, and the number of individual-level samples from each of these group-level samples (“n.phi.samples” and “n.theta.samples”, respectively) must now be specified. The second, and less important sampling specification, is the maximum number of evaluations the GPU can handle at any one time (“maxEvalsAtOnce”), which may need to be tuned to specific GPUs to allow optimal performance, depending on their memory limitations.

Table 5 Displays the variables that are contained within the Monte-Carlo estimator code (BFcode_AUTOMATIC) - both individual and hierarchical - for which user input is needed, what type of input is needed, and a brief description of what the variables are used for
Full size table

The model specification includes all the remaining parameters listed in Table 5, and are explained in detail both within the table and in the README.txt file. Generally speaking, the model specification parameters give three things; which parameters will be set to differ across within-subjects conditions, what the prior distribution mean and standard deviation will be (the code assumes a truncated-normal distribution, and that identical priors will be used for the same parameters across each condition), and the contamination process allowed in the data (if any).

When calculating Bayes factors using our Monte-Carlo integration code, it is very important to specify the data structure correctly; failure to do so will result in either an error, or even worse, the method performing incorrect and potentially misleading analysis. Although this is explained in both comments in the code, and the README.txt file, we will re-iterate it here due to its importance. In the case of the individual subjects code, the name of the .Rdata file containing the data should be placed within the variable datasetToFit. This file should contain a single variable, called “data”, which is a data frame with at least three columns, and a different row for each data point. One of these columns should be called “Time”, and contain the reaction time for each data point in seconds. Another of these columns should be called “Correct”, and contain whether the participant was correct or incorrect on the trial, represented as a 1 or 2, respectively. Lastly, a column should be called “Cond”, and contain the within-subjects condition that the trial was from, with the conditions being integers starting at 1 (e.g. 1, 2, 3, etc.). In the hierarchical case, the variable “data” should be a list, with each element of the list being a different subject, and each list element having the same structure as is required for the individual subjects code.

The output that will be saved from the code is displayed in Table 6. The key part of this output is the variable “log.PdataGivenModel”, which contains the natural logarithm of the marginal probability for the model, log(P(Data|Model)). In order to obtain the natural logarithm of the Bayes factor for any two models, simply subtract the “log.PdataGivenModel” values from one another to get the log Bayes factor in favor of the first model.

Table 6 Displays the variables that are output from the Monte-Carlo estimator code (BFcode_AUTOMATIC) - both individual and hierarchical - which are saved off into a “.Rdata” file, what type of output is to be expected, and a brief description of what the variables contain
Full size table

Lastly, the CUDA code can obviously be used as a replacement density function for other types of LBA analyses. However, as this is not the main focus of this paper, we will not further discuss this in text, and have included the relevant information within Table 7.

Table 7 Important functions and arguments written in C and/or CUDA, of interest only to users who may wish to implement non-standard computations
Full size table