Every school child knows that arithmetic involves facts (e.g., 1 + 2 = 3) and rules (1 × 2 = 2, 0 × 2 = 0), the latter corresponding to elementary algebraic principles. The present research concerned adults’ memory processes underlying instantiation of the multiplicative identity principle (1 × N = N), zero-product principle (0 × N = 0), and the additive identity principle (0 + N = N). Research has consistently indicated that the rule-governed zero and one problems are normally solved by applying the appropriate rule rather than by retrieval of individually stored facts in memory. The research supporting this view includes behavioral (Butterworth, Zorzi, Girelli & Jonkheere, 2001; Campbell & Metcalfe, 2007; LeFevre, Bisanz, Daley, Buffone, Greenham & Sadesky, 1996), imaging (Jost, Beinhoff, Hennighausen & Rösler, 2004), and neuropsychological evidence (Pesenti, Depoorter & Seron, 2000; Sokol, McCloskey, Cohen, & Aliminosa, 1991).

Of central interest here is the phenomenon of retrieval-induced forgetting (RIF) and performance of fact-retrieval based and rule-based arithmetic. Repeated retrieval practice of a memory item can impair retrieval of related, unpracticed items (Anderson, Bjork & Bjork, 1994). RIF is observed in a wide variety of memory domains (e.g., Anderson, 2003; Storm & Levy, 2012) including memory for basic addition facts (Campbell & Thompson, 2012a). The addition RIF research uses a version of the standard RIF retrieval-practice paradigm (Anderson, 2003) in which participants repeatedly practice a set of multiplication problems (e.g., 2 × 5, 3 × 3, etc.) and then are tested on the addition counterparts (i.e., 2 + 5, 3 + 3) and control addition problems. Several experiments have shown that multiplication practice slows response time (RT) or increases errors for the counterpart addition problems (e.g., Campbell, Chen & Maslany, 2013; Campbell & Dowd, 2012; Campbell & Thompson, 2012a). In the RIF literature broadly the effect is usually measured as failures of recall. Applying the term RIF to reduced memory accessibility without memory failure (expressed in longer retrieval times, for example) implies a continuum of RIF that ranges from weakened memory strength or efficiency to more complete forgetting in which the desired memory is inaccessible.

Campbell and Therriault (2013) proposed that the addition RIF effect is potentially diagnostic of specific instances of 0 × N = 0 and 1 × N = N problems stored in memory. RIF is most likely to occur for memory items that are competitors of the target memory (Anderson, 2003; Levy, McVeigh, Marful & Anderson, 2007; Norman, Newman & Detre, 2007; but see Jakab & Raaijmakers, 2009). This competition dependence of RIF (see Storm & Levy, 2012, for a recent review) would explain why Campbell and Thompson (2012a; Campbell et al., 2013) observed RIF of small addition problems with sums ≤10 (e.g., 2 + 4, 3 + 5) following the practice of multiplication counterparts, but larger additions (e.g., 7 + 9, 6 + 8) did not present RIF. This implies competition dependency because small addition facts have high memory strength and would be strong competitors for their multiplication counterparts whereas the relatively weaker memory for large addition facts would not (Campbell & Thompson, 2012a). If RIF of addition is competition dependent, we would not expect RIF for the addition counterparts of the 0 × N = 0 and 1 × N = N problems because answering 0 × N and 1 × N problems by reference to their respective rules would not encounter competition from addition counterparts at the item level. Such item-level competition would occur only when there are fact-based representations for both multiplication and addition counterparts. Campbell and Therriault found the usual RIF effect of multiplication practice on subsequent performance of addition facts with sums ≤10 (e.g., 2 + 3) but practicing 0 × N and 1 × N multiplication problems did not yield RIF of the addition counterpart 0 + N or 1 + N problems. This result reinforces the theory that rule-based and fact-based multiplication are mediated by different types of memory processes and that arithmetic RIF requires item-level retrieval competition.

The present experiment

RIF of addition fact memory from practice of multiplication counterparts is a robust phenomenon, but no research has examined RIF in the other direction; that is, RIF of multiplication by practice of the addition counterparts. The previous research focused on measuring RIF with multiplication practice followed by an addition test because a variety of findings had demonstrated an asymmetry whereby multiplication interfered with addition more than addition interfered with multiplication (Campbell & Arbuthnott, 2010; Miller & Paredes, 1990; Zbrodoff & Logan, 1986). For example, RT costs on answering simple addition and multiplication problems in mixed-operation blocks, relative to single-operation blocks, are greater for addition than for multiplication. These effects are observed in adults’ performance, but Miller and Paredes (1990) proposed that the asymmetry in interference between addition and multiplication is a relic of early learning. Addition is learned before multiplication, and the subsequent learning of multiplication therefore requires suppression of addition. This creates a permanent asymmetry in the extent of mutual retrieval interference between the operations. One purpose of the present research was to determine if this asymmetry extended to the RIF paradigm. In this case, an asymmetrical mixture effect in mixed addition and multiplication blocks could arise, in part, from asymmetrical RIF.

The other purpose was to complete the taxonomy of practice-test combinations of fact-based and rule-based addition and multiplication counterpart problems using the RIF paradigm. Table 1 presents this taxonomy and also the predictions for RIF based on the assumption that RIF will only occur when both the practiced items and test items are answered by retrieval of individual facts and the test item is a strong competitive memory for the target item (Campbell & Therriault, 2013). When multiplication was practiced followed by an addition test, we expected to replicate Campbell and Therriault. Specifically, RIF will only occur when both practice and test conditions are fact based and not when either is rule based. By extension, we expected the same pattern when addition was practiced followed by a multiplication test, unless the previously discussed asymmetry in inter-operation interference favoring multiplication is so complete that no RIF is observed in any multiplication test condition.

Table 1 Predictions for RIF of arithmetic problems following practice of operation counterparts
Full size table

The design of the experiment also afforded measurement of generalization of practice across different problems within operations. Because procedures are assumed to be algorithms applicable to any appropriate problem, improving the efficiency of the procedure through practice of one set of problems should generalize to other problems (Singley & Anderson, 1989). Consequently, generalization effects provide a converging diagnostic test for procedure-based versus fact-retrieval based arithmetic. Campbell and Beech (2014) examined simple addition for evidence of generalization for fact-based additions and also addition with zero, which is governed by the additive identity rule (e.g., 0 + 8 = 8). The procedure-based 0 + N = N problems presented evidence of generalization (i.e., practicing a subset of 0 + N problems facilitated a different subset of 0 + N problems), but there was no evidence of such generalization for the non-zero problems (see also Campbell & Therriault, 2013). The present experiment afforded the first examination of generalization of practice for all three rule-governed problem types of addition and multiplication (i.e., 0 + N = N, 1 × N = N, and 0 × N = 0).

Method

Participants

Seventy-two volunteers participated for bonus marks in their introductory psychology course at the University of Saskatchewan. None had participated in previous arithmetic RIF studies. Alternating participants were assigned to the addition practice/multiplication test or multiplication practice/addition test groups. In the former group, there were 23 women and 13 men, aged 17–26 years (M =19.5), of whom 34 were right-handed and two were left-handed. Twenty-eight reported English as their first language for arithmetic, three reported Spanish, and one each reported Chinese, Cantonese, Mandarin, Turkish, and Tagalog. For the latter group, there were 26 women and ten men, aged 16–28 years (M =18.9), all right-handed. Thirty-four reported English as their first language for arithmetic and one each reported Chinese and Korean. All participants answered the arithmetic problems in English.

Apparatus

Stimuli were presented on two CRT monitors using Eprime 2.0 (Psychology Software Tools, Pittsburgh, PA, USA) with one monitor viewed by the participant and the other by the experimenter. The participant sat about 50 cm from the monitor and held a microphone connected to the computer through Eprime’s SRbox. Detection of the participant’s verbal response by the microphone provided response time accuracy to within ±1 ms.

Stimuli and design

The stimuli and design were identical to Campbell and Therriault (2013) and the group that had multiplication practice followed by addition test constituted a replication of that study. For the other group, the experiment was the same except that they received addition practice followed by multiplication test. Stimuli appeared in black Courier New 14 font on a white background. Problems occupied five horizontal character spaces and appeared with the smaller operand on the left (e.g., 0 + 2). Addition and multiplication problems were created from the 32 pairs of single-digit numbers that sum to ten or less, excluding pairs comprised of only 0 and/or 1. Sixteen pairs corresponded to rule-related problems and 16 corresponded to fact-based problems. The rule-related pairs were divided into two sets of eight (03 04 05 08 12 16 17 19 and 02 06 07 09 13 14 15 18). Each set contained four 0-related and four 1-related pairs, with 0 and 1 each combined with two odd and two even numbers in the range 2–9. Note that the 0 + N = N, 0 × N = 0, and 1 × N = N problems are rule governed, but the 1 + N = ? problems are not because their solution does not correspond to one of the presented operands. They may be considered rule-related, however, because Campbell and Metcalfe (2007) found rule intrusions to be the most common error type for these items (i.e., 1 + N = N). The fact-based pairs were also divided into two sets of eight (24 25 27 28 33 34 46 55 and 22 23 26 35 36 37 44 45). Each set included two “tie” pairs (e.g., 33, 44).

A rule-related and fact-based set were combined to make the practice set of 16 pairs and the other two sets were combined for the unpracticed set. The four combinations of rule-related and fact-based sets for the practice phase were counterbalanced over four consecutive participants within each group. In the practice phase, participants received four blocks of the practice set of 16 problems (either multiplication or addition). For the test phase, participants received two blocks of 32 problems in the other, unpracticed operation. Following Campbell and Therriault (2013), no operation sign was presented during the test phase so that the problem stimulus did not explicitly identify the required operation. This might increase the opportunity to observe RIF from practice of the competing operation. The order of problems in both the practice and test phases was independently randomized for each participant.

Procedure

The 30-min experiment took place in a quiet testing room with an experimenter present. Prior to the arithmetic task, microphone sensitivity was tested by asking participants to quickly name eight single letters a though h presented sequentially at the centre of the screen in random order in Courier New 14 font. The arithmetic practice phase comprised four blocks of 16 trials. Participants were asked to state the correct answer aloud for each problem with an emphasis on accuracy. The test phase consisted of two blocks of 32 problems in the unpracticed operation, including both the operation-counterpart practiced and unpracticed sets. Participants were instructed to state the sum or product of the digit pair that appeared on each trial as quickly as possible.

Each trial began with a central fixation dot for 1 s followed by the problem centered at fixation. Response timing began when the problem appeared and continued until the participant’s verbal response stopped the timer. When the response was detected, the problem immediately disappeared from the screen. This allowed the experimenter to identify failures of the microphone to detect response onset and flag those RTs for exclusion. The experimenter entered the participant’s answer and then the fixation dot appeared to signal the beginning of the next trial. No feedback regarding speed or accuracy was provided during either the practice or test phase.

Results

ANOVA tests had F(1,70) degrees of freedom unless otherwise indicated. We analyzed median RT owing to the relatively small number of observations per cell (Miller, 1988).

Practice phase

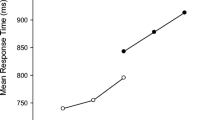
A total of 15 practice RTs (0.7 %) were marked for exclusion by the experimenter. The error rate during multiplication practice was 0.7 % with a total of 15 errors, too few for a systematic analysis. Median RT for correct responses received an Operation (addition vs. multiplication) × Problem type (fact based vs. rule related) × Block (1 and 2 vs. 3 and 4) ANOVA with operation as a between-participants factor and problem type and block as repeated measures. The corresponding means appear in Fig. 1 with 95 % repeated-measures confidence intervals based on the MSE for the three-way interaction (Jarmasz & Hollands, 2009; Masson & Loftus, 2003).Footnote 1

Fig. 1
figure 1

Mean multiplication and addition response time during the practice phase. Facts = fact-based problems. Rule-related = both 0 × N and 1 × N for multiplication and both 0 + N and 1 + N for addition. Error bars are 95 % repeated-measures confidence intervals based on the MSE for the Operation × Problem type × Block interaction

Full size image

Overall, mean median addition RT (666 ms) was faster than multiplication RT (736 ms) [F =5.42, p = .023, MSE =66033.28, \( {\upeta}_{\mathrm{p}}^2 \) = .072]. All other main and interaction effects were also significant with p ≤ .002. As the pattern of differences is apparent from the means and confidence intervals in Fig. 1 we do not report all the ANOVA tests in detail [F =9.98, p = .002, MSE =1086.08, \( {\upeta}_{\mathrm{p}}^2 \) = .125 for the three-way interaction]. As Campbell and Therriault (2013) observed, rule-related problems (649 ms) were answered more quickly than fact-based problems (753 ms) and participants responded more quickly later in practice (673 ms) than earlier in practice (729 ms). As Fig. 1 shows, the amount of speed-up was approximately proportional to the mean RT early in practice (i.e., Blocks 1 and 2). Proportional speed-up would occur primarily because the faster problem types were closer to their speed-up asymptote from the outset of the experiment, which would limit their RT gains from practice. The fact-based multiplication problems were clearly the slowest problem type early in practice, and sped up the most; consequently, proportional speed-up produced the three-way interaction shown in Fig. 1.

Median RT for the 0 and 1 problems received a separate Operation × Problem type (0 vs. 1) × Blocks (1 and 2 vs. 3 and 4) ANOVA (see Fig. 2 for the corresponding means and 95 % confidence intervals based on the MSE for the three-way interaction). Again, as the pattern of differences is apparent from the means and confidence intervals we do not report all the ANOVA tests in detail [F =8.44, p = .005, MSE =1226.23, \( {\upeta}_{\mathrm{p}}^2 \) = .11 for the three-way interaction]. For addition, the rule-based 0 + N problems were answered more quickly (587 ms) than the 1 + N problems (682 ms), which were more similar in mean response time to the other fact-based addition problems (700 ms). For multiplication, the mean RT for 0 × N problems was 49 ms slower than 1 × N in Block 1, but this difference was largely eliminated in Block 2. The greater speed-up for 0 × N compared to the other three rule-related problem types produced the three-way interaction. The relatively small amount of speed-up for 1 + N problems, despite being the slowest of the rule-related problem types overall, appears to violate the general observation that speed-up was proportional to mean RT early in practice. As we show in the subsequent test phase analyses, however, among the rule-related problems only the 1 + N problems did not benefit from generalization of practice across different instances (i.e., practicing 0 + 3 benefited subsequent performance of 0 + 5, but practicing 1 + 3 did not facilitate subsequent performance of 1 + 5) (see also Campbell & Beech, 2014). This absence of generalization would limit speed-up for the 1 + N problems.

Fig. 2
figure 2

Mean multiplication and addition response time for 0 and 1 problems during the practice phase. Error bars are 95 % repeated-measures confidence intervals based on the MSE for the Operation × Problem type × Block interaction

Full size image

Test phase

A total of 119 test phase RTs (5.2 %) were marked as spoiled by the experimenter. There were 43 errors committed on fact-based problems (3.7 % of trials) and 21 errors on the rule-related problems (0.9 % of trials), too few for a meaningful factorial analysis. Twenty of the 21 rule-related errors were consistent with rule confusions or intrusions (e.g., 0 × N = N, 1 + N = N). Median RT for correct answers received an Operation (multiplication vs. addition) × Problem type (rule-related vs. facts) × Practice Set (operation-counterpart practiced vs. unpracticed) × Block (1 vs. 2) mixed-factor ANOVA. The corresponding mean RTs appear in Fig. 3. Error bars are 95 % repeated-measures confidence intervals based the MSE for the Problem type × Practice Set × Block interaction.

Fig. 3
figure 3

Mean multiplication and addition response time during the test phase. Facts = fact-based problems. Rule-related = both 0 × N and 1 × N for multiplication and both 0 + N and 1 + N for addition. Error bars are 95 % repeated-measures confidence intervals based on the MSE for the Problem type × Practice Set × Block interaction

Full size image

Fact-based problems had a slower mean RT (855 ms) than rule-related problems (688 ms) [F =174.87, p < .001, MSE =22952.79, \( {\upeta}_{\mathrm{p}}^2 \) = .71] and RT sped up from Block 1 (810 ms) to Block 2 (734 ms) [F =98.94, p < .001, MSE =8461.00, \( {\upeta}_{\mathrm{p}}^2 \) = .59]. As Fig. 3 shows, the amount of speed-up across blocks was approximately proportional to Block 1 RT, which produced an Operation × Problem type × Block interaction [F =7.64, p = .007, MSE =4142.79, \( {\upeta}_{\mathrm{p}}^2 \) = .10]. With respect to RIF, problems whose other-operation counterpart had been practiced were answered slower on average (785 ms) than counterpart-unpracticed problems (758 ms) [F =13.86, p < .001, MSE =7349.17, \( {\upeta}_{\mathrm{p}}^2 \) = .17], but this overall RIF effect was greater for fact-based problems [46 ms, t(71) =4.08, p = .0001, SE =11.31] than rule-related problems [7 ms, t(71) =0.97, p = .334, SE =7.19] [F =9.90, p = .002, MSE =5585.53, \( {\upeta}_{\mathrm{p}}^2 \) = .12 for the Problem type × Practice Set interaction].Footnote 2 There was no evidence that this effect differed between operations (p = .97 for the Operation × Problem type × Practice Set interaction and p = .79 for the four-way interaction).

Nonetheless, because the finding of RIF of fact-based multiplication problems by practice of their addition counterparts is a new finding, it is important to confirm this effect separately. The observed RIF for fact-based multiplication was 74 ms in Block 1[t(35) =2.81, p = .008, SE =26.18] and 37 ms in Block 2 [t(35) =2.38, p = .02, SE =15.48]. A relatively conservative BIC-based Bayesian hypothesis test (Campbell & Thompson, 2012b; Masson, 2011) of the overall 55 ms RIF effect (SE =16.79) for fact-based multiplication yielded a Bayes Factor of .047, indicating that the data provided strong evidence for the effect. Thus, the RIF effect for fact-based multiplication was robust and Fig. 2 shows the effect was at least as large as the well established RIF effect observed for addition here (49 ms and 25 ms in Blocks 1 and 2, respectively) and in several previous experiments (e.g., Campbell & Therriault, 2013; Campbell & Thompson, 2012a).

To directly compare the 0 and 1 rule-related problems, median RT for the rule-related problems received an Operation (multiplication vs. addition) × Problem type (0 vs. 1) × Practice Set (operation-counterpart practiced vs. unpracticed) × Block (1 vs. 2) ANOVA. Means for the 0 and 1 rule-related problems appear in Fig. 4 with 95 % repeated measures confidence intervals based on the MSE for the Problem Type × Practice Set × Block interaction. Although participants’ median RTs for this analysis were based on only four trials per cell, the very low variability for these problems, together with relatively large samples, provided very good precision of measurement.

Fig. 4
figure 4

Mean multiplication and addition response time for 0 and 1 problems during the test phase. Error bars are 95 % repeated-measures confidence intervals based on the MSE for the Problem type × Practice Set × Block interaction

Full size image

As would be expected given the results of the preceding analysis, there was a main effect of block in which Block 2 had faster mean RT (660 ms) than Block 1 (716 ms) [F =44.05, p < .001, MSE =10285.69, \( {\upeta}_{\mathrm{p}}^2 \) = .39]. Zero-problems had a faster mean RT (671 ms) than 1-problems (707 ms) [F =21.07, p < .001, MSE =8625.56, \( {\upeta}_{\mathrm{p}}^2 \) = .23], but an Operation × Problem type interaction occurred [F =53.10, p < .001, MSE =8625.56, \( {\upeta}_{\mathrm{p}}^2 \) = .43] because multiplication problems were faster for 1-times problems than 0-times problems (21 ms), whereas addition problems were substantially slower for 1-plus problems than 0-plus problems (−92 ms) (see also Campbell & Therriault, 2013). The Problem type × Practice Set interaction [F =4.52, p = .04, MSE =4926.60, \( {\upeta}_{\mathrm{p}}^2 \) = .06] reflected a RIF effect for 1-problems [21 ms, t(71) =2.16, p = .03, SE =9.83] but not for 0-problems (-4 ms). As Fig. 4 shows, however, the RIF effect for 1-problems originated entirely with the 1 × N multiplication condition. Specifically, 1 × N problems presented a 37-ms RIF effect [t(35) =2.88, p = .007, SE =12.7, η2 = .19], whereas 1 + N presented a non-significant 6-ms difference [t(35) =0.39, p = .70, SE =13.9, η2 = .004].

As the RIF effect for 1 × N is a new finding we conducted a separate test of rule-based multiplication problems, which confirmed a Problem type (0 × N vs. 1 × N) × Practice Set interaction owing to RIF for 1 × N but not 0 × N [F(1, 35) =4.33, p = .05, MSE =6627.05, \( {\upeta}_{\mathrm{p}}^2 \) = .11]. The RIF effect for 1 × N was significant both in Block 1 [43 ms, t(35) =2.65, p = .01, SE =16.3, η2 = .17] and Block 2 [30 ms, t(35) =2.06, p = .05, SE =14.6, η2 = .11]. A BIC-based Bayesian hypothesis test of the overall 37 ms RIF effect (SE =12.69) for 1 × N problems yielded a Bayes Factor of .129, which indicates that the data provided substantial evidence for the effect. Thus, the identity rule for multiplication proved to be the RIF exception among the rule-related addition and multiplication problems. Before considering possible explanations for this finding it is important to examine generalization effects for the rule-related problems in the test phase. Generalization (i.e., positive transfer of practice across different items) is expected for rule-based but not fact-based processing.

Generalization of practice

The following analysis examined generalization of practice for the rule-related problems by comparing RT for the first four instances versus the second four different instances of each problem type within the first test block. We conducted this sub-block analysis on the test phase data, rather than the practice phase data, because the test phase data allow us to examine generalization effects in the same trials analyzed for RIF effects. Additionally, at the beginning of the practice phase, participants might show a general speed-up across all problems types as they gain confidence in their ability to respond very quickly but accurately (Pirolli & Anderson, 1985). We expect generalization of practice (i.e., speed-up across sub-blocks) for problems that are solved using a common procedure whereas performance based on retrieval of individual facts should not display generalization. We used the nominally rule-related (but not rule-based) 1 + N problems to represent individual-fact problems because they were similar in mean RT to the other 0 and 1 problems and therefore would provide a similar opportunity for speed-up owing to generalization. Previously, both Campbell and Beech (2014) and Campbell and Therriault (2013) found no generalization of practice among 1 + N problems, suggesting that they were retrieved as individuals facts.

Figure 5 presents mean median RT by operation (multiplication vs. addition), problem Type (0 vs. 1) and sub-block (1 vs. 2). The corresponding ANOVA indicated a three-way interaction [F =6.98, p = .01, MSE =4434.88, \( {\upeta}_{\mathrm{p}}^2 \) = .09]. As Fig. 5 shows, this occurred because both rule-based multiplication problem types (0 × N and 1 × N) and the rule-based 0 + N additions showed robust speed-up across sub-blocks, but the non-rule-based 1 + N addition problems did not. Specifically, mean speed-up across sub-blocks was 69 ms for 0 × N [t(35) =4.2, p < .001, SE =16.6], 62 ms for 1 × N [t(35) =3.5, p = .001, SE =17.9], 102 ms for 0 + N [t(35) =5.49, p < .001, SE =18.6], whereas 1 + N problems presented a non-significant 12-ms difference between sub-blocks [t(35) =0.67, p = .51, SE =18.1].

Fig. 5
figure 5

Mean multiplication and addition response time during Block 1 of the test phase by sub-blocks for the rule-related problems sets. Error bars are 95 % repeated-measures confidence intervals based on the MSE for the Operation × Problem type × Sub-block interaction

Full size image

Perhaps some part of the speed-up across sub-blocks for 0 + N, 0 × N and 1 × N problems in Fig. 5 reflected recovery from interference owing to counterpart practice during the practice phase. The same pattern of results held, however, when only the counterpart-unpracticed items were included in the analysis [F(1, 63) =8.18, p = .006, MSE =150150.15, \( {\upeta}_{\mathrm{p}}^2 \) = .12 for the three-way interaction.Footnote 3 For the counterpart-unpracticed problems, mean speed-up across sub-blocks was 70 ms for 0 × N [t(34) =2.82, p = .008, SE =24.7], 68 ms for 1 × N [t(32) =2.98, p = .005, SE =22.7], 183 ms for 0 + N [t(32) =4.29, p < .001, SE =42.7], and the 1 + N problem were 3 ms slower on average in the second sub-block. As these items were the control condition for which operation-counterparts were not practiced, the speed-up across sub-blocks for these rule-governed problems cannot reflect recovery from item-specific interference created during the practice phase. These results confirm generalization for 0 + N but not 1 + N (see also Campbell & Beech, 2014; Campbell & Therriault, 2013) and extend the evidence for procedure-based generalization to the identity rules of multiplication. The corresponding analysis of the other fact-based problems indicated no generalization (i.e., speed-up across sub-blocks in Block 1) for either fact-based addition [mean slowing of –13 ms, t(35) = −0.53, p = .60, SE =23.8] or multiplication [4 ms, t(35) =0.14, p = .89, SE =26.2].

Discussion

Campbell and Thompson (2012a; Campbell & Dowd, 2012; Campbell & Therriault, 2013) proposed that item-specific RIF of arithmetic facts is competition dependent and reflects active inhibition of the competitor item below pre-RIF baseline rather than, for example, retrieval blocking by strengthened cue-target associations. There is also support for the competitor-inhibition theory in the general RIF literature (Storm & Levy, 2012). The present RIF findings for 1 × N problems, however, cannot be explained by item-level competitor inhibition. The generalization results for 1 × N indicated that participants retrieved an item-general procedure used for all 1 × N instances. This implies that there would not be item-specific representations of distinct instances of the rule (such as 1 × 2 = 2, 1 × 4 = 4, etc.) stored in long-term memory. Answering 1 + N problems during the practice phase therefore would not encounter competition from individual 1 × N counterparts. Therefore, the item-specific RIF for 1 × N occurred in the absence of item-level competition. Furthermore, inhibitory RIF is assumed to be recruited specifically in response to item-level competition (Anderson, 2003; Storm & Levy, 2012); thus, the inhibition theory of RIF would not predict RIF for the 1 × N problems. Consequently, the item-specific RIF for 1 × N must reflect item-specific interference rather than competition-based inhibition. We propose that the practiced 1 + N items (e.g., 1 + 3 = 4, 1 + 5 = 6, 1 + 6 = 7) were individually strengthened during the practice phase and were readily reactivated by the 1 × N counterpart stimuli (e.g., 1 × 3, 1 × 5, 1 × 6) during the test phase. This cue-based interference blocked initiation of the item-general procedure required for the counterpart problems, producing item-specific RIF for 1 × N = N problems. Such interference would not occur in the reverse direction (i.e., RIF of 1 + N) because practicing the procedure for 1 × N problems specifically strengthened execution of the item-general procedure rather than strengthen item-specific associations.

The RIF observed for 1 × N problems is evidence that item-specific RIF does not necessarily require competition at the item level or item-level inhibition. Does this imply that the RIF observed for non-rule-based problems here, and in numerous previous experiments, also could be due to blocking or interference rather than competitor-dependent inhibition? We think it would be premature to draw this conclusion. Campbell and Thompson (2012a; Campbell et al., 2013) found RIF of small addition problems with sums ≤10 (e.g., 2 + 3, 3 + 4) following practice of multiplication counterparts, whereas larger additions (e.g., 7 + 8, 6 + 7) did not present RIF. Small arithmetic problems usually have much greater memory strength compared to the larger problems. This suggests competition dependency of the effect because small addition problems would be strong competitors for their multiplication counterparts whereas the large addition problems would not. Furthermore, Campbell and Thompson (see also Campbell & Phenix, 2009; Maslany & Campbell, 2013; but see Galfano et al., 2011) showed that the effect, at least for non-ruled-based problems, occurs only following retrieval practice of multiplication facts (repeatedly answering 4 × 6 = ?) and not following study practice (reading equations silently and stating the answer; e.g., 4 × 6 = 24). The retrieval dependency of RIF supports an inhibitory model of the effect over a model based only on cue-related retrieval interference (Anderson, 2003; Storm & Levy, 2012). Nonetheless, the item-specific RIF observed for 1 × N rule-based problems provides an existence proof that the effect can occur in the absence of item-level competition.

The experiment also demonstrated robust RIF of small fact-based multiplications, and the effect was as large as the RIF effect observed for small fact-based additions (Fig. 2). This confirms that the effect exists for both addition and multiplication fact retrieval and that retrieval-induced interference between the operations is approximately symmetrical. Previous research using several different paradigms has found an asymmetry in interference between addition and multiplication whereby multiplication interferes more with addition than vice versa (see Campbell & Arbuthnott, 2010, for a review). The present results imply that the asymmetrical interference observed in previous research does not arise from asymmetrical RIF; but why would RIF of addition and multiplication not present the asymmetry demonstrated in other interference paradigms? One consideration is that the asymmetrical effects emerged from paradigms that required participants to select or discriminate between the two operations on each trial (e.g., asymmetrical mixing costs in mixed vs. single-operation blocks; asymmetrical operation switch costs in mixed trials; asymmetrical slowing of verification stimuli with the cross-operation answer). The RIF paradigm used here, however, did not require this type of explicit trial by trial discrimination of the operations, but rather involved blocks of one operation (practice phase) followed by a global switch to the other operation (test phase), which may have avoided asymmetrical interference effects. Our results suggest therefore that asymmetrical interference is not inherent in retrieval from addition and multiplication memory but emerges when task demands require trial by trial operation switching or discrimination.

Finally, the experiment demonstrated for the first time that generalization of practice occurs for items governed by the multiplicative identity principle (1 × N = N) and zero-product principle (0 × N = 0), and also replicated the finding of generalization of practice across different instances of the rule-based 0 + N problems, but not fact-based 1 + N problems (Campbell & Beech, 2014).The generalization effects observed selectively for the rule-governed problems strongly supports the hypothesis that these problems were answered by reference to algebraic principles each implemented as a procedure that was shared across items. Conversely, the absence of generalization of practice for 1 + N problems argues against the possibility that these items were solved in the present experiment by a common shared procedure. Recently, researchers have proposed that simple addition problems may be solved by automatic counting algorithms, at least in expert performers (Barrouillet & Thevenot, 2013; Campbell, Chen & Maslany, 2013; Fayol & Thevenot, 2012). The absence of generalization for non-zero additions (see also Campbell & Beech, 2014; Campbell & Therriault, 2013), especially its absence for 1 + N, single-increment problems that might be likely candidates for automatic counting, suggests that development of automated procedures for simple addition is not the norm. Instead, development of skilled simple addition generally proceeds from counting-based skills to direct memory retrieval, as a variety of previous research has proposed (e.g., Ashcraft & Guillaume, 2009; Barrouillet & Fayol, 1998; Shrager & Siegler, 1998).

Conclusions

By including all practice-test combinations of fact-based and rule-based counterpart conditions (Table 1) the experiment filled all the conditions to complete the basic picture for inter-operation RIF in simple addition and multiplication, at least for the population sampled. The results indicated that memory for simple fact-based addition and multiplication was similarly susceptible to item-specific inter-operation RIF. Practicing a procedure does not produce RIF of cross-operation counterpart problems, but the results showed that an item-general process (i.e., the procedure for answering 1 × N = N problems) can be subject to item-specific interference from practice of counterpart fact-based problems (i.e., the 1 + N = ? problems). The item-specific RIF for 1 × N must reflect item-specific interference rather than item-level competitor inhibition given that there is no item-level representation of 1 × N = N facts in long-term memory. To our knowledge, there is no well developed theory or computer model of cognitive arithmetic (e.g., Campbell, 1995; Lebiere & Anderson, 1998; Siegler & Shrager, 1984; Verguts & Fias, 2005) that predicts or explains any of the RIF findings observed in the present research. These RIF phenomena of arithmetic memory represent an important empirical benchmark for future theory development in cognitive arithmetic.