1 Introduction

After liberalization of the electric power industry and launching of competitive electric markets, precise short-term load forecasting (STLF) has become much more important for both electricity system operators and market participants. Considering the fact that electricity load always suffers from various unstable factors, including weather conditions, social activities, and dynamic electricity prices, the load series often shows highly nonlinear and nonstationary characteristics that make forecasting very difficult. Inaccurate load forecasting may increase operating costs (Bunn, 2000). On the contrary, with an accurate electric load forecasting method, essential operating functions such as unit commitment, reliability analysis, and unit maintenance can be operated more effectively (Senjyu et al., 2005). Thus, developing a method to improve the accuracy of electric load forecasting is essential.

The STLF method can be broadly divided into two categories: traditional approaches and modern intelligent approaches. The traditional approaches are mainly time series analysis methods based on mathematical statistics, such as regression analysis approach (Goia et al., 2010), Kalman filtering approach (Trudnowski et al., 2001), Box-Jenkins’ autoregressive integrated moving average (ARIMA) approach (Wang and Schulz, 2006), exponential smoothing (Wu et al., 2013), and so on. Although these methods have the advantage of a simple algorithm, they are not suitable for forecasting the nonlinear and nonstationary electric load series, because they are based on linear analysis. Modern intelligent approaches such as expert system approach (Rahman and Bhatnagar, 1988), fuzzy logic-based approach (Che et al., 2012), and artificial neural networks (Hernandez et al., 2013) can improve the performance of electric load forecasting efficiently. However, these methods cannot yield the desired accuracy in all forecasting problems. Just as Chatfield (1988) and Jenkins (1982) concluded, there is no single best prediction method that can be applied to any specific situation. As a result, many combination short-term forecasting methods that combine two or more models are proposed to enhance the performance and eliminate the limitations of existing individual models (Xiong et al., 2014; Chen et al., 2015; Liu et al., 2015; Sudheer and Suseelatha, 2015; Yang et al., 2015). Among these, hybrid models that integrate empirical mode decomposition (EMD) with other techniques have been widely used for STLF because the former considers the inherent characteristics of the data. Liu et al. (2015) combined EMD with an improved recursive autoregressive integrated moving average model to the forecast of short-term wind speed. Yang et al. (2015) used EMD to decompose a rotor’s nonlinear response into a series of intrinsic mode functions (IMFs) and further predicted the nonlinear response of a cracked rotor by adding all the prediction results obtained based on the maximal local Lyapunov exponent. However, Guo et al. (2012) and Huang et al. (2014) pointed out that the forecasting accuracy of the classical EMD-based hybrid model will be decreased without the denoising process because the electric load series have certain random volatility, which would introduce noises. To solve this problem, Guo et al. (2012) and Huang et al. (2014) removed the high frequency (namely IMF1) obtained through EMD, which is regarded as noise, and predicted each remaining component respectively to achieve the final forecasting results. However, the IMF1 obtained in traditional EMD is always a mixture of the real intrinsic mode and noise under the influence of the mode mixing problem; thus, removing it directly would result in the loss of useful information, which will lead to the decrease of forecasting accuracy.

To alleviate the mode mixing problem of EMD, the ensemble empirical mode decomposition (EEMD) was presented by Wu and Huang (2009) recently. EEMD is a noise-assisted data analysis method that has been widely applied in many areas, such as forecasting (Wang et al., 2015), fault diagnosis (Yang and Wu, 2015), and signal denoising (Mariyappa et al., 2015). However, in the EEMD process, the two ends of the signals disperse, which is termed as the end effect, and this would “empoison” the whole time series, gradually causing distortion in the results. As a result, severe distortion would occur on the two sides of the predicted electric load series, which render the predicted results unreliable. To eliminate the end-effect problem in the traditional EEMD, an improved EEMD (IEEMD) is proposed in this study based on the degree of wave similarity.

Considering the simplicity and the ability to extract useful information from samples of back propagation neural networks (BPNNs), which are successfully used in forecasting applications, such as forecasting time series (Wang et al., 2015), electric load (Wang et al., 2014), and traffic flow (Li et al., 2013), a hybrid STLF model that integrates IEEMD with BPNN is proposed in this study. In the hybrid model, the original load data are first decomposed into a finite and often small number of stationary IMFs and a residual using the IEEMD to reduce its instability. Next, the high frequency (namely IMF1) obtained through IEEMD, which is the major source of noise and has little contribution to model fitting, is removed for denoising. Then, the remaining IMFs and residual are forecast by BPNN. Finally, the electric load is forecast by combining the predicted values of each subseries through BPNN.

In this paper, the fundamental principles of IEEMD and BPNN are illustrated first, and a hybrid STLF model for an electricity system is constructed based on the IEEMD and BPNN, then experiments are carried out to evaluate our forecasting model and the experimental results are discussed.

2 Analyzing techniques

2.1 IEEMD

EMD is a direct, a posteriori, and self-adaptive method for signal decomposition, first proposed by Huang et al. (1998). It is developed from the simple assumption that any signal consists of different simple intrinsic modes of oscillations. Any signal can be decomposed into a finite number of IMFs, each of which must satisfy the following definition: (1) in the whole data set, the number of extrema and the number of zero-crossings must either be equal or differ at the most by one; (2) at any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero. After EMD decomposition, the original signal x(t) can be represented as

$$x(t) = \sum\limits_{i = 1}^n {{c_i}} (t) + {r_n}(t){.}$$
(1)

Thus, we can achieve a decomposition of the signal into IMFs c1(t), c2(t), …, c n (t), and a residual r n (t), which is the mean trend of x(t). However, there are still limitations in this algorithm. One of the most crucial problems is mode mixing. Mode mixing is the phenomenon of disparate frequencies existing in a single IMF. The occurrence of mode mixing is mostly caused by signal intermittency and may be interpreted incorrectly as a different physical meaning represented by this mode.

To alleviate the problem of mode mixing inherent in the use of EMD, Wu and Huang (2009) proposed an effective EEMD method. The principle of EEMD is simple: adding white noise to the data, which becomes distributed uniformly in the whole time-frequency space; the bits of signals of different scales can be automatically designed onto proper scales of reference established by the white noise. The procedures of EEMD are as follows:

  1. 1.

    Add a random white noise signal n j (t) to x(t):

    $${x_j}(t) = x(t) + {n_j}(t),$$
    (2)

    where x j (t) is the noise-added signal, j=1, 2, …, M, and M is the number of trials.

  2. 2.

    Decompose x j (t) into a series of IMFs c i,j utilizing EMD as follows:

    $${x_j}(t) = \sum\limits_{i = 1}^{{N_j}} {{c_{i,j}}} (t) + {r_{{n_j}}}(t),$$
    (3)

    where c i,j denotes the ith IMF of the jth trial, \({r_{{n_j}}}\) denotes the residue of the jth trial, and N j is the number of IMFs of the jth trial.

  3. 3.

    If j<M, then repeat steps 1 and 2, and add different random white noise signals each time.

  4. 4.

    Obtain I=min(N1, N2, …, N M ) and calculate the ensemble means of corresponding IMFs of the decompositions as the final result:

    $${c_i} = \left({\sum\limits_{j = 1}^M {{c_{i,j}}} } \right)\Bigg/M,$$
    (4)

    where c i (i=1, 2, …, I) is the ensemble mean of the corresponding IMF of the decompositions.

EEMD is a fully data-adaptive method, which provides an efficient analysis method for nonstationary and nonlinear signals. However, the two ends of the signals become dispersed while the series is decomposed by the EEMD, and this dispersion, termed as the end effect, would “empoison” the whole time series, gradually causing distortion in the results. To restrain the end effect in traditional EEMD, an IEEMD is proposed to restrain the end-effect issue, and the process is detailed as follows:

  1. 1.

    Take the left end processing procedure for instance. The left end point (t0) of the original signal is set as the starting point of the wave (ω) to be matched. Then, the n pieces of data t1 after t0 are set as the terminal point of ω. In this study, \(n = {{1440} \over T}\) is used, where T (min) is the sampled time.

  2. 2.

    According to Eq. (5), the degree (ρ) of wave similarity between ω and all the sub waves (ω i ) in the original signal are calculated and compared to achieve the most similar sub wave (ωmatch) that has the biggest ρ.

    $$\rho (\omega, {\omega _i}) = {{{\rm{cov}}(\omega, {\omega _i})} \over {\sqrt {\sigma (\omega)\sigma ({\omega _i})} }},$$
    (5)

    where cov(ω, ω i ) is the covariance of the two waves, and σ(ω) and σ(ω i ) are the variances of ω and ω i , respectively.

  3. 3.

    According to Eq. (6), the data correlation between ω and ωmatch is calculated through the linear regression method.

    $$Y = a + bX,$$
    (6)

    where X and Y are the amplitude vectors of ω and ωmatch, respectively, and a and b are the correlation coefficients.

  4. 4.

    The left end point (t′0) of ωmatch is set as the starting point of the wave (ωmatch-left) used for extension, and then, the n pieces of data t′1 after t′0 are set as the terminal point of ωmatch-left.

  5. 5.

    The left end of the signal is extended with a wave (ωextension), which can be calculated according to Eq. (7). Then, the right end of the signal is extended in the same way.

    $${\omega _{{\rm{extension}}}} = {{{\omega _{{\rm{match}} - {\rm{left}}}} - b} \over a}{.}$$
    (7)
  6. 6.

    The EEMD method is applied for decomposing the signal after extension. After decomposition, the extended data on both sides of the obtained IMFs and residual are removed. The remaining data section of the IMFs and residual are the decomposition results of the original data set obtained through the IEEMD.

2.2 BPNN

The BPNN is one of the most widely used artificial neural networks and it has infinite potential in the load forecasting area due to its strong nonlinear processing ability and approaching capability. A typical BPNN is a multilevel hierarchical feedback structure, which is used to adjust the network weights through the back propagation algorithm, including input layer, hidden layer, and output layer. There are full internet connections between the upper and lower layer, and no connections among neurons in the same layer. Connection weights of each layer can be adjusted by learning. When the network obtains a learning sample, neural activation values are transmitted from the input layer to the output layer through the hidden layer, and the input response of the network is received in the output layer. If the output value cannot be as desired, an error signal should return along the original connection path in the back propagation process. The error of the output layer node should transmit reversely to the input layer to adjust the connection weights and thresholds to adapt the requirements of mapping. The model structure of BPNN is given in Fig. 1.

Fig. 1
figure 1

Structural diagram of BPNN

Full size image

3 A Hybrid STLF model

To reduce the instability of the original load series, IEEMD is used to decompose the original load series into a finite and often small number of IMFs and one residual. Then these components are forecast by BPNN respectively, such that the tendencies of these components can be predicted. Finally, aggregation of the prediction results of all components through BPNN produces the final forecasting result for the original electric load series (this model can be denoted by IEEMD-BPNN).

Our studies showed that the high frequency (namely IMF1) of IEEMD results is always so small that it has little contribution to model fitting, while it sometimes proves to be a great disturbance for the forecasting precision of an electric load. The reason is that after IEEMD decomposition, the real intrinsic mode and noise of the original signal are separated as a result of eliminating the mode mixing problem. Therefore, the obtained IMF1 contains almost no useful information and is the main source of noise. Considering the insignificance of IMF1, it is removed in the IEEMD-BPNN to improve the forecasting precision of a disordered electric load series.

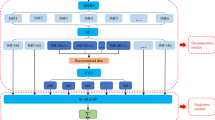
In other words, this study proposes a novel hybrid model that integrates IEEMD with BPNN to provide a quick and accurate way for STLF. The specific process of the proposed model is described below, and the flowchart is shown in Fig. 2.

  • Step 1: Non-stability reduction. Decompose the electric load series with IEEMD to obtain a series of IMFs and a residual.

  • Step 2: Noise reduction. Remove the IMF1 obtained in Step 1, which is the main source of noise and contains limited useful information.

  • Step 3: BPNN forecasting. Input each remaining component obtained in Steps 1 and 2 to the BPNN to achieve its future values respectively. Here, multiinput and mono-output method is taken to construct the input and output matrices of time series to build the training samples of the BPNN model. The structure of the training samples is shown in Table 1. In Table 1, [x(i), x(i+1), x(i+2), …, x(i+k−1)] is the input vector, while [x(i+k)] is the output vector; k is the embedding dimension of the input vector. If k is too small, the forecasting accuracy of BPNN would decline. If k is too large, the convergence speed of BPNN would decrease. In this study, the embedding dimension (k) of the input vector was set as six through the neural network simulation.

  • Step 4: Gain the final forecasts. Use the BPNN to combine these forecasting results of each component to achieve the final results.

Fig. 2
figure 2

Overall process of the proposed IEEMD-BPNN model

Full size image
Table 1 Input and output vectors of BPNN
Full size table

4 Experimental analyses

4.1 Statistical measures of forecasting performance

In this study, the following three criteria were used to evaluate the STLF methods. They are the root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE), which are calculated as follows:

$${\rm{RMSE}} = \sqrt {{1 \over N}\sum\limits_{i = 1}^N {{{({x_i} - {{\dot x}_i})}^2}}},$$
(8)
$${\rm{MAE}} = {1 \over N}\sum\limits_{i = 1}^N {\left\vert {{x_i} - {{\dot x}_i}} \right\vert},$$
(9)
$${\rm{MAPE}} = {1 \over N}\sum\limits_{i = 1}^N {\left\vert {{{{x_i} - {{\dot x}_i}} \over {{x_i}}}} \right\vert } \times 100\%,$$
(10)

where ẋ i represents the actual value, represents the forecast value, and N is the number of test samples for the prediction model. Clearly, the above criteria represent three types of deviation between the forecasts and the actual values: the smaller they are, the better the forecasting accuracy is.

4.2 Study 1: examination of the IEEMD-BPNN model

First, the URL (http://neuron.tuke.sk) of the web site is entered to download the electric load data of the Eastern Slovakian Electricity Corporation (ESEC) from 1997 to 1998. The load data include the readings for 30 min per sampling point. The feasible data used in this study are the data from April 8, 1998 to April 26, 1998 (19 days in all). Among these data, the electric load data from April 8, 1998 to April 19, 1998 are used for model fitting and training, and then the constructed models are applied to forecast the electric load from April 20, 1998 to April 26, 1998. The electric loads of the ESEC from April 8, 1998 to April 19, 1998 are outlined in Fig. 3.

Fig. 3
figure 3

Electric load data of the ESEC from April 8, 1998 to April 19, 1998

Full size image

Rolling forecasting process is undertaken in this study. For example, the data from April 8, 1998 to April 19, 1998 are used to forecast the electric data of April 20, 1998; the data from April 9, 1998 to April 20, 1998, together with the forecast electric data of April 20, 1998, are used to forecast the electric data for April 21, 1998. Then, in the same way, 12 days’ electric load data are used to forecast the next day’s electric load data.

From Fig. 3, we can see that the actual electric load time series has certain random volatility, due to which denoising is necessary. Decomposing the load series shown in Fig. 3 is achieved using IEEMD. After removing IMF1, the reconstructed denoised signal is shown in Fig. 4. Compared with Fig. 3, it can be seen that the denoised data is a little smoother than the original data. Hence, instead of using all the components, the IEEMD-BPNN removes the IMF1 and uses the remaining components for model fitting and training.

Fig. 4
figure 4

Reconstructed denoised electric load signal

Full size image

Prediction results of all IMFs and the residual component of Fig. 4 are illustrated in Fig. 5. These IMF components, IMF2–IMF8 (IMF1 is removed), are the decomposed results whose frequency bands range from high to low respectively, while the residual component maintains the original shape of the curve of the whole electric load data. It is obvious that the prediction accuracy is improved gradually with the decreasing of IMF frequency although the forecast result of IMF2 is not perfect.

Fig. 5
figure 5

Predicted load curves of IMFs and the residual component

Figs. 5a–5g represent the predicted load curves of IMF2-IMF8, respectively; Fig. 5h represents the predicted load curve of the residual

Full size image

After combining these forecasting results of each remaining component with BPNN, the final forecasting result of electric load on April 20, 1998 can be acquired, as shown in Fig. 6a. The electric load data from April 21, 1998 to April 26, 1998 are forecast in the same way, and the results are shown in Figs. 6b–6g. It is clear that the predicted load data obtained through the IEEMD-BPNN are in good agreement with the actual load data for a whole week. The proposed IEEMD-BPNN has good performance for the STLF of electricity systems.

Fig. 6
figure 6

The actual and predicted electric load data for April 20–26 ((a)–(g), respectively), 1998 obtained by the IEEMD-BPNN method

Full size image

To highlight the advantage of the proposed IEEMD-BPNN, it is compared with the other three methods, i.e., basic BPNN, EMD-BPNN, and EEMD-BPNN. All the three methods used the BPNN to predict; while the basic BPNN simulated the original data directly, the EMD-BPNN simulated the data decomposed with traditional EMD and the EEMD-BPNN simulated the data decomposed with traditional EEMD. The RMSE, MAE, and MAPE of the four methods were calculated and listed in Table 2. It can be observed from Table 2 that the basic BPNN has the worst performance compared with the other three methods. The EMD-BPNN and EEMD-BPNN both have good performances compared with basic BPNN. However, among all the methods, it is the IEEMD-BPNN that has the best performance and it outperforms the other three methods in terms of all the three standard statistical indicators.

Table 2 Three statistical measures of the four forecasting methods
Full size table

To clearly illustrate the forecast value, the actual and predicted electric load values obtained by the four methods for April 20, 1998 are shown in Fig. 7. It can be seen that the predicted data obtained through the basic BPNN has the maximum error with the original data, compared with the other three methods; this is because the original electric load data have certain random volatility, which makes it difficult for the BPNN to predict directly. EMD-BPNN has better performance than basic BPNN, but there is still a certain error in the predicted data due to its limited denoising ability; EEMD-BPNN has better performance than both basic BPNN and EMD-BPNN due to its strong denoising ability, but it is influenced by the end effect severely, which leads to a large error in the ends of the predicted data; IEEMD-BPNN is more consistent with the original data than the other three methods; furthermore, it has a small error in the ends of the predicted data, because it eliminates the end effect in traditional EEMD effectively. Therefore, the proposed IEEMD can eliminate the end effect in traditional EEMD effectively, and the proposed IEEMD-BPNN is the most accurate forecasting method compared with the other three methods.

Fig. 7
figure 7

Actual and predicted load values for April 20, 1998 obtained by basic BPNN (a), EMD-BPNN (b), EEMD-BPNN (c), and IEEMD-BPNN (d)

Full size image

4.3 Study 2: comparison with a seasonal ARIMA-BPNN model

In this section, the electric load demand data of the South Australia (SA) state of Australia (AEMO, 2007) are applied to compare the efficiency of the proposed IEEMD-BPNN model with the seasonal ARIMA-BPNN (SARIMA-BPNN) model presented by Yang et al. (2013). Thus, the results of this method are compared with the results of Yang et al. (2013) to forecast the load on July 14, 2007. For this purpose, the same training and testing samples of Yang et al. (2013) are used in this study. Namely, the load demand data of SA on June 23, June 30, and July 7 are used to forecast the load demand of SA on July 14 through IEEMD-BPNN. The load demand data include the readings for 30 min per sampling point.

The results of the STLF for July 14, 2007 obtained through IEEMD-BPNN are shown in Fig. 8 and compared with the method presented by Yang et al. (2013) in Table 3. In the IEEMD-BPNN, the MAPE and RMSE values obtained for July 14, 2007 are 0.548% and 15.401 MW, respectively. These measures are approximately 89.32% and 83.28% less than those in literature (Yang et al., 2013), respectively. Therefore, it can be concluded that the forecast accuracy of the proposed method is significantly better than that presented by Yang et al. (2013).

Fig. 8
figure 8

Predicted load demand results obtained by IEEMD-BPNN for July 14, 2007

Full size image
Table 3 Comparing the results of STLF for July 14, 2007
Full size table

4.4 Study 3: comparison with other well-known hybrid models

To further examine the proposed IEEMD-BPNN forecasting model, the electric load data of New York networks (NYISO, 2004) are used. The load data include the readings for 1 h per sampling point. The results of the proposed IEEMD-BPNN are compared with the results of other well-known hybrid models, WTNNEA and WGMIPSO presented by Amjady and Keynia (2009) and Bahrami et al. (2014), respectively, to forecast the load on July 1, 2004. For this purpose, the load data of the previous 10 d are used to forecast the electric load on July 1, 2004.

The forecast results of the IEEMD-BPNN and the methods in the literature (Amjady and Keynia, 2009; Bahrami et al., 2014) for July 1, 2004 are shown in Fig. 9, while the values of the forecast load, the actual load, and the error of load forecasting of the three methods are presented in Table 4. According to Table 4, the error of the load forecasting method proposed by Amjady and Keynia (2009) is more than 100 MW in 18 h. In the method proposed by Bahrami et al. (2014), the value of the error is less than 60 MW in 14 h. However, in the proposed IEEMD-BPNN, the value of the error is less than 55 MW in 16 h. Obviously, the proposed IEEMD-BPNN enjoys higher accuracy for load forecasting.

Fig. 9
figure 9

Actual and predicted electric load values obtained by the three methods for July 1, 2004

Full size image
Table 4 Actual load, forecast load, and forecast error for the power system of New York for July 1, 2004
Full size table

The results of the electric load forecasting for July 1, 2004 are compared with the proposed methods in the literature (Amjady and Keynia, 2009; Bahrami et al., 2014) in Table 5 (p.112). In the method proposed by Amjady and Keynia (2009), the MAPE, MAE, and RMSE values obtained for July 1, 2004 are 1.931%, 132.11 MW, and 145.19 MW, respectively, which are approximately 64.68%, 64.71%, and 63.01% less than those of Bahrami et al. (2014), respectively. However, among these methods, it is the IEEMD-BPNN that has the lowest MAPE, MAE, and RMSE values, which are approximately 72.40%, 71.82%, and 68.47% less than those of Amjady and Keynia (2009). The maximum and the minimum errors occurred at 7:00 pm and 1:00 pm, respectively. The maximum and the minimum absolute errors are equal to 83.76 MW (at 7:00 pm) and 0.75 MW (at 1:00 pm), respectively. Finally, it can be concluded that the forecast accuracy of the proposed IEEMD-BPNN is significantly better than that of the other models presented in the literature (Amjady and Keynia, 2009; Bahrami et al., 2014).

Table 5 Comparison of the electric load forecasting results for July 1, 2004
Full size table

Conclusions

STLF is an important issue when operating an electricity system reliably and economically. In this paper, a hybrid forecasting model based on IEEMD and BPNN is constructed. The IEEMD method is used to decompose the original load series into several IMFs and one residual component. This can reduce the nonstationarity of the original load series and enhance the prediction accuracy. Here, IEEMD is an improvement of EEMD proposed in this study. In the IEEMD, end-points continuation based on the degree of wave similarity is used to restrain the end effect in traditional EEMD. After removing the high-frequency component (namely IMF1) obtained through IEEMD, the remaining IMFs and the residual are forecast by BPNN. The final forecasting result for electric load is produced by combining all the forecasting results obtained through BPNN.

The IEEMD-BPNN model is compared with the basic BPNN, EMD-BPNN, and EEMD-BPNN models. The comparison results show that the basic BPNN has the worst performance compared with the other models. The EMD-BPNN and EEMD-BPNN both have a better performance compared with the basic BPNN: the EMD-BPNN reduces the average RMSE, average MAE, and average MAPE by 26.99%, 24.42%, and 23.68%, respectively, compared with the basic BPNN, and the EEMD-BPNN reduces the average RMSE, average MAE, and average MAPE by 39.39%, 35.38%, and 36.18%, respectively, compared with the basic BPNN. Among all the models, the IEEMD-BPNN model has the best performance and it outperforms the basic BPNN, EMD-BPNN, and EEMD-BPNN models in terms of all the standard statistical measures, acquiring the average RMSE, average MAE, and average MAPE statistics of 8.13 MW, 6.55 MW, and 6.19%, respectively; these RMSE, MAE, and MAPE values are reduced by 62.10%, 60.11%, and 60.86%, respectively, compared with the basic BPNN. In addition, considering the three parameters RMSE, MAE, and MAPE, the IEEMD-BPNN model performs the best with the lowest RMSE, MAE, and MAPE for all days of the week. To further examine the IEEMD-BPNN model, three models proposed in other studies, i.e., SARIMA-BPNN (Yang et al., 2013), WTNNEA (Amjady and Keynia, 2009), and WGMIPSO (Bahrami et al., 2014), are used for comparison. Similarly, the forecasting results show that the IEEMD-BPNN has the best performance compared with the SARIMA-BPNN, WTNNEA, and WGMIPSO models in terms of all the three standard statistical indicators (RMSE, MAE, and MAPE). Therefore, this study concludes that the IEEMD-BPNN model can obviously improve the electric load forecasting accuracy and can provide a very powerful tool for market players and regulators to control and arrange their electricity supply.

In addition to electricity load, the proposed IEEMD-BPNN model might be used for other nonlinear and nonstationary time series forecasting task in the energy market such as wind power, which requires further evidence. Furthermore, this study devotes attention exclusively to STLF, whereas middleterm and long-term load forecasting procedures are of greater value than STLF to decision-makers in the energy market. We will look into these issues in future research.