Abstract
Stability is an important and fruitful avenue of research for liquid crystal elastomers. At constant temperature, upon stretching, the homogeneous state of a nematic body becomes unstable, and alternating shear stripes develop at very low stress. Moreover, these materials can experience classical mechanical effects, such as necking, void nucleation and cavitation, and inflation instability, which are inherited from their polymeric network. We investigate the following two problems: First, how do instabilities in nematic bodies change from those found in purely elastic solids? Second, how are these phenomena modified if the material constants fluctuate? To answer these questions, we present a systematic study of instabilities occurring in nematic liquid crystal elastomers, and examine the contribution of the nematic component and of fluctuating model parameters that follow probability laws. This combined analysis may lead to more realistic estimations of subsequent mechanical damage in nematic solid materials. Because of their complex material responses in the presence of external stimuli, liquid crystal elastomers have many potential applications in science, manufacturing, and medical research. The modeling of these materials requires a multiphysics approach, linking traditional continuum mechanics with liquid crystal theory, and has led to the discovery of intriguing mechanical effects. An important problem for both applications and our fundamental understanding of nematic elastomers is their instability under large strains, as this can be harnessed for actuation, sensing, or patterning. The goal is then to identify parameter values at which a bifurcation emerges, and how these values change with external stimuli, such as temperature or loads. However, constitutive parameters of real manufactured materials have an inherent variation that should also be taken into account, thus the need to quantify uncertainties in physical responses, which can be done by combining the classical field theories with stochastic methods that enable the propagation of uncertainties from input data to output quantities of interest. The present study demonstrates how to characterize instabilities found in nematic liquid crystal elastomers with probabilistic material parameters at the macroscopic scale, and paves the way for a systematic theoretical and experimental study of these fascinating materials.
Similar content being viewed by others
Introduction
Liquid crystal elastomers (LCEs) are advanced multifunctional materials that combine the flexibility of polymeric networks with the nematic structure of liquid crystals.1,2 Because of their complex molecular architecture, they are capable of exceptional responses, such as large spontaneous deformations and phase transitions, which are reversible and repeatable under certain external stimuli, namely heat, light, solvents, electric, or magnetic fields. These properties render them as promising candidates for future “animate materials” and could be harnessed for a range of technological applications, including soft actuators and soft tissue engineering. Nevertheless, a better understanding of these materials is needed before they can be exploited on an industrial scale.3,4,5,6,7,8,9,10,11,12,13,14,15,16
Since the early discovery of liquid crystalline solids, probing their intriguing material properties has been the focus of research laboratories around the world, and the importance of such essential work is hard to overstate. However, their accurate description can only be useful if fully integrated in a multiphysics framework combining elasticity and liquid crystal theories. Many nematic solids are synthesized as polydomains, where the liquid crystal mesogens are separated into different domains, and in every domain, they are aligned along a preferred direction, known as the local director.17,18,19,20,21,22 Depending on the fabrication process, polydomains may have very different material properties and behaviors. Monodomains, where mesogen molecules are uniformly aligned throughout the material, can be formed from polydomains through mechanical stretching or by cooling an isotropic material under an external stress field to reach the nematic phase.
An ideal continuum model for monodomains is provided by the neoclassical strain-energy function.23,24,25 This is a phenomenological model based on the molecular network theory of rubber elasticity.26 The parameters appearing in the neo-Hookean-type strain energy can be obtained through statistical averaging at microscopic scale or derived from macroscopic shape changes at small strain.27,28 Since elastic stresses dominate over Frank elasticity induced by the distortion of mesogens alignment,29,30,31 Frank effects are generally ignored.32,33 The neoclassical formulation has been extended to polydomains by assuming that every domain has the same strain-energy density as a monodomain.34,35 These descriptions have been generalized to include nematic strain-energy densities based on phenomenological hyperelastic models (e.g., Mooney–Rivlin, Gent, Ogden) that better capture the non-linear elastic behavior at large strains36,37,38 (molecular interpretations of the Mooney–Rivlin and Gent constitutive models for rubber are presented in References 39, 40). Further generalizations are proposed in References 41, 42.
Another important characteristic of most materials is that physical properties are subject to random variations. Typically, average properties are used, and any variations around the mean are neglected when computing the response of a material. However, as we show here, one can employ information theory43 and the maximum entropy principle44,45,46 to include some stochastic variations of the material parameters, then propagate their uncertainty to output physical responses. Comprehensive reviews on the information-theoretic approach in elasticity can be found in References 47,48,49.
Our main focus is on large strain instabilities of LCE bodies acted upon by external loads. In addition to the recurring phenomenon of soft elasticity, where alternating shear stripes develop at very low stress if a nematic body is stretched, we explore theoretically a set of classical instabilities inherited from parent polymeric networks, namely necking under tensile load, cavitation of a nematic sphere where a void nucleates at its center when uniform tensile traction is imposed, and inflation instability of an internally pressurized shell, where the pressure increases, decreases, and then increases again. The aim is to determine conditions for the onset of instability and show how nematic materials perform compared to their purely elastic analog. Moreover, for these problems, the propagation of stochastic variation from input material parameters to output mechanical behavior is mathematically traceable, making our stochastic approach both mathematically and mechanically transparent. The main effect of random variations is to replace a well-defined bifurcation point by a probability that a material will undergo an instability as a function of the bifurcation parameter. Such fundamental problems are important in their own right and may stimulate related mechanical testing of nematic materials.
General set-up
Following the classical work of Flory50 on polymer elasticity, we use the stress-free state of a virtual isotropic phase at high temperature as the reference configuration,29,38,51,52,53,54 rather than the nematic phase in which the cross-linking might have been produced.23,24,25,41,42,55,56 Within this theoretical framework, the material deformation due to the interaction between external stimuli and mechanical loads can be expressed as a composite deformation from a reference configuration to the current configuration via an elastic deformation followed by a natural (stress-free) shape change. The multiplicative decomposition of the associated gradient tensor is similar in some respects to those found in the constitutive theories of thermoelasticity, elastoplasticity, and growth57,58 (see also References 59 and 60) but is different on one major aspect: the stress-free geometrical change is superposed on the elastic deformation, which is applied directly to the reference state. This difference is important because although the elastic configuration obtained by this deformation may not be observed in practice, it still may be possible for the nematic body to assume such a configuration under suitable external stimuli. The resulting elastic stresses then can be used to analyze the final deformation, where the particular geometry also plays a role (Figure 1).61,62
Multiplicative decomposition of the deformation gradient for a nematic elastomer. Unlike traditional theories of anelasticity, the elastic deformation is applied first to the reference configuration and then followed by an anelastic strain deformation. F = GA is the deformation gradient tensor with respect to the reference isotropic state.
To describe an incompressible nematic material, we combine isotropic hyperelastic and neoclassical strain-energy density functions as follows:63
where, on the right-hand side, the first term is the energy of the “parent” elastic matrix, and the second term is the neoclassical-type function. Specifically, n is a unit vector for the localized direction of uniaxial nematic alignment in the present configuration; F = GA is the deformation gradient tensor with respect to the reference isotropic state (see Figure 1 and also Figure 1 of Reference 38), with G = a1/3n ⊗ n + a−1/6 (I − n ⊗ n) as the “spontaneous” (or “natural”) deformation tensor and A the (local) elastic deformation tensor; G0 = a1/3n0 ⊗ n0 + a−1/6 (I − n0 ⊗ n0) is the spontaneous deformation tensor with n0 the director orientation at cross-linking, which may be spatially varying; and a > 0 is a temperature-dependent shape parameter, which we assume to be spatially independent (i.e., no differential swelling). We denote by ⊗ the usual tensor product of two vectors, and by I = diag(1,1,1) the identity second-order tensor.
Recognizing that some uncertainties may arise in the mechanical responses of liquid crystal elastomers, and inspired by recent developments in stochastic finite elasticity,64,65,66,67,68,69,70,71,72,73,74,75,76,77 we assume that the model parameters are defined as random variables drawn from given probability distributions. In practice, material parameters take on different values, corresponding to possible outcomes of experimental tests. The maximum entropy principle then allows us to explicitly construct prior probability laws for the model parameters, given the available information. Explicit derivations of probability distributions for the elastic parameters of stochastic homogeneous isotropic hyperelastic models calibrated to experimental data for rubber-like material and soft tissues were previously presented.64,69,75 Intuitively, such a stochastic body can be regarded as an ensemble (or population) of bodies that are equal in size and have the same geometry, and each body in the ensemble is made from a single homogeneous material with uncertain parameters but distributed according to probability density functions that are calibrated to macroscopic experimental measurements. These models reduce to the usual deterministic ones when the parameters are single-valued constants.
Soft elasticity and stress plateaus
Many macroscopic deformations of nematic liquid crystal elastomers induce a re-orientation of the director with a general tendency for the director to become parallel to the direction of the largest principal stretch. This re-orientation is typically uniform across the material. However, non-uniform behaviors are also possible. In particular, under appropriate uniaxial tension or biaxial stretch, bifurcation to a pattern of stripe domains is generated, where adjacent stripes deform by the same shear but in opposite directions. Early experimental investigations of this phenomenon, known as soft elasticity,56,78,79 were reported.80,81,82,83 Its theoretical explanation for these materials is that the energy is minimized by passing through a state exhibiting a microstructure of many homogeneously deformed parts.38,53,81,84,85,86,87 A natural question is then: How does soft elasticity depend on the material parameters? For simplicity, we selected an incompressible neo-Hookean-type strain-energy function,88
where the superscript “T” represents the transpose operator, “tr” denotes the trace operator, and µ(1) ≥ 0 is constant, together with the neoclassical strain-energy function38,51,53
with µ(2) ≥ 0 constant. For the composite model function defined by Equation 1, the shear modulus at infinitesimal strain is µ = µ(1) + µ(2) > 0.89 However, our results can be easily extended to other choices of strain-energy density functions.63
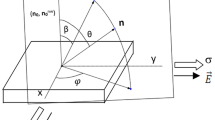
We analyzed shear striping under biaxial stretch, and assumed that the nematic director can only rotate in the biaxial plane. To achieve this, we set n0 = [0,0,1]T and n = [0,sinθ,cosθ]T, where θ ∈ [0,π/2], in a Cartesian system of reference, and examined small shear perturbations of biaxial extensions, with gradient tensor63
where a > 1 is the nematic shape parameter, λ > 0 is the stretch ratio, and ε > 0 is the small perturbation. Denoting w(λ,ε,θ) = \(\overline{W}^{(nc)}\) (F,n), for sufficiently small values of ε and θ, we found that when µ(1) > 0 and µ(2) = 0 (purely elastic case), the equilibrium state with parameters ε = 0 (Figures 2 and 3), and θ = 0 is stable. If µ(2) > 0, then this equilibrium state is unstable for
where the elasto-nematic ratio η = µ(1)/µ(2) gives the relative magnitude of the elastic and neoclassical contributions. There is also an equilibrium state with ε = 0 and θ = π/2, where the nematic director is fully rotated so that it aligns uniformly with the direction of macroscopic extension. By symmetry arguments, this state is unstable for
(a) and (b) The strain-energy function w(λ,ε,θ) for (ε,θ) = (0,0) and (ε,θ) = (ε0,θ0), with ε0 and θ0 shown in Equation 7, and (ε,θ) = (0,π/2) when \(a\) = 2 and (a) µ(1) = 4.05 or (b) µ(1) = 0, while µ(2) = 4.05. The two vertical lines correspond to the lower and upper bounds on λ, given by Equations 5 and 6, respectively. Between these bounds, the second solution, with (ε,θ) = (ε0,θ0), minimizes the energy. The lower and upper bounds on λ, given in (c) (Equations 5 and 6) and (d) (Equations 8 and 9), respectively, are functions of the parameter ratio η = µ(1)/µ(2) when \(a\) = 2. For η → ∞, the model approaches a purely elastic form where the homogeneous deformation is always stable. For η = 0, the bounds are the same, and correspond to the neoclassical form.
The stochastic shear parameter ε0 and director angle θ0, given in Equation 7, when (a) and (b) \(a\) = 2, while the shear modulus µ follows a Gamma distribution with shape and scale parameters ρ1 = 405 and ρ2 = 0.01, respectively, and R(1) = µ(1)/µ is drawn from a Beta distribution with hyperparameters ξ1 = 100 and ξ2 = 100. (c) and (d) µ = 4.05 and R(1) = µ(1)/µ = 0.5, while the shape parameter \(a\) follows a Gamma distribution with ρ1 = 200, ρ2 = 0.01. In (a) and (b), the dashed black lines correspond to the deterministic solutions based only on the mean values µ = ρ1ρ2 = 4.05 and R1 = ξ1/(ξ1 + ξ2) = 0.5, whereas the red versions show the arithmetic mean value solutions. In (c)–(d), the dashed black lines correspond to the deterministic solutions based only on the mean value \(a\) = ρ1ρ2 = 2, whereas the red versions show the arithmetic mean value solutions. In this case, there is a significant difference between the mean value solutions and the deterministic solutions.
When λ satisfies Equations 5 or 6, we obtain
For the resulting strip pattern, the gradient tensors of alternating shear deformations in two adjacent stripe domains are F± with ε = ± ε0, respectively. The two deformations are geometrically compatible in the sense that there are two non-zero vectors q and p, such that the Hadamard jump condition F+ − F− = q ⊗ p is satisfied, where p is the normal vector to the interface between the two phases corresponding to the deformation gradients F+ and F−.90,91,92,93 In other words, F+ and F− are rank-one connected (i.e., rank(F+ − F−) = 1). If η = 0, then the above equilibrium states are unstable for \(\uplambda \in (a^{{-1/6}} ,a^{1/12} )\) and \(\uplambda \in (a^{1/12} ,a^{1/3} )\), respectively. Thus, soft elasticity is always presented by the purely neoclassical model.38,84 When η → ∞, there is no shear striping since the material is practically elastic.
The strain-energy function w(λ,ε,θ) is illustrated in Figure 2a and b. Note that for λ, with values between the lower and upper bounds given by Equations 5 and 6, respectively, the minimum energy is attained for (ε,θ) = (ε0,θ0). Assuming that loading is applied in the second direction, the first Piola–Kirchhoff axial stress in this direction is equal to \(P_{2}^{(nc)} = dw(\uplambda ,\varepsilon ,\uptheta )/d\uplambda\). Figure 2b then suggests that when µ(1) = 0 (i.e., for the purely neoclassical form), the director rotates and alternating shear stripes develop for \(\uplambda \in (a^{{-1/6}} ,a^{1/3} )\), at zero load, since the slope of the curve is equal to zero within this interval. In contrast, if µ(1) > 0, then from Figure 2a, we infer that the applied load increases with deformation and is almost constant but non-zero while the director rotates.
Because of the geometric compatibility, and since the intervals for stretch ratios λ, where shear striping occurs are at a maximum length when n0 = [0,0,1]T, the bounds in Equations 5 and 6 also provide the maximum interval for shear striping when n0 is not uniformly aligned. The minimum length of those intervals is attained for monodomains with n0 = [0,1,0]T. Experimental results for monodomains, where the tensile load forms different angles with the initial nematic director were also reported.94,95 If G0 = I,34 then the solution with ε = 0 and θ = 0 is unstable for
and that with ε = 0 and θ = π/2 is unstable for
For example, when a = 2, the bounds given by Equations 5 and 6 and by Equations 8 and 9, respectively, are plotted as functions of the parameter ratio η in Figure 2c and d.
In addition, when the model parameters are random variables, characterized by probability distributions, we are interested in the probability where shear striping occurs under a given stretch. Here, we show the effects of fluctuations in the shear modulus µ and the shape parameter a separately (i.e., we first set µ as a random variable, while a is a single-valued constant), then keep µ constant and let a fluctuate. In Figure 3a and b, the stochastic shear parameter ε0 and director angle θ0, given in Equation 7, are represented when the stochastic material parameters were chosen such that their mean values are the same as the deterministic values in Figure 2a. For both stochastic versions, to increase the probability of homogeneous deformation, one must increase the value of η, whereas shear striping is certain only if the model reduces to the neoclassical one (i.e., when η = 0). However, while η > 0, the inherent variability in the probabilistic system means that there will always be competition between the homogeneous and inhomogeneous deformations.
Cavitation
Cavitation in solids is the formation of a void within a solid under tensile loads through analogy to the similar phenomenon observed in fluids. For rubber-like materials, following early studies of damage under loads,96,97 this phenomenon was first reported by Gent (1959)98 who showed experiments where rubber cylinders ruptured under relatively small tensile-dead loads by opening an internal cavity. The non-linear elastic analysis by Ball (1982)99 provided the first systematic theory for the formation of a spherical cavity at the center of a sphere of isotropic incompressible hyperelastic material under a radially symmetric tensile load. Mathematically, cavitation was treated as a bifurcation from the trivial state at a critical value of the surface traction or displacement, at which the trivial solution became unstable. This work paved the way for numerous applied and theoretical studies devoted to this inherently non-linear mechanical effect, which is not captured by the linear elasticity theory. In addition to the well-known stable cavitation post-bifurcation at the critical dead load, such that the cavity radius monotonically increases with the applied load, it was shown68 that unstable (snap) cavitation is also possible for some homogeneous isotropic incompressible hyperelastic materials, where Backer–Ericksen inequalities100,101 hold. Static and dynamic cavitation in radially inhomogeneous spheres with stochastic parameters were also analyzed.72
To study the cavitation of a nematic sphere, we consider an initially unit sphere described by the neoclassical model given by Equation 3 where either the shear modulus µ or the nematic parameter a is a random variable. Expressing all tensors in the spherical coordinates (R,Θ,Φ) in the reference configuration, we assume that the sphere is deformed by radially symmetric inflation with deformation gradient F = diag (λ−2, λ, λ), while the natural deformation tensor is G = diag (a−1/3, a1/6, a1/6), and λ > a1/6 > 1. When this deformation is caused by a radial dead-load traction applied uniformly on the sphere surface in the reference configuration, we are interested in the critical load that will cause a spherical cavity to open at its center. The radial traction at the outer surface is necessary for an inner cavity of radius c to form (see Figure 4). For the onset of cavitation, the critical load is found by letting c → 0. Since the bifurcation is supercritical, cavitation is stable (i.e., the cavity radius increases as the applied dead load increases). A comparison72 shows that for the nematic sphere, cavitation nucleates at a larger critical load, \(P_{0}^{(nc)} ,\) than the corresponding load, P0, for the elastic sphere with the same shear modulus, and \(P_{0}^{(nc)} = a^{1/3} P_{0}\). For the neo-Hookean sphere, P0 = 5µ/2.
Probability distribution of the applied dead-load traction causing cavitation of radius c at the center of an initially unit sphere of neoclassical liquid crystal elastomers material when (a) \(a\) = 2, while the shear modulus µ follows a Gamma distribution with hyperparameters ρ1 = 405, ρ2 = 0.01, and (b) µ = 4.05, while the shape parameter \(a\) follows a Gamma distribution with ρ1 = 200, ρ2 = 0.01. The dashed black lines correspond to the deterministic solutions based only on the mean values of the parameters, whereas the red versions show the arithmetic mean value solutions. The probabilistic interval for the critical load at which the cavity nucleates is found when c → 0. As the bifurcation from trivial solution is supercritical, cavitation is stable (i.e., the cavity radius increases as the applied dead load increases).
When the LCE strain-energy function includes an additional elastic component, as in Equation 1, so that the elasto-nematic ratio is η > 0 while the shear modulus µ remains the same, the critical dead load decreases toward P0. For example, if G0 = I, then the critical applied load is equal to \(\overline{P}_{0}^{(nc)} = [a^{1/3} + (1 - a^{1/3} )\upmu^{(1)} /\upmu ]P_{0}\), and \(P_{0} < \overline{P}_{0}^{(nc)} < P_{0}^{(nc)}\) (see Figure 4).
Shell inflation
Internally pressurized hollow spheres and tubes are relevant in many biological and engineering structures.57 For rubber spherical and tubular balloons, the first experimental observations of inflation instabilities under internal pressure were reported by Mallock (1891).102 Cylindrical tubes of homogeneous isotropic incompressible hyperelastic material subject to finite symmetric inflation and stretching were theoretically analyzed for the first time by Rivlin (1949).103 Finite radially symmetric inflation of elastic spherical shells was initially initially investigated by Green & Shield (1950)104 and then later by Adkins & Rivlin (1952) and Shield (1972).105,106 For both elastic tubular and spherical shells, it was shown107 that depending on the material model, the internal pressure may increase monotonically; increase and then decrease; or increase, decrease, and then increase again. These classical results were extended to elastic materials with stochastic parameters.65,66,67 Theoretical investigations of inflated nematic cylindrical balloons were presented recently as well.108,109
To compare inflation instabilities in nematic and in purely elastic spheres, we consider the hyperelastic Mooney–Rivlin model110,111 given by
where µ = µ1 + µ2 > 0 is the shear modulus at infinitesimal strain. A Mooney–Rivlin-type neoclassical strain-energy function for the nematic material then takes the form
Taking a spherical coordinates system with coordinates (R,Θ,Φ) in the reference configuration, we assume that the sphere is deformed by radially symmetric inflation with deformation gradient F = diag (λ−2, λ, λ), while the natural deformation tensor is G = diag (a−1/3, a1/6, a1/6) and λ > a1/6 > 1. We denote W(nc)(λ,n) = W(nc)(F,n) and further assume that the shell is thin (i.e., 0 < ϵ = (B − A)/A << 1), where A and B represent the inner and outer radii of the reference shell, respectively (Figure 5). When the deformation is due to a radial pressure applied uniformly on the inner surface in the present configuration, the corresponding radial Cauchy stress at the inner surface can be approximated as \(T^{(nc)} = \upepsilon a^{1/2} \uplambda^{ - 2} {\text{d}}{\text{W}}^{\text{(nc)}} /{\text{d}}\uplambda\). The relation between the Cauchy stress at the inner surface in the nematic and purely elastic shell with the same shear modulus is T(nc) = T. Figure 5a and b shows that if the parameter ratio µ1/µ is sufficiently small, the required stress changes from increasing to decreasing (i.e., the material displays inflation instability), and for the nematic model, instability is expected at larger deformation than for the hyperelastic model. However, this value will decrease if the model is modified to include an additional elastic energy, as in Equation 1, so that the elasto-nematic ratio is η > 0, while the shear modulus µ remains the same. For the nematic shell in Figure 5c and d, either the shear modulus µ = µ1 + µ2 or the shape parameter a is a random variable. In both cases, the critical load for instability resides in a probabilistic interval where the stable and unstable states compete. To decrease the chance of stable deformation, one must increase the value of µ1/µ, and only when µ1 = µ is unstable is deformation certain.
The normalized internal pressure for an inflated spherical shell of (a) Mooney–Rivlin hyperelastic material, defined by Equation 10, when A = diag (α−2, α, α), with α > 1. (b) Mooney–Rivlin liquid crystal elastomer (LCE) material, defined by Equation 11, when F = diag (λ−2, λ, λ) and G = diag (a−1/3, a1/6, a1/6), with \(a\) = 2 and λ > \(a\)1/6 ≈ 1.1225. (c) Mooney–Rivlin LCE material with \(a\) = 2, while the shear modulus µ follows a Gamma distribution with ρ1 = 405, ρ2 = 0.01, and R1 = µ1/µ is drawn from a Beta distribution with ξ1 = 900 and ξ2 = 100. (d) Mooney–Rivlin LCE material with µ = 4.05 and R1 = µ1/µ = 0.9, while the shape parameter \(a\) follows a Gamma distribution with ρ1 = 200, and ρ2 = 0.01. (a) and (b) When the parameter ratio µ1/µ is sufficiently small, the required stress changes from increasing to decreasing (i.e., the material displays inflation instability). For the nematic model, instability is expected at larger deformation than for the underlying hyperelastic model. (c) and (d) The dashed black lines correspond to the deterministic solutions based only on the mean values of the parameters, whereas the red versions show the arithmetic mean value solutions. When the material parameters are stochastic, the critical load for instability is found in a probabilistic interval, where both stable and unstable states are observed with a given probability.
Necking
Similar to other rubber-like materials, LCEs may suffer from necking instability under stretch.17,18 When homogeneous isotropic incompressible hyperelastic materials are subject to large tension, necking occurs if there is a maximum load or if a critical extension ratio exists, such that the force required to extend the material beyond this critical value changes from increasing to decreasing.112,113,114,115,116,117,118 The relationship between the onset of necking and the maximum load was originally analyzed for ductile materials.119 For a class of hyperelastic materials, where the load–displacement curve does not possess a maximum,120 it was proven that the homogeneous deformation is the only absolute minimizer of the elastic energy. In particular, incompressible neo-Hookean or Mooney–Rivlin hyperelastic models do not exhibit necking, and this property is inherited by the associated nematic LCE models. For example, a necking instability observed experimentally under uniaxial tension could not be captured by the neoclassical LCE model based on the neo-Hookean strain-energy function alone.121 In that case, since necking was initiated during director rotation, a composite model consisting of a purely neoclassical form and an additional elastic form, as presented previously, should be used to predict the non-zero stress plateau associated with the neck formation. Necking instability during director rotation in stretched monodomain nematic elastomers was previously reported.122
To further explore necking instability that may occur when the director is parallel to the applied tensile force, and compare that with the same behavior in a purely elastic material, we consider the hyperelastic Gent–Thomas model123 defined by
where µ = µ1 + µ2 > 0 is the shear modulus at small strain. A Gent–Thomas-type neoclassical strain-energy function for the nematic material then reads
We take F = diag (λ−1/2, λ, λ−1/2), while G = diag (a−1/6, a1/3, a−1/6) and λ > a1/3 > 1.
In this case, denoting W(nc)(λ,n) = W(nc)(F,n), the uniaxial tensile load is given by the first Piola–Kirchhoff stress \(P_{0}^{(nc)} = {\text{d}}{\text{W}}^{\text{(nc)}} /{\text{d}}\uplambda\), and necking occurs when the ratio µ1/µ is sufficiently small. The relation between the first Piola–Kirchhoff tensile stress in the nematic and purely elastic case with the same shear modulus is \(P_{2}^{(nc)} = a^{-1/3} P_{2}\). As shown in Figure 6a and b, for the nematic model, necking is expected at larger deformation and lower maximum dead load than for the hyperelastic model. However, the maximum load will increase if the model is modified to include an additional elastic energy, as in Equation 1, so that the elasto-nematic ratio is η > 0, while the shear modulus µ remains the same. Figure 6c and d illustrates the stochastic tensile load in the deformed LCE.
The effect of changing the value of parameter ratio µ1/µ on the normalized tensile-first Piola–Kirchhoff stress for (a) the Gent–Thomas model, defined in Equation 12, where A = diag (α−1/2, α, α−1/2) with α > 1. (b) The Gent–Thomas-type liquid crystal elastomers (LCE) model, defined in Equation 13, where F = diag (λ−1/2, λ, λ−1/2) and G = diag (\(a\)−1/6, \(a\)1/3, \(a\)−1/6), with \(a\) = 2 and λ > \(a\)1/3 ≈ 1.2599. (c) The LCE model, where \(a\) = 2, while the shear modulus µ follows a Gamma distribution with ρ1 = 405, ρ2 = 0.01, and R1 = µ1/µ is drawn from a Beta distribution with ξ1 = 12 and ξ2 = 100. (b) The LCE model where µ = 4.05 and R1 = µ1/µ = 0.11, while the shape parameter \(a\) follows a Gamma distribution with ρ1 = 200 and ρ2 = 0.01. In (c) and (d), the dashed black lines correspond to the deterministic solutions based only on the mean values of the parameters, whereas the red versions show the arithmetic mean value solutions. In all cases, when the parameter ratio is sufficiently small, the required dead load changes from increasing to decreasing, and the material displays necking instability. For the nematic model, necking is expected at larger deformation and lower maximum load than for the underlying hyperelastic model. When the material parameters are stochastic, both stable and unstable states are presented with a given probability.
Conclusion
Instabilities in liquid crystalline solids can be of potential interest in a range of applications. Here, we present various situations to understand some new possibilities offered by LCEs. Specifically, we combine for the first time non-linear elastic instabilities with nematic elastomer theory, within a stochastic setting where the material parameters are probabilistic, and compare the results with those from classical non-linear elasticity. While shear striping instabilities are specific to LCEs, as they do not occur in rubber, instabilities such as cavitation, shell inflation, and necking have been widely studied in the context of purely hyperelastic materials. In recent years, we have reviewed such results and extended them to a stochastic elasticity framework by building directly on the deterministic non-linear theory. For LCEs, similar interesting phenomena can occur, and we offer a perspective on the general methodology to analyze them. Moreover, each of these instability problems could be further formulated and treated under slightly different hypotheses, where the external forces or the type of nematic material might change to reflect different experimental setups and observations. Our scope is to present some key theoretical ingredients to study this class of problems.
The particular choice of numerical values in our calculations are for illustrative purposes only. To compare the stochastic results with the deterministic ones, we sampled from distributions where the parameters have mean values corresponding to the deterministic system. The stochastic results mostly follow the deterministic ones, but transform a single critical value for instability into a large probability of an instability taking place close to that value. However, both stable and unstable states have a quantifiable chance to be observed with a given probability, and small variations in the input model parameters can have a significant impact on whether an instability occurs at a certain load. Moreover, we observed that, as deformation progresses, the solution variance tends to change non-uniformly around the mean value, suggesting that the average value may be less significant from a physical point of view if fluctuations become large.
The results presented here are universal in the sense that they hold for families of LCE models for which their classic hyperelastic counterparts exhibit a similar instability. To gain significant insight into the macroscopic mechanical properties of these materials, it is imperative that they are analyzed and tested under more complex multiaxial deformations and loads before they can be incorporated into real industrial systems. Therefore, we hope that the general field of instabilities for LCE materials may serve as an inspiration for new devices or for systematic testing. For example, inflation instabilities were reported124 for elongated nematic balloons. The inflation of cylindrical elastic balloons is often accompanied by different types of instabilities, such as bulging and necking. These phenomena have been analyzed theoretically for hyperelastic balloons,125,126,127 but remain new territory for LCEs. The possibility of activation of LCEs may finally fulfill the early promises of the rational mechanics pioneers who first demonstrated the existence of non-linear elastic instabilities and understood that they could be used to design new devices.
Data availability
Some technical details are provided in a supplementary file. There are no additional data associated with this paper.
References
P.G. de Gennes, Physique moleculaire - reflexions sur un type de polymeres nematiques. C. R. Acad. Sci. Ser. 281, 101 (1975)
H. Finkelmann, H.J. Kock, G. Rehage, Investigations on liquid crystalline polysiloxanes 3, Liquid crystalline elastomers—A new type of liquid crystalline material. Makromol. Chem. Rapid Commun. 2, 317 (1981). https://doi.org/10.1002/marc.1981.030020413
L.T. de Haan, A.P. Schenning, D.J. Broer, Programmed morphing of liquid crystal networks. Polymer 55(23), 5885 (2014). https://doi.org/10.1016/j.polymer.2014.08.023
Z.C. Jiang, Y.Y. Xiao, Y. Zhao, Shining light on liquid crystal polymer networks: Preparing, reconfiguring, and driving soft actuators. Adv. Opt. Mater. 7, 1900262 (2019). https://doi.org/10.1002/adom.201900262
A.S. Kuenstler, R.C. Hayward, Light-induced shape morphing of thin films. Curr. Opin. Colloid Interface Sci. 40, 70 (2019). https://doi.org/10.1016/j.cocis.2019.01.009
Z. Mahimwalla, K.G. Yager, J.I. Mamiya, A. Shishido, A. Priimagi, C.J. Barrett, Azobenzene photomechanics: Prospects and potential applications. Polym. Bull. 69, 967 (2019). https://doi.org/10.1007/s00289-012-0792-0
J.M. McCracken, B.R. Donovan, T.J. White, Materials as machines. Adv. Mater. 32(20), 1906564 (2020). https://doi.org/10.1002/adma.201906564
X. Pang, J.-A. Lv, C. Zhu, L. Qin, Y. Yu, Photodeformable azobenzenecontaining liquid crystal polymers and soft actuators. Adv. Mater. 31(52), 1904224 (2019). https://doi.org/10.1002/adma.201904224
T. Ube, T. Ikeda, Photomobile polymer materials with crosslinked liquid-crystalline structures: Molecular design, fabrication, and functions. Angew. Chem. Int. Ed. 53(39), 10290 (2014). https://doi.org/10.1002/anie.201400513
S.W. Ula, N.A. Traugutt, R.H. Volpe, R.P. Patel, K. Yu, C.M. Yakacki, Liquid crystal elastomers: An introduction and review of emerging technologies. Liq. Cryst. Rev. 6, 78 (2018). https://doi.org/10.1080/21680396.2018.1530155
G. Wan, C. Jin, I. Trase, S. Zhao, Z. Chen, Helical structures mimicking chiral seedpod opening and tendril coiling. Sensors 18(9), 2973 (2018). https://doi.org/10.3390/s18092973
M. Warner, Topographic mechanics and applications of liquid crystalline solids. Annu. Rev. Condens. Matter Phys. 11, 125 (2020). https://doi.org/10.1146/annurev-conmatphys031119-050738
Z. Wen, K. Yang, J.M. Raquez, A review on liquid crystal polymers in free-standing reversible shape memory materials. Molecules 25, 1241 (2020). https://doi.org/10.3390/molecules25051241
T.J. White, Photomechanical effects in liquid crystalline polymer networks and elastomers. J. Polym. Sci. B Polym. Phys. 56, 695 (2018). https://doi.org/10.1002/polb.24576
T.J. White, D.J. Broer, Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 14, 1087 (2015). https://doi.org/10.1038/nmat4433
Y. Xia, A. Honglawan, S. Yang, Tailoring surface patterns to direct the assembly of liquid crystalline materials. Liq. Cryst. Rev. 7(1), 30 (2019). https://doi.org/10.1080/21680396.2019.1598295
S.M. Clarke, E.M. Terentjev, Slow stress relaxation in randomly disordered nematic elastomers and gels. Phys. Rev. Lett. 81(20), 4436 (1998). https://doi.org/10.1103/PhysRevLett.81.4436
S.M. Clarke, E.M. Terentjev, I. Kundler, H. Finkelmann, Texture evolution during the polydomain-monodomain transition in nematic elastomers. Macromolecules 31(15), 48624872 (1998). https://doi.org/10.1021/ma980195j
J. Küpfer, H. Finkelmann, Nematic liquid single crystal elastomers. Makromol. Chem. Rapid Commun. 12, 717 (1991). https://doi.org/10.1002/marc.1991.030121211
M.O. Saed, A.H. Torbati, C.A. Starr, R. Visvanathan, N.A. Clark, C.M. Yakacki, Thiolacrylate main-chain liquid-crystalline elastomers with tunable thermomechanical properties and actuation strain. J. Polym. Sci. 55(2), 157 (2017). https://doi.org/10.1002/polb.24249
N.A. Traugutt, R.H. Volpe, M.S. Bollinger, M.O. Saed, A.H. Torbati, K. Yu, N. Dadivanyan, C.M. Yakacki, Liquid-crystal order during synthesis affects main-chain liquid-crystal elastomer behavior. Soft Matter 13, 7013 (2017). https://doi.org/10.1039/c7sm01405h
K. Urayama, E. Kohmon, M. Kojima, T. Takigawa, Polydomain-monodomain transition of randomly disordered nematic elastomers with different cross-linking histories. Macromolecules 42, 4084 (2009). https://doi.org/10.1021/ma9004692
P. Bladon, E.M. Terentjev, M. Warner, Deformation-induced orientational transitions in liquid crystal elastomers. J. Phys. II 4, 75 (1994). https://doi.org/10.1051/jp2:1994100
M. Warner, K.P. Gelling, T.A. Vilgis, Theory of nematic networks. J. Chem. Phys. 88, 4008 (1998). https://doi.org/10.1063/1.453852
M. Warner, X.J. Wang, Elasticity and phase behavior of nematic elastomers. Macromolecules 24, 4932 (1991). https://doi.org/10.1021/ma00017a033
L.R.G. Treloar, The Physics of Rubber Elasticity, 3rd ed. (Oxford University Press, Oxford, UK, 2005)
M. Warner, E.M. Terentjev, Nematic elastomers—A new state of matter? Prog. Polym. Sci. 21, 853 (1996)
M. Warner, E.M. Terentjev, Liquid Crystal Elastomers (Oxford University Press, Oxford, UK, 2007)
R. Bai, K. Bhattacharya, Photomechanical coupling in photoactive nematic elastomers. J. Mech. Phys. Solids 144, 104115 (2020). https://doi.org/10.1016/j.jmps.2020.104115
C.D. Modes, K. Bhattacharya, M. Warner, Disclination-mediated thermo-optical response in nematic glass sheets. Phys. Rev. E 81, 060701(R) (2010). https://doi.org/10.1103/PhysRevE.81.060701
C.D. Modes, K. Bhattacharya, M. Warner, Gaussian curvature from flat elastica sheets. Proc. Royal Soc. A 467, 1121 (2011). https://doi.org/10.1098/rspa.2010.0352
P.G. de Gennes, J. Prost, The Physics of Liquid Crystals (Clarendon Press, Oxford, UK, 1993)
F.C. Frank, I. Liquid crystals. On the theory of liquid crystals. Discuss. Faraday Soc. 25, 19 (1958)
J.S. Biggins, M. Warner, K. Bhattacharya, Supersoft elasticity in polydomain nematic elastomers. Phys. Rev. Lett. 103, 037802 (2009). https://doi.org/10.1103/PhysRevLett.103.037802
J.S. Biggins, M. Warner, K. Bhattacharya, Elasticity of polydomain liquid crystal elastomers. J. Mech. Phys. Solids 60, 573 (2012). https://doi.org/10.1016/j.jmps.2012.01.008
V. Agostiniani, G. Dal Maso, A. DeSimone, Attainment results for nematic elastomers. Proc. Royal Soc. Edinb. A 145, 669 (2015). https://doi.org/10.1017/S0308210515000128
V. Agostiniani, A. DeSimone, Ogden-type energies for nematic elastomers. Int. J. Non Linear Mech. 47(2), 402 (2012). https://doi.org/10.1016/j.ijnonlinmec.2011.10.001
A. DeSimone, L. Teresi, Elastic energies for nematic elastomers. Eur. Phys. J. E 29, 191 (2009). https://doi.org/10.1140/epje/i2009-10467-9
E. Fried, An elementary molecular-statistical basis for the Mooney and Rivlin-Saunders theories of rubber elasticity. J. Mech. Phys. Solids 50, 571 (2002). https://doi.org/10.1016/S0022-5096(01)00086-2
C.O. Horgan, G. Saccomandi, A molecular-statistical basis for the Gent constitutive model of rubber elasticity. J. Elast. 68, 167 (2002). https://doi.org/10.1023/A:1026029111723
D.R. Anderson, D.E. Carlson, E. Fried, A continuum-mechanical theory for nematic elastomers. J. Elast. 56, 33 (1999). https://doi.org/10.1023/A:1007647913363
Y. Zhang, C. Xuan, Y. Jiang, Y. Huo, Continuum mechanical modeling of liquid crystal elastomers as dissipative ordered solids. J. Mech. Phys. Solids 126, 285 (2019). https://doi.org/10.1016/j.jmps.2019.02.018
C.E. Shannon, A mathematical theory of communication. Bell Syst. Tech. J. 27(379–423), 623–659 (1948)
E.T. Jaynes, Information theory and statistical mechanics I. Phys. Rev. 108, 171 (1957)
E.T. Jaynes, Information theory and statistical mechanics II. Phys. Rev. 106, 620 (1957)
E.T. Jaynes, Probability Theory: The Logic of Science (Cambridge University Press, Cambridge, New York, 2003)
J. Guilleminot, Modelling Non-Gaussian Random Fields of Material Properties in Multiscale Mechanics of Materials, in Uncertainty Quantification in Multiscale Materials Modeling, Y. Wang, F.L. McDowell (Eds.) (Elsevier, Cambridge, MA, 2020)
J. Guilleminot, C. Soize, “Non-Gaussian Random Fields in Multiscale Mechanics of Heterogeneous Materials,” in Encyclopedia of Continuum Mechanics (Springer, Berlin, Germany, 2017)
C. Soize, Uncertainty Quantification: An Accelerated Course with Advanced Applications in Computational Engineering, Interdisciplinary Applied Mathematics Book 47 (Springer, New York, 2017)
P.J. Flory, Thermodynamic relations for high elastic materials. Trans. Faraday Soc. 57, 829 (1961). https://doi.org/10.1039/TF9615700829
F. Cirak, Q. Long, K. Bhattacharya, M. Warner, Computational analysis of liquid crystalline elastomer membranes: Changing Gaussian curvature without stretch energy. Int. J. Solids Struct. 51(1), 144 (2014). https://doi.org/10.1016/j.ijsolstr.2013.09.019
A. DeSimone, Energetics of fine domain structures. Ferroelectrics 222(1), 275 (1999). https://doi.org/10.1080/00150199908014827
A. DeSimone, G. Dolzmann, Material instabilities in nematic elastomers. Phys. D 136(1–2), 175 (2000)
A. DeSimone, G. Dolzmann, Macroscopic response of nematic elastomers via relaxation of a class of SO(3)-invariant energies. Arch. Ration. Mech. Anal. 161, 181204 (2002). https://doi.org/10.1007/s002050100174
G.C. Verwey, M. Warner, E.M. Terentjev, Elastic instability and stripe domains in liquid crystalline elastomers. J. Phys. 6(9), 1273 (1996). https://doi.org/10.1051/jp2:1996130.
M. Warner, P. Bladon, E. Terentjev, “Soft elasticity”—Deformation without resistance in liquid crystal elastomers. J. Phys. II 4, 93 (1994). https://doi.org/10.1051/jp2:1994116
A. Goriely, The Mathematics and Mechanics of Biological Growth (Springer-Verlag, New York, 2017)
V.A. Lubarda, Constitutive theories based on the multiplicative decomposition of deformation gradient: Thermoelasticity, elastoplasticity and biomechanics. Appl. Mech. Rev. 57(2), 95 (2004). https://doi.org/10.1115/1.1591000
C. Goodbrake, A. Goriely, A. Yavari, The mathematical foundations of anelasticity: Existence of smooth global intermediate configurations. Proc. R. Soc. A 477, 20200462 (2021). https://doi.org/10.1098/rspa.2020.0462
S. Sadik, A. Yavari, On the origins of the idea of the multiplicative decomposition of the deformation gradient. Math. Mech. Solids 22(4), 771 (2017). https://doi.org/10.1177/1081286515612280
L.A. Mihai, A. Goriely, A plate theory for nematic liquid crystalline solids. J. Mech. Phys. Solids 144, 104101 (2020). https://doi.org/10.1016/j.jmps.2020.104101
L.A. Mihai, A. Goriely, A pseudo-anelastic model for stress softening in liquid crystal elastomers. Proc. R. Soc. A 476, 2243 (2020). https://doi.org/10.1098/rspa.2020.0558
L.A. Mihai, A. Goriely, Likely striping in stochastic nematic elastomers. Math. Mech. Solids 25(10), 1851 (2020). https://doi.org/10.1177/1081286520914958
D. Fitt, H. Wyatt, T.E. Woolley, L.A. Mihai, Uncertainty quantification of elastic material responses: Testing, stochastic calibration and Bayesian model selection. Mech. Soft Mater. 1, 13 (2019). https://doi.org/10.1007/s42558-019-0013-1
L.A. Mihai, M. Alamoudi, Likely oscillatory motions of stochastic hyperelastic spherical shells and tubes. Int. J. Non Linear Mech. 130, 103671 (2021). https://doi.org/10.1016/j.ijnonlinmec.2021.103671
L.A. Mihai, D. Fitt, T.E. Woolley, A. Goriely, Likely equilibria of stochastic hyperelastic spherical shells and tubes. Math. Mech. Solids 24(7), 2066 (2019). https://doi.org/10.1177/108128651881188
L.A. Mihai, D. Fitt, T.E. Woolley, A. Goriely, Likely oscillatory motions of stochastic hyperelastic solids. Trans. Math. Appl. 3(1), tnz003 (2019). https://doi.org/10.1093/imatrm/tnz003
L.A. Mihai, D. Fitt, T.E. Woolley, A. Goriely, Likely cavitation in stochastic elasticity. J. Elast. 137(1), 27 (2019). https://doi.org/10.1007/s10659-018-9706-1
L.A. Mihai, T.E. Woolley, A. Goriely, Stochastic isotropic hyperelastic materials: Constitutive calibration and model selection. Proc. R. Soc. A 474, 20170858 (2018). https://doi.org/10.1098/rspa.2017.0858
L.A. Mihai, T.E. Woolley, A. Goriel, Likely equilibria of the stochastic Rivlin cube. Phil. Trans. R. Soc. A 377, 20180068 (2019). https://doi.org/10.1098/rsta.2018.0068
L.A. Mihai, T.E. Woolley, A. Goriely, Likely chirality of stochastic anisotropic hyperelastic tubes. Int. J. Non Linear Mech. 114, 9 (2019). https://doi.org/10.1016/j.ijnonlinmec.2019.04.004
L.A. Mihai, T.E. Woolley, A. Goriely, Likely cavitation and radial motion of stochastic elastic spheres. Nonlinearity 33(5), 1987 (2020). https://doi.org/10.1088/1361-6544/ab7104
B. Staber, J. Guilleminot, Stochastic modeling of a class of stored energy functions for incompressible hyperelastic materials with uncertainties. C. R. Mech. 343, 503 (2015). https://doi.org/10.1016/j.crme.2015.07.008
B. Staber, J. Guilleminot, Stochastic modeling of the Ogden class of stored energy functions for hyperelastic materials: The compressible case. J. Appl. Math. Mech. 97, 273 (2016). https://doi.org/10.1002/zamm.201500255
B. Staber, J. Guilleminot, Stochastic hyperelastic constitutive laws and identification procedure for soft biological tissues with intrinsic variability. J. Mech. Behav. Biomed. Mater. 65, 743 (2017). https://doi.org/10.1016/j.jmbbm.2016.09.022
B. Staber, J. Guilleminot, A random field model for anisotropic strain energy functions and its application for uncertainty quantification in vascular mechanics. Comput. Meth. Appl. Mech. Eng. 333, 94 (2018). https://doi.org/10.1016/j.cma.2018.01.001
B. Staber, J. Guilleminot, C. Soize, J. Michopoulos, A. Iliopoulos, Stochastic modeling and identification of an hyperelastic constitutive model for laminated composites. Comput. Meth. Appl. Mech. Eng. 347, 425 (2019). https://doi.org/10.1016/j.cma.2018.12.036
G.C. Verwey, M. Warner, Soft rubber elasticity. Macromolecules 28, 4303 (1995)
P. Olmsted, Rotational invariance and Goldstone modes in nematic elastomers and gels. J. Phys. II 4(12), 2215 (1994). https://doi.org/10.1051/jp2:1994257
H. Finkelmann, I. Kundler, E.M. Terentjev, M. Warner, Critical stripe-domain instability of nematic elastomers. J. Phys. II 7, 1059 (1997). https://doi.org/10.1051/jp2:1997171
I. Kundler, H. Finkelmann, Strain-induced director reorientation in nematic liquid single crystal elastomers. Macromol. Rapid Commun. 16, 679 (1995). https://doi.org/10.1002/marc.1995.030160908
R.V. Talroze, E.R. Zubarev, S.A. Kuptsov, A.S. Merekalov, T.I. Yuranova, N.A. Plate, H. Finkelmann, Liquid crystal acrylate-based networks: Polymer backbone-LC order interaction. Reac. Funct. Polym. 41, 1 (1999). https://doi.org/10.1016/S1381-5148(99)00032-2
E.R. Zubarev, S.A. Kuptsov, T.I. Yuranova, R.V. Talroze, H. Finkelmann, Monodomain liquid crystalline networks: Reorientation mechanism from uniform to stripe domains. Liq. Cryst. 26, 1531 (1999). https://doi.org/10.1080/026782999203869
S. Conti, A. DeSimone, G. Dolzmann, Soft elastic response of stretched sheets of nematic elastomers: A numerical study. J. Mech. Phys. Solids 50, 1431 (2002)
E. Fried, S. Sellers, Free-energy density functions for nematic elastomers. J. Mech. Phys. Solids 52(7), 1671 (2004). https://doi.org/10.1016/j.jmps.2003.12.005
E. Fried, S. Sellers, Orientational order and finite strain in nematic elastomers. J. Chem. Phys. 123(4), 043521 (2005). https://doi.org/10.1063/1.1979479
E. Fried, S. Sellers, Soft elasticity is not necessary for striping in nematic elastomers. J. Appl. Phys. 100, 043521 (2006). https://doi.org/10.1063/1.2234824
L.R.G. Treloar, Stress-strain data for vulcanized rubber under various types of deformation. Trans. Faraday Soc. 40, 59 (1944). https://doi.org/10.1039/TF9444000059
L.A. Mihai, A. Goriely, How to characterize a nonlinear elastic material? A review on nonlinear constitutive parameters in isotropic finite elasticity. Proc. R. Soc. A 473, 20170607 (2017). https://doi.org/10.1098/rspa.2017.0607
J.M. Ball, Fine phase mixtures as minimizers of energy. Arch. Ration. Mech. Anal. 100, 13 (1987)
J.M. Ball, R.D. James, Proposed experimental tests of a theory of fine microstructure, and the two-well problem. Phil. Trans. R. Soc. Lond. A 338, 389 (1992)
L.A. Mihai, P. Neff, Hyperelastic bodies under homogeneous Cauchy stress induced by non-homogeneous finite deformations. Int. J. Non Linear Mech. 89, 93 (2017)
L.A. Mihai, P. Neff, Hyperelastic bodies under homogeneous Cauchy stress induced by three-dimensional non-homogeneous deformations. Math. Mech. Solids (2017). https://doi.org/10.1177/1081286516682556
D. Mistry, H.F. Gleeson, Mechanical deformations of a liquid crystal elastomer at director angles between 0̊ and 90̊: Deducing an empirical model encompassing anisotropic nonlinearity. J. Polym. Sci. 57, 1367 (2019). https://doi.org/10.1002/polb.24879
S. Okamoto, S. Sakurai, K. Urayama, Effect of stretching angle on the stress plateau behavior of main-chain liquid crystal elastomers. Soft Matter 17, 3128 (2021). https://doi.org/10.1039/d0sm02244f
W.F. Busse, Physics of rubber as related to the automobile. J. Appl. Phys. 9(7), 438 (1939). https://doi.org/10.1063/1.1710439
F.L. Yerzley, Adhesion of neoprene to metal. Ind. Eng. Chem. 31(8), 950 (1939). https://doi.org/10.1021/ie50356a007
A.N. Gent, P.B. Lindley, Internal rupture of bonded rubber cylinders in tension. Proc. R. Soc. Lond. A 249, 195 (1959)
J.M. Ball, Discontinuous equilibrium solutions and cavitation in nonlinear elasticity. Phil. Trans. R. Soc. A 306(1496), 557 (1982). https://doi.org/10.1098/rsta.1982.0095
M. Baker, J.L. Ericksen, Inequalities restricting the form of stress-deformation relations for isotropic elastic solids and Reiner-Rivlin fluids. J. Wash. Acad. Sci. 44(2), 33 (1954)
M. Marzano, An interpretation of Baker-Ericksen inequalities in uniaxial deformation and stress. Meccanica 18, 233 (1983). https://doi.org/10.1007/BF02128248
A. Mallock, Note on the instability of India-rubber tubes and balloons when distended by fluid pressure. Proc. R. Soc. Lond. 49, 458 (1891). https://doi.org/10.1098/rspl.1890.0116
R.S. Rivlin, Large elastic deformations of isotropic materials. VI. Further results in the theory of torsion, shear and flexure. Phil. Trans. R. Soc. Lond. A 242(845), 173 (1949)
A.E. Green, R.T. Shield, Finite elastic deformations in incompressible isotropic bodies. Proc. R. Soc. Lond. A 202, 407 (1950)
J.E. Adkins, R.S. Rivlin, Large elastic deformations of isotropic materials. IX. The deformation of thin shells. Phil. Trans. R. Soc. Lond. A 244, 505 (1952)
R.T. Shield, On the stability of finitely deformed elastic membranes. II. Stability of inflated cylindrical and spherical membranes. Z. Angew. Math. Phys. 23, 16 (1972)
M.M. Carroll, Pressure maximum behavior in inflation of incompressible elastic hollow spheres and cylinders. Q. Appl. Math. 45, 141 (1987)
A. Giudici, J.S. Biggins, Giant deformations and soft-inflation in LCE balloons. Europhys. Lett. 132(3), 36001 (2020). https://doi.org/10.1209/0295-5075/132/36001
V. Lee, K. Bhattacharya, Actuation of cylindrical nematic elastomer balloons. J. Appl. Phys. 129, 114701 (2020)
M. Mooney, A theory of large elastic deformation. J. Appl. Phys. 11, 582 (1940)
R.S. Rivlin, Large elastic deformations of isotropic materials. IV. Further developments of the general theory. Phil. Trans. R. Soc. Lond. A 241, 379 (1948)
S.S. Antman, Nonuniqueness of equilibrium states for bars in tension. J. Math. Anal. Appl. 44(2), 333 (1973). https://doi.org/10.1016/0022-247X(73)90063-2
S.S. Antman, E.R. Carbone, Shear and necking instabilities in nonlinear elasticity. J. Elast. 7(2), 125 (1977). https://doi.org/10.1007/BF00041087
B. Audoly, J.W. Hutchinson, Analysis of necking based on a one-dimensional model. J. Mech. Phys. Solids 97, 68 (2016). https://doi.org/10.1016/j.jmps.2015.12.018
B.D. Coleman, D.C. Newman, On the rheology of cold drawing. I. Elastic materials. J. Polym. Sci B Polym. Phys. 26, 1801 (1988). https://doi.org/10.1002/polb.1988.090260901
J.L. Ericksen, Equilibrium of bars. J. Elast. 5(3–4), 191 (1975). https://doi.org/10.1007/BF00126984
R. Hill. J.W. Hutchinson, Bifurcation phenomena in the plane tension test. J. Mech. Phys. Solids 23(4–5), 239 (1975). https://doi.org/10.1016/0022-5096(75)90027-7
N. Owen, Existence and stability of necking deformations for nonlinearly elastic rods. Arch. Ration. Mech. Anal. 98, 357 (1987). https://doi.org/10.1007/BF00276914
A. Consid´ere, M´emoire sur l’emploi du fer et de l’acier dans les constructions. Ann. Ponts Chaussees 6 (9), 574 (1885)
J. Sivaloganathan, S.J. Spector, On the stability of incompressible elastic cylinders in uniaxial extension. J. Elast. 105(1–2), 313 (2011). https://doi.org/10.1007/s10659-011-9330-9
X. He, Y. Zheng, Q. He, S. Cai, Uniaxial tension of a nematic elastomer with inclined mesogens. Extreme Mech. Lett. 40, 100936 (2020). https://doi.org/10.1016/j.eml.2020.100936
H. Higaki, T. Takigawa, K. Urayama, Nonuniform and uniform deformations of stretched nematic elastomers. Macromolecules 46, 5223 (2013). https://doi.org/10.1021/ma400771z
A.N. Gent, A.G. Thomas, Forms for the stored (strain) energy function for vulcanized rubber. J. Polym. Sci. 28, 625 (1958)
Q. He, Y. Zheng, Z. Wang, X. He, S. Cai, Anomalous inflation of a nematic balloon. J. Mech. Phys. Solids 142, 104013 (2020). https://doi.org/10.1016/j.jmps.2020.104013
Y.B. Fu, J.L. Liu, G.S. Francisco, Localized bulging in an inflated cylindrical tube of arbitrary thickness–The effect of bending stiffness. J. Mech. Phys. Solids 90, 45 (2016)
Y. Fu, L. Jin, A. Goriely, Necking, beading, and bulging in soft elastic cylinders. J. Mech. Phys. Solids 147, 104250 (2021). https://doi.org/10.1016/j.jmps.2020.104250
Y. Ye, Y. Liu, Y. Fu, Weakly nonlinear analysis of localized bulging of an inflated hyperelastic tube of arbitrary wall thickness. J. Mech. Phys. Solids 135, 103804 (2020). https://doi.org/10.1016/j.jmps.2019.103804
Acknowledgments
We gratefully acknowledge the support by the Engineering and Physical Sciences Research Council of Great Britain under research grant EP/R020205/1 to Alain Goriely and grant EP/S028870/1 to L. Angela Mihai.
Author information
Authors and Affiliations
Corresponding author
Supplementary information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mihai, L.A., Goriely, A. Instabilities in liquid crystal elastomers. MRS Bulletin 46, 784–794 (2021). https://doi.org/10.1557/s43577-021-00115-2
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1557/s43577-021-00115-2