Abstract
The infrared solar spectrum contains a wealth of physical data about our Sun, and is explored using modern detectors and technology with new ground-based solar telescopes. The scientific motivation behind exploring these wavelengths is presented, along with a brief look at the rich history of observations here. Several avenues of solar physics research exploiting and benefiting from observations at infrared wavelengths from roughly 1000 nm to 12 400 nm are discussed, and the instrument and detector technology driving this research is briefly summarized. Finally, goals for future work at infrared wavelengths are presented in conjunction with ground and space-based observations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
“Why does anyone still observe the Sun using visible wavelengths of light?” a colleague recently asked of me. Certainly night-time astronomers have been exploiting the infrared spectrum for many years to address critical science questions in that field. The spatial resolution, flux, and background problems are even more extreme at night than they are for observations of the Sun. Infrared detector and instrument technology is clearly robust, and the scientific advantages are important. So then why is not the majority of solar data, particularly ground-based solar data, taken in the infrared spectrum? The best answer I could conceive was simply that of tradition. Solar observations have been made in visible wavelengths for hundreds if not thousands of years, and many of those observations have produced breakthrough science. But one thing is certain: the Sun is still stubbornly keeping secrets from us. The goal of this review is to clearly show how we can attack those outstanding questions in solar physics by looking through the window provided by the infrared spectrum.
From the discovery of infrared radiation by William Hershel (Herschel, 1800) infrared referred to light with a wavelength too long to be detected by the human eye. As the human eye is replaced in astronomy by a plethora of different types of detectors, this definition falters, and we must look for other ways to define the infrared spectrum. One technique which is often used (Jefferies, 1994) simply defines the infrared spectrum as three decades of wavelength, from a wavelength of 1000 nm to a wavelength of 1 mm. On the short wavelength side, this definition roughly agrees with a detector-based definition. Silicon detectors are sensitive to visible wavelengths, and drop to very little sensitivity at a wavelength around 1000 nm. On the long wavelength end, this definition includes some of the sub-mm or terahertz radation (usually 0.1 to 1 mm). For the purposes of this review paper, these three decades of wavelength will be used to define infrared radiation.
Since the visible spectrum covers a wavelength range of only a factor of two, and the infrared spectrum covers a factor of 1000, it is useful to sub-divide the infrared spectrum into smaller wavelength ranges. Table 1 shows a list of commonly used names for the different parts of the infrared spectrum. While this nomenclature is often used, it is not strictly defined for the three regions of Near-IR, Mid-IR, and Far-IR, and one should expect to see the terms used only loosely especially in fields outside of astronomy. Table 1 also includes lists of the corresponding wavenumber and frequency intervals for these bands, again only approximately computed due to the informal nature of the definitions. The last column shows the temperatures corresponding to black body radiation curves with peaks at the wavelength boundaries, computed using Wien’s displacement law, where T = 2897/λmax in degrees Kelvin when the wavelength is written in microns. Recalling the fact that solar telescopes and their associated optics operate near room temperature of 300 K, the meaning for the term thermal IR becomes clear: at wavelengths from about 4000 nm and longer, photon flux emitted from background sources can dominate even solar photon flux. Measurements at these wavelengths become background dominated, and clever observational techniques must often be used.
Instead of using these labels, a simple division of the infrared spectrum by factors of ten is appealing. In the first decade of wavelengths (1000 to 10000 nm) the spectrum is explored using array detectors which are similar to those used at visible wavelengths. In the longest wavelength decade (from 0.1 to 1 mm) measurements are often made using heterodyne receivers or radiation waveguides which resemble radio detectors. Here I will focus on results in the first decade of the infrared wavelength range, from about 1000 to 10 000 nm including just a few notable exceptions outside of this range. Studies of the Sun at longer wavelengths have been reviewed by Deming et al. (1991b) and new exciting results continue to be made, especially by Kaufmann et al. (2013); but these wavelengths will be left for future discussion.
Within this smaller wavelength range, it is useful to consider both atmospheric transmission and detectors again. Figure 1 from Hinkle et al. (2003) shows a diagram of the Earth’s atmospheric transmission. There are several clear wavelength regions where a high percentage of light is transmitted to the surface of the Earth, and there are several blocked wavelength regions where light is very effectively absorbed by the Earth’s atmosphere. In astronomy, these atmospheric transmission windows were exploited for stellar photometry, and the early work of stellar astronomers, (especially Johnson, 1962) established the nomenclature for the infrared wavelength bands in the 1000 to 5000 nm range known as J, H, K, L, and M. The central wavelengths of these bands are roughly 1300, 1600, 2200, 3600, and 5000 nm. and the names are often used to describe infrared solar spectral observations.
Atmospheric transmission from 560 to 21000 nm as measured from the McMath-Pierce facility at Kitt Peak. The molecules which are responsible for the various absorption bands are marked. Image reproduced with permission from Hinkle et al. (2003), copyright by AAS.
Finally, it is useful to briefly discuss the detectors used for study in the Near-IR region. In order to detect a photon with a reasonable level of efficiency, a detector pixel needs to be roughly the size of the photon wavelength or larger. At these wavelengths, array detectors with pixel sizes of order 10 or 100 microns (just as for visible wavelengths) can be used as efficient detectors. Silicon array detectors, including both CMOS and CCD cameras, have a quantum efficiency which drops to near zero at roughly 1100 nm, as the silicon substrate becomes transparent to longer wavelength photons.
Infrared detectors are highly desirable items for many industrial purposes, and so the technology is changing constantly. Several reviews of the applications of these new arrays to astronomy have been published and make useful resources (for two examples, see Wynn-Williams and Becklin, 1987; Rieke, 2007). In general, arrays which use new technology strive for high efficiency within the wavelength range of interest, as well as high uniformity of response with a low dark current. Ease-of-use and expense are also factors which enter into the development process. At the current date, infrared observations at different wavelengths are regularly made with a handful of different types of detectors. These include arrays with detectors of HgCdTe (roughly 1000–2200 nm), InGaAs (roughly 1000–1800 nm), InSb (1000–5000 nm), Si:X doped silicon arrays (2000–30000 nm), Ge:X doped germanium arrays (28 000–20 0000 nm), and PtSi diode arrays Ge bolometer arrays. There are many new detector technologies under development, and solar physics research is often the first place that these new technologies can achieve scientific results. The quantum well infrared photodetector (QWIP) cameras offer a new and inexpensive route for measuring infrared photons, and are currently being tested at the NSO McMath-Pierce Solar Facility (McM-P).
2 Science and Instrumentation Considerations for Infrared Solar Observations
There are several advantages which can be realized by observing the Sun at infrared wavelengths compared to observations at shorter wavelengths. These advantages concern the behavior of the Earth’s atmosphere and the telescope, as well as the physics of atoms and solar radiative transfer. While these factors play an important role in studies of the solar disk, they can be absolutely critical for studies of the faint solar corona. To be fair, there are also disadvantages to observing at infrared wavelengths, and these will also be discussed below. Borrowing from Harvey and Hall (1971), presented below is a discussion of the advantages and disadvantages of making observations of the Sun at infrared wavelengths.
2.1 Instrument advantages in the infrared
2.1.1 Better atmospheric seeing
It has been known for a long time that seeing improves at longer wavelengths, and early work at infrared wavelengths suggested that atmospheric seeing was so minimal that many telescopes were seen to achieve their diffraction limit (Turon and Léna, 1970). Most modern ground-based solar observations do not settle for seeing limitations imposed by the atmosphere. New progress in the field of adaptive optics has resulted in superb image quality for images of the solar surface. Image stability is also key for spectroscopic and polarimetric studies of the Sun, especially when scanning the solar image is required to build a map of the solar surface.
Adaptive optics (AO) correction techniques have been discussed in many places and a good reference is the Living Reviews article by Rimmele and Marino (2011). The general aim of an AO system is to correct the effects of atmospheric turbulence on the wavefront measured by the telescope so that the total optical transfer function (OTF) of the telescope and the atmosphere approaches the OTF of the diffraction limit of the telescope. The wavefront distortions introduced by changing atmospheric refraction depend on the wavelength of the light observed. A quantity known as the Fried parameter r0 is used to characterize the atmospheric distortions integrated through the atmosphere. Early work from Karo and Schneiderman (1978) with stellar sources (and even earlier lab work) showed that the Fried parameter increase with wavelength as r0 ≈ λ6/5.
This enters into the performance of an AO system in two ways. First the angular extent over which an image can be corrected by an AO system (also known as the isoplanatic patch) increases as r0 increases, and so at infrared wavelengths an AO system can correct a larger area of the solar image than at visible wavelengths.
The second advantage comes from a physical description of the Fried parameter; it represents a typical atmospheric size-scale with little distortion; a region of the atmosphere across which diffractive changes of the incident wavefront are minimal. The time-scale associated with the image distortions is given by the Fried parameter divided by the atmospheric wind speed (which moves the distortions across the telescope’s line of sight) TAO r0/υatm. So for larger Fried parameter values, the time scale is larger, and the image changes more slowly. This means that AO system can work more slowly, and this is the second way in which AO correction is easier at longer wavelengths.
2.1.2 Less atmospheric scattering
Atmospheric scattered light has been studied for many years. The scattering at visible wavelengths in a clear sky was explained well by Lord Rayleigh (J. Strutt) as early as 1871 (Strutt, 1871) with single scattering from molecules in the atmosphere. Approximate solutions of electromagnetic scattering from particles smaller than the wavelength of light show a dependence on wavelength which varies as λ−4. Thus blue light is highly scattered, while red and infrared light is scattered less and transmitted more. Early infrared observations (Knestrick et al., 1962) confirmed that while the amount of infrared scattering was much smaller than visible scattering, the wavelength dependence was flatter (see Figure 2). At infrared wavelengths the particle size is closer to the wavelength of the radiation, and so the Rayleigh approximation does not work.
Atmospheric scattered light as a function of wavelength from sea level measurements over water, taken in 1959–1960. Corrections for water vapor and methane absorption were made. The wavelength behavior of the scattering changes on different days, presumably depending on the particulates present during the testing. These particular measurements show at best a λ−1.7 change, but at other times are nearly flat. Image reproduced with permission from Knestrick et al. (1962), copyright by OSA.
At infrared wavelengths, the Mie solution to the scattering problem must be used. Mie scattering solutions can be computed using a variety of scattering source sizes, and can represent different types of atmospheric particulates. Results of such calculations show only a small decrease with wavelength, and also show more complex wavelength behavior, determined by the molecules found in the scattering sources (Whittet et al., 1987).
2.1.3 Less instrumental scattering
Scattered light is present in all telescopes, reflecting and refracting. In the simplest model, a manufactured mirror will have small-scale deviations from the ideal shape. The root mean square of this deviation is known as the surface roughness, σ, and in the best case the surface roughness is small compared to the wavelength of light. Bennet and Porteus (1961) show that the diffuse reflection from such a surface will vary as (σ/λ)2, and Harvey et al. (2012) define the total integrated scatter (TIS) as the ratio of the diffuse reflectance to the specular reflectance, which also varies as TIS ≈ (σ/λ)2. Harvey et al. (2012) also point out that it is important to use the relevent spatial scale of the surface roughness (generally the surface deviations on length scales of less than 1 mm) for these calculations. While deviations on larger spatial scales (sometimes known as figure errors) also contribute to scattering, and a more complete discussion of scattering is provided by calculating the bidirectional reflectance-distribution function (Nicodemus, 1970), the wavelength dependence of the BRDF is encapsulated in the TIS. So as observations move from visible to infrared wavelengths, the scattered light which disturbs those measurements decreases sharply.
For mirrors which are not perfectly clean, the situation becomes more complicated. As might be expected from the discussion of atmospheric scattering, the telescope scattering at infrared wavelengths is limited by scattering from dust contamination rather than from diffuse reflection caused by surface roughness. Surface contamination of the mirror by dust particles can be examined with Mie scattering solutions, but models of mirror BRDF at 10 600 nm reproduce the measured BRDF values only to a factor of 5 (Spyak and Wolfe, 1992a). So while moving from 1150 nm to 10 600 nm wavelength, the total scattering from an ideal mirror should decrease by a factor of 100, real measurements and also predictions from dust scattering models show that the actual scattering decreases by only a factor of about 20 (Spyak and Wolfe, 1992b). Scattering from dust on mirror surfaces is the dominant source at infrared wavelengths, and while the total scatter does decrease with wavelength, it decreases about a factor of 5 more slowly than surface roughness arguments alone would predict.
What scattered light has been observed at real solar telescopes? Staveland (1970) reports a wavelength dependence in the combined telescopic and atmospheric scatter, which drops faster than λ−1 but not as steep as λ−4. Work at the McM-P telescope by Johnson (1972) provides total scattered light observations at the limb of the Sun from about 1000 nm to 20 000 nm. The data show a drop of only a factor of two from 1000 nm to 5000 nm, and then rather uniform scattered light at wavelengths towards 20000 nm. This work also provides a numerical fit of TIS = 0.026 + 0.06(1 + λ/1000nm)e−λ/1000 nm, but this 40 year-old work should be re-examined with modern instrumentation.
2.1.4 Smaller instrumental polarization
A telescope introduces polarization to change the input polarization of light it recieves in ways which mix the different states, sometimes making it difficult to retrieve the original polarized signal. This process has been studies in great detail, and the parameter used to measure this change is the Mueller matrix. The Mueller matrix acts on the input polarization to produce the measured polarization state output by the telescope, which is given by: \({\vec S}_{\rm out} = M{\vec S}_{\rm in}\). Here \({\vec S} = [I, Q, U, V]\) represents the intensity of the four Stokes components of polarized light. In an ideal system the Mueller matrix is fully diagonal, and in the best case with no instrumental polarization it is equal to the identity matrix.
In a telescope with many optical elements, the total Mueller matrix can be constructed by multiplying the matrices from the individual elements. Balasubramaniam et al. (1985) specify the Mueller matrix for a reflection off of a single mirror as:
where the terms X and tan(τ) are dependent upon the angle of incidence, and the real (n) and imaginary (k) components of the index of refraction. For values of X approaching 1.0 and τ approaching zero, the Mueller matrix becomes diagonal and instrumental polarization effects are reduced. This occurs for increasing values of either n or k.
Aluminum is often used as a mirror surface, and the index of refraction of aluminum has been measured through a large wavelength range. In the infrared spectrum, the value of k increases, and for values of wavelength greater than about 1250 nm, the value of n also increases (Rakić, 1995). An aluminum mirror introduces less instrumental polarization through the infrared spectrum.
While many infrared telescopes and instruments use all-reflecting optical systems, some telescopes also use transmissive optics in the infrared. Additionally, as metal coatings on mirrors are exposed to the air, metal oxide layers build up which also act as transmission elements in the optical system. With these added complications, do real telescopes also show a decreasing instrumental polarization at infrared wavelengths? Socas-Navarro et al. (2011) made measurements of the Mueller matrix of the NSO/DST (which includes transmissive optics) as a function of wavelength from 470 nm to 1413 nm. The infrared coverage is not large, but clear trends can be seen from 1000 to 1413 nm in their analysis. All the off-diagonal terms in the matrix decrease in value and in some cases are already very close to zero at 1413 nm (see Figure 3). At the all-reflecting NSO/McM-P facility, studies at 12 000 nm show that the off-diagonal terms in the telescope matrix were expected to be at the level of about 1% or less, (Deming et al., 1991a) and measured to have an upper limit of 4% (Hewagama, 1991).
A schematic representation of the wavelength variation of the Mueller matrix of the DST. In each box the wavelength dependence of the value of the matrix element is plotted from 400–1600 nm. What is important to note is that the off-diagonal elements, which represent the polarization cross-talk, approach a value of 0 as the wavelength increases. Image reproduced with permission from Socas-Navarro et al. (2011), copyright by ESO.
2.2 Instrument disadvantages in the infrared
2.2.1 Larger diffraction limit
At longer wavelengths, a given telescope will have less spatial resolution. The diffraction limit of a telescope represents the ability to resolve small objects, or to distinguish two closely space objects. The diffraction limit is often defined as the distance between the central peak and the first minimum of the Airy pattern resulting from diffraction by a telescope’s primary aperture. With a diameter of D the angular separation in radians is given by θ = 1.22λ/D but this is often simplified as just θ = λ/D. To compute the diffraction limit in arcseconds when λ is in units of nm and D is in units of mm, we find θ ≈ 0.2λ/D.
2.2.2 Increased background levels
According to Wien’s displacement law, a black body with a temperature of 300 K will have its continuum emission peak at a wavelength of 9656 nm, but at wavelengths shorter than that value, such a body will emit a large amount of radiation. Starting at wavelengths of about 3000 nm, room temperature telescopes and feed optics glow and this emission provides a background value against which a target object must be measured. This increasing background level is the other key disadvantage of observing the Sun at infrared wavelengths.
Cryogenic cooling is used to minimize this thermal background. Infrared arrays are cooled to much lower temperatures than visible cameras are cooled. Often several feed optics upstream of the infrared array are cooled, and of particular importance is the cooling of a narrowband filter. Interference filters or, in some cases, diffraction gratings are used to limit the spectral range of flux incident on the infrared array in order to avoid thermal contamination. To be effective, these filters must themselves be cooled to cryogenic temperatures, usually at or below the temperature of liquid nitrogen (77 K). Such cooling efforts then required evacuated dewars to house the cold detectors and optics.
Even with excellent cooling, some infrared observations are still subject to high levels of background contamination. Such observations fall into the realm of background-limited observations, in a similar way that ground-based observations of the solar corona at infrared and even shorter wavelengths are background-limited (Penn et al., 2004b). In an effort to accurately measure the large background and subtract it, a variety observational methods have been developed, including chopping between on-target and off-target.
2.2.3 Atmospheric and transmissive optics absorption
Absorption bands from the Earth’s atmosphere in the solar spectrum are not limited to infrared wavelengths; there are several in the visible spectrum, and the ultraviolet and some radio and sub-mm wavelengths are also impacted. Larger swaths of the infrared solar spectrum are not visible from the surface of the Earth, and so this is a disadvantage when compared to the visible spectrum.
Finally, some well-known optical materials do not transmit some infrared wavelengths. For example, telescopes with transmissive optical elements made from the commonly used BK7 crown glass have an wavelength cutoff at about 2500 nm; fused silica lenses have a wavelength cutoff at about 2300 nm. This issue is no longer a large difficulty, as transmissive lenses made from CaF2 or MgF2 are readily available and transmit up to about 6000 nm, and other optical materials are available for wavelengths longer than this.
2.3 Scientific advantages in the infrared
2.3.1 Increased Zeeman resolution
The wavelength splitting of atomic sublevels in the presence of a magnetic field increases as geff λ2 increases, where geff is the effective Landé g-factor for the electron transitions forming a particular spectral line. The Landé g-factor is usually calculated with atomic models that couple total orbital angular momentum and total spin angular momentum first (known as Russell-Saunders or LS coupling) and the work of Beckers (1969) provides values of geff for many lines. While many lines have values of geff between 1.0 and 3.0, there are spectral lines seen from the Sun which can have larger values (Harvey, 1973a).
The Doppler broadening of spectral lines due to macro and micro-turbulent velocities on the Sun increases linearly as λ increases. Magnetic field measurements measure a shift in the components of a spectral line, and this shift is most easily measured if it is large relative to the observed line width (see Figure 4). So the ratio of the Zeeman splitting divided by the spectral line width gives us a measure of the magnetic resolution of a spectral line, and that value is geff λ. In order to make observations with the highest possible magnetic sensitivity, lines with large values of geff λ are sought in the solar spectrum, and while some spectral lines can be found with increasing values of geff (for example, selecting a different line may change the magnetic sensitivity by a factor of 4) it is usually more advantageous to increase the wavelength of the observations (changing from 500 nm to 5000 nm can increase the magnetic sensitivity by a factor of 10). Ideally spectral lines with inherently large geff and with long wavelengths are the best for making sensitive magnetic measurements.
The benefit of making magnetic field Zeeman observations in the infrared is shown in this figure. On the left is a plot showing the separation of the Stokes V peaks for various Voigt profiles at a magnetic field of 1 kG for a visible line and an IR line. On the right is a plot showing the value of the Stokes V amplitude. The Zeeman splitting of the 1565 nm IR line is fully resolved at this magnetic field strength, and the weak field approximation does not need to be used to interpret the spectra. Image reproduced with permission from Stenflo et al. (1987), copyright by ESO.
Table 2 lists the magnetic sensitivies of some spectral lines with their respective magnetic sensitivies.
2.3.2 Large number of molecular rotation-vibration lines
Due to the structure of the several common molecules, the energy difference between rotation-vibration states of the molecule produces spectral lines which are found at infrared wavelengths. While the energies involved in these transitions are only completely described by a quantum mechanical treatment of the molecule, a simple classical physics analysis gives some insight about why this occurs. Setting the molecular rotational energy equal to the thermal energy of the solar plasma gives us \(I {\omega} \ (mr^{2}) {\omega_{\rm char}^{2}} \ kT\). Using T = 6000 K and order of magnitude masses for an oxygen atom and distances found in a water molecule, we can compute the rotational frequency to be ω ≈ 104 GHz. This corresponds to a wavelength of about 25 microns, and this is one way to consider why the solar IR spectrum contains many molecular transitions. On the Sun molecules exist in only the coolest regions but are destroyed by dissociation in all other regions. In this way, molecular spectral lines provide unique ways to probe cool regions around sunspots and near the temperature minimum region of the quiet solar atmosphere. Also of note is that molecular transitions have a range of Zeeman sensitivities and, thus, provide a unique probe into the solar magnetic fields in this cool plasma. Molecular spectral lines also provide a convenient way to measure atomic isotopes, as the subtle nuclear mass changes can result in larger wavelength shifts for molecular lines than atomic lines.
2.3.3 Ability to probe different heights in the solar atmopshere using continuum radiation
From 1000 to 10 000 nm, the height of formation of the solar continuum emission varies from roughly z = −40 km to z = 140 km. While the dominant form of continuum opacity at visible wavelengths is caused by H-minus bound-free transitions, at infrared wavelengths longer than about 1600 nm the dominant process changes to H-minus free-free opacity. The transition between the two processes allows photons to escape most easily from the solar plasma, and because of this we can view the deepest layers of the solar photosphere with observations of the continuum at 1600 nm. According to the VAL models (Vernazza et al., 1976) photons at 1600 nm originate from about 40 km below the level at which photons at 500 nm escape. While this may seem like a small height difference, due to the photosphere’s which large density gradient there are changes in the solar magnetic fields which can be seen across this height change. Thus, spectral lines in the IR probe deeper regions where the magnetic fields are stronger than the regions measured by spectral lines at visible wavelengths. Over the range of heights probed by the infrared continuum, the solar convective granulation undergoes a radical change, reversing the intensity contrast completely. At the lowest layers probed by the infrared continuum, the center of granules are bright and the intergranular lanes are dark, whereas in the upper layers the reverse is true (Leenaarts and Wedemeyer-Böhm, 2005; Cheung et al., 2007). The height change of the infrared continuum thus provides a critical probe of the vertical structure of solar granulation.
At wavelengths longward of 1600 nm, the H-minus free-free continuum opacity increases and photons which we observe originate at higher levels in the solar atmosphere. At wavelengths near 1600 nm the τ =1 level moves up through the solar atmosphere about 25 m per nm of wavelength, but at wavelengths near 10 000 nm the change decreases to about 15 m per nm. We can generate approximate fits predicted by various models using the log10 of the reciprocal of the wavelength. The approximate height of the τ = 1 level (in units of km) according to the VAL model is z = −776 − 227 log10(1/λ) (see Figure 5), and from another calculation by Gezari et al. (1999) z = −1049 − 303 log10(1/λ), where λ is in units of nm. Each of these approximations is valid only at wavelengths between about 2000 nm to 20 000 nm.
The height of formation of the infrared continuum radiation is shown in this figure. The continuum radiation is formed at the deepest level in the Sun at 1600 nm, and then the continuum formation height increases with increasing wavelength in the infrared spectrum. The bottom plot shows that the dominant source of opacity is from Hydrogen free-free transitions. See also Fontenla et al. (2006) for more recent work. Image reproduced with permission from Vernazza et al. (1976), copyright by AAS.
2.4 Scientific disadvantages in the infrared
2.4.1 Fewer solar photons
The solar spectral intensity closely follows a black-body curve with an effective temperature between about 5800 K and 4300 K (Boreiko and Clark, 1987) although this varies with spatial position on the solar surface. At this temperature the peak of the black-body curve is in the visible spectrum and so the Sun radiates fewer photons in the infrared spectrum than it does at visible wavelengths. For wavelengths much longer than the peak of the black-body spectrum, the Rayleigh-Jeans law can be used to express the number of photons per second, per unit surface area, per solid angle, and per wavelength bin emitted by a black-body. The wavelength form for this Law is Bλ(T) = 2ckT/λ4. In order to maintain a constant spectral resolving power given by R = λ/Δλ, one must increase the wavelength bin size Δλ as λ increases, to achieve the same velocity and Doppler broadening sensitivity. But even with the ability to bin in wavelength more, the number of IR photons available to observe the Sun at the same effective Doppler resolution changes as λ−3. Since the signal to noise of a particular measurement varies as the square-root of the number of photons which are measured, the signal to noise of a given spectrum decreases due to fewer solar photons as λ−3/2 at infrared wavelengths compared to visible wavelengths.
2.4.2 Fewer atomic absorptions
The energy range of photons for the infrared spectrum as we defined in Section 1, spans about 1 eV to 10−3 eV. In order to form absorption lines at these low photon energies, the energy difference between the atomic levels must be small. Such small energy differences are usually found in upper levels (with large total quantum number n) of most atoms. The level populations of these high n states are usually quite low in solar plasma, so there are few opportunities for atoms to absorb infrared light. The infrared solar spectrum contains fewer atomic absorption lines than shorter wavelength regimes, and they are usually weaker. Some exceptions exist, such as spectral lines formed by electrons cascading through these upper levels after recombination of electrons, but, in general, atomic absorption lines decrease in their predominance as the wavelength increases. One advantage of this is that with fewer lines the infrared spectrum contains cleaner line profiles, free from the blending seen at shorter wavelengths.
3 Key Science using Solar Infrared Observations
Infrared solar physics has enjoyed contributions from a large number of excellent experimental scientists. Several reviews and status updates of the field have been made and published, i.e., Rabin et al. (1994), Kuhn and Penn (1995), and Lin (2009). While reading John Jefferies’ introduction to the 1992 IAU Symposium (Jefferies, 1994), it is inspirational to see how much real progress has been made over the past 20 years. The initial magnetic field measurements with an infrared array detector observing the highly advantageous Fe I 1564.8 nm spectral line were being made at the time of that meeting (Rabin, 1994), and now they are routine (Jaeggli et al., 2010). Observations of the solar corona, including the potential for magnetic field measurements, were just being discussed (Kumar and Davila, 1994), and now coronal magnetic field measurements are made using the favorable 1074.7 nm emission line on a regular basis (Tomczyk et al., 2008). Perhaps most importantly, as the initial scientific results started to be realized at infrared wavelengths, discussions had started about the scientific need for a large, unobstructed-aperture infrared optimized solar telescope (Livingston, 1994). Now, as the all-reflecting 4-m Advanced Technology Solar Telescope (recently renamed the Daniel K. Inouye Solar Telescope, or DKIST) is under construction on Haleakala (Keil et al., 2001), we are looking forward to a new era where we can use several known tools in the infrared spectrum, and where we can also anticipate fundamentally new discoveries in this wavelength range.
3.1 IR solar spectral tools
The IR solar disk spectrum has been mapped; two important references are the series of quiet Sun and sunspot spectral atlases taken with the FTS at the McM-P telescope (Wallace et al., 1996) and the NASA ATMOS mission spectral atlas (Farmer and Norton, 1989b). The ground-based spectra contain useful information about telluric absorption lines where the lines are relatively weak, but where they are strong the ground data cannot observe the solar spectrum; here the space atlas must be used. The ground-based spectra are available onlineFootnote 1. Modern sources for lists of atomic absorption lines must be used for IR wavelengths, since the historical line lists from Roland stop at about 720 nm. A comprehensive source is that from Kurucz (2009) and the databaseFootnote 2 of these lines. Another very useful listFootnote 3 of theoretical wavelengths was compiled by van Hoof at the University of Kentucky. Other sources are available and provide useful reference in special cases: the NIST Atomic Spectra DatabaseFootnote 4, the CHIANTI databaseFootnote 5, and for molecular species, the HITRAN databaseFootnote 6 (Rothman et al., 2013). A sequence of three papers are available where the authors examine the infrared solar spectrum and discuss interesting unblended lines useful for magnetic field measurements from 1490 to 1800 nm (Solanki et al., 1990), survey the quiet Sun lines which are unblended with atmospheric absorption from 1000 to 1800 nm (Ramsauer et al., 1995a), and survey the Stokes I, Q, and V profiles in a plage and a sunspot umbra from 1050 to 2500 nm (Rüedi et al., 1995a). An online database for the unblended 1000 to 1800 nm line list is also available (Ramsauer et al., 1995b).
The following sections discuss five of the key solar science items being explored using various diagnostics in the IR solar spectrum, plus a selection of other topics where some interesting work has been done. This list is by no means complete, and will certainly change with time. A brief discussion of the telescopes and instruments which are used to observed this spectral region is presented, and then the key science addressed by the diagnostics is discussed.
3.2 The impact of CO 4666 nm observations on solar models
3.2.1 Telescopes, instruments, and detectors
The fundamental CO absorption lines near 4666 nm have been observed from the ground at the McM-P telescope (Hall et al., 1972), and have been seen in space data taken during the NASA Space Shuttle ATMOS mission (Farmer and Norton, 1989b). Instrumentation has involved warm spectrographs including the FTS, (Ayres and Testerman, 1981) and cryogenically cooled spectrographs including Phoenix (Ayres, 1998). Detectors have evolved from single bolometers (Hall et al., 1972) to 10242 InSb array cameras (Penn et al., 2011).
3.2.2 Early work
There is an excellent discussion of the history of CO observations of the Sun provided by Ayres (1998). In summary, the discovery that the lines in the fundamental band of CO absorption were so strong (Hall et al., 1972; Ayres and Testerman, 1981) meant that there was a large amount of cool gas present in the quiet Sun. At the same height as this cool gas, chromospheric Ca II and Mg II emission line intensities require the plasma to be at higher temperatures (Ayres and Linsky, 1976). To explain this apparent contradiction, a major shift was required in both solar (Ayres, 1981) and stellar (Wiedemann et al., 1994) atmospheric models (see Figure 6). Static radiative cooling by the strong CO lines was proposed to be an important part of the atmospheric energy balance at high altitudes (Ayres, 1981), but recent detailed modeling of the hydrodynamics and non-equilibrium molecular chemistry in these low chromosphere layers suggests instead a highly dynamic situation in which strong adiabatic cooling and shock wave heating play key roles (Wedemeyer-Böhm and Steffen, 2007). Nevertheless, the numerical treatment of the hydrodynamics is still in an experimental state, and whether radiative effects or dynamics is the dominant force in creating cool regions in the low chromosphere remains an open question. This issue can be addressed by high-resolution measurements of the mid-IR CO bands by the DKIST, or by high-resolution sub-mm continuum imaging from ALMA (Wedemeyer-Böhm et al., 2007).
This figure shows the types of changes needed in the solar atmosphere models in order to bring the CO observations into agreement with other chromospheric measurements. The diagram on the left shows an early simple atmospheric model, and the diagram on the right shows the updated model after the discovery of strong CO lines and dynamic shock waves in the chromosphere. Image reproduced with permission from Ayres (2002), copyright by AAS.
3.2.3 Height of formation
It has been 20 years since the discovery of CO emission at the solar limb (Solanki et al., 1994). Direct measurements of the height of formation of limb emission from an eclipse (Clark et al., 1995) suggest a geometric height of formation at the limb of 450 km above the τ500 = 1 limb layer. Direct measurements from the McM-P telescope show heights are different for various lines, ranging from 400 km (Uitenbroek et al., 1994) to 480 km (Ayres and Rabin, 1996) (see Figure 7); some observations even show CO emission extending to heights of 1000 km (Ayres, 2002). Helioseismic oscillations measurement of the I-V phase difference in the CO lines (Penn et al., 2011) shows a changing height between 425 and 560 km moving from the center of the solar disk to μ = 0.5 The dynamical model of CO formation from Asensio Ramos et al. (2003) agrees with the observations by finding an upper limit of 700 km for the CO bulk of the CO formation. More recent models from Wedemeyer-Böhm et al. (2005) suggest a geometric formation height near 200 km, presumably where the molecular density peaks (Ayres et al., 2013). In general, CO in the solar atmosphere probes a range of heights from the upper photosphere to the middle chromosphere, with the weaker CO lines (such as those at 2300 nm) probing the lower layers, and the strongest lines having a double-peaked contribution function which also probe the low chromosphere (Ayres et al., 2006).
The limb extensions in arcseconds of several CO lines near 4666 nm are shown in this plot. Image reproduced with permission from Ayres and Rabin (1996), copyright by AAS.
3.2.4 Spatial structure and flows
The spatial structure of cold clouds of CO gas has been investigated, but only through spectroheliograms which have low spatial and temporal resolution. Early observations of Ayres and Rabin (1996) suggested that the solar atmosphere consisted mostly of cool material forming CO molecules which were punctuated by hotter regions associated with magnetic field concentrations. Observations from Uitenbroek (2000) using the McM-P facility and the NIM instrument showed granulation sized regions of CO structure, and regions of the internetwork (correlating with magnetic field concentrations) which lack significant CO line absorption. Unpublished high-resolution images and movies taken by at the McM-P also show granulation-sized CO absorption regions and evidence for loop-like structure.
The CO atmosphere is a highly dynamic system, with time dependent models of the quiet Sun showing significant changes during over less than one minute of time (Wedemeyer-Böhm et al., 2005). Dynamical events around sunspots and solar active regions have been observed. Uitenbroek et al. (1994) showed that the CO lines reveal the inverse Evershed flow in sunspot penumbra, with a flow pattern moving from the quiet Sun back into the umbra. The same inverse flow was seen in the strong CO lines by Clark et al. (2004) and this flow pattern showed a different morphology than shown by the penumbral continuum intensity fibrils. Clark et al. (2004) also noted that the weaker CO lines showed a normal, radially outward Evershed flow. Highly sheared flows in the solar plasma near sunspots were seen by Penn and Schad (2012) in the decay phase of a large X-class flare in 2011.
3.2.5 Helioseismology using CO lines at 4666 nm
Some of the earliest observations of the CO line showed large intensity oscillations in the line core. With a single element InSb detector and a warm slit spectrograph at the McM-P, Noyes and Hall (1972) showed that the oscillations at a single position on the Sun had a roughly 5 minute period with amplitudes of several percent in the line core intensity. The work had a cadence of 1 second and a duration of about 1000 seconds. That early work also claimed that the line formed in the high photosphere where the plasma was nearly adiabatic, and the temperature and velocity oscillations were 90 degrees out of phase, although specific measurements were not made. Observations from the FTS at the McM-P (Ayres and Brault, 1990) with 40 minutes durations and with 15 second cadence showed both Doppler velocity oscillations and line core intensity oscillations at several pointings on the solar disk. The phase difference between the velocity and the intensity oscillations was measured to be between 40 and 70 degrees, rather far from the assumed 90 degree adiabatic value. The application of these phase differences for probing the solar atmosphere were pointed out. Using a single slit position, but with a 2562 InSb array detector, Uitenbroek et al. (1994) made observations with 8.6 second cadence during a 36 minutes period in the quiet Sun. Oscillations were seen in both line center intensity and Doppler velocity, but the line center intensity showed primarily 3-minute oscillations while the Doppler velocity showed the typical 5-minute period. Observations in a sunspot by Solanki et al. (1996a) also showed different peaks in the power spectra for CO intensity versus the CO Doppler velocity. These observations were made with a slit spectrograph and a single-element detector, with 32 second cadence and 64 minute duration. Time sequences from this study in the quiet Sun and in plages showed primarily 5-minute periods, except for intensity oscillations near the solar limb which showed mostly 3-minute period oscillations. The phase differences between intensity and velocity were also examined in these different structures and compared with phases seen in other spectral lines. Most recently, full-disk Doppler and intensity measurements were made using the McM-P and the NAC detector (Penn et al., 2011). The full solar disk was scanned at 50 second cadence for 133 minutes with effectively rectangular pixels about 4 × 12 arcseconds. Three strong CO lines were observed and the spectral lines were fit. Diagnostic diagrams were made for velocity and intensity, and the phase and the coherence between the two. As shown in Figure 8 the diagnostic diagrams show ridges which are aligned with the known global p-mode frequencies, show strong coherence in these ridges, and show a shift from the expected 90-degree adiabatic phase difference. The phase shift is used to compute a value for the atmospheric radiative relaxation frequency. Using the center-to-limb variation of the phase, and comparing to far-IR continuum observations from Kopp et al. (1992) a height of formation for the lines is also derived.
Diagnostic l-ν diagrams for full disk oscillations observed with the Doppler shifts and depths of CO 4666 nm lines. The CO oscillations show the same power ridges as the global p-mode oscillations, but show an I–V phase which is different from the expected adiabatic phase shift and which allows an investigation of the dynamics of the solar atmosphere. Image reproduced with permission from Penn et al. (2011), copyright by AAS.
3.3 The Fe I 1564.83 nm line: sunspots, flux tubes, and the solar cycle
3.3.1 Telescopes, instruments, and detectors
The Zeeman splitting displayed by the magnetically sensitive Fe I 1565 nm absorption line is large (see Figure 9), and observations of the line were started at the McM-P telescope at Kitt Peak (Harvey and Hall, 1975), but since this wavelength is transmitted through most refractive optics, further observations have been made at many telescopes, especially the NSO Dunn Solar Telescope (DST) at Sunspot, the KIS Vacuum Tower Telescope (VTT) at Tenerife, and the NJIT New Solar Telescope (NST) at Big Bear. Instrumentation used to make spectroscopic and spectropolarimetric observations of this line started with single element PbS detector on the main spectrograph at the McM-P (Hall and Noyes, 1969) or used a cooled InSb diode detector on the FTS at the McM-P (Stenflo et al., 1987). But the instruments used to study this line have evolved from these single-element systems. Instruments using grating spectropolarimeters with arrays include the NIM (Rabin et al., 1992), the TIP (Mártinez Pillet et al., 1999), and the NAC (Plymate and Penn, 2007). Imaging Fabry-Perot spectropolarimeters include the NIM-2 (Rabin et al., 1996) and IRIM (Cao et al., 2004). And, finally, a new facility-class instrument at the NSO/DST is the FIRS instrument, a multi-slit grating spectropolarimeter with a 1024 × 1024 HgCdTe detector (Jaeggli et al., 2010).
A figure showing the polarization spectra of a sunspot. The spectrograph slit crossed a sunspot umbra, and the Zeeman spitting in Stokes I, Q, U, and V are shown in this figure, with the continuum intensity removed from the Stokes I panel. The 1565 nm g = 3 line is shown at the center of each panel, and other atomic and molecular lines are identified in each spectrum. Image reproduced with permission from Penn et al. (2004a), copyright by AAS.
3.3.2 Early work
The first observations of the magnetically sensitive Fe I 1565 nm absorption line in sunspots appeared in Harvey and Hall (1975), and the first observations of non-spot magnetic fields between 1200 and 1700 G are shown and briefly discussed in Harvey (1977). A more detailed analysis of the full Stokes (I, Q, U, and V) profiles from this line taken at several points on the solar surface was first done by Stenflo et al. (1987). The FTS spectra in this work clearly show the spectral line is fully split for magnetic fields of about 1000 G and greater, where the Zeeman displacement of the σ components is greater than the Doppler width of the line. Here it is emphasized that the fully resolved splitting shown by the 1565 nm Fe I g = 3 line reveals the magnetic field strength B, rather than the spatially averaged magnetic flux ϕ. This work also shows that this line probes stronger magnetic fields than absorption lines in the visible spectrum, because the height of formation of the line is lower and magnetic fields on the Sun strengthen with decreasing height. Later work in Solanki et al. (1992b) (which is part of a highly informative 15 paper series on IR solar spectroscopy and spectropolarimetry) showed that the 1565 nm line could be used in conjunction with the nearby Fe I line to measure magnetic fields as weak as 100 G.
3.3.3 Quiet Sun magnetic fields
Measurements of Rüedi et al. (1992) probe magnetic fields outside of sunspots in active region plages. Here field strengths from about 400 to 1700 G were measured, and this provided strong evidence against the idea that all of the Sun’s magnetic field was concentrated into flux tubes of about 1 kG in strength. Maps of the solar surface at higher spatial resolution were produced by Lin (1995) using this spectral line at both the DST and BBSO 26-inch Vacuum Telescope. Histograms of the magnetic field strength showed two components to solar magnetic field: first, active region spots and plage showed a distribution of magnetic field strengths ranging from about 2500 G down to about 300 G with an average of about 1400 G, and then quiet Sun regions showed magnetic field strengths ranging from about 2000 G down to about 200 G, but with an average of only 500 G. It was proposed that the smaller field strength regions were internetwork fields and had a fundamentally different origin from the active region fields. More recent work using the amplitudes of the 1565 nm line (combined with the well-known visible line at 630 nm) has lowered the strength of the internetwork field by more than an order of magnitude to about 20 G (Khomenko et al., 2005). The behavior of these weaker fields in the solar plasma at the photosphere was examined by Solanki et al. (1996b), who found evidence for a more vertical arrangement of fields occuring at 1500 G, and ascribed that to the process of convective collapse. This behavior has also been seen in more recent work which has combined the IR line with the visible 630 nm line (Domínguez Cerdeña et al., 2006).
3.3.4 Sunspot magnetic fields
Exploiting the ability of the 1565 nm line to measure the true magnetic field strength in sunspots, McPherson et al. (1992) mapped the changes of magnetic field and plasma velocities across a sunspot. Kopp and Rabin (1992) measured the relationship between B and intensity (plasma temperature) in several sunspots. This data showed a rough agreement with the expected B ≈ T2 variation expected from a horizontal magnetostatic argument (Martínez Pillet and Vázquez, 1990) and visible observations. Subsequent work (Solanki et al., 1993) confirmed this and measured horizontal gradients of the magnetic field strength and inclination across a sunspot. Magnetic observations of many spots (Livingston, 2002) showed that the relationship between the magnetic field and continuum intensity at one spatial position in the center of many sunspots followed the same relationship as different spatial positions within one sunspot. A comparison between many infrared and visible measurements (Penn et al., 2003c) showed that the scatter between the results from the visible and IR data was reduced when the temperature and magnetic differences between the heights of formation were taken into account. However, much more recent work has shown that the simple hydrostatic models cannot account for the behavior seen in many of the darkest parts of sunspot umbrae, where the formation of molecules in the cool solar plasma changes the pressure balance and, thus, the relationship between magnetic field and temperature (Jaeggli et al., 2012).
The analysis techniques used to understand spectropolarimetric data have advanced considerably, and for some time the analysis of visible and IR data followed separate paths, with the analysis of the IR data lagging the visible data by a year or two. Milne-Eddington models were used to invert 1565 nm sunspot observations in Solanki et al. (1992a) and then atmospheric gradients were included in the analysis first done by Bellot Rubio et al. (2000), and later by Mathew et al. (2003) where the spectropolarimetric wavelength response function of both the atomic Fe lines and the molecular OH lines were used to measure the magnetic fields (see Figure 10). Analysis of both visible and IR data (taken of the same sunspot but with different telescopes and instruments) have been done using wavelength response functions (Cabrera Solana et al., 2006).
Fits to the Stokes spectra for the 1565 nm Fe line pair. Here the Fe and OH lines are both fit using response functions computed for each line. Image reproduced with permission from Mathew et al. (2003), copyright by ESO.
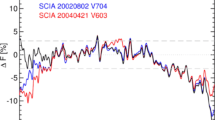
Early work done by Livingston to measure the magnetic fields in many sunspots using 1565 nm data showed a temporal decrease in the magnetic fields between two years of data (Livingston, 2002). Subsequent work showed that the decrease seemed linear over several years and independent of solar cycle (Penn and Livingston, 2006) and that extrapolations of the trend, combined with the lower limit of 1500 G sunspot magnetic field strengths, might lead to a lack of sunspots for solar Cycles 24 and 25. Comparison of over 3000 sunspot observations with radio observations at 21 cm confirmed the initial observations (Livingston et al., 2012) although results from 99 sunspot observations at 1565 nm, combined with magnetic measurements from other spectral lines, do not show a temporal decrease (Rezaei et al., 2012). While Cycle 24 has currently only shown about one-half of the sunspots seen in Cycle 23, the result remains controversial.
3.3.5 Helioseismology using Fe I 1565 nm
While some early work discussed making helioseimic observations in the continuum at 1600 nm near the wavelength of this line (Li et al., 1994), there seems to be only one research effort in this category which has been published. Bellot Rubio et al. (2000) use the 1565 nm geff = 3.0 line and two others to measure velocity and magnetic field oscillations in a sunspot umbra. Using a SIR inversion procedure, the authors invert the Stokes profiles for 6 pixels and examine a time sequence of 22 minutes with a cadence of about 5 seconds. Velocity observations are seen in the data with amplitudes on the order of 100 m/s, and changes in the magnetic field are seen with amplitudes of up to ± 50 gauss. The phase difference between the velocity and the magnetic field oscillations is measured to be 105 ± 30 degrees. The authors point out that if there are significant gas density changes in the umbral atmosphere which produce a vertical displacement of the line-forming region, then the fact that sunspots have a vertical gradient in the magnetic field suggests that the magnetic field is not changing during the observations, but rather the spectral line probes regions of different magnetic field strength at different times. The phase difference expected for this scenario is 90 degrees, and the measurement error of these data are consistent with this interpretation.
3.4 He I spectral line at 1083 nm
3.4.1 Telescopes, instruments, and detectors
The He I absorption line at 1083 nm lies well within the transmission range of common refracting optics, and at the long wavelength edge of the sensitivity of silicon-based CCD detectors. Thus, many telescope, instrument, and detector combinations have been used to observe this spectral feature, and below is an incomplete list of just a few. The discovery of the He I 1083 nm absorption line on the disk of the Sun was made at the Mt. Wilson Observatory using film (Babcock and Babcock, 1934) and then the line was also observed with the Mount Wilson 60-foot tower and an ITT FW-167 infrared image converter tube (Zirin and Howard, 1966). Full disk observations, capturing the above-limb emission, were done synoptically for many years with silicon-based detectors at the KPVT (see Livingston et al., 1976; Jones et al., 1992), and those observations are continued by SOLIS VSM and FDP (Keller et al., 2003) (see Figure 11), which again use silicon detectors. With a tunable Lyot filter based on liquid-crystal retarders, the CHIP instrument provides full-disk line observations of 1083 nm with rapid cadence (MacQueen et al., 1998). At the McM-P, spectropolarimetric observations of this line were first done using a spectrograph with polarization optics and silicon photodiodes (Harvey and Hall, 1971). Infrared array detectors (256 × 256 HgCdTe) were used with a slit spectrograph and liquid crystal polarization optics with simultaneous dual-beam feeds at the DST (Penn and Kuhn, 1995), and work there continues with the 1024 × 1024 HgCdTe detector in the FIRS instrument (Schad et al., 2013). Full-disk vector magnetic measurements using He I 1083 nm have been taken at the NOAJ Solar Flare Telescope since about 2010 (Hanaoka et al., 2011). Using ferroelectric liquid crystals, the ProMag instrument observes He 1083 nm line profiles again using a dual-beam feed and a slit spectrograph at the JESF (Elmore et al., 2008).
A full disk spectroheliogram in He I 1083 nm from the NSO/VSM instrument; solar north is up. The image shows polar coronal holes as regions of less absorption, and a low latitude coronal hole in the northern hemisphere. Dark absorption accompanies active regions, and the quiet Sun shows less absorption, but reveals the internetwork pattern. Limb prominences and limb emission are seen as bright regions off the solar limb, and a dark filament is visible on the disk in the northern hemisphere. Credits: NSO/AURA/NSF.
While it is accessible from a variety of telescopes and detectors, accurate spectral analysis of the He I 1083 nm line is challenging. The absorption line is normally very weak, reaching depths of only a few percent of the continuum intensity in the quiet Sun, but it can become very dark in filaments or solar active regions, increasing its absorption ten-fold. The line is blended with the red wing of the nearby strong Si I 1082.7 nm photospheric line, and several telluric absorption lines populate this spectral region. Finally, the Doppler shifts seen in the line often reveal multiple components, sometimes at high velocities. Thus, for analysis and scientific reasons, it is best to observe a large spectral region surrounding the line center (Malanushenko and Jones, 2004).
3.4.2 Early work
While the element of Helium was discovered using its yellow line in the visible spectrum at a solar eclipse by Janssen (1869), studies of the infrared spectral line began only after film was regularly used. Early spectra and spectroheliograms (Richardson and Minkowski, 1939) revealed line emission in a solar flare near disk center, as well as in an erupting prominence at the limb. Spectra from McMath-Hulbert Observatory in Michigan (Mohler and Goldberg, 1956) showed that the line had a large width corresponding to a kinetic temperature of 50 000 K and, thus, it likely originated in hot regions of the solar chromosphere. Athay and Johnson (1960) did a careful examination of the physical conditions involved in the excitation of the He I 1083 nm line (and other lines) by including both radiative and collisional excitation mechanisms, and explained previously observed disk emission in the line with high temperatures and large electron densities. Spectroheliograms from Zirin and Howard (1966) showed that the disk absorption seemed to follow the Ca II and Hα network, and those regions were thought to support the high temperatures needed to form the line. The high temperature was confirmed with the analysis of several visible lines from orthohelium (Hirayama, 1971) and combined with the lack of He emission from coronal holes (Zirin, 1975) found support for the photo-ionization and recombination process (PR) of line formation for the 1083 nm line, originally suggested in the work of Goldberg (1939). Early CCD observations of He 1083 nm structures revealed Doppler velocities in the line, but also showed small structures of about 1 arcsecond of size, and the formation of such structures would be difficult if PR were the only line formation mechanism (Lites et al., 1985). A “mixed formation mechanism” for the line formation of He I 1083 nm was proposed by Andretta and Jones (1997) where a combination of collisional excitation and the PR mechanism instigate the line formation, and recent models (Centeno et al., 2009) support this idea today.
3.4.3 Height of formation
Many observations of the height of formation of the visible He I D3 emission shell have been made, and the average of these measurements is 1.45 Mm with a standard deviation of 0.25 Mm (Penn and Jones, 1996). However, there are fewer measurements of the He I 1083 nm emission shell height. Early data from Giovanelli and Hall (1977) show the emission maximum at 1.6 Mm above the limb, while Schmidt et al. (1994) show peak formation at a height of 2.4 Mm above the limb. Using two different telescopes, Penn and Jones (1996) measure the emission shell to be at 1.74 ± 0.05 Mm with the DST and 2.11 ± 0.12 Mm with the KPVT. Most recently, Muglach and Schmidt (2001) show measurements of both He I D3 and 1083 nm limb emission, which are consistent to within about 100 km of one another, and range from 1100 to 1800 km in height above the solar limb.
3.4.4 Ground-based observations of coronal holes
The He I 1083 nm line provides a useful ground-based method for studying coronal features on the disk of the Sun. By comparing Skylab X-ray telescope observations with He I 1083 nm spectroheliograms, Harvey et al. (1975) found that the coronal holes seen in the X-ray data also displayed a lack of He I 1083 nm absorption against the disk of the Sun. Sheeley Jr (1980) used KPVT 1083 observations to show that the polar coronal holes contracted in size when the solar polar magnetic field changed sign near sunspot maximum, and then Webb et al. (1984) observed the polar coronal holes reform after the polar field reversed. Harvey and Recely (2002) present a more thorough study of the evolution of the polar coronal holes using 11 years of He I 1083 nm data to observe changes during solar Cycles 22 and 23. Not only polar coronal holes, but also low-latitude transient coronal holes (often associated with solar flares and now known as coronal dimmings), have been observed using He I 1083 nm observations initially by Harvey and Recely (1984), and more recently using higher-cadence CHIP observations in de Toma et al. (2005). The position of coronal structures known as X-ray bright points (XBP) are closely correlated with regions of stronger He I 1083 nm absorption (Golub et al., 1989), but while dark absorption regions on the disk do not identify all the XBPs, the strongest XBPs have the darkest He I 1083 nm absorption, and even the faintest XBPs correspond to regions of weakly enhanced disk absorption.
3.4.5 Quiescent prominences
A set of four papers by Tandberg-Hanssen and colleagues investigated quiescent prominences using the infrared lines from He I. Line profile shapes and intensity ratios between the two resolved components of the line were studied by Tandberg-Hanssen (1962) and the authors concluded that the prominences showed regions which were optically thick in this line. A He I line at 2058 nm was observed in prominences simultaneously with 1083 nm by Streete et al. (1973) and the authors concluded that, based on the fact that 2058 nm was more than 100 times fainter than 1083 nm (instead of about 50 times fainter), LTE conditions were not present in the prominence and the incident radiation field played a large role in determining the level populations, which was also verified by Streete and Tandberg-Hanssen (1974). In the last of the series, Heasley et al. (1975) make a more rigorous analysis of the intensity ratio between the components of the 1083 nm line and determine a hydrogen density value of about 1010 cm−3. More prominences were observed and analyzed by Landman (1976). In addition to He I 1083, Chang and Deming (1996) observed much fainter emission from He I lines at 1278 and 1700 nm using the FTS instrument at the McM-P. Using both space-based and ground-based instrument, Stellmacher et al. (2003) investigate prominence emission using many lines, including He I 1083 nm. Again, the authors find that parts of prominences are optically thick (with τ = 2.0 for one prominence) and deduce an excitation temperature of only 3750 K in this line.
3.4.6 Solar flares
While emission from solar flares in He I 1083 nm was seen early, the slow cadence of many observations made it difficult to observe in detail. Observations by Harvey and Recely (1984) of a large two-ribbon M4.0-class flare showed two dark He I 1083 nm ribbon structures which lasted more than 60 hours. Observations in the decay phase of a C9.7-class flare by Penn and Kuhn (1995) showed line center emission at 1.3 times the level of the continuum emission, and downflows in the active region filament of 30–60 km/s. Zeeman splitting in the emission kernal revealed a magnetic field of 735 gauss, which then dropped to 622 gauss at the same spatial position after the emission faded. Limb emission during a large solar flare of X20-class was observed on 16 Aug 1989 (see You and Oertel, 1992; You et al., 2004). The line profiles were extremely broadened, were best fit with a gaussian large half-width of 0.42 nm, and showed multiple narrow absorption components against this wide spectral emission. Similar behavior was seen in a limb flare from 11 Jan 2002 (Li and You, 2009), which was also observed by a variety of space instruments. Ding et al. (2005) suggest that He I 1083 nm is a powerful diagnostic of non-thermal effects in flares. A flare-associated erupting active region filament was observed near disk center using He I 1083 nm during a joint run with SOHO/CDS (Penn, 2000). The He I 1083 nm profiles show multiple components, with a seemingly undisturbed solar chromosphere at the rest wavelength, and an erupting filament with a 200–300 km/s blueshift which moves transversly across the field-of-view. The CDS line profiles also show two spectral components, which allows easy line ratios to be computed without needing to subtract a background. Computing the column depth of the filament using the EUV lines gives a value of (4.8 ± 2.5) × 1017 cm−2. Very bright emission at a level of 2.5 times the continuum intensity was observed in He 1083 nm during an X1.8-class flare using the NAC instrument at the McM-P (Penn, 2006) (see Figure 12). Strong downflows with amplitudes of 100 km/s were seen during the flare decay phase. Dark absorption with a very large line width was observed with full Stokes polarimetry during a C2.0-class flare by Sasso et al. (2011). By fitting up to five different velocity components to the line profiles, some with redshifts as high as 100 km/s, they find magnetic field strengths in the range of 100–250 G in the active region filament.
A plot of flare emission seen in the He I 1083 nm line. The bottom spectrum shows very strong absorption in an active region filament, the central spectrum shows strong active region absorption, and the top spectrum shows emission in a flare kernel. In all cases both He I line components are seen. Image reproduced with permission from Penn and Kuhn (1995), copyright by AAS.
3.4.7 Magnetic measurements
Some of the earliest He I 1083 nm measurement included spectropolarimetric data. Harvey and Hall (1971) measured the line-of-sight component of the magnetic field using the He I line and a nearby line from Si I (formed in the photosphere). The He I magnetograms showed a magnetic field which was more diffuse and appeared more extended around an active region than the photospheric magnetic field. The He I magnetic measurements showed a reduced flux compared to the Si I data, and the authors concluded that the magnetic field at the He I height was more horizontal. Infrared array detectors were used to measure magnetic fields in both spectral lines by Penn and Kuhn (1995) around an active region, and the measurements again showed a weaker magnetic field in He than in Si. A linear relationship between the two gave BHe = 0.84 ± 0.01BSi, and using a formation height difference of 2000 km, the authors compute a logarithmic vertical gradient δ ln B/δz = (8.7 ± 0.6) × 10−5 km−1. They also noted that the photospheric magnetic field appears more bipolar than the He I field, with some pixels showing very different magnetic fields in the two lines. Observations of a sunspot by Rüedi et al. (1995b) also showed evidence for a vertical magnetic gradient which changed depending on the field strength, as the measured vertical gradient in an umbra (about 0.5 G/km) was more than twice that measured in the penumbra (about 0.2 G/km).
As the on-disk counterpart to off-limb prominences, filaments are highly visible in He I 1083 nm, showing increased absorption. In a filament region, Lin et al. (1998) made full Stokes spectropolarimetric observations of He I 1083 nm. By using a classical model for the polarization of the scattered radiation field, they developed expressions for the filament’s magnetic field in terms of the measured Stokes values. Mapping the field showed that the axial component of the magnetic field changed sign across the filament, which was consistent with having the filament embedded in a tilted magnetic loop system. The model failed to explain some of the observations however, especially the apparent reversal of the Stokes parameters between the red and the blue components of the He I 1083 nm triplet.
Measuring the vector chromospheric magnetic field has been a long-standing goal of those doing spectropolarimetry with the He I 1083 nm line, and recent efforts have shown that this goal may be achieved soon (Solanki et al., 2006). Observations of an emerging flux region using full Stokes spectropolarimetry show a set of rising magnetic loops, and also reveal that non-linear force-free extrapolations of the photospheric field (measured simultaneously with Si I) provide the closest fit to the observed chromospheric loops (see Solanki et al., 2003; Wiegelmann et al., 2005). These inversions included a simple implementation of the Hanle effect, and later work has used Milne-Eddington inversions and the Paschen-Back effect (Sasso et al., 2006).
A more complete theorectical framework for interpreting spectropolarimetric observations of He I 1083 nm was presented by Trujillo Bueno and Asensio Ramos (2007). Their work addresses atomic-level polarization, and discusses potential modifications to the anisotropy of the local radiation field. Based this framework, Lagg et al. (2009) produced the HELIX+ analysis package, and examined the polarization along chromospheric fibrils. They found the local magnetic field was nearly aligned with the fibrils, and recent work from Schad et al. (2013) using a version of the HAZEL code developed by Asensio Ramos et al. (2008) found a tighter alignment of the magnetic field direction with superpenumbral fibrils (aligned within ± 10 degrees). Finally, recent work by Schad et al. (2012) measured the magnetic field at coronal heights using a downflowing He I event (see Figure 13).
A composite spectrum of a strong He I 1083 nm downflow. At every pixel, the normal spectral line at the rest wavelength is seen along with a highly red-shifted second spectral line. The Stokes IQUV spectra are taken from along a curved path following a coronal condensation event. The upper panels show the measurements, while the lower panels show the resulting fitted spectra from the analysis, with the telluric and weak photospheric lines removed. The magnetic field measured in this event varies with height from approximately 100 G at 50 Mm to over 1000 G at 10 Mm and below. Image reproduced with permission from Schad (2013), copyright by the author.
3.4.8 Helioseismology using He I 1083 nm
Oscillations in the He I 1083 nm line have been used to examine the dynamics of the chromosphere. Lites (1986) examined the behavior of the He I line and the Ca II K line simultaneously above a sunspot umbra. One set of observations used a 42-second cadence for about 25 minutes, and the second set used 5-second cadence for 50 minutes. Oscillation power at 5 mHz dominated the observations, and the oscillation waveforms showed irregular shapes which were suggested to be evidence for shock formation. No phase relationship between the two lines could be determined. In several solar filaments, Yi et al. (1991) made maps of the Doppler velocity with a cadence of 140 seconds, spanning 140 to 210 minutes of time. They found several oscillation periods between 5 and 15 minutes, and noted that there was a long delay between Doppler shifts and intensity variations of about one period. Fleck et al. (1994) observed velocity and intensity oscillations in the quiet Sun with 24-second cadence during 90 minutes. They found both 5-minute and 3-minute oscillation periods in the velocity signal, but no power peaks in the intensity measurements. The coherence between the intensity and velocity was high through about 4 mHz, and at those frequencies a phase shift near 210 degrees was measured, well off from the adiabatic shift of 90 degrees (see Figure 14). Oscillations near the north pole of the Sun were observed by Penn and Allen (1997) and the He 1083 nm line showed mostly radial oscillations with a small 22 m/s horizontal component. In that work no oscillations were seen in the off-limb emission, although Muglach and Schmidt (2001) did report oscillations in the emission shell as observed with both He D3 and 1083 nm. In Centeno et al. (2006) the authors observe oscillations in a facular region and a sunspot umbra; an analysis of the phase diagrams between the velocity in the photosphere (using Si I) and higher (using He I) showed propagating waves in both features, and computed radiative cooling times and height differences in both objects.
Oscillations observations in He I 1083 nm. Both velocity and intensity oscillations were seen, but power peaks are only visible in the velocity signal. The coherence is high at low frequencies, but the phase shift is very different from the adiabatic value of 90 degrees. Image reproduced with permission from Fleck et al. (1994), copyright by IAU.
3.5 Mg I Emission at 12318 nm: the most sensitive magnetic probe
3.5.1 Telescopes, instruments, and detectors
Observations of this region of the spectrum are challenging due to the low solar flux and the high backgrounds from the atmosphere and telescope. The McM-P telescope is where the majority of the observations of this line have been made; exceptions include of early observations from the South Pole and Boulder, CO, and eclipse observations from the NASA IRTF on Mauna Kea during the 1991 total eclipse, and from the Apache Point ARC 3.5-m telescope during the 1994 partial eclipse. Detector technology used to observe this line has ranged from single element arsenic-doped silicon photodiode in early work (Brault and Noyes, 1983) to modern imaging Stokes spectropolarimetry using the Celeste instrument, currently equiped with a 128 × 128 array of arsenic doped silicon BIB detectors (McCabe et al., 2003).
3.5.2 Early work
Chang (1994) provides a discussion of the history of the study of the Mg I emission line at 12 318 nm. To briefly summarize: the first observations of emission from Mg I at 12 000 nm was by Goldman et al. (1980), although the first published observations can be seen in Murcray et al. (1981). After observations from the McM-P telescope by Brault and Noyes (1983) and from space data from the ATMOS program Farmer and Norton (1989a), the lines were identified as high-l Rydberg transitions by Chang and Noyes (1983). The narrow emission line sits atop a broad spectral absorption feature (i.e., see Figure 1 of Deming et al., 1988).
3.5.3 Height of formation
While Chang and Noyes (1983) predicted that the line was formed in the low chromosphere, work by Lemke and Holweger (1987) using NLTE calculations suggested that the line originated in the upper photosphere. Measurements from Zirin and Popp (1989) at the McM-P suggested that the formation height was above the temperature minimum in the low chromosphere. The formation height mystery continued until eclipse measurements from Deming et al. (1992) and Deming et al. (1998) showed that the emission originated below the temperature minimum in the upper photosphere. Subsequent modeling with plane-parallel atmosphere and NLTE effects (see Carlsson et al., 1992) agreed with the upper photospheric formation height, and predicted that the line formation occurred at roughly log τ500 = −3.5, corresponding to z = 400 km.
3.5.4 Magnetic field measurements
The earliest measurements of the Mg I line profiles revealed split emission profiles in sunspots, which suggested that Zeeman splitting was being observed. Laboratory measurements by Lemoine et al. (1988) showed that the transition had a Landé geff = 1.0. Since the magnetic sensitivity of a spectral line varies as the product of geff λ, this line is the most magnetically sensitive line currently known in the solar spectrum.
Exploitation of the very favorable Zeeman sensitivity of this line began with the work of Chang and Noyes (1983); progress on the use of the spectral line is presented in a series of papers from Deming and coworkers. Deming et al. (1988) measured quiet Sun p-mode oscillations using the line, found Zeeman splitting in the line profiles through a sunspot indicating magnetic fields of between 850 and 1400 gauss, and measured an inverse Evershed flow in the penumbra of a sunspot. Hewagama et al. (1993) made the first full-Stokes measurements of a sunspot magnetic field using this spectral line. In this work they emphasized that the broadening of the Zeeman-shifted σ emission line components was due to a distribution of magnetic fields within their spatial pixels rather than from Doppler broadening. (This was confirmed with a polarized line profile synthesis done by Bruls et al., 1995.) The third paper in the sequence (Moran et al., 2000) provided simultaneous measurements at 1565 nm and 12 318 nm in sunspots and plage, and showed that the vertical gradients of the magnetic field varied between these different solar structures (see Figure 15). Finally, Jennings et al. (2002) produced maps of the vector magnetic fields around an active region and observed a solar flare. By using the spectral line to measure the distribution of magnetic fields (rather than assigning a single-value as with some magnetogram analysis, see Figure 16), the magnetic energy involved in the flaring regions was larger than the X-ray luminosity of the flare. More recently the vector field properties of a solar active region have been explored in Moran et al. (2007).
Simultaneous spectra from a sunspot umbra showing the Mg I 12318 nm (top) and the Fe I 1565 nm (bottom) lines. The larger splitting of the Mg I line components is clearly visible, and the width of the Zeeman shifted components reveals a large range in the magnetic field strengths seen at this spatial position. Image reproduced with permission from Moran et al. (2000), copyright by AAS.
Maps of the magnetic field strength in a magnetically complex active region. The Zeeman shifted sigma components of the line are sliced at different wavelength positions corresponding to the magnetic field values listed in each sub-image. Magnetic fields of various strengths are seen to occur in the same spatial pixels, while the stronger magnetic fields are limited to the umbral regions. Image reproduced with permission from Jennings et al. (2002), copyright by AAS.
3.5.5 Helioseismology using Mg I 12318 nm
It seems that currently only one study of solar oscillations has been published using this line. Deming et al. (1988) measure quiet Sun p-mode oscillations using the line. With two quiet Sun time sequences of about 120 minutes and 90-second cadence, the authors measured solar velocity oscillations at disk center with single-point apertures of 2.3 and 4.6 arcseconds. The power spectrum clearly showed peaks near 5-minute periods, but little power at 3 minutes. The average period was measured to be 276 seconds, and the rms velocity amplitude was in the range of 500 m/s. All three of these features led the authors to conclude that the line originated from atmospheric heights of between 300–475 km, and so concluded that the line was from the upper photosphere and not chromospheric in origin. No intensity oscillations were seen in the emission lines above an amplitude corresponding to a temperature fluctuation of about 7 K, which is surprising given the observations of oscillations of lines formed at similar heights.
3.6 Coronal measurements
3.6.1 Telescopes, instruments, and detectors
Infrared observations of the corona are made from both eclipse experiments and from ground-based coronagraphs. Eclipse experiments are often specially designed, but have included a range of experiments from simple reflecting telescopes with spectrographs and IR array detectors (Kuhn et al., 1996) to aircraft equipped with gyroscopic-stabilized telescopes, spectrographs, and infrared detectors which fly through the path of totality (i.e., Münch et al., 1967; Kuhn et al., 1999). Several ground-based coronagraphs have been used to observe the solar corona at infrared wavelengths including the Pic du Midi and Climax coronagraphs, (Firor and Zirin, 1962) the ESF, (Penn and Kuhn, 1994a) COMP, (Tomczyk et al., 2008), and Solar-C. (Lin et al., 2004). Taking advantage of the fact that both atmospheric and telescopic scattered light are reduced at infrared wavelengths, observations of coronal emission lines have also been made from the non-coronagraphic all-reflecting McM-P telescope (Judge et al., 2002).
3.6.2 Early work
Infrared coronal physics has a long history. Quickly summarizing the excellent review by Malville (1967), the 1075 and 1080 nm emission lines from [Fe XIII] were first observed by Lyot in 1936 from the Pic du Midi coronagraph, and then were properly identified in the solar coronal spectrum as ions of iron by Edlen in 1942. Using an infrared sensitive high-voltage photomultiplier tube, observations of Fe XIII 10747 were from Climax coronagraph by Firor and Zirin (1962). Subsequent observations using a cooled photomultiplier tube during the May 1965 total eclipse (Eddy and Malville, 1967) showed for the first time strong linear polarization signal in the 1075 nm line.
The theory of polarization for many coronal emission lines was discussed in Hyder (1965), where the 1075/1080 nm [Fe XIII] line pair was shown to be an excellent choice for making magnetic field observations of the corona. A thorough discussion of the ability of the lines to measure the coronal magnetic field was given by House (1977). Initial observations of the coronal magnetic field of a limb sunspot using the the linear polarization of the 1075 nm line were reported in Querfeld and Elmore (1976), and subsequent work at the ESF by this group using cooled GaAsSb heterojunction photo-diodes provided maps of the coronal emission line polarization at many heights during many observing days (i.e., Querfeld and Smartt, 1984; Arnaud and Newkirk Jr, 1987).
Other infrared emission lines from the corona were predicted to be seen by Münch (1966) at longer wavelengths, including 1431 nm [Si X], 2047 nm [Al IX], 3032 nm [Mg VIII], and 3859 nm [Si IX]. Observations of the 1431 nm line were reported by Mangus and Stockhausen (1966), and later observations from Münch et al. (1967) using a PbS also measured the 3032 nm line. Eclipse observations (Olsen et al., 1971) using a 1 mm diameter InSb detector produced a more complete survey of emission lines from roughly 1000 to 3000 nm. Two low temperature lines (H I 1876 nm and He I 1083 nm) were observed, along with 9 high temperature lines and two unidentified emission lines. The measured wavelengths for the [Al IX] (2744–2749 nm) and the [Mg VIII] (3016–3021 nm) differed from previous predictions and observations. Recently, more work has been done to compute the wavelengths and intensities of infrared coronal emission lines, and a series of papers describing this work begins with Judge (1998). Using a model for a coronal loop structure, this work predicts many new useful lines to observe and confirms some of the calculations from early authors. Brage et al. (2000) point out that in particular, the [Si IX] line at 3935 nm promises to be an important diagnostic of the coronal magnetic field. Table 3 lists several coronal emission lines with wavelengths adapated from Judge (1998).
In addition to diagnosing the polarization of these emission lines, ratios of the emission from these lines can provide insight into the physical parameters of the coronal plasma. The line ratio of the two [Fe XIII] emission lines was computed to be sensitive to the local coronal electron density, and the analysis presented in Flower and Pineau des Forets (1973) facilitates this conversion. Early measurements of these emission lines (Byard and Kissell, 1971) from eclipse data from 1966 showed that the electron density from these two lines was related to the electron density computed with the continuum intensity. Observations from Mauna Kea during the 1991 total solar eclipse with a 61-cm telescope (Penn et al., 1994) provided calibrated images in both lines and nearby continuum. The line ratio was calculated and mapped in a variety of structures in a 180 × 270 arcsecond field of view (see Figure 17), and resulted in lower line ratio values for a given continuum brightness than seen in the earlier eclipse data (Byard and Kissell, 1971).
A map of the ratio of emission from the two infrared [Fe XIII] lines near 1075 nm from the 1991 eclipse. The line ratio is sensitive to the local coronal electron density and reveals structures in the hot plasma near a cool prominence, seen in the lower right of this figure. Image reproduced with permission from Penn et al. (1994), copyright by AAS.
3.6.3 Search for thermal emission from interplanetary dust
Infrared observations are used to explore dust in interstellar regions, and the idea of observing interplanetary dust near the Sun was examined by Peterson (1963). A review of previous eclipse experiments prompted Peterson to suggest that thermal emission from dust might be visible as a ring of infrared light around the Sun. Here the idea is that meteoric or cometary dust which gradually spirals into the Sun would reach a distance (and temperature) where it would sublimate. The region closer to the Sun would be dust free, and so thermal emission observed from this dust would gradually increase towards the Sun and then disappear at this sublimation radius. During an eclipse, observers at the Earth would be able to map this thermal emission. Dust with different chemical composition would be expected to sublimate at different solar distances, and so in principal a set of thermal emission rings might be observed near the Sun.
Observations of thermal excess were seen during an eclipse experiment and also with observations from a stratospheric balloon-borne coronagraph flight at a wavelength of 2200 nm (MacQueen, 1968). In both experiments, a single element PbS detector was used to scan the solar corona. During the eclipse experiment, an excess emisison bump was seen between 3.8 and 4.1 R⊙ and during the balloon flight, excess IR emission was observed between 3.9 and 4.2 R⊙, as well as between 8.5 and 9.5 R⊙. Emission at a radial distance of about 4 R⊙ was also seen at a wavelength of 10 000 nm in a famous airborne eclipse experiement in 1973 (Lena et al., 1974). The instrumentation for this experiement was a liquid-Helium cooled Ge-bolometer (Beckman et al., 1973), and again the solar corona was scanned with this single element detector. Not only was an IR excess detected at 4 R⊙, but many peaks were seen between 3–17 R⊙. A low-resolution spectrum of the emission was also taken between 8000 and 13 000 nm, showing a few peaks from which the authors concluded that the dust was composed of silicates.
With great anticipation, imaging IR detectors were used in several experiments from Mauna Kea during the 1991 eclipse (Lamy et al., 1992; Hodapp et al., 1992). Here intensity and polarization measurements were taken between 1000 and 2500 nm, and in all cases the IR intensity away from the Sun dropped smoothly with radius; no rings were seen at all. A follow-up observation from the 1998 eclipse covering the same spectral bands again showed no dust (Ohgaito et al., 2002), and no recent observations have been made. One idea is that earlier observations likely saw temporary dust enhancement deposited by a sun grazing comet.
3.6.4 Coronal IR spectroscopy
Exploration of the coronal spectrum using modern IR array detectors started with some work from the JESF using a HgCdTe 256 × 26 array. Penn and Kuhn (1994a,b) present observations of the 1075 nm and 1431 nm lines. A new detection of [S IX] emission at 1252 nm the 1994 solar eclipse was done by Kuhn et al. (1996), and the 1431 nm [Si X] 1075 and 1080 nm [Fe XIII] and 1083 nm He I lines were also observed. Unfortunately, no other spectral lines were seen from about 1000 to 1500 nm (excluding wavelengths of strong atmospheric absorption, see Figure 18). Further observations of He I 1083 nm emission from the corona were done using a coronagraph at the Mees solar observatory by Kuhn et al. (2007). Initially the source of these cold neutral Helium atoms was thought to be the local interstellar wind, but subsequent work (Moise et al., 2010) has shown that the measurements are more consistent with ionized helium becoming neutral and scattering solar photons. Finally, new observations of the longer wavelength [Si IX] line predicted by Münch (1966) have revealed the emission at a new wavelength of 3934 nm. Although the line was likely detected in an airborne eclipse experiment during the 1998 eclipse (Kuhn et al., 1999), ground-based observations using the non-coronagraphic McM-P telescope (Judge et al., 2002) have provided the only observed spectrum of this line so far, and produced an accurate central wavelength measurement (see Figure 19).
The coronal spectrum from 1000 to 1500 nm of the 1994 eclipse. The left panel shows the raw counts, and the right panel is normalized to the disk center solar intensity. Lines are seen at 1075, 1080, 1083, 1251, and 1431 nm. Image reproduced with permission from Kuhn et al. (1996), copyright by AAS.
A spectrum of the 3934 nm [Si IX] coronal emission. The top panel shows the observed coronal spectrum with the emission line fit with a Gaussian line profile; the middle panel shows the coronal spectrum and a disk spectrum for reference; and the bottom panel shows a graph approximating the expected Stokes V profile for this line. Image reproduced with permission from Judge et al. (2002), copyright by AAS.
3.6.5 Coronal magnetic field measurements using 1075 nm [Fe XIII]
The circular polarization of the infrared spectral line of [Fe XIII] was examined by Kuhn (1995) using the JESF 40 cm coronagraph and a 1282 HgCdTe array detector. The measurements were made in a dual-beam system where the Stokes I+V and I–V spectra were recorded simultaneously. An upper limit of 40 gauss was determined for the magnetic field strength. Subsequent work at the JESF by Lin et al. (2000) measured all four Stokes states and made a first order correction for the telescopic induced polarization cross-talk. The resulting Stokes V profile was fit with a magnetic field strength of 33 gauss. Using a fiber-fed spectrograph on a 0.5-m reflecting coronagraph at the Mees Solar Observatory on Haleakala, Lin et al. (2004) measured all four Stokes states and again corrected for telescopic induced polarization. Maps of the linear polarization were produced using Stokes Q and U, and then a map of the magnetic field strength was made from the splitting measurements done with the Stokes V profiles. In the coronal area observed, above a limb active region, magnetic fields of about 4 gauss were observed (see Figure 20).
The coronal magnetic field variation with height in the corona over an active region at the solar limb. Measurements are shown (with error bars) as the solid line, and the polarity of the observed magnetic field is seen to vary. Expected magnetic field values from an extrapolation of the active region fields are shown with the points. Image reproduced with permission from Lin et al. (2004), copyright by AAS.
The linear polarization signals from this coronal emission line are several times larger than the circular polarization. Using the Stokes Q and U the COMP instrument has been used with forward models (Ba̧k-Stȩślicka et al., 2013) to explain the linear polarizations observed around coronal voids with a model of a magnetic flux rope. Since the signal to noise of this data is becoming very good now, and improving the data is likely to occur with the DKIST telescope, a full tomographic inversion may be used in the future to measure the magnetic field strength and topology in many coronal structures. Work in this direction has been demonstrated recently by Kramar et al. (2013). And finally, the classical theory regarding the measurement of magnetic fields using the polarization of coronal emission lines was recently updated (Lin and Casini, 2000), and a good review of work using observations of coronal emission line polarization to determine the coronal magnetic field can be found in Judge et al. (2013).
3.6.6 Helioseismology using IR coronal lines
Many new techniques to probe the structure of the solar corona using waves have been developed recently, and infrared observations have provided an important tool. Using the Doppler shift of the [Fe XIIII] 1075 nm spectral line, Tomczyk et al. (2007) found evidence for wave oscillations in many large-scale coronal structures. The COMP observations have 4.5 arcsec pixels, and measure from about 1.05 to 1.35 R⊙ across a segment of about one-quarter of the solar corona. The observations have a cadence of 29 seconds, and while some sequences run for over 9 hours, the published analysis from this work usually include 2 or 3 continuous hours of the best data. The instrument measures all four Stokes parameters at three wavelength positions bracketing the rest wavelength of the 1075 nm spectral line.
Doppler oscillations with a rms velocity of about 300 m/s are found in the velocity observations with periods near 5 minutes. Early work did not find any oscillations in line width, although they have been seen recently (Threlfall et al., 2013). No intensity oscillations have been observed at the level of 3 × 10−3, although observations with SDO/AIA instruments cotemporal with COMP observations have seen oscillations in the line intensity (Threlfall et al., 2013).
The waves have been found to move along the coronal loops, (presumably along the magnetic field lines) and were first thought to be Alfvén waves, but may instead be magneto-acoustic kink waves. With phases speeds greater than 500 km/s, these waves are thought to carry on the order of 100 erg cm−2 s−1, and show more outgoing power than ingoing power (see Figure 21), indicating that the wave energy must be damped in the loops on the time scale of a few oscillation periods. The energy estimated to be carried by the observed waves is many orders of magnitude less than the value canonically quoted to produce coronal heating, but the authors suggest that currently unseen small-scale waves may carry more energy (Tomczyk and McIntosh, 2009).
A map of the outgoing and ingoing power seen in 5-minute period coronal waves for a section of the corona. The oscillations are measured with the [Fe XIII] 1075 nm Doppler shift, and the waves are classified as outgoing and ingoing using their propagation direction. The outgoing waves are measured to have more power than the ingoing waves. Image reproduced with permission from Tomczyk and McIntosh (2009), copyright by AAS.
3.7 Miscellaneous
There are many other areas of solar physics research which have employed infrared detectors. Topics of recent interest include impulsive phase continuum brightening during flares at 10 000 nm (Kaufmann et al., 2013) and long-term infrared solar irradiance variations (Harder et al., 2009; Pagaran et al., 2011). Research in these areas will be discussed in future updates to this review. Some additional research areas are discussed in more detail below, but the topics discussed in this section are in no way a complete survey.
3.7.1 Granulation at different heights
Models of solar granulation (Cheung et al., 2007) predict that the contrast of the solar convective flow will reverse sign at heights as low as z = 130 km. Such reversal has been observed in visible spectral lines which form at roughly z = 350 km (Leenaarts and Wedemeyer-Böhm, 2005) Observations in the CO absorption lines near 4666 nm have been made and show an inverse granulation pattern (Uitenbroek et al., 1994) but the uniqueness of IR diagnostics lies in continuum observations. Continuum emission observed at infrared wavelengths from 1000 to 10 000 nm probes heights in the solar atmosphere from about z = −40 km to z = 140 km, and longer wavelengths can probe above these heights. The radiative transfer involved with continuum is simple compared to that in spectral lines, and so the infrared continuum provides powerful diagnostics for studying the upper layers of solar convection.
Turon and Léna (1973) used an infrared linear array to scan across the solar surface, and mapped sunspots and granulation at 1650 nm. Using the NSO McM-P Main telescope, they produced images of sunspots showing penumbral structure, and images of the quiet Sun with structures near the size of solar granulation. Scanning the solar surface over 2-dimensions with a single element PbS photometer Koutchmy and Lebecq (1986) found intensity fluctuations comparable to the size of granulation at a wavelength of 1750 nm. These observations, and imaging observations using an IR vidicon also in that work suggested that granulation at these wavelengths showed rapid evolution with a timescale of only 3.25 minutes as opposed to 6 minutes seen in visible data (Koutchmy, 1989, 1994). This difference was not seen by Keil et al. (1994) who used an IR array (128 × 128 HgCdTe) to simultaneous observe granulation at 1640 nm while a CCD observed at 558 nm. The Keil et al. (1994) work actually showed evidence for slightly longer-lived features in the infrared dat a as compared to the visible data.
Observations of solar granulation at wavelengths longer than 2000 nm are limited. Observations at McM-P using 1200, 1600, 2200 and 4666 nm channels (see Figure 22) show a surprisingly large contrast at 2200 nm and a low contrast but normal granulation pattern using the 4666 nm continuum (Penn, 2008). Measurements at 4800, 12 400, and 18 000 nm from Gezari et al. (1999) show rapid time fluctuations at the longer wavelengths, suggestive of the dynamics of internetwork regions associated with reverse granulation. The short duration of these observations and the lack of simultaneous visible data strongly suggest that the observations should be repeated.
Images of solar granulation in the infrared J, H, K bands. In each case a sequence of short exposure images was processed using the Multi-Object Multi-Frame Blind Deconvolution (MOMFBD) reconstruction algorithm. In some images artifacts from the reconstruction are visible. The images are not from the same regions of the Sun and are taken at different times under different seeing conditions. The axes are marked in units of arcseconds. Comparison of the contrasts at these wavelengths shows larger than expected contrast in the K-band images. Image reproduced with permission from Penn (2008), copyright by AGU.
3.7.2 Spectropolarimetry with molecular lines
Molecular lines dominate some regions of the infrared and spectropolarimetric observations of molecular lines have been made. Early observations using the vertical spectrograph at the Mc-Math/Pierce telescope showed that CN lines near 1100 nm displayed Stokes V profiles which were reversed from the profiles seen in atomic lines and showed sigma components with unequal depths (Harvey, 1973b). Later, FTS observations of OH spectral lines at 1541 nm showed Stokes V profiles which were also reversed (see Figure 23 and Harvey, 1985; and more recently Rüedi et al., 1995a). New calculations of the Zeeman effect in diatomic molecules have explained the effectively negative Landé-g factor for some OH molecular transitions, which produced the reversed profiles (Berdyugina and Solanki, 2001). CN lines in this spectral region also displayed odd Stokes profiles; in this case the linear polarization signals were anti-symmetric about the rest wavelength. A new theory about the Paschen-Back effect in these molecular lines was needed and developed by Asensio Ramos et al. (2005) to explain the observed profiles. The spectropolarimetric observations of OH lines near 1565 nm were inverted along with the Fe I lines there to obtain the magnetic field in a sunspot (Mathew et al., 2003). Observations at sunspot umbra using the 1006 nm absorption lines of FeH also show rather strong Stokes V profiles. Recent efforts to model the circular polarization of these lines has met with mixed results; the model does a good job for the 1006 nm profiles, but fails for other FeH lines observed near 990 nm (Afram et al., 2007).
The Zeeman Stokes V splitting patterns for several molecular lines. Although the molecular lines measure the same magnetic field, the properties of the particular lines produce positive and negative polarity Stokes V profiles. Image reproduced with permission from Harvey (1985), copyright by NASA.
3.7.3 Hyperfine splitting of Mn I 1526 nm
Asensio Ramos et al. (2007) identified a line from Mn I at 1526.2 nm which originates from an atomic transition that is very sensitive to the Paschen-Back effect for hyperfine structure (see Figure 24) Weak magnetic fields on the order of a few hundred gauss or less can produce Zeeman splitting which is significant compared to the Doppler width of this line in the solar spectrum. This type of observation has the advantage over Stokes V observations that opposite polarities of magnetic fields which may be spatially unresolved do not produce cancelling signals. Observations of this line were made in quiet Sun regions, and a magnetic field of about 250 G was determined. Simulations of the line produced with photospheric models show that an 80 G field will reproduce the observed quiet Sun line profile seen in the FTS spectrum (Asensio Ramos, 2009).
The Stokes profiles for the 1526 nm Mn I absorption line for various magnetic field strengths are shown in this figure. For magnetic fields less than about 1000 G, the two spectral components in the Mn I line show different strengths, and then for fields at higher values the spectral components more apart in wavelength. The special hyperfine structure involved in this line provides a uniquely sensitive measurement of the solar magnetic field. Image reproduced with permission from Asensio Ramos et al. (2007), copyright by AAS.
3.7.4 Ti I lines near 2200 nm
Identified in solar spectral atlases and mentioned in the line list of Rüedi et al. (1995a), a group of several Ti I absorption lines near 2200 nm are excellent probes of the cool plasma in and around sunspot umbrae. Observations of several of the Ti I lines near 2200 nm were made by Rüedi et al. (1998). Several point observations using the FTS and one dimensional cuts through a sunspot using the NIM instrument measured the intensity and Stokes V spectral behavior of the lines through the sunspot umbra, penumbra, and then the quiet Sun. The equivalent width of the lines are strongest in the coolest parts of the umbrae, and then the line virtually disappears in the quiet Sun. Radiative transfer calculations done in this work showed that in the lowest temperature regions the formation of TiO molecules becomes an important factor, and may reduce the line strength. A normal Evershed outflow was observed using these lines by Rüedi et al. (1999). The flow was seen to be nearly horizontal across the solar surface, and the Zeeman splitting of the line suggested a low field strength of 500–900 gauss. Two dimensional maps of a sunspot were made using the 2231 nm line by Penn et al. (2003b), and magnetic fields up to 3300 gauss were observed (see Figure 25). The continuum at 2230 nm was used to compute the temperature of the solar plasma, and then the equivalent width of the line was compared with temperature. The measurements agreed with the observations of Rüedi et al. (1998). Penn et al. (2003a) used the Stokes V spectra from the 2231 nm Ti I absorption line to map the azimuthal variation of the penumbral magnetic field and the Evershed outflow. High values of the Evershed outflow of 6 km/s were seen (consistent with the outflow speeds from a 1564 nm CN line and an unidentified molecular line at 2232.2 nm) and the penumbral magnetic field was measured to be 1400 G.
Stokes V spectral profiles of a Ti I line at 2231 nm. The two Zeeman split components are completely resolved in the sunspot umbra, and the line does not form in the high temperatures of the solar photosphere. With a magnetic sensitivity larger than the Fe I 1565 nm spectral line, this line is uniquely suited for probing the magnetic fields in sunspot umbrae. Image reproduced with permission from Penn et al. (2003b), copyright by Springer.
4 Future Prospects for Infrared Solar Observations
As we have seen in the previous section, our understanding of the Sun has been profoundly shaped by observations made in the infrared spectrum. Spectropolarimetry of IR lines with high magnetic sensitivity clearly demonstrated that kilo-gauss flux tubes were not the building blocks of the Sun’s photospheric magnetism, and instead a variety of magnetic field strengths exist there. Infrared molecular spectroscopy revolutionized our understanding of the temperature structure and the dynamics of the solar atmosphere from the upper photosphere to the lower chromosphere. And now IR spectropolarimetry of both hot and cold lines from the solar corona provide a new window into the critical magnetic processes which drive flares and cause the space weather around the Earth.
More work remains ahead. While IR observations have already changed our physical understanding of the Sun in important ways, at the current time the behavior of our Sun presents us with many problems. The strange trends seen in the current sunspot Cycle 24 and the difficulty with making accurate predictions of the solar magnetic dynamo loom large as of this writing. The exact heating mechanism for the solar corona remains elusive. The evolution of magnetic fields in the chromosphere and the corona, especially the conditions which generate solar flares and coronal mass ejections, is a key problem with a direct connection to spaceweather here at Earth. Having enjoyed the advancements from the past 20 years of work in this field, we must recognize that for continued advancement in the next two decades, we have to continue in the tradition of the original experimentalists. While some infrared observations have become a new comfort zone for solar physics, the hard work of observing new wavelengths must be done. New technology must be used to develop new instrumentation to allow those windows to be opened, and these instruments must be used by careful observers to explore the questions posed by our Sun.
4.1 New telescopes and new instruments
We are at an exciting time in the history of infrared solar physics research with the development of new instruments and new telescopes. At the recently built NST a cooled-grating spectrograph spectropolarimeter is planned to come on-line soon, the Cyra instrument (Cao et al., 2010). Cyra will have dual-beam polarimetric capability from 1000 to 5000 nm, and the cryogenic spectrograph will give much lower background signals for studies from 3000 to 5000 nm. The 1.5-m GREGOR solar telescope at the Observatorio del Teide on Tenerife is home to the GRIS instrument (Schmidt et al., 2012; Collados et al., 2012), which is designed to perform spectroscopy from 1000–2300 nm and spectropolarimetry from 1000–1800 nm. Initial intensity spectra from GRIS show excellent image quality can be obtained with the system, and this promises that future polarimetric data from the instrument will be scientifically very interesting.
A new 4-m all-reflecting IR optimized telescope at the NSO was proposed by Livingston (1994); currently under construction, the 4-m DKIST telescope will deliver 3 times the spatial resolution of the McM-P or the NST facilities. The telescope and the AO system is designed to achieve 0.08 arcsecond resolution at 1565 nm. The infrared instruments planned for the DKIST, the Cryo-NIRSP, and the DL-NIRSP (Lin, 2003; Rimmele et al., 2005) will provide unprecedented observations from 1000 to 5000 nm, on the solar disk, at the limb, and into the solar corona. With these instruments, the DKIST will deliver all of the scientific and technical advantages of observing in the IR solar spectrum at the highest spatial resolution we can now achieve from the ground.
Building on work done by the COMP instrument, Gallagher et al. (2012) have proposed a large coronagraph for the COSMO project which will examine the coronal magnetic fields of the Sun using the polarization of the 1075 nm [Fe XIII] spectral lines. This instrument would operate in a more synoptic manner than would the DKIST Cryo-NIRSP, and it would have a larger field-of-view.
4.1.1 Simultaneous wavelengths and polarizations
Spectropolarimetric observations analyze the spatial distribution of solar radiation across wavelength and polarization state, and the result is that the measured intensity is a function of four variables I(x, y, λ, p). The solar radiation varies inherently as structures change on the Sun, and also as the Earth’s atmosphere alters the incoming wavefronts of sunlight, and so ideally all four of these parameters would be sampled simultaneously. Unfortunately detectors are only 2d, and so modern solar instrumentation divides these four variables in different ways and samples them across short intervals of time. As detector sizes become larger though, it becomes possible to limit the area of the Sun which is observed and to measure more variables simultaneously. Using a slit spectrograph fed with a 64 × 32 array of fiber optics, the SPIES instrument Lin and Jaeggli (2012) simultaneously measures I(x, y, λ) using a 2048 × 2048 array detector. Preliminary results have been shown for spectropolarimetry of 1083 and 1565 nm. Nearly simultaneous I(x, y, λ) measurements are possible with quantum well infrared photodetector (QWIP) cameras as changing the bias voltage applied to the array can alter the wavelength response (Li et al., 2002). Dual beam systems measuring orthogonal polarization are common in solar physics now, and coupled with a slit spectrograph and they minimize the problems caused when atmospheric distortion changes between polarimetric measurements. However, a quad-beam polarimetric system to measure linear I, Q, U Stokes vectors simultaneously has been used for comet observations (Geyer et al., 1996) and, more recently, it has been coupled with a large format array (Kawabata et al., 2008). With the introduction of circular polarization analysis as is currently done with optimal chopping techniques, one may truly measure I(x,λ,p) simultaneously. Stokes measurements at the pixel level using QWIP detectors has been discussed by Serna Jr (2002); one may envision sampling I(x, y,p) simultaneously with a device like this. While the problem of sampling the solar intensity in all of the desired ways is not a unique problem to infrared observations, the unique capabilities of some IR detectors may facilitate a solution in the IR spectrum sooner than at shorter wavelengths.
4.2 What is the wavelength of the next key line?
We currently know that the Mg I 12 318 nm line is the most sensitive probe of the solar magnetic field. However, with a value for geff = 1.0 the wavelength of the line is the key in determining its magnetic sensitivity. A line at a shorter wavelength which was found to have a significantly larger geff value would supercede the Mg I line.
4.2.1 Spectropolarimetry near 4000 nm
A set of weak lines at 4135 nm have been observed recently and are a key target for the Cyra instrument. The lines are weak and have a strong dependence on temperature; they almost completely disappear at the low temperatures of a sunspot umbra. Some of the lines are currently not well-understood, and one shows some very large Zeeman splitting according to Clark (2005) and as seen in more recent data taken at the McM-P (see Figure 26). While the line may be absent from sunspots and active regions, it has the potential to provide critical diagnostics for the weak magnetic fields of the quiet Sun.
4.2.2 Mostly unexplored: 5000–10 000 nm
Until the DKIST comes on-line, the NST and McM-P are the two telescopes that can explore this region of the spectrum, with the McM-P having the advantage of being at a drier site. The Celeste instrument (McCabe et al., 2003) currently represents the only cooled-grating instrument dedicated to solar use at these wavelengths, though other instruments may have abilities here. For use on warm spectrographs, a camera system which functions at these wavelengths is the Si:Ga array detector used by Gezari et al. (1992) and employed for solar observations by Gezari et al. (1999). This array is nominally sensitive from 5000 to 18000 nm. Newer camera systems which can be used in this wavelength range include QWIP cameras, which were used for astronomical imaging by Ressler et al. (2001) and have been fabricated in large formats of 1024 × 1024 (Jhabvala et al., 2004). This particular array is sensitive from 8400 to 9000 nm, although during fabrication the wavelength response of the array can be modified.
4.3 Spectropolarimetry of molecules
Because the IR spectrum is dominated by spectral lines from molecules, a full understanding of the magnetic sensitivity of molecules is imperative if this part of the solar spectrum is to be fully exploited. While the development of some spectropolarimetric diagnostics has been mentioned already, a more thorough review is presented in Berdyugina (2011). An entire session of the Solar Polarization Workshop 4 (Casini and Lites, 2006) was devoted to a description of the state of the art in molecular line spectropolarimetry, and especially interesting work was presented by Trujillo Bueno et al. (2006) and Asensio Ramos (2006). Observations must be done in order to push the development of these theories, and so recent efforts for spectropolarimeters to explore the 1000 to 5000 nm region will provide important results, and efforts beyond 5000 nm are needed as well.
4.4 Space-based solar IR instrumentation
With the exception of only one option for the upcoming Japanese Aerospace Exploration Agency mission to be an infrared spectropolarimeter, prospects for infrared space-based solar observations are surprisingly lacking, although past proposals for space-based solar IR missions have been made, including the SIRE mission (Deming et al., 1991c). This oversight needs to be corrected. While the spatial resolution of a space-based solar telescope operating in the IR is less than if it operated at shorter wavelengths, the magnetic sensitivity such an instrument gains opens new realms of possible science. Night-time astronomy has long exploited the advantages offered in the infrared spectrum through a variety of space missions from IRAS to WISE, from Spitzer to Herschel, and now to the upcoming JWST. Clearly the technology is available to develop cutting-edge solar physics missions to observe the Sun from space in the infrared spectrum. The recent excellent results from the Hinode spacecraft (i.e., Lites et al., 2008) clearly show that a new solar mission with three times the magnetic sensitivity of Hinode would be revolutionary.
References
Afram, N., Berdyugina, S. V., Fluri, D. M., Semel, M., Bianda, M. and Ramelli, R., 2007, “First polarimetric observations and modeling of the FeH F4Δ-X4Δ system”, Astron. Astrophys., 473, L1–L4. [DOI], [ADS], [arXiv:0708.0298]. (Cited on page 41.)
Andretta, V. and Jones, H. P., 1997, “On the Role of the Solar Corona and Transition Region in the Excitation of the Spectrum of Neutral Helium”, Astrophys. J., 489, 375–394. [DOI], [ADS]. (Cited on page 26.)
Arnaud, J. and Newkirk Jr, G., 1987, “Mean properties of the polarization of the Fe XIII 10747 Å coronal emission line”, Astron. Astrophys., 178, 263–268. [ADS]. (Cited on page 34.)
Asensio Ramos, A., 2006, “Theory, Observation, and Modeling of the Zeeman and Paschen-Back Effects in Molecular Lines”, in Solar Polarization 4, Proceedings of the conference held in Boulder, Colorado, USA, 19–23 September, 2005, (Eds.) Casini, R., Lites, B. W., ASP Conference Series, 358, p. 301, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 47.)
Asensio Ramos, A., 2009, “The Magnetic Sensitivity of the Stokes I Profile of the 15260 Å Line of Mn I”, Astrophys. J., 690, 416–426. [DOI], [ADS]. (Cited on page 42.)
Asensio Ramos, A., Trujillo Bueno, J., Carlsson, M. and Cernicharo, J., 2003, “Nonequilibrium CO Chemistry in the Solar Atmosphere”, Astrophys. J. Lett., 588, L61–L64. [DOI], [ADS], [arXiv:astro-ph/0303460]. (Cited on page 18.)
Asensio Ramos, A., Trujillo Bueno, J. and Collados, M., 2005, “Observation and Modeling of Anomalous CN Polarization Profiles Produced by the Molecular Paschen-Back Effect in Sunspots”, Astrophys. J. Lett., 623, L57–L61. [DOI], [ADS], [arXiv:astro-ph/0505076]. (Cited on page 40.)
Asensio Ramos, A., Martínez González, M. J., Lóopez Ariste, A., Trujillo Bueno, J. and Collados, M., 2007, “A Near-Infrared Line of Mn I as a Diagnostic Tool of the Average Magnetic Energy in the Solar Photosphere”, Astrophys. J., 659, 829–847. [DOI], [ADS], [arXiv:astro-ph/0612389]. (Cited on pages 42 and 43.)
Asensio Ramos, A., Trujillo Bueno, J. and Landi Degl’Innocenti, E., 2008, “Advanced Forward Modeling and Inversion of Stokes Profiles Resulting from the Joint Action of the Hanle and Zeeman Effects”, Astrophys. J., 683, 542–565. [DOI], [ADS], [arXiv:0804.2695 [astro-ph]]. (Cited on page 29.)
Athay, R. G. and Johnson, H. R., 1960, “The Excitation of He I in the Spectrum”, Astrophys. J., 131, 413. [DOI], [ADS]. (Cited on page 26.)
Ayres, T. R., 1981, “Thermal bifurcation in the solar outer atmosphere”, Astrophys. J., 244, 1064–1071. [DOI], [ADS]. (Cited on page 18.)
Ayres, T. R., 1998, “CO and the temperature structure of the solar atmosphere”, in New Eyes to See Inside the Sun and Stars, Proceedings of IAU Symposium 185 held in Kyoto, Japan, 18–22 August, 1997, (Eds.) Deubner, F.-L., Christensen-Dalsgaard, J., Kurtz, D., IAU Symposia, 185, p. 403, Kluwer, Dordrecht; Boston. [ADS]. (Cited on page 18.)
Ayres, T. R., 2002, “Does the Sun Have a Full-Time COmosphere?”, Astrophys. J., 575, 1104–1115. [DOI], [ADS]. (Cited on pages 18 and 19.)
Ayres, T. R. and Brault, J. W., 1990, “Fourier transform spectrometer observations of solar carbon monoxide. III. Time-resolved spectroscopy of the Δυ = 1 bands”, Astrophys. J., 363, 705–717. [DOI], [ADS]. (Cited on page 20.)
Ayres, T. R. and Linsky, J. L., 1976, “The Mg II H and K lines. II. Comparison with synthesized profiles and Ca II K”, Astrophys. J., 205, 874–894. [DOI], [ADS]. (Cited on page 18.)
Ayres, T. R. and Rabin, D., 1996, “Observations of Solar Carbon Monoxide with an Imaging Infrared Spectrograph. I. Thermal Bifurcation Revisited”, Astrophys. J., 460, 1042. [DOI], [ADS]. (Cited on pages 18, 19, and 20.)
Ayres, T. R. and Testerman, L., 1981, “Fourier Transform Spectrometer observations of solar carbon monoxide. I. The fundamental and first overtone bands in the quiet sun”, Astrophys. J., 245, 1124–1140. [DOI], [ADS]. (Cited on page 18.)
Ayres, T. R., Plymate, C. and Keller, C. U., 2006, “Solar Carbon Monoxide, Thermal Profiling, and the Abundances of C, O, and Their Isotopes”, Astrophys. J. Suppl. Ser., 165, 618–651. [DOI], [ADS], [arXiv:astro-ph/0606153]. (Cited on page 18.)
Ayres, T. R., Lyons, J. R., Ludwig, H.-G., Caffau, E. and Wedemeyer-Böhm, S., 2013, “Is the Sun Lighter than the Earth? Isotopic CO in the Photosphere, Viewed through the Lens of Three-dimensional Spectrum Synthesis”, Astrophys. J., 765, 46. [DOI], [ADS], [arXiv:1301.5281 [astro-ph.SR]]. (Cited on page 18.)
Babcock, H. D. and Babcock, H. W., 1934, “Some New Features of the Solar Spectrum”, Publ. Astron. Soc. Pac., 46, 132. [DOI], [ADS]. (Cited on page 25.)
Ba̧k-Stȩślicka, U., Gibson, S. E., Fan, Y., Bethge, C., Forland, B. and Rachmeler, L. A., 2013, “The Magnetic Structure of Solar Prominence Cavities: New Observational Signature Revealed by Coronal Magnetometry”, Astrophys. J. Lett., 770, L28. [DOI], [ADS], [arXiv:1304.7388 [astro-ph.SR]]. (Cited on page 37.)
Balasubramaniam, K. S., Venkatakrishnan, P. and Bhattacharyya, J. C., 1985, “Measurement of vector magnetic fields. I. heoretical approach to the instrumental polarisation of the Kodaikanal Solar Tower”, Solar Phys., 99, 333–348. [DOI], [ADS]. (Cited on page 10.)
Beckers, J. M., 1969, A table of Zeeman Multiplets, Physical Science Research Papers, no. 371, SPO and Air Force Cambridge Research Laboratories, Bedford, MA. [ADS]. (Cited on page 13.)
Beckman, J., Begot, J., Charvin, P., Hall, D., Lena, P., Soufflot, A., Liebenberg, D. and Wraight, P., 1973, “Eclipse Flight of Concorde 001”, Nature, 246, 72–74.[DOI]. (Cited on page 36.)
Bellot Rubio, L. R., Collados, M., Ruiz Cobo, B. and Rodríguez Hidalgo, I., 2000, “Oscillations in the Photosphere of a Sunspot Umbra from the Inversion of Infrared Stokes Profiles”, Astrophys. J., 534, 989–996. [DOI], [ADS]. (Cited on pages 23 and 24.)
Bennet, H. E. and Porteus, J. O., 1961, “Relation Between Surface Roughness and Specular Reflectance at Normal Incidence”, J. Opt. Soc. Am., 51(2), 123–129. [DOI]. (Cited on page 9.)
Berdyugina, S. V., 2011, “Polarimetry of Cool Atmospheres: From the Sun to Exoplanets”, in Solar Polarization 6, Proceedings of a conference held in Maui, Hawaii, USA, May 30–June 4, 2010, (Eds.) Kuhn, J. R., Harrington, D. M., Lin, H., Berdyugina, S. V., Trujillo-Bueno, J., Keil, S. L., Rimmele, T. R., ASP Conference Series, 437, p. 219, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:1011.0751 [astro-ph.SR]]. (Cited on page 47.)
Berdyugina, S. V. and Solanki, S. K., 2001, “Zeeman-split opposite-polarity OH lines in sunspot spectra: Resolution of a puzzle”, Astron. Astrophys., 380, L5–L8. [DOI], [ADS]. (Cited on page 40.)
Boreiko, R. T. and Clark, T. A., 1987, “Solar brightness temperature at submillimeter wavelengths”, Astrophys. J., 318, 445–450. [DOI], [ADS]. (Cited on page 16.)
Brage, T., Judge, P. G., Jönsson, P. and Edwards, D. P., 2000, “Spectral Lines for Polarization Measurements of the Coronal Magnetic Field. III. Atomic Data for Si IX”, Astrophys. J., 540, 1114–1118. [DOI], [ADS]. (Cited on page 35.)
Brault, J. and Noyes, R., 1983, “Solar emission lines near 12 microns”, Astrophys. J., 269, L61–L66. [DOI], [ADS]. (Cited on page 30.)
Bruls, J. H. M. J., Solanki, S. K., Rutten, R. J. and Carlsson, M., 1995, “Infrared lines as probes of solar magnetic features. VIII. Mg I 12µm diagnostics of sunspots”, Astron. Astrophys., 293, 225–239. [ADS]. (Cited on page 32.)
Byard, P. L. and Kissell, K. E., 1971, “Observations of the Infrared Fe XIII Lines in the Solar Corona of 12 November, 1966”, Solar Phys., 21, 351–359. [DOI], [ADS]. (Cited on page 35.)
Cabrera Solana, D., Bellot Rubio, L. R., Beck, C. and Del Toro Iniesta, J. C., 2006, “Inversion of Visible and IR Stokes Profiles in Sunspots”, in Solar Polarization 4, Proceedings of the conference held in Boulder, CO, USA, 19–23 September, 2005, (Eds.) Casini, R., Lites, B. W., ASP Conference Series, 358, pp. 25–30, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 23.)
Cao, W., Denker, C. J., Wang, H., Ma, J., Qu, M., Wang, J. and Goode, P. R., 2004, “Characteristic evaluation of a near-infrared Fabry-Perot filter for the InfraRed Imaging Magnetograph (IRIM)”, in Telescopes and Instrumentation for Solar Astrophysics, San Diego, California, USA, August 3, 2003, (Eds.) Fineschi, S., Gummin, M. A., Proc. SPIE, 5171, pp. 307–315, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 21.)
Cao, W., Gorceix, N., Coulter, R., Ahn, K., Rimmele, T. R. and Goode, P. R., 2010, “Scientific instrumentation for the 1.6 m New Solar Telescope in Big Bear”, Astron. Nachr., 331, 636. [DOI], [ADS]. (Cited on page 45.)
Carlsson, M., Rutten, R. J. and Shchukina, N. G., 1992, “The formation of the Mg I emission features near 12 microns”, Astron. Astrophys., 253, 567–585. [ADS]. (Cited on page 31.)
Casini, R. and Lites, B. W. (Eds.), 2006, Solar Polarization 4, Proceedings of the conference held in Boulder, Colorado, USA, 19–23 September, 2005, ASP Conference Series, 358, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 47.)
Centeno, R., Collados, M. and Trujillo Bueno, J., 2006, “Oscillations and Wave Propagation in Different Solar Magnetic Features”, in Solar Polarization 4, Proceedings of the conference held in Boulder, Colorado, USA, 19–23 September, 2005, (Eds.) Casini, R., Lites, B. W., ASP Conference Series, 358, p. 465, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 30.)
Centeno, R., Trujillo Bueno, J., Uitenbroek, H. and Collados, M., 2009, “Influence of Coronal EUV Irradiance on the Stokes Profiles of the He I 10830 Å Multiplet”, in Solar Polarization 5: In Honor of Jan Stenflo, Proceedings of the conference held 17–21 September, 2007 in Ascona, Switzerland, (Eds.) Berdyugina, S. V., Nagendra, K. N., Ramelli, R., ASP Conference Series, 405, p. 297, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 26.)
Chang, E. S., 1994, “Atomic Physics of the 12-µm and Related Lines”, in Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, (Eds.) Rabin, D. M., Jefferies, J. T., Lindsey, C., IAU Symposia, 154, pp. 297–307, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on page 30.)
Chang, E. S. and Deming, D., 1996, “Observation of infrared lines in a prominence at 1–5 microns”, Solar Phys., 165, 257–274. [DOI], [ADS]. (Cited on page 27.)
Chang, E. S. and Noyes, R. W., 1983, “Identification of the solar emission lines near 12 microns”, Astrophys. J., 275, L11–L13. [DOI], [ADS]. (Cited on pages 30 and 31.)
Cheung, M. C. M., Schüssler, M. and Moreno-Insertis, F., 2007, “The origin of the reversed granulation in the solar photosphere”, Astron. Astrophys., 461, 1163–1171. [DOI], [ADS], [arXiv:astro-ph/0612464]. (Cited on pages 15 and 39.)
Clark, A., 2005, personal communication. (Cited on page 46.)
Clark, T. A., Lindsey, C., Rabin, D. M. and Livingston, W. C., 1995, “Eclipse Measurements of the Distribution of CO Emission Above the Solar Limb”, in Infrared tools for solar astrophysics: What’s next?, Proceedings of the 15th NSO/Sacramento Peak Summer Workshop, held in Sunspot, NM, USA, 19–23 September 1994, (Eds.) Kuhn, J. R., Penn, M. J., p. 133, World Scientific, Singapore. [ADS]. (Cited on page 18.)
Clark, T. A., Plymate, C., Bergman, M. W. and Keller, C. U., 2004, “Evershed Flow of CO at Different Depths in a Sunspot Penumbra”, Bull. Am. Astron. Soc., 36, 712. [ADS]. (Cited on page 19.)
Collados, M., López, R., Páez, E. et al., 2012, “GRIS: The GREGOR Infrared Spectrograph”, Astron. Nachr., 333, 872–879. [DOI], [ADS]. (Cited on page 45.)
de Toma, G., Holzer, T. E., Burkepile, J. T. and Gilbert, H. R., 2005, “Transient Coronal Holes as Seen in the HeI 1083 nm MLSO Observations”, Astrophys. J., 621, 1109–1120. [DOI], [ADS]. (Cited on page 26.)
Deming, D., Boyle, R. J., Jennings, D. E. and Wiedemann, G., 1988, “Solar magnetic field studies using the 12 micron emission lines. I. Quiet sun time series and sunspot slices”, Astrophys. J., 333, 978–995. [DOI], [ADS]. (Cited on pages 30, 31, and 32.)
Deming, D., Hewagama, T., Jennings, D. E. and Wiedemann, G., 1991a, “Polarimetry in the infrared”, in Solar Polarimetry, Proceedings of the 11th NSO/Sacramento Peak Summer Workshop, held in Sunspot, NM, USA, 27–31 August 1990, (Ed.) November, L. J., pp. 341–355, National Solar Observatory, Sunspot, NM. [ADS]. (Cited on page 11.)
Deming, D., Jennings, D. E., Jefferies, J. and Lindsey, C., 1991b, “Physics of the infrared spectrum”, in Solar Interior and Atmosphere, (Eds.) Cox, A. N., Livingston, W. C., Matthews, M. S., pp. 933–963, University of Arizona Press, Tucson, AZ. [ADS]. (Cited on page 6.)
Deming, D., Kostiuk, T. and Glenar, D., 1991c, “The Solar Infrared Explorer (SIRE): A Small Explorer Mission for Solar Physics”, Bull. Am. Astron. Soc., 23, 1038. [ADS]. (Cited on page 47.)
Deming, D., Jennings, D. E., McCabe, G., Noyes, R., Wiedemann, G. and Espenak, F., 1992, “Limb observations of the 12.32 micron solar emission line during the 1991 July total eclipse”, Astrophys. J., 396, L53–L56. [DOI], [ADS]. (Cited on page 30.)
Deming, D., Jennings, D. E., McCabe, G., Moran, T. and Loewenstein, R., 1998, “Limb observations of the 12.32-micron MgI emission line during the 1994 annular eclipse”, Solar Phys., 182, 283–291. [DOI], [ADS]. (Cited on page 30.)
Ding, M. D., Li, H. and Fang, C., 2005, “On the formation of the He I 10830 Å line in a flaring atmosphere”, Astron. Astrophys., 432, 699–704. [DOI], [ADS]. (Cited on page 27.)
Domínguez Cerdeña, I., Sánchez Almeida, J. and Kneer, F., 2006, “Quiet Sun Magnetic Fields from Simultaneous Inversions of Visible and Infrared Spectropolarimetric Observations”, Astrophys. J., 646, 1421–1435. [DOI], [ADS], [arXiv:astro-ph/0604381]. (Cited on page 23.)
Eddy, J. A. and Malville, J., 1967, “Observations of the Emission Lines of Fe XIII during the Solar Eclipse of May 30, 1965”, Astrophys. J., 150, 289. [DOI], [ADS]. (Cited on page 34.)
Elmore, D. F., Casini, R., Card, G. L., Davis, M., Lecinski, A., Lull, R., Nelson, P. G. and Tomczyk, S., 2008, “A new spectro-polarimeter for solar prominence and filament magnetic field measurements”, in Ground-based and Airborne Instrumentation for Astronomy II, Marseille, France, June 23, 2008, (Eds.) McLean, I. S., Casali, M. M., Proc. SPIE, 7014, 701416, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 25.)
Farmer, C. B. and Norton, R. H., 1989a, A High-Resolution Atlas of the Infrared Spectrum of the Sun and the Earth Atmosphere from Space: A Compilation of ATMOS Spectra of the Region from 650 to 4800 cm−1 (2.3 to 16 µm), Volume I: The Sun, NASA Reference Publication, 1224, NASA, Washington, DC. [ADS]. Online version (accessed 6 May 2014): http://ntrs.nasa.gov/search.jsp?R=19900004577. (Cited on page 30.)
Farmer, C. B. and Norton, R. H., 1989b, A High-Resolution Atlas of the Infrared Spectrum of the Sun and the Earth Atmosphere from Space. A Compilation of ATMOS Spectra of the Region from 650 to 4800 cm−1 (2.3 to 16 µm), Volume II: Stratosphere and Mesosphere, 650 to 3350 cm−1, NASA Reference Publication, 1224, NASA, Washington, DC. [ADS]. Online version (accessed 6 May 2014): http://ntrs.nasa.gov/search.jsp?R=19890019598. (Cited on pages 17 and 18.)
Firor, J. and Zirin, H., 1962, “Observations of Five Ionization Stages of Iron in the Solar Corona”, Astrophys. J., 135, 122. [DOI], [ADS]. (Cited on page 34.)
Fleck, B., Deubner, F.-L., Maier, D. and Schmidt, W., 1994, “Observations of Solar Oscillations in He I 10830 Å”, in Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, (Eds.) Rabin, D. M., Jefferies, J. T., Lindsey, C., IAU Symposium, 154, pp. 65–70, Kluwer, Dordrecht. [DOI], [ADS]. (Cited on pages 30 and 31.)
Flower, D. R. and Pineau des Forets, G., 1973, “Excitation of the Fe XIII Spectrum in the Solar Corona”, Astron. Astrophys., 24, 181. [ADS]. (Cited on page 35.)
Fontenla, J. M., Avrett, E. H., Thuillier, G. and Harder, J., 2006, “Semiempirical Models of the Solar Atmosphere. I. The Quiet- and Active Sun Photosphere at Moderate Resolution”, Astrophys. J., 639, 441–458. [DOI], [ADS]. (Cited on page 15.)
Gallagher, D., Tomczyk, S., Zhang, H. and Nelson, P. G., 2012, “Optical design of the COSMO large coronagraph”, in Ground-based and Airborne Telescopes IV, Amsterdam, Netherlands, July 1, 2012, (Eds.) Stepp, L. M., Gilmozzi, R., Hall, H. J., Proc. SPIE, 8444, 84443P, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 45.)
Geyer, E. H., Jockers, K., Kiselev, N. N. and Chernova, G. P., 1996, “A novel quadruple beam imaging polarimeter and its application to Comet Tanaka-Machholz 1992 X”, Astrophys. Space Sci., 239, 259–274. [DOI], [ADS]. (Cited on page 45.)
Gezari, D., Livingston, W. and Varosi, F., 1999, “Thermal Structure in Sunspots and Dynamic Solar Infrared Granulation Imaged at 4.8, 12.4, and 18.1 Microns”, in High Resolution Solar Physics: Theory, Observations, and Techniques, Proceedings of the 19th NSO/Sacramento Peak Summer Workshop, held in Sunspot, NM, USA, 28 September–2 October 1998, (Eds.) Rimmele, T. R., Balasubramaniam, K. S., Radick, R. R., ASP Conference Series, 183, p. 559, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on pages 15, 40, and 46.)
Gezari, D. Y., Folz, W. C., Woods, L. A. and Varosi, F., 1992, “A 5–18 µm Array Camera for High-Background Astronomical Imaging”, Publ. Astron. Soc. Pac., 104, 191–203. [DOI], [ADS]. (Cited on page 46.)
Giovanelli, R. G. and Hall, D., 1977, “The helium 10830 Å line in the undisturbed chromosphere”, Solar Phys., 52, 211–228. [DOI], [ADS]. (Cited on page 26.)
Goldberg, L., 1939, “The Temperature of the Solar Chromosphere”, Astrophys. J., 89, 673. [DOI], [ADS]. (Cited on page 26.)
Goldman, A., Blatherwick, R. D., Murcray, F. H., Van Allen, J. W., Bradford, C. M., Cook, G. R. and Murcray, D. G., 1980, New Atlas of IR Solar Spectra, NASA Technical Report, NASA-CR-163499, NASA / University of Denver, Hampton, VA; Denver, CO. [ADS]. Online version (accessed 6 May 2014): http://ntrs.nasa.gov/search.jsp?R=19800022793. (Cited on page 30.)
Golub, L., Harvey, K. L., Herant, M. and Webb, D. F., 1989, “X-ray bright points and He I λ 10830 dark points”, Solar Phys., 124, 211–217. [DOI], [ADS]. (Cited on page 27.)
Hall, D. N. B. and Noyes, R. W., 1969, “Observation of Hydrogen Fluoride in Sunspots and the Determination of the Solar Fluorine Abundance”, Astrophys. Lett., 4, 143. [ADS]. (Cited on page 21.)
Hall, D. N. B., Noyes, R. W. and Ayres, T. R., 1972, “The Identification of 13C16O in the Infrared Sunspot Spectrum and the Determination of the Solar 12C/13C Abundance Ratio”, Astrophys. J., 171, 615. [DOI], [ADS]. (Cited on page 18.)
Hanaoka, Y., Sakurai, T., Shinoda, K. et al., 2011, “Infrared Stokes Spectro-Polarimeter at the National Astronomical Observatory of Japan”, in Solar Polarization 6, Proceedings of a conference held in Maui, Hawaii, USA, May 30–June 4, 2010, (Eds.) Kuhn, J. R., Harrington, D. M., Lin, H., Berdyugina, S. V., Trujillo-Bueno, J., Keil, S. L., Rimmele, T. R., ASP Conference Series, 437, p. 371, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 25.)
Harder, J. W., Fontenla, J. M., Pilewskie, P., Richard, E. C. and Woods, T. N., 2009, “Trends in solar spectral irradiance variability in the visible and infrared”, Geophys. Res. Lett., 36, L07801. [DOI], [ADS]. (Cited on page 39.)
Harvey, J., 1985, “Trends in measurement of solar vector magnetic fields using the Zeeman effect”, in Measurements of Solar Vector Magnetic Fields, Proceedings of the MSFC workshop held at George C. Marshall Space Flight Center, Huntsville, AL, USA, May 15–18, 1984, (Ed.) Hagyard, M. J., NASA Conference Publication, 2374, pp. 109–120, NASA, Washington, DC. [ADS]. (Cited on pages 40 and 41.)
Harvey, J. and Hall, D., 1971, “Magnetic Fields Measured with the 10830 Å He I Line”, in Solar Magnetic Fields, Proceedings of IAU Symposium 43 held in Paris, France, August 31–September 4, 1970, (Ed.) Howard, R., IAU Symposia, 43, p. 279, Reidel, Dordrecht. [ADS]. (Cited on pages 8, 25, and 28.)
Harvey, J. and Hall, D., 1975, “Magnetic Field Observations with Fe I λ15648 Å”, Bull. Am. Astron. Soc., 7, 459. [ADS]. (Cited on pages 21 and 22.)
Harvey, J., Krieger, A. S., Timothy, A. F. and Vaiana, G. S., 1975, “Comparison of Skylab X-ray and Ground-based Helium Observations”, in Skylab Solar Workshop, Prelimary Results from the S-054 X-Ray Telescope and the Correlated Ground-Based Observations, Florence, Italy, 21–22 March 1974, (Ed.) Righini, G., Oss. Mem. Oss. Astrofis. Arcetri, 104, pp. 50–58, Baccini & Chiappi, Florence. [ADS]. (Cited on page 26.)
Harvey, J. E., Schröder, S., Choi, N. and Duparré, A., 2012, “Total integrated scatter from surfaces with arbitrary roughness, correlation widths, and incident angles”, Opt. Eng., 51(1), 013402. [DOI]. (Cited on page 10.)
Harvey, J. W., 1973a, “Fraunhofer Lines with Large Zeeman Splitting”, Solar Phys., 28, 9–13. [DOI], [ADS]. (Cited on page 13.)
Harvey, J. W., 1973b, “Polarization of Red System CN Lines in Sunspots”, Solar Phys., 28, 43–47. [DOI], [ADS]. (Cited on page 40.)
Harvey, J. W., 1977, “Observations of Small-Scale Photospheric Magnetic Fields”, in Highlights of Astronomy, Vol. 4, As Presented at the XVIth General Assembly of the IAU 1976, (Ed.) Müller, E. A., pp. 223–239, D. Reidel, Dordrecht; Boston. [DOI], [ADS]. (Cited on page 22.)
Harvey, K. L. and Recely, F., 1984, “He I 10830 observations of the 3N/M4.0 flare of 4 September, 1982”, Solar Phys., 91, 127–139. [DOI], [ADS]. (Cited on pages 26 and 27.)
Harvey, K. L. and Recely, F., 2002, “Polar Coronal Holes During Cycles 22 and 23”, Solar Phys., 211, 31–52. [DOI], [ADS]. (Cited on page 26.)
Heasley, J. N., Tandberg-Hanssen, E. and Wagner, W. J., 1975, “Study of HeI emission lines in the solar atmosphere. III. The triplet-singlet line intensity ratios in solar prominences”, Astron. Astrophys., 40, 391–395. [ADS]. (Cited on page 27.)
Herschel, W., 1800, “Experiments on the Refrangibility of the Invisible Rays of the Sun”, Philos. Trans. R. Soc. London, 90, 284–292. [DOI], [ADS]. (Cited on page 5.)
Hewagama, T., 1991, An infrared polarimetric study of sunspots, Ph.D. thesis, Maryland University, College Park, MD. [ADS]. (Cited on page 11.)
Hewagama, T., Deming, D., Jennings, D. E., Osherovich, V., Wiedemann, G., Zipoy, D., Mickey, D. L. and Garcia, H., 1993, “Solar magnetic field studies using the 12 micron emission lines. II. Stokes profiles and vector field samples in sunspots”, Astrophys. J. Suppl. Ser., 86, 313–332. [DOI], [ADS]. (Cited on page 32.)
Hinkle, K. H., Wallace, L. and Livingston, W., 2003, “Atmospheric Transmission Above Kitt Peak, 0.5 to 5.5 microns”, Bull. Am. Astron. Soc., 35, 1260. [ADS]. (Cited on pages 6 and 7.)
Hirayama, T., 1971, “The Abundance of Helium in Prominences and in the Chromosphere”, Solar Phys., 19, 384–400. [DOI], [ADS]. (Cited on page 26.)
Hodapp, K.-W., MacQueen, R. M. and Hall, D. N. B., 1992, “A search during the 1991 solar eclipse for the infrared signature of circumsolar dust”, Nature, 355, 707–710. [DOI], [ADS]. (Cited on page 36.)
House, L. L., 1977, “Coronal emission-line polarization from the statistical equilibrium of magnetic sub-levels. I. Fe XIII”, Astrophys. J., 214, 632–652. [DOI], [ADS]. (Cited on page 34.)
Hyder, C. L., 1965, “The Polarization of Emission Lines in Astronomy. III. The Polarization of Coronal Emission Lines”, Astrophys. J., 141, 1382. [DOI], [ADS]. (Cited on page 34.)
Jaeggli, S. A., Lin, H., Mickey, D. L., Kuhn, J. R., Hegwer, S. L., Rimmele, T. R. and Penn, M. J., 2010, “FIRS: a new instrument for photospheric and chromospheric studies at the DST”, Mem. Soc. Astron. Ital., 81, 763. [ADS]. (Cited on pages 17 and 21.)
Jaeggli, S. A., Lin, H. and Uitenbroek, H., 2012, “On Molecular Hydrogen Formation and the Magneto-hydrostatic Equilibrium of Sunspots”, Astrophys. J., 745, 133. [DOI], [ADS], [arXiv:1110.0575 [astro-ph.SR]]. (Cited on page 23.)
Janssen, M., 1869, “The Total Solar Eclipse of August 1868. Part I”, Astron. Reg., 7, 107–110. [ADS]. (Cited on page 26.)
Jefferies, J. T., 1994, “Overview of Infrared Solar Physics”, in Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, (Eds.) Rabin, D. M., Jefferies, J. T., Lindsey, C., IAU Symposia, 154, pp. 1–8, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on pages 5 and 17.)
Jennings, D. E., Deming, D., McCabe, G., Sada, P. V. and Moran, T., 2002, “Solar Magnetic Field Studies Using the 12 Micron Emission Lines. IV. Observations of a Delta Region Solar Flare”, Astrophys. J., 568, 1043–1048. [DOI], [ADS], [arXiv:astro-ph/0112116]. (Cited on pages 32 and 33.)
Jhabvala, M., Choi, K., Goldberg, A. C., La, A. T. and Gunapala, S. D., 2004, “Development of a 1K × 1K GaAs QWIP far IR imaging array”, in Focal Plane Arrays for Space Telescopes, San Diego, California, USA, August 3, 2003, (Eds.) Grycewicz, T. J., McCreight, C. R., Proc. SPIE, 5167, pp. 175–185, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 46.)
Johnson, H. L., 1962, “Infrared Stellar Photometry”, Astrophys. J., 135, 69. [DOI], [ADS]. (Cited on page 6.)
Johnson, N. J., 1972, Solar Infrared Limb Profiles, Ph.D. thesis, The University of Michigan, Ann Arbor, MI. [ADS]. (Cited on page 10.)
Jones, H. P., Duvall Jr, T. L., Harvey, J. W., Mahaffey, C. T., Schwitters, J. D. and Simmons, J. E., 1992, “The NASA/NSO spectromagnetograph”, Solar Phys., 139, 211–232. [DOI], [ADS]. (Cited on page 25.)
Judge, P. G., 1998, “Spectral Lines for Polarization Measurements of the Coronal Magnetic Field. I. Theoretical Intensities”, Astrophys. J., 500, 1009. [DOI], [ADS]. (Cited on page 35.)
Judge, P. G., Tomczyk, S., Livingston, W. C., Keller, C. U. and Penn, M. J., 2002, “Spectroscopic Detection of the 3.934 Micron Line of Si IX in the Solar Corona”, Astrophys. J. Lett., 576, L157–L160. [DOI], [ADS]. (Cited on pages 34, 37, and 38.)
Judge, P. G., Habbal, S. and Landi, E., 2013, “From Forbidden Coronal Lines to Meaningful Coronal Magnetic Fields”, Solar Phys., 288, 467–480. [DOI], [ADS], [arXiv:1304.3863 [astro-ph.SR]]. (Cited on page 38.)
Karo, D. P. and Schneiderman, A. M., 1978, “Speckle interferometry at finite spectral bandwidths and exposure times”, J. Opt. Soc. Am., 68, 480–485. [DOI], [ADS]. (Cited on page 8.)
Kaufmann, P., White, S. M., Freeland, S. L. et al., 2013, “A Bright Impulsive Solar Burst Detected at 30 THz”, Astrophys. J., 768, 134. [DOI], [ADS], [arXiv:1303.5894 [astro-ph.IM]]. (Cited on pages 6 and 39.)
Kawabata, K. S., Nagae, O., Chiyonobu, S. et al., 2008, “Wide-field one-shot optical polarimeter: HOW-Pol”, in Ground-based and Airborne Instrumentation for Astronomy II, Marseille, France, June 23, 2008, (Eds.) McLean, I. S., Casali, M. M., Proc. SPIE, 7014, 70144L, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 45.)
Keil, S., Kuhn, J., Lin, H. and Reardon, K., 1994, “Simultaneous IR and Visible Light Measurements of the Solar Granulation”, in Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, (Eds.) Rabin, D. M., Jefferies, J. T., Lindsey, C., IAU Symposia, 154, pp. 251–257, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on page 40.)
Keil, S. L., Rimmele, T. R. and Keller, C. U. [ATST Team], 2001, “The Advanced Technology Solar Telescope”, in Advanced Solar Polarimetry — Theory, Observation, and Instrumentation, Proceedings of the 20th NSO/Sacramento Peak Summer Workshop, held in Sunspot, NM, USA, 11–15 September 2000, (Ed.) Sigwarth, M., ASP Conference Series, 236, p. 597, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 17.)
Keller, C. U., Harvey, J. W. and Giampapa, M. S., 2003, “SOLIS: an innovative suite of synoptic instruments”, in Innovative Telescopes and Instrumentation for Solar Astrophysics, Waikoloa, Hawaii, USA, August 22–28, 2002, (Eds.) Keil, S. L., Avakyan, S. V., Proc. SPIE, 4853, pp. 194–204, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 25.)
Khomenko, E. V., Martínez González, M. J., Collados, M., Vögler, A., Solanki, S. K., Ruiz Cobo, B. and Beck, C., 2005, “Magnetic flux in the internetwork quiet Sun”, Astron. Astrophys., 436, L27–L30. [DOI], [ADS]. (Cited on page 23.)
Knestrick, G. L., Cosden, T. H. and Curcio, J. A., 1962, “Atmospheric Scattering Coefficients in the Visible and Infrared Regions”, J. Opt. Soc. Am., 52(9), 1010–1016. [DOI]. (Cited on page 9.)
Kopp, G. and Rabin, D., 1992, “A relation between magnetic field strength and temperature in sunspots”, Solar Phys., 141, 253–265. [DOI], [ADS]. (Cited on page 23.)
Kopp, G., Lindsey, C., Roellig, T. L., Werner, M. W., Becklin, E. E., Orrall, F. Q. and Jefferies, J. T., 1992, “Chromospheric dynamics based on infrared solar brightness variations”, Astrophys. J., 388, 203–210. [DOI], [ADS]. (Cited on page 20.)
Koutchmy, S., 1989, “Photoelectric Analysis of the Solar Granulation in the Infrared”, in Solar and Stellar Granulation, Proceedings of the 3rd Workshop of the Astronomical Observatory of Capodimonte (OAC 3) and the NATO Advanced Research Workshop held at Capri, Italy, June 21–25, 1988, (Eds.) Rutten, R. J., Severino, G., NATO ASI Series C, 263, p. 347, Kluwer, Dordrecht; Boston. [ADS]. (Cited on page 40.)
Koutchmy, S., 1994, “The Infrared Granulation — Observations”, in Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, (Eds.) Rabin, D. M., Jefferies, J. T., Lindsey, C., IAU Symposia, 154, pp. 239–250, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on page 40.)
Koutchmy, S. and Lebecq, C., 1986, “The solar granulation. II. Photographic and photoelectric analysis of photospheric intensity fluctuations at the meso-granulation scale”, Astron. Astrophys., 169, 323–328. [ADS]. (Cited on page 39.)
Kramar, M., Inhester, B., Lin, H. and Davila, J., 2013, “Vector Tomography for the Coronal Magnetic Field. II. Hanle Effect Measurements”, Astrophys. J., 775, 25. [DOI], [ADS]. (Cited on page 38.)
Kuhn, J. R., 1995, “Infrared Coronal Magnetic Field Measurements”, in Infrared tools for solar astrophysics: What’s next?, Proceedings of the 15th NSO/Sacramento Peak Summer Workshop, held in Sunspot, NM, USA, 19–23 September 1994, (Eds.) Kuhn, J. R., Penn, M. J., p. 89, World Scientific, Singapore. [ADS]. (Cited on page 37.)
Kuhn, J. R. and Penn, M. J. (Eds.), 1995, Infrared tools for solar astrophysics: What’s next?, Proceedings of the 15th NSO/Sacramento Peak Summer Workshop, held in Sunspot, NM, USA, 19–23 September 1994, World Scientific, Singapore. [ADS]. (Cited on page 17.)
Kuhn, J. R., Penn, M. J. and Mann, I., 1996, “The Near-Infrared Coronal Spectrum”, Astrophys. J. Lett., 456, L67. [DOI], [ADS]. (Cited on pages 34, 36, and 37.)
Kuhn, J. R., MacQueen, R. M., Streete, J. et al., 1999, “Probable Detection of a Bright Infrared Coronal Emission Line of Si IX near 3.93 Microns”, Astrophys. J., 521, 478–482. [DOI], [ADS]. (Cited on pages 34 and 37.)
Kuhn, J. R., Arnaud, J., Jaeggli, S., Lin, H. and Moise, E., 2007, “Detection of an Extended Near-Sun Neutral Helium Cloud from Ground-based Infrared Coronagraph Spectropolarimetry”, Astrophys. J. Lett., 667, L203–L205. [DOI], [ADS]. (Cited on page 37.)
Kumar, C. K. and Davila, J., 1994, “Potential IR Observations of the Solar Corona”, in Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, (Eds.) Rabin, D. M., Jefferies, J. T., Lindsey, C., IAU Symposia, 154, pp. 81–84, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on page 17.)
Kurucz, R. L., 2009, “Including All the Lines”, in Recent Directions in Astrophysical Quantitative Spectroscopy and Radiation Hydrodynamics, Proceedings of the International Conference in Honor of Dimitri Mihalas for His Lifetime Scientific Contributions on the Occasion of His 70th Birthday, Boulder, Colorado, 30 March–3 April 2009, (Eds.) Hubeny, I., Stone, J. M., MacGregor, K., Werner, K., AIP Conference Proceedings, 1171, pp. 43–51, American Institute of Physics, Melville, NY. [DOI], [ADS], [arXiv:0912.5371 [astro-ph.SR]]. (Cited on page 17.)
Lagg, A., Ishikawa, R., Merenda, L., Wiegelmann, T., Tsuneta, S. and Solanki, S. K., 2009, “Internetwork Horizontal Magnetic Fields in the Quiet Sun Chromosphere: Results from a Joint Hinode/VTT Study”, in The Second Hinode Science Meeting: Beyond Discovery-Toward Understanding, Proceedings of a meeting at the NCAR, Boulder, CO, USA, held 29 September–3 October, 2008, (Eds.) Lites, B., Cheung, M., Magara, T., Mariska, J., Reeves, K., ASP Conference Series, 415, p. 327, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 29.)
Lamy, P., Kuhn, J. R., Lin, H., Koutchmy, S. and Smartt, R. N., 1992, “No evidence of a circumsolar dust ring from infrared observations of the 1991 solar eclipse”, Science, 257, 1377–1380. [DOI], [ADS]. (Cited on page 36.)
Landman, D. A., 1976, “A study of the He λ 10830 line emission from quiescent prominences”, Solar Phys., 50, 383–394. [DOI], [ADS]. (Cited on page 27.)
Leenaarts, J. and Wedemeyer-Böhm, S., 2005, “DOT tomography of the solar atmosphere. III. Observations and simulations of reversed granulation”, Astron. Astrophys., 431, 687–692. [DOI], [ADS]. (Cited on pages 15 and 39.)
Lemke, M. and Holweger, H., 1987, “A non-LTE study of the solar emission lines near 12 microns”, Astron. Astrophys., 173, 375–382. [ADS]. (Cited on page 30.)
Lemoine, B., Demuynck, C. and Destombes, J. L., 1988, “Rydberg transitions of neutral magnesium in the infrared: Frequency measurements and Zeeman effect”, Astron. Astrophys., 191, L4–L6. [ADS]. (Cited on page 31.)
Lena, P., Hall, D., Soufflot, A. and Viala, Y., 1974, “The thermal emission of the dust corona, during the eclipse of June 30, 1973. II. Photometric and spectral observations”, Astron. Astrophys., 37, 81–86. [ADS]. (Cited on page 36.)
Li, H. and You, J., 2009, “Observational Study of a Peculiar Solar Limb Event Occurred on 11 January 2002”, Solar Phys., 258, 89–104. [DOI], [ADS]. (Cited on page 27.)
Li, R., Ye, B., Chen, H., Liu, S., Deng, B., Ma, J., Hill, H. A. and Oglesby, P. H., 1994, “Solar Oscillations Instrument at an Infrared Wavelength of 1.6 µm at Yunnan Observatory”, in Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, (Eds.) Rabin, D. M., Jefferies, J. T., Lindsey, C., IAU Symposia, 154, pp. 283–286, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on page 24.)
Li, S. S., Kim, S.-H., Moon, J.-H., Lee, J. H., Tidrow, M. Z. and Dyer, W. R., 2002, “Two-stack three-color quantum well infrared photodetector for mid- and long-wavelength infrared detection”, in Infrared Detectors and Focal Plane Arrays VII, Orlando, Florida, USA, April 1, 2002, (Eds.) Dereniak, E. L., Sampson, R. E., Proc. SPIE, 4721, pp. 204–211, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 45.)
Lin, H., 1995, “On the Distribution of the Solar Magnetic Fields”, Astrophys. J., 446, 421. [DOI], [ADS]. (Cited on page 23.)
Lin, H., 2003, “ATST near-IR spectropolarimeter”, in Innovative Telescopes and Instrumentation for Solar Astrophysics, Waikoloa, Hawaii, USA, August 22, 2002, (Eds.) Keil, S. L., Avakyan, S. V., Proc. SPIE, 4853, pp. 215–222, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 45.)
Lin, H., 2009, “Infrared Solar Polarimetry”, in Solar Polarization 5: In Honor of Jan Stenflo, Proceedings of the conference held 17–21 September, 2007 in Ascona, Switzerland, (Eds.) Berdyugina, S. V., Nagendra, K. N., Ramelli, R., ASP Conference Series, 405, p. 413, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 17.)
Lin, H. and Casini, R., 2000, “A Classical Theory of Coronal Emission Line Polarization”, Astrophys. J., 542, 528–534. [DOI], [ADS]. (Cited on page 38.)
Lin, H. and Jaeggli, S., 2012, “SPIES — Spectral Polarimetric Imager For The Energetic Sun”, Bull. Am. Astron. Soc., 44, 123.06. [ADS]. (Cited on page 45.)
Lin, H., Penn, M. J. and Kuhn, J. R., 1998, “He I 10830 Å Line Polarimetry: A New Tool to Probe the Filament Magnetic Fields”, Astrophys. J., 493, 978–995. [DOI], [ADS]. (Cited on page 28.)
Lin, H., Penn, M. J. and Tomczyk, S., 2000, “A New Precise Measurement of the Coronal Magnetic Field Strength”, Astrophys. J. Lett., 541, L83–L86. [DOI], [ADS]. (Cited on page 37.)
Lin, H., Kuhn, J. R. and Coulter, R., 2004, “Coronal Magnetic Field Measurements”, Astrophys. J. Lett., 613, L177–L180. [DOI], [ADS]. (Cited on pages 34, 37, and 39.)
Lites, B. W., 1986, “Photoelectric observations of chromospheric sunspot oscillations. IV. The Ca II H line and He I 10830 Å”, Astrophys. J., 301, 1005–1017. [DOI], [ADS]. (Cited on page 29.)
Lites, B. W., Keil, S. L., Scharmer, G. B. and Wyller, A. A., 1985, “Steady flows in active regions observed with the He I 10830 Å line”, Solar Phys., 97, 35–49. [DOI], [ADS]. (Cited on page 26.)
Lites, B. W., Kubo, M., Socas-Navarro, H. et al., 2008, “The Horizontal Magnetic Flux of the Quiet-Sun Internetwork as Observed with the Hinode Spectro-Polarimeter”, Astrophys. J., 672, 1237–1253. [DOI], [ADS]. (Cited on page 47.)
Livingston, W., 1994, “A 4-meter McMath Telescope for the Infrared”, in Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, (Eds.) Rabin, D. M., Jefferies, J. T., Lindsey, C., IAU Symposia, 154, pp. 589–594, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on pages 17 and 45.)
Livingston, W., 2002, “Sunspots Observed to Physically Weaken in 2000–2001”, Solar Phys., 207, 41–45. [DOI], [ADS]. (Cited on page 23.)
Livingston, W., Penn, M. J. and Svalgaard, L., 2012, “Decreasing Sunspot Magnetic Fields Explain Unique 10.7 cm Radio Flux”, Astrophys. J. Lett., 757, L8. [DOI], [ADS]. (Cited on page 23.)
Livingston, W. C., Harvey, J., Pierce, A. K., Schrage, D., Gillespie, B., Simmons, J. and Slaughter, C., 1976, “Kitt Peak 60-cm vacuum telescope”, Appl. Opt., 15, 33–39. [DOI], [ADS]. (Cited on page 25.)
MacQueen, R. M., 1968, “Infrared Observations of the Outer Solar Corona”, Astrophys. J., 154, 1059. [DOI], [ADS]. (Cited on page 35.)
MacQueen, R. M., Blankner, J. G., Elmore, D. F., Lecinski, A. R. and White, O. R., 1998, “Initial CHIP He I Observations of Solar Limb Activity”, Solar Phys., 182, 97–105. [DOI], [ADS]. (Cited on page 25.)
Malanushenko, O. V. and Jones, H. P., 2004, “Analysis of HeI 1083 nm Imaging Spectroscopy Using a Spectral Standard”, Solar Phys., 222, 43–60. [DOI], [ADS]. (Cited on page 25.)
Malville, J., 1967, “Excitation of the Infrared Lines of Fe XIII in the Solar Corona”, Astrophys. J., 148, 229. [DOI], [ADS]. (Cited on page 34.)
Mangus, J. and Stockhausen, R., 1966, Near Infrared Solar Eclipse Observations, NASA Technical Papers, X-614-66-29, NASA Goddard Space Flight Center, Greenbelt, MD. Online version (accessed 6 May 2014): http://ntrs.nasa.gov/search.jsp?R=19660015354. (Cited on page 34.)
Martínez Pillet, V. and Vázquez, M., 1990, “On the continuum intensity-magnetic field relation along the decay phase of sunspots”, Astrophys. Space Sci., 170, 75–79. [DOI], [ADS]. (Cited on page 23.)
Mártinez Pillet, V., Collados, M., Sánchez Almeida, J. et al., 1999, “LPSP & TIP: Full Stokes Polarimeters for the Canary Islands Observatories”, in High Resolution Solar Physics: Theory, Observations, and Techniques, Proceedings of the 19th NSO/Sacramento Peak Summer Workshop, held in Sunspot, NM, USA, 28 September–2 Ocotber 1998, (Eds.) Rimmele, T. R., Balasubramaniam, K. S., Radick, R. R., ASP Conference Series, 183, p. 264, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 21.)
Mathew, S. K., Lagg, A., Solanki, S. K. et al., 2003, “Three dimensional structure of a regular sunspot from the inversion of IR Stokes profiles”, Astron. Astrophys., 410, 695–710. [DOI], [ADS]. (Cited on pages 23, 24, and 41.)
McCabe, G. H., Jennings, D. E., Deming, D., Sada, P. and Moran, T., 2003, “Stokes polarimeter for mid-IR solar magnetic field measurements”, in Polarimetry in Astronomy, Waikoloa, Hawaii, USA, August 22, 2002, (Ed.) Fineschi, S., Proc. SPIE, 4843, pp. 39–44, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on pages 30 and 46.)
McPherson, M. R., Lin, H. and Kuhn, J. R., 1992, “Infrared array measurements of sunspot magnetic fields”, Solar Phys., 139, 255–266. [DOI], [ADS]. (Cited on page 23.)
Mohler, O. C. and Goldberg, L., 1956, “The Width of the Infrared Helium Line in the Solar Spectrum”, Astrophys. J., 124, 13. [DOI], [ADS]. (Cited on page 26.)
Moise, E., Raymond, J. and Kuhn, J. R., 2010, “Properties of the Diffuse Neutral Helium in the Inner Heliosphere”, Astrophys. J., 722, 1411–1415. [DOI], [ADS]. (Cited on page 37.)
Moran, T., Deming, D., Jennings, D. E. and McCabe, G., 2000, “Solar Magnetic Field Studies Using the 12 Micron Emission Lines. III. Simultaneous Measurements at 12 and 1.6 Microns”, Astrophys. J., 533, 1035–1042. [DOI], [ADS]. (Cited on page 32.)
Moran, T. G., Jennings, D. E., Deming, L. D., McCabe, G. H., Sada, P. V. and Boyle, R. J., 2007, “Solar Magnetograms at 12 µm Using the Celeste Spectrograph”, Solar Phys., 241, 213–222. [DOI], [ADS]. (Cited on page 32.)
Muglach, K. and Schmidt, W., 2001, “Height and dynamics of the quiet solar chromosphere at the limb”, Astron. Astrophys., 379, 592–600. [DOI], [ADS]. (Cited on pages 26 and 30.)
Münch, G., 1966, “Infrared Lines of the Solar Corona. I. Prediction”, Astrophys. J., 145, 237. [DOI], [ADS]. (Cited on pages 34 and 37.)
Münch, G., Neugebauer, G. and McCammon, D., 1967, “Infrared Coronal Lines. II. Observation of [Si X] λ1.43 µ and [Mg VIII] A3.03 µ”, Astrophys. J., 149, 681. [DOI], [ADS]. (Cited on page 34.)
Murcray, F. J., Goldman, A., Murcray, F. H., Bradford, C. M., Murcray, D. G., Coffey, M. T. and Mankin, W. G., 1981, “Observation of new emission lines in the infrared solar spectrum near 12.33, 12.22, and 7.38 microns”, Astrophys. J., 247, L97–L99. [DOI], [ADS]. (Cited on page 30.)
Nicodemus, F. E., 1970, “Reflectance Nomenclature and Directional Reflectance and Emissivity”, Appl. Opt., 9(6), 1474–1475. [DOI]. (Cited on page 10.)
Noyes, R. W. and Hall, D. N. B., 1972, “Thermal Oscillations in the High Solar Photosphere”, Astrophys. J. Lett., 176, L89. [DOI], [ADS]. (Cited on page 19.)
Ohgaito, R., Mann, I., Kuhn, J. R., MacQueen, R. M. and Kimura, H., 2002, “The J- and K-Band Brightness of the Solar F Corona Observed during the Solar Eclipse on 1998 February 26”, Astrophys. J., 578, 610–620. [DOI], [ADS]. (Cited on page 36.)
Olsen, K. H., Anderson, C. R. and Stewart, J. N., 1971, “Some Newly Discovered Coronal Emission Lines from High Altitude Infrared Observations of the 7 March, 1970, Solar Eclipse”, Solar Phys., 21, 360–371. [DOI], [ADS]. (Cited on page 34.)
Pagaran, J., Weber, M., DeLand, M. T., Floyd, L. E. and Burrows, J. P., 2011, “Solar Spectral Irradiance Variations in 240–1600 nm During the Recent Solar Cycles 21–23”, Solar Phys., 272, 159–188. [DOI], [ADS]. (Cited on page 39.)
Penn, M., 2008, “Near Infrared Observations of Solar Granulation”, Eos Trans. AGU, 89(23), SP41B–01. [ADS]. (Cited on pages 40 and 41.)
Penn, M. J., 2000, “An Erupting Active Region Filament: Three-Dimensional Trajectory and Hydrogen Column Density”, Solar Phys., 197, 313–335. [DOI], [ADS]. (Cited on page 27.)
Penn, M. J., 2006, “NAC Observations of an X1.8 Flare”, Bull. Am. Astron. Soc., 38, 232. [ADS]. (Cited on page 27.)
Penn, M. J. and Allen, C. L., 1997, “He I 1083 nm Oscillations and Downflows Near the North Solar Pole”, Solar Phys., 174, 359–366. [DOI], [ADS]. (Cited on page 30.)
Penn, M. J. and Jones, H. P., 1996, “Limb Observations of He I 1083 nm”, Solar Phys., 168, 19–35. [DOI], [ADS]. (Cited on page 26.)
Penn, M. J. and Kuhn, J. R., 1994a, “Ground-based detection of an infrared (Si X) coronal emission line and improved wavelengths for the infrared (Fe XIII) emission lines”, Astrophys. J., 434, 807–810. [DOI], [ADS]. (Cited on pages 34 and 36.)
Penn, M. J. and Kuhn, J. R., 1994b, “How bright is the (Si X) 1431 nm coronal emission line?”, Solar Phys., 151, 51–56. [DOI], [ADS]. (Cited on page 36.)
Penn, M. J. and Kuhn, J. R., 1995, “Imaging spectropolarimetry of the HeI 1083 nanometer line in a flaring solar active region”, Astrophys. J. Lett., 441, L51–L54. [DOI], [ADS]. (Cited on pages 25, 27, and 28.)
Penn, M. J. and Livingston, W., 2006, “Temporal Changes in Sunspot Umbral Magnetic Fields and Temperatures”, Astrophys. J. Lett., 649, L45–L48. [DOI], [ADS]. (Cited on page 23.)
Penn, M. J. and Schad, T., 2012, “Sunspot Dynamics as seen with CO 4666 nm Spectroscopy”, Bull. Am. Astron. Soc., 44, 206.10. [ADS]. (Cited on page 19.)
Penn, M. J., Arnaud, J., Mickey, D. L. and Labonte, B. J., 1994, “Near-infrared emission-line and continuum observations from the 1991 eclipse”, Astrophys. J., 436, 368–371. [DOI], [ADS]. (Cited on pages 35 and 36.)
Penn, M. J., Cao, W. D., Walton, S. R., Chapman, G. A. and Livingston, W., 2003a, “Weak Infrared Molecular Lines Reveal Rapid Outflow in Cool Magnetic Sunspot Penumbral Fibrils”, Astrophys. J. Lett., 590, L119–L122. [DOI], [ADS]. (Cited on page 42.)
Penn, M. J., Cao, W. D., Walton, S. R., Chapman, G. A. and Livingston, W., 2003b, “Imaging Spectropolarimetry of Ti I 2231 nm in a Sunspot”, Solar Phys., 215, 87–97. [DOI], [ADS]. (Cited on pages 42 and 44.)
Penn, M. J., Walton, S., Chapman, G., Ceja, J. and Plick, W., 2003c, “Temperature Dependence of Molecular Line Strengths and Fei 1565 nm Zeeman Splitting in a Sunspot”, Solar Phys., 213, 55–67. [DOI], [ADS]. (Cited on page 23.)
Penn, M. J., Jaeggli, S. A., Henney, C. J., Walton, S. R. and Ceja, J. A., 2004a, “IR Vector Magnetic Fields II: Atomic and Molecular Line Polarization in a Sunspot”, Bull. Am. Astron. Soc., 36, 709. [ADS]. (Cited on page 22.)
Penn, M. J., Lin, H., Tomczyk, S., Elmore, D. and Judge, P., 2004b, “Background-Induced Measurement Errors of the Coronal Intensity, Density, Velocity, and Magnetic Field”, Solar Phys., 222, 61–78. [DOI], [ADS]. (Cited on page 12.)
Penn, M. J., Schad, T. and Cox, E., 2011, “Probing the Solar Atmosphere Using Oscillations of Infrared CO Spectral Lines”, Astrophys. J., 734, 47. [DOI], [ADS], [arXiv:1012.2371 [astro-ph.SR]]. (Cited on pages 18, 20, and 21.)
Peterson, A. W., 1963, “Thermal Radiation from Interplanetary Dust”, Astrophys. J., 138, 1218. [DOI], [ADS]. (Cited on page 35.)
Plymate, C. and Penn, M. J., 2007, “Recent Results From The NSO Array Camera”, Bull. Am. Astron. Soc., 39, 130. [ADS]. (Cited on page 21.)
Querfeld, C. W. and Elmore, D. E., 1976, “Observation of Polarization in Fe XIII 10747 Å Coronal Emission Line”, Bull. Am. Astron. Soc., 8, 368. [ADS]. (Cited on page 34.)
Querfeld, C. W. and Smartt, R. N., 1984, “Comparison of coronal emission-line structure and polarization”, Solar Phys., 91, 299–310. [DOI], [ADS]. (Cited on page 34.)
Rabin, D., 1994, “Near Infrared Imaging Magnetometry”, in Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, (Eds.) Rabin, D. M., Jefferies, J. T., Lindsey, C., IAU Symposia, 154, pp. 449–457, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on page 17.)
Rabin, D., Jaksha, D., Kopp, G. and Mahaffey, C., 1992, “NIM — A Near Infrared Magnetograph”, Bull. Am. Astron. Soc., 24, 1251. [ADS]. (Cited on page 21.)
Rabin, D., Keller, C. and Jaksha, D., 1996, “NIM-2 — A Near Infrared Imaging Vector Magnetograph”, Bull. Am. Astron. Soc., 28, 934. [ADS]. (Cited on page 21.)
Rabin, D. M., Jefferies, J. T. and Lindsey, C. (Eds.), 1994, Infrared Solar Physics, Proceedings of IAU Symposium 154 held in Tucson, AZ, USA, March 2–6, 1992, IAU Symposia, 154, Kluwer, Dordrecht; Boston. [DOI], [ADS]. (Cited on page 17.)
Rakić, A. D., 1995, “Algorithm for the determination of intrinsic optical constants of metal films: application to aluminum”, Appl. Opt., 34(22), 4755–4767. [DOI]. (Cited on page 11.)
Ramsauer, J., Solanki, S. K. and Biemont, E., 1995a, “Interesting lines in the infrared solar spectrum. II. Unblended lines between λ1.0 and λ1.8 µm”, Astron. Astrophys. Suppl., 113, 71. [ADS]. (Cited on page 17.)
Ramsauer, J., Solanki, S. K. and Biemont, E., 1995b, “Lines in the infrared solar spectrum (Ramsauer+, 1995)”, web interface to database, Harvard-Smithsonian Center for Astrophysics. URL (accessed 6 May 2014): http://vizier.cfa.harvard.edu/viz-bin/VizieR?-source=J/A+AS/113/71. (Cited on page 17.)
Ressler, M. E., Bock, J. J., Bandara, S. V., Gunapala, S. D. and Werner, M. W., 2001, “Astronomical imaging with quantum well infrared photodetectors”, Infrared Phys. Technol., 42, 377–383. [DOI], [ADS]. (Cited on page 46.)
Rezaei, R., Beck, C. and Schmidt, W., 2012, “Variation in sunspot properties between 1999 and 2011 as observed with the Tenerife Infrared Polarimeter”, Astron. Astrophys., 541, A60. [DOI], [ADS], [arXiv:1203.1444 [astro-ph.SR]]. (Cited on page 24.)
Richardson, R. S. and Minkowski, R., 1939, “The Spectra of Bright Chromospheric Eruptions from λ 3300 TO λ 11500”, Astrophys. J., 89, 347. [DOI], [ADS]. (Cited on page 26.)
Rieke, G. H., 2007, “Infrared Detector Arrays for Astronomy”, Annu. Rev. Astron. Astrophys., 45, 77–115. [DOI], [ADS]. (Cited on page 6.)
Rimmele, T. R. and Marino, J., 2011, “Solar Adaptive Optics”, Living Rev. Solar Phys., 8, lrsp-2011-2. [DOI], [ADS]. URL (accessed 28 April 2014): http://www.livingreviews.org/lrsp-2011-2. (Cited on page 8.)
Rimmele, T. R., Balasubramaniam, K., Berger, T. et al., 2005, “First-Light Instrumentation for the Advanced Technology Solar Telescope”, Eos Trans. AGU, 86(18), SP34A–03. [ADS]. (Cited on page 45.)
Rothman, L. S., Gordon, I. E., Babikov, Y. et al., 2013, “The HITRAN2012 molecular spectroscopic database”, J. Quant. Spectrosc. Radiat. Transf., 130, 4–50. [DOI], [ADS]. (Cited on page 17.)
Rüedi, I., Solanki, S. K., Livingston, W. and Stenflo, J. O., 1992, “Infrared lines as probes of solar magnetic features. III. Strong and weak magnetic fields in plages”, Astron. Astrophys., 263, 323–338. [ADS]. (Cited on page 22.)
Rüedi, I., Solanki, S. K., Livingston, W. and Harvey, J., 1995a, “Interesting lines in the infrared solar spectrum. III. A polarimetric survey between 1.05 and 2.50 µm”, Astron. Astrophys. Suppl., 113, 91. [ADS]. (Cited on pages 17, 40, and 42.)
Rüedi, I., Solanki, S. K. and Livingston, W. C., 1995b, “Infrared lines as probes of solar magnetic features. X. He I 10830 Å as a diagnostic of chromospheric magnetic fields”, Astron. Astrophys., 293, 252–262. [ADS]. (Cited on page 28.)
Rüedi, I., Solanki, S. K., Keller, C. U. and Frutiger, C., 1998, “Infrared lines as probes of solar magnetic features. XIV. Ti I and the cool components of sunspots”, Astron. Astrophys., 338, 1089–1101. [ADS]. (Cited on page 42.)
Rüedi, I., Solanki, S. K. and Keller, C. U., 1999, “Infrared lines as probes of solar magnetic features. XV. Evershed flow in cool, weak penumbral fields”, Astron. Astrophys., 348, L37–L40. [ADS]. (Cited on page 42.)
Sasso, C., Lagg, A. and Solanki, S. K., 2006, “Milne-Eddington inversions of the HeI 10830 Å Stokes profiles: influence of the Paschen-Back effect”, Astron. Astrophys., 456, 367–371. [DOI], [ADS], [arXiv:1102.0898 [astro-ph.SR]]. (Cited on page 29.)
Sasso, C., Lagg, A. and Solanki, S. K., 2011, “Multicomponent He I 10 830 Å profiles in an active filament”, Astron. Astrophys., 526, A42. [DOI], [ADS], [arXiv:1101.5563 [astro-ph.SR]]. (Cited on page 27.)
Schad, T. A., 2013, Spectropolarimetry of Fine Magnetized Structures in the Upper Solar Atmosphere, Ph.D. thesis, The University of Arizona, Tucson, AZ. [ADS]. URL (accessed 28 April 2014): http://hdl.handle.net/10150/301683. (Cited on page 29.)
Schad, T. A., Penn, M. J. and Pietarila, A., 2012, “Coronal Rain Observed On-disk with HeI Spectropolarimetry from DST/FIRS”, Bull. Am. Astron. Soc., 44, 310.05. [ADS]. (Cited on page 29.)
Schad, T. A., Penn, M. J. and Lin, H., 2013, “HeI Vector Magnetometry of Field-aligned Superpenumbral Fibrils”, Astrophys. J., 768, 111. [DOI], [ADS], [arXiv:1303.4463 [astro-ph.SR]]. (Cited on pages 25 and 29.)
Schmidt, W., Knoelker, M. and Westendorp Plaza, C., 1994, “Limb observations of the He I 1083.0 nm line”, Astron. Astrophys., 287, 229–232. [ADS]. (Cited on page 26.)
Schmidt, W., von der Lühe, O., Volkmer, R. et al., 2012, “The 1.5 meter solar telescope GREGOR”, Astron. Nachr., 333, 796–809. [DOI], [ADS]. (Cited on page 45.)
Serna Jr, M., 2002, “Quantum-well-detector concept for hyperspectral coregistered full-Stokes-vector detection”, in Photonics for Space Environments VIII, Seattle, Washington, USA, July 7, 2002, (Ed.) Taylor, E. W., Proc. SPIE, 4823, pp. 113–123, SPIE Digital Library, Bellingham, WA. [DOI], [ADS]. (Cited on page 45.)
Sheeley Jr, N. R., 1980, “The evolution of the polar coronal holes”, Solar Phys., 65, 229–235. [DOI], [ADS]. (Cited on page 26.)
Socas-Navarro, H., Elmore, D., Asensio Ramos, A. and Harrington, D. M., 2011, “Characterization of telescope polarization properties across the visible and near-infrared spectrum. Case study: the Dunn Solar Telescope”, Astron. Astrophys., 531, A2. [DOI], [ADS], [arXiv:1009.2866 [astro-ph.IM]]. (Cited on page 11.)
Solanki, S. K., Biemont, E. and Muerset, U., 1990, “Interesting lines in the infrared solar spectrum between 1.49 and 1.8 microns”, Astron. Astrophys. Suppl., 83, 307–315. [ADS]. (Cited on page 17.)
Solanki, S. K., Rüedi, I. and Livingston, W., 1992a, “Infrared lines as probes of solar magnetic features. V. The magnetic structure of a simple sunspot and its canopy”, Astron. Astrophys., 263, 339–350. [ADS]. (Cited on page 23.)
Solanki, S. K., Rüedi, I. K. and Livingston, W., 1992b, “Infrared lines as probes of solar magnetic features. II. Diagnostic capabilities of Fe I 15648.5 Å and 15652.9 Å”, Astron. Astrophys., 263, 312–322. [ADS]. (Cited on page 22.)
Solanki, S. K., Walther, U. and Livingston, W., 1993, “Infrared lines as probes of solar magnetic features. VI. The thermal-magnetic relation and Wilson depression of a simple sunspot”, Astron. Astrophys., 277, 639–647. [ADS]. (Cited on page 23.)
Solanki, S. K., Livingston, W. and Ayres, T., 1994, “New Light on the Heart of Darkness of the Solar Chromosphere”, Science, 263, 64–66. [DOI], [ADS]. (Cited on page 18.)
Solanki, S. K., Livingston, W., Muglach, K. and Wallace, L., 1996a, “The beat of the solar chromosphere’s cold heart”, Astron. Astrophys., 315, 303–311. [ADS]. (Cited on page 20.)
Solanki, S. K., Zufferey, D., Lin, H., Rüedi, I. and Kuhn, J. R., 1996b, “Infrared lines as probes of solar magnetic features. XII. Magnetic flux tubes: evidence of convective collapse?”, Astron. Astrophys., 310, L33–L36. [ADS]. (Cited on page 23.)
Solanki, S. K., Lagg, A., Woch, J., Krupp, N. and Collados, M., 2003, “Three-dimensional magnetic field topology in a region of solar coronal heating”, Nature, 425, 692–695. [DOI], [ADS]. (Cited on page 29.)
Solanki, S. K., Lagg, A., Aznar Cuadrado, R. et al., 2006, “Measuring the Magnetic Vector with the He I 10830 Å Line: A Rich New World”, in Solar Polarization 4, Proceedings of the conference held in Boulder, Colorado, USA, 19–23 September, 2005, (Eds.) Casini, R., Lites, B. W., ASP Conference Series, 358, p. 431, Astronomical Society of the Pacific, San Francisco. [ADS]. (Cited on page 29.)
Spyak, P. R. and Wolfe, W. L., 1992a, “Scatter from particulate-contaminated mirrors. Part 3: Theory and experiment for dust and λ = 10.6µm”, Opt. Eng., 31(8), 1764–1774. [DOI]. (Cited on page 10.)
Spyak, P. R. and Wolfe, W. L., 1992b, “Scatter from particulate-contaminated mirrors. Part 4: Properties of scatter from dust for visible to far-infrared wavelengths”, Opt. Eng., 31(8), 1775–1784. [DOI]. (Cited on page 10.)
Staveland, L., 1970, “Determination of the Spread Function for Solar Stray Light”, Solar Phys., 12, 328–331. [DOI], [ADS]. (Cited on page 10.)
Stellmacher, G., Wiehr, E. and Dammasch, I. E., 2003, “Spectroscopy of Solar Prominences Simultaneously From Space and Ground”, Solar Phys., 217, 133–155. [DOI], [ADS]. (Cited on page 27.)
Stenflo, J. O., Solanki, S. K. and Harvey, J. W., 1987, “Diagnostics of solar magnetic fluxtubes with the infrared line Fe I A15648.54 Å”, Astron. Astrophys., 173, 167–179. [ADS]. (Cited on pages 13, 21, and 22.)
Streete, J. L. and Tandberg-Hanssen, E., 1974, “Study of HeI Emission Lines in the Solar Atmosphere. III. The Chromospheric 10830 Å and 20581 Å Lines Observed at the Eclipse of June 30, 1973”, Astron. Astrophys., 33, 385–387. [ADS]. (Cited on page 27.)
Streete, J. L., MacQueen, R. M. and Tandberg-Hanssen, E., 1973, “Study of He I Emission Lines in the Solar Atmosphere. II. The Infrared Lines at 10830 Å and 20581 Å”, Astron. Astrophys., 28, 125–130. [ADS]. (Cited on page 27.)
Strutt, J., 1871, “On the light from the sky, its polarization and colour”, Philos. Mag., 41, 107–120. (Cited on page 8.)
Tandberg-Hanssen, E., 1962, “Études des raies d’émission de He I dans l’atmosphére solaire I. — Les profils de la raie triplet infrarouge, λ 10830 Å”, Ann. Astrophys., 25, 357–366. [ADS]. (Cited on page 27.)
Threlfall, J., De Moortel, I., McIntosh, S. W. and Bethge, C., 2013, “First comparison of wave observations from CoMP and AIA/SDO”, Astron. Astrophys., 556, A124. [DOI], [ADS], [arXiv:1306.3354 [astro-ph.SR]]. (Cited on page 38.)
Tomczyk, S. and McIntosh, S. W., 2009, “Time-Distance Seismology of the Solar Corona with CoMP”, Astrophys. J., 697, 1384–1391. [DOI], [ADS], [arXiv:0903.2002 [astro-ph.SR]]. (Cited on pages 39 and 40.)
Tomczyk, S., McIntosh, S. W., Keil, S. L., Judge, P. G., Schad, T., Seeley, D. H. and Edmondson, J., 2007, “Alfvén Waves in the Solar Corona”, Science, 317, 1192–1196. [DOI], [ADS]. (Cited on page 38.)
Tomczyk, S., Card, G. L., Darnell, T. et al., 2008, “An Instrument to Measure Coronal Emission Line Polarization”, Solar Phys., 247, 411–428. [DOI], [ADS]. (Cited on pages 17 and 34.)
Trujillo Bueno, J. and Asensio Ramos, A., 2007, “Influence of Atomic Polarization and Horizontal Illumination on the Stokes Profiles of the He I 10830 Å Multiplet”, Astrophys. J., 655, 642–650. [DOI], [ADS], [arXiv:astro-ph/0610128]. (Cited on page 29.)
Trujillo Bueno, J., Asensio Ramos, A. and Shchukina, N., 2006, “The Hanle Effect in Atomic and Molecular Lines: A New Look at the Sun’s Hidden Magnetism”, in Solar Polarization 4, Proceedings of the conference held in Boulder, Colorado, USA, 19–23 September, 2005, (Eds.) Casini, R., Lites, B. W., ASP Conference Series, 358, p. 269, Astronomical Society of the Pacific, San Francisco. [ADS], [arXiv:astro-ph/0612678]. (Cited on page 47.)
Turon, P. J. and Léna, P., 1973, “First Observations of the Granulation at 1.65µ, Center to Limb Variation of the Contrast”, Solar Phys., 30, 3–14. [DOI], [ADS]. (Cited on page 39.)
Turon, P. J. and Léna, P. J., 1970, “High resolution solar images at 10 microns: Sunspot details and photometry”, Solar Phys., 14, 112–124. [DOI], [ADS]. (Cited on page 8.)
Uitenbroek, H., 2000, “The CO Fundamental Vibration-Rotation Lines in the Solar Spectrum. I. Imaging Spectroscopy and Multidimensional LTE Modeling”, Astrophys. J., 531, 571–584. [DOI], [ADS]. (Cited on page 19.)
Uitenbroek, H., Noyes, R. W. and Rabin, D., 1994, “Imaging spectroscopy of the solar CO lines at 4.67 microns”, Astrophys. J. Lett., 432, L67–L70. [DOI], [ADS]. (Cited on pages 18, 19, 20, and 39.)
Vernazza, J. E., Avrett, E. H. and Loeser, R., 1976, “Structure of the solar chromosphere. II. The underlying photosphere and temperature-minimum region”, Astrophys. J. Suppl. Ser., 30, 1–60. [DOI], [ADS]. (Cited on pages 14 and 15.)
Wallace, L., Livingston, W., Hinkle, K. and Bernath, P., 1996, “Infrared Spectral Atlases of the Sun from NOAO”, Astrophys. J. Suppl. Ser., 106, 165. [DOI], [ADS]. (Cited on page 17.)
Webb, D. F., Davis, J. M. and McIntosh, P. S., 1984, “Observations of the reappearance of polar coronal holes and the reversal of the polar magnetic field”, Solar Phys., 92, 109–132. [DOI], [ADS]. (Cited on page 26.)
Wedemeyer-Böhm, S. and Steffen, M., 2007, “Carbon monoxide in the solar atmosphere. II. Radiative cooling by CO lines”, Astron. Astrophys., 462, L31–L35. [DOI], [ADS], [arXiv:astro-ph/0612197]. (Cited on page 18.)
Wedemeyer-Böhm, S., Kamp, I., Bruls, J. and Freytag, B., 2005, “Carbon monoxide in the solar atmosphere. I. Numerical method and two-dimensional models”, Astron. Astrophys., 438, 1043–1057. [DOI], [ADS], [arXiv:astro-ph/0503496]. (Cited on pages 18 and 19.)
Wedemeyer-Böhm, S., Ludwig, H. G., Steffen, M., Leenaarts, J. and Freytag, B., 2007, “Inter-network regions of the Sun at millimetre wavelengths”, Astron. Astrophys., 471, 977–991. [DOI], [ADS], [arXiv:0705.2304]. (Cited on page 18.)
Whittet, D. C. B., Bode, M. F. and Murdin, P., 1987, “The extinction properties of Saharan dust over La Palma”, Vistas Astron., 30, 135–144. [DOI], [ADS]. (Cited on page 9.)
Wiedemann, G., Ayres, T. R., Jennings, D. E. and Saar, S. H., 1994, “Carbon Monoxide Fundamental Bands in Late-Type Stars. III. Chromosphere or CO-mosphere?”, Astrophys. J., 423, 806–816. [DOI], [ADS]. (Cited on page 18.)
Wiegelmann, T., Lagg, A., Solanki, S. K., Inhester, B. and Woch, J., 2005, “Comparing magnetic field extrapolations with measurements of magnetic loops”, Astron. Astrophys., 433, 701–705. [DOI], [ADS], [arXiv:0801.4519]. (Cited on page 29.)
Wynn-Williams, C. G. and Becklin, E. E. (Eds.), 1987, Infrared Astronomy with Arrays, Proceedings of the Workshop on Ground-based Astronomical Observations with Infrared Array Detectors, University of Hawaii at Hilo, HI, USA, 24–26 March 1987, University of Hawaii, Hilo, Hawaii. [ADS]. (Cited on page 6.)
Yi, Z., Engvold, O. and Keil, S. L., 1991, “Structure and oscillations in quiescent filaments from observations in He I λ 10830 Å”, Solar Phys., 132, 63–80. [DOI], [ADS]. (Cited on page 30.)
You, J., Li, H. and Hiei, E., 2004, “Unusual spectral absorption observed in the 16 August 1989 limb flare”, Solar Phys., 223, 169–180. [DOI], [ADS]. (Cited on page 27.)
You, J. Q. and Oertel, G. K., 1992, “What caused an unusually broad HeI 10830 Å emission line in a solar limb flare?”, Astrophys. J. Lett., 389, L33–L35. [DOI], [ADS]. (Cited on page 27.)
Zirin, H., 1975, “The helium chromosphere, coronal holes, and stellar X-rays”, Astrophys. J. Lett., 199, L63–L66. [DOI], [ADS]. (Cited on page 26.)
Zirin, H. and Howard, R., 1966, “The Structure of the Solar Chromosphere. II. Spectroheliograms in λ 10830 Å and Their Interpretation”, Astrophys. J., 146, 367. [DOI], [ADS]. (Cited on pages 25 and 26.)
Zirin, H. and Popp, B., 1989, “Observations of the 12 micron Mg I lines in various solar features”, Astrophys. J., 340, 571–578. [DOI], [ADS]. (Cited on page 30.)
Acknowledgements
It is humbling to review the work that dedicated scientists have done on this subject, and it is a joy to be able to work in the same field with these insightful researchers. Many discussions with many people have helped to improve this paper, and an incomplete list of colleagues who have helped me follows below. Tom Ayres reviewed much of the discussion of the CO lines and provided crucial help on a first draft of that section. Jack Harvey provided many insightful comments on the entire paper, and important pointers to early work done in this field. Tilak Hewagama was kind enough to provide a copy of his dissertation containing measurements of the McMath-Pierce polarization at 12 318 nm. Don Jennings reviewed the discussion of the Mg I 12 318 nm line and provided comments. Harrison Jones provided a critical review and key suggestions for improving the section about He I 1083 nm. Jeff Kuhn reinforced the importance of molecular transitions and provided a summary of the 1991 eclipse experiments. Claude Plymate provided suggestions overall and specific comments on the CO section. Referee comments by D. M. Rabin and a second anonymous referee improved the content and the flow of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Change summary
I forgot to include one of the new, very relevant telescopes in my discussion in Section 4.1, the GREGOR telescope.
Change details
-
Page 45: Added mention of GREGOR and GRIS and two respective references.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Penn, M.J. Infrared Solar Physics. Living Rev. Solar Phys. 11, 2 (2014). https://doi.org/10.12942/lrsp-2014-2
Published:
DOI: https://doi.org/10.12942/lrsp-2014-2