New traveling wave solutions of MHD micropolar fluid in porous medium

Abstract

This paper aims to determine the exact solutions of non-Newtonian fluid namely micropolar fluid with MHD in a porous medium by traveling wave method. The governing equations of incompressible micropolar fluid with MHD in a porous medium are non-linear PDEs reduced to ODEs through wave parameter ξ=mx+ny+Ut. The set of new exact solutions are determined for five different cases. In special cases, the solution for micropolar fluid with and without MHD and porous effects can also be obtained from general solutions. Furthermore, these solution reduces to a Newtonian solution if we put vortex viscosity κ→0. Finally, the influence of the material and other parameters of interest on the fluid motion, as well as a comparison among micropolar and Newtonian fluids is also analyzed by 2D and 3D graphical illustrations.

Introduction

In the present, many researchers are working on the non-Newtonian fluid from both essential and sensible point of view [1]. These fluids have immediate effects on the processing of polymer, animal blood, liquid crystal, and geological flows in the earth mantle. The general conditions of non-Newtonian fluid are exceptionally non-linear and higher-arrangement than Navier-Stokes equations. Therefore, many analytical and numerical solutions are accessible to non-Newtonian fluid on the topic.

The electrically conducting fluid and magnetic properties are sufficiently studied in magnetohydrodynamics (MHD). MHD has specific applications like engineering science, metallurgical industry, electromagnetic pump, power generation, and flow meter. Hydromagnetic movements have a major part of study in the fields of the aerospace, astronomical, and planetary magnetosphere. The cleansing of liquid metals from non-metallic presence through the use of the attractive field is another basic component of MHD [2, 3]. Khalid et al. [4] have evaluated the exact solution of wall couple stress in MHD by Laplace transform and convolution. Fatunmbi et al. [5] have numerically studied the MHD stagnation point flow of a micropolar fluid by applying RK (Runge-Kutta) method. Hammouch [6] investigated the numerous solution of steady magnetohydrodynamics flow of dilatant fluids by various method techniques. Interesting recent studies on non-newtonian fluids with magnetohydrodynamics have been given by different researchers [7–11].

Micropolar fluid theory was proposed by Eriggen [12]. Mekheimer et al. [13] showed that the micropolar fluid model is a kind of non-Newtonian fluid which depends upon a microstructure and belongs to non-symmetrical stress tensor. Physically, micropolar fluid may be rigid particles, at random oriented (spherical) elements suspended in a viscous medium where the change of fluid elements is disregarded. Micropolar fluid can perform a better model for animal blood. Raza et al. [14] studied the different branches of the solution of micropolar fluid in a channel with permeable walls. Hussanan et al. [15] examined the heat and mass transfer in a micropolar fluid. Sheikholeslami et al. [16] evaluated the micropolar fluid flow in a channel by homotopy perturbation method (HPM). Lukaszewicz [17] explored the nature of the micropolar fluid. Ravi and Prasad [18] studied the relations of pulsatile and peristaltic stream of couple stress fluid through a porous medium in an elastic route.

There are many methods for solving non-linear partial differential equations such as bilinear transformation [19, 20], homotopy perturbation method [21, 22], $\phantom {\dot {i}\!}(G^{'}\setminus G)$ expansion method [23], Exp-function [24, 25], modified simple equation (MSE) method [26], and fingero-imbibition method [27]. The traveling wave method is useable for solving non-linear partial differential equations because it provides a simple exact solution of non-linear partial differential equations. Due to the many importance of this method in theory of non-linear partial differential equations, this method is applicable in the field of fluid mechanics, chemical kinematics, electromagnetic, and nonlinear mechanics. Some important work-related traveling wave solutions recently appeared in [28–34] and references presented there.

In the present communication, the traveling wave solution, and transformation method are used to find the exact solutions of unsteady incompressible two-dimensional laminar flow of MHD micropolar fluid in a porous medium. The mathematical model that considered here are carefully entrenched and judge with many general cases. It is noticed that the present model is capable of covering such benchmark cases and can give new information on the parameter determination of the dynamical system which governed micropolar fluid equations. To the best of our knowledge, only one study, which deals with the flows of unsteady incompressible two-dimensional laminar flow of micropolar fluid via traveling wave transformation appeared in [28]. Therefore, this communication aims to extend the results of [28] for unsteady two-dimensional incompressible laminar flow of MHD micropolar fluid in a porous medium. The family of new exact solutions is found for five distinct cases. Particularly, the solutions for micropolar fluid with and without MHD and porous effects can also be established from present general solutions. The solutions for MHD Newtonian fluid in the porous medium may for all cases easily be determined if we substitute vortex viscosity κ→0 in respective equations. Finally, the impact of parameters defines micropolar fluid and other parameters are analyzed through 2D and 3D graphical illustrations and differences among micropolar and Newtonian fluids are also discussed. For the present paper, we adopted the method [28–33] in the following pattern. In the “Basic governing equations” section, we provide the basic governing equations and the theoretical development of the traveling wave method. In the “Traveling wave solutions” section, we present the solution of our governing equations by the traveling wave methods along with five different cases for MHD micropolar fluid in a porous medium. Some initial and boundary conditions are discussed in the “Making initial and boundary conditions” section. In the “Numerical results and discussions” section, we discuss the numerical results with the help of graphical illustrations.

Basic governing equations

The equation of continuity and the conservation equations of linear momentum and angular momentum for an incompressible unsteady micropolar fluid, in the presence of magnetohydrodynamic through a porous medium, by neglecting the body force and body couple are as follows:

$$\begin{array}{@{}rcl@{}}\label {1} {}\nabla \cdot \overrightarrow{V} &=& 0, \end{array} $$

(1)

$$\begin{array}{@{}rcl@{}}\label {2} {}\rho\frac{D \overrightarrow{V}}{Dt}&=& - \nabla p + (\mu + \kappa) \nabla^{2}\overrightarrow{V} + \kappa \nabla \times \overrightarrow{\Omega} + \overrightarrow{J} \times \overrightarrow{B} - \left(\frac{\nu}{k^{\ast}}\right) \overrightarrow{V}, \end{array} $$

(2)

$$\begin{array}{@{}rcl@{}} {\kern10pt}\rho j \frac{D \overrightarrow{\Omega}}{D t}&=& \big (\alpha+\beta+\gamma \big) \nabla \big(\nabla \cdot \overrightarrow{\Omega} \big) - \gamma\nabla\times \left(\nabla\times \overrightarrow{\Omega}\right) + \kappa\nabla\times \overrightarrow{V} - 2 \kappa \overrightarrow{\Omega}. \end{array} $$

(3)

In the above equations, $\overrightarrow {V}$ is a velocity; $\overrightarrow {\Omega }$ is a microrotation; p be the pressure; ρ is the fluid density; j be the gyration parameters of the fluid; μ and κ are the dynamic and vortex viscosities; α,β, and γ are the respective coefficients of coupled viscosities [29]; $\overrightarrow {B}$ is the total magnetic force vector; $\overrightarrow {J}$ is the current density; and κ^∗ is the porosity parameter.

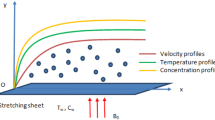
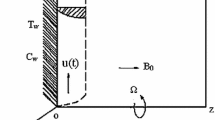
The velocity, microrotation, and magnetic component porous plate are (u,v,0),(0,0,N), and (0,0,B_o), respectively, where u and v are the second and third components of velocity, respectively, and N is the second component of microrotation while $\overrightarrow {B}$ is total magnetic filed, so that $\overrightarrow {B}= \overrightarrow {B_{o}}+\overrightarrow {b}$, $\overrightarrow {B}$ is the induced magnetic filed and using $\overrightarrow {J} \times \overrightarrow {B}= -\sigma B_{o} \overrightarrow {V}$, where σ is the electrically conductively of fluid and then Eqs. (1–3) provide the following governing equations (see Fig. 1):

$$\begin{array}{@{}rcl@{}}\label {4} {}\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y}= 0, \end{array} $$

(4)

Fig. 1

Two dimensional flow of micropolar fluid in the presence of normal magnetic field on porous plane

$$\begin{array}{@{}rcl@{}}\label {5} \frac{\partial u}{\partial t} + u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}= -\frac{\partial p}{\partial x} + \left(\nu + \frac{\kappa}{\rho}\right) \left(\frac{\partial^{2} u}{\partial x^{2}}+ \frac{\partial^{2} u}{\partial y^{2}}\right) + \frac{\kappa}{\rho}\frac{\partial N}{\partial y} - \left (\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) u, \end{array} $$

(5)

$$\begin{array}{@{}rcl@{}}\label {6} \frac{\partial v}{\partial t} + u \frac{\partial v}{\partial x}+v \frac{\partial v}{\partial y}= -\frac{\partial p}{\partial y} + \left(\nu + \frac{\kappa}{\rho}\right)\left(\frac{\partial^{2} v}{\partial x^{2}}+ \frac{\partial^{2} v}{\partial y^{2}} \right) - \frac{\kappa}{\rho}\frac{\partial N}{\partial x} - \bigg (\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\bigg) v, \end{array} $$

(6)

$$\begin{array}{@{}rcl@{}}\label {7} {}\frac{\partial N}{\partial t} + u \frac{\partial N}{\partial x} + v \frac{\partial N}{\partial y}= \frac{\gamma}{\rho j}\left(\frac{\partial^{2} N}{\partial x^{2}}+ \frac{\partial^{2} N}{\partial y^{2}} \right) - \frac{\kappa}{\rho j}\left(2N - \frac{\partial v}{\partial x}+ \frac{\partial u}{\partial y}\right). \end{array} $$

(7)

Procedure of traveling wave method

Suppose the non-linear partial differential equations include four dependent variables u, v, N,and p three variables t, x,and y.

$$\begin{array}{@{}rcl@{}}\label {8} {\kern90pt}M_{1} \left(u_{x}, v_{y} \right)=0, \end{array} $$

(8)

$$\begin{array}{@{}rcl@{}}\label {9} M_{2} \left(u,v,u_{t},u_{x},u_{y},u_{x x},u_{y y},N_{y},p_{x} \right)=0, \end{array} $$

(9)

$$\begin{array}{@{}rcl@{}}\label {10} M_{3} \left(u,v,v_{t},v_{x},v_{y},v_{x x},v_{y y},N_{x},p_{y} \right)=0, \end{array} $$

(10)

$$\begin{array}{@{}rcl@{}}\label {11} M_{4} \left(N_{t},N_{x},N_{y},N_{x x},N_{y y},N,u_{y}, u_{x} \right)=0. \end{array} $$

(11)

Here, M_i is a polynomial function of u,v,N,and p which contain the non-linear terms and higher order of derivative; where i=1,2,3,4., we display traveling wave solution as follows:

$$\begin{array}{@{}rcl@{}}\label {12} u(x,y,t)= u(\xi), v(x,y,t)= v(\xi), N(x,y,t)= N(\xi), p(x,y,t)= p(\xi), \end{array} $$

(12)

where ξ=mx+ny+Ut. The system Eqs. (8–11) can be converted into the system of ordinary differential equations.

$$\begin{array}{@{}rcl@{}}\label {13} {\kern45pt}M_{1} \left(u^{'}, v^{'} \right) = 0, \end{array} $$

(13)

$$\begin{array}{@{}rcl@{}}\label {14} M_{2} \left(u,v,u^{'}, u^{\prime\prime}, N^{'}, p^{'} \right)=0, \end{array} $$

(14)

$$\begin{array}{@{}rcl@{}}\label {15} M_{3} \left(u,v,v^{'}, v^{\prime\prime}, N^{'}, p^{'} \right)=0, \end{array} $$

(15)

$$\begin{array}{@{}rcl@{}}\label {16} M_{4} \left(N,N^{'}, N^{\prime\prime}, u^{'}, v^{'} \right)=0. \end{array} $$

(16)

This system of ordinary differential equations are may or may not be solvable. In our case, these system are solvable.

Traveling wave solutions

In this section, we will determine the traveling wave solutions of governing Eqs. (4–7). The traveling wave parameter type can be taken, and then, the solution has the following representation.

$$\begin{array}{@{}rcl@{}} u= u(\xi),\ v= v(\xi),\ N= N(\xi),\ p= p(\xi)\ \text{and} \ \xi= m x+n y+ U t. \end{array} $$

Here, U is the constant phase velocity and m and n are constants. On using the traveling wave parameter ξ into Eqs. (4–7), we get representation of the form

$$\begin{array}{@{}rcl@{}}\label {17} {}m u^{'}+ n v^{'}=0, \end{array} $$

(17)

$$\begin{array}{@{}rcl@{}}\label {18} \left (U + m u + n v \right) u^{'}= -mp^{'}+ \left(\nu + \frac{\kappa}{\rho}\right) \left (m^{2}+ n^{2} \right)u^{\prime\prime} + \frac{n \kappa}{\rho} N^{'} - \bigg(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\bigg)u, \end{array} $$

(18)

$$\begin{array}{@{}rcl@{}}\label {19} \left(U + m u + n v \right) v^{'}= -np^{'}+ \left(\nu + \frac{\kappa}{\rho}\right) \left (m^{2}+ n^{2}\right)v^{\prime\prime} - \frac{m \kappa}{\rho} N^{'} - \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right)v, \end{array} $$

(19)

$$\begin{array}{@{}rcl@{}}\label {20} \left(U + m u + n v \right) N^{'}= \frac{\gamma}{\rho j} \left(m^{2}+ n^{2} \right)N^{\prime\prime}- \frac{\kappa}{\rho j}\left(2N - m v^{'}+ n u^{'}\right), \end{array} $$

(20)

where the prime denotes the differentiation with respect to ξ. Integration to Eq. (17), w.r.t ξ on both side yields

$$\begin{array}{@{}rcl@{}}\label {21} m u + n v = c_{0}, \end{array} $$

(21)

where c₀ is an arbitrary constant. Using Eq. (21) in Eqs. (18)–(20) reduced to

$$\begin{array}{@{}rcl@{}}\label {22} \left(U+c_{0} \right)u^{'}=-mp^{'}+ \left(\nu + \frac{\kappa}{\rho}\right) \left (m^{2}+ n^{2}\right)u^{\prime\prime} + \frac{n \kappa}{\rho} N^{'} - \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right)u, \end{array} $$

(22)

$$\begin{array}{@{}rcl@{}}\label {23} \left(U+c_{0}\right)v^{'} = -np^{'}+ \left(\nu + \frac{\kappa}{\rho}\right) \left(m^{2}+ n^{2}\right)v^{\prime\prime} - \frac{m \kappa}{\rho} N^{'} - \left (\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right)v, \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}}\label {24} \left (U+c_{0} \right)N^{'}=\frac{\gamma}{\rho j} \left(m^{2}+ n^{2} \right) N^{\prime\prime}- \frac{\kappa}{\rho j}\left (2N - m v^{'}+ n u^{'}\right). \end{array} $$

(24)

To find u,v,N, and p from the above three equations, the following five cases will be discussed.

Case-I: U+c₀≠0

Eliminating p from Eqs. (22) and (23), we get

$$\begin{array}{@{}rcl@{}}\label {25} \left (U+c_{0}\right)\left(n u^{'}- m v^{'}\right)= \left(m^{2}+n^{2}\right) \left(\nu + \frac{\kappa}{\rho}\right) \left(n u^{\prime\prime} - m v^{\prime\prime} \right) + \frac{\kappa}{\rho}\left(m^{2}+n^{2} \right)N^{'} \end{array} $$

(25)

$$\begin{array}{@{}rcl@{}} - \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right)\left(n u - m v \right). \end{array} $$

Again, using Eq. (21) and converting v into u in Eq. (25), we arrive

$$\begin{array}{@{}rcl@{}}\label {26} N^{'}= \frac{\rho}{\kappa}\left[\frac{1}{n} \left(U + c_{o}\right)u^{'} - \frac{1}{n} \left(m^{2} + n^{2}\right)\left(\nu + \frac{\kappa}{\rho}\right) u^{\prime\prime} + \frac{1}{n} \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) u\right. \end{array} $$

(26)

$$\begin{array}{@{}rcl@{}} -\left. \frac{m c_{o}}{n \left(m^{2} + n^{2}\right)} \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) \right]. \end{array} $$

Eliminating N from Eqs. (24) and (26), we get

$$\begin{array}{@{}rcl@{}}\label {27} a_{1} u^{i \mathrm{v}} - a_{2} u^{\prime\prime\prime} + a_{3} u^{\prime\prime} + a_{4} u^{'}+ a_{5} u= a_{6}, \end{array} $$

(27)

where

$${}\begin{aligned} a_{1}&= \frac{\gamma}{n j \kappa} \left(m^{2}+ n^{2}\right)^{2} \left(\nu + \frac{\kappa}{\rho}\right), \end{aligned} $$

$$\begin{aligned} {}a_{2}&= \left[\frac{\rho}{n \kappa}\left(U+c_{0}\right)\left(m^{2}+ n^{2}\right) \left (\nu + \frac{\kappa}{\rho}\right)+\frac{\gamma}{n j \kappa} \left(m^{2}+ n^{2}\right) \left(U+c_{o}\right)\right], \end{aligned} $$

$$\begin{aligned} a_{3}= \left[\frac{\rho}{n \kappa}\left(U+c_{0}\right)^{2}+\frac{\kappa}{n j \rho}\left(m^{2}+ n^{2}\right)-\frac{\gamma}{n j \kappa} \left(m^{2}+ n^{2}\right) \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right)-\frac{2}{n j}\left(m^{2}+ n^{2}\right)\left(\nu + \frac{\kappa}{\rho}\right)\right], \end{aligned} $$

$${}\begin{aligned} a_{4}=\left[\frac{\rho}{n \kappa}\left(U+c_{0}\right) \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) + \frac{2}{n j}\left(U+c_{0}\right) \right], \end{aligned} $$

$${}\begin{aligned} a_{5}=\frac{2}{n j}\left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) \ and \ a_{6}=\frac{2m c_{0}}{n j \left(m^{2}+n^{2}\right)}\left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right). \end{aligned} $$

The solution of Eq. (27) is

$$\begin{array}{@{}rcl@{}}\label {28} u(\xi)= a_{7}e^{r_{11} \xi} + a_{8}e^{r_{12} \xi}+ a_{9}e^{r_{13} \xi} + a_{10}e^{r_{14} \xi} + a_{11}, \end{array} $$

(28)

where r₁₁, r₁₂, r₁₃, and r₁₄ are the roots of the auxiliary equation

$$\begin{array}{@{}rcl@{}} a_{1} m^{4} - a_{2} m^{3} + a_{3} m^{2} + a_{4} m + a_{5} = 0. \end{array} $$

Putting the Eq. (28) into Eq. (21), we get

$$\begin{array}{@{}rcl@{}}\label {29}\ v(\xi)= a_{12}e^{r_{11} \xi} + a_{13}e^{r_{12} \xi}+ a_{14}e^{r_{13} \xi} + a_{15}e^{r_{14} \xi} + a_{16}, \end{array} $$

(29)

where $a_{i+5} = - \frac {a_{i} \ m}{n} \ ; \ i= 7,8,9,10,$ and

$$\begin{array}{@{}rcl@{}} a_{16}= \frac{1}{n} \left (c_{0} - a_{11} \ m \right). \end{array} $$

Substituting Eq. (28) into Eq. (26), we get

$$\begin{array}{@{}rcl@{}}\label {30} N(\xi)= a_{17}e^{r_{11} \xi} + a_{18}e^{r_{12} \xi}+ a_{19}e^{r_{13} \xi} + a_{20}e^{r_{14} \xi} + a_{21} \xi + a_{22}, \end{array} $$

(30)

where

$$\begin{array}{@{}rcl@{}} a_{i}= \frac{1}{r_{i-6}} \left[\frac{a_{i-10} \ r_{i-6} \ \rho}{n \kappa} \left(U+c_{0}\right) - \frac{a_{i-10} \ r_{i-6}^{2} \ \rho}{n \kappa} \left(m^{2}+n^{2}\right) \left(\nu +\frac{\kappa}{\rho}\right)\right. \end{array} $$

$$\begin{array}{@{}rcl@{}} +\left. \frac{a_{i-10} \ \rho}{n \kappa}\left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) \right],\,\,i=17,18,19,20, \end{array} $$

and

$$\begin{array}{@{}rcl@{}} a_{21}= \bigg[\left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) \left(\frac{a_{11} \ \rho}{ n \kappa} - \frac{m \ \rho \ c_{0}}{ n \kappa \left(m^{2}+ n^{2}\right)}\right)\bigg]. \end{array} $$

Putting the Eqs. (28) and (30) into Eq. (22), we get

$$\begin{array}{@{}rcl@{}} \label {31} p(\xi)= a_{23}e^{r_{11} \xi} + a_{24}e^{r_{12} \xi}+ a_{25}e^{r_{13} \xi} + a_{26}e^{r_{14} \xi} + a_{27} \xi^{2} + a_{28} \xi + a_{29}, \end{array} $$

(31)

where

$$\begin{array}{@{}rcl@{}} a_{i}= \frac{1}{r_{i-12}}\left[\frac{a_{i-16} \ r_{i-12}^{2}}{m} \left(m^{2}+n^{2}\right) \left(\nu +\frac{\kappa}{\rho}\right)- \frac{a_{i-16} \ r_{i-12}}{m}\left(U+c_{0}\right) + \frac{a_{i-6} \ n \ \kappa}{r_{i-12}\ \rho}\right. \end{array} $$

$$\begin{array}{@{}rcl@{}} {}-\left. a_{i-16} \ \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right)\right],\,\,i=23,24,25,26, \end{array} $$

and

$$\begin{array}{@{}rcl@{}} a_{27}= \frac{a_{21} \ n \ \kappa}{2 \rho},\,\, a_{28}= \frac{a_{22}\ n \ \kappa}{\rho}. \end{array} $$

Hence, the velocity components, microrotation, and pressure in the original variables form are

$$\begin{array}{*{20}l} u(x,y,t)&= a_{7}e^{r_{11}(m x + ny +U t)} + a_{8}e^{r_{12} (m x + ny +U t)}+ a_{9}e^{r_{13}(m x + ny +U t)} \\&\quad+ a_{10}e^{r_{14}(m x + ny +U t)} + a_{11}, \end{array} $$

(32)

$$\begin{array}{*{20}l} v(x,y,t)&= a_{12}e^{r_{11}(m x + ny +U t)} + a_{13}e^{r_{12}(m x + ny +U t)}+ a_{14}e^{r_{13}(m x + ny +U t)} \\&\quad+ a_{15}e^{r_{14}(m x + ny +U t)} + a_{16}, \end{array} $$

(33)

$$\begin{array}{*{20}l} N(x,y,t)&= a_{17} e^{r_{11} (m x + ny +U t)} + a_{18} e^{r_{12} (m x + ny +U t)}+ a_{19} e^{r_{13}(m x + ny +U t)} \\ &\quad+ a_{20} e^{r_{14} (m x + ny +U t)} + a_{21} (m x + ny +U t)+ a_{22}, \end{array} $$

(34)

$$\begin{array}{*{20}l} p(x,y,t)&= a_{23}e^{r_{11}(m x + ny +U t)} + a_{24}e^{r_{12} (m x + ny +U t)}+ a_{25}e^{r_{13}(m x + ny +U t)}\\ &\quad+ a_{26}e^{r_{14}(m x + ny +U t)}+ a_{27} (m x + ny +U t)^{2} + a_{28} (m x + ny +U t) + a_{29}. \end{array} $$

(35)

Case-II: U+c_o=0

For this case, Eqs. (22–24) reduce to

$$\begin{array}{@{}rcl@{}}\label {36} -mp^{'}+ \left(\nu + \frac{\kappa}{\rho}\right) \left(m^{2}+ n^{2} \right)u^{\prime\prime} + \frac{n \ \kappa}{\rho} N^{'} - \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right)u = 0, \end{array} $$

(36)

$$\begin{array}{@{}rcl@{}}\label {37} -n p^{'}+ \left(\nu + \frac{\kappa}{\rho}\right) \left(m^{2}+ n^{2} \right)v^{\prime\prime} - \frac{m \ \kappa}{\rho} N^{'} - \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right)v = 0, \end{array} $$

(37)

$$\begin{array}{@{}rcl@{}}\label {38} \frac{\gamma}{\rho j} \left(m^{2}+ n^{2}\right)N^{\prime\prime} - \frac{2\kappa}{\rho j} \ N - \frac{\kappa}{\rho j}\left(n u^{'} - m v^{'}\right)= 0. \end{array} $$

(38)

Eliminating p from Eqs. (36) and (37)

$$ \begin{aligned} \left(\nu + \frac{\kappa}{\rho}\right)\left(m^{2} + n^{2}\right) \left(n u^{\prime\prime}- m v^{\prime\prime}\right) + \frac{\kappa}{\rho} \left(m^{2} + n^{2}\right)N^{'} - \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) \left(n u - m v\right)=0. \end{aligned} $$

(39)

Converting v into u in Eq. (39), then

$$\label {40} \begin{aligned} N^{'}= \frac{\rho}{\kappa} \bigg[ \frac{1}{n}\left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) u - \frac{1}{n} \left(m^{2}+ n^{2} \right) \left(\nu + \frac{\kappa}{\rho}\right) u^{\prime\prime} - \frac{m \ c_{o}}{n \left(m^{2}+n^{2}\right)} \left(\frac{\sigma B^{2}_{o}}{\rho}+\frac{\nu}{k^{\ast}}\right) \bigg]. \end{aligned} $$

(40)

Eliminating N from Eqs. (38) and (40), we get

$$\begin{array}{@{}rcl@{}}\label {41} b_{1}u^{i \mathrm{v}}+b_{2} u^{\prime\prime} + b_{3} u = b_{4}. \end{array} $$

(41)

where

$$\begin{array}{*{20}l} {}b_{1}= \frac{\gamma}{ n \ j \ \kappa} \left (m^{2}+ n^{2}\right)^{2} \left(\nu+\frac{\kappa}{\rho} \right), \end{array} $$

$$\begin{array}{@{}rcl@{}} b_{2}= \bigg [ \frac{\kappa}{ n \ \rho \ j} \left (m^{2}+ n^{2}\right) - \frac{\gamma}{n \ j \ \kappa}\left (m^{2}+ n^{2}\right) \left (\frac{\sigma B_{o}^{2}}{\rho}+\frac{\nu}{k^{\ast}}\right) -\frac{2 \left (m^{2}+n^{2}\right)}{n \ j} \left(\nu +\frac{\kappa}{\rho} \right) \bigg], \end{array} $$

$$\begin{array}{*{20}l} {}b_{3}= \frac{2}{n \ j} \left (\frac{\sigma B_{o}^{2}}{\rho}+\frac{\nu}{k^{\ast}}\right) \,\, \text{and} \,\, b_{4}= \frac{2 \ m \ c_{o}}{n \ j \ \left (m^{2}+n^{2}\right)} \left (\frac{\sigma B_{o}^{2}}{\rho}+\frac{\nu}{k^{\ast}}\right). \end{array} $$

The solution of Eq.(41) is

$$\begin{array}{@{}rcl@{}}\label {42} u(\xi)= b_{5}e^{r_{21} \xi}+b_{6}e^{r_{22} \xi} + b_{7}e^{r_{23} \xi}+ b_{8}e^{r_{24} \xi} + b_{9}, \end{array} $$

(42)

where r₂₁, r₂₂, r₂₃, and r₂₄ are the roots of the auxiliary equation.

$$\begin{array}{@{}rcl@{}} b_{1} m^{4} + b_{2} m^{2} + b_{3} = 0. \end{array} $$

Putting Eq. (42) into Eq.(21) provides

$$\begin{array}{@{}rcl@{}}\label {43} v(\xi)= b_{10}e^{r_{21} \xi}+ b_{11}e^{r_{22} \xi} + b_{12}e^{r_{23} \xi}+ b_{13}e^{r_{24} \xi} + b_{14}, \end{array} $$

(43)

where

$$\begin{array}{@{}rcl@{}} b_{i}= -\frac{m \ b_{i-5}}{n},\,\, \text{for} \, i=10,11,12,13, \end{array} $$

$$\begin{array}{@{}rcl@{}} b_{14}= \frac{1}{n} \left (c_{0} - m \ b_{9} \right). \end{array} $$

Putting the Eq. (42) in Eq. (40)

$$\begin{array}{@{}rcl@{}}\label {44} N(\xi)= b_{15}e^{r_{21} \xi}+b_{16}e^{r_{22} \xi} + b_{17}e^{r_{23} \xi}+ b_{18}e^{r_{24} \xi} + b_{19}\xi + b_{20}, \end{array} $$

(44)

where

$$\begin{aligned} b_{i}= \frac{1}{r_{i+6}}\left[\frac{b_{i-10} \ \rho}{n \kappa}\left (\frac{\sigma B_{o}^{2}}{\rho}+\frac{\nu}{ k^{\ast}}\right)-\frac{b_{i-10} \ r_{i+6}^{2} \ \rho}{n \kappa}\left(m^{2}+n^{2} \right)\left(\nu +\frac{\kappa}{\rho} \right)\right],\,\text{for} \,\, i=15,16,17,18, \end{aligned} $$

and

$$\begin{array}{@{}rcl@{}} b_{19}= \left (\frac{\sigma B_{o}^{2}}{\rho}+\frac{\nu}{k^{\ast}}\right) \left [\frac{b_{9} \ \rho}{n \kappa} - \frac{m \ c_{0} \ \rho}{n \kappa \left(m^{2}+n^{2}\right)} \right]. \end{array} $$

Substituting the Eqs. (42) and (44) in Eq. (36), we get

$$\begin{array}{@{}rcl@{}}\label {45} p(\xi)= b_{21}e^{r_{21} \xi}+b_{22}e^{r_{22} \xi} + b_{23}e^{r_{23} \xi}+ b_{24}e^{r_{24} \xi} + b_{25} \xi + b_{26}, \end{array} $$

(45)

where

$$\begin{aligned} b_{i}= \frac{1}{r_{i}}\left[\frac{b_{i-16} \ r_{i}^{2}}{m}\left(m^{2}+n^{2} \right)\left(\nu +\frac{\kappa}{\rho} \right)+ \frac{b_{i-6} \ n \ \kappa}{m \rho}-\frac{b_{i-16}}{m}\left (\frac{\sigma B_{o}^{2}}{\rho}+\frac{\nu}{k^{\ast}}\right)\right], \, \text{for} \, i=21,22,23,24, \end{aligned} $$

and

$$\begin{array}{@{}rcl@{}} b_{25}= \frac{b_{19} \ n \ \kappa}{m \ \rho} - \frac{b_{9}}{m}\left (\frac{\sigma B_{o}^{2}}{\rho}+\frac{\nu}{ k^{\ast}}\right). \end{array} $$

Returning the original variable in Eqs. (42–45), we have

$$\begin{array}{*{20}l} u(x,y,t)&= b_{5}e^{r_{21}(m x + n y + U t)}+b_{6}e^{r_{22}(m x + n y + U t)} + b_{7}e^{r_{23}(m x + n y + U t)}\\&\quad+ b_{8}e^{r_{24}(m x + n y + U t)} + b_{9}, \end{array} $$

(46)

$$\begin{array}{*{20}l} v(x,y,t)&= b_{10}e^{r_{21}(m x + n y + U t)}+ b_{11}e^{r_{22}(m x + n y + U t)} + b_{12}e^{r_{23}(m x + n y + U t)}\\&\quad+ b_{13}e^{r_{24}(m x + n y + U t)} + b_{14}, \end{array} $$

(47)

$$\begin{array}{*{20}l} N(x,y,t)&= b_{15}e^{r_{21}(m x + n y + U t)}+b_{16}e^{r_{22}(m x + n y + U t)} + b_{17}e^{r_{23}(m x + n y + U t)}\\&+ b_{18}e^{r_{24}(m x + n y + U t)} + b_{19}(m x + n y + U t)+ b_{20}, \end{array} $$

(48)

$$\begin{array}{*{20}l} p(x,y,t)&= b_{21}e^{r_{21} (m x + n y + U t)}+b_{22}e^{r_{22}(m x + n y + U t)} + b_{23}e^{r_{23}(m x + n y + U t)}\\&+ b_{24}e^{r_{24}(m x + n y + U t)} + b_{25} (m x + n y + U t) + b_{26}. \end{array} $$

(49)

Case - III : m=0

In this case, Eqs. (4–7) will be

$$\begin{array}{*{20}l}\label {50} {\kern40pt}v'=0, \end{array} $$

(50)

$$\begin{array}{*{20}l}\label {51} \left(U + n v \right) u^{'} = n^{2} \left(\nu + \frac{\kappa}{\rho} \right) u^{\prime\prime} + \frac{n \ \kappa}{\rho} N^{'} -\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) u, \end{array} $$

(51)

$$\begin{array}{*{20}l}\label {52} \left(U + n v \right) v^{'} = n^{2}\left(\nu + \frac{\kappa}{\rho}\right) v^{\prime\prime} - n p^{'} -\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) v, \end{array} $$

(52)

$$\begin{array}{@{}rcl@{}}\label {53} \left(U + n v \right) N^{'} = \frac{n^{2} \ \gamma}{\rho j} N^{\prime\prime} - \frac{2 \kappa}{\rho j} N -\frac{n \ \kappa}{ \rho j} u^{'}. \end{array} $$

(53)

From Eq. (51)

$$\begin{array}{@{}rcl@{}}\label {54} N^{'} = \frac{\rho}{n \kappa} \bigg[{\left(U+ n v \right)u^{'} - n^{2} \left(\nu + \frac{\kappa}{\rho}\right) u^{\prime\prime} + \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) u }\bigg]. \end{array} $$

(54)

Putting the Eq. (54) in Eq. (53), we find

$$\begin{array}{@{}rcl@{}}\label {55} c_{1} u^{i \mathrm{v}} - c_{2}u^{\prime\prime\prime} + c_{3} u^{\prime\prime} + c_{4} u^{'} + c_{5} u = 0, \end{array} $$

(55)

where

$$\begin{array}{*{20}l} c_{1}= \frac{n^{4} \ \gamma}{n \ \kappa \ j} \left(\nu + \frac{\kappa}{\rho}\right), \end{array} $$

$$\begin{array}{*{20}l} c_{2}= \bigg[\frac{n \ \rho}{\kappa} \left(U + n v \right)\left(\nu + \frac{\kappa}{\rho}\right)+ \frac{n \gamma}{\kappa j} \left (U+ n v \right) \bigg], \end{array} $$

$$\begin{array}{*{20}l} c_{3}= \left[\frac{\rho}{n \kappa} \left(U + n v \right)^{2} + \frac{n \ \kappa}{\rho j} - \frac{n \ \gamma}{j \kappa}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) - \frac{2 n}{j} \left(\nu + \frac{\kappa}{\rho}\right) \right], \end{array} $$

$$\begin{array}{*{20}l} c_{4}= \left[\frac{\rho}{n \kappa} \left(U + n v \right)\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) +\frac{2 n}{j} \left (U+ n v \right) \right], \end{array} $$

$$\begin{array}{*{20}l} c_{5}= \frac{2}{ n j}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right). \end{array} $$

The solution of Eq.(55) is

$$\begin{array}{@{}rcl@{}}\label {56} u(\xi)= c_{6} e^{r_{31} \xi} + c_{7} e^{r_{32} \xi} + c_{8} e^{r_{33} \xi} + c_{9} e^{r_{34} \xi}, \end{array} $$

(56)

where r₃₁, r₃₂, r₃₃, and r₃₄ are the roots of the auxiliary equation.

$$\begin{array}{@{}rcl@{}} c_{1} m^{4} - c_{2} m^{3} + c_{3} m^{2} + c_{4} m + c_{5} = 0. \end{array} $$

Integrating Eq. (50), we have

$$\begin{array}{@{}rcl@{}}\label {57} v(\xi)= c_{10}. \end{array} $$

(57)

Putting the Eq. (56) in Eq. (54)

$$\begin{array}{@{}rcl@{}}\label {58} N(\xi)= c_{11} e^{r_{31} \xi} + c_{12} e^{r_{32} \xi} + c_{13} e^{r_{33} \xi} + c_{14} e^{r_{34} \xi} + c_{15}. \end{array} $$

(58)

where

$$\begin{aligned} c_{i}=\frac{1}{r_{i+20}}\bigg[\frac{c_{i-5} \ r_{i+20} \ \rho}{n \kappa}(U+ n v)-\frac{c_{i-5} \ r_{i+20}^{2} \ m^{2} \ \rho}{n \kappa}\left(\nu +\frac{\kappa}{\rho} \right) + c_{i-5}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{ k^{\ast}}\right)\bigg], \, \text{for} \, i= 11,12,13,14. \end{aligned} $$

Putting Eqs. (50) and (57) into Eq. (52)

$$\begin{array}{@{}rcl@{}}\label {59} p(\xi) = c_{16} \xi + c_{17}. \end{array} $$

(59)

where

$$\begin{array}{@{}rcl@{}} c_{16}= - \frac{c_{10}}{n}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right). \end{array} $$

Returning the original variable, we get

$$\begin{array}{*{20}l}\label {60} u(x,y,t)&= c_{6} e^{r_{31}(mx+ny+Ut)} + c_{7} e^{r_{32}(mx+ny+Ut)} + c_{8} e^{r_{33}(mx+ny+Ut)} \\&\quad+ c_{9} e^{r_{34}(mx+ny+Ut)}, \end{array} $$

(60)

$$\begin{array}{*{20}l}\label {61} v(x,y,t)= c_{10}, \end{array} $$

(61)

$$\begin{array}{*{20}l}\label {62} N(x,y,t)&= c_{11} e^{r_{31} (mx+ny+Ut)} + c_{12} e^{r_{32}(mx+ny+Ut)} + c_{13} e^{r_{33}(mx+ny+Ut)} \\&\quad+ c_{14} e^{r_{34}(mx+ny+Ut)} + c_{15}, \end{array} $$

(62)

$$\begin{array}{*{20}l}\label {63} p(x,y,t) = c_{16}(mx+ny+Ut) + c_{17}. \end{array} $$

(63)

Case- IV: n=0

Equations (4 - 7) reduces to

$$\begin{array}{*{20}l}\label {64} {\kern42pt}u'=0, \end{array} $$

(64)

$$\begin{array}{*{20}l}\label {65} \left(U + mu\right) u^{'} = -m p^{'}+ m^{2} \left(\nu +\frac{\kappa}{\rho}\right) u^{\prime\prime} - \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) u, \end{array} $$

(65)

$$\begin{array}{*{20}l}\label {66} \left(U + mu\right) v^{'} = m^{2}\left(\nu +\frac{\kappa}{\rho}\right) v^{\prime\prime} - \frac{m \kappa}{\rho} N^{'} - \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) v, \end{array} $$

(66)

$$\begin{array}{*{20}l}\label {67} \left(U + mu\right) N^{'} = \frac{m^{2} \ \gamma}{\rho j} N^{\prime\prime} - \frac{2 \kappa}{\rho j} N + m v^{'}. \end{array} $$

(67)

Integrating Eq. (64), we get

$$\begin{array}{@{}rcl@{}}\label {68} u(\xi)= d_{1}. \end{array} $$

(68)

From Eq. (66), we have

$$\begin{array}{@{}rcl@{}}\label {69} N^{'}= \frac{\rho}{ m \kappa} \bigg[m \left(\nu +\frac{\kappa}{\rho}\right) v^{\prime\prime} - \frac{1}{m} \left(U+ d_{1} m\right) v^{'} - \frac{1}{m} \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right)v \bigg]. \end{array} $$

(69)

Putting Eq. (69) into Eq. (67)

$$\begin{array}{@{}rcl@{}}\label {70} d_{2} v^{i \mathrm{v}} - d_{3} v^{\prime\prime\prime} - d_{4} v^{\prime\prime} + d_{5} v^{'} + d_{6} v = 0, \end{array} $$

(70)

where

$$\begin{array}{@{}rcl@{}} d_{2}= \frac{m^{3} \ \gamma}{\kappa j} \left(\nu +\frac{k}{\rho}\right), \end{array} $$

$$\begin{array}{@{}rcl@{}} d_{3}=\bigg[\frac{m \ \gamma}{\kappa j}\left(U+d_{1} m \right)-\frac{m \ \rho}{\kappa}\left(U+d_{1} m \right)\left(\nu +\frac{\kappa}{\rho}\right)\bigg], \end{array} $$

$$\begin{array}{@{}rcl@{}} d_{4}=\bigg[\frac{m \ \gamma}{\kappa j}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right)-\frac{ \rho}{m \kappa}\left(U+d_{1} m \right)^{2}+\frac{2 m}{j}\left(\nu+\frac{\kappa}{\rho}\right) -m \bigg], \end{array} $$

$$\begin{array}{@{}rcl@{}} d_{5}=\bigg[\frac{2}{m j}\left(U+d_{1}m \right)+\frac{\rho}{m \kappa}\left(U+d_{1}m \right)\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right)\bigg], \end{array} $$

$$\begin{array}{@{}rcl@{}} d_{6}=\frac{2}{m j}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right). \end{array} $$

The solution of Eq. (70) is

$$\begin{array}{@{}rcl@{}}\label {71} v(\xi)= d_{7} e^{r_{41} \xi} + d_{8} e^{r_{42} \xi} + d_{9} e^{r_{43} \xi} + d_{10} e^{r_{44} \xi}, \end{array} $$

(71)

where r₄₁, r₄₂, r₄₃, and r₄₄ are the roots of the auxiliary equation

$$\begin{array}{@{}rcl@{}} d_{2} m^{4} - d_{3} m^{3} - d_{4} m^{2} + d_{5} m + d_{6} = 0. \end{array} $$

Putting the Eq. (71) in Eq. (69)

$$\begin{array}{@{}rcl@{}}\label {72} N(\xi)= d_{11} e^{r_{41} \xi} + d_{12} e^{r_{42} \xi} + d_{13} e^{r_{43} \xi} + d_{14} e^{r_{44} \xi} + d_{15}, \end{array} $$

(72)

where

$$\begin{aligned} d_{i}=\frac{1}{r_{i+30}}\bigg[\frac{d_{i-4} \ r_{i+30}^{2} \ m \rho}{\kappa}\left(\nu +\frac{\kappa}{\rho}\right)-\frac{d_{i-4} \ r_{i+30} \ \rho}{m \kappa}\left(U+d_{1} m \right)-\frac{d_{i-4} \ \rho}{m \kappa}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right)\bigg]. \, \text{for}\, i= 11,12,13,14, \end{aligned} $$

Substituting the Eq. (68) in Eq. (65)

$$\begin{array}{@{}rcl@{}}\label {73} p(\xi)= d_{16} \xi + d_{17}, \end{array} $$

(73)

where

$$\begin{array}{@{}rcl@{}} d_{16}= - \frac{d_{1}}{m}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right). \end{array} $$

The exact solutions in term of the original variables are

$$\begin{array}{*{20}l}\label {74} u(x,y,t)= d_{1}, \end{array} $$

(74)

$$\begin{array}{*{20}l}\label {75} v(x,y,t)&= d_{7} e^{r_{41}(mx+ny+Ut)} + d_{8} e^{r_{42}(mx+ny+Ut)} + d_{9} e^{r_{43}(mx+ny+Ut)}\\&\quad + d_{10} e^{r_{44}(mx+ny+Ut)}, \end{array} $$

(75)

$$\begin{array}{*{20}l}\label {76} N(x,y,t)&= d_{11} e^{r_{41}(mx+ny+Ut)} + d_{12} e^{r_{42}(mx+ny+Ut)} + d_{13} e^{r_{43}(mx+ny+Ut)} \\&\quad+ d_{14} e^{r_{44}(mx+ny+Ut)} + d_{15}, \end{array} $$

(76)

$$\begin{array}{*{20}l}\label {77} p(x,y,t)= d_{16}(mx+ny+Ut) + d_{17}. \end{array} $$

(77)

Case-V: U=0

For this case, Eqs. (22)–(24) become

$$\begin{array}{@{}rcl@{}}\label {78} c_{0} u^{'}= - m p^{'}+ \left(m^{2} + n^{2} \right) \left(\nu + \frac{\kappa}{\rho} \right) u^{\prime\prime} + \frac{n \kappa}{\rho} N^{'} - \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) u, \end{array} $$

(78)

$$\begin{array}{@{}rcl@{}}\label {79} c_{0} v^{'}= - n p^{'}+ \left(m^{2} + n^{2}\right) \left(\nu + \frac{\kappa}{\rho}\right) v^{\prime\prime} - \frac{m \kappa}{\rho} N^{'} - \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) v, \end{array} $$

(79)

$$\begin{array}{@{}rcl@{}}\label {80} {}c_{0} N^{'}= \frac{\gamma}{\rho j} \left(m^{2} + n^{2}\right) N^{\prime\prime} - \frac{2 \kappa}{\rho j} N - \frac{\kappa}{\rho j}\left(n u^{'} - m v^{'}\right). \end{array} $$

(80)

Eliminating p from Eqs. (78) and (79), we get

$$\begin{array}{*{20}l}\label {81} c_{0} \left(n u^{'} - m v^{'}\right) &= \left(m^{2}+n^{2}\right) \left(\nu + \frac{\kappa}{\rho}\right) \left(n u^{\prime\prime} -m v^{\prime\prime}\right) + \frac{\kappa}{\rho}\left(m^{2}+ n^{2} \right) N^{'} \\&\quad- \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{ k^{\ast}}\right) \left(n u - m v \right). \end{array} $$

(81)

Convert ing v into u in Eq. (81), we arrive

$$\begin{array}{*{20}l}\label {82} \frac{c_{0}}{n}\left(m^{2}+n^{2} \right)u^{'}&= \frac{1}{n}\left(m^{2} + n^{2} \right)^{2} \left(\nu + \frac{\kappa}{\rho} \right) u^{\prime\prime}+ \frac{\kappa}{\rho} \left(m^{2}+n^{2}\right)N^{'} \\&\quad- \frac{\left(m^{2} + n^{2} \right)}{n} \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) u \end{array} $$

$$\begin{array}{*{20}l} \qquad\qquad\qquad\quad+ \frac{m \ c_{0}}{n} \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right). \end{array} $$

(82)

From Eq. (82), we have

$$\label {83} \begin{aligned} N^{'}= \frac{\rho}{\kappa}\bigg[\frac{c_{0}}{n} u^{'} -\frac{1}{n} \left(m^{2} + n^{2} \right)\left(\nu + \frac{\kappa}{\rho}\right) u^{\prime\prime} + \frac{1}{n}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right)u - \frac{m \ c_{0}}{n\left(m^{2}+n^{2}\right)}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) \bigg]. \end{aligned} $$

(83)

Putting Eq. (83) in Eq. (78)

$$\begin{array}{@{}rcl@{}}\label {84} e_{1} u^{i \mathrm{v}} - e_{2} u^{\prime\prime\prime} + e_{3} u^{\prime\prime} + e_{4} u^{'}+ e_{5}u= e_{6}, \end{array} $$

(84)

where

$$\begin{array}{*{20}l} {}e_{1}=\frac{\gamma \ \left(m^{2}+n^{2}\right)^{2}}{ n \kappa j}\left(\nu + \frac{\kappa}{\rho}\right), \end{array} $$

$$\begin{array}{*{20}l} {}e_{2}=\bigg[\frac{c_{0} \ \rho}{n \kappa}\left(m^{2}+n^{2}\right)\left(\nu + \frac{\kappa}{\rho}\right)+\frac{c_{0} \ \gamma}{n j \kappa}\left(m^{2}+n^{2}\right) \bigg], \end{array} $$

$$\begin{array}{@{}rcl@{}} e_{3}=\bigg[\frac{\rho \ c_{0}^{2}}{n \kappa} - \frac{\gamma \ \left(m^{2}+n^{2}\right)}{n j \kappa}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right)- \frac{2\left(m^{2}+n^{2}\right)}{n j}\left(\nu + \frac{\kappa}{\rho}\right)+ \frac{\kappa}{\rho j}\left(m^{2}+n^{2}\right)\bigg], \end{array} $$

$$\begin{array}{*{20}l} {}e_{4}=\bigg[\frac{\rho \ c_{o}}{n \kappa}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right)+\frac{2 \ c_{o}}{n j}\bigg], \end{array} $$

$$\begin{array}{@{}rcl@{}} e_{5}=\frac{2}{n j}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right) \ and \ e_{6}= \frac{2 \ m \ c_{o}}{n \left(m^{2}+n^{2}\right)} \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right). \end{array} $$

The solution of Eq. (84) is

$$\begin{array}{@{}rcl@{}}\label {85} u(\xi) = e_{7} e^{r_{51} \xi} + e_{8}e^{r_{52} \xi} + e_{9} e^{r_{53} \xi} + e_{10} e^{r_{54} \xi} + e_{11}, \end{array} $$

(85)

where r₅₁, r₅₂, r₅₃, and r₅₄ are the roots of the auxiliary equation

$$\begin{array}{@{}rcl@{}} e_{1} m^{4} - e_{2} m^{3} + e_{3} m^{2} + e_{4} m + e_{5} = 0. \end{array} $$

Substituting Eq. (85) into Eq. (21)

$$\begin{array}{@{}rcl@{}}\label {86} v(\xi) = e_{12} e^{r_{51} \xi} + e_{13}e^{r_{52} \xi} + e_{14} e^{r_{53} \xi} + e_{15} e^{r_{54} \xi} + e_{16}, \end{array} $$

(86)

where

$$\begin{array}{@{}rcl@{}} e_{i}= -\frac{m \ e_{i-5}}{n}, \, \text{for} \, i=12,13, 14,15,\,\,\text{and} \end{array} $$

$$\begin{array}{@{}rcl@{}} e_{16}= \frac{1}{n} \left (c_{0} - m \ e_{11} \right). \end{array} $$

Putting the Eq. (85) in Eq. (83)

$$\begin{array}{@{}rcl@{}}\label {87} N(\xi) = e_{17} e^{r_{51} \xi} + e_{18}e^{r_{52} \xi} + e_{19} e^{r_{53} \xi} + e_{20} e^{r_{54} \xi} + e_{21} \xi + e_{22}. \end{array} $$

(87)

where

$$\begin{array}{*{20}l} e_{i}=\frac{1}{r_{i+34}}\left[\frac{e_{i-10} \ r_{i+34} \ \rho c_{0}}{n \kappa} -\frac{e_{i-10} \ r_{i+34}^{2}\ \rho}{n \kappa} \left(m^{2}+n^{2}\right)\right. \end{array} $$

$$\begin{array}{@{}rcl@{}} \times\left.\left(\nu + \frac{\kappa}{\rho}\right)+\frac{e_{i-10} \ \rho}{n \kappa} \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right)\right],\, \text{for}\, i= 17,18,19,20\,\,\,\text{and} \end{array} $$

$$\begin{array}{*{20}l} e_{21}= - \frac{\rho \ m \ c_{o}}{n \kappa \left(m^{2}+n^{2}\right)} \left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{ k^{\ast}}\right). \end{array} $$

Substituting Eqs. (85) and (87) in Eq. (78), we get

$$\begin{array}{@{}rcl@{}}\label {88} p(\xi) = e_{23} e^{r_{51} \xi} + e_{24}e^{r_{52} \xi} + e_{25} e^{r_{53} \xi} + e_{26} e^{r_{54} \xi} + e_{27} \xi^{2} + e_{28} \xi + e_{29}, \end{array} $$

(88)

where

$$\begin{array}{@{}rcl@{}} e_{i}=\frac{1}{r_{i+28}}\bigg[\frac{e_{i-16} \ r_{i+28}^{2}}{m}\left(m^{2}+n^{2}\right) \left(\nu +\frac{\kappa}{\rho}\right)-\frac{e_{i-16} \ r_{i+28} c_{0}}{m}+\frac{e_{i-6} \ n \ \kappa}{\rho} \end{array} $$

$$\begin{array}{@{}rcl@{}} -e_{i-16}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{k^{\ast}}\right)\bigg],\, \text{for}\, i= 23,24,25,26,\,\, \text{and} \end{array} $$

$$\begin{array}{@{}rcl@{}} e_{27}=\frac{e_{21} \ n \ \kappa}{2 \rho} \,\,\, \text{and} \,\,\, e_{28}= -e_{11}\left(\frac{\sigma B^{2}_{o}}{\rho} + \frac{\nu}{ k^{\ast}}\right). \end{array} $$

Returning to the original variables, the exact solutions are

$$\begin{array}{*{20}l}\label {89} u(x,y,t) &= e_{7} e^{r_{51}(mx+ny+Ut)} + e_{8}e^{r_{52} (mx+ny+Ut)} + e_{9} e^{r_{53}(mx+ny+Ut)}\\&\quad + e_{10} e^{r_{54}(mx+ny+Ut)} + e_{11}, \end{array} $$

(89)

$$\begin{array}{*{20}l}\label {90} v(x,y,t) &= e_{12} e^{r_{51}(mx+ny+Ut)} + e_{13}e^{r_{52}(mx+ny+Ut)} + e_{14} e^{r_{53}(mx+ny+Ut)}\\&\quad + e_{15} e^{r_{54}(mx+ny+Ut)} + e_{16}, \end{array} $$

(90)

$$\begin{array}{*{20}l}\label {91} N(x,y,t) &= e_{17} e^{r_{51}(mx+ny+Ut)} + e_{18}e^{r_{52}(mx+ny+Ut)} + e_{19} e^{r_{53}(mx+ny+Ut)}\\ &\quad + e_{20} e^{r_{54}(mx+ny+Ut)}+ e_{21}(mx+ny+Ut) + e_{22}, \end{array} $$

(91)

$$\begin{array}{*{20}l}\label {92} p(x,y,t) &= e_{23} e^{r_{51}(mx+ny+Ut)} + e_{24}e^{r_{52}(mx+ny+Ut)} + e_{25} e^{r_{53}(mx+ny+Ut)}\\ &\quad + e_{26} e^{r_{54}(mx+ny+Ut)}e_{27}(mx+ny+Ut)^{2} + e_{28}(mx+ny+Ut) + e_{29}. \end{array} $$

(92)

Making initial and boundary conditions

Some exact traveling solutions are determined for Eqs. (4)–(7) in the “Traveling wave solutions” section, without initial and boundary conditions. Definitely, the initial and boundary conditions can be made from these solutions. For instance, if governing Eqs. (4)–(7) is assumed that they are satisfied Rayleigh-Stokes problem for an edge, then for two perpendicular plates (yz and xz−planes), we have x,y∈[0,∞]. Utilizing t=0, x=0 and y=0 into Eqs. (32)–(35), then some initial and boundary conditions are achieved.

∙Equations (32)–(35) satisfy the following initial conditions:

$$\begin{array}{*{20}l}\label {32} u(x,y,0)&= a_{7}e^{r_{11}(m x + ny)} + a_{8}e^{r_{12} (m x + ny)}+ a_{9}e^{r_{13}(m x + ny)} + a_{10}e^{r_{14}(m x + ny)}\\&\quad + a_{11},\,\,\,x,\,y>0, \end{array} $$

(93)

$$\begin{array}{*{20}l}\label {33} v(x,y,0)&= a_{12}e^{r_{11}(m x + ny)} + a_{13}e^{r_{12}(m x + ny)}+ a_{14}e^{r_{13}(m x + ny)} + a_{15}e^{r_{14}(m x + ny)}\\&\quad + a_{16},\,\,\,x,\,y>0, \end{array} $$

(94)

$$\begin{array}{*{20}l} N(x,y,0)&= a_{17} e^{r_{11} (m x + ny)} + a_{18} e^{r_{12} (m x + ny)}+ a_{19} e^{r_{13}(m x + ny)} + a_{20} e^{r_{14} (m x + ny)}\\ &\quad + a_{21} (m x + ny)+ a_{22},\,\,\,x,\,y>0, \end{array} $$

(95)

$$\begin{array}{*{20}l}\label {35} p(x,y,0)&= a_{23}e^{r_{11}(m x + ny)} + a_{24}e^{r_{12} (m x + ny)}+ a_{25}e^{r_{13}(m x + ny)} + a_{26}e^{r_{14}(m x + ny)}\\ &\quad + a_{27} (m x + ny)^{2} + a_{28} (m x + ny) + a_{29},\,\,\,x,\,y>0. \end{array} $$

(96)

∙Equations (32)–(35) satisfy the following boundary conditions on the upper plate (yz-plane):

$$\begin{array}{*{20}l}\label {32} u(0,y,t)&= a_{7}e^{r_{11}(ny +U t)} + a_{8}e^{r_{12} (ny +U t)}+ a_{9}e^{r_{13}(ny +U t)} + a_{10}e^{r_{14}(ny +U t)}\\&\quad + a_{11},\,\,\,t>0, \end{array} $$

(97)

$$\begin{array}{*{20}l}\label {33} v(0,y,t)&= a_{12}e^{r_{11}(ny +U t)} + a_{13}e^{r_{12}(ny +U t)}+ a_{14}e^{r_{13}(ny +U t)} + a_{15}e^{r_{14}(ny +U t)} \\&\quad+ a_{16},\,\,\,t>0, \end{array} $$

(98)

$$\begin{array}{*{20}l}\label {34} N(0,y,t)&= a_{17} e^{r_{11} (ny +U t)} + a_{18} e^{r_{12} (ny +U t)}+ a_{19} e^{r_{13}(ny +U t)} + a_{20} e^{r_{14} (ny +U t)}\\ &\quad+ a_{21} (ny +U t)+ a_{22},\,\,\,t>0, \end{array} $$

(99)

$$\begin{array}{@{}rcl@{}}\label {35} p(0,y,t)= a_{23}e^{r_{11}(ny +U t)} + a_{24}e^{r_{12} (ny +U t)}+ a_{25}e^{r_{13}(ny +U t)} + a_{26}e^{r_{14}(ny +U t)} \end{array} $$

(100)

$$\begin{array}{@{}rcl@{}} + a_{27} (ny +U t)^{2} + a_{28} (ny +U t) + a_{29},\,\,\,t>0. \end{array} $$

∙Equations (32)–(35) satisfy the following boundary conditions on the lower plate (xz-plane):

$$\begin{array}{*{20}l}\label {32} u(x,0,t)&= a_{7}e^{r_{11}(m x+U t)} + a_{8}e^{r_{12} (m x +U t)}+ a_{9}e^{r_{13}(m x +U t)} + a_{10}e^{r_{14}(m x +U t)} \\&\quad+ a_{11},\,\,\,t>0, \end{array} $$

(101)

$$\begin{array}{*{20}l}\label {33} v(x,0,t)&= a_{12}e^{r_{11}(m x +U t)} + a_{13}e^{r_{12}(m x +U t)}+ a_{14}e^{r_{13}(m x +U t)} + a_{15}e^{r_{14}(m x +U t)}\\&\quad + a_{16},\,\,\,t>0, \end{array} $$

(102)

$$\begin{array}{@{}rcl@{}}\label {34} N(x,0,t)= a_{17} e^{r_{11} (m x +U t)} + a_{18} e^{r_{12} (m x +U t)}+ a_{19} e^{r_{13}(m x +U t)} + a_{20} e^{r_{14} (m x+U t)} \end{array} $$

(103)

$$\begin{array}{@{}rcl@{}} {}+ a_{21} (m x +U t)+ a_{22},\,\,\,t>0, \end{array} $$

$$\begin{array}{@{}rcl@{}}\label {35} p(x,0,t)= a_{23}e^{r_{11}(m x +U t)} + a_{24}e^{r_{12} (m x +U t)}+ a_{25}e^{r_{13}(m x +U t)} + a_{26}e^{r_{14}(m x +U t)} \end{array} $$

(104)

$$\begin{array}{@{}rcl@{}} {}+ a_{27} (m x +U t)^{2} + a_{28} (m x +U t) + a_{29},\,\,\,t>0. \end{array} $$

Similarly, we can made the initial and boundary conditions to the other many cases.

Numerical results and discussions

In this paper, we obtain exact traveling wave solutions of MHD flow of micropolar fluid in a porous medium. The methodology in the recent work is easily reduced to the non-linear partial differential equations of MHD micropolar fluid to linearized ordinary differential equations. The method has been used directly without any restrictive assumption and laborious calculation. These exact traveling solutions are obtained for five different cases. From these solutions, we can find special solutions for with and without MHD and porous effects. It is also noted that when κ,N→0, we obtain the solutions for viscous fluid flow. Furthermore, in all cases, we write general solutions in the exponential form; however, we can also write general solutions in the oscillatory form by assuming some suitable restriction on the roots of the equations, but we avoid it due to the length of the paper.

Now, in order to reveal some relevant physical aspect of the determine results the diagram of the velocity fluid components u(x,t),v(x,t), and the microrotation N(x,t) are present against x for different values of t and of the important parameters of the micropolar fluid. For the sake of convenience, we present a graph only for case I, U+c₀≠0, and a similar prediction can be done by other cases. Figures 2, 3, and 4 showed the influence of time, space variable x, and three-dimensional representation of u, v, and N. From Figs. 2 and 3, it is clear that u is increasing function of time t and space variable x; however, v and N are also increasing functions (in absolute value) of these variables. The combined effects of these variables are shown in 3D graphs of Fig. 4. It is more clear from 3D pictures of u, v, and N that they are becoming strengthen with the strengthening values of t and x. The influence of the vortex viscosity κ is shown in Fig. 5; from these figures, we can see that velocity components u, v, and microrotation N (in absolute sense) increase with the increasing values of κ. The influence of kinematic viscosity ν is shown in Fig. 6. The effect of kinematic viscosity ν on a fluid motion is quite opposite to that of vortex viscosity κ. The effect of magnetic parameter B₀ is shown in Fig. 7. It is clear that the effect of the magnetic parameter B₀ is similar to u and v. For instance, the velocity component u is increasing while v is also increasing function (in absolute value) of B₀ because the particle of micropolar fluid always travel rotationally, which may cause increment in velocity. However, the influence of magnetic parameter B₀ on the microrotation profile N is decreasing in the two-third domain and increasing in the remaining domain. In Fig. 8, the effect of porosity parameter k^∗ is depicted on the velocity components and microrotation profiles. It is noted that the porosity parameter k has opposite effects on the profiles of u and v in comparison to the magnetic parameter B₀. The microrotation N is decreasing the function of the porosity parameter. The influence of the parameter m appears in the traveling wave parameter ξ is shown in Fig. 9. It comes to the notice that increasing values of the parameter m reduce the values of u and N; however, the values of v are increased very shortly.

Fig. 2

Profiles of the velocity field u(x,t),v(x,t), and microrotation N(x,t) for MHD micropolar fluid given by Eqs. (32), (33), and (34), for U=0.1, ν=0.045, μ=0.5, κ=0.2, B₀=2, k^∗=0.2, σ=0.2, j=0.03, m=n=1, y=1, c₀=0.01, and different values of x

Fig. 3

Profiles of the velocity field u(x,t),v(x,t) and microrotation N(x,t) for MHD micropolar fluid given by Eqs. (32), (33), and (34), for U=0.1, ν=0.045, μ=0.5, κ=0.2, B₀=2, k^∗=0.2, σ=0.2, j=0.03, m=n=1, y=1, c₀=0.01, and different values of t

Fig. 4

3D profiles of the velocity field u(x,t),v(x,t), and microrotation N(x,t) for MHD micropolar fluid given by Eqs. (32), (33), and (34), for U=0.1, ν=0.045, μ=0.5, κ=0.2, B₀=2, k^∗=0.2, σ=0.2, j=0.03, m=n=1, y=1, c₀=0.01

Fig. 5

Profiles of the velocity field u(x,t),v(x,t), and microrotation N(x,t) for MHD micropolar fluid given by Eqs. (32), (33), and (34), for U=0.1, ν=0.045, μ=0.5, B₀=2, k^∗=0.2, σ=0.2, j=0.03, m=n=1, y=1, c₀=0.01, t=2s, and different values of κ

Fig. 6

Profiles of the velocity field u(x,t),v(x,t), and microrotation N(x,t) for MHD micropolar fluid given by Eqs. (32), (33), and (34), for U=0.1, ρ=12, κ=0.2, B₀=2, k^∗=0.2, σ=0.2, j=0.03, m=n=1, y=1, c₀=0.01, t=2s, and different values of ν

Fig. 7

Profiles of the velocity field u(x,t),v(x,t), and microrotation N(x,t) for MHD micropolar fluid given by Eqs. (32), (33), and (34), for U=0.1, ν=0.045, μ=0.5, κ=0.2, k^∗=0.2, σ=0.2, j=0.03, m=n=1, y=1, c₀=0.01, t=2s, and different values of B₀

Fig. 8

Profiles of the velocity field u(x,t),v(x,t), and microrotation N(x,t) for MHD micropolar fluid given by Eqs. (32), (33), and (34), for U=0.1, ν=0.045, μ=0.5, κ=0.2, B₀=2, σ=0.2, j=0.03, m=n=1, y=1, c₀=0.01, t=2s, and different values of k^∗

Fig. 9

Profiles of the velocity field u(x,t),v(x,t), and microrotation N(x,t) for MHD micropolar fluid given by Eqs. (32), (33), and (34), for U=0.1, ν=0.045, μ=0.5, κ=0.2, B₀=2, k^∗=0.2, σ=0.2, j=0.03, n=1, y=1, c₀=0.01, t=2s, and different values of m

Finally for comparison, the profile of the velocity components u(x,t) and v(x,t) corresponding to the motion of the three types of fluids (MHD micropolar fluid in porous medium, micropolar, and MHD Newtonian in porous medium fluids) are together presented in Fig. 10 for similar values of material constants. It is clear from these figures that MHD Newtonian in a porous medium fluid is the fastest, and the simple micropolar fluid is slowest. It is also brought to the knowledge that magnetic and porosity parameters fasten the fluid motion in this case that we have considered here. SI units are used in making all these graphs and Mathcad software is used for making these graphs.

Fig. 10

Profiles of the velocity field u(x,t) and v(x,t) for MHD micropolar fluid with porous effect, micropolar fluid, and MHD Newtonian fluids with porous given by Eqs. (32), (33), and (34), for U=0.1, ν=0.045, μ=0.5, κ=0.2, B₀=0.2, k^∗=0.2, σ=0.2, j=0.03, m=n=1, y=1, c₀=0.01, and t=2s