Accelerated fitted operator finite difference method for singularly perturbed delay differential equations with non-local boundary condition

Abstract

In this paper, accelerated fitted finite difference method for solving singularly perturbed delay differential equation with non-local boundary condition is considered. To treat the non-local boundary condition, Simpson’s rule is applied. The stability and parameter uniform convergence for the proposed method are proved. To validate the applicability of the scheme, two model problems are considered for numerical experimentation and solved for different values of the perturbation parameter ε and mesh size h. The numerical results are tabulated in terms of maximum absolute errors and rate of convergence, and it is observed that the present method is more accurate and ε-uniformly convergent for h ≥ ε where the classical numerical methods fails to give good result, and it also improves the results of the methods existing in the literature.

Introduction

A differential equation is said to be singularly perturbed delay differential equation, if it includes at least one delay term, involving unknown functions occurring with different arguments, and also, the highest derivative term is multiplied by a small parameter. Such type of delay, differential equations play a very important role in the mathematical models of science and engineering, such as, the human pupil light reflex with mixed delay type [1], variational problems in control theory with small state problem [2], models of HIV infection [3], and signal transition [4]. Any system involving a feedback control almost involves time delay. The delay occurs because a finite time is required to sense the information and then react to it. Finding the solution of singularly perturbed delay differential equations, whose application mentioned above, is a challenging problem. In response to these, in recent years, there has been a growing interest in numerical methods on singularly perturbed delay differential equations. The authors of [5,6,7] have developed various numerical schemes on uniform meshes for singularly perturbed first and second order differential equations with integral boundary conditions. The authors of [8,9,10] have proved that the problem of differential equations with integral boundary conditions is well posed. The authors of [11] proposed a first order uniform convergent fitted finite difference scheme for singularly perturbed boundary value problem for a linear second order delay differential equation with large delay in reaction term.

The standard numerical methods used for solving singularly perturbed differential equation are sometime ill posed and fail to give analytical solution when the perturbation parameter ε is small.

Therefore, it is necessary to develop suitable numerical methods which are uniformly convergent to solve this type of differential equations. In [12,13,14,15], finite difference and finite element methods are proposed to solve this kind of equations with large and small shifts.

As far as the researchers’ knowledge is concerned, numerical solution of singularly perturbed boundary value problem containing integral boundary condition via accelerated exponential fitted operator method is first being considered. The basic essence of accelerated fitted operator finite difference method is fitting an operator into a finite difference scheme, determining the value for the operator, formulating the intended scheme, and then applying Richardson extrapolation that can be explained as whenever the leading term in the error for an approximation formula is known; we can combine two approximations obtained from the formula using different values of the mesh sizes h and 0.5h to obtain a higher order approximation, and the technique is known as Richardson extrapolation. This procedure is a convergence acceleration technique which consists of a linear combination of two computed approximations of a solution (applied on two nested meshes). The linear combination turns out to be a better approximation. Therefore, the main objective of this study is to develop ε-uniformly convergent and more accurate numerical method for solving singularly perturbed delay differential equations with non-local boundary condition. Hence, in the present paper, motivated by the works of [16], we developed a fitted operator finite difference scheme on uniform mesh for the numerical solution for second order singularly perturbed convection-diffusion equations with negative shift and non-local boundary condition.

The present paper is organized as follows. Statement of the problem is given in the “Statement of the problem” section. In the “Properties of continuous solution” section, properties of continuous solution are presented. The “Formulation of the numerical scheme” section describes formulation of the numerical scheme. Convergence analysis for approximate solution is given in the “Convergence analysis” section. Numerical results are given in the “Numerical examples and results” section. Discussion and conclusion is given in the “Discussion and conclusion” section.

Throughout our analysis, C is a generic positive constant that is independent of the parameter ε and number of mesh points 2N. We assume that $\overline{\varOmega}=\left[0,2\right],\varOmega =\left(0,2\right),\kern0.5em {\varOmega}_1=\left(0,1\right),{\varOmega}_2=\left(1,2\right)$. Further, ${\varOmega}^{\ast }={\varOmega}_1\cup {\varOmega}_2,{\overline{\varOmega}}^{2N}$ is denoted by $\left\{0,1,2,...,2N\right\},{\overline{\varOmega}}_1^{2N}$ is denoted by $\left\{1,2,...,N-1\right\},{\varOmega}_2^{2N}$ is denoted by {N + 1, N + 2, ..., 2N − 1}.

Statement of the problem

Consider the following singularly perturbed problem:

$$ Ly(x)=-\varepsilon {y}^{{\prime\prime} }(x)+a(x){y}^{\prime }(x)+b(x)y(x)+c(x)y\left(x-1\right)=f(x),\kern0.5em x\in \varOmega =\left(0,2\right),\kern5.75em $$

(1)

$$ y(x)=\phi (x),\kern0.75em x\in \left[-1,0\right],\kern19.75em $$

(2)

$$ Ky(2)=y(2)-\varepsilon \underset{0}{\overset{2}{\int }}g(x)y(x) dx=l,\kern6.75em $$

(3)

where ϕ(x) is sufficiently smooth on [−1, 0]. For all x ∈ Ω, it is assumed that the sufficient smooth functions a(x), b(x) and c(x) satisfy a(x) > α₁ > α > 0, b(x) ≥ β ≥ 0, c(x) ≤ γ ≤ 0, and α + β + γ > 0. Furthermore, g(x) is non-negative and monotonic with $\underset{0}{\overset{2}{\int }}g(x) dx<1$. The above assumptions ensure that y ∈ X = C⁰(Ω) ∩ C¹(Ω) ∩ C²(Ω₁ ∪ Ω₂) [16].

Eqs. (1)–(3) is equivalent to

$$ Ly(x)=F(x) $$

(4)

where

$$ Ly(x)=\left\{\right){\displaystyle \begin{array}{l}{L}_1y(x)=-\varepsilon {y}^{{\prime\prime} }(x)+a(x){y}^{\prime }(x)+b(x)y(x),\kern7em x\in {\varOmega}_1=\left(0,1\right)\\ {}{L}_2y(x)=-\varepsilon {y}^{{\prime\prime} }(x)+a(x){y}^{\prime }(x)+b(x)y(x)+c(x)y\left(x-1\right),\kern1.25em x\in {\varOmega}_2=\left(1,2\right)\end{array}} $$

(5)

$$ F(x)=\left\{\right){\displaystyle \begin{array}{l}f(x)-c(x)\phi \left(x-1\right),\kern1em x\in {\varOmega}_1\\ {}f(x),\kern6.5em x\in {\varOmega}_2\end{array}} $$

(6)

with boundary conditions

$$ {\displaystyle \begin{array}{l}y(x)=\phi (x),x\in \left[-1,0\right],\\ {}y\left({1}^{-}\right)=y\left({1}^{+}\right),\kern0.5em {y}^{\prime}\left({1}^{-}\right)={y}^{\prime}\left({1}^{+}\right),\\ {} Ky(2)=y(2)-\varepsilon \underset{0}{\overset{2}{\int }}g(x)y(x) dx=l,\end{array}}\left(\right\} $$

(7)

Properties of continuous solution

Lemma 1: (Maximum Principle) Let ψ(x) be any function in X such that ψ(0) ≥ 0, Kψ(2) ≥ 0, L₁ψ(x) ≥ 0, ∀ x ∈ Ω₁, L₂ψ(x) ≥ 0, ∀ x ∈ Ω₂ and [ψ^′](1) ≤ 0 then $\psi (x)\ge 0,\forall x\in \overline{\varOmega}$.

Proof: Define the test function

$$ s(x)=\left\{\right){\displaystyle \begin{array}{l}\frac{1}{8}+\frac{x}{2},\kern0.5em x\in \left[0,1\right]\\ {}\frac{3}{8}+\frac{x}{4},\kern0.5em x\in \left[1,2\right]\end{array}} $$

(8)

Note that $s(x)>0,\forall x\in \overline{\varOmega}, Ls(x)>0,\forall x\in {\varOmega}_1\cup {\varOmega}_2,s(0)>0, Ks(2)>0$, and [s^′](1) < 0.

Let $\mu =\max \left\{\frac{-\psi (x)}{s(x)}:x\in \overline{\varOmega}\right\}$. Then, there exists ${x}_0\in \overline{\varOmega}$ such that ψ(x₀) + μs(x₀) = 0 and $\psi (x)+\mu s(x)\ge 0,\forall x\in \overline{\varOmega}$. Therefore, the function (ψ + μs) attains its minimum at x = x₀. Suppose the theorem does not hold true, then μ > 0.

Case (i):x₀ = 0; 0 < (ψ + μs)(0) = ψ(0) + μs(0) = 0, it is a contradiction.

Case (ii):x₀ ∈ Ω₁ 0 < L(ψ + μs)(x₀) =  − ε(ψ + μs)^″(x₀) + a(x₀)(ψ + μs)^′(x₀) + b(x₀)(ψ + μs)(x₀) ≤ 0, it is a contradiction.

Case (iii):x₀ = 1; 0 ≤ [(ψ + μs)^′](1) = [ψ^′](1) + μ[s^′](1) < 0, it is a contradiction.

Case (iv):x₀ ∈ Ω₂

${\displaystyle \begin{array}{l}0<L\left(\psi +\mu s\right)\left({x}_0\right)=-\varepsilon {\left(\psi +\mu s\right)}^{{\prime\prime}}\left({x}_0\right)+a\left({x}_0\right){\left(\psi +\mu s\right)}^{\prime}\left({x}_0\right)+b\left({x}_0\right)\left(\psi +\mu s\right)\left({x}_0\right)\\ {}\kern7.75em +c\left({x}_0\right)\left(\psi +\mu s\right)\left({x}_0-1\right)\le 0,\mathrm{it}\ \mathrm{is}\ \mathrm{a}\ \mathrm{contradiction}.\end{array}}$

Case (v):x₀ = 2; $0\le K\left(\psi +\mu s\right)(2)=\left(\psi +\mu s\right)(2)-\varepsilon \underset{0}{\overset{2}{\int }}g(x)\left(\psi +\mu s\right)(x) dx\le 0,\mathrm{it}\ \mathrm{is}\ \mathrm{a}\ \mathrm{contradiction}.$

Hence, the proof of the theorem.

Lemma 2: (Stability Result) The solution y(x) for the problems (1)–(3) satisfies the bound

$$ \left|y(x)\right|\le C\max \left\{\left|y(0)\right|,\left| Ky(2)\right|,\underset{x\in {\Omega}^{\ast }}{\sup}\left| Ly(x)\right|\right\},x\in \overline{\Omega} $$

Proof: This theorem can be proved by using Lemma 1, and the barrier functions ${\theta}^{\pm }(x)= CMs(x)\pm y(x),x\in \overline{\varOmega}$, where $M=\max \left\{\left|y(0)\right|,\left| Ky(2)\right|,\underset{x\in {\Omega}^{\ast }}{\sup}\left| Ly(x)\right|\right\}$ and s(x) are the test function as in Lemma 1.

Lemma 3: Let y(x) be the solution for (1)–(3). Then we have the following bounds:

$$ {\left\Vert {y}^{(k)}(x)\right\Vert}_{\varOmega^{\ast }}\le C{\varepsilon}^{-k},\mathrm{for}\ k=1,2,3. $$

Proof: For the proof, refer to [16].

Lemma 4: The bound for derivative of the solution y(x) of the problems (1)–(3) when x ∈ Ω₁ = (0, 1) is given by:

$$ \mid {y}^{(k)}(x)\mid \le C\left(1+{\varepsilon}^{-k}\exp \left(\frac{-\alpha \left(1-{x}_j\right)}{\varepsilon}\right)\right),\kern0.5em k=0\le k\le 4,\kern0.5em j=1,2,...,N-1. $$

Proof: For the proof, refer to [17].

Formulation of the numerical scheme

For small values of ε, the boundary value problem, (1)–(3) exhibit strong boundary layer at x = 2 and interior layer at x = 1 (see [16]).

The linear ordinary differential Eq. (1) cannot, in general, be solved analytically because of the dependence of a(x), b(x), and c(x) on the spatial coordinate x. We divide the interval [0, 2] into 2N equal parts with constant mesh length h. Let 0 = x₀, x₂, ..., x_N = 1, x_N + 1, x_N + 2, ..., x_2N = 2 be the mesh points. Then, we have x_i = ih, i = 0, 1, 2, ...2N. If we consider, the interval x ∈ (0, 1) and the coefficients of (1) are evaluated at the midpoint of each interval; then, we will obtain the differential equation:

$$ \left\{\right){\displaystyle \begin{array}{l}-\varepsilon {y}^{{\prime\prime} }(x)+a(x){y}^{\prime }(x)+b(x)y(x)=f(x)-c(x)\phi \left(x-1\right),\kern0.5em x\in {\varOmega}_1=\left(0,1\right)\\ {}{y}_0=y(0)=\phi (0)\end{array}} $$

(9)

Now, the domain [0, 1] is discretized into N equal number of subintervals, each of length h. Let 0 = x₀ < x₁ < ... < x_N = 1 be the points such that x_i = ih, i = 0, 1, 2, ..., N. For the discretization, we apply a exponentially fitted operator finite difference method (FOFDM).

From (9), we have

$$ -\varepsilon {y}^{{\prime\prime} }(x)+a(x){y}^{\prime }(x)+b(x)y(x)=F(x),\kern0.5em x\in {\varOmega}_1=\left(0,1\right) $$

(10)

where F(x) = f(x) − c(x)ϕ(x − 1).

To find the numerical solution of (10), we use the theory applied in asymptotic method for solving singularly perturbed BVPs. In the considered case, the boundary layer is in the right side of the domain, i.e., near x = 1. From the theory of singular perturbations given by O’Malley [18] and using Taylor’s series expansion for a(x) about x = 1 and restriction to their first terms, we get the asymptotic solution as follows:

$$ y(x)={y}_0(x)+\left(\theta -{y}_0(1)\right)\exp \left(-\frac{a(1)\left(1-x\right)}{\varepsilon}\right),\kern0.75em $$

(11)

where y₀(x) is the solution of the reduced problem (obtained by setting ε = 0) of (10) which is given by:

a(x)y^′(x) + b(x)y(x) = F(x) with y₀(0) = ϕ(0).(12)

Considering h is small enough, the discretized form for (11) becomes

$$ y(ih)={y}_0(ih)+\left(\theta -{y}_0(1)\right)\exp \left(-\frac{a(1)\left(1- ih\right)}{\varepsilon}\right), $$

which is simplified to

$$ y(ih)={y}_0(ih)+\left(\theta -{y}_0(1)\right)\exp \left(-a(1)\left(\frac{1}{\varepsilon }- i\rho \right)\right), $$

(13)

where $\rho =\frac{h}{\varepsilon },h=\frac{1}{N}$.

To handle the effect of the perturbation parameter, artificial viscosity (an exponentially fitting factor σ(ρ)) is multiplied on the term containing the perturbation parameter as follows:

$$ -\varepsilon \sigma \left(\rho \right){y}^{{\prime\prime} }(x)+a(x){y}^{\prime }(x)+b(x)y(x)=F(x),\kern11.5em $$

(14)

with boundary conditions y₀(0) = ϕ(0)  and  y(N) = θ, where y(N) is evaluated by Runge-Kutta method from the reduced solution of (12).

Next, we consider the difference approximation of (9) on a uniform grid ${\overline{\varOmega}}^N={\left\{{x}_i\right\}}_{i=0}^N$ and denote h = x_i + 1 − x_i.

For any mesh function z_i, define the following difference operators:

$$ {D}^{+}{z}_i=\frac{z_{i+1}-{z}_i}{h},\kern0.5em {D}^{-}{z}_i=\frac{z_i-{z}_{i-1}}{h},\kern0.5em {D}^0{z}_i=\frac{z_{i+1}-{z}_{i-1}}{2h},\kern0.5em {D}^{+}{D}^{-}{z}_i=\frac{z_{i+1}-2{z}_i+{z}_{i-1}}{h^2}, $$

(15)

by applying the central finite difference scheme on (14) takes the form:

$$ -\varepsilon \sigma \left(\rho \right)\left({D}^{+}{D}^{-}y\left({x}_i\right)\right)+a\left({x}_i\right)\left({D}^0y\left({x}_i\right)\right)+b\left({x}_i\right)y\left({x}_i\right)=F\left({x}_i\right),\kern1.25em $$

(16)

with the boundary conditions y₀(0) = ϕ(0)  and  y(N) = θ.

Using operator, (10) is rewritten as follows:

$$ {L}^h{y}_i={F}_i $$

(17)

with the boundary conditions y₀ = ϕ(0)  and  y_N = θ.

where

$$ {L}^h{y}_i=-\varepsilon \sigma \left(\rho \right)\left(\frac{y_{i+1}-2{y}_i+{y}_{i-1}}{h^2}\right)+a\left({x}_i\right)\left(\frac{y_{i+1}-{y}_{i-1}}{2h}\right)+b\left({x}_i\right){y}_i={F}_i,\kern0.5em $$

(18)

multiplying (18) by h and considering h is small and truncating the term h(F_i − , result

$$ \frac{\sigma \left(\rho \right)}{\rho}\left({y}_{i-1}-2{y}_i+{y}_{i+1}\right)+\frac{a\left({x}_i\right)}{2}\left({y}_{i-1}-{y}_{i+1}\right)=0.\kern8.5em $$

(19)

Now, by using Taylor’s series for y_i − 1 and y_i + 1 up to first term and substituting the results in (19) into (16) and simplifying, the exponential fitting factor is obtained as follows:

$$ \sigma \left(\rho \right)=\frac{\rho a(1)}{2}\coth \left(\frac{\rho a(1)}{2}\right).\kern15.75em $$

(20)

Assume that ${\overline{\varOmega}}^{2N}$ denotes partition of [0, 2] into 2N subintervals such that 0 = x₀ < x₁ < ... < x_N = 1 and 1 < x_N + 1 < x_N + 2 < ... < x_2N = 2 with ${x}_i= ih,h=\frac{2}{2N}=\frac{1}{N},i=0,1,2,....,2N$.

Case 1: Consider (4) on the domain Ω₁ = (0, 1) which is given by:

$$ -\varepsilon {y}^{{\prime\prime} }(x)+a(x){y}^{\prime }(x)+b(x)y(x)=f(x)-c(x)\phi \left(x-1\right) $$

(21)

Hence, the required finite difference scheme becomes

$$ \left(\frac{-\varepsilon \sigma \left(\rho \right)}{h^2}-\frac{a\left({x}_i\right)}{2h}\right){y}_{i-1}+\left(\frac{2\varepsilon \sigma \left(\rho \right)}{h^2}+b\left({x}_i\right)\right){y}_i+\left(\frac{-\varepsilon \sigma \left(\rho \right)}{h^2}+\frac{a\left({x}_i\right)}{2h}\right){y}_{i+1}={f}_i-{c}_i\phi \left({x}_i-N\right) $$

(22)

for i = 0, 1, 2, ..., N.

The numerical scheme in (22) can be written in three-term recurrence relation as follows:

$$ {E}_i{y}_{i-1}+{F}_i{y}_i+{G}_i{y}_{i+1}={H}_i,\kern0.96em i=1,2,...,N, $$

(23)

where ${E}_i=\frac{-\varepsilon \sigma}{h^2}-\frac{a_i}{2h},\kern0.5em {F}_i=\frac{2\varepsilon \sigma}{h^2}+{b}_i,\kern0.5em {G}_i=\frac{-\varepsilon \sigma}{h^2}+\frac{a_i}{2h},\kern0.5em {H}_i={f}_i-{c}_i\phi \left({x}_i-N\right)$.

Case 2: Consider (4) on the domain Ω₂ = (1, 2), for right layer in the domain Ω₂ using exponentially fitted finite difference method, which is given by:

$$ -\varepsilon \sigma \left(\rho \right)\left(\frac{y_{i+1}-2{y}_i+{y}_{i-1}}{h^2}\right)+{a}_i\left(\frac{y_{i+1}-{y}_{i-1}}{2h}\right)+{b}_i{y}_i+{c}_iy\left({x}_i-1\right)+{\tau}_1={f}_i. $$

Similarly, this equation can be written as follows:

$$ {c}_i{y}_j+{E}_i{y}_{i-1}+{F}_i{y}_i+{G}_i{y}_{i+1}={H}_i,\kern0.96em i=N+1,N+2,...,2N-1, $$

(24)

$$ \mathrm{where}{y}_j=y\left({x}_i-1\right),\kern0.72em j=1,2,...,N $$

$$ {E}_i=\frac{-\varepsilon \sigma}{h^2}-\frac{a_i}{2h},\kern0.5em {F}_i=\frac{2\varepsilon \sigma}{h^2}+{b}_i,\kern0.5em {G}_i=\frac{-\varepsilon \sigma}{h^2}+\frac{a_i}{2h},\kern0.5em {H}_i={f}_i. $$

Case 3: For i = 2N, the composite Simpson’s rule approximates the integral of g(x)y(x) by:

$$ \underset{0}{\overset{2}{\int }}g(x)y(x) dx=\frac{h}{3}\left(g(0)y(0)+g(2)y(2)+2\sum \limits_{i=1}^{2N-1}g\left({x}_{2i}\right)y\left({x}_{2i}\right)+4\sum \limits_{i=1}^{2N}g\left({x}_{2i-1}\right)y\left({x}_{2i-1}\right)\right).\kern4.25em $$

(25)

Substituting (25) into (3) gives:

$$ y(2)-\frac{\varepsilon h}{3}\left(g(0)y(0)+g(2)y(2)+2\sum \limits_{i=1}^{2N-1}g\left({x}_{2i}\right)y\left({x}_{2i}\right)+4\sum \limits_{i=1}^{2N}g\left({x}_{2i-1}\right)y\left({x}_{2i-1}\right)\right)=L $$

Since y(0) = ϕ(0), from (2), this equation can be re-written as follows:

$$ -\frac{4\varepsilon h}{3}\sum \limits_{i=1}^{2N}g\left({x}_{2i-1}\right)y\left({x}_{2i-1}\right)-\frac{2\varepsilon h}{3}\sum \limits_{i=1}^{2N-1}g\left({x}_{2i}\right)y\left({x}_{2i}\right)+\left(1-\frac{\varepsilon h}{3}g(2)\right)\;y(2)=L+\frac{\varepsilon h}{3}g(0)y(0).\kern2.75em $$

(26)

Therefore, on the whole domain $\overline{\varOmega}=\left[0,2\right]$, the basic schemes to solve (1)–(3) are the schemes given in (23), (24), and (26) together with the local truncation error of τ₁.

Convergence analysis

The discrete scheme corresponding to the original problem (1)–(3) is as follows:

$$ \mathrm{For}\;i=1,2,...,N-1,\kern0.6em {L}_1^N{Y}_i={f}_i-{b}_i{\phi}_{i-N,} $$

(27)

$$ \mathrm{For}\;i=N+1,...,2N-1,\kern0.6em {L}_2^N{Y}_i={f}_i, $$

(28)

subject to the boundary conditions is as follows:

$$ {Y}_i={\phi}_i,i=-N,-N+1,...,0,\kern3.25em $$

(29)

$$ {K}^N{Y}_{2N}={Y}_{2N}-\sum \limits_{i=1}^{2N}\frac{g_{i-1}{Y}_{i-1}+4{g}_i{Y}_i+{g}_{i+1}{Y}_{i+1}}{3}{h}_i,\kern1.25em $$

(30)

and

$$ {D}^{-}{Y}_N={D}^{+}{Y}_N, $$

where

$$ {\displaystyle \begin{array}{l}{L}_1^N{Y}_i=-\varepsilon {\delta}^2Y\left({x}_i\right)+a\left({x}_i\right){D}^0Y\left({x}_i\right)+b\left({x}_i\right)Y\left({x}_i\right)\\ {}{L}_2^N{Y}_i=-\varepsilon {\delta}^2Y\left({x}_i\right)+a\left({x}_i\right){D}^0Y\left({x}_i\right)+b\left({x}_i\right)Y\left({x}_i\right)+c\left({x}_i\right)Y\left({x}_{i-N}\right)\end{array}}. $$

Lemma 5: (Discrete Maximum Principle) Assume that

$$ \sum \limits_{i=1}^{2N}\frac{g_{i-1}+4{g}_i+{g}_{i+1}}{3}{h}_i=\rho <1 $$

and mesh function ψ(x_i) satisfy ψ(x₀) ≥ 0 and K^Nψ(x_2N) ≥ 0. Then, ${L}_1^N\psi \left({x}_i\right)\ge 0,\forall {x}_i\in {\varOmega}_1^{2N},{L}_2^N\psi \left({x}_i\right)\ge 0,\forall {x}_i\in {\varOmega}_2^{2N}$ and D⁺(ψ(x_N)) − D⁻(ψ(x_N)) ≤ 0 imply that $\psi \left({x}_i\right)\ge 0,\forall {x}_i\in {\overline{\varOmega}}^{2N}$.

Proof: Define

$$ s\left({x}_i\right)=\Big\{{\displaystyle \begin{array}{l}\frac{1}{8}+\frac{x_i}{2},\kern0.5em {x}_i\in \left[0,1\right]\cap {\overline{\varOmega}}^{2N},\\ {}\frac{3}{8}+\frac{x_i}{4},\kern0.5em {x}_i\in \left[1,2\right]\cap {\overline{\varOmega}}^{2N},\end{array}} $$

Note that $s\left({x}_i\right)>0,\forall {x}_i\in {\overline{\varOmega}}^{2N}, Ls\left({x}_i\right)>0,\forall {x}_i\in {\varOmega}_1^{2N}\cup {\varOmega}_2^{2N},s(0)>0, Ks\left({x}_{2N}\right)>0$, and[s^′](x_N) < 0.

Let $\mu =\max \left\{\frac{-\psi \left({x}_i\right)}{s\left({x}_i\right)}:{x}_i\in {\overline{\varOmega}}^{2N}\right\}$. Then, there exists ${x}_k\in {\overline{\varOmega}}^{2N}$ such that ψ(x_k) + μs(x_k) = 0 and $\psi \left({x}_i\right)+\mu s\left({x}_i\right)\ge 0,\forall {x}_i\in {\overline{\varOmega}}^{2N}$. Therefore, the function (ψ + μs) attains its minimum at x = x_k. Suppose the theorem does not hold true, then, μ > 0.

Case (i):x_k = x₀, 0 < (ψ + μs)(x₀) = 0, it is a contradiction.

Case (ii):${x}_k\in {\varOmega}_1^{2N}$, $0<{L}_1^N\left(\psi +\mu s\right)\left({x}_k\right)\le 0$, it is a contradiction.

Case (iii):x_k = x_N, 0 ≤ [D(ψ + μs)^′](x_N) < 0, it is a contradiction.

Case (iv):${x}_k\in {\varOmega}_2^{2N}$, $0<{L}_2^N\left(\psi +\mu s\right)\left({x}_k\right)\le 0$, it is a contradiction.

Case (v):x_k = x_2N

$$ 0<{K}^N\left(\psi +\mu s\right){x}_{2N}=\left(\psi +\mu s\right){x}_{2N}-\sum \limits_{i=1}^{2N}\frac{g_{i-1}\left(\psi +\mu s\right){x}_{i-1}+4{g}_i\left(\psi +\mu s\right){x}_i+{g}_{i+1}\left(\psi +\mu s\right){x}_{i+1}}{3}{h}_i\le 0 $$

It is a contradiction. Hence the proof of the theorem.

Lemma 6: Let ψ(x_i) be any mesh function then for 0 ≤ i ≤ 2N,

$$ \left|\psi \left({x}_i\right)\right|\le C\max \left\{\left|\psi \left({x}_o\right)\right|,\left|{K}^N\psi \left({x}_{2N}\right)\right|,\underset{i\in {\Omega}_1^{2N}\cup {\Omega}_2^{2N}}{\max}\left|{L}^N\psi \left({x}_i\right)\right|\right\}. $$

Proof: For the proof, refer to [16].

The following theorem shows the parameter uniform convergence of the scheme developed.

Theorem 1:

Let y(x_i) and y_i be respectively the exact solution of (1)–(3) and numerical solutions of (17). Then, for sufficiently large N, the following parameter uniform error estimate holds:

$$ \underset{0<\varepsilon \le 1}{\sup}\left\Vert y\left({x}_i\right)-{y}_i\right\Vert \le C{N}^{-2} $$

(32)

Proof: Let us consider the local truncation error defined as follows:

$$ {L}^h\left(y\left({x}_i\right)-{y}_i\right)=-\varepsilon \sigma \left(\rho \right)\left(\frac{d^2}{d{x}^2}-{D}^{+}{D}^{-}\right)y\left({x}_i\right)+a\left({x}_i\right)\left(\frac{d}{dx}-{D}^0\right)y\left({x}_i\right),\kern4.25em $$

(33)

where $\varepsilon \sigma \left(\rho \right)=a(1)\frac{N^{-1}}{2}\coth \left(a(1)\frac{N^{-1}}{2\varepsilon}\right)$ since $\rho =\frac{N^{-1}}{\varepsilon }$. In our assumption, ε ≤ h = N⁻¹.

By considering N is fixed and taking the limit for ε → 0, we obtain the following:

$$ \underset{\varepsilon \to 0}{\lim}\varepsilon \sigma \left(\rho \right)=\underset{\varepsilon \to 0}{\lim }a(1)\frac{N^{-1}}{2}\coth \left(a(1)\frac{N^{-1}}{2\varepsilon}\right)=C{N}^{-1}. $$

From Taylor’s series expansion, the bound for the difference becomes:

$$ \Big\{{\displaystyle \begin{array}{l}\left\Vert \left(\frac{d^2}{d{x}^2}-{D}^{+}{D}^{-}\right)y\left({x}_i\right)\right\Vert \le C{N}^{-3}\left\Vert \frac{d^4\left(y\left({x}_i\right)\right)}{d{x}^4}\right\Vert \\ {}\left\Vert \left(\frac{d}{dx}-{D}^0\right)y\left({x}_i\right)\right\Vert \le C{N}^{-2}\left\Vert \frac{d^3\left(y\left({x}_i\right)\right)}{d{x}^3}\right\Vert \end{array}}, $$

where $\left\Vert \frac{d^k\left(y\left({x}_i\right)\right)}{d{x}^k}\right\Vert =\underset{x_i\in \left({x}_0,{x}_N\right)}{\sup}\left(\frac{d^ky\left({x}_i\right)}{d{x}^k}\right),k=3,4$.

Now, using the bounds and the assumption ε ≤ N⁻¹, (33) reduces to:

$$ {\displaystyle \begin{array}{l}\left\Vert {L}^h\left(y\left({x}_i\right)-{y}_i\right)\right\Vert =\left\Vert -\varepsilon \sigma \left(\rho \right)\left(\frac{d^2}{d{x}^2}-{D}^{+}{D}^{-}\right)y\left({x}_i\right)+a\left({x}_i\right)\left(\frac{d}{dx}-{D}^0\right)y\left({x}_i\right)\right\Vert \\ {}\kern6em \le \left\Vert -\varepsilon \sigma \left(\rho \right)\left(\frac{d^2}{d{x}^2}-{D}^{+}{D}^{-}\right)y\left({x}_i\right)\right\Vert +\left\Vert a\left({x}_i\right)\left(\frac{d}{dx}-{D}^0\right)y\left({x}_i\right)\right\Vert \\ {}\kern6.25em \le C{N}^{-3}\left\Vert \frac{d^4\left(y\left({x}_i\right)\right)}{d{x}^4}\right\Vert +C{N}^{-2}\left\Vert \frac{d^3\left(y\left({x}_i\right)\right)}{d{x}^3}\right\Vert \end{array}}. $$

(34)

Here, the target is to show the scheme convergence independent on the number of mesh points.

By using the bounds for the derivatives of the solution in Lemma 4, we obtain:

$$ {\displaystyle \begin{array}{l}\left\Vert {L}^h\left(y\left({x}_i\right)-{y}_i\right)\right\Vert \le C{N}^{-3}\left\Vert \frac{d^4\left(y\left({x}_i\right)\right)}{d{x}^4}\right\Vert +C{N}^{-2}\left\Vert \frac{d^3\left(y\left({x}_i\right)\right)}{d{x}^3}\right\Vert \\ {}\kern6em \le C{N}^{-3}\left(1+{\varepsilon}^{-4}\exp \left(\frac{-\alpha \left(1-{x}_j\right)}{\varepsilon}\right)\right)+C{N}^{-2}\left(1+{\varepsilon}^{-3}\exp \left(\frac{-\alpha \left(1-{x}_j\right)}{\varepsilon}\right)\right)\\ {}\kern6em \le C{N}^{-2}\left(1+{\varepsilon}^{-4}\exp \left(\frac{-\alpha \left(1-{x}_j\right)}{\varepsilon}\right)\right),\kern0.5em \mathrm{since}\kern0.5em {\varepsilon}^{-4}\ge {\varepsilon}^{-3}\end{array}}. $$

(35)

Lemma 7: For a fixed mesh and for ε → 0, it holds:

$$ \underset{\varepsilon \to 0}{\lim}\underset{1\le j\le N-1}{\max}\frac{\exp \left(\frac{-\alpha \left(1-{x}_j\right)}{\varepsilon}\right)}{\varepsilon^m}=0,\kern0.5em m=1,2,3,... $$

(36)

Proof: Refer to [19].

By using Lemma 7 into (35), results to

$$ \left\Vert {L}^h\left(y\left({x}_i\right)-{y}_i\right)\right\Vert \le C{N}^{-2} $$

(37)

Hence, by discrete maximum principle, we obtain:

$$ \left\Vert y\left({x}_i\right)-{y}_i\right\Vert \le C{N}^{-2}.\kern13em $$

(38)

Thus, result of (38) shows (32). Hence, the proof.

Remark: A similar analysis for convergence may be carried out for the finite difference scheme (24).

Richardson Extrapolation

This technique is acceleration technique which involves combination of two computed approximations of a solution. The combination goes out to be an improved approximation. From the local truncation term, we have:

$$ \mid y\left({x}_i\right)-{y}_i\mid \le C(h) $$

(39)

where y(x_i)  and  y_i are exact and approximate solutions respectively, and C is constant free from mesh size h.

Let Ω^4N be the mesh found by dividing each mesh interval in Ω^2N and symbolize the calculation of the solution on Ω^4N by ${\overline{y}}_i$. Consider (39) works for any h ≠ 0, which implies:

$$ y\left({x}_i\right)-{y}_i\le C(h)+{R}^{2N},\kern0.84em {x}_i\in {\varOmega}^{2N} $$

(40)

So that it works for any $\frac{h}{2}\ne 0$ yields:

$$ y\left({x}_i\right)-{\overline{y}}_i\le C\left(\frac{h}{2}\right)+{R}^{4N},\kern0.84em {x}_i\in {\varOmega}^{4N} $$

(41)

where the remainders R^2N and R^4N are O(h²). Combination of inequalities in (40) and (41) leads to $y\left({x}_i\right)-\left(2{\overline{y}}_i-{y}_i\right)\approx O\left({h}^2\right)$ which proposes that

$$ {\left({y}_i\right)}^{ext}=2{\overline{y}}_i-{y}_i $$

(42)

is also a rough calculation of y(x_i). By means of this approximation to estimate the truncation error, we obtain:

$$ \mid y\left({x}_i\right)-{\left({y}_i\right)}^{ext}\mid \le C\left({h}^2\right) $$

(43)

where C is free of mesh size h. Thus, using Richardson extrapolation first order convergent method is accelerated into second order convergent as provided in (43). Thus, we can say that the proposed method is second order convergent.

Numerical examples and results

In this section, two examples are considered to illustrate the applicability of the numerical method discussed above. The exact solutions of these test problems are not known. Therefore, double mesh principle is used to estimate the errors and compute the numerical rate of convergence to the computed solution. The double mesh formula to determine maximum absolute error is defined as follows:

$$ {E}_{\varepsilon}^h=\underset{0\le i\le 2N}{\max}\mid {Y}_i^N-{Y}_{2i}^{2N}\mid $$

where ${Y}_i^N$ and ${Y}_{2i}^{2N}$ are the i^th components of the numerical solutions for N and 2N, respectively. We compute the uniform error and the rate of convergence using the formula:

$$ {E}^h=\underset{\varepsilon }{\max }{E}_{\varepsilon}^h\;\mathrm{and}\;{R}^h={\log}_2\left(\frac{E^N}{E^{2N}}\right) $$

The numerical results are presented for the values of the perturbation parameter ε ∈ {10⁻⁴, 10⁻⁸, ..., 10⁻²⁰}.

Example 1:

$$ {\displaystyle \begin{array}{l}-\varepsilon {y}^{{\prime\prime} }(x)+3{y}^{\prime }(x)+y(x)-y\left(x-1\right)=1,\kern0.72em x\in \left(0,1\right)\cup \left(1,2\right)\\ {}\kern0.48em y(x)=1,\kern0.72em x\in \left[-1,0\right]\\ {}\kern0.48em y(2)-\varepsilon \underset{0}{\overset{2}{\int }}\frac{x}{3}y(x) dx=2\end{array}} $$

Example 2:

$$ {\displaystyle \begin{array}{l}-\varepsilon {y}^{{\prime\prime} }(x)+5{y}^{\prime }(x)+\left(x+1\right)y(x)-y\left(x-1\right)={x}^2,\kern0.72em x\in \left(0,1\right)\cup \left(1,2\right)\\ {}\kern0.48em y(x)=1,\kern0.72em x\in \left[-1,0\right]\\ {}\kern0.48em y(2)-\varepsilon \underset{0}{\overset{2}{\int }}\frac{x}{3}y(x) dx=2\end{array}} $$

Discussion and conclusion

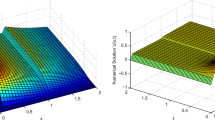
This study introduces accelerated fitted operator numerical method for solving singularly perturbed delay differential equations with integral boundary condition. The behavior of the continuous solution of the problem is studied and shown that it satisfies the continuous stability estimate, and the derivatives of the solution are also bounded. The numerical scheme is developed on uniform mesh using fitted operator finite difference method in the given differential equation. The integral boundary condition is treated by using Simpson’s rule. The stability of the developed numerical method is established, and its uniform convergence is proved. To validate the applicability of the method, two model problems are considered for numerical experimentation for different values of the perturbation parameter and mesh points. The numerical results are tabulated in terms of maximum absolute errors, numerical rate of convergence, and uniform errors (see Tables 1, 2, 3 and 4). Further, Figs. 1 and 2 show that for small values of ε, the solution of the problem under consideration exhibits strong boundary layer at x = 2, and interior layer at x = 1. Figures 3 and 4 show that as the mesh size decrease or as the number of mesh point increase, the absolute error decreases. The log-log scale plot in Figs. 5 and 6 depicted the ε-uniformly convergence of the method for h ≥ ε where the classical numerical methods fail to converge. The method is shown to be ε-uniformly convergent with order of convergence O(h²). The performance of the proposed scheme is investigated by comparing with prior study (Tables 2 and 4). The proposed method is stable, more accurate, and convergent independent of the values of the perturbation parameter and the mesh size. The authors suggested that one can extend the work or solve the problem under consideration by applying higher order fitted operator numerical methods or Bakhavlov-type fitted mesh numerical method to obtain more accurate numerical results.

Table 1 Maximum absolute errors for Example 1 at number of mesh points 2N

Table 2 Comparison of maximum absolute errors for Example 1 at number of mesh points 2N

Table 3 Maximum absolute errors for Example 2 at number of mesh points 2N

Table 4 Comparison of maximum absolute errors for Example 2 at number of mesh points 2N

Fig. 1

The behavior of the numerical solution for Example 1 at ε = 10⁻¹² and N = 32

Fig. 2

The behavior of the numerical solution for Example 2 at ε = 10⁻¹² and N = 32

Fig. 3

Point wise absolute error of Example 1 at ε = 10⁻¹² with different mesh points N

Fig. 4

Point wise absolute error of Example 2 at ε = 10⁻¹² with different mesh points N

Fig. 5

ε-uniform convergence with fitted operator in log-log scale for Example 1

Fig. 6

ε-uniform convergence with fitted operator in log-log scale for Example 2