Generalization of soft topological groups

Abstract

There exists two different definitions for soft topological groups, the first due to Hida and the other due to Tariq Shah. In this paper, we give a generalization for both of them, and also, we study the topological properties for the construction of finer soft topology made by Nazmul and use the same technique to construct a soft topological group via Hida concept starting from a parametrized family of topological groups. Then, we introduce the concept of soft rough and rough soft topological group to generalize the concept of rough and soft topological group.

Introduction

In 2014, Hida [1] introduced a definition for the soft topological group as a soft topological structure on a crisp group under suitable conditions; otherwise, Tariq Shah [2] introduced the soft topological group as a soft set over a group, although both have the same title but they refer to different structures, while in 2013, Nazmul and Samanta [3] construct a soft topological space from a parametrized family of topological spaces but he did not study the properties for this structure and the relation between the parametrized topologies and the resulting one. In this paper, we introduce a generalization for the two different definitions of soft topological groups showing that each one of the two definitions is a special case of our definition, study the structure made by Nazmul and Samanta [3], and use the same technique to obtain a soft topological group via Hida [1]’s concept. Also, we introduce the soft rough and rough soft topological group showing the relation between the two definitions.

Preliminaries and notations

In this section, we list the main basic definitions we need in this paper, starting by the definition of ordinary topological group.

Definition 1

[4] Topological group is a group (G,∗) together with a topology on G satisfies:

• 1 The mapping f:G×G→G defined by f(x,y)=x∗y is continuous.

• 2 The inverse mapping i:G→G defined by i(x)=x⁻¹ is continuous.

Then, we need the basic definitions of soft set and soft topology.

Definition 2

[5] Let U be an initial universe and A be a set of parameters. Then, a soft set over U is a function F:A→P(U).

In what follows, we use tilde $\tilde {(.)}$ to distinguish “soft” objects from usual ones. For example, for a subset X of U, $\tilde {X}$ denotes the soft set satisfying that X(a)=X for all a∈A. The set of all soft sets over U is denoted by S(U).

Definition 3

[6] Let (F,A) and (F^′,A) be soft sets over U where A is a set of parameters. Then

• (Soft subset) F is a soft subset of F^′, denoted by $F \tilde \subset F'$, if F(a)⊂F^′(a) for all a∈A.

• (Soft equality) F is soft equal to F^′, denoted by $F \tilde = F'$, if both $F \tilde \subset F'$ and $F' \tilde \subset F$ hold.

• (Soft intersection) The soft intersection of F and F^′, denoted by $F \tilde \cap F'$, is defined by $(F \tilde \cap F')(a) = F (a) \cap F'(a)$ for every a∈A.

• (Soft union) The soft union of F and F^′, denoted by $F \tilde \cup F'$, is defined by $(F \tilde \cup F')(a) = F (a) \cup F '(a)$ for every a∈A.

• (Soft complement) The soft complement of F, denoted by $F^{\tilde {c}}$, is defined by $F^{\tilde {c}}(a) = U \setminus F (a)$ for every a∈A.

There are more than one definition for the soft point; we will depend on the following one.

Definition 4

[7] A soft set (F,A) is called a soft point in (X,A), denoted by x_e if:

$x_{e}(e') =\left \{ \begin {array}{ll} \{x\}, & e' = e;\\ \phi, & e' \not = e. \end {array} \right.$

Definition 5

([8,9]). A family τ of soft sets over U is called a soft topology on U if it satisfies:

• $\tilde \phi$ and $\tilde U \in \tau$,

• τ is closed under finite soft intersection,

• τ is closed under (arbitrary) soft union.

We refer to a triplet 〈U,τ,A〉 as a soft topological space. Each member of τ is called a soft open set.

Definition 6

[ 10 ]

• A soft topological space 〈X,τ,A〉 is said to be a soft T₀-space if for every two different soft points $\phantom {\dot {i}\!}x_{e}, y_{e'}$ there exists a soft set (G,A) such that $x_{e} \tilde \in G, y_{e'} \tilde {\not \in } G$ or $x_{e} \tilde {\not \in } G, y_{e'} \tilde \in G$.

• A soft topological space 〈X,τ,A〉 is said to be a soft T₁-space if for every two different soft points $\phantom {\dot {i}\!}x_{e}, y_{e'}$ there exists soft sets (G,A),(F,A) such that $x_{e} \tilde \in G, y_{e'} \tilde {\not \in } G$, and $x_{e} \tilde {\not \in } F, y_{e'} \tilde \in F$.

• A soft topological space 〈X,τ,A〉 is said to be a soft T₂-space if for every two different soft points $\phantom {\dot {i}\!}x_{e}, y_{e'}$ there exists soft sets (G,A),(F,A) such that $x_{e} \tilde \in G, y_{e'} \tilde {\not \in } G, x_{e} \tilde {\not \in } F, y_{e'} \tilde \in F$, and $(G,A) \tilde {\cap } (F,A) = \tilde \phi$.

Definition 7

[11] A soft topological space 〈X,τ,A〉 is called a soft connected space if (X,A) cannot be expressed as a soft union of two separated soft sets. Otherwise, it is called a soft disconnected space.

Definition 8

[12] A family Ψ of soft sets is a cover of a soft set (F,A) if $(F, A) \tilde \subseteq \cup \{(F_{i}, A) : (F_{i}, A) \in \Psi, i \in I \}$. It is a soft open cover if each member of Ψ is a soft open set. A subcover of Ψ is a subfamily of Ψ which is also a cover.

Definition 9

[12] A soft topological space 〈U,τ,A〉 is compact if each soft open cover of U has a finite subcover.

The first definition of the soft topological group is the following:

Definition 10

[1] Let G=(G,∗) be a group. We say that 〈G,τ,E〉 is a soft topological group if τ is a soft topology on G with a parameter set E and the following conditions are satisfied:

• 1. For every (g,h)∈G×G and a soft neighborhood F of g∗h∈G, there exist soft neighborhoods F_g and F_h of g and h, respectively, such that $F_{g} * F_{h} \tilde {\subset } F$.

• 2 The inversion function i:G→G, where i(x):x→x⁻¹,∀x∈G is soft continuous.

While the second definition is as follows:

Definition 11

[2] Let τ be a topology defined on a group (G,∗). Let (F,A) be a non-null soft set defined over G. Then, the triplet (F,A,τ) is called soft topological group over G if:

• 1 F(a) is a subgroup of G for all a∈A.

• 2 The mapping (x,y)→x∗y⁻¹ of the topological space F(a)×F(a) onto F(a) is continuous for all a∈A.

Finally, we will need the definitions of rough set, rough group, and topological rough groups.

Definition 12

[13] Let U be a finite non-empty set called universe and R be an equivalence relation on U. The pair (U,R) is called an approximation space, denoted by K=(U,R).

Definition 13

[13] Let K=(U,R) be an approximation space and X be a subset of U. The set $\overline {X} = \{x|[x]R \cap X \not = \phi \}$ is called upper approximation of X in K.

Definition 14

[14] Let K=(U,R) be an approximation space and ∗ be a binary operation defined on U. A subset G of U is called a rough group if:

• 1. $\forall x, y \in G, x* y \in \overline {G}$.

• 2. ∗ is associative over $\overline {G}$.

• 3. $\exists e \in \overline {G}$ such that ∀x∈G,x∗e=e∗x=x.

• 4. ∀x∈G,∃y∈G such that x∗y=y∗x=e.

Definition 15

[15] A topological rough group is a rough group (G,∗) together with a topology τ on $\overline G$ satisfying the following two properties:

• 1. The mapping $f : G \times G \rightarrow \overline G$ defined by f(x,y)=x∗y is continuous with respect to the product topology on G×G and the topology τ_G on G induced by τ.

• 2. The inverse mapping g:G→G defined by g(x)=x⁻¹ is continuous with respect to the topology τ_G on G induced by τ.

Generalized soft topological group

The two different definitions of topological groups can be generalized in the following one.

Definition 16

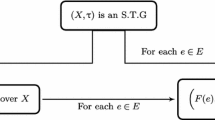
Let (G,∗) be a group, 〈G,τ,A〉 be a soft topology on G, and (F,E) be a non-null soft set defined on G, where A,E are two different sets of parameters. Then, 〈F,τ,A,E,∗〉 is called a generalized soft topological group over G if:

• 1. F(α) is a subgroup of G for all α∈E.

• 2. For every α∈E with the restricted soft topology τ|_F(α), for every (g,h)∈F(α)×F(α) and a soft neighborhood K of g∗h∈F(α), there exist soft neighborhoods K_g and K_h of g and h, respectively, such that $K_{g} * K_{h} \tilde {\subset } F(\alpha).$

• 3 For every α∈E with the restricted soft topology τ|_F(α), the inversion function i_α:F(α)→F(α) is soft continuous.

The following remark shows that the two definitions of topological group are a special case of ours.

Remark 1

• 1. If $(F,E) \tilde {=} \tilde {G}$, then 〈F,τ,A,E,∗〉 is a soft topological group via Hida’s concept.

• 2. If A contains one parameter, then 〈F,τ,A,E,∗〉 is a soft topological group via Tariq Shah’s concept.

Example 1

Let $G= (\mathbb {Z}_{4}, +_{4}), A=\{a_{1}, a_{2}\}, E = \{e_{1}, e_{2}\}, \tau =\{ \tilde \phi, \tilde {\mathbb {Z}_{4}}, \{(a_{1}, \{\bar 0, \bar 2\}), (a_{2}, \phi)\}, \{(a_{1}, \{\bar 1, \bar 3\}), (a_{2}, \mathbb {Z}_{4})\}\}$, and $(F,E)=\{ (e_{1},\{\bar 0, \bar 2\}), (e_{2}, \mathbb {Z}_{4})\}$.

Note that $\tau |_{F(e_{1})} = \{ \tilde \phi,\widetilde {\{\bar 0, \bar 2\}}, \{(a_{1}, \{\bar 0, \bar 2\}), (a_{2}, \phi)\}, \{(a_{1}, \phi), (a_{2},\{\bar 0, \bar 2\})\}\}$, and $\tau |_{F(e_{2})} =\tau$. Clearly, 〈F,τ,A,E,+₄〉 is a generalized soft topological group.

Definition 17

Let 〈F,τ,A,E,∗〉 be a generalized soft topological group over a group G and F^′ be a soft subset of F. Then, 〈F^′,τ,A,E,∗〉 is substructure of 〈F,τ,A,E,∗〉 if itself is a generalized soft topological group over G.

Example 2

Consider 〈F,τ,A,E,+₄〉 in Example 1, 〈F,τ,A,E,+₄〉,〈F,τ,{a₁},E,+₄〉, and $\langle \mathbb {Z}_{4}, \tau, A, E, +_{4}\rangle$ are a substructures of 〈F,τ,A,E,+₄〉.

Definition 18

Let (G,∗₁) and (H,∗₂) be two groups, and M⊂G,L⊂H such that 〈M,τ,A,E,∗₁〉 and 〈L,σ,A,E,∗₂〉 are two generalized soft topological groups over G,H, respectively. Then, F=(f₁,f₂) is called a morphism if:

• 1. f₁:〈G,τ,A〉→〈H,σ,A〉 is soft continuous.

• 2. f₂:(G,∗₁)→(H,∗₂) is a group homomorphism.

Theorem 1

The image of a generalized soft topological group under a morphism F is, also, a generalized soft topological group.

Proof

Let (G,∗₁) and (H,∗₂) be two groups, and M⊂G,L⊂H such that 〈M,τ,A,E,∗₁〉 and 〈L,σ,A,E,∗₂〉 are two generalized soft topological groups over G,H, respectively, and let F=(f₁,f₂) be a morphism. Then, F{〈M,τ,A,E,∗₁〉} is a generalized soft topological group. Since for all α∈E,f₂(F(α))≤H as f₂ is a group homomorphism, and the second and third conditions follow from the fact that the composition of two continuous functions is continuous. □

Definition 19

The generalized soft topological group 〈F,τ,A,E,∗〉 is said to be T_i generalized soft topological group if 〈G,τ,A〉 is a soft T_i topological space.

Theorem 2

Let (G,∗₁) and (H,∗₂) be two groups, and K⊂G,L⊂H such that 〈K,τ,A,E,∗₁〉 and 〈L,σ,A,E,∗₂〉 are two generalized soft topological groups over G,H. If 〈K,τ,A,E,∗₁〉 is a T_i generalized soft topological group, then F(〈K,τ,A,E,∗₁〉) is a T_i generalized soft topological group.

Proof

Straight forward from the definition. □

Theorem 3

For any generalized soft topological group 〈F,τ,A,E,∗〉, the following are equivalents:

• 1. 〈F,τ,A,E,∗〉 is T₀ generalized soft topological group.

• 2. 〈F,τ,A,E,∗〉 is T₁ generalized soft topological group.

• 3. 〈F,τ,A,E,∗〉 is T₂ generalized soft topological group.

Proof

Straight forward from the definition. □

New soft topological structure

The following proposition is introduced by Nazmul and Samanta [3], but the authors did not study the properties of their construction, so we study the relation between this construction and the crisp topologies.

Proposition 1

[3] Let 〈X,A,τ〉 be a soft topological space and τ^α be the topologies on X. Let τ^∗={(G,A)∈S(X):G(α)∈τ^α,∀α∈A}. Then, τ^∗ is a soft topology on X with [τ^∗]^α=τ^α,∀α∈A.

Corollary 1

Given a soft topological space 〈X,A,τ〉,τ^∗={(G,A)∈S(X):G(α)∈τ^α,∀α∈A} is the finest soft topological space containing 〈X,A,τ〉 and satisfying [τ^∗]^α=τ^α,∀α∈A.

Note that it is not necessary that the parametrized topologies come from a soft topological space; they may be any set of topological structures defined on the same universal set and assign a parameter to each one of them.

Theorem 4

Let X be a universal set. Given a collection $\mathscr {A}$, where $\mathscr {A}=\{\tau _{\alpha }, \alpha \in A\}$ and A is a set of parameters of topological spaces over X, and let τ^∗={(G,A)∈S(X):G(α)∈τ_α,∀α∈A}.

• 1. If τ_α is T_i topological space ∀α∈A, then τ^∗ is a soft T_i space for i=0,1,2.

• 2. If τ_α is compact topological space ∀α∈A, A is a finite set of parameters, then τ^∗ is a soft compact space.

• 3. If τ_α is disconnected topological space for some α∈A, then τ^∗ is a soft disconnected space.

Proof

• 1

  • For i=0, let $\phantom {\dot {i}\!}x_{\alpha }, y_{\alpha '} \in \tau ^{*}$ be two different soft points, where x,y∈X and α,α^′∈A. If α=α^′, then x≠y, ∃G∈τ_α such that x∈G,y∉G. Then, ∃(G,A)∈τ^∗such that

    $G(\alpha '')=\left \{ \begin {array}{ll} G, & \alpha '' = \alpha ;\\ \phi, & \alpha '' \not = \alpha. \end {array} \right.$

    Thus, x_α∈(G,A),y_α∉(G,A). Then, τ^∗ is a soft T₀ topological space.

    If α^″≠α, then ∃(G,A)∈τ^∗such that

    $G(\alpha '')=\left \{ \begin {array}{ll} X, & \alpha '' = \alpha ;\\ \phi, & \alpha '' \not = \alpha. \end {array} \right.$

    Thus, x_α∈(G,A),y_α∈(G,A). Then, τ^∗ is a soft T₀ topological space.

  • For i=1, let x_α∈τ^∗, where x∈X and α∈A.

    $x_{\alpha }^{c}(\alpha ')=\left \{ \begin {array}{ll} X -\{x\}, & \alpha ' = \alpha ;\\ X, & \alpha ' \not = \alpha. \end {array} \right.$

    $x_{\alpha }^{c}(\alpha ') \in \tau ^{*}.$ Then, the soft point x_α is closed ∀α∈A,∀x∈X. Thus, τ^∗ is a soft T₁ topological space.

  • For i=2, let $\phantom {\dot {i}\!}x_{\alpha }, y_{\alpha '} \in \tau ^{*}$ be two different soft points, where x,y∈X and α,α^′∈A. If α=α^′, then x≠y, ∃G,H∈τ_α such that x∈G,y∈H,G∩H=ϕ. Then, ∃(G,A),(H,A)∈τ^∗such that

    $G(\alpha '')=\left \{ \begin {array}{ll} G, & \alpha '' = \alpha ;\\ \phi, & \alpha '' \not = \alpha. \end {array} \right.$

    and $H(\alpha '')= \left \{\begin {array}{ll} H, & \alpha '' = \alpha ;\\ \phi, & \alpha '' \not = \alpha. \end {array} \right.$

    Thus, x_α∈(G,A),y_α∈(H,A), and $(G, A) \tilde \cap (H, A) =\phi.$ Then, τ^∗ is a soft T₂ topological space.

    If α≠α^′, then ∃(G,A),(H,A)∈τ^∗such that

    $G(\alpha '')=\left \{ \begin {array}{ll} X, & \alpha '' = \alpha ;\\ \phi, & \alpha '' \not = \alpha. \end {array} \right.$

    and $H(\alpha '')=\left \{ \begin {array}{ll} X, & \alpha '' = \alpha ';\\ \phi, & \alpha '' \not = \alpha '. \end {array} \right.$

    Thus, x_α∈(G,E),y_α∈(H,A), and $(G, A) \tilde \cap (H, A) =\phi.$ Then, τ^∗ is a soft T₂ topological space.

• 2. Let $\mathfrak {C}$ be a soft open cover for $\tilde X.$ Then, $\mathfrak {C}^{\alpha }$ is an open cover ∀α∈E, but τ^α is compact ∀α∈E, then there exists a finite open cover $(\mathfrak {C}^{\alpha })'$ for $\mathfrak {C}^{\alpha } \forall \alpha \in E$. Set $n = \text {max} |(\mathfrak {C}^{\alpha })'|$. Assume, without loss of generality, that $|(\mathfrak {C}^{\alpha })'| = n, \forall \alpha \in E.$ Then, there exists a finite open cover $\mathfrak {C}' = \{(C_{i}, E), i=1,2,..., n\}$, where C_i(α)=(C_i)^α,∀∈E.

• 3. Let $\tau _{\alpha _{1}}$ be disconnected, α₁∈A. Then, $\exists G_{\alpha _{1}}, H_{\alpha _{1}} \in \tau _{\alpha _{1}}$ such that $G_{\alpha _{1}} \cup H_{\alpha _{1}} = X$ and $G_{\alpha _{1}} \cap H_{\alpha _{1}} = \phi$. Set

  $G(\alpha)=\left \{ \begin {array}{ll} G_{\alpha _{1}}, & \alpha = \alpha _{1};\\ X, & \alpha \not = \alpha _{1}. \end {array} \right.$

  and $H(\alpha)=\left \{ \begin {array}{ll} H_{\alpha _{1}}, & \alpha = \alpha _{1};\\ \phi, & \alpha \not = \alpha _{1}. \end {array} \right.$

  Thus, $(G,A) \tilde \cup (H,A) = \tilde X$ and $(G,A) \tilde \cap (H,A) = \tilde \phi$, and τ^∗ is soft disconnected space.

Note that the set of parameters A, in Theorem 4, should be finite. □

Example 3

Let $X= \mathbb {N},\tau _{n} = \{\mathbb {N}, P(A_{n})\}$, where A_n is a set consisting of n elements. Each τ_n is a compact topological space because it consists of 2ⁿ+1 open sets, but $(\mathbb {N}, \tau ^{*}, \mathbb {N})$ is not a soft compact topological space.

Remark 2

Let (X,τ,A) be a soft topological space which is not T₂ soft topological space and for all α∈A,(X,τ^α) is a T₂ topological space. Then, (X,τ^∗,A) is a finer soft topological space of (X,τ,A) which is soft T₂ topological space.

Example 4

Consider $(\mathbb {Z}_{2}, \tau, A), A=\{ \alpha _{1}, \alpha _{2}\}$ and $\tau =\{ \tilde \phi, \{(\alpha _{1}, \{\bar {0}\}), (\alpha _{2},\{\bar {1}\})\},\\ \{(\alpha _{1}, \{\bar {1}\}), (\alpha _{2},\{\bar {0}\})\}, E \times \mathbb {Z}_{2} \}$. We have $\tau ^{\alpha _{1}}= \{\phi,\mathbb {Z}_{2}, \{\bar {0}\}, \{\bar {1}\} \} =\tau ^{\alpha _{2}}$ which is T₂ topological spaces.

Remark 3

Let (X,τ,A) be a soft connected topological space and for some α∈A,(X,τ^α) is a disconnected topological space. Then, (X,τ^∗,A) is a finer soft disconnected topological space of (X,τ,A).

Example 5

Consider $(\mathbb {Z}_{3}, \tau, A), A=\{ \alpha _{1}, \alpha _{2}\}$ and $\tau =\{\tilde \phi, \{(\alpha _{1}, \{\bar {0}\})\},\\ \{(\alpha _{1}, \{\bar {1}, \bar {2}\}), (\alpha _{2},\{\bar {0}, \bar {1}\})\}, E \times \mathbb {Z}_{3} \}$. We have $\tau ^{\alpha _{1}}= \{\phi,\mathbb {Z}_{3}, \{\bar {0}\}, \{\bar {1}, \bar {2}\} \}$ which is not a connected topological spaces and $\tau ^{\alpha _{2}}= \{\phi,\mathbb {Z}_{3}, \{\bar {0}, \bar {1}\} \}$, and we have $F_{1}=\{(\alpha _{1}, \{\bar {0}\}), (\alpha _{2}, \mathbb {Z}_{3})\}$ and $F_{2}=\{(\alpha _{1}, \{\bar {1}, \bar {2}\}), (\alpha _{2}, \phi \}$ which is a soft disconnection for τ^∗.

Now, we can use the same technique to construct a soft topological group via Hida’s concept starting from a parametrized family of topological groups. We shall not repeat the proof for the soft topology, and we will prove the algebraic condition.

Theorem 5

Let G be a group, given a collection $\mathscr {A}=\{\langle G,*,\tau _{\alpha } \rangle, \alpha \in A\}$, where A is a set of parameters, of topological groups over G and let τ^∗={(F,A)∈S(G):F(α)∈τ_α,∀α∈A}. Then, 〈G,∗,τ^∗〉 is a soft topological group via Hida [1] concept and [τ^∗]^α=τ^α,∀α∈A, where A is a parameter set.

Proof

Consider the soft topological space τ^∗ constructed in [3] Proposition 2.11. Let x,y∈G,(F,A) be soft open set such that $x y^{-1} \tilde \in F.$ Then, ∀α∈A,xy⁻¹∈F(α)∈τ^α. But τ^α is a topological group ∀α∈A, then ∃H^α,K^α such that x∈H^α,y∈K^αand xy⁻¹∈F(α). Set F_x(α)=H^α and F_y(α)=K^α, then F_x,F_y∈τ^∗. □

Remark 4

A soft topological group via Hida [1] concept may not generate a parametrized family of topological groups, as it was shown in the following example.

Example 6

[1] Let us consider the soft space $(\mathbb {Z}_{2}, \tau, E)$, with E={e₁,e₂} and τ is generated by $\{ \tilde \phi, \{(e_{1}, \{\bar {1}\})\},\{(e_{2},\{ \bar {0}\})\}, E \times \mathbb {Z}_{2}$}. Note that $\bar {0}$ and $\bar {1}$ have exactly one soft neighborhood, namely $E \times \mathbb {Z}_{2}$. It is then evident that, with the additive structure on $\mathbb {Z}_{2}$, the soft space$(\mathbb {Z}_{2}, \tau, E)$ is indeed a soft topological group. However, a trivial verification shows that neither $(\mathbb {Z}_{2}, \tau _{e_{1}})=(\mathbb {Z}_{2}, \{ \mathbb {Z}_{2}, \phi, \{\bar {1}\}\})$ nor $(\mathbb {Z}_{2},\tau _{e_{2}})=(\mathbb {Z}_{2}, \{ \mathbb {Z}_{2}, \phi, \{\bar {0}\}\})$ is a topological group.

Soft rough and rough soft topological group

Another generalization for soft topological group is putting it in the rough form and putting the topological rough group in the soft form. In this section, we introduce a definition for both showing the relation between them.

Definition 20

Let (U,R) be an approximation space, U^′⊂U,〈U,τ,A〉 be a soft topology on U where A is a set of parameters, and let ∗ be a binary operation defined on U. Then, 〈U^′,τ,R,∗,A〉 is called a soft rough topological group if (U^′,∗) is topological rough group with τ_α,∀α∈A. In other words, a soft rough topological group is a parametrized family of topological rough groups.

Example 7

We introduce two examples for soft rough topological group as follows:

• Let $U=\mathbb {Z}_{9}, U/R =\{E_{1}, E_{2}, E_{3}\}$, where $E_{1}= \{\bar {0}, \bar {1}, \bar {2}\}, E_{2} =\{\bar {3}, \bar {4}, \bar {5}\}, E_{3}= \{\bar {6}, \bar {7}, \bar {8}\}, A=\{a_{1}, a_{2}\}$, and let $\tau _{1} =\{ \tilde U,\tilde \phi, {\{(a_{1}, \{\bar {2}, \bar {4}, \bar {5},\bar {7}\}), (a_{2}, \{\bar {2},\bar {3},\bar {6},\bar {7}\})\}.}$ Then, 〈U^′,τ₂,R,∗,A〉 is a soft rough topological group.

• Let $U=\mathbb {Z}_{9}, U/R =\{E_{1}, E_{2}, E_{3}\}$, where $E_{1}= \{\bar {0}, \bar {1}, \bar {2}\}, E_{2} =\{\bar {3}, \bar {4}, \bar {5}\}, E_{3}= \{\bar {6}, \bar {7}, \bar {8}\}, A=\{a_{1}, a_{2}\}$, and let $\tau _{2} =\{ \tilde U,\tilde \phi, {\{(a_{2}, \{\bar {2}, \bar {4}, \bar {5},\bar {7}\}), (a_{1}, \{\bar {2},\bar {3},\bar {6},\bar {7}\})\}}$. Then, 〈U^′,τ₂,R,∗,A〉 is a soft rough topological group.

Remark 5

The intersection between two soft rough topological groups is not necessary a soft rough topological group.

Example 8

Consider the two examples above.

We have $\tau _{1} \cap \tau _{2} = \{\tilde U,\tilde \phi, \{(a_{1}, \{\bar {2},\bar {7}\}), (a_{2}, \{\bar {2},\bar {7}\})\} \}$ which is not a topological rough group for all a∈A since $\{\bar {2},\bar {7}\}$ is not a rough group because $\bar {2} * \bar {2} = \bar {4} \not \in \overline {H(a)} = E_{1} \cup E_{3}$.

Remark 6

Let 〈U^′,τ,R,∗,A〉 be a soft rough topological group. If A contains one element, then (U^′,∗) is isomorphic to a rough topological group.

Definition 21

Let 〈X,τ,A〉 be a soft topological space, (X,R) be an approximation space, and ∗ be a binary relation on X and G⊂X. We say that 〈G,τ,R,∗,A〉 is a rough soft topological group if the following conditions are satisfied:

• 1. For every (g,h)∈G×G and a soft neighborhood F of $g*h \in \overline G$, there exist soft neighborhoods F_g and F_h of g and h, respectively, such that $F_{g} * F_{h} \tilde {\subset } F$.

• 2. The inversion function i:G→G is soft continuous.

Example 9

Let $U=\mathbb {Z}_{9}, U/R =\{E_{1}, E_{2}, E_{3}\}$ where $E_{1}= \{\bar {0}, \bar {1}, \bar {2}\}, E_{2} =\{\bar {3}, \bar {4}, \bar {5}\}, E_{3}= \{\bar {6}, \bar {7}, \bar {8}\}, A=\{a_{1}, a_{2}\}, V= \{\bar {2}, \bar {4}, \bar {5},\bar {7}\}, W= \{\bar {2},\bar {3},\bar {6},\bar {7}\}$, and let $\tau = \{\tilde U,\tilde \phi, \tilde {V}, \tilde {W}, \{(a_{1}, \phi), (a_{2}, V)\}, \{(a_{1}, \phi), (a_{2}, W)\}, \{(a_{1}, \phi), (a_{2}, U)\}, \{(a_{1}, V), (a_{2}, \phi)\},\\ \{(a_{1}, V), (a_{2}, W)\}, \{(a_{1}, V), (a_{2}, U)\}, \{(a_{1}, W), (a_{2}, \phi)\}, \{(a_{1}, W), (a_{2}, V)\}, \{(a_{1}, W),\\ (a_{2}, U)\}, \{(a_{1}, U), (a_{2}, \phi)\}, \{(a_{1}, U), (a_{2}, V)\}, \{(a_{1}, U), (a_{2}, W)\} \}$. Then, 〈U,τ,R,∗,A〉 is a rough soft topological group.

Again, we can use the same method to construct a rough soft topological group starting from a soft rough topological group.

Theorem 6

Let (U,R) be an approximation space, (U,τ,A) be a soft topology on U, ∗ be a binary operation on U, and G⊂U such that 〈G,τ,R,∗,A〉 is a soft rough topological group. Consider τ^∗={(G,A)∈S(U):G(α)∈τ^α,∀α∈A}. Then, 〈G,τ^∗,R,∗,A〉 is a rough soft topological group.

Proof

(1) Let (g,h)∈G×G, F be a soft neighborhood of g∗h. Then, for all α∈A such that g∗h∈G(α), there exist neighborhoods F_g,F_h of g,h such that $F_{g} * F_{h} \tilde {\subset } F$, since (G,τ^α) is a topological rough group. (2) Let F be a soft open set in G, then i(G) is soft open since (G,∗) together with τ^α is a topological rough group for all α∈A. □

Remark 7

Let (U,R) be an approximation space, (U,τ,A) be a soft topology on (U,∗) be a binary operation on U, and G⊂U such that 〈G,τ,R,∗,A〉 is a rough soft topological group. Then, 〈G,τ,R,∗,A〉 is not necessarily a soft rough topological group.

Example 10

Let $U=\mathbb {Z}_{9}, U/R =\{E_{1}, E_{2}, E_{3}\}$ where $E_{1}= \{\bar {0}, \bar {1}, \bar {2}\}, E_{2} =\{\bar {3}, \bar {4}, \bar {5}\}, E_{3}= \{\bar {6}, \bar {7}, \bar {8}\}, A=\{a_{1}, a_{2}\}, U'= \{\bar {2},\bar {7}\}$, and let $\tau =\{\tilde U,\tilde \phi,{\{(a_{1}, \{\bar {2},\bar {7}\}), (a_{2}, \{\bar {2},\bar {7}\})\}} \}$. Then, 〈U^′,τ,R,∗,A〉 is a rough soft topological group which is not soft rough topological group.