1 Introduction

Operation and control of the power system under various operating conditions and configurations is always a challenging, difficult task to the power system engineers as it suffers from a variety of disturbances. During the disturbances, generators in the interconnected power system will oscillate and causes loss of synchronism. Oscillations in the range of low frequencies have considerable effect on the system dynamic stability. To counter these disturbances, PSS is developed as an auxiliary controller to damp out these oscillations by providing sufficient damping torque to the system [1, 2]. PSS tuning procedure guidelines using various signals are mentioned in [3, 4]. Later Kundur [5] had developed a systematic methodology for PSS tuning and implemented on Ontario Hydro station. Coordinated fixed gain PSS tuning on a wide range of operating conditions is given in [6]. In line with these methods, various PSS design techniques are developed from the last few decades, which includes robust control techniques [7, 8], sliding mode control techniques [9,10,11] optimization methods [12,13,14], H∞ techniques [15, 16], artificial intelligence techniques based PSS is given in [17,18,19]. Some of the disadvantages of the above mentioned techniques are that they need number of particles and hence much time for the design of PSS for multi machine interconnected systems, operating on various conditions and configurations. In recent years, heuristic algorithms have been developed by various researchers to solve complex problems in the field of science and technology. These include Simulated annealing [20], tabu search [21], genetic algorithm [22, 23], particle swarm optimization [24, 25], differential evolution [26], artificial bee colony [27, 28], honey –bee algorithm [29], harmony search algorithm [30, 31], cuckoo algorithm [32], chaotic – teaching, learning methods [33], gray wolf algorithm [34], bat algorithm [35, 36], back tacking algorithm [37] were developed for the PSS design from the last few years. Though several methods are developed, optimal PSS design for a highly nonlinear interconnected power system under variable operating conditions is still essential for robust operation. PSS design technique using WOA is proposed in this paper, and is tested on various test systems under a variety of disturbances to get the robust damping performance of the system. WOA [38] was developed by Seyedali. Mirjalili by observing the foraging method of Humpback whales. These whales have very special hunting method named as bubble- net feeding method, in which whale creates two paths for reaching the prey. Based on this unique hunting method of the whales, WOA is developed. PSS design using WOA is developed based on the locations of the lightly damped electromechanical modes of the system to enhance the damping performance of the system. The proposed method is tested on three multi-machine inter connected systems: three- generator nine- bus system, two- area four-generator system and ten- generator thirty-nine bus system working on various operating conditions under several disturbances. The efficacy of proposed WOA based PSS is compared with the famous optimization algorithm based PSSs such as PSO based and DE based PSS. The proposed design technique would become better substitute to the conventional stabilizers, as they need lots of calculations for the design purpose, when the power system operates on variable operating conditions.

2 Problem statement

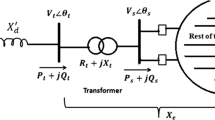
The complex, interconnected power system can be represented by n machines. Each generator in the power system can be represented by Heffron-Philips model. The problem in this paper is to design parameters of PSS of the inter connected multi-machine power system. Here two multi-machine interconnected power systems are considered. For any nth machine, the equations that govern the dynamics of the interconnected power system are as follows.

$$ \delta ={\omega}_m{S}_m $$
(1)
$$ {S}_m=\frac{1}{2H}\left\{{T}_{mech}-{T}_{elec}-{DS}_m\right\} $$
(2)
$$ {E}_q^{\hbox{'}}=\frac{1}{T_{d_0}}\left\{-{E}_q^{\hbox{'}}+\left({X}_d-{X}_d^{\hbox{'}}\right){i}_d+{E}_{fd}\right\} $$
(3)
$$ {E}_{fd}=\frac{1}{T_e}\left\{-{E}_{fd}+{K}_e\left({V}_{ref}+{V}_{pss}-{V}_t\right)\right\} $$
(4)
$$ {T}_{elec}={E}_q^{\hbox{'}}{i}_q+\left({X}_d^{\hbox{'}}-{X}_q^{\hbox{'}}\right){i}_d{i}_q $$
(5)

where δ, ωm are the rotor angle and angular speed, Sm is slip speed, H is inertia constant, Tmech is mechanical torque, Telec is electrical torque, D is damping coefficient, Eq’ is field flux emf in transient state, Td0 is open circuit time constant of d-axis, Xd’ is d-axis transient reactance and Xq’ is q-axis transient reactance, Efd is field voltage, Ke is gain of the exciter, Vref is the reference voltage, Vpss is PSS input, Vt is terminal voltage id and iq are the d and q-axis are respectively.

2.1 Structure of PSS

The main role of PSS is to provide damping torque to the excitation system of the generator in order to damp out electromechanical oscillations in the range of low frequencies which arose from small disturbances. This can be done by three major components of the PSS. The first component is the gain component that provides sufficient gain value to the system in order to damp out the oscillations, second component is the washout component, which acts as a high pass filter and the third one is a phase compensation component, which improves the phase lag through the system. The transfer function of PSS can be represented as

$$ {V}_s={K}_{PSSi}\frac{sT_{Wi}}{1+{sT}_{Wi}}\left[\frac{\left(1+{sT}_{1i}\right)\left(1+{sT}_{2i}\right)}{\left(1+{sT}_{3i}\right)\left(1+{sT}_{4i}\right)}\right]\Delta {\omega}_i(s) $$
(6)

Where Kpssi is PSS gain, Twi is the time constant of washout component, T1, T2, T3,T4 are the time constants of the phase compensation component, and Δωi is the speed deviation. When these parameters are evaluated properly, PSS can work effectively and enhance the dynamic performance of the system during the disturbances. Hence PSS parameters are assumed as control parameters and are evolved on a given objective function using proposed algorithm.

3 Proposed whale optimization algorithm for PSS design

WOA is proposed by Seyedali Mirjalili, in the year 2016 by impersonating the behavior of humpback whales. Humpback whales have very special hunting method, which is named as bubble – net feeding method. Based on this foraging method this algorithm was developed. Figure 1 shows Bubble – net feeding method of humpback whales. The motivation behind using WOA method is to design PSS parameters is, WOA has very good properties as follows; due to the less number of control parameters (two), WOA takes minimum time for evolution process, when compared to DE and PSO. For any optimization algorithm, exploitation (integration) and exploration (diversification) are very important stages and a good balance between these two stages will enhance the performance of search problem to get optimum solution. In WOA, the transit between exploitation and exploration operation can be done in a smoother manner and it can be done with only one parameter. More ever, the literature says that there is always a room for the improvement of the current techniques to get better solutions [39]. This motivation has lead to use WOA for the design of PSS to the interconnected multi- machine power system.

Fig. 1
figure 1

Bubble - net feeding method of humpback whale

Full size image

WOA method in this paper is used to optimize the PSS parameters of all the generators of test systems operating on a wide range of operating conditions and system configurations on a given objective function. Several typical disturbances have been considered at various locations of the test systems to test the robustness of WOA-PSS. The performance of WOA-PSS is compared with DE-PSS and PSO-PSS to prove its superiority in suppressing the oscillations.

WOA is developed to evolve the PSS parameters of various test systems. The following are the various steps involved in implementing WOA for PSS design.

Step1: Initialization

To start with, population size of the algorithm is chosen as 40, total number of generations is taken as 100 and the range of control variables are selected and listed in Table 1. PSS parameters are realized as control variables. The initial populations are randomly generated by using the given expression.

$$ {X}_{j_i}^0={X}_j^{min}+\mathit{\operatorname{rand}}.\kern0.5em \left({X}_j^{min}-{X}_j^{max}\right) $$
(7)
Table 1 Ranges of control parameters to be evolved
Full size table

Where X is the control variable and \( {X}_j^{\mathrm{min}} \), \( {X}_j^{\mathrm{max}} \) are the lowest and highest value of the control variables. j = 1, 2… N, N is the number of control variables, i = 1, 2, 3………. Np, Np is population size, rand∈ [0, 1] is a number varies between 0 and 1 randomly.

Step 2: Evaluating objective function

Eigenvalues of test systems are determined to find the objective function. To shift the eigenvalues of the test system into desired locations of the s-plane, here an objective function is formulated. Only lightly damped eigenvalues are considered to construct the objective function as these are responsible for the oscillatory behavior of the system. Hence, only these poles are considered throughout the study and shifted into desired locations by minimizing the following objective function.

$$ J={J}_1+c\ {J}_2 $$
(8)
$$ {}_{Where\ {J}_1=\sum \limits_{j=1}^{Np}\sum \limits_{\sigma i\ge \sigma o}{\left({\sigma}_0-{\sigma}_i\right)}^2} $$
(9)
$$ {}_{and{J}_2=\sum \limits_{j=1}^{Np}\sum \limits_{\varsigma_i\le {\varsigma}_0}{\left({\varsigma}_0-{\varsigma}_i\right)}^2} $$
(10)

Here Np is population size considered, σi is real part of ith eigenvalue of the population and σ0 is relative stability and is chosen as − 0.3, ζi damping ratio of the ith eigenvalue of the population . Here ζ0value is taken as 0.15. Eigen values will place in the highlighted regions of Fig. 2a, if J1alone is considered. Eigenvalues will move in the marked regions of Fig. 2b, if J2alone is considered. Two single objective functions J1 and J2can be combined together by assigning them a weighing factor, C to get the single objective function, J to place the eigen valuses into the desired locations. All the considered roots will move in the desired locations with the single objective function as shown in Fig. 2c. The value of C chosen as 10. For each particle, the fitness function is calculated by using eq. 8 and the best fitness function is identified among them.

Fig. 2
figure 2

Regions of closed loop eigenvalues for multi objective function

Full size image

Step 3 Search agent updation using Shrinking encircle mechanism (exploration phase)

Here the WOA is used to identify the best solution obtained so far. After fitness function is calculated on a random basis, since optimum position is not known initially, in the search place, the present best solution is considered as target prey or close to the optimum. Then other search agents will update their position after the best search agent is identified according to the following equation

$$ \overrightarrow{X_{j_i}}\left(t+1\right)={\overrightarrow{X_{j_i}}}^{\ast }(t)-\overrightarrow{A}.\overrightarrow{D} $$
(11)
$$ \overrightarrow{D}=\left|\right.\overrightarrow{C.}{\overrightarrow{X}}_{j_i}{(t)}^{\ast }-{\overrightarrow{X}}_{j_i}(t)\left.\right| $$
(12)

Here t represents present iteration, \( \overrightarrow{A} \), \( \overrightarrow{C} \) are the coefficient vectors, X∗is the best solution obtained so far, \( \overrightarrow{X} \)is the position vector ║ is the absolute value, and ‘.’represents a multiplication of elements to the elements. The vectors\( \overrightarrow{A},\overrightarrow{C} \) are represented as

$$ \overrightarrow{A}=2\overrightarrow{a}.\overrightarrow{r}-\overrightarrow{a} $$
(13)
$$ \overrightarrow{C}=2.\overrightarrow{r} $$
(14)

Here value of \( \overrightarrow{A} \)varies between -a, a randomly. Where a varies from 2 to 0 during the course of iterations. For each search agent a, A, C values are updated. If value of \( \overrightarrow{A} \) is less than 1, then the the search agent updates its position by Eq. 11.

Step 4 Particle updation using a spiral mechanism

As humpback whales swim around the prey within a shrinking circle and spiral – shaped path, a spiral equation is created between whale’s position and the prey to mimic the helix – shaped movement of the humpback whales. All the search agents follow the equation below.

$$ \overrightarrow{X_{j_i}}\left(t+1\right)={\overrightarrow{D}}^{\hbox{'}}{e}^{bl}.\cos \left(2\Pi l\right)+{X_{j_i}}^{\ast }(t)-\overrightarrow{A}.\overrightarrow{D} $$
(15)

Where

$$ {\overrightarrow{D}}^{\hbox{'}}=\left|\right.{{\overrightarrow{X}}_{j_i}}^{\ast }(t)-{\overrightarrow{X}}_{j_i}(t)\left.\right| $$
(16)

Where l is a random number varies between 0 and 1. To combine both shrinking circle path and spiral path, here 50% probability is given for the paths to update the positions of the whales. Finally search agent follows the equation below.

$$ \overrightarrow{X_{j_i}}\left(t+1\right)= $$
$$ {\overrightarrow{X_{j_i}}}^{\ast }(t)-\overrightarrow{A}.\overrightarrow{D}\; if\;\rho \le 0.5 $$
(17)
$$ {\overrightarrow{D}}^{\hbox{'}}{e}^{bl}.\cos \left(2\Pi l\right)+{X_{j_i}}^{\ast }(t)-\overrightarrow{A}.\overrightarrow{D}\kern0.28em if\kern0.28em \rho \ge 0.5 $$
(18)

Step 5 Search for prey (exploitation phase)

If the value of \( \overrightarrow{A} \) is greater than 1, to have an exploitation phase position of the search agent is updated according to randomly chosen search agent instead of best search agent. The search agent follows the equation below.

$$ \overrightarrow{X_{j_i}}\left(t+1\right)=\overrightarrow{X_{j_i}}\mathit{\operatorname{rand}}-\overrightarrow{A}.\overrightarrow{D} $$
(19)
$$ \overrightarrow{D}=\left|\right.\overrightarrow{C.}\overrightarrow{X_{j_i}}\mathit{\operatorname{rand}}\_{\overrightarrow{X}}_{j_i}(t)\left.\right| $$
(20)

Where \( \overrightarrow{X_{j_i}}\mathit{\operatorname{rand}} \) is the random position vector selected from the current population. The flow chart for implmentation of proposed algorithm is shown in Fig. 3.

Fig. 3
figure 3

Flow chart for WOA

Full size image

4 Case studies

4.1 Case 1 three generator nine bus system

The operating conditions in per unit values of this case are listed in Table 2. Figure 4 shows the block diagram of Heffron-Philips model for multi machine systems [40]. A modified Heffron-Philphs model [41] is considered in the development of multi-machine system. The advantage of this model is PSS design can be done with the information available with the generating station. With this model PSS tuning could be done in a decentralized manner. Figure 5 shows the three generator nine bus test system [42].

Table 2 Operating conditions of case 1
Full size table
Fig. 4
figure 4

Heffron - Philips model for multi-machine system

Full size image
Fig. 5
figure 5

Three generator nine bus test system

Full size image

4.2 Case 2 two- area four machine system

This test system has been taken from [43] which is a very popular test system for the study of power system stability. Two generators serves each area of the of this test system and each area is connected by two 220 km, 230 KV transmission lines. Figure 6 depicts two- area four- generator interconnected system. Power system stabilizer is connected at each generator and a sustained three phase fault is created at the midpoint of the line to test the performance of the proposed technique.

Fig. 6
figure 6

Two area system

Full size image

5 Simulation results and discussions

5.1 Case 1

Initially design approach is made by taking this case for evaluating PSS parameters. Whale algorithm is run several times to optimize the PSS parameters. Evolved parameters are listed in Table 3. Efficacy of WOA -PSS is then tested with a disturbance of 10% step change at Vref at each generator.

Table 3 Optimized Parameters using PSO,DE and WOA for case 1
Full size table

The performance curves are depicted in Figs. 7, 8, 9, 10, 11 and 12. These figures show the speed deviation plots for disturbances of 10% step change at Vref and 10% step change at turbine input. The Figures show that intensity of the oscillations is greatly reduced and duration of this intensity is much lesser with WOA-PSS when the proposed stabilizer is established in the system. From these observations it is concluded that the WOA-PSS shows superior performance in minimizing the oscillations when compared to DE, and PSO based stabilizers.

Fig. 7
figure 7

Speed deviation of G1 for 10% step change at Vref

Full size image
Fig. 8
figure 8

Speed deviation of G2 for 10% step change at Vref

Full size image
Fig. 9
figure 9

Speed deviation of G3 for 10% step change at Vref

Full size image
Fig. 10
figure 10

Speed deviation of G1 for 10% step change at turbine input

Full size image
Fig. 11
figure 11

Speed deviation of G2 for 10% step change at turbine input

Full size image
Fig. 12
figure 12

Speed deviation of G3 for 10% step change at turbine input

Full size image

To prove the robustness of WOA -PSS, eigenvalue analysis is made on the system and is compared with DE-PSS and PSO-PSS.

Table 4 shows the eigenvalue comparison of the test case with proposed WOA-PSS and DE-PSS and PSO-PSS. It is observed that the real part of considered eigenvalues of all the generators are increased, i.e., eigenvalues are shifted into moves away to desired locations from the previous locations with WOA-PSS. Hence it is proved that WOA- PSS is very effective in placing the lightly damped oscillating modes of the system into the desired regions.

Table 4 Eigen value analysis with PSO,DE and WOA
Full size table

5.2 Case 2

This test case is a very popular one in the field of stability and control. Total four generators are interconnected with each generator is equipped with one power system stabilizer. PSS parameters are optimized with the proposed method over a given objective function and listed in Table 5. Table 5 depicts the evolved parameters of PSS with WOA, DE and PSO. PSS are embedded with these parameters and tested on a severe sustained three phase fault.

Table 5 Evolved parameters with WOA, DE and PSO
Full size table

Performance plots of four generators with WOA, DE and PSO based power system stabilizers are shown in Figs. 13, 14, 15, 16, 17, 18 and 19 under severe sustained three phase fault at t = 10 s condition. It can be seen from the simulation results that the oscillations at generator one, generator two, generator three and generator four of two area systems are reduced and settled in a lesser time when the PSSs are designed with WOA than the other stabilizers. It is to be noted that the peak overshoot is greatly reduced with the proposed stabilizer than the other stabilizers for all the generators. This shows the efficacy of the proposed stabilizer over the other stabilizers.

Fig. 13
figure 13

Speed deviatio n of G1 under 3-φ fault at t = 10 s

Full size image
Fig. 14
figure 14

speed deviation of G2 under 3-φ fault at t = 10 s

Full size image
Fig. 15
figure 15

speed deviation of G3 under 3-φ fault at t = 10 s

Full size image
Fig. 16
figure 16

speed deviation of G4 under 3-φ fault at t = 10 s

Full size image
Fig. 17
figure 17

delta deviation of G1 under 3-φ fault at t = 10 s

Full size image
Fig. 18
figure 18

delta deviation of G2 under 3-φ fault at t = 10 s

Full size image
Fig. 19
figure 19

delta deviation of G3 under 3-φ fault at t = 10 s

Full size image

Further, to have more emphasis, eigenvalue analysis is made for all the generators and shown in Table 6. Table 6 depicts eigenvalue analysis of the two area system. It is observed from the results that low damped oscillating electromechanical modes are shifted more away from the imaginary axis with the WOA based stabilizer than the other stabilizers.

Table 6 Eigen value analysis of two area system
Full size table

Time specifications are also found to test the dynamic performance of WOA-PSS and shown in Table 7. It is clear from these results that overshoot and the settling time are reduced with WOA-PSS in all the generators. At G1 with WOA-PSS, settling time is 1.6879 s, which is lesser than other stabilizers. Further, settling time is decreased from 2.8499 s to 1.5374 s with WOA-PSS at G2. Oscillations are settled very quickly with lesser over shoot with proposed stabilizers than the other stabilizers at G3. The same observation is made at G4 also. Hence WOA–PSSs greatly enhances the damping characteristics of the system. Figure 20 Shows the convergence characteristics comparison of WOA with DE and PSO.

Table 7 Time response specifications of two area system
Full size table
Fig. 20
figure 20

convergence characteristics WOA,DE and PSO

Full size image

6 Conclusion

A PSS design technique using whale optimization algorithm for the interconnected power system working on various operating conditions is proposed in this paper. The design technique has been successfully implemented on two case studies: three generator nine bus system and two area systems working at various operating conditions under typical disturbances. It is concluded from simulation results that the proposed WOA based stabilizer exhibited better damping performance than the DE and PSO based Stabilizers From the eigenvalue analysis, it is proved that weakly damped eigenvalues placed into desired locations with whale based PSS, when compared to other stabilizers in all the cases.