Introduction

Preparation and transfer of maximum coherent quantum states are requisite in the applications of quantum measurements and sensing. Traditionally, adiabatic passage (AP), in order to transfer the population coherently and adiabatically in a two-level quantum system, is one of the most popular protocols used for initializing and manipulating quantum systems [1–4], with many applications ranging from large-area atom interferometry [5], atomic frequency standards [6], quantum information processing [7], nuclear magnetic resonance [8], coherent superposition of molecular vibration states [9], to quantum dots [10], etc.

AP approach and its variants including (fractional) stimulated Raman adiabatic passage (STIRAP) depend on the off-resonant coupling between descrete states and laser pulse to achieve a steady-state superposition. In the pseudo polarization representation [11], a two-level state superposition is considered as a state vector, and the phase, intensity, and detuning of the optical field is defined as a field vector. The state vector precesses about this adjustable field vector. Provided that this field vector varies sufficiently slowly, the population can be transferred from one state to the other with an arbitrary fidelity, that is, the state can be transferred perfectly. If this adiabatic condition is not met, the nonadiabatic coupling between eigenstates results in decoherence and the target state can not be reached perfectly. Therefore, in an AP process, the price to get a perfect target state is at expense of long time, which is the limitation for the application of AP technique in the case where a fast state preparation is demanding under the existence of decoherence.

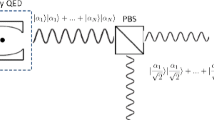
Subsequently, a technique called shortcuts to adiabaticity (STA) [12–23] was proposed theoretically and demonstrated experimentally to speed up slow AP, whose concepts, methods, and applications are well reviewed by Guery et al. [23]. One of STA is counterdiabatic driving [14, 16, 17], in which an additional counterdiabatic term is introduced to eliminate the nonadiabatic coupling, and thus make it possible for quantum state preparation to be rapidly realized. However, the cost for this fast state preparation is the increase of energy consumption due to the introduction of counterdiabatic driving. The existing studies about STA have focused on a Hermitian system, but recently, an increasing interest is blooming in a non-Hermitian system [24–26]. For example, as for a parity-time (PT) symmetric non-Hermitian system [27, 28], it can produce a faster-than-Hermitian evolution, while keeping the eigenenergy difference fixed [27, 29]. Some proposals for the realization of PT-symmetric Hamiltonian have been put forth [24] as well as some extensions related to the Landau-Zener (LZ) model [25, 30, 31]. In addition, the approximated adiabatic condition for a non-Hermitian Hamiltonian system has also been obtained [32]. And dissipation-assisted adiabatic passages was applied to prepare entangled-state [33]. However, as far as we know, no one consider STA-based creation of maximum coherence or beam splitting in a non-Hermitian system, even in a Hermitian system. The beam splitting is very useful in optical waveguides and coherent quantum state preparation, especially in quantum sensing and metrology.As shown in the following, by exploiting the fast shortcuts population transfer in a non-Hermitian Hamiltonian system, one can overcome some decoherence processes and achieve a perfect quantum state preparation. By properly choosing the driving field the maximum coherence and beam splitting can be obtained exactly. The creation of maximum coherence and beam splitting based on counterdiabatic driving or non-Hermitian STA is faster than that based on AP. But the counterdiabatic driving cost more coupling to speed up adiabatic evolution, while non-Hermitian STA modulates non-Hermitian terms without increasing coupling. Therefore, non-Hermitian STA can work in an arbitrarily small coupling and has more advantages.

The above STA in quantum systems can be moved into optical waveguide systems if just substituting time by spatial coordinates [34, 35], which favors a more compact device integration. Furthermore, non-Hermitian terms can be introduced and controlled by ion doping and laser pumping [36], and thus non-Hermitian STA can be implemented in non-Hermitian optical waveguides [36, 37].

In this paper, we firstly present the creation of maximum coherence and beam splitting of AP in a two-level Hermitian system. Secondly, the theoretical description of the counterdiabatic driving creation of maximum coherence and beam splitting in the Hermitian system is given. Then creation of maximum coherence and beam splitting of STA in a non-Hermitian system is described in detail and the physical implementation is considered in optical waveguides systems. The main conclusion is summarized in the end.

Results and discussion

First, for convenience of description, we use a two-level system to describe a directional coupler of two waveguides, and briefly introduce the conventional AP in a simple two-level Hermitian system, whose coherent excitation is described by the Schrödinger equation [38],

$$ i\hbar\partial_{t}c(t)=H_{0}(t)c(t), $$
(1)

where the vector c(t)=[cg1(t),cg2(t)]T comprises two probability amplitudes of states |g1〉 and |g2〉. The Hamiltonian under the rotating wave approximation (RWA) is written as

$$ H_{0}(t)= \frac{\hbar}{2} \left(\begin{array}{ll} 0 & \Omega(t) \\ \Omega(t)& 2\delta(t) \end{array}\right), $$
(2)

where Ω(t) is the Rabi frequency, which characterizes the strength of the field-induced coupling between states |g1〉 and |g2〉, and δ(t) is the detuning between field frequency ω(t) and the transition frequency ω0(t), δ(t)=ω0(t)−ω(t).

The instantaneous eigenstates of this time-dependent Hamiltonian H0(t) are

$$\begin{array}{*{20}l} \vert -\rangle=\cos \theta \vert g1\rangle-\sin \theta \vert g2\rangle, \notag\\ \vert +\rangle=\sin \theta \vert g1\rangle+\cos \theta \vert g2\rangle, \end{array} $$
(3)

with eigenvalues

$$ \hbar\varepsilon_{\pm}(t)=\frac\hbar2\left[\delta(t)\pm\sqrt{\Omega^{2}(t)+\delta^{2}(t)}\right], $$
(4)

and the mixing angle θ(t) is defined as tan2θ(t)=Ω(t)/δ(t). The states |−〉 and |+〉 are the adiabatic states. They are connected with the diabatic vector c(t) via the rotation matrix

$$ R(\theta)= \left(\begin{array}{ll} \cos\theta & \sin\theta\\ -\sin\theta & \cos\theta \end{array}\right), $$
(5)

as c(t)=R(θ(t))a(t), where a(t)=[a−(t),a+(t)]T contains the probability amplitudes of the adiabatic states |−〉 and |+〉. Similarly, the Schrödinger equation in the adiabatic basis reads

$$ i\hbar\partial_{t} a(t)=H_{a}(t)a(t), $$
(6)

where

$$ H_{a}(t)=\hbar \left(\begin{array}{ll} \varepsilon_{-}(t)&-i\dot{\theta}(t)\\ i\dot{\theta}(t)&\varepsilon_{+}(t) \end{array}\right). $$
(7)

Here, an overdot means a time derivative.

The adiabatic condition \(\vert \dot {\theta }(t)\vert \ll \varepsilon _{+}(t)-\varepsilon _{-}(t)=\varepsilon (t)\) means the nonadiabatic coupling in the Hamiltonian Ha(t) is negligible compared with the eigenenergy difference. If the system is initially prepared in |+(0)〉=|g1〉, then under the adiabatic condition, this system will always maintain on the instantaneous eigenstate |+(t)〉. Then by controlling the final mixing angle θf according to Eq. (3), one can achieve an arbitrary target state. This means that the AP makes the initial population in state |g1〉 be exactly split into two parts respectively populated in states |g1〉 and |g2〉, with a population radio of tan2θf. It is needed to be pointed out that the above creation passage of maximum coherence and beam splitting is limited by the adiabatic condition \(\vert \dot {\theta }(t)\vert \ll \varepsilon (t)\), which requires a slow evolution. As an example, we numerically demonstrate this AP for creation of maximum coherence or beam splitting under a Gaussian shape pulse. The mixing angle is required to satisfy θ(0)→π/2 and θ(tf)→π/4, which means

$$ \frac{\Omega(t)}{\delta(t)}\bigg|_{t=0}\to0^{-},\qquad \frac{\Omega(t)}{\delta(t)}\bigg|_{t=t_{f}}\to-\infty. $$
(8)

And as shown in Fig. 1a, the Rabi frequency and detuning for the field are

$$\begin{array}{*{20}l} \Omega(t)=\Omega_{0}\exp\left[-\frac{\left(t-t_{f}/2-\tau\right)^{2}}{\sigma^{2}}\right],\notag\\ \delta(t)=\delta_{0} \exp\left[-\frac{\left(t-t_{f}/2+\tau\right)^{2}}{\sigma^{2}}\right]. \end{array} $$
(9)
Fig. 1
figure 1

AP for creation of maximum coherence or beam splitting in a two-level system. a Gaussin Rabi frequency (solid) and detuning (dashed) defined by Eq. (9). b Adiabatic condition. c Population of state |g1〉 (solid) and state |g2〉 (dashed). Parameters: Ω0=5 MHz, δ0=−0.5 MHz, tf=8 ms, τ=tf/8.5, σ=tf/6

Full size image

In Eq. (9), Ω0 and δ0 are the peak values of Rabi frequency Ω and detuning δ, and σ is full width at half maximum. The τ is separation time between detuning and Rabi frequency, which guarantees to satisfy the boundary conditions in Eq. (8), and tf is the operation time. In the creation process of maximum coherence and beam splitting, the adiabatic condition is always satisfied, if one can check the time evolution of \(\varepsilon (t)/\vert \dot {\theta }(t)\vert \) (Fig. 1b) where this ratio is much larger than 1. Thus the state |g1〉 is equally split into state |g1〉 and state |g2〉 (Fig. 1c).

Although the AP can be used to obtain a precise quantum state preparation, it requires an extremely long operation time to avoid the influence of nonadiabatic effect in the evolution process. To speed up the slow evolution process, researchers have proposed the counterdiabatic driving [14, 16, 17], which is one of STA methods. The addition of an additional counterdiabatic term [14] can effectively suppress the nonadiabatic effect, which is written as

$$ H_{cd}(t)=\hbar \left(\begin{array}{cc} 0 & i\dot{\theta}(t)\\ -i\dot{\theta}(t) & 0 \end{array}\right). $$
(10)

And then the total Hamiltonian is constructed as

$$ {}H=H_{0}+H_{cd}=\frac \hbar 2 \left(\begin{array}{cc} 0 & \sqrt{\Omega^{2}+4\dot{\theta}^{2}}e^{-i\alpha} \\ \sqrt{\Omega^{2}+4\dot{\theta}^{2}}e^{i\alpha} & 2 \delta \end{array}\right), $$
(11)

where \(\alpha (t)=-\arctan {2\dot \theta (t)/\Omega (t)}\). By using the unitary transformation,

$$ U(t)= \left(\begin{array}{cc} e^{-i\frac\alpha2} & 0\\ 0 & e^{i\frac\alpha2} \end{array}\right), $$
(12)

modified Hamiltonian, \(H_{m}(t)=U^{-1}HU-i\hbar U^{-1}\dot {U}\), can be calculated as

$$ H_{m}=\frac \hbar 2 \left(\begin{array}{cc} -\dot\alpha & \sqrt{\Omega^{2}+4\dot{\theta}^{2}}\\ \sqrt{\Omega^{2}+4\dot{\theta}^{2}} & 2\delta+\dot\alpha \end{array}\right). $$
(13)

The modified Rabi frequency Ωm(t) and detuning δm(t) are obtained as

$$\begin{array}{*{20}l} \Omega_{m}(t)=\sqrt{\Omega^{2}(t)+4\dot{\theta}^{2}(t)}, \end{array} $$
(14)
$$\begin{array}{*{20}l} \delta_{m}(t)=\delta(t)+\dot\alpha(t). \end{array} $$
(15)

To demonstrate the advantages of counterdiabatic driving for accelerating quantum evolution, we set the same Rabi frequency and detuning defined by Eq. (9) with the same amplitude of Rabi frequency and detuning (Ω0=5 MHz and δ0=−0.5 MHz) as shown in Fig. 1a, but for a very short operation time, tf=1μs. According Eq. (15), one can see that the amplitudes of the modified Rabi frequency and detuning obviously increase (Fig. 2b). This means that the counterdiabatic driving costs more coupling to achieve an accurate adiabatic evolution (Fig. 2c). Here, an operation time of 1 μs is an example, in fact, the theoretically speeding operation time can be arbitrarily short. In addition, it is necessary to point out that there is a phase difference α(0) between states |g1〉 and |g2〉 at the initial moment.

Fig. 2
figure 2

STA for creation of maximum coherence or beam splitting. a Original Rabi frequencies (solid) and detuning (dashed) defined by Eq. (9). b Modified Rabi frequencies (solid) and detuning (dashed) defined by Eq. (15). c Population of state |g1〉 (solid) and state |g2〉 (dashed). Parameters: Ω0=5 MHz, δ0=−0.5 MHz, tf=1μs, τ=tf/12, σ=tf/6

Full size image

As for a non-Hermitian system, there is gain or loss of state population. One can nullify the nonadiabatic coupling by controlling gain or loss instead of the counterdiabatic term in a Hermitian system. For this goal, two nonzero terms are added in the Hamiltonian H0(t), and we obtain

$$ H^{\Gamma}(t)=\frac\hbar2 \left(\begin{array}{cc} -i\Gamma_{1}(t)&\Omega(t)\\ \Omega(t)&2\delta(t)+i\Gamma_{2}(t) \end{array}\right), $$
(16)

where Γ1(t) and Γ2(t) are both real numbers and represent the loss rate of the state |g1〉 and the gain rate of the state |g2〉 respectively.

As illustrated in AP, the Hamiltonian \(H^{\Gamma }_{a}(t)\) in the basis |±〉 has the form

$$ H^{\Gamma}_{a}(t) =\hbar \left(\begin{array}{cc} A_{11}&A_{12}\\ A_{21}&A_{22} \end{array} \right), $$
(17)

where

$$\begin{array}{*{20}l} A_{11}=\varepsilon_{-}-\frac i2\left(\Gamma_{1}\cos^{2}\theta-\Gamma_{2}\sin^{2}\theta\right),\notag\\ A_{12}=-\frac i4(\Gamma_{1}+\Gamma_{2})\sin{2\theta}-i\dot{\theta},\notag\\ A_{21}=-\frac i4(\Gamma_{1}+\Gamma_{2})\sin{2\theta}+i\dot{\theta},\notag\\ A_{22}=\varepsilon_{+}-\frac i2\left(\Gamma_{1}\sin^{2}\theta-\Gamma_{2}\cos^{2}\theta\right). \end{array} $$
(18)

The ε±(t) are again defined by Eq. (4). We assume that initially the system only populates in state |g1〉. According to the initial condition θ(0)=π/2 and Eq. (3), the initial state coincides completely with the state |+〉. To nullify the nonadiabatic coupling, it requires that the nondiagonal terms are zero, which means

$$ \Gamma_{1}(t)+\Gamma_{2}(t)=-\frac {4\dot{\theta}(t)}{\sin{2\theta}}. $$
(19)

During the evolution, the system follows the state |+〉, and the state |−〉 has never received any populations.

We obtain the evolution of the amplitudes of the adiabatic state by using Eq. (6)

$$ a_{-}(t_{f})=0, $$
(20a)
$$\begin{array}{@{}rcl@{}} a_{+}(t_{f})&=&\exp\left\{-i\int^{t_{f}}_{0}\varepsilon_{+}(t')-\frac i2\left[\Gamma_{1}(t')\sin^{2}\theta(t')-\right.\right.\\ &&\left.\left.\Gamma_{2}(t')\cos^{2}\theta(t')\right]dt'\right\}, \end{array} $$
(20b)

where tf is the final time of the evolution process. In order to guarantee the final state |a+(tf)|2=1, we require that the real part in Eq. (20b) is zero. It means

$$ \int^{t_{f}}_{0}\left[\Gamma_{1}(t')\sin^{2}\theta(t')-\Gamma_{2}(t')\cos^{2}\theta(t')\right]dt'=0. $$
(21)

Eq. (21) ensures that the total population at the end of the process is conserved. In particular, the total population in the system remains constant throughout the process, if the Γ1 and Γ2 satisfy

$$ \Gamma_{1}(t)\sin^{2}\theta(t)-\Gamma_{2}(t)\cos^{2}\theta(t)=0. $$
(22)

So we obtain

$$\begin{array}{*{20}l} \Gamma_{1}(t)&=-\frac{2\dot{\theta}(t)}{\tan{\theta(t)}},\notag\\ \Gamma_{2}(t)&=-2\dot{\theta}(t)\tan{\theta(t)}. \end{array} $$
(23)

So far, we have obtained the exact analytic solutions to equations about loss rate Γ1(t) of the state |g1〉 and gain rate Γ2(t) of the state |g2〉. From Eq. (23), it can be seen that there are Γ1(t) and Γ2(t), which satisfy Eq. (23), to ensure that the total population is conservable, regardless of any set of field parameters (Ω(t) and δ(t)) selected.

After obtaining the relation between Γ1,2 and mixing angle, the corresponding field parameters can be selected according to our purposes. Now, efficiency of creation of maximum coherence and beam splitting based on non-Hermitian STA in a Gaussian model described by Eq. (9) is investigated as well as that of a Hermitian STA. We set the same parameters (Ω0=5 MHz, δ0=−0.5 MHz, tf=1μs, τ=tf/10, and σ=tf/6) as Fig. 2. In our method, we introduce a non-Hermitian term (Fig. 3b) to cancel the nonadiabatic coupling, and Rabi frequency and detuning (Fig. 3a) are neither modified nor increased. And the accurate and rapid creation of maximum coherence or beam splitting is obtained in Fig. 3c. Same as Hermitian STA, non-Hermitian STA is three-order or even arbitrarily faster than AP. Non-Hermitian STA which is better than Hermitian one can be applied under arbitrarily small coupling.

Fig. 3
figure 3

Non-Hermitian STA for creation of maximum coherence or beam splitting with Gaussian model. a Rabi frequency (solid) and detuning (dashed). b Gain rate Γ1(t) (solid) of the state |g1〉 and loss rate Γ2(t) (dashed) of the state |g2〉. c Population of state |g1〉 (solid) and state |g2〉 (dashed). Parameters: Ω0=5 MHz, δ0=−0.5 MHz, tf=1μs, τ=tf/10, σ=tf/6

Full size image

In fact, the above creation of maximum coherence or beam splitting is not limited to a Gaussian model, and the non-Hermitian STA beam splitting can be realized in other models, such as the widely used Allen-Eberly (AE) model [39]. The Rabi frequency and detuning in the AE model are

$$\begin{array}{*{20}l} \Omega(t)&=\Omega_{0} \text{sech}\left({\frac{t-t_{f}/2}{\sigma}}\right),\notag\\ \delta(t)&=\delta_{0} \left[1-\tanh\left({\frac{t-t_{f}/2}{\sigma}}\right)\right]. \end{array} $$
(24)

Here the detuning is a transformed hyperbolic tangent function, which is a little different from that used in the traditional AE model, in order to ensure that the boundary conditions (8) are satisfied. Under the parameters Ω0=5 MHz, δ0=−0.5 MHz, tf=1μs, and σ=tf/12, a perfect creation of maximum coherence and beam splitting are achieved in short time, as shown in Fig. 4c.

Fig. 4
figure 4

Non-Hermitian STA for creation of maximum coherence or beam splitting with AE model. a Rabi frequency (solid) and detuning (dashed). b Gain rate Γ1(t) (solid) of the state |g1〉 and loss rate Γ2(t) (dashed) of the state |g2〉. c Population of state |g1〉 (solid) and state |g2〉 (dashed). Parameters: Ω0=5 MHz, δ0=−0.5 MHz, tf=1μs, σ=tf/12

Full size image

With a further discussion, our suggested STA technique in non-Hermitian systems could be physically realized in waveguide optics [36, 37]. A PT-symmetric directional coupler consisting of two waveguides, waveguide |L〉 and waveguide |R〉, placed in proximity with propagation constants βL(z) and βR(z) is considered. The refractive index or geometry of the two waveguides are allowed to vary along the propagation direction z. Light is coupled into the device at input plane z=zi(=0) and out at output plane z=zf. The waveguides |L〉 and |R〉 here substitute for the above quantum states |g1〉 and |g2〉, and time t in Eq. (16) is replaced by direction z. Light propagation in the coupler is described by coupled-mode equation [40, 41]

$$ {}i \frac{d}{dz}\left(\begin{array}{l}A_{L}\\A_{R}\end{array}\right) =\left(\begin{array}{cc}\beta_{L}(z)-i \gamma_{l}(z)& \kappa(z)\\\kappa(z)& \beta_{R}(z)+i \gamma_{g}(z)\end{array}\right) \left(\begin{array}{l}A_{L}\\A_{R}\end{array}\right), $$
(25)

where AL and AR are mode amplitudes of two waveguides, κ is coupling coefficient, γl and γg are respectively the loss of waveguide |L〉 and the gain of waveguides |R〉. The relation between the mismatch Δ=(βR−βL)/2 and width difference δW of two waveguides can be approximated by a linear relation [35, 42], and the coupling coefficient scales exponentially with the waveguide separation d(z) according to the law κ(z)=κ0 exp[−k(d(z)−d0)] [35, 40] (where κ0 and k are two constant parameters to be determined from the fabrication process). A practical consideration of experimental realization of this system can be Ti in-diffused Fe:LiNb O3 optical waveguides which have recently been applied to demonstrate PT-symmetric directional couplers in the visible spectrum [36]. The loss rate γl is dependent on the number of Fe2+ dopants and can be controlled easily. The laser pumping through the two-wave mixing process can provid the gain γg [36]. Thus, non-Hermitian STA can be experimentally verified in optical waveguide systems. Better yet, although we focus on equal mode splitting of optical waveguides, our technique can be applied to arbitrary ratio mode splitting and can be applied in more fields.

Conclusion

In this paper, we have presented the fast creation of maximum coherence and beam splitting via shortcuts to adiabaticity technique in Hermitian and non-Hermitian systems. In a Hermitian system, one achieved a fast adiabatic creation of maximum coherence and beam splitting by introducing an additional counterdiabatic term to eliminate the nonadiabatic coupling in evolution. Theoretical analysis and numerical results verified that shortcuts to adiabaticity is three-order or even arbitrarily faster than conventional adiabatic passage, but this realization is at the cost of increasing coupling. Instead, a novel non-Hermitian STA scheme proposed here can be used to achieve perfect creation of maximum coherence and beam splitting without increasing coupling. By tuning non-Hermitian terms and field parameters, it is convenient to control the dynamic evolution of the system. Moreover, even for an arbitrarily small coupling between two states, non-Hermitian STA succeeds in perfect creation of maximum coherence and beam splitting, but counterdiabatic driving fails. The feasibility of non-Hermitian STA method has demonstrated in Gaussian and Allen-Eberly models and its experimental realization in optical waveguide systems is described. The fast quantum state manipulation based on shortcuts to adiabaticity demonstrated here possesses unique advantages in quantum sensing and metrology in a noisy environment.