Introduction

Investigation of the electromagnetic traits of plasma waveguide structures reveals attractive features that are very significant for potential applications in communication, cancer treatment, advancement in methods of charge particle acceleration, transport of high current charge particle beams, and generation of high-power electromagnetic radiation [1,2,3]. Theoretical and plasma physicists categorize plasma as anisotropic plasma and isotropic plasma. Anisotropic plasma is direction dependent and has an external magnetic field, while in the case of isotropic plasma, there is no external magnetic field and it has the same properties in all directions. Isotropic plasma supports high-frequency electromagnetic waves, which see the plasma as a simple dielectric owing to the response of free electrons to the wave. In the case of cold plasma, these waves exhibit simple oscillation at the plasma frequency, which is the function of number density, below which electromagnetic waves do not propagate.

Recently, ferrite materials have attracted considerable attention in different areas of nanotechnology research. Ferrite is an anisotropic magnetic material having superior fabrication and design properties widely used in passive and Antenna microwave devices such as filters, circulators, phase shifters, and isolators [4,5,6,7,8,9,10,11]. Since ferrite magnetic tensors can be altered by tailoring the DC magnetic bias, ferromagnetic materials are used to design many reconfigurable electromagnetic devices. Due to their adjustable magnetic traits, ferrite materials are widely used for designing the latest reconfigurable antennae [12]. These traits motivate us to study the ferrite-filled waveguide, which has not yet been studied. Many researchers carried out research on surface wave and wave propagation for waveguides [13,14,15,16,17,18,19].

The presented work of this manuscript deals with a waveguide made of a plasma-ferrite-plasma planar interface in the GHz operating surface wave frequency. In this work, we present the analysis and computation of the propagation constant and field distribution. The dispersion relations for the guided TE surface waves are derived and used to acquire the propagating mode and normalized field distribution. The influence of the number density of electrons, separation distance, and dielectric permittivity of the ferrite material on the propagation constant is studied. Moreover, the normalized field distribution for plasma and ferrite medium is also presented in this manuscript.

Geometry and equations

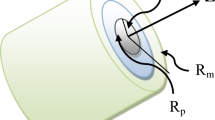
The geometric configuration of the proposed dielectric/ferrite/dielectric sandwich structure for the propagation of the guided TE surface waves is presented in Fig. 1. The structure consists of ferrite medium bounded by isotropic plasma materials. We assume that the electric and magnetic field components are proportional to ei(kz − ωt) and y independent i. e. ∂/∂y = 0 where ω is the operating surface wave frequency and k is the propagation vector in the z direction. To obtain uniform intensity H0 within the ferrite film, we apply static magnetic field B0 along the y direction. The electric and magnetic field components for the propagation of TE surface waves along the z for the presented geometry have the following form as presented in [20].

$$ E=\left[0,{E}_y,0\right]{e}^{i\left({k}_z-\omega t\right)} $$
(1a)
$$ H=\left[{H}_x,0,{H}_z\right]{e}^{i\left({k}_z-\omega t\right)}. $$
(1b)
Fig. 1
figure 1

Geometry for plasma parallel plate waveguide filled with ferrite

Full size image

Field component for plasma medium (x < 0) and (d < x)

We consider that a plasma medium with region 1 (x < 0) and with region 3 (d < x) as shown in Fig. 1. By assuming the time-dependent perturbations, the momentum transfer, equation of continuity and Maxwell’s equations can be used to express the plasma medium in the absence of electric field and an equilibrium drift velocity [21, 22]:

$$ nm\left(- i\omega \boldsymbol{V}+v\boldsymbol{V}\right)=- en\boldsymbol{E}-\nabla \mathrm{p} $$
(2)
$$ i\omega p= nm{v}_{th}^2\nabla .\mathbf{V} $$
(3)
$$ \nabla \times \boldsymbol{H}=- en\boldsymbol{V}- i\omega {\varepsilon}_0\boldsymbol{E} $$
(4)
$$ \nabla \times \boldsymbol{E}= i\omega {\mu}_0\boldsymbol{H} $$
(5)

Where n, m, v, V, e, p and \( {v}_{th}=\sqrt{KT\gamma /m} \) are electron number density, mass of electron, collision frequency, velocity, charge on electron, pressure and thermal velocity respectively whereas K, T and γ are Boltzmann constant, temperature of plasma and ratio of specific heat. By using value of V in equation (4) from equations (2, 3) we get

$$ \nabla \left(\nabla .\mathbf{E}\right)-{\nabla}^2\boldsymbol{E}=\frac{\omega^2}{c^2}\left[\left(1-\frac{\omega_p^2}{\omega^2+ i\omega v}\right)\boldsymbol{E}+\left(\frac{v_{th}^2}{\omega^2+ i\omega v}\right)\nabla \left(\nabla .\mathbf{E}\right)\right] $$
(6)

where plasma frequency is defined as \( {\omega}_p={\left({e}^2n/{\varepsilon}_0m\right)}^{\frac{1}{2}} \) In our proposed model the electric field \( \boldsymbol{E}={E}_y\hat{j} \) and \( \nabla .\mathbf{E}=\left(\hat{i}\partial /\mathrm{\partial x}+\hat{k}\partial /\mathrm{\partial z}\right).\left({E}_y\hat{j}\right)=0 \). The equation (6) becomes as presented in [20].

$$ \frac{d^2{E}_y}{d{x}^2}-{k}_p^2{E}_y=0 $$
(7)

where \( {k}_p^2 \) = \( {\beta}^2-{k}_0^2{\varepsilon}_p \) with propagation constant β, \( {k}_0^2={\omega}^2/{c}^2 \) and \( {\varepsilon}_p=1-\frac{\omega_p^2}{\omega^2+ i\omega v} \) .

The solution of equation (5) for region 1 (x < 0) and region 3 (d < x) are given below respectively

$$ {E}_{y1}=C{e}^{k_px}. $$
(8)
$$ {E}_{y3}=D{e}^{-{k}_px} $$
(9)

where C and D are unknown constants.

Field component for ferrite medium (0 < x and <x)

In this structure, a ferrite film is sandwiched between plasma materials. For this region, Maxwell’s equations can be written as

$$ \nabla \times \boldsymbol{H}=- i\omega {\varepsilon}_0{\varepsilon}_f\boldsymbol{E} $$
(10)
$$ \nabla \times \boldsymbol{E}= i\omega {\mu}_0\overline{\mu}\boldsymbol{H}. $$
(11)

The model field for ferrite medium is

$$ {E}_{y2}= Acosh\left({k}_fx\right)+ Bsinh\left({k}_fx\right) $$
(12)

where A, B are unknown constants, \( {k}_f=\sqrt{\beta^2-{k}_0^2{\varepsilon}_f{\mu}_v} \) is wave number in ferrite films, μv = μxx2 − μzx2/μxx is called Voigt permeability as presented in [20] and εf is the dielectric constant for the ferrite material. The \( \overline{\mu} \) is the Polder permeability tensor as:

$$ \overline{\mu}=\left(\begin{array}{ccc}{\mu}_{xx}& 0& i{\mu}_{zx}\\ {}0& {\mu}_{yy}& 0\\ {}-i{\mu}_{zx}& 0& {\mu}_{xx}\end{array}\right). $$
(13)

Here, \( {\mu}_{xx}=\left(1+\frac{\omega_m{\omega}_0}{{\omega_0}^2-\omega}\right)\ {\mu}_b \), \( {\mu}_{zx}=\left(1+\frac{\omega_m\omega }{{\omega_0}^2-\omega}\right)\ {\mu}_b \), and μyy = μb are the Polder tensor elements; μb is the optical magnon permeability; and ωm and ω0 are given as ωm = μ0γM0, M0 is the static magnetization and ω0 = μ0γH0. Here, H0 is the uniform intensity within the ferrite film resulting from the applied static magnetic field B0 and γ is the gyromagnetic ratio [23, 24]. Owing to the anisotropy of the ferrite material, the analysis of the ferrite waveguide is complicated. The following boundary conditions are used to solve the proposed structure:

$$ \hat{\boldsymbol{x}}\times \left({\boldsymbol{H}}_{\mathbf{2}}-{\boldsymbol{H}}_{\mathbf{1}}\right)=\mathbf{0} $$
(14)
$$ \hat{\boldsymbol{x}}\times \left({\boldsymbol{E}}_{\mathbf{2}}-{\boldsymbol{E}}_{\mathbf{1}}\right)=\mathbf{0} $$
(15)

By applying these boundary conditions at the plasma-ferrite and ferrite-plasma interfaces following matrix is yielded as:

$$ \left[\begin{array}{cc}\begin{array}{c}\begin{array}{c}{a}_{11}\kern0.5em {a}_{12}\\ {}{a}_{21}\kern0.5em {a}_{22}\end{array}\\ {}\begin{array}{cc}{a}_{31}& {a}_{32}\end{array}\end{array}& \begin{array}{c}\begin{array}{c}\begin{array}{cc}{a}_{13}& {a}_{14}\end{array}\\ {}\begin{array}{cc}{a}_{23}& {a}_{24}\end{array}\end{array}\\ {}\begin{array}{cc}{a}_{33}& {a}_{34}\end{array}\end{array}\\ {}\begin{array}{cc}{a}_{41}& {a}_{42}\end{array}& \begin{array}{cc}{a}_{43}& {a}_{44}\end{array}\end{array}\right]\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}A\\ {}B\end{array}\\ {}C\end{array}\\ {}D\end{array}\right]=0 $$
(16)

The entities in matrix are defined as a11 = 1, a12 = 0, a13 =  − 1, a14 = 0, a21 = 0, \( {a}_{22}=-\frac{i{k}_f}{\varepsilon_f{\mu}_0} \), \( {a}_{23}=\frac{i{k}_p}{\varepsilon_p{\mu}_0\omega } \), a24 = 0, a31 =  − cosh(dkf), a32 = sinh(dkf), a33 = 0, \( {a}_{34}={e}^{-{k}_pd} \), \( {a}_{41}=\frac{i{k}_f\sinh \left(d{k}_f\right)}{\varepsilon_f{\mu}_0\omega } \), \( {a}_{42}=\frac{i{k}_f\cosh \left(d{k}_f\right)}{\varepsilon_f{\mu}_0\omega } \), a43 = 0 and \( {a}_{44}=\frac{i{e}^{-{k}_pd}{k}_p}{\varepsilon_p{\mu}_0\omega } \),

After solving the matrix, we get dispersion relation:

$$ \mathrm{Tanh}\left[d{\mathrm{k}}_f\right]+\frac{2{\mathrm{k}}_f{\mathrm{k}}_p{\varepsilon}_f{\varepsilon}_p}{\left({\left({\mathrm{k}}_p{\varepsilon}_f\right)}^2+{\left({\mathrm{k}}_f{\varepsilon}_p\right)}^2\right)}=0 $$
(17)

Results and discussion

The derived characteristic equation for the plasma-ferrite-plasma structure was computed numerically. The numerically simulated results are presented in graphical form using the computer software MATHEMATICA. In all the graphical results, the separation distance is kept at d = 10−6 m. We can numerically illustrate the normalized propagation constant Re(β) with respect to the operating surface wave frequency ω for the different values of plasma frequency, separation distance d, and dielectric constant of ferrite film εf. The ferrite film parameter values are εf = 1, ωm = 3.08 ∗ 1010 Hz, ω0 = 0.343 ∗ 1010 × ωm Hz, and μb = 1. We have assumed that (v/ω) <  < 1. Since guided TE surface waves are interlinked with Hx and Hz, they depend upon the frequency-dependent μxx and μzx components of the Voigt permeability, and its function is given as μv = (μ2xx − μ2zx)/μxx.

Fig. 2 illustrates the computed dispersion curve of TE surface waves for the different values of number densities i.e., n = 1 ∗ 1020 m−3 (black dashed line), n = 1.2 ∗ 1020 m−3 (red thick line), n = 1.3 ∗ 1020 m−3 (blue dashed line) and n = 1.4 ∗ 1020 m−3 (green thick line). Since the electron plasma frequency can be tuned by the number density of free electrons, in Fig. 2, the propagation constant Re(β) with respect to the operating surface wave frequency ω in the GHz range is analyzed using the dispersion relation of equation (17). We have assumed over dense plasma material due its importance in theoretical as well experimental researches. The typical values of number density of electron are assumed to obey the condition of over dense plasma regime for ω < ωp when \( {\varepsilon}_p=1-\frac{\omega_p^2}{\omega^2}=1-\frac{\left({e}^2n/{\varepsilon}_0m\right)}{\omega^2}<0 \) . It can be observed that as the number density of electrons increases, the normalized phase constant tends to decrease and peaks are shifted toward the higher frequency region in a certain frequency range as reported in [20]. As the propagation constant Re(β) decreases, the band gap also decreases, and thus, the band gap has potential practical applications for waveguide devices. It is concluded that the number density of electrons controls the surface wave propagation in the plasma-ferrite-plasma structure.

Fig. 2
figure 2

Influence of number density on propagation constant

Full size image

To study the confinement of guided surface waves, which is a significant parameter for the practical aspects of the proposed geometry, the normalized propagation constant Re(β) with respect to the operating surface wave frequency using the dispersion relation of equation (17) under the different values of plate separation i.e., d = 5 ∗ 10−6m (black dashed line), d = 6 ∗ 10−6m (red thick line), d = 7 ∗ 10−6m (blue dashed line), and d = 8 ∗ 10−6m (green thick line) is presented in Fig. 3. It is obvious that as the separation distance (distance between the layers of plasma) can be varied by considerably varying the separation distance. It is noted that if separation distance plasma layer increases the normalized phase constant decreases as expected to obey the condition of over dense plasma. The numerical calculations are performed at the different values of dielectric permittivity of ferrite film i.e., εf = 1 (black dashed line), εf = 2.3 (red thick line) and εf = 14 (blue dashed line) with respect to the operating surface wave frequency for the plasma-ferrite-plasma structure is analyzed in Fig. 4. As dielectric permittivity of ferrite film increases, the propagation constant Re(β) increases due to dielectric constant property of ferrite film and peaks shift toward the low-frequency region. Moreover, by decreasing the dielectric permittivity of ferrite, the band gap increases, which is very useful for the waveguide community. Representative modal fields are shown in Figures 5 and 6 of ferrite medium and plasma medium respectively for the plasma-ferrite-plasma structure with d = 5 ∗ 10−6m and n = 1 ∗ 1020 m−3. Figures 5 and 6 illustrate the normalized field distribution of ferrite medium and plasma medium respectively for TE surface wave components Ey and Hz. The surface wave has two conditions: (1) it moves away from the interface and (2) it undergoes exponential decay. Therefore, these simulations results verify the surface wave conditions.

Fig. 3
figure 3

Influence of plate separation on propagation constant

Full size image
Fig. 4
figure 4

Influence of dielectric permittivity of ferrite material on propagation constant

Full size image
Fig. 5
figure 5

Normalized field distribution of ferrite medium

Full size image
Fig. 6
figure 6

Normalized field distribution of plasma medium

Full size image

Conclusion

We presented an analysis of guided TE surface waves for a ferrite medium surrounded by plasma layers. The dispersion relation was computed by applying the boundary conditions approach, and the following conclusions were drawn:

  1. (i)

    Surface waves propagate along the plasma-ferrite-plasma interface.

  2. (ii)

    The normalized propagation constant is very sensitive to the number density of free electrons, which is the key parameter of isotropic plasma, dielectric permittivity of ferrite film, and separation distance of plasma layers.

  3. (iii)

    To verify the surface waves, the normalized field distribution of plasma and ferrite medium was also discussed.

  4. (iv)

    The presented work has potential applications in cancer treatment, communication, drug delivery, and ferrite-based waveguide devices in the GHz frequency range.