Background

A pure-phase spatial light modulator (SLM) is a diffractive optical device with a high energy efficiency. The generation of random phase illumination by an SLM has been used in many applications such as phase retrieval [1] and microscopic imaging [2, 3]. In single-pixel imaging [4] and structured illumination imaging [5, 6] applications, an SLM may also be used to generate random amplitude patterns. As the device only modulates the phase, its energy efficiency will be higher than conventional projection devices based on amplitude modulation. In most current applications, SLMs are generally used only for a single-wavelength beam. If an SLM can be used for full-color or multi-spectral beam control, the usage of the above applications can be extended, thereby obtaining more information in the spectral dimension. As the LC-SLM technology is mature and cheap, it is the most commonly used SLM device in laboratory and commercial use. Thus, our study is focused in LC-SLM. For the sake of simplicity, we will still use SLM to refer to LC-SLM in the following paper.

McManamon analyzed the use of an SLM for steering a broadband beam and found that a beam with different wavelengths will be steered to different angles and orders owing to the dispersion caused by the wavelength-dependent response of the SLM [7]. Gruneisen theoretically analyzed broadband beam control and pointed out that the use of an SLM with a very large modulation range could avoid beams pointed to the wrong orders. However, they are still dispersed to different angles [8]. Stockley studied a chiral smectic liquid crystal (CSLC) writable grating that can minimize the wavelength dependence of the phase-shifting elements, thereby steering multi-spectral beams to the same order. However, such devices are not common and still need an achromatic optical system to offset the angle dispersion [9]. These explorations pointed out the difficulties for SLM multi-spectral beam control without a very ideal solution.

The use of an SLM for full-color holographic displays has been widely studied. In one approach, three SLMs are utilized for the corresponding red, green, and blue (RGB) channels [10]. However, this obviously increases the complexity of the system. Another approach is the time-division method (TDM), which cannot simultaneously modulate a multi-spectral beam [11]. In the space-division method (SDM), beams with different spectra are projected onto different areas of the SLM [12]. The beams generated using this method cannot utilize all of the units of an SLM; thus, the resolution is lowered.

In summary, it is difficult to utilize an SLM to generate a certain multi-spectral projection efficiently. However, it may be feasible for multi-spectral random illumination, which is the focus of this study. To improve the performance of SLM-based phase retrieval, Chen et al. [13] generated the random illumination by a designed phase pattern which can eliminate the zeroth-order beam and let the light be more evenly distributed. While, this method is only for the single-wavelength random illuminate. Inspired by this approach, we generate the multi-spectral random illumination by designing the phase pattern of SLM. According to our investigation, this is the first research generating the multi-spectral random illumination using an LC-SLM without time-division or spacial-division methods.

Methods

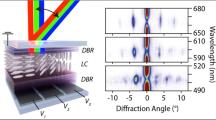
The configuration of the optical system is shown in Fig. 1. Three (or more) lasers are fused in a beam spliter and expand by a beam expander then modified by a LC-SLM. After that the modified light is imaged on the screen through the lens.

Fig. 1
figure 1

The configuration of the optical system

Full size image

The light field in the focal plane of an SLM can be obtained with the Fourier transform of the emitted light. Thus, I=|FFT(U)|2, where I is the intensity of beam in the far field, and U is the light field of emitted beam. If the phase of U is randomly distributed, then beams are scattered to spots with a random intensity in the far field. To obtain random spots with a large bandwidth, the size of the SLM should be large. With a larger scattering angle, the spatial correlation of the random phase should be weak. If a particular device is selected, the optimal values of these parameters are fixed.

When an SLM is used, it is important to reduce the intensity of the zeroth-order of the far-field beam because it is often very strong, which seriously deteriorates the performance of structured light illumination and phase retrieval. Because of the wavelength-dependent response of the SLM, strong zeroth-orders will appear in each spectrum if arbitrary voltages are applied to the device. In this study, we are aiming to design a control voltage to eliminate these zeroth-order spots.

For the k-th beam spectrum, the zeroth-order intensity is related to the phase of the modulated beam; that is,

$$ I_{0k} = A_{k}\left|\sum_{m,n}^{N}\exp\left(i\phi_{k}\left(m,n\right)\right)\right|^{2}. $$
(1)

Where I0k denotes the zeroth-order intensity of the k-th spectrum; Ak is a fixed intensity factor; N is the total number of rows (and columns), i.e., the resolution of the SLM is N×N; and ϕk denotes the phase retardation of the corresponding spectrum. Accounting for the crosstalk effect in liquid crystal SLM, we have

$$ \phi_{k}\left(m,n\right) = f_{k}\left[x\left(m,n\right)\right]\otimes h\left(m,n\right). $$
(2)

Where fk[] denotes the voltage-phase response of the k-th spectrum, x(m,n) is the control voltage. h(m,n) is the point spread function (PSF) of the crosstalk [14], which has non-zero values only in a small region around (0,0). ⊗ represents the convolution operator.

To reduce every I0k, we need to solve for the control voltages. An apparent way is to optimize x(m,n) with the objective function \(J = \sum _{k}\ I_{0k}\). However, it is very hard.

In order to generate random illumination, x(m,n) should be independent random variables to broaden the scattering angle. Assuming that they are identically distributed, as N→∞, the expectation of the zeroth-order intensity is

$$ \overline{I_{0k}}=A_{k}N^{2}\left|\overline{\exp\left(i\phi_{k}\right)}\right|^{2}. $$
(3)

The objective function can then be converted to

$$ J^{\prime} = \sum_{k}\ \left|\overline{\exp\left(i\phi_{k}\right)}\right|^{2} $$
(4)

and

$$ \overline{\exp\left(i\phi_{k}\right)} = \overline{\exp\left(i\sum_{a,b}^{N}f_{k}\left[x\left(m-a,n-b\right)\right] h\left(a,b\right)\right)}. $$
(5)

To convert the two-dimensional convolution to one-dimensional vector multiplication, we reshape h(m,n) into a S×1 vector h′, and x(m,n) into a N2×S matrix x′. Here, S equals to the number of non-zero elements in h(m,n). We assign a new index t to represent the t-th row of x′. Further, we denote the PDF of x by p(x). Thus, we have

$$\begin{array}{*{20}l} \overline{\exp\left(i\phi_{k}\right)} &= \overline{\exp\left(i\sum_{t}^{N^{2}}f_{k}\left[x^{\prime}_{t}\right] h^{\prime}\right)} \end{array} $$
(6)
$$\begin{array}{*{20}l} &= \int_{-\pi}^{\pi}\cdots\int_{-\pi}^{\pi}\prod_{t}^{N^{2}} \left(\exp\left(if_{k}\left[x^{\prime}_{t}\right]h^{\prime}\right) p\left(x^{\prime}_{t}\right)\right) dx^{\prime}_{1} \cdots dx^{\prime}_{N^{2}} \end{array} $$
(7)
$$\begin{array}{*{20}l} &= \prod_{t}^{N^{2}} \int_{-\pi}^{\pi}\exp\left(if_{k}\left[x^{\prime}_{t}\right]h^{\prime}\right) p\left(x^{\prime}_{t}\right) dx^{\prime}_{t} \end{array} $$
(8)
$$\begin{array}{*{20}l} &= \prod_{i}^{S}\prod_{t}^{N^{2}} \int_{-\pi}^{\pi}\exp\left(if_{k}\left[x^{\prime}_{t}(i)\right]h^{\prime}(i)\right) p\left(x^{\prime}_{t}(i)\right) dx^{\prime}_{t}(i) \end{array} $$
(9)
$$\begin{array}{*{20}l} &\ \dot{=} \prod_{i}^{S}J^{\prime\prime}(i). \end{array} $$
(10)

Since p(x)>0 and the range of fk[] is only a few multiples of 2πs, reducing any of J′′(i) will reduce the J. To simplify the optimization, let hmax=max(h′), and choose the corresponding term \(J^{\prime \prime }_{max} = J^{\prime \prime }(i_{max})\) as the objective function. Where, imax is the index of the maximum of h′. We denote \(x^{\prime }_{t}(i_{max})\) as \(x_{t}^{\prime \prime }\), then the objective function becomes

$$ J^{\prime\prime}_{max} = \sum_{k}\ \prod_{t}^{N^{2}}\left|\int_{-\pi}^{\pi}\exp\left(if_{k}\left[x_{t}^{\prime\prime}\right]h_{max}\right)p\left(x^{\prime\prime}_{t}\right) dx^{\prime\prime}_{t}\right|^{2}. $$
(11)

Further, \(x^{\prime \prime }_{t}\) is independent and identically distributed, then

$$\begin{array}{@{}rcl@{}} J^{\prime\prime}_{max} &=& \sum_{k}\ \left|\int_{-\pi}^{\pi}\exp\left(if_{k}\left[x_{t}^{\prime\prime}\right]h_{max}\right)p\left(x^{\prime\prime}_{t}\right)dx^{\prime\prime}_{t}\right|^{2N^{2}}. \end{array} $$
(12)

In order to solve this problem with a computer, p(x) is discretized. Finally, by ignoring the N2-th power,the objective function becomes

$$\begin{array}{@{}rcl@{}} J^{\prime\prime}_{max} &=& \sum_{k}\ \left|\int_{-\pi}^{\pi}\exp\left(if_{k}[x^{\prime\prime}]h_{max}\right)p\left(x^{\prime\prime}\right)dx^{\prime\prime}\right|^{2} \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} &=& \sum_{k}\ \left|\sum_{l}^{M}\exp\left(if_{k}\left[x_{l}^{\prime\prime}\right]h_{max}\right)p_{l}\right|^{2}. \end{array} $$
(14)

Here, p(x) is a discrete PDF that has a probability of pl at \(x^{\prime \prime }_{l}\). Then, only 2M parameters need to be optimized to minimize \(J^{\prime \prime }_{max}\), thereby suppressing the zeroth-order of every spectrum.

Result and discussion

The nonlinearity of the optimization problem is very strong. Traditional optimization methods may easily converge to the local maxima. Thus, we use the genetic algorithm function ga in MATLAB to optimize the parameters in Eq. 14. After that, the function fminsearch is utilized for further optimization. In the simulation, in order to demonstrate the results clearly, we assume that there are three spectra (k=1,2,3): 632 nm (R), 514 nm (G), and 454 nm (B), and the SLM has modulation ranges of 2.4π, 3.4π, and 3.7π, respectively. Namely, the minimum modulation range appears in the red band (the longest wavelength), which is slightly greater than 1λ. However, they are larger in other spectra due to the dispersion of the liquid crystal. The PDF of the crosstalk is a Gaussian kernel with a standard deviation of 0.4 pixels. The voltage-phase response curves are similar to the one in literature [5], as shown in Fig. 2. In our simulation experiment, the number of points of the discrete PDF is eight. The optimization function only requires 10s to find a result. The optimized PDF is summarized in Table 1. In the tests, one of the results is shown in Fig. 3. A random voltage pattern with the optimized PDF is shown in Fig. 3a, and the random intensity pattern in the far-field (in RGB color) is shown in Fig. 3b.

Fig. 2
figure 2

Voltage-phase response curve for each spectra

Full size image
Fig. 3
figure 3

a Control voltage pattern and b random intensity pattern from our simulation experiment

Full size image
Table 1 Optimized PDF
Full size table

We calculated 1000 random patterns in the far field to validate the performance of our random illumination. In the simulation, we set the SLM parameters as mentioned above with the following additional parameters: device resolution: 128×128, electrode interval: 10 μm and fill factor: 100% (in fact, the fill factor only affects the PDF h). Simulation experiments were carried out using an Intel Core i3-2130 3.4-GHz central processing unit (CPU) using MATLAB version 2013a. It takes 1.26 s to generate 1000 voltage patterns, i.e., the refresh rate could be higher than 800 Hz, which is far greater than the frame rate of most commercial SLMs. In comparison, the pattern generated without optimization is also presented. An average intensity image of the random spots is shown in Fig. 4.

Fig. 4
figure 4

The average intensity of the random spots. a Before optimization, b after optimization

Full size image

As shown in Fig. 4a, there exists an extremely bright zeroth-order spot; therefore, it must be saturated in the visualization. However, in Fig. 4b, the average intensity distribution of the random spots is uniform without any large fluctuations. Upon closer inspection, a brighter spot could be found in the zeroth-order, which is mainly attributed to the residuals of the optimization. The zeroth-order intensities are 1.5, 2, and 1.2 times larger than their neighborhoods in the R, G, and B bands, respectively, but their powers are only 0.009, 0.011, and 0.004% of the entire beam in each spectrum. In contrast, in the nonoptimized case, the zeroth-order intensities are 6000 times lager then their neighborhoods, and they take up 7.2, 6.7, and 3.8% of the entire energy, respectively. Hence, our algorithm successfully suppressed the zeroth-order spot. If we increase the modulation range of the SLM or use a PDF with a larger number of degrees of freedom, the zeroth-order intensities will be reduced more significantly.

In Fig. 4b, if the average intensity of the spot is greater than 1/e2 of the maximum value (except the zeroth-order), we define this area as a valid area (VA). In this area, if an 8-bit camera is used, the average gray value of the random spot will be greater than 35, which is sufficient for measurement. For the R, G, and B bands, the angles of the VAs are approximately 5.3°, 4.3°, and 3.8°, respectively. Although they are narrow, the VAs can be increased through a telescope system. In addition, the energy utilization efficiency is greater than 75% in the VA of each spectrum. If we choose the minimum VA as the VA of entire system, i.e., 3.8%, the efficiencies of each spectrum are 57, 70, and 76%, which are also far higher than the efficiency of the random spots generated by amplitude modulation (< 45%).

By analyzing the autocorrelation of the spot intensity, the widths of the correlation peaks can be obtained as 0.028°, 0.023°, and 0.020° for R, G, and B, respectively, which determine the average size of a random spot. A high-resolution SLM can be used to obtain a finer spot. Moreover, we find that the spots of the three spectra are nearly independent, and the cross-correlations of RG, GB, and BR are 0.007, 0.004, and 0.005, respectively, which means that the random spots are independent.

Experimental results show that we can use a single SLM to generate multi-spectral random illumination which is close to the wight uniform distribution with high energy efficiency. The method in this paper can be used for multi-spectral phase-retrieval, multi-spectral microscopy imaging, single pixel imaging and other fields.

Conclusions

In summary, we have developed a method to generate multi-spectral random illumination by a piece of an SLM whose modulation range is a slightly greater than 1λ. This method has a high energy efficiency and computing efficiency. Moreover, it does not require a complex system, and the complexities of the system and algorithm will not significantly increase when a new spectrum is added. In our method, every spectrum illuminates the entire area of the SLM; thus, the random illumination has a very high resolution. We also suppressed the zeroth-order spot in the far field to improve the illumination quality. This method can be used for multi-spectral microscopy, phase retrieval, structured illumination imaging, single-pixel imaging, and other applications.