Background

The spiral axicon is known for generating a field with an on-axis helical wavefront [1–4]. This wave field carries an optical angular momentum (OAM) of \(l \hbar \) per photon [5] which can be transferred to particles. In general, optical vortices (OVs) are connected to points of zero intensity where the real and imaginary parts are both zero [6]. These points are phase singularities. In the case of a helical wavefront, they are also called screw dislocations (SD). Moreover, these SDs exhibit a topological charge (TC) of ±l in respect of the phase increasing/decreasing by ±l 2π along one circumference around the SD. OVs are of widespread interest and have found applications in various areas like atom trapping and micromanipulation [7], imaging [8], plasmonics [9], optical data communication [10] and active OAM-emitter in vertical-cavity surface-emitting lasers (VCSEL) [11].

Multiple optical vortices have also been demonstrated in 2D geometries, referred to as optical vortex lattice (OVL) or optical vortex arrays [12–14]. OVLs can be created, for instance, by coaxial or noncoaxial superposition of vortices with different or same TC [13–19]. In the following these are called fundamental vortex modes (FVM). Moreover, the motion and the position of the vortices in an OVL along propagation depends on the kind of superposition (addition of the complex amplitude or phase term) and the kind of the (host) beam [14, 19–21]. In our investigations we consider the coaxial superposition of the complex amplitudes of non-diffracting Bessel beams. The corresponding resulting field distribution can be described by

$$\begin{array}{@{}rcl@{}} u(r,\theta,z) \propto \sum\limits_{\tilde{m}=1}^{\infty} \sum\limits_{\tilde{n}=1}^{\infty} & a_{\tilde{n},\tilde{m}}\, J_{\tilde{n}} \left(k_{r,\tilde{m}} r \right) e^{i \left(\tilde{n}\theta+k_{z,\tilde{m}}z+k_{r,\tilde{m}}r \right)} \end{array} $$
(1)

where r,θ,z are the cylindrical coordinates in the observation plane and \(\tilde {n},\tilde {m}\) address the corresponding radial and azimuthal component. Here, the \(\tilde {n}\)th order of the Bessel function determines the TC of the vortex so that \(l=\tilde {n}\). The radial and longitudinal components of the wave vector are denoted by kr and kz, respectively, and \( a_{\tilde {n},\tilde {m}}\) denotes the corresponding weighting factor.

Experimentally, Eq. 1 could also be introduced on a spatial light modulator (SLM) [2, 22]. Next to the possibility of the precise adjustment of the radial and azimuthal parameters, the generated wavefield is limited by the spatial bandwidth product (SBP) due to the resolution of the SLM. This leads to a reduction of the efficiency of the helical wavefront [23–25], especially in case of the superposition of higher order of Bessel modes [17]. As it can be seen by the following results, the structured diffractive spiral axicon represents another method for the direct generation of an optical vortex lattice equivalent to the coaxial superposition of fundamental vortex modes, analogous to Eq. 1. By the use of the structured spiral axicon, the generated wavefield is not restricted by any limitation of the SBP and there is no necessity of additional optical components in order to perform the superposition [16, 19]. Here, we consider the case of an element with binary amplitude transmission, however, results are very similar for a binary phase transmission.

This article is organized as follows: first, we will introduce the resulting object structure due to the modulation. Then we will present the analytical investigations describing the resulting field distribution which involves the determination of optical vortices. A comparison between analytical and experimental results shows good agreement.

Methods

Transmission function of the discretized spiral axicon

Discretization of conventional diffractive elements like Fresnel zone plates and spiral axicons was discussed earlier in [26–28]. Discretization leads to additional degrees of freedom for the optical design, on the one hand, and thus more functionality on the other. Here, we consider the situation of a discretized spiral axicon as an element, generally described by Eq. 2.

$$ \begin{aligned} {}\tau(r_{0},\theta_{0})=\sum\limits_{n=0}^{N-1} \sum\limits_{m=1}^{M} \text{rect} \left(\frac{r_{0}-\delta r_{0}(m,n)}{\, a_{r} r_{\mathrm{p}}} \right) \, \text{rect} \left(\frac{\theta_{0}-\delta \theta_{0}(n)}{\, a_{\phi} \theta_{\mathrm{p}}} \right). \end{aligned} $$
(2)

The mathematical treatment is performed in polar coordinates. In this particular example we express the object by a product of rect-functions [29] with the center coordinates δr0(m,n) and δθ0(n) described in Eq. 2. The object’s coordinates are expressed by r0 and θ0. The structure is divided into N blades. This leads to an azimuthal fragmentation with a period of θp=2π/N, each with a constant radial component (see Fig. 1b). The offset of the radial period increases linearly with each blade. Therefore, the center coordinates in radial direction of the transparent sections are also dependent on N. We introduce the following center coordinates as follows: δθ0(n)=(n+0.25)θp and δr0(m,n) = rp(m−0.75+n/N), with rp denoting the radial period, n and m are the indices of the transparent sections in azimuthal and radial direction, and M denotes the number of radial periods.

Fig. 1
figure 1

Structured spiral axicon with N=3 in (a) Cartesian (x0,y0) and (b) polar coordinates (r0,ϕ0). The transparent sections of the object are indicated in black

Full size image

From Eq. 2, various structures may result, depending on the variables. Here, in order to understand and show the basic phenomena that occur due to discretization, we restrict our investigation to a specific element described by ar=1/2 and aϕ=1/2, a Ronchi division in radial and azimuthal direction as shown in Fig. 1a. Different of other values for ar and aϕ lead to interesting observations, as described in [30], but will be left out of consideration here.

The resulting transmission function can be developed as a Fourier series expansion, similar to the mathematical expression reported in [31, 32], and inserted into the scalar diffraction formula with Fresnel approximation [23]. First, the diffraction integral is solved for the azimuthal coordinate using Jacobi-Anger identity [33] and second, for the radial coordinate using the method of stationary phase [34, 35], respectively. Here, the object function is limited by a circ - function with circ(r0/R0) in the objects plane. The resulting Fourier components \(\tilde {m}\) and \(\tilde {n}\) can be seen as the order of the radial and azimuthal harmonic, respectively. The contribution of the radial harmonics is limited to the first order for

$$\begin{array}{@{}rcl@{}} \frac{r_{\mathrm{p}} R_{0}}{\lambda} \geq z_{\tilde{m}=1} \geq \frac{r_{\mathrm{p}} R_{0}}{3\lambda} \end{array} $$
(3)

in the near-field - region. At a distance \(z_{\tilde {m}=1} \) behind the diffractive mask, the field distribution can be described as:

$$ \begin{aligned} {}u(r,\theta,z,N) &\propto 2 \, A \, C \sum\limits_{\tilde{n}=1}^{\infty} \sum\limits_{n=0}^{N-1} \, \text{sinc} \left(\frac{\tilde{n}}{2N} \right) \\ &\times J_{\tilde{n}} \left(\frac{r}{\rho} \right) \, \left(-i \right)^{\tilde{n}} \cos \left(\tilde{n} \left(\theta-\tilde{\theta} \right) \right) e^{i2 \pi \left(\frac{1}{4}+\frac{n}{N} \right) } \end{aligned} $$
(4)

with:

$$\begin{array}{@{}rcl@{}} A &=& \frac{1}{i\lambda z}e^{ikz}e^{i\frac{kr^{2}}{2z}} e^{-i \frac{z}{2k\rho^{2}}} \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} C &=& \text{circ} \left(\frac{z \lambda}{r_{\mathrm{p}}\,R_{0}} \right) \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} \rho &=& \frac{r_{\mathrm{p}}}{2\pi} \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} \tilde{\theta} &=& \left(n+\frac{1}{4} \right) \frac{2\pi}{N} \end{array} $$
(8)

Results and discussion

Near-field distribution

Evaluation of Eq. 4 shows that depending on each N, certain terms of the series are equal zero. Therefore, only a finite number of azimuthal harmonics \(\tilde {n}\) have to be taken into account generating the resulting field distribution in the near-field region. Figure 2 gives an overview on the corresponding intensity distribution of each contributing azimuthal harmonic \(\tilde {n}\) along the radial component r in the transversal observation plane.

Fig. 2
figure 2

Azimuthal harmonics \(\tilde {n}\) contributing to the field according to Eq. 4. Here, the cases (a) N=3 (b) N=4 (c) N=5 (d) N=6 are shown as a function of r. For all examples, we assume rp=32 μm,M=15 and z=12 mm

Full size image

The analysis shows that in each case the contributing azimuthal harmonics can be expressed by \( \tilde {n}=1, qN\pm 1\) with \( q \in \mathbb {N} \backslash \{0\} \). Each contribution results in a weighted Bessel beam with a TC of \(\mid l \mid =\tilde {n}\). Here, these Bessel modes are referred to as fundamental vortex modes (FVMs). Successive FVMs have alternating algebraic sign. The first sign results from the orientation of the object as for an increasing slope of the structure (Fig. 1b) it is positive, for an negative slope negative, respectively. Thus, the result can also be seen as axial superposition of different isotropic fundamental vortex modes [32]. Note that not all high harmonics \(\tilde {n}\) have to be taken into account as their contribution is either comparatively low or near zero as they cause high orders of the Bessel function (see Eq. 4). With respect of a high number of blades (N), the field distribution of the discretized spiral axicon resembles the not discretized spiral axicon, as the second contribution does not influence the contribution of the first harmonic \(\tilde {n}=1\). Therefore, for high N, the resulting field distribution near the optical axis solely consists of a Bessel beam with the TC l=1.

The resulting field distributions with corresponding symmetry axis for different N of the object structure are illustrated in Fig. 3. All intensity distributions exhibit zero intensity in the center. Comparing the zero contours of real- and imaginary part (see right column in Fig. 3) and the phase distributions (see middle column in Fig. 3), all distributions contain an on-axis screw dislocation (SD) in the center.

Fig. 3
figure 3

Resulting field distribution for rp=32 μm,M=15,λ=632.8 nm and z=12 mm: (left column) intensity distribution, (middle column) phase distribution with vortices indicated by black circles, (right column) zero contour lines of real and imaginary part with positive and negative charged vortices indicated by blue and red circles, respectively, for (a)–(c) N=3, (d)-(f) N=4, (g)-(i) N=5 and (j)-(l) N=6 blades

Full size image

Further examination of the real and imaginary zero contour identifies additional off-axis SD at their intersections. The SDs are arranged symmetrically around the center leading to an optical vortex lattice. The optical vortices with positive and negative charge are indicated by blue and red circles in the right column of Fig. 3. Each phase profile around these singularities exhibits a decreasing/increasing phase with a phase step of Δϕ=±2π corresponding to an optical vortex. Here, the ring integral was used for the determination of the SDs. The result leads in all cases to an single charged optical vortex with the corresponding TC of

$$\begin{array}{@{}rcl@{}} l=\frac{1}{2\pi} \oint \nabla \phi \,d \vec s =1 \quad \text{or} \quad l=-1 \end{array} $$
(9)

depending on the orientation. Both, the positions of the PS, and the closed path integral were determined numerically based on the analytical calculations. Note the geometrical position of the SD depending on the symmetry given by N and the corresponding anticorrelated (alternating) charge so that OVs of the same charge are no direct neighbours. For N=3, Fig. 3 does not indicate all OVs as their spatial extend is small, as they are to close to neighbouring OVs or they are connected to a low intensity level.

The angles of the intersection of the zero contour lines of the real- and imaginary part reveal further characteristics of the vortices [36, 37]. While for a conventional isotropic on-axis vortex, the contour lines for ℜ(u)=0 and I(u)=0 intersect under an angle of 90°, this is not true for the off-axis vortices shown in Fig. 3. Instead, here one observes anisotropic characteristics. Such optical vortices are referred to as non-canonical vortices, which here also correlates with a non circular symmetry of the intensity distribution of off-axis vortices. This behaviour is also depicted in Fig. 4a– c, which outlines the phase distribution along one circumference around the SDs with the radius rps. With smaller division ratio in azimuthal direction of the grating further off-axis vortices occur as the amplitudes of the higher azimuthal harmonics rise [30]. More over, the first order off-axis vortices shown in Fig. 3 develop a more isotropic behaviour whereas the second order off-axis vortices have comparable anisotropic behaviour like presented in Fig. 4.

Fig. 4
figure 4

Phase distribution of the on-axis vortex as a function of θ for different N at z=12 mm and with the radius of the circumference of (a) rps=1 μm; (b) rps=5 μm; (c) rps=11 μm. (d) Phase distribution around the SD at xps=yps=26.38 μm for N=6 at z=12 mm with rps as parameter. Note that the phase distributions for different N (a-c) and different rps (d) were each shifted by different multiples Δθ=0.25π for a better overview

Full size image

The on-axis vortex of the modulated spiral axicon with N=3 exhibits rising anisotropic character with increasing rps. The strong anisotropic character in Fig. 4c, on the one hand, results from the low distance of the circumference to the adjacent negative charged off-axis SD and on the other hand can also be derived from the strong curvature of the real and imaginary contour. Equivalent but weaker behaviour with rising rps can be observed for N=4 and N=5. The phase distribution’s inclination becomes more constant with increasing N at higher rps. Note that the higher the number of blades N of the structure gets, the more the field distribution corresponds to the unmodulated spiral axicon.

In the following, the structure with N=6 will be considered in detail. In contrast to the on-axis vortex, the off-axis vortices are unlikely to be isotropic. Figure 4d shows the phase distribution around one particular off-axis singularity (xps=yps=26.38 μm for different values of rps at z=12 mm for N=6 blades.

For better comparison, Fig. 5a and b depict the azimuthal phase gradient along one circumference with different radii rps around the SD of the on-axis and off-axis vortex, respectively.

Fig. 5
figure 5

N=6 and z=12 mm: azimuthal phase gradient along the circumference with different rps (a) around the on-axis SD; (b) around the off-axis SD at xps=yps=26.38 μm

Full size image

The azimuthal gradient of the on-axis vortex exhibits sixfold rotational symmetry, which correlates to the six corners of the on-axis intensity maximum with donut shape. Moreover, the OV can be seen as isotropic within a certain range, as the oscillations are comparatively small for rps≤9.25 μm, where the intensity of the on-axis vortex reaches its maximum. The off-axis vortex shown in Fig. 5b has in general strong anisotropic behaviour which increases for higher rps of the circumference, as in this case, the circumferences also approach adjacent off-axis SDs.

Further investigations reveal that neither the position of the SDs changes along z, nor the azimuthal phase gradient illustrated in Fig. 5 changes along the propagation direction. The calculated gradient in z-direction ∂ϕ(r,θ,z)/∂z, resulting from Eq. 4, has no azimuthal dependencies:

$$\begin{array}{@{}rcl@{}} \frac{\partial \phi(r,\theta,z)}{\partial z} = k-\frac{1}{2k} \left(\frac{2\pi}{r} \right)^{2}- \frac{kr^{2}}{2z^{2}} \end{array} $$
(10)

The first and the second terms are the derivative of the phase connected to the traveling plane wave and the longitudinal phase variation, respectively. The third term is the derivative of a quadratic phase front which remains from the approximation by the method of stationary phase [35]. Both, the second and the third term are negligible compared to the first term. Therefore, Eq. 10 shows that the transversal vortex lattice structure persists along propagation in z-direction in the above defined near-field region.

The resulting 2D - phase gradients in Cartesian coordinates are depicted in Fig. 6 for the on- (top row) and off-axis vortex (bottom row). The value of the gradient is limited to ±5×105 for a better overview.

Fig. 6
figure 6

Calculated transversal phase gradient in Cartesian coordinates at z=18 mm (left column) or (a)+(c) \(\frac {\partial \phi (x,y)}{\partial x}\); (right column) or (b)+(d) \(\frac {\partial \phi (x,y)}{\partial y}\); (top row) or (a)+(b) on-axis vortex; (bottom row) or (c)+(d) off-axis vortex. The value of the gradient is limited to ±5×105 for a better overview. The solid curves represent lines of zero gradient on the x-axis (y-axis) for the x- (y-) component of the gradient. The dashed lines indicate maximum/minimum of the lobes of the corresponding gradient distribution

Full size image

In case of an isotropic vortex, the azimuthal phase gradient, given by \(\frac {1}{r} \frac {\partial \phi }{ \partial \theta }\), is proportional to the inverse of the radial coordinate, irrespective of the angle θ. In general, the phase gradient in azimuthal coordinates is associated with the Cartesian coordinates by:

$$\begin{array}{@{}rcl@{}} \frac{\partial \phi (x,y)}{\partial x} &=& \frac{\partial \phi (r,\theta)}{\partial r} \cos \left(\theta \right) - \frac {1}{r} \frac{\partial \phi (r,\theta)}{\partial \theta} \sin \left(\theta \right) \end{array} $$
(11)
$$\begin{array}{@{}rcl@{}} \frac{\partial\phi (x,y)}{\partial y} &=& \frac{\partial \phi (r,\theta)}{\partial r} \sin \left(\theta \right) + \frac {1}{r} \frac{\partial \phi (r,\theta)}{\partial \theta} \cos \left(\theta \right). \end{array} $$
(12)

For an isotropic vortex the gradient distributions on the coordinates axes are linked by:

$$\begin{array}{@{}rcl@{}} \frac{\partial \phi(x,y)}{\partial x} &=& - \frac{1}{r}\frac{\partial \phi (r,\theta)}{\partial \theta} \sin \left(\theta \right) \quad \text{for} \quad x=0 \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \frac{\partial \phi(x,y)}{\partial y} &=& \frac{1}{r}\frac{\partial \phi (r,\theta)}{\partial \theta} \cos \left(\theta \right) \quad \text{for} \quad y=0 \end{array} $$
(14)

Therefore, in both cases, the gradient distributions in Cartesian coordinates exhibit lobes with different algebraic sign above and underneath the x-axis, and right and left of the y-axis, respectively. This behaviour can be seen for the x- and y- components of the gradient for the on-axis vortex (see Fig. 6a, b). The black curve in Fig. 6 indicates the zero-value on the x- and y-axis, respectively. Furthermore, the dashed lines indicate the axis, where the absolute value of the x- and y-component equals the azimuthal phase gradient without respect to the sign. The orientation of the TC (positive/negative), is given by the direction of the azimuthal phase gradient. This can in turn be calculated from the gradient distribution in Cartesian coordinates, where characteristic lobes are recognizable. Near the middle point, the solid (which is straight near the middle point) and the dashed lines are perpendicular to each other. In the outer region of the distribution shown in Fig. 6a, b, the distribution loses its mirror symmetry correlating to the results from Fig. 5.

Figure 6 (bottom row) illustrates the distribution of the x- and y- component of the gradient for the off-axis vortex in Cartesian coordinates. Here, this distribution again exhibits lobes similar to Fig. 6 (top row). In the off-axis case, the dashed lines in the x- and y - gradient distribution are curved and not perpendicular to the zero lines. The gradient distribution exhibits no mirror symmetry. This represents the anisotropy and correlates with the results indicated in Fig. 5. The amount of the x-component of the gradient in Cartesian coordinates does not equal the azimuthal phase gradient on the dashed line in this case, neither does the y-component on the other dashed line. This is owed to the fact of an off-axis vortex which requires a coordinate transformation for further investigation. Here, we concentrate on an qualitative considerations.

Experimental results

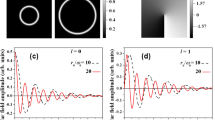
Figure 8 depicts the experimental results obtained with an helium-neon laser at λ=632.8 nm. The experimental setup is presented in Fig. 7. The structured spiral axicon with N=6 blades has an radial period rp=32 μm and a diameter D0=960 μm. The measured intensity distribution at z=18 mm can be seen in Fig. 8a showing one intensity maximum in donut shape in the center (on-axis) and six maxima in donut shape arranged symmetrically around the on-axis maximum. The transversal intensity distribution was 20× magnified. The pixel size of the CCD camera was 4.75 μm×4.75 μm. The corresponding wavefront measurement, obtained with a Shack-Hartmann-sensor, can be seen in Fig. 8b and c for the on-axis and off-axis vortex, respectively.

Fig. 7
figure 7

Experimental set up

Full size image
Fig. 8
figure 8

Measurement of the discretized spiral axicon with N=6, rp=32 μm, aperture diameter D0=960 μm at z=18 mm illuminated by a helium-neon laser with λ=632.8 nm and 5mW power (a) intensity distribution with CCD-camera (4.75 μm×4.75 μm pixel) with 20× magnification; measured spot deviation obtained with a Shack-Hartmann sensor and 50× magnification of (b) on-axis and (c) off-axis vortex. Note, that the arrows representing the spot displacement are stretched by the same factor for a better overview

Full size image

The Shack-Hartmann sensor used in the measurement has a pitch of 130 μm. In order to resolve the wavefront of the vortices, a sufficient magnification had to be used. In our experiments, this magnification was 50× to yield a donut diameter on the sensor camera about 1.5 mm.

The vector fields shown in Fig. 8b and c demonstrate the isotropic character of the on-axis vortex and the anisotropy of the off-axis vortex, respectively. Both are in agreement with Fig. 6. We would like to explain the asymmetric behaviour of the off-axis vortices in more detail with a qualitative and geometrical evaluation of the experimental data. The resulting phase gradient can easily be calculated from the measured spot displacement shown in Fig. 9.

Fig. 9
figure 9

Calculated phase gradients from spot displacement in Cartesian coordinates at z=18 mm: (left column) or (a)+(c) \(\frac {\partial \phi (x,y)}{\partial x}\); (right column) or (b)+(d) \(\frac {\partial \phi (x,y)}{\partial y}\); (top row) or (a)+(b) on-axis vortex; (bottom row) or (c)+(d) off-axis vortex

Full size image

The axes shown here (continuous and dashed lines) are used to demonstrate the same behavior of the phase gradient for the on- and off-axis situation. By comparison with the calculated results shown in Fig. 6, on can observe that the experimental distribution in Fig. 9 match the predictions.

Conclusion

We have discussed and demonstrated the use of discretization as a design tool for the generation of complex vortex fields. Theory was described for the general case, and experimental results have been presented for a specific example of a six-pronged element where both, radial and azimuthal coordinate, were discretized. As a result, we obtained a non-diffracting optical vortex lattice in the near-field region. The positions of the SDs are fixed along propagation. The longitudinal phase gradient exhibits no azimuthal dependencies. Further examination have revealed the characteristics of the on- and off-axis vortices. The on-axis vortex shows isotropic characteristics near the vortex middle point, whereas the off-axis vortices, which are arranged symmetrically around the on-axis vortex, involve an anisotropic phase distribution. The resulting field distribution can be seen as superposition of different non-diffracting fundamental vortex modes. In addition to the theoretical analysis, we have shown several experimental results obtained with lithographically fabricated diffractive elements. In particular, we would like to emphasize the measurements of the phase gradients which were carried out with a Shack-Hartmann sensor. The SHS has proven to be a practical tool for this purpose, yielding quantitative results which can be further analyzed. Theoretical and experimental results are in good agreement.