Background

Phase-shifting interferometry (PSI) is a technique used in optical interference metrology. This technique has high precision and good stability, can be implemented through a variety of hardware, and has been consistently observed by researchers. Many algorithms have been developed to retrieve phase from a group of phase-shifted interferograms. Classical phase-shifting algorithms include fixed steps, variable steps, or random phase-shifting [1]. In recent years, researchers proposed a lot of interesting algorithms, including the two-frame phase shifting algorithms with regularized fringe pattern [2,3,4], the unknown or uncalibrated extraction algorithms [5, 6], and the generalized phase shifting method [7], etc. On some occasions, global phase-shifting value is a known value. The estimated value can be provided through existing information from previous measurements. However, many PSI algorithms need to calibrate the influence of phase-shifted errors from environment vibration, nonlinear response or unbalanced piezo-electric effect. In some other cases, global phase-shifting itself is unknown, which needs to be determined from a series of interferograms.

With respect to solutions of global phase-shifting values among interferograms, Farrell and Player proposed a method based on Lissajous figure fitting [8]. Brug proposed a method based on calculation of the correlation between two images [9]. Goldberg and Bokor, et al., proposed a method based on single-point Fourier transform [10], which calculates global phase-shifting by comparing the changes in power of the carrier frequency between two interferograms. However, all interference signals have limited length; carrier frequency is not a single frequency; spectral leakage may occur on the + 1 (or − 1) order signal frequency spectrum. Calculated the power change in a single frequency, alone, cannot comprehensively reflect the change in the global phase-shifting and cause the loss of calculation precision. Guo and Rong, et al., proposed an Energy-minimum Fourier Transform algorithm (EMFT) [11]. This method attempts to locate the best range of + 1 (or − 1) order signal frequency spectrum from the power spectrum, and therefore can increase the calculation precision for global phase-shifting under the same conditions. However, the interferograms from the measurements are affected by a variety of factors such as the effect of interferograms apodization, the uneven background, the signal envelope and the random noise. As a result, spectral aliasing may occur between the sideband of + 1 (or − 1) order spectrum and zero order signal frequency spectrum. This issue significantly reduces the precision of the calculation results, especially when the carrier frequency is low. Therefore, some methods for zero order spectrum elimination or suppression were proposed [12, 13]. In recent years, methods with Hilbert Transform (HT) and Hilbert-Huang Transform (HHT), aided by Empirical Mode Decomposition (EMD) have been used to suppress the unevenness of background [14,15,16]. On one hand, this issue reduces the robustness of the algorithms; on the other hand, because the generation of interferograms are constraint by the detector and hardware configuration, the choice of carrier frequency is not unlimited. In order to resolve this problem, Vishnyakov and Levin, et al., proposed a method to first do subtraction between two interferograms and then perform the Fourier Transform. This can effectively avoid the spectral aliasing and preserve relatively high calculation precision even when the carrier frequency is low [17, 18]. However, under this method, three interferograms are required for calculation, which limits its applicability.

In this paper, we propose a global phase shifting extraction method which is simple and direct. This method performs algebraic calculation of two interferograms with the assistance of Hilbert transform, and inserts the attempted global phase shift value into assessment function for calculation. The process is repeated until the value of the global phase shift in determined. The proposed method has better precision and robustness in scenarios of spectral aliasing or non-periodic apodization and potential applicability in various aspects of digital holography, interferometry, surface metrology, etc. [19,20,21,22]. This paper introduces the theory behind the method, analyzes the accuracy and adaptability with numerical simulations and experiment.

Methods

A common expression for an interferogram can be written as:

$$ {I}_t=a(x)+b(x)\cos \left[\varphi (x)+ kx+{\delta}_m\right]. $$
(1)

In which α(x) is the background, b(x) is amplitude modulation, kx is the carrier frequency, both of which are functions of x. φ(x) represents phase distribution, δ m represents the global phase shift at the mth measurement, which is the value to be estimated in this article. The algorithm in this article applies to scenarios with one-dimensional or two-dimensional interference signals. One or more row/column of data needs to be selected to determine the global phase shift of the interferogram. Generally speaking, assuming that the background and the modulation intensities are unchanged in the entire phase shifting process, the intensity before and after the phase shift can be written as:

$$ {I}_1=a+b\cos \left[\varphi + kx\right], $$
(2)
$$ {I}_2=a+b\cos \left[\varphi + kx+\delta \right]. $$
(3)

The part of zero order frequency is background intensity. The possibility of spectral aliasing can be reduced by eliminating uneven background. Subtract Eq. (3) from (2) and use trigonometric identities to get:

$$ {\displaystyle \begin{array}{c}{I}_m=\left({I}_1-{I}_2\right)/\left(-2\right)\\ {}=b\left[\cos \left(\varphi + kx+\delta \right)-\cos \left(\varphi + kx\right)\right]\\ {}=b\sin \left(\frac{\delta }{2}\right)\sin \left(\varphi + kx+\frac{\delta }{2}\right)\end{array}} $$
(4)
$$ {\displaystyle \begin{array}{c}{I}_p=\left({I}_1+{I}_2\right)/2\\ {}=a+b\left[\cos \left(\varphi + kx+\delta \right)+\cos \left(\varphi + kx\right)\right]\\ {}=a+b\cos \left(\frac{\delta }{2}\right)\cos \left(\varphi + kx+\frac{\delta }{2}\right)\end{array}} $$
(5)

In which I m is generated after uneven background is eliminated and can be seen as a cosine signal with envelope. Perform the Hilbert Transform and take its imaginary part to obtain the cosine expression of Eq. (4). Because the Hilbert Transform of a sine signal takes the negative value of its cosine signal:

$$ {\displaystyle \begin{array}{c}{I}_{mc}=-\mathrm{H}\left[{I}_m\right]\\ {}=b\sin \left(\frac{\delta }{2}\right)\cos \left(\varphi + kx+\frac{\delta }{2}\right).\end{array}} $$
(6)

In which H[⋅] represents the Hilbert Transform of the function; Take the phase shift value δ as the variable and incorporate Eqs.(5) and (6) to get:

$$ F\left(\delta \right)={\int}_l\left|{I}_p(x)-{I}_{mc}(x)\cdot \cot \left(\delta /2\right)\right| dx. $$
(7)

This is the test function for the determination of the global phase shift. I p and I mc are functions of x; the range of integral is the length of the entire signal l. For discretely sampled signals, summation instead of integration is used. The value to be determined is δ, the global phase shift corresponding to the minimum value of Eq. (7). The basic steps of the algorithm elaborated in this article include:

  1. 1.

    Capture two linear carrier interferograms, I1 and I2, that include unknown global phase shift;

  2. 2.

    Calculate for I p , I m and I mc in accordance with Eqs. (4), (5), (6);

  3. 3.

    Set the initial value of δ and incorporate Eq. (7) to calculate the value of the assessment function;

  4. 4.

    Set the range for δ and the step interval ∆δ, adjust the value of δ, and incorporate F(δ) for additional calculation;

  5. 5.

    Repeat this step until all F(δ) are solved;

  6. 6.

    Find the minimum value of F(δ), which is the global phase shift to be determined.

    Note that when δ → 2πn(n = 0,1,2,---), cot(δ / 2) → ∞. In this situation, this algorithm is invalid as there seems to be no phase shift between the two interferograms. The difference interferograms should be analyzed if this occurs. If only random noise exists and there is no periodic change in intensity, then it should be concluded that no phase shift occurs between the two interferograms.

Results and discussion

Numerical simulation

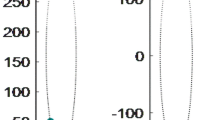
To confirm the validity of the method proposed in this article, we simulated a set of one-dimensional signals with relatively high carrier frequency, as shown in Fig. 1a. The corresponding power spectrum of I1 is shown in Fig. 1b. The range of the selected + 1 order frequency spectrum is marked in the figure. In the expression of this signal, α = -0.3x2, b=-0.3(x - 0.02)2 +0.9, the phase distribution φ = 0.1x2, and the carrier frequency k = 6.6π. 3% random noise is added to this set of signals. The horizontal coordinates for this set of signals x ∈[–1.02, 0.90]; the corresponding kx ∈[–6.7π,5.94π]. The cutoff point of the signal is not selected to be at the position of a full cycle of the carrier frequency. The envelope is not centrally symmetrical. The phase shift between the two interference signals is δ = π/3. Sampling includes 201 points. The odd number for the sampling is for the easy search for central frequency under the EMFT method. The above described interference signal module is commonly seen in practice. The uneven background intensity is included in this pair of interferograms. The amplitude modulation differs at different positions of the interference fringes. We can see from Fig. 1a that this set of interference signals include about 6 fringes. We call it a “high” carrier frequency signal, in comparison with the signal described later in this article that includes only 0.5 fringes. It is relative in our discussion.

Fig. 1
figure 1

High carrier frequency interference signal; part of the power spectrum curve of I1 and the range of the selected + 1 order window

Full size image

We move along the Y-axis the assessment function curve for the EMFT method in Fig. 2 for comparison with the assessment function for the method introduced in this article. As seen in the figure, the EMFT method can accurately capture the + 1 order when the carrier frequency is high. The global phase shift determined under the method in this article and under the EMFT method are respectively 1.044rad and 1.045rad. Both are consistent with the set value.

Fig. 2
figure 2

The curves of the assessment functions under the method proposed in this article and under the EMFT method (~ 6 fringes)

Full size image

When we keep the other parameters unchanged, decrease the carrier frequency to k = 0.7π, and include approximately 0.35 fringe in the entire signal, the two interference signal curves are shown as in Fig. 3a. The corresponding power spectrum is shown as in Fig. 3b. In this scenario, the error will be greater than under EMFT if we perform calculation with the single point Fourier Transform method. Meanwhile, the EMFT method is useful to increase the precision of determination as it adjusts the location and the range of the integration based on different carrier frequencies, but its potential impacts on the assessment functions from inappropriately chosen windows are also evident. As the carrier frequency decreases, the + 1 order frequency spectrum is not readily determinable. We carefully select the range of the + 1 order frequency spectrum and mark it with a dotted square in Fig. 3b. Based on the + 1 order frequency spectrum range as shown in the figure, we use the EMFT method to calculate the assessment function and portray it, along with the result from the method from this article, in Fig. 4. As seen from the curves in the figure, the results from the two methods are patently different. The result from the method in this article is δ = 1.025rad, whereas the phase shift calculated from the EMFT assessment function is δ = 1.113rad. As our set phase shift value is δ = 1.047rad, the relative errors for the two methods are 2.1% and 6.3%. The comparison results show that the precision from the two methods are comparable if the fringes are relatively many; but as fringes are significantly fewer, the reported method is superior to the EMFT method in its functionality.

Fig. 3
figure 3

Low carrier frequency interference signal; part of the power spectrum curve of I1 and the range of the selected + 1 order window

Full size image
Fig. 4
figure 4

The curves of the assessment functions under the method proposed in this article and under the EMFT method (~ 0.5 fringes)

Full size image

In order to further compare the relatively errors between the two methods, we gradually increase the carrier frequency of the simulated signal, i.e. to increase the number of the interference fringes, and perform calculation based on the two methods. We report the relatively error curves in Fig. 5. When the fringes are few, the calculation errors from both methods increase; as the fringes increase, the relative errors gradually decrease. Generally, the method in this article generates lower errors than EMFT; its curve depicting the change in error is rather flatter, showing that the error values are relatively stable. EMFT, in comparison with the method in this article, generates higher relatively errors; the fluctuation is also higher. The method introduced in this article is evidently more advantageous, particularly, when the fringes are rare.

Fig. 5
figure 5

Comparison of relative errors

Full size image

From the perspective of signal shapes, the above described simulated signals include various interfering factors that may impact the calculation of global phase shifts, including, as documented in Literature ([21], 33–34), unevenness in background intensity and modulation envelopes (α ≠ constant, b ≠ constant), low carrier frequency, signal noises, non-periodic apodization, and etc. For a linear carrier interferogram, if the signal is non-periodic, the sideband of the carrier frequency signal will be broader; if the carrier frequency is not high enough, then it will spectrally aliased with the baseband signal. In practice, however, most interference signals are usually not single frequency. The location of apodization is not readily selected for reasons such as background and modulation unevenness.

Experimental results

In this section, we will verify the performance of the algorithm with experiment data. A group of linear carrier interferograms with a Zygo GPI interferometer has been recorded. Fig. 6 shows these phase shift interferograms, the resolution of these images is 256 × 256 pixels. These interferograms do not have any pre-processed including filtering or background removal etc. For these interferograms, we perform calculation of data of each row and column between M1 (Fig. 6a) and M2 (Fig. 6b) with method mentioned in the previous section. The global phase shift range to try into the Eq.7 should be [0, 2π], but in order to avoid infinity, we choose a variable range of [0.03π, 1.94π] and search step is 0.0047π. And the corresponding assessment function values of all rows and columns are shown in Fig. 7a and b respectively.

Fig. 6
figure 6

Linear carrier interferograms. (a) M1 (b) M2 (c) M3

Full size image
Fig. 7
figure 7

Assessment function value of each row and column. (a) row (b)column

Full size image

Each column data in Fig. 7 shows the assessment function calculated from one slice data, x-axis indicates the phase step, and the color map means evaluation value. From the graph above, we can find the minimum point for each column in the graph, and display the result in Fig. 8. The solid line in blue and the dot line in red are represent estimated phase step from each row and column respectively. The RMS of two curves are 0.018rad and 0.028rad, while the average values are 1.597rad and 1.610rad. We use the average of the two averages as the final estimated global phase shift. The running time is 0.32s (mean of 10 independent runs) based on a computer with a 3.3GHz i5 CPU and 8GB RAM using MATLAB®.

Fig. 8
figure 8

Curves of estimated phase step from each row and column

Full size image

Using the same method, we calculate the global phase step between M1 (Fig. 6a) and M3 (Fig. 6c), and plot the result in Fig. 9. The result indicates the phase step between these two frame is 3.14rad. From those three phase-shift interferograms, the sought phase distribution ϕ(x, y) can be extracted by the equations below.

$$ \left[\begin{array}{ccc}3& \sum \cos \left({\delta}_i\right)& \sum \sin \left({\delta}_i\right)\\ {}\sum \cos \left({\delta}_i\right)& \sum {\cos}^2\left({\delta}_i\right)& \sum \sin \left({\delta}_i\right)\cos \left({\delta}_i\right)\\ {}\sum \sin \left({\delta}_i\right)& \sum \sin \left({\delta}_i\right)\cos \left({\delta}_i\right)& \sum {\sin}^2\left({\delta}_i\right)\end{array}\right]\left[\begin{array}{c}{D}_1\\ {}{D}_2\\ {}{D}_3\end{array}\right]=\left[\begin{array}{c}\sum {M}_i\\ {}\sum {M}_i\cos \left({\delta}_i\right)\\ {}\sum {M}_i\sin \left({\delta}_i\right)\end{array}\right], $$
(8)
$$ \phi \left(x,y\right)=- arc\tan \left[\frac{D_3}{D_2}\right], $$
(9)
Fig. 9
figure 9

Curves of estimated phase step from each row and column between M1 and M3

Full size image

Where, i = 1,2,3, δ1 = 0, δ2 = 1.6037rad, δ3 = 3.146rad. The phase demodulation result for the considered experimental data is shown in Fig. 10. The linear carrier frequency pattern has been removed from the unwrapping map.

Fig. 10
figure 10

Wrapped (a) and unwrapped (b) phase extracted from the experimental data

Full size image

Conclusions

This article reports a method to estimation the global phase shift with two interferograms. Compared with existing methods, this method requires no pre-filtering, nor does it have specific requirement for the carrier frequency of the interferograms. During the calculation, this method does not require the selection of a window for integration. It therefore increases the algorithmic adaptability and provides easy automatic processing. The method in this article may resolve the problem of global phase shift calculation when the interference signal faces a variety of factors such as nonperiodic apodization, uneven background and modulation. It also has better precision and robustness than previous methods in scenarios of spectral aliasing between the + 1 order spectrum and the zero order spectrum. The method in this article can calculate the global phase shift with only two interferograms. We believe that this method has broad potential applicability in various aspects of interferogram processing. And it could be extending to process the closed fringe patterns. In practice, this method can be used to screen out one or more sets of interferograms that meet the global phase shift needs from a series of interferograms for further calculation and analysis. This article provides the rationale and process of the calculation under this method, compares it with the existing method that needs Fourier Transform based on simulated interference signals, demonstrates the superiority of the method in this article, and confirms the precision of calculation with this method with data from experimental measurements.