Introduction

The North Anatolian fault (NAF) system across the Turkey is a right lateral strike-slip fault about 1500 km from Karlıova triple junction to the Sea of Marmara. It plays an important geodynamic role between Anatolian and Eurasia plates by moving with an average slip rate at 20–30 mm/year (McKenzie 1972; McClusky et al. 2000; Barka 1992; Fichtner et al. 2013; Dresen et al. 2007). The western part of NAF system enters the Sea of Marmara in the Gulf of Izmit and then splits into two distinct branches that define, tectonically, northern and southern boundaries of the Marmara region. The complex tectonic structure of NAF system was responsible for many destructive earthquakes in the past (Ambraseys and Jackson 2000), and the recent seismic activity showed an apparently westward propagating sequence of earthquakes since 1939 (Barka 1996; Hubert-Ferrari et al. 2000; Parsons et al. 2000; Stein et al. 1997; Toksöz et al. 1979; Reilinger et al. 2000), leaving a long segment within Marmara Sea near Istanbul as a seismic gap (Le Pichon et al. 2001; Oglesby et al. 2008). On the western part of northern branch of the North Anatolian fault, two strike-slip faults are connected with a fault zone consisting of three basins (Çınarcık, Central and Tekirdağ) in the Marmara Sea. The faults ruptured after 1912 Ganos and 1999 İzmit earthquakes (Le Pichon et al. 2003; Armijo et al. 2002). Also, a pull-apart structure accompanying with normal faulting components seems to control Çınarcık and Central basins (Armijo et al. 2005). Some active faults in the Marmara basin were also historically tsunamigenic (Altinok and Ersoy 2000; Altinok et al. 2011; Ambraseys 2002; Armijo et al. 2005; Hancilar 2012; Ozel et al. 2011; Ozcicek et al. 1966–1967).

The knowledge of the historical earthquakes which occurred in the Marmara Region indicates that İstanbul has been affected by high intensity (I o  = VIII–IX) events for the interval of 250–300 years (e.g., 1509, 1766) (Ambraseys 2002, 2009; Guidoboni et al. 1994; Duman et al. 2016). This available evidence and the existing seismic gap suggest the idea that the destructive earthquake probability in this city is above 65 % in 30 years (Ozel et al. 2011; Parsons 2004; Parsons et al. 2000). Undoubtedly, the high level of seismic hazard poses a major threat to the lives of one-third of total Turkish population (13 millions of inhabitant only in Istanbul) around this city (Altinok et al. 2011; Hancilar 2012; Hubert-Ferrari et al. 2000; Kalkan et al. 2009; Ozel et al. 2011; Parsons 2004; Parsons et al. 2000). Since the earthquake cycle has long period of time, examining historical events can give new insights about the seismotectonics of their respective region (Kanamori 1988). Although the historical earthquakes are so important to the understanding of the seismic characteristics of a region, our knowledge about these earthquakes is very limited, except defining them by macroseismic, paleoseismologic and geological data. In that respect, analyzing historical earthquakes using their original seismograms which were recorded instrumentally comes into prominence which will enable seismologists to expand their knowledge about the seismicity of long period of time of a region (Kanamori 1988; Lee et al. 1988; Batlló et al. 2008). However, this process entails much effort because of the deficiencies in technology of the historical recording systems. Usually the information necessary for all the process of the analyzing of these records, such as instrument constants and time accuracy, is missing or doubtful (Batlló et al. 2008; Kanamori 1988; Abe 1994). The importance of studying historical earthquakes by analyzing original records through the modern techniques has been realized by many researchers over the world (e.g., Baskoutas et al. 2000; Dineva et al. 2002; Kanamori et al. 2010; Lee et al. 1988; Pino et al. 2000, 2008; Schlupp 1996; Schlupp and Cisternas 2007; Stich et al. 2003, 2005; Teves-Costa et al. 1999; Cadek 1987; Abe 1994; Rivera et al. 2002; Kikuchi et al. 2003), which presented different methods and stimulated to carry out more comprehensive investigations about historical earthquakes over the world.

To date, collection and distribution of these early records necessitated too much effort. In recent years, there has been increasing interest in historical seismograms and many initiatives around the world have been intended to create digital forms of the early seismograms and their related material to preserve seismological heritage of the world such as International Data Centre (IDC), World Wide Seismographic Stations Network (WWSSN), and International Association of Seismology and Physics of the Earth’s Interior (IASPEI) (Michelini et al. 2005; Batlló et al. 2008). More recently, SISMOS (Michelini et al. 2005) and EUROSEISMOS (Ferrari and Pino 2003; Ferrari and Roversi Monaco 2005) projects undertook the scanning, archiving and distribution of historical seismograms. KOERI also have taken part of this project which enabled us to obtain old records analyzed in this study to understand the seismological properties of the 1935 and 1963 Earthquakes that occurred in the Marmara Region.

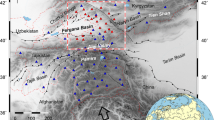
The seismic hazard analysis of Marmara Region is also related to the evaluation of historical earthquakes, especially those which are believed to have taken place in the Sea of Marmara (Ambraseys 2002; Ambraseys and Finkel 1991) (Fig. 1). Understanding seismological properties of the instrumentally recorded 1935 Erdek–Marmara Island and 1963 Çınarcık Earthquakes to understand the seismotectonics of the Marmara Region has also great importance in this assessment. Particularly, the ambiguity of the locations, magnitudes and fault mechanisms of these earthquakes inspired us to study the 1935 and 1963 historical events. Illuminating whether these earthquakes are related to the so-called faults, on the northern branches of the western continuation of the NAF system (Le Pichon et al. 2001), may also contribute to the knowledge of the seismotectonic structure of the region. Several studies had been published on the 1935 and 1963 Earthquakes (e.g., Ambraseys and Finkel 1987; Ambraseys 1988; Özçiçek 1996; Taymaz et al. 1991; Toksöz et al. 1979); however, many of these studies were based on only geological and macroseismic data, which may not be as accurate as found by an assessment using instrumental earthquake records.

Fig. 1
figure 1

Important historical earthquakes (M s  ≥ 7.0) that occurred in the Marmara Region given by Ambraseys (2002)

Full size image

In this study, the historical 1935 Erdek–Marmara Islands M s  = 6.4 and 1963 Çınarcık M s  = 6.3 Earthquakes were investigated using P and S waveform data at regional seismic stations. To carry out this process, the seismic traces recorded on the analog seismograms were obtained in digital form through the vectorization method. The seismic traces acquired in digital form were corrected geometrically to avoid the distortions caused by the needle mechanisms of old-time seismic instruments. In addition, the epicenters of the 1935 Erdek–Marmara Islands M s  = 6.4 and the 1963 Çınarcık M s  = 6.3 Earthquakes were re-determined using the arrival times obtained from ISS Bulletins as well as the P and S readings based on original seismograms through the HYPOCENTRE 3.2. by Lienert (1994). Fault plane solutions were also obtained for the 1935 Erdek–Marmara Islands M = 6.4 and 1963 Çınarcık M s  = 6.3 Earthquakes using the moment tensor inversion time-domain moment tensor inversion (TDMT-INV) algorithm produced by Dreger (2002).

04.01.1935, Erdek–Marmara Island Earthquakes

On 04.01.1935, three successive events occurred in Erdek and Marmara Islands (Figs. 2, 3; Pinar and Lahn 1952). The first shock (M s  = 6.4) was reported to have occurred at 14:41:29 (GMT) and located at 40.64N, 27.51E, with an intensity I o  = IX (MSK) assigned by Ambraseys (1988). The damage caused 5 death and 30 injured. This event was followed by 15:18:57 (GMT) (M s  = 4.6), 15:19:24 (GMT) (M s  = 4.5) Earthquakes. Shortly after these events, there has been another shock which took place at 16:20:05 (GMT) (M s  = 6.3) (Ambraseys and Jackson 2000) and was strongly felt in a large area. The aftershocks were monitored through the recording systems of that period for 3 months. (Pinar and Lahn 1952). The depths of these two earthquakes that occurred at 14:41:29 and 16:20:05 were reported as 20 and 30 km, respectively, by Ayhan et al. (1981). Table 1 shows the epicentral locations given by different sources for 04.01.1935-14:41 and 16:20 (GMT) Earthquakes. It should be noted the large ambiguity of the location.

Fig. 2
figure 2

Epicenter locations for 04.01.1935-14:41 Erdek Earthquake: 1 this study, 2 by Ambraseys (1988) and 3 by ISS Bulletin

Full size image
Fig. 3
figure 3

Epicenter locations for 04.01.1935-16:20 Erdek Earthquake: 1 this study, 2 by Ambraseys and Jackson (2000), 3 by ISS Bulletin

Full size image
Table 1 Epicentral locations given in various sources mostly based on the macroseismic investigations, for the 04.01.1935-14:41 and 16:20 (GMT) Earthquakes
Full size table

Although a seismological study based on original seismic waveforms was not carried out for these two earthquakes that occurred on 04.01.1935, the focal mechanism for the fault concerned has been proposed as 100/40/−90 (strike/dip/rake) by Nalbant et al. (1998) who investigated the Coulomb stress change after these shocks. There are some reports that this earthquake caused tsunami, and its effects were published in some newspapers. One of them is the Kurun newspaper on January 10, 1935, reporting the words of an eyewitness, named Mr. Kevork, of the earthquake. He claimed that when the third shock came, which occurred 45 min after the first shock, he was able to see the sea, which was not normally visible in his position, which may imply an evidence of seismic seawave, as stated by Altınok and Alpar (2006).

18.09.1963, Çınarcık Earthquake

The Çınarcık Earthquake which occurred on 18.09.1963 at 16:58 GMT was located in the western Marmara, with a magnitude of M s  = 6.3 (Fig. 4). It was reported by Ozcicek (1966–1967) that after the earthquake, the seashells were noticed on the coastline of the Mudanya Bay in the east–west direction. Kuran and Yalciner (1993) stated that the sea waves reached about 1 m height along the shore in some region, which may be the evidence that the earthquake is tsunamigenic. Ergin et al. (1967) reported that 4 buildings were destroyed and 2 buildings were damaged and the damage was observed mostly in Çınarcık. There were also reports of damage in Yalova. In total, 7 buildings were demolished in Yalova and Çınarcık Regions. This earthquake caused 1 dead (Ergin, et al. 1967). The locations and the mechanism solutions estimated before are significantly scattered. Different epicentral locations and fault mechanism solutions for 18.09.1963-16:58 (GMT) Earthquake are given in Table 2.

Fig. 4
figure 4

Epicenter locations for 18.09.1963-16:58 Çınarcık Earthquake: 1 this study, 2 by ISS Bulletin, 3 by Taymaz et al. (1991)

Full size image
Table 2 Earthquake parameters given by different sources for 18.09.1963-16:58 (GMT) Earthquake
Full size table

Epicenter estimations

It is a well-known fact that, before the 1960s, for seismological observatories in many places including Mediterranean countries, the quality of input data containing the arrival times is not sufficient for an accurate epicentral location procedure, and the biggest problem is the accuracy of the ISS epicenters, especially before 1960 (Ambraseys and Melville 1982). This fact inspired us to analyze the epicenter of these significant events that occurred in the Marmara Region by assessing the available P and S arrival times using modern approximation.

In order to re-determine the epicenters of the 1935 and 1963 events, we used P and S arrival times based on original seismograms, original bulletins to cross-check the data reported by International Seismological Summary (ISS) Bulletins. We also checked the difference between the theoretical phase readings from travel time tables for ISS Bulletin and also especially the original records which are not in the list of available readings. It has been possible to see the reliability of a station time by comparing the phases with the theoretical arrival times to see whether there are large clock bias, misidentification of the seismic phases, or typing mistakes and so on. We also compared the available seismic stations’ bulletins with the ISS Bulletin data.

Epicentral location was performed using the program HYPOCENTRE 3.2. (Lienert 1994) and the velocity model of Kalafat et al. (1987). The estimated results are shown in Table 3 and Fig. 5. We also used the IASPEI91 velocity model (Kennett and Engdahl 1991) to check the reliability of the results, but the results did not change significantly, which do not exceed 3 km for both events that occurred on ​04.01.1935, and 1 km for the 18.09.1963 Earthquake. The first earthquake that occured in 1935 (at 14:41) has confidence limits of 8 km in longitude and latitude, which defines the epicenter quality. The second event in 1935 (at 16:20) shows errors about 13 km in longitude and latitude. 18.09.1963 Earthquake has errors of about 11 km in longitude and 10 km in latitude. Although errors in longitude and latitude seem to be large for these events, it is possible to observe the large confidence limits for the historical earthquakes, also in the published papers such as Kanamori et al. (2010), Batlló et al. (2008, 2010) and Tobin and Sykes (1968). The data obtained from the ISS Bulletin for this earthquake indicated large errors during the process of epicentral location. For this reason, we followed the process of removing the arrival time readings that show time residuals above 100 s. However, the total RMS value was still too large after the first run. Then, the readings with time residuals larger than 10 s were removed to obtain smaller total RMS value.

Table 3 Location Results of the 04.01.1935, 14:41, 16:20 and 18.09.1963, 16:58 Earthquakes
Full size table
Fig. 5
figure 5

Error ellipses in the location results for both velocity model: 1 04.01.1935-14:41, 2 04.01.1935-16:20, 3 18.09.1963-16:58. Red ellipses indicate the velocity model estimated by Kalafat et al. (1987). Black ellipses indicate the global IASPEI91 velocity model

Full size image

For 04.01.1935-14:41 event, in addition to data from ISS Bulletin, the readings from obtained original records which are not in the list of ISS Bulletin and are seismograms of ISK, ATH, MNH, FBR, COI stations were included. The readings of P and S arrival times from the seismograms of ZUR, STR, PRA, JENA, DBN, COP, BER, ZAG, VIE, PCN stations, which are also available in the ISS Bulletin, were reevaluated. The same procedure was followed also for 04.01.1935-16:20 Erdek–Marmara Island Earthquake. The readings of P and S arrival times obtained from ISS Bulletins indicated large errors for 04.01.1935-14:41 as in the case of first event. The readings based on available original records enabled to compare P and S arrival times with ISS Bulletin and reduce large residuals. As a result, the RMS values were obtained as 2.47 and 3.44 for 04.01.1935-14:41 and 16:20 Earthquakes, respectively.

For 18.09.1963-16:58 Çınarcık Earthquake, the readings based on original seismograms were also available in the list of ISS Bulletins. Therefore, we included these readings in our epicenter solution. Most of the readings for P and S waves based on original records agree with the readings of ISS Bulletins. During the process of epicenter location of the historical earthquakes interest of this study, P and S arrival times in original seismograms were also checked and the large residuals were reduced. The RMS value was acquired as 2.82 for this event. In most cases, our readings for P and S wave agree with the readings of ISS Bulletins. Theoretical arrival times (Additional file 1: Appendix C; Table C1, C2 and C3) were calculated for the velocity model used to compare with the phase reading data. By doing this comparison, the inconsistencies may be recognized in the data of the phases, such as large clock bias, misidentification of the seismic phases or typing mistakes.

We have azimuthal gap in station coverage 139° for ​04.01.1935, 14:41 Earthquake, while the azimuthal gap is 87° for the second event of ​04.01.1935. For 18.09.1963, 16:58 Earthquake, the azimuthal gap is 38°. These azimuthal gap values are sufficient to constrain location accuracy for these events as the largest azimuthal gap is, at worst, 180° as also specified by several authors such as Engdahl et al. (1998, 2007). Furthermore, global bulletins such as those reported by the International Seismologcal Center and the US Geological Survey National Earthquake Information Center (NEIC) that contain predominantly teleseismic arrival time data have an accuracy of 10–15 km when the largest azimuthal gap is < 200° in continental regions, reported by Sweeney (1996) and Zare et al. (2004).

Vectorization and correction procedure of historical seismograms

The historical seismograms used in this study were obtained from the SISMOS seismogram archive in the framework of the EUROSEISMOS Project. European countries were scanned at a resolution of 1016 dpi using very high-quality scanners at the SEISMOS laboratories of the Istituto Nazionale di Geofisica e Vulcanologia in Rome (Michelini et al. 2005; Pintore et al. 2005; Ferrari and Pino 2003; Batlló et al. 2008). In order to use historical seismograms, the raster images of the interested recorded waveform must be converted into vector format with a vectorization procedure. However, it may not be possible to use all the scanned paper seismograms due to the poor quality of the recorded signal and seismograms without recorded earthquakes.

In this study, we obtained 81 seismograms from 23 seismic stations for the 04.01.1935 14:41:29 and 16:20:05 Earthquakes that occurred at Marmara Island–Erdek and 38 seismograms from 11 stations for 18.09.1963-16:58 Çınarcık-Yalova Earthquake. During the analysis of the analog records, we realized that earthquakes of our interest were not registered on some seismograms. Also, it was not possible for some records to be vectorized due to the poor quality of recorded waveforms on paper seismograms. Consequently, we have vectorized 35 seismograms from 16 stations for 04.01.1935 14:41:29, 33 seismograms from 15 stations for 04.01.1935-16:20:05 Erdek Earthquake, and 29 seismograms from 10 stations for 18.09.1963-16:58:08 Çınarcık Earthquake. Figure 6 shows the station locations of obtained seismograms for 04.01.1935-14:41 and 16:20 Marmara Island–Erdek Earthquakes and 18.09.1963-16:58 Çınarcık-Yalova Earthquake.

Fig. 6
figure 6

Station locations of obtained seismograms for 04.01.1935-14:41 and 16:20 Marmara Island–Erdek 18.09.1963-16:58 Çınarcık-Yalova Earthquakes

Full size image

In this study, manual vectorization method that is based on redrawing seismic traces on old record by using the mouse pointer has been used to convert seismic traces recorded on paper to a digital time series. Vectorization process is of considerable effort due to many problems that arise from quality of trace on the paper and the mechanism of traditional seismometers. Examples are pen slipping on the paper and little oscillations that are interpreted as noise on the trace because of instrumentation (Batlló et al. 2008; Kanamori et al. 2010). Correct identification of the earthquake to be studied can also be troublesome, which necessitates counting very carefully time marks available on records. Yet, some of the historical records do not have well-marked time marks, and therefore it is essential to obtain some bulletins for stations and regard delay times of the first arrival times in relation to station distances. Besides, the needle mechanism leads to curvatures of the traces. Inadequate contrast between recorded waveform and the background poses a serious problem during the digitization of the historical seismograms, which may be seen in the case of mechanical recording when the paper was insufficiently smoked (Batlló et al. 1997, 2008, 2010; Kanamori et al. 2010). In this study, we have also encountered some problems that complicate the vectorization process. For example, we observed seismic traces in mesh on historical records (Additional file 1: Figure F1). Since the historical records were exposed to many external factors, it is possible to encounter records including erased parts of traces, which is also another problem that makes difficult to vectorize old seismograms when a part of trace is erased on the paper. If the missing part is small, the erased part can be completed; however, they do not provide a reliable basis when large parts are missing from the records as it seems in Additional file 1: Figure F2 which shows the historical seismogram recorded at KAS (Kastamonu, Turkey) station for the 1963 Earthquake.

After obtaining vectorized scanned seismic traces, it is necessary to carry out some corrections, such as the geometry of the recording system, deconvolution with the instrument response, etc. One of the major problems with the historical seismograms is the curvatures on vectorized seismic traces, which is the result of the mechanism of needle mounted on a finite-length pivoting arm of mechanical seismometer. In such a case, the abscissa of the seismogram cannot be obtained as linear function of time (Grabrovec and Allegretti 1994). In this study, the geometrical distortions such as the pen curvature, uneven paper speed and skew on seismic traces have been corrected by applying the formula of Grabrovec and Allegretti (1994) and Samardjieva et al. (1998).

In that respect, it is necessary to find some parameters for the geometrical corrections as the arm length of the mechanical recording system. In cases where the proper seismic traces could not be obtained after correction process, we tried different solutions to find especially the arm length value of the recording systems of the seismograms. For example, we observed a big problem for the records of ISK (Kandilli) station. Since it has been possible for us to obtain the arm length values by measuring directly from instruments available at ISK (Kandilli) station, we used these values to remove circular arcs on original seismograms for the 1935 Earthquake. This effort considerably changed the seismic traces on the records from its first solutions with wrong arm length value (Fig. 7). The arm length value of the Wiechert ISK (Kandilli) station seismometer was measured as 150 mm, while the value of the arm length of Mainka seismometer was measured as 450 mm. Despite the fact that we obtained more proper seismograms to analyze, there were still problems with the records of ISK station. Probably, this situation arises from the traces that are very close to each other, which also requires a considerable effort during vectorization process. Another example of the curvature correction of the seismogram recorded by Tromometrograph Omori instrument at PRT (Italy) station for the 1935 Earthquake can be seen in Additional file 1: Figure F3.

Fig. 7
figure 7

Comparison between the uncorrected and corrected seismic traces recorded at ISK (Kandilli, İstanbul) station; a the original record from ISK (Turkey) station for the 1935 Earthquake, b seismic traces before curvature correction, c seismic traces after curvature correction

Full size image

The vectorized points of seismic signal recorded on original seismogram were scaled to time (X) and amplitude (Y) axes considering the length between two time marks on the original records to obtain equal time intervals on time (X) axis. In order to acquire equally spaced points on the time axis, a polynomial interpolation method has been used. Interpolated data have been sampled using 0.1 s sampling rate.

The instrument response correction

In order to carry out instrument response correction, the seismic traces have been corrected by specifying transfer function with the free period of pendulum (T o ), damping constant (h) and the magnification (V) of the instrument for mechanical sensors (Herak et al. 1998). In fact, it is sometimes possible to find these values on the original seismograms even though it is a low possibility. However, in general, it is a difficult task to obtain the collection of the instrument constants which are essential to perform the process, for the old seismic recording systems since the necessary documents are not available. For this purpose, a special effort has been made to gather every possible source. These sources include Uccle (UCC), Prague (PRA), Fabra (FBR), DeBilt (DBN), Copenhagen (COP) seismic station bulletins for the year 1935 and Timisoara (TIM) seismic station bulletin for the year 1963, Bulletin of National Research Council in McComb and West (1931) and INGV (http://storing.ingv.it/es_web/Data/Es_map.html, EUROSEISMOS Project). Also, some European observatories (SPC, BRA) have been consulted for the documentation and bulletins of the stations (see Additional file 1: Appendix D; Table D1, D2). Here, it is important to note that the instrument constants given in the Bulletin of the National Research Council cannot be considered of the same value of the station bulletins. We used these values only in the case that we could not obtain the instrument constants from the seismic station bulletins.

Moment tensor inversion

For the moment tensor inversion, three component seismograms of DBN, ZAG, JENA, COP stations for the 1935 Earthquakes and BRA, COP, DBN, PAV, ROM for the 1963 Earthquake were selected. We tried to find more seismograms for this process. We used the locations that we previously obtained for these events to perform this application (Figs. 2, 3, 4). However, as pointed out by many researchers (Kanamori 1988; Lee et al. 1988; Batlló et al. 2008; Stich et al. 2005), studied on analyzing historical records, it is a big deal to find adequate and high-quality old seismograms for the seismological process and to provide much better azimuthal coverage. We had to exclude seismograms from other stations for this analysis since most of them do not have all the three components (usually they have one component), which does not allow us to rotate seismogram components into the cylindrical or spherical coordinate system, which is essential for this process. Vectorized and geometrically corrected seismic traces were converted to SAC format in order to perform the essential operations such as filtering, rotating and integration. TDMT-INV algorithm produced by Dreger (2002) was used to moment tensor inversion. The synthetic data were generated using an algorithm named FKRPROG (Saikia 1994), which calculates the Green’s functions in the frequency domain. The Green’s functions were modeled using the velocity model estimated by Kalafat et al. (1987). The procedure of the coherency between the synthetic and observed waveform is assessed with variance reduction (VR). Here, the objective is the correlation between these synthetic waveforms and the waveforms produced with the earthquake source. In Eq. (1), data i represents the observed waveforms, whereas the synth i indicates the synthetic waveforms (Dreger 2002). The non-DC component, compensated-linear-vector-dipole (CLVD) component, is also depicted in Figs. 8, 9and 10

$$R = \left[ {1 - \mathop \sum \limits_{i} \frac{{\sqrt {\left( {{\text{data}}_{i} - {\text{synth}}_{i} } \right)^{2} } }}{{\sqrt {{\text{data}}_{i}^{2} } }}} \right] \times 100.$$
(1)
Fig. 8
figure 8

VR, CLVD, seismic moment, M w and fault mechanism with corresponding depth for 04.01.1935-14:41 Erdek Earthquake

Full size image
Fig. 9
figure 9

VR, CLVD, seismic moment, M w and fault mechanism with corresponding depth for 04.01.1935-16:20 Erdek Earthquake

Full size image
Fig. 10
figure 10

VR, CLVD, seismic moment, Mw and fault mechanism with corresponding depth for 18.09.1963-16:58 Çınarcık Earthquake

Full size image

We used 0.025–0.075-Hz filter for the both events (14:41:30 and 16:20:05) that occurred on 04.01.1935 and 0.035–0.085-Hz filter for the 18.09.1963 event. For this process, the instrumental correction was performed by multiplying the amplitudes with a coefficient to approximate to synthetic waveforms. These coefficients (Additional file 1: Appendix E) were determined by trying different values by approximating these values to the magnitudes of these events which were previously reported (Tables 1, 2).

In the application of moment tensor inversion, we encountered the common problems also cited by Stich et al. (2005) such as the absence of three components of the historical seismograms, uneven time marks on the records (which results in an incoherency between seismic waveforms when they are superposed to each other). For two earthquakes, the seismograms were obtained from the eastern part of the epicenter, which is a trouble for estimating earthquake fault mechanism. The process of cutting three components from the starting time is troublesome due to the fact that the starting times of the waveforms are usually doubtful on the original seismograms. Radial and transversal components must be obtained by rotating the NS–EW components.

The comparison of the moment tensor solutions for 04.01.1935-14:41 and 16:20 Erdek Earthquakes is given in Fig. 11: (1) the result of this study found for the 14:41 Earthquake 140/56/−98 (strike/dip/rake); (2) the result found for the 16:20 Earthquake 352/51/−77 (strike/dip/rake); (3) the fault mechanism for 04.01.1935-14:41 Earthquake given by Nalbant et al. (1998) as 100/40/−90 (strike/dip/rake). However, it must be reminded that this solution is a preference for modeling this event by examining Coulomb stress changes, not based on the analyzing original records. We believe that we obtained best coherency of the observed and synthetic waveforms (Figs. 12, 13). The moment tensor inversion solutions of this study for fault mechanisms of these two events may contribute to the seismotectonic of the Marmara Region, since no study was carried out using original seismograms. In addition, this rigorous effort contains valuable importance as it clarifies for the first time the fault characteristics of the couple of 1935 Earthquakes. Also, a reasonable consistency between observed and synthetic waveforms was achieved using moment tensor inversion application (Fig. 14) for the 18.09.1963 16:58 Çınarcık Earthquake. We can also see a comparison of the moment tensor solutions for this event in Fig. 15, which seems below.

Fig. 11
figure 11

Comparison of the fault plane solutions for 04.01.1935-14:41 and 16:20 Erdek Earthquakes; 1 the study result for 04.01.1935-14:41 Earthquake; 2 the study result for 04.01.1935-16:20 Earthquake; 3 the fault mechanism for 04.01.1935-14:41 Earthquake given by Nalbant et al. (1998)

Full size image
Fig. 12
figure 12

Fault plane solution and the coherency of the waveforms obtained for 04.01.1935-14:41 Erdek Earthquake

Full size image
Fig. 13
figure 13

Fault plane solution and the coherency of the waveforms obtained for 04.01.1935-16:20 Erdek Earthquake

Full size image
Fig. 14
figure 14

Fault plane solution and the coherency of the waveforms obtained for 18.09.1963 16:58 Çınarcık Earthquake

Full size image
Fig. 15
figure 15

Fault plane solutions for the 1963 Çınarcık Earthquake with their epicenter locations; 1 the result of this study, which gave the normal fault mechanism with 285/59/−101 (strike/dip/rake); 2 the fault solution 304/56/−82 (strike/dip/rake) of Taymaz et al. (1991); 3 the fault mechanism as 152/40/−32 given by Jackson and McKenzie (1984)

Full size image

Discussion

The seismic parameters and fault mechanism solutions were obtained for 04.01.1935-14:41 and 16:20 Earthquakes through the modern seismological techniques based on original seismograms. There are reports about epicenter locations by Ambraseys (1988) and some catalogues, but these are not beyond the macroseismic observations. Also, the accuracy of the ISS epicenter results for pre-1960 earthquakes is discussed by Ambraseys and Melville (1982), which predominates the idea that epicenter locations determined by ISS (1935) for both earthquakes of 04.01.1935 are unreasonable since they are located so far away from macroseismic results (Figs. 2, 3). Therefore, we tried to relocate these events using ISS and seismic station bulletin data and also compare them with available original records. We obtained 40.72N–27.72E for the 04.01.1935-14:41 Earthquake, which is located about 19 km NE of the epicentral location determined by Ambraseys (1988). The second large shock that occurred at 16:20 was located 40.61N–27.43E, which is situated at about 27 km NW of the epicentral location (40.55N–27.75E) determined by Ambraseys and Jackson (2000). Semi-major axes are <30 km for the error ellipses for both earthquakes that occurred in 1935 (at 14:41 and 16:20) (Fig. 5). The confidence limits obtained for these events may seem relatively large compared to those found for some recent earthquakes as in Pierri et al. (2013), which is probably the result of the poor arrival time data of historical earthquakes as pointed out by Kanamori et al. (2010). However, the confidence errors may be obtained with semi-major axis reaching to the values at least 50 km reported by Okal et al. (2012) and Kanamori et al. (2010) for the historical events and also for more recent earthquakes given by Schweitzer and Kennett (2007) and Henry and Das (2002). A thorough re-assessment of the fault mechanism of these earthquakes was one of the objectives of this work since the information of fault characteristics is not available. We investigated the fault characteristics of these two earthquakes, which were not determined previously by analyzing of original seismograms. Nalbant et al. (1998) modeled these two earthquakes as resulted from one rupture for investigating Coulomb stress changes. The appropriate focal mechanism assumption when modeling these earthquakes was chosen as 100/40/−90 (strike/dip/rake). In our study, the fault characteristics of these two earthquakes have been determined for the first time using modern seismological analysis. We found fault characteristics for these two shocks by applying moment tensor inversion on the waveforms obtained by vectorizing on the original records. Comparing the observed and synthetic waveforms, the coherency between them may present reliable solutions.

Our preferred moment tensor solution for the first shock that occurred in 1935 indicates predominantly normal faulting at 4 km depth. The nodal planes have orientations of 140/56/−98 (strike/dip/rake) and 335/34.8/−77.23. As a non-double-couple component, the compensated linear dipole vector (CLVD) of the moment tensor inversion is 4.1, which indicates the smallest CLVD value of the all solutions for this earthquake. Inversion produces a total seismic moment of M o  = 4.112 × 1025 dyn cm (M w  = 6.4). The hypocentral depth with the best fit is 4 km, which indicates that the focus of this earthquake was closer to the surface than previously reported as 20 km by Ayhan et al. (1981). Moment tensor inversion solutions for the second large shock, which occurred at 16:20, gave the Nodal Plane 1, 2 as 352/51/−77 and 153/40/−105 (strike/dip/rake). Seismic moment is M o  = 1.32 × 1025 dyn cm. We choose the fault plane solution for the second event as 352/51/−77 at a depth of 10 km which is much shallower than previous estimate of 40 km (Ayhan et al. 1981). Also, it can be seen that the faulting type changes from normal to reverse fault type in deeper parts (14–20 km) for the first event, and the variance reduction (VR) does not change so much with these different fault mechanisms at different depths, but the CLVD of the chosen solution with respect to depth is much smaller than other (Figs. 8, 16). For the second event, the mechanism changes from normal to reverse at the depth 12 km (Figs. 9, 17). However, the largest VR value is obtained at the depth of 10 km. Also, it should also be noted that VR is not the one aspect that we take into consideration to assess the fault mechanism solutions. One can obtain smaller VR by using more stations with a good azimuthal coverage (Yılmazer 2009), which was one of the problems for us to obtain more seismograms during the process of this study and it may be the result of the variation of mechanisms at some depths. Although the acquired fault mechanism solutions are given by the high degree of sensitivity with respect to the depth with a little change of variance reduction values, normal faulting type of the solutions at the shallower depths found in this study corresponds to the tectonic structure of the Marmara region. Also, the preferences for the solutions of the two possible planes (fault plane and auxiliary plane) were made by the tectonic properties and the knowledge of this region. Some studies show the existence of the normal faulting system in this area such as Parke et al. (1999, 2002) who mentions the basins that are half graben, formed on north dipping fault planes, in the southern Sea of Marmara by using regional grid of high-resolution seismic reflection profiles. They also reported that there is most likely a zone of deformation on the north of Marmara Island. In addition, normal faults dip both north and south bound the deep basins in the Sea of Marmara, which may be interpreted as the uplift of the Islands including the Marmara, Imralı and Princes Island (Taymaz et al. 1991). Some recent studies also report that normal faults observed at a shallow level in the sediment are not deeply rooted (Zitter et al. 2012). In the southern part of the Eastern Ganos Offshore cluster, on the surroundings Marmara Island (especially north, northwest and western parts of the island) which was investigated in detail by Korkusuz (2012) and Korkusuz Öztürk et al. (2015), has extensional fault plane solutions results which backs up the fault mechanism of two events of 1935 that indicated NW–SE normal faulting type.

Fig. 16
figure 16

Fault plane solutions and the variance reduction with corresponding depth for 04.01.1935-14:41 Erdek Earthquake

Full size image
Fig. 17
figure 17

Fault plane solutions and the variance reduction with corresponding depth for 04.01.1935-16:20 Erdek Earthquake

Full size image

Other finding related to these two earthquakes occurred in 1935 is that they are two separate events. We realized the waveforms are not similar to each other in terms of their shape by comparing available original seismograms. This can be seen dominantly on the original seismograms of ISK station. Their nearly equal magnitude and the proximity of occurring time are also indications that the second shock at 16:20 is not the aftershock of the first shock at 14:41.

It can be seen that both events (14:41 and 16:20) in 1935 were located in the vicinity of the Marmara Islands which are northward continuations of Kapidag Peninsula in geological and geomorphological aspect (Altınok and Alpar 2006). It was also reported by Papazachos and Papazachhou (1997) that there has been a similar historical earthquake that occurred in Marmara Island on 11.08.1265. The magnitude and epicenter of this event are given as M = 6.6 and 40.7N, 27.4E, respectively (Papazachos and Papazachhou 1997). The locations of these historical and instrumental earthquakes are not on the main fault zone (Fig. 1) and on the extending southern branch of NAF (Altınok and Alpar 2006).

The location of the 1963 Yalova Earthquake is a significant question since the rupture of this event and western termination of the 1999 Izmit Earthquake are debated (Muller et al. 2006). In this study, epicenter of the 1963 Çınarcık Earthquake is found to be at 40.80N–29.18E, based on the readings on the original seismograms and ISC Bulletin data, in the Sea of Marmara. The semi-major axis of the error ellipse for the 1963 Earthquake is about 10 km (Fig. 5), which is relatively small compared to two events relocated in this study. Our result is closer to the epicenter location (40.80N–29.13E) of ISS Bulletin data for the year 1963. The epicenter location found by Taymaz et al. (1991) is 15 km northeast of the fault of Princes’ Island and 25 km northeast of the Çınarcık Fault pointed out by Muller et al. (2006) (Fig. 4). The epicenter location result determined by this study is 11 km southwest of the location found by Taymaz et al. (1991) and is closer to the Princes’ Island Fault and the margin of the Çınarcık Basin. Another study by Bulut and Aktar (2007) using seismological method for this event creates an uncertainty, especially in the epicenter location. They re-determined the location of the 1963 event using ISC Bulletin data that includes the stations within a 12° distance and found that this event occurred on the north of the Armutlu Peninsula. In that study, they also compared two waveform pairs including mainshocks and aftershocks of 1963 Çınarcık Earthquake and 1999 İzmit Earthquake, which suggested that the similarity of first motion polarity of the compared waveforms may be interpreted as the same fault mechanism of aftershocks of two earthquakes.

The preferred result for 18.09.1963-16:58 Çınarcık Earthquake from moment tensor inversion applications is a fault mechanism with 285/59/−101 (strike/dip/rake) at 12 km. The other nodal plane is obtained as 126/32/−71 (strike/dip/rake). A total seismic moment of M o  = 2.04 × 1025 dyn cm (M w  = 6.2) is found. Taymaz et al. (1991) determined fault characteristics of the 1963 event using P and SH waveforms and first motion polarities of P waves. They found almost pure normal slip on south and north dipping nodal planes with 304/56/−82 (strike/dip/rake). Our preferred solution (285/59/−101) is close to the solution, NE-dipping, pure normal fault which was thought to have ruptured to NE margin of the Çınarcık Basin (Fig. 1), found by Taymaz et al. (1991). Also, NE-dipping plane of our solution is a little steeper and has more easterly strike than their result. As already mentioned, the pull-apart mechanism in the Marmara Sea is thought to have formed the basin structures in this region. The solutions obtained are normal faulting mechanisms with changing the strike that rotates to some degree at the depths 22 and 24 km. Looking at Figs. 10 and 18, the variance reduction values seem to have close values to each other at the different depths. We preferred the solution 285/59/−101 (strike/dip/rake) at 12 km, consistent with the stress tensor alignments of the Northern Çınarcık Basin (Korkusuz Öztürk et al. 2015), by indicating WNW–ESE-trending normal faults as the solution reported by Taymaz et al. (1991). Despite the fact that there are researches implying that Çınarcık basin exhibits compressional (Pinar et al. 2009) and strike-slip motions (Özalaybey et al. 2002), recent studies indicate that there are normal and oblique structures in the Çınarcık area from the analyses of the focal mechanism applications (Karabulut et al. 2002, 2011; Tunç et al. 2011; Örgülü and Aktar 2001). In a very recent study, the present stress state in the Marmara Region was investigated by Korkusuz Öztürk et al. (2015) who analyzed the fault plane solutions with a comprehensive and high-quality data of small earthquakes, finding the normal components in the area that correspond to our fault mechanism solutions. The study demonstrated that normal and oblique faulting system dominates in Çınarcık Basin and Yalova cluster, which matches with the pull-apart mechanism suggested by Armijo et al. (2005). Also, deep basins, resulting of the normal faults, in the Marmara Sea (Taymaz et al. 1991) may also back up this mechanism in the region.

Fig. 18
figure 18

Fault plane solutions and the variance reduction with corresponding depth for 18.09.1963-16:58 Çınarcık Earthquake

Full size image

Conclusion

To conclude, the seismic parameters of three large historical earthquakes, 04.01.1935 (GMT) 14:41 and 16:20 (GMT) Marmara Island–Erdek and 18.09.1963-16:58 (GMT) Çınarcık-Yalova Earthquakes, which occurred in the Marmara Region, have been assessed using original records from mechanical and also electromagnetic (Galitzin 1914) seismographs. The epicenter estimations gave the results 40.72N–27.72E and 40.61N–27.43E for the 04.01.1935-14:41 (GMT) and 16:20 (GMT) Earthquakes, respectively. Furthermore, 18.09.1963-16:58 (GMT) Earthquake was located at 40.80N–29.18E. Despite the fact that we had some deficits in the seismogram quality and limited azimuthal coverage, the fault mechanisms for these events that occurred in 1935 were determined for the first time. Our preferred solution showed that the fault mechanisms for the three events are normal faults and coincide with the seismotectonic structure of the Marmara Region, considering the recent studies (Korkusuz Öztürk et al. 2015; Karabulut et al. 2002, 2011; Tunç et al. 2011; Örgülü and Aktar 2001). These findings may be developed by analyzing also other historical earthquakes in the Marmara Region and attribute to understanding of its complicated seismotectonic structure and seismic hazard analysis.