Abstract
In this article, a technique is proposed for obtaining better and accurate results for nonlinear PDEs. We constructed abundant exact solutions via exp\( ( - \varphi \left( \eta \right)) \)-expansion method for the Zakharov–Kuznetsov-modified equal-width (ZK-MEW) equation and the (2 + 1)-dimensional Burgers equation. The traveling wave solutions are found through the hyperbolic functions, the trigonometric functions and the rational functions. The specified idea is very pragmatic for PDEs, and could be extended to engineering problems.
Similar content being viewed by others
Background
Over the past few decades, researchers have shown keen interest in the solutions of nonlinear partial differential equations (PDEs).In the study of nonlinear physical phenomena, the investigation of solitary wave solutions [1–44] of nonlinear wave equations shows an important role. Scientific problems arise nonlinearly in numerous fields of mathematical physics, such as fluid mechanics, plasma physics, solid-state physics and geochemistry. Due to exact interpretation of nonlinear phenomena, these problems have gained much importance. However, in recent years, a variety of effective analytical methods has been developed to study soliton solutions of nonlinear equations, such as Backlund transformation method [1], tanh method [2–6], extended tanh method [7–12], pseudo-spectral method [13], trial function [14], sine–cosine method [15], Hirota method [16], exp function method [17–25], \( (G^{'} /G) \)-expansion method [26–30], homogeneous balance method [31, 32], F-expansion method [33–35] and Jacobi elliptic function expansion method [36–38]. Ma et al. [39–44] established the complexiton solutions for Toda lattice equation. The theme of the method is that the exact solutions of nonlinear evolution equations can be articulated by exp\( ( - \varphi \left( \eta \right)) \), where \( \varphi \left( \eta \right) \) gratifies the ordinary differential equation (ODE):
where \( \eta = x - Vt. \)
Explanation of exp\( ( - \varphi \left( \eta \right)) \)-expansion method
Now, the exp\( ( - \varphi \left( \eta \right)) \)-expansion method will be explained for constructing traveling wave solutions. Consider the general nonlinear partial differential equation for \( u\left( {x,t} \right) \) is given by,
where \( u\left( \eta \right) = u\left( {x,t} \right), \) \( \phi \) is a polynomial of \( u \) and its derivatives. Solving (2), the following steps are as.
Step 1 We Combine the variables by \( \eta , \)
where V is the speed of wave. Using Eqs. (3, 2) reduced to the following ODE for \( u = u\left( \eta \right) \)
Step 2 The solution of Eq. (4) can be articulated as
where \( a_{n} 0 \le n \le M \) are constants such that \( a_{n} \ne 0 \) and \( \varphi \left( \eta \right) \) satisfies Eq. (1). Our solutions now depend on the parameters involved in (1).
Family 1: When \( \lambda^{2} - 4\mu > 0, \) we have
Family 2: When \( \lambda^{2} - 4\mu < 0, \) we have
Family 3: When \( \lambda^{2} - 4{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu > 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu = 0 \) and \( \lambda \ne 0, \)
Family 4: When \( \lambda^{2} - 4{\kern 1pt} {\kern 1pt} {\kern 1pt} \mu = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda \ne 0, \) and \( \mu \ne 0, \)
Family 5: When \( \lambda^{2} - 4{\kern 1pt} {\kern 1pt} {\kern 1pt} \mu = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda = 0, \) and \( \mu = 0, \)
Step 3 By considering the homogenous principal, in Eq. (4). Considering Eqs. (1, 4, 5), we have \( {\text{e}}^{M\varphi \left( \eta \right)} \). We get algebraic equations with \( a_{n} ,V,\lambda , \mu , \) after comparing the same powers of \( {\text{e}}^{\varphi \left( \eta \right)} \) to zero. We put the above values in Eq. (5) and with Eq. (1), we get some valuable traveling wave solutions of Eq. (2).
Solution procedure
Zakharov–Kuznetsov-modified equal-width equation
Consider the equation,
where \( \alpha ,{\kern 1pt} \beta \) and \( \delta \) are some nonzero parameters. We use \( u = u\left( \eta \right),\eta = x + y - Vt, \) we can convert Eq. (11) into an ODE.
where the dash denotes the derivative w. r. t. \( \eta \). Now integrating Eq. (12), we have,
Using homogenous principle, balancing \( u^{\prime\prime}\) and \( u^{2} \), we have
The trial solution of Eq. (12) can be stated as,
where \( a_{2} \ne 0,{\kern 1pt} {\kern 1pt} a_{1} \) and \( a_{0} \) are constants, while \( \lambda ,\mu \) are any constants.
Putting \( u, u^{\prime} , u^{\prime\prime} , u^{2} \) in Eq. (13) and comparing, we get,
By solving the algebraic equations, the required solution is given below.
where \( \lambda \) and \( \mu \) are any constants.
Now putting the values in Eq. (14), we obtain
where \( \eta = x - Vt. \) By putting (6–10) in (16), we obtain the solutions which are given below.
Case 1 When \( \lambda^{2} - 4\mu > 0 \) and \( \mu \ne 0, \) we have,
where \( \eta = x - \frac{1}{6}\frac{{\alpha a_{2} + 6\delta }}{\beta }t \) and where \( c_{1} \) is any constant.
Case 2 When \( \lambda^{2} - 4\mu < 0 \) and \( \mu \ne 0, \) we have,
where \( \eta = x - \frac{1}{6}\frac{{\alpha a_{2} + 6\delta }}{\beta }t \) and where \( c_{1} \) is any constant.
Case 3 When \( \mu = 0 \) and \( \lambda \ne 0, \) we have,
where \( \eta = x - \frac{1}{6}\frac{{\alpha a_{2} + 6\delta }}{\beta }t \) and where \( c_{1} \) is any constant.
Case 4 When \( \lambda^{2} - 4\mu = 0,{\kern 1pt} \lambda \ne 0, \) and \( \mu \ne 0, \) we obtain,
where \( \eta = x - \frac{1}{6}\frac{{\alpha a_{2} + 6\delta }}{\beta }t \) and where \( c_{1} \) is any constant.
Case 5 When \( \lambda = 0, \) and \( \mu = 0, \) we have, \( u_{5} \left( \eta \right) = a_{0} + \frac{{a_{2} }}{{\left( {\eta + c_{1} } \right)^{2} }}, \) where \( \eta = x - \frac{1}{6}\frac{{\alpha a_{2} + 6\delta }}{\beta }t \) and where \( c_{1} \) is any constant.
Graphical demonstration
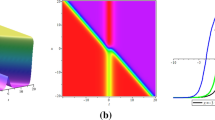
The graphs are given in Figs. 1, 2, 3, 4 and 5.
Singular kink wave solution \( u_{2} \) when \( {\kern 1pt} a_{2} = 10, {\kern 1pt} {\kern 1pt} a_{0} = 8,{\kern 1pt} {\kern 1pt} {\kern 1pt} y = 0, {\kern 1pt} {\kern 1pt} {\kern 1pt} \lambda = 7,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu = 5,{\kern 1pt} {\kern 1pt} {\kern 1pt} c_{1} = - 10 \)
(2 + 1)-dimensional Burger’s equation
Consider the equation,
where \( \alpha ,\beta \) and \( \delta \) are some nonzero parameters. We have, \( u = u\left( \eta \right) \), \( \eta = x + y - Vt, \) we can convert Eq. (17) into an ODE.
where dash denotes the derivative w. r. t.\( \eta.\)
Integrating Eq. (18), we have,
Using homogenous principle, balancing the \( u' \) and \( u^{2} , \) we have, \( M = 1 \).
The trial solution of Eq. (18) can be stated as,
where \( a_{1} \ne 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} a_{0} \) is a constant, while \( \lambda ,\mu \) are any constants. By putting \( u, u^{\prime} , u^{\prime\prime} , u^{2} \) in Eq. (19) and comparing, we get
By solving the algebraic equations, the required solution is given below.
where \( \lambda \) and \( \mu \) are any constants. Now putting the values in Eq. (20), we obtain,
where \( \eta = x - Vt. \)
Now putting (6–10) in (22), we obtain the solutions as.
Case 1 When \( \lambda^{2} - 4\mu > 0 \) and \( \mu \ne 0, \) we have,
where \( \eta = x - {\text{V}}t \) and where \( c_{1} \) is any constant.
Case 2 When \( \lambda^{2} - 4\mu < 0 \) and \( \mu \ne 0, \) we obtain,
where \( \eta = x - {\text{V}}t \) and where \( c_{1} \) is any constant.
Case 3 When \( \mu = 0 \) and \( \lambda \ne 0, \) we have,
where \( \eta = x - Vt \) and where \( c_{1} \) is any constant.
Case 4 When \( \lambda^{2} - 4\mu = 0, \lambda \ne 0, \) and \( \mu \ne 0, \) we obtain,
where \( \eta = x - Vt \) and where \( c_{1} \) is any constant.
Case 5 When \( \lambda = 0, \) and \( \mu = 0, \) we have,
where \( \eta = x - Vt \) and where \( c_{1} \) is any constant.
Graphical illustration
The graphs are given in Figs. 6, 7, 8, 9 and 10.
Conclusions
The exp\( ( - \varphi \left( \eta \right)) \)-expansion method has been successfully applied to find the exact solutions of (ZK-MEW) equation and the Burger’s equation. The attained results show that the proposed technique is effective and capable for solving nonlinear partial differential equations. In this study, some exact solitary wave solutions, mostly solitons and kink solutions, are obtained through the hyperbolic and rational functions. This study shows that the proposed method is quite proficient and practically well organized in finding exact solutions of other physical problems.
References
Ablowitz MJ, Clarkson PA (1991) Solitons, nonlinear evolution equations and inverse scattering. Cambridge University Press, New York
Wazwaz AM (2004) The tanh-method for traveling wave solutions of nonlinear equations. Appl Math Comput 154:713–723
Malfliet W, Hereman W (1996) The tanh method: exact solutions of nonlinear evolution and wave equations. Phys Scr 54:563–568
Wazwaz AM (2007) The tanh-method for traveling wave solutions of nonlinear wave equations. Appl Math Comput 187:1131–1142
Zayed EME, Abdel Rahman HM (2010) The tanh-function method using a generalized wave transformation for nonlinear equations. Int J Nonlinear Sci Numer Simul 11:595–601
Wazwaz AM (2004) The tanh method for travelling wave solutions of nonlinear equations. Appl Math Comput 154:713–723
Abdou MA (2007) The extended tanh method and its applications for solving nonlinear physical models. Appl Math Comput 190:988–996
El-Wakil SA, Abdou MA (2007) New exact traveling wave solutions using modified extended tanh-function method. Chaos Solit Fract 31:840–852
Zayed EME, AbdelRahman HM (2010) The extended tanh-method for finding traveling wave solutions of nonlinear PDEs. Nonlinear Sci Lett A 1(2):193–200
Fan EG (2000) Extended tanh-function method and its applications to nonlinear equations. Phys Lett A 277:212–218
Wazwaz AM (2008) The extended tanh-method for new compact and non-compact solutions for the KP–BBM and the ZK–BBM equations. Chaos Solit Fract 38:1505–1516
Yaghobi Moghaddam M, Asgari A, Yazdani H (2009) Exact travelling wave solutions for the generalized nonlinear Schrödinger (GNLS) equation with a source by extended tanh–coth, sine–cosine and Exp-function methods. Appl Math Comput 210:422–435
Rosenau P, Hyman JM (1993) Compactons: solitons with finite wavelengths. Phys Rev Lett 70:564–567
Wazwaz AM (2003) An analytic study of compactons structures in a class of nonlinear dispersive equations. Math Comput Simul 63:35–44
Wazwaz AM (2004) A sine-cosine method for handling nonlinear wave equations. Math Comput Model 40:499–508
Hirota R (1971) Exact solutions of the Korteweg–de-Vries equation for multiple collisions of solitons. Phys Lett A 27:1192–1194
Mohyud-Din ST (2009) Solution of nonlinear differential equations by exp-function method. World Appl Sci J 7:116–147
Noor MA, Mohyud-Din ST, Waheed A (2008) Exp-function method for solving Kuramoto–Sivashinsky and Boussinesq equations. J Appl Math Comput. 29:1–13. doi:10.1007/s12190-008-0083-y
Wu HX, He JH (2006) Exp-function method and its application to nonlinear equations. Chaos Solit Fract 30:700–708
Mohyud-Din ST, Noor MA, Waheed A (2009) Exp-function method for generalized travelling solutions of good Boussinesq equations. J Appl Math Comput 30:439–445
Abdou MA, Soliman AA, Basyony ST (2007) New application of exp-function method for improved Boussinesq equation. Phys Lett A 369:469–475
Bekir A, Boz A (2008) Exact solutions for nonlinear evolution equation using Exp-function method. Phys Lett A 372:1619–1625
Naher H, Abdullah FA, Akbar MA (2012) New travelling wave solutions of the higher dimensional nonlinear partial differential equation by the Exp-function method. J Appl Math 2012:14. doi:10.1155/2012/575387
Zhu SD (2007) Exp-function method for the discrete m KdV lattice. Int J Nonlinear Sci Numer Simul 8:465–469
Wu XH, He JH (2008) Exp-function method and its application to nonlinear equations. Chaos Solit Fract 38:903–910
Wang M, Li X, Zhang J (2008) The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys Lett A 372:417–423
Ebadi G, Biswas A (2011) The (G′/G)-expansion method and topological soliton solution of the K(m, n) equation. Commun Nonlinear Sci Numer Simulat 16:2377–2382
Zayed EME, Gepreel KA (2009) The (G′/G)-expansion method for finding traveling wave solutions of nonlinear partial differential equations in mathematical physics. J Math Phys 50:013502–013512
Zayed EME, EL-Malky MAS (2011) The Extended (G′/G)-expansion method and its applications for solving the(3 + 1)-dimensional nonlinear evolution equations in mathematical physcis. Glob J Sci Front Res 11:13
Ekici M, Duran D, Sonmezoglu A (2014) Constructing of exact solutions to the (2 + 1)-dimensional breaking soliton equations by the multiple (G′/G)-expansion method. J Adv Math Stud 7:27–44
Fan E, Zhang H (1998) A note on the homogeneous balance method. Phys Lett A 246:403–406
Wang M (1995) Solitary wave solutions for variant Boussinesq equations. Phys Lett A 199:169–172
Ebaid A, Aly EH (2012) Exact solutions for the transformed reduced Ostrovsky equation via the F-expansion method in terms of Weierstrass-elliptic and Jacobian-elliptic functions. Wave Motion 49:296–308
Filiz A, Ekici M, Sonmezoglu A (2014) F-expansion method and new exact solutions of the SchrÄodinger-KdV equation. Sci World J 2014:14
Abdou MA (2007) The extended F-expansion method and its applications for a class of nonlinear evolution equations. Chaos Solit Fract 31:95–104
Dai CQ, Zhang JF (2006) Jacobian elliptic function method for nonlinear differential-difference equations. Chaos Solit Fract 27:1042–1047
Liu D (2005) Jacobi elliptic function solutions for two variant Boussinesq equations. Chaos Solit Fract 24:1373–1385
Chen Y, Wang Q (2005) Extended Jacobi elliptic function rational expansion method and abundant families of Jacobi elliptic functions solutions to (1 + 1)-dimensional dispersive long wave equation. Chaos Solit Fract 24:745–757
Ma WX, Maruno K (2004) Complexiton solutions of the Toda lattice equation. Phys A 343:219–237
Ma WX, Zhou DT (1997) Explicit exact solution of a generalized KdV equation. Acta Math Scita 17:168–174
Ma WX, You Y (2004) Solving the Korteweg—de Vries equation by its bilinear form: Wronskian solutions. Trans Am Math Soc 357:1753–1778
Ma WX, You Y (2004) Rational solutions of the Toda lattice equation in Casoratian form. Chaos Solit Fract 22:395–406
Ma WX, Fuchssteiner B (1996) Explicit and exact solutions of Kolmogorov–PetrovskII–Piskunov equation. Int J Nonlinear Mech 31(3):329–338
Ma WX, Wu HY, He JS (2007) Partial differential equations possessing Frobenius integrable decompositions. Phys Lett A 364:29–32
Authors’ contributions
The work was carried out in cooperation among all the authors (STM-D, AA and MAI). All authors have a good involvement to plan the paper, and to execute the analysis of this research work together. All authors read and approved the final manuscript.
Compliance with ethical guidelines
Competing interests The authors declare that they have no competing interests.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mohyud-Din, S.T., Ali, A. & Iqbal, M.A. Traveling wave solutions of Zakharov–Kuznetsov-modified equal-width and Burger’s equations via \( {\text{exp}}( - \varphi \left( \eta \right)) \)-expansion method. Asia Pac. J. Comput. Engin. 2, 2 (2015). https://doi.org/10.1186/s40540-015-0014-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s40540-015-0014-y