Background

With advancement in 3D imaging and processing, collections of 3D models have become an increasingly prominent in many fields, such as engineering, entertainment, and medical imaging (Liu et al. 2006). In order to find relevant objects from a given query, measuring the similarity between different objects has become acute. Since many shapes manifest rich variability, retrieval is required to be invariant to different kinds of deformations. One of the most challenging tasks is to deal with non-rigid shapes, in which transformation category is very broad.

The key component of 3D shape analysis is to define a descriptor, for distinguishing different parts of the shapes. Elad (2001) extended a series of rigid descriptors for non-rigid shapes by replacing Euclidean metric space with geodesic distance, which is invariant to inelastic deformations. However, it suffers from a huge flaw because of its strong sensitivity to topological noise, which limits the usefulness of such descriptors (Li and Hamza 2013).

Recently, research efforts have shown growing popularity of spectral analysis of the Laplace–Beltrami (LB) operator. An isometry-invariant global descriptor was proposed by Reuter (2006) which used eigenvalues of LB operator as Shape-DNA for a 3D manifold. Despite the good performance for non-rigid shapes, it cannot be used for local shape analysis. Rustamov (2007) proposed to construct global point signature (GPS) at each point based on diffusion geometry. A major drawback of such a descriptor is the problem of eigenfunctions’ switching whenever the associated eigenvalues are close to each other. A remedy was proposed lately by Sun (2009) through constructing heat kernel signature, which was based on the fundamental solutions of the heat equation. It is a point-based signature which has a number of desirable properties, including invariance to isometric transformations, robustness to small perturbations (Abdelrahman et al. 2012), and a multi-scale interpretation (Sun et al. 2009) of the shapes. As of today, this descriptor achieves state-of-art performance in shape retrieval and other applications.

HKS successes in wide applications, however, it highly depends on the information derived from low frequencies corresponding to the global structure of the shape (Aubry et al. 2011). The information of low frequency is effective to discriminate distinct shapes, which usually differ greatly at coarse scales; however, the loss of high-frequency information damages the ability to conduct feature localization precisely (Aflalo et al. 2012).

To solve the problem that high frequencies are avoided, in this study, we proposed a novel framework for shape retrieval by integrating the advantages of both global geometry for discriminative power and microgeometry for localization. In proposed method, not only the macroshape information, but also the microshape information is considered. In the experiment, some cases from the standard benchmark (SHREC 2010) are employed for testing and validating the proposed approach; and a well-studied approach (Ovsjanikov et al. 2009) based on heat kernel signature is utilized for comparison. Experimental results demonstrate that the proposed method is effective and accurate for 3D shape retrieval.

The rest of this study is organized as follows. “The proposed method” section describes our framework in details. “Object representation and matching” section presents our retrieval procedure using Bag of words. “Results and discussion” section shows some experimental results on a 3D shape benchmark. Finally, we conclude in “Conclusions” section.

The proposed method

We proposed a new framework to handle the loss information of heat kernel signature.

Highlight details

The heat kernel h t (x, y) is the fundamental solution of the heat equation (Sun et al. 2009), which is closely associated with Laplace–Beltrami operator by:

$$\frac{{\partial h_{t} (x,y)}}{\partial t} + \Delta h_{t} (x,y) = 0.$$
(1)

It can be further defined in terms of the eigenvalues and eigenfunctions of ∆ as follows:

$$h_{t} (x,y) = \sum\limits_{i} {e^{{ - \lambda_{i} t}} \phi_{i} (x)\phi_{i} (y)}.$$
(2)

Intuitively, h t (x, x) denotes the amount of heat remaining at point x after time t. Therefore, HKS at point x is represented in the discrete temporal domain by a n-dimensional feature vector:

$${\text{HKS}}(x) = [h_{t1} (x,x),h_{t2} (x,x), \ldots ,h_{tn} (x,x)],$$
(3)

where t is the time scale.

The function exp(−λt) is mainly dominated by low frequencies, which correspond to the macrostructure. In this study, we use heat mean signature (HMS) (Fang et al. 2011) to evaluate the weight of a point. The bigger is the value of HMS, the more influential of a point is. Using weight, we can further enhance the importance of salient points so that highlighting their corresponding details.

$${\text{weight}}(x) = {\text{HMS}}_{t} (x) = \frac{1}{m}\sum\limits_{y \ne x} {h_{t} (x,y)}$$
(4)

We empirically choose a smaller parameter t to compute the weight of a point. A new descriptor, enhanced heat kernel signature (EHSK) is defined:

$${\text{EHKS}}(x) = {\text{weight}}(x) \cdot {\text{HKS}}(x)$$
(5)
$$= {\text{weight}}\left( x \right) \cdot \left[ {h_{t1} \left( {x,x} \right), \ldots ,h_{{t{\text{n}}}} \left( {x,x} \right)} \right].$$
(6)

Microgeometry structure

Besides highlighting details by introducing the weight, we also directly capture microgeometry of a point. In our method, we use the wave kernel. The wave kernel is from Schrodinger’s equation (Aubry et al. 2011)

$$\frac{\partial \varphi (x,t)}{\partial t} = i\Delta \varphi (x,t).$$
(7)

The wave function \(\varphi\) (x, t), which governs the evolution of a quantum particle on the surface, is the solution of Schrodinger’s equation and can be further expressed as following:

$$\varphi_{e} (x,t) = \sum\limits_{k} {e^{{i\lambda_{k} t}} } \varphi_{k} (x)f_{e} (\lambda_{k} ),$$
(8)

where e is the energy of the particle at t = 0. f e is the initial distribution. The probability to measure the particle at point x is then |φ e (x, t)|2. Thus, the average probability is obtained by integrating over time as following:

$$P_{e} (x) = \mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int\limits_{0}^{T} {|\varphi {}_{E}(x,t)|^{2} } = \sum\limits_{k} {\varphi_{k} (x)^{2} f_{e} (\lambda_{k} )^{2} },$$
(9)

where we use a log-normal energy distribution.

$$f_{e} \left(\uplambda \right) \propto \exp \left( { - \frac{{\left( {\log e - \log \lambda } \right)^{2} }}{{2\sigma^{2} }}} \right).$$
(10)

Finally, the wave kernel signature at point x is defined as:

$${\text{WKS }}(x) = (P_{e1} (x),P_{e2} (x), \ldots ,P_{\text{en}} (x)),$$
(11)

where e i is the logarithmic energy scale. The function \(\exp \left( { - \frac{{(\log e - \log \lambda )^{2} }}{{\sigma^{2} }}} \right)\) yielding WKS can be considered as band-pass filters. Thus, it provides an access to high frequencies, which corresponds to the microgeometry of a point. Thus, we use wave kernel signature to remedy HKS’s poor feature location capability.

Analysis of the proposed method

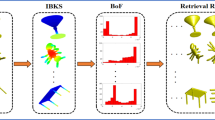
HKS can capture global geometry of shapes well, but it suppressed the local structure. In order to compensate this, we proposed an approach from two aspects. First, we consider the weights of the points. In shape representation, salient points make significantly greater contribution. After applying the weights, we define the EHKS which will not only to further enhance details of salient points but also maintain HKS’s global geometry property. Second, we use WKS as band-pass filters to obtain high-frequency information and thus to capture the local structures of shapes. Thus, we can obtain full information of the shape both local and global, which is critical for shape analysis. In order to avoid overlapping of the two types of descriptors, we create two codebooks based on EHKS and WKS, respectively. Using Bag of words representation, we can finally obtain the global geometry distribution and local geometry distribution based on different codebooks which will be explained in “Object representation and matching” section in detail.

Object representation and matching

Codebook construction

Given a set of point-wise signatures, we use a codebook to represent the distribution of a shape. In our framework, each point has two types of signatures based on EHKS and WKS, respectively. To avoid the influence of different frequencies, we create two codebooks based on different type of descriptors.

To create a codebook \(D = \left\{ {c_{1} ,\,c_{2} \,, \ldots c_{w} } \right\}\), we just employ simple k-means clustering on the set of descriptors and use the center of the cluster as a visual word.

Bag of words representation and matching

For a given model M with a set of descriptors Q = {q i , i = 1, 2,…,n}, where n is the number of points. The codebook \(D = \left\{ {c_{1} ,\,c_{2} \,, \ldots c_{w} } \right\}\) is obtained as discussed above. In this study, we use visual word uncertainty to describe M as the distribution of visual words. Hence, we assign a descriptor q i over all visual words instead of its nearest visual word. Relevancy between q i and word c j is evaluated by a Gaussian kernel K σ  (q i , c j ). The distribution on word c j is obtained as follow:

$${\text{rel}}\,(c_{j} ) = \sum\limits_{i = 1}^{n} {K_{\sigma } (q_{i} ,c_{j} )}$$
(12)

According EHKS and codebook D 1—we can obtain distribution histogram h 1 —on macro structures using above word uncertainty method. Similarly, we can obtain distribution histogram h 2 —on local structures. So, for a given shape X, the fully representation is h X  = [h 1, h 2]. To compare two shapes X and Y, we define their distance as follow:

$$d(X,Y) = ||h_{X} - h{}_{Y}||{}_{1}.$$
(13)

The summary of the proposed approach is given in Fig. 1.

Fig. 1
figure 1

Retrieval procedure of the proposed approach

Full size image

Results and discussion

Dataset and measures

To test the proposed approach, we conducted experiments on a benchmark: SHREC 2010. The dataset contains three collections: TOSCA, Sumner and Princeton (Bronstein et al. 2011). TOSCA contained seven shape classes, and Sumner contained six shape classes. After applying different transformations on 13 shape classes, the total set size has 596 shapes used as positives, while Princeton contained 347 shapes (exclude the shapes as the positives) used as negatives. Retrieval quality is assessed by following measures. Mean Average Precision (mAP) is defined as:

$${\text{mAP}} = \sum\limits_{r} {P(r) \cdot {\text{rel}}(r)},$$
(14)

where P(r) is the percentage of relevant shapes in the first r top-ranked retrieved shapes and rel(r) is the relevance of a given rank. False positive rate (FPR) is the percentage of dissimilar shapes wrongfully identified as similar. False negative rate (FNR) is the percentage of similar shapes wrongfully identified as dissimilar. Equal error rate (EER) is the value of FPR at which it equals FNR.

Results

We compared results with the state-of-art method proposed by Ovsjanikov (2009). In this study, we use the largest 200 eigenvalues and eigenfunctions of LB operator. For EHKS, we choose six time scales with α = 1.32 and t i  = 1024 · αi−1 (i = 1, 2,…,6). For WKS, we select energy scale N = 20 and variance σ = 1 with the best results through repeating experiments.

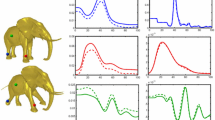
Figure 2a and b shows the results of a query “man.” Ovsjanikov’s method considers only the global geometry, so it cannot discriminate man and woman. Our method is more accurate in capturing both global and local structures. Figure 2c and d shows results of a query “dog.” In this query experiment, a large number of noise samples were added. Ovsjanikov’s method retrieved 3 wrong shapes, while our method retrived only 1 shape. This demonstrates the robust of our method.

Fig. 2
figure 2

Retrieval results. Left: query; Right: first six retrieved shapes; Green-color: wrongly matched shapes. a Results of method in (Ovsjanikov et al. 2009); b results of our method; c results of method in (Ovsjanikov et al. 2009); d results of our method; Left query

Full size image

To evaluate accuracy of each transformation, we conducted another experiment. Ovsjanikov’s results and our method are shown in Tables 1 and 2, respectively. The higher mAP of our method indicates that the retrieved related shapes have a top ranking, while the low EER denotes better identification capability. The overall superior performance validates the effectiveness and accuracy of the proposed approach.

Table 1 Results of our method with vocabulary of size 48
Full size table
Table 2 Results of Ovsjanikov’s method based on heat kernel signature
Full size table

Conclusions

In this study, we proposed a novel retrieval framework. Althrough enhancing the details and capturing microstructures, this approach can handle the substantial loss of high frequencies of the state-of-art heat kernel signature; therefore, it can obtain both the global geometry and local geometry of the shapes. The experimental results also demonstrate that the proposed method is more accurate and robust compared with state-of-the-art methods. In future work, we would develop a more general and flexible way to obtain the shape’s geometric features at different frequencies.