1 Introduction

It is well known that some special type of exact solutions [1–7], including soliton (it has ionic and stability properties), lump (localized in all directions in the space), breather (localized in one certain direction with periodic structure), and rogue wave (localized in both time and space) of nonlinear evolution equations (NLEEs) depict many physical scenarios occurring in diverse areas of physics. In the past few decades, these exact solutions of NLEEs, such as the KP equation [8], the Konopelchenko–Dubrovsky equation [9], the potential Yu–Toda–Sasa–Fukuyama equation [10], and the \((3+1)\)-dimensional Hirota bilinear equation, have been studied [11, 12]. Meanwhile, several effective methods have been established by mathematicians and physicists to obtain the exact solutions of NLEEs, for instance, Painlevé analysis [13], Hirota bilinear method [14–18], Darboux transformation (DT) [19, 20], and so on [21]. In particular, it is clear that the long wave limit method is a powerful technique for deriving rational solutions from the exponential solutions of nonlinear evolution equations, which helps us to obtain new analytical solutions more easily than some classical methods for finding the exact solutions of NLEEs.

Recently, interaction phenomena concerning solitons and other types of solutions have attracted wide attention in the field of mathematical physics. As early as 2003, Fokas and Pogrebkov investigated the collision of lump and line soliton in the Kadomtsev–Petviashvili I equation [22]. In addition, various studies show that there are interaction solutions between solitons and another exact solutions of nonlinear integrable equation [23, 24]. Thereafter, more and more scholars have been devoting themselves to the study of interaction solutions of NLEEs because of their strong practical significance in many fields.

In 2012, a new type of KP equation (called B-type KP equation) was presented as follows [25]:

$$ u_{ty}-u_{xxxy}-3(u_{x}u_{y})_{x}+3u_{xz}=0. $$
(1.1)

We have noticed that the above equation is nonintegrable equation and can be reduced to the \((2+1)\)-dimensional BKP equation [26, 27] when we take \(z=y\). A lot of meaningful works of the above equation, including the Bäcklund transformation, multiple soliton solutions, and lump waves, have been published [28, 29]. Until 2017, the Wazwaz and El-Tantawy derived another KP-type equation by adding a linear term \(u_{tt}\) to the generalized form of the B-type KP Eq. (1.1) [30]. In this paper, we mainly investigate the \((3+1)\)-dimensional B-type Kadomtsev–Petviashvili–Boussinesq equation

$$ u_{ty}-u_{xxxy}-3(u_{x}u_{y})_{x}+u_{tt}+3u_{xz}=0, $$
(1.2)

where u is a differential function about x, y, z, and t. This equation has a strong application background as it can be used to describe not only the processes of interaction of exponentially localized structures but also the propagation of long waves in shallow water. Therefore, Eq. (1.2) has attracted wide attention in the field of mathematical physics [31, 32]. In 2017, the soliton solutions of Eq. (1.2) were constructed [27]. Besides, the integrability, bilinearization, and analytic study of Eq. (1.2) were also investigated by Verma and Kaur [33]. Despite all that, there are still many interesting properties that need to be thoroughly explored. The main purpose of the present paper is to derive the localized waves and interaction solutions based on the complex conjugate approach and the long wave limit method.

The outline of the paper is organized as follows. In Sect. 2, we give the bilinear form of the \((3+1)\)-dimensional B-type KP-Boussinesq equation and the expression of N-soliton solutions (\(N=1,2,3,4\)), respectively. Then, based on the complex conjugate approach, the breather solutions, lump solutions, rogue waves, and their interaction solutions of Eq. (1.2) are resolved. Moreover, we provide some graphical analyzes to discuss the properties for the dynamic behaviors of these solutions in different planes. Section 3 is devoted to conclusion and discussion.

2 Localized wave and interaction solutions

With the aid of early work of Eq. (1.2) [30], its bilinear form has been given as

$$ \bigl(D_{t}D_{y}-D_{x}^{3}D_{y}+D_{t}^{2}+3D_{x}D_{z} \bigr)f\cdot f=0, $$
(2.1)

under the following transformation:

$$ u=2(\ln f)_{x}, $$
(2.2)

where \(D_{s}\) (\(s=x,y,z,t\)) denotes some Hirota’s bilinear operators [34].

Based on transformation (2.2), the N-order soliton solutions of the B-type KP-Boussinesq equation can be obtained through assuming that f of Eq. (1.2) has the form

$$ f=\sum_{\mu=0,1}\exp \Biggl(\sum _{i=1}^{N}\mu_{i}\eta_{i}+\sum _{1\leq i< j}^{N}\mu_{i} \mu_{j}\ln(A_{ij}) \Biggr). $$
(2.3)

Combining Eq. (2.2) and Eq. (2.3), the one soliton, two solitons, three solitons, and four solitons can be read in the following expression by taking \(N=1,2,3,4\) in Eq. (2.3), respectively:

$$ \begin{gathered} (N=1) \quad f_{1}=1+\mathrm{exp}^{\eta_{1}}, \\ (N=2) \quad f_{2}=1+\mathrm{exp}^{\eta_{1}}+\mathrm{exp}^{\eta_{2}}+A_{12}\mathrm{exp}^{\eta _{1}+\eta_{2}}, \\ (N=3) \quad f_{3}=1+\mathrm{exp}^{\eta_{1}}+\mathrm{exp}^{\eta_{2}}+\mathrm{exp}^{\eta _{3}}+A_{12}\mathrm{exp}^{\eta_{1}+\eta_{2}}+A_{13}\mathrm{exp}^{\eta_{1}+\eta _{3}} \\ \phantom{(N=3) \quad f_{3}=}{}+A_{23}\mathrm{exp}^{\eta_{2}+\eta_{3}}+A_{12}A_{13}A_{23}\mathrm{exp}^{\eta_{1}+\eta_{2}+\eta_{3}}, \\ (N=4) \quad f_{4}=1+\mathrm{exp}^{\eta_{1}}+\mathrm{exp}^{\eta_{2}}+\mathrm{exp}^{\eta _{3}}+\mathrm{exp}^{\eta_{4}}+A_{12}\mathrm{exp}^{\eta_{1}+\eta_{2}}+A_{13}\mathrm{exp}^{\eta _{1}+\eta_{3}} \\ \phantom{(N=4) \quad f_{4}=}{}+A_{14}\mathrm{exp}^{\eta_{1}+\eta_{4}}+A_{23}\mathrm{exp}^{\eta _{2}+\eta_{3}}+A_{24}\mathrm{exp}^{\eta_{2}+\eta_{4}}+A_{34}\mathrm{exp}^{\eta_{3}+\eta _{4}}\\ \phantom{(N=4) \quad f_{4}=}{}+A_{12}A_{13}A_{23}\mathrm{exp}^{\eta_{1}+\eta_{2}+\eta _{3}}+A_{12}A_{14}A_{24}\mathrm{exp}^{\eta_{1}+\eta_{2}+\eta _{4}}+A_{13}A_{14}A_{34}\mathrm{exp}^{\eta_{1}+\eta_{3}+\eta_{4}}\hspace{-36pt} \\ \phantom{(N=4) \quad f_{4}=}{}+A_{23}A_{24}A_{34}\mathrm{exp}^{\eta_{2}+\eta_{3}+\eta _{4}}+A_{12}A_{13}A_{14}A_{23}A_{24}A_{34}\mathrm{exp}^{\eta_{1}+\eta_{2}+\eta _{3}+\eta_{4}}, \end{gathered} $$
(2.4)

where

$$ \begin{gathered} \eta_{i}=k_{i}(x+p_{i}y+q_{i}z+ \omega_{i}t)+\eta_{i0}, \qquad\omega _{i}=- \frac{1}{2}p_{i}+\frac {1}{2}\bigl(4k_{i}^{2}p_{i}+p_{i}^{2}-12q_{i} \bigr)^{\frac{1}{2}} \quad (i,j=1,2,3,4), \\ A_{ij}=\frac {-6k_{i}^{2}p_{i}-2k_{i}^{2}p_{j}+6k_{i}p_{i}k_{j}+6k_{i}k_{j}p_{j}-2k_{j}^{2}p_{i}-6k_{j}^{2}p_{j}+(2\omega _{i}+p_{i})(2\omega _{j}+p_{j})-p_{i}p_{j}+6q_{i}+6q_{j}}{-6k_{i}^{2}p_{i}-2k_{i}^{2}p_{j}-6k_{i}p_{i}k_{j}-6k_{i}k_{j}p_{j}-2k_{j}^{2}p_{i}-6k_{j}^{2}p_{j}+(2\omega _{i}+p_{i})(2\omega_{j}+p_{j})-p_{i}p_{j}+6q_{i}+6q_{j}}.\hspace{-12pt} \end{gathered} $$
(2.5)

Here \(k_{i}\), \(p_{i}\), \(q_{i}\), and \(\eta_{i0}\) are arbitrary constants. In 2017, Wazwaz constructed the multiple solitons of Eq. (1.2) by using the above expression [30], so we will not repeat it here. This section is devoted to investigating some localized waves and their interaction phenomena.

2.1 The breather solutions

By resorting to Eq. (2.4), one can obtain the analytical expressions of breather solutions for Eq. (1.2) based on the complex conjugate approach. For example, in this case of \(N=2\) of Eq. (2.4), the \(f_{2}\) can be written as follows:

$$ \begin{aligned}[b] f_{2}&=1+\exp \biggl(ix+iy-z+i \biggl(- \frac{1}{2}+\frac{1}{2}\sqrt {-3-12i} \biggr)t \biggr)\\ &\quad+\exp \biggl(-ix-iy-z-i \biggl(-\frac {1}{2}+\frac{1}{2}\sqrt{-3+12i} \biggr)t \biggr) \\ &\quad+ \biggl(\frac{27+3\sqrt{17}}{3+3\sqrt{17}} \biggr)\exp \biggl(-2z+i \biggl(-\frac{1}{2}+ \frac{1}{2}\sqrt{-3-12i} \biggr)t-i \biggl(-\frac{1}{2}+ \frac{1}{2}\sqrt{-3+12i} \biggr)t \biggr) \end{aligned} $$
(2.6)

with the following parameters:

$$\begin{gathered} k_{1}=i, \qquad k_{2}=-i, \qquad p_{1}=1, \qquad p_{2}=1, \qquad q_{1}=i, \qquad q_{2}=-i, \\ \eta_{10}=\eta_{20}=0. \end{gathered} $$
(2.7)

Therefore, the breather solutions for Eq. (1.2) read

$$ u=2(\ln f_{2})_{x}. $$
(2.8)

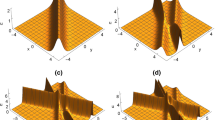
The general breathers (2.8) can be described in the \((x,z)\), \((y,z)\), \((z,t)\) planes, respectively, whose three-dimensional graphics are illustrated in Fig. 1. It is not hard to see that these breathers have the same period in the \((x,z)\) and \((y,z)\) planes from Fig. 1a and 1b. They are localized in space directions and have different propagation path in the \((z,t)\) plane. In addition, it is also worth pointing out that we observed different dynamic characteristics (called line breathers) with the same parameters of Fig. 1 in the \((x,y)\) plane, which are visually shown in Fig. 2. As shown in Fig. 2a, the line breathers are produced in a constant background and reach their maximum peak when \(t=0\). Over time, the line breather disappears in the constant background.

Figure 1
figure 1

Breathers of Eq. (1.2) in different planes with parameters constrained by \(k_{1}=k_{2}^{*}=i\), \(p_{1}=p_{2}=1\), \(q_{1}=q_{2}^{*}=i\), \(\eta_{10}=\eta_{20}=0\)

Full size image
Figure 2
figure 2

Line breathers of Eq. (1.2) in the \((x,y)\) plane with parameters constrained by \(k_{1}=k_{2}^{*}=i\), \(p_{1}=p_{2}=1\), \(q_{1}=q_{2}^{*}=i\), \(\eta_{10}=\eta_{20}=0\)

Full size image

For \(N=3\) in Eq. (2.4), the interaction solutions between one soliton and breather of Eq. (1.2) can be displayed in three different planes by selecting the following suitable parameters:

$$ \begin{gathered} k_{1}=i, \qquad k_{2}=1, \qquad k_{3}=-i, \qquad p_{1}=2+i, \qquad p_{2}=2, \qquad p_{3}=2-i, \\ q_{1}=2i, \qquad q_{2}=1, \qquad q_{3}=-2i, \qquad\eta_{10}=\eta_{20}= \eta_{30}=0. \end{gathered} $$
(2.9)

Based on the parameters selected above, one has

$$ \begin{aligned}[b] f_{3}&=1+\exp \biggl( (-3+2i )y-2z+ix+i \biggl(-1-\frac {3}{2}i+\frac{1}{2}\sqrt{-13-24i} \biggr)t \biggr) \\ &\quad+\exp (x+2y+z-t )+\exp \biggl( (-3-2i )y-2z-ix-i \biggl(-1+\frac{3}{2}i+ \frac{1}{2}\sqrt{-13+24i} \biggr)t \biggr) \\ &\quad+ \biggl(-\frac{143}{109}+\frac{186}{109}i \biggr)\exp \biggl( (i+1 )x+ (-1+2i )y-z+i \biggl(-1-\frac{1}{2}i+\frac {1}{2}\sqrt{-13-24i} \biggr)t \biggr) \\ &\quad+ \biggl(-\frac{143}{109}-\frac{186}{109}i \biggr)\exp \biggl( (-i+1 )x+ (-1-2i )y-z+i \biggl(-1+\frac{1}{2}i+\frac {1}{2}\sqrt{-13+24i} \biggr)t \biggr) \\ &\quad+ \biggl(\frac{43+\sqrt{745}}{-5+\sqrt{745}} \biggr)\exp \biggl(-6y-4z+ \biggl(3+ \frac{1}{2}i\sqrt{-13-24i}-\frac{1}{2}i\sqrt {-13+24i} \biggr)t \biggr) \\ &\quad+ \biggl(\frac{21715+505\sqrt{745}}{-545+109\sqrt{745}} \biggr)\exp \biggl(x-4y-3z+ \biggl(2+ \frac{1}{2}i\sqrt{-13-24i}-\frac {1}{2}i\sqrt{-13+24i} \biggr)t \biggr). \end{aligned} $$
(2.10)

Hence the interaction solutions between soliton and general breather of Eq. (1.2) can be expressed as follows:

$$ u=2(\ln f_{3})_{x}, $$
(2.11)

whose dynamical phenomena are exhibited in Fig. 3. Figures 3a, 3b, and 3c show different interaction phenomena between one soliton and breather, respectively. But the propagation path of the breather does not change after interaction with the solitons (see Figs. 3d, 3e, and 3f).

Figure 3
figure 3

The interaction solutions between soliton and general breather of Eq. (1.2) in different planes with parameters constrained by \(k_{1}=k_{3}^{*}=i\), \(p_{1}=p_{3}^{*}=2+i\), \(q_{1}=q_{3}^{*}=2i\), \(k_{2}=1\), \(p_{2}=2\), \(q_{2}=1\), \(\eta_{10}=\eta _{20}=\eta_{30}\)

Full size image

In the case of \(N=4\), we can get the interaction solutions of two groups of breathers. The collision process is shown in Figs. 4 and 5 with the following parameters:

$$ \begin{gathered} k_{1}=i, \qquad k_{2}=-i, \qquad k_{3}=2i, \qquad k_{4}=-2i, \\ p_{1}=1+i, \qquad p_{2}=1-i, \qquad p_{3}=2+i, \qquad p_{4}=2-i, \\ q_{1}=1, \qquad q_{2}=1, \qquad q_{3}=2, \qquad q_{4}=2, \qquad\eta _{10}=\eta_{20}= \eta_{30}=\eta_{40}=0. \end{gathered} $$
(2.12)

When \(t\ll0\), the two-line breathers appear from a constant plane and the latter catches up with the former in the course of propagation. The interaction of two-line breathers reaches the maximum peak at \(t=0\). Subsequently, the latter line breather surpasses the former and keeps the original characteristic propagating forward (see Fig. 4c). Furthermore, the two-line breathers can be constructed in the \((x,z)\) plane, whose collision processes are illustrated in Figs. 6 and 7.

Figure 4
figure 4

The interaction solutions between two general breathers of Eq. (1.2) in the \((x,y)\) plane with parameters constrained by Eq. (2.12)

Full size image
Figure 5
figure 5

The interaction solutions between two general breathers of Eq. (1.2) in the \((y,z)\) plane with parameters constrained by Eq. (2.12)

Full size image
Figure 6
figure 6

The interaction solution between two general breathers of Eq. (1.2) in the \((x,z)\) plane with parameters constrained by Eq. (2.12)

Full size image
Figure 7
figure 7

The interaction solution between two general breathers of Eq. (1.2) in the \((x,z)\) plane with parameters constrained by Eq. (2.12)

Full size image

2.2 The lump solutions

The lump wave, as one kind of rational solutions, draws much attention in the field of mathematical physics [35, 36]. In 1979, Ablowitz and Satsuma proposed a method called ’long wave limit method’ to help us derive lump waves on multi-soliton solutions [37]. That means we can obtain the lump waves by choosing suitable parameters in the soliton solutions (2.4). In order to obtain the single lump, put

$$ k_{1}=l_{1}\epsilon, \qquad k_{2}=l_{2} \epsilon, \qquad\eta_{10}=\eta _{20}=i\pi $$
(2.13)

in the case of \(N=2\) for Eq. (2.4) and take the limit as \(\epsilon\rightarrow0\). Then the \(f_{2}\) can be simplified and the single lump solution can be constructed as follows:

$$ u=\frac{2(\theta_{1}+\theta_{2})}{\theta_{1}\theta_{2}+\theta_{0}}, $$
(2.14)

where

$$ \begin{gathered} \theta_{i}=\frac{1}{2} \Bigl(p_{i}t-\sqrt {p_{i}^{2}-12q_{i}}t-2p_{i}y-2q_{i}z-2x \Bigr) \quad(i=1,2), \\ \theta_{0}=\frac{12(p_{1}+p_{2})}{\sqrt {(p_{1}^{2}-12q_{1})(p_{2}^{2}-12q_{2})}-p_{1}p_{2}+6q_{1}+6q_{2}}.\end{gathered} $$
(2.15)

From what has been discussed above, we can recognize that the solution u is nonsingular if we set \(p_{1}=p_{2}^{*}\) and \(q_{1}=q_{2}^{*}\). Next, assuming that \(p_{1}=a_{1}+ib_{1}\) and \(q_{1}=a_{2}+ib_{2}\) without loss of generality, the characteristics of solution (2.14) can be illustrated. But before that, if we consider that \(a_{1}\neq0\), the trajectory of solution (2.14) can be defined along the path \([x(t),y(t)]\) as follows:

$$\begin{aligned}& \frac{1}{2}a_{1}t-a_{1}y-a_{2}z-x\\& \quad{}- \frac{1}{4} \Bigl(2\sqrt {\bigl(a_{1}^{2}-b_{1}^{2}-12a_{2} \bigr)^{2}+(2a_{1}b_{1}-12b_{2})^{2}}+2a_{1}^{2}-2b_{1}^{2}-24a_{2} \Bigr)^{\frac{1}{2}}t=0, \\& \frac{1}{2}b_{1}t-b_{1}y-b_{2}z\\& \quad{}+ \frac{1}{4}\varGamma \Bigl(2\sqrt {\bigl(a_{1}^{2}-b_{1}^{2}-12a_{2} \bigr)^{2}+(2a_{1}b_{1}-12b_{2})^{2}}-2a_{1}^{2}+2b_{1}^{2}+24a_{2} \Bigr)^{\frac{1}{2}}t=0, \\& \varGamma=\operatorname{csgn}\bigl(a_{1}^{2}i-b_{1}^{2}i-12a_{2}i-2a_{1}b_{1}+12b_{2} \bigr), \end{aligned}$$
(2.16)

which tell us that solution (2.14) keeps the permanent lump condition in motion on six different planes. As shown in Fig. 8, the single lump waves are plotted in six different planes, and they are all clearly localized in all directions.

Figure 8
figure 8

The lump solutions for Eq. (1.2) in different planes with parameters \(a_{1}=2\), \(b_{1}=0\), \(a_{2}=b_{2}=1\)

Full size image

For \(N=4\), we also introduce the parameters similar to Eq. (2.13) as follows:

$$\begin{gathered} k_{1}=l_{1}\epsilon, \qquad k_{2}=l_{2} \epsilon, \qquad k_{3}=l_{3}\epsilon, \qquad k_{4}=l_{4}\epsilon, \\\eta_{10}=\eta _{20}=\eta_{30}=\eta_{40}=i\pi. \end{gathered} $$
(2.17)

Under the above parameter constraints, we take \(\epsilon\rightarrow0\) and we have

$$ \begin{aligned}[b] f&=(\theta_{1}\theta_{2} \theta_{3}\theta_{4}+a_{12}\theta _{3} \theta_{4}+a_{13}\theta_{2}\theta_{4}+a_{14} \theta_{2}\theta _{3}+a_{23}\theta_{1} \theta_{4}+a_{24}\theta_{1}\theta _{3}+a_{34}\theta_{1}\theta_{2} \\ &\quad+a_{12}a_{34}+a_{13}a_{24}+a_{14}a_{23})l_{1}l_{2}l_{3}l_{4} \epsilon ^{4}+O\bigl(\epsilon^{5}\bigr), \end{aligned} $$
(2.18)

where

$$ \begin{gathered} \theta_{i}=\frac{1}{2} \Bigl(p_{i}t-\sqrt {p_{i}^{2}-12q_{i}}t-2p_{i}y-2q_{i}z-2x \Bigr), \\ a_{ij}=\frac{12(p_{i}+p_{j})}{\sqrt {(p_{i}^{2}-12q_{i})(p_{j}^{2}-12q_{j})}-p_{i}p_{j}+6q_{i}+6q_{j}} \quad(i,j=1,2,3,4). \end{gathered} $$
(2.19)

Finally, the collision process of two lumps can be demonstrated in Fig. 9 with the following appropriate parameters:

$$ p_{1}=p_{2}^{*}=1+i, \qquad p_{3}=p_{4}^{*}=1+2i, \qquad q_{1}=q_{2}^{*}=2+i, \qquad q_{3}=q_{4}^{*}=2+3i. $$
(2.20)

Obviously, we can draw a conclusion that the two-lump waves propagate in a constant state by looking at Fig. 9.

Figure 9
figure 9

Two-lump solutions for Eq. (1.2) in the \((x,y)\) plane with the parameters defined in Eq. (2.19)

Full size image

2.3 The rogue wave solutions

In this part, another kind of dynamical phenomenon localized in both time and space will be mentioned with the long wave limit method. For \(N=2\) and \(N=3\) of Eq. (2.4), it is easy to find that the corresponding dynamic behavior under the same parameters is shown as one-order line rogue wave and the interaction between soliton and line rogue wave, respectively. In the following, we only consider the rogue waves and interaction solutions for Eq. (2.4) in the case of \(N=4\). The rogue waves also have different dynamic characteristics in different planes. For instance, in Fig. 10, the two-line rogue waves are described in the \((x,z)\) plane with the following suitable parameters:

$$ p_{1}=p_{2}^{*}=1+i, \qquad p_{3}=p_{4}^{*}=3+2i, \qquad q_{1}=q_{2}=1, \qquad q_{3}=q_{4}=2. $$
(2.21)

Obviously, the above dynamic process presents a periodicity. The two-line rogue waves will reach a large peak over time (see Fig. 10b) and eventually return to their original state. Besides that, the interaction between line rogue wave and lump can be constructed in the \((y,z)\) plane if we choose the following parameters:

$$ p_{1}=p_{2}^{*}=1+i, \qquad p_{3}=p_{4}^{*}=3+2i, \qquad q_{1}=q_{2}=2+i, \qquad q_{3}=q_{4}=1. $$
(2.22)
Figure 10
figure 10

Two-line rogue waves for Eq. (1.2) in the \((x,z)\) plane with the parameters defined in Eq. (2.21)

Full size image

3 Conclusion and discussion

To conclude, based on the Hirota bilinear forms (2.1) of the \((3+1)\)-dimensional B-type Kadomtsev–Petviashvili–Boussinesq equation, the breather waves and interaction solutions are discussed by the complex conjugate method on soliton solutions (2.4). It seems clear that the breathers have different dynamic characteristics in different planes (see Figs. 1 and 2). In addition, in case of \(N=3\) (or \(N=4\)), we obtained the interaction between breather and single soliton (or interaction between two breathers) by selecting some special parameters (as shown in Figs. 3 and 4, respectively). Through a long wave limit method, we further investigated the lump waves and rogue waves of Eq. (1.2) by Taylor expansion of breathers. According to our understanding, the same research on soliton solutions with periodic properties has been published in [33] and the same expressions of solitons have been given in [30]. However, no previous research has explored results similar to our interaction between solitons and breathers, lumps, and rogue waves. We have obtained some completely new types of solutions based on all the published work on the solution of Eq. (1.2). The lumps, single lump solutions, and two-lump solutions of Eq. (1.2) are displayed in Figs. 8 and 9, respectively. Furthermore, another kind of dynamical phenomenon (Rogue waves) is mentioned, and its dynamic characteristics vary greatly in different planes (see Figs. 10 and 11). Our results of some nonlinear wave interactions are closely related to some interesting dynamical phenomena in physical systems. It is worth further exploring in the future.

Figure 11
figure 11

The interaction between line rogue wave and lump for Eq. (1.2) in the \((y,z)\) plane with the parameters defined in Eq. (2.22): (a) three-dimensional plot at \(t=0\), (b) the density plot, (c) the corresponding contour plot

Full size image