1 Introduction

From the beginning of creation, human beings were interested in discovering the mechanism of various processes of the world around in order to be able to answer some important questions. For this reason, by increasing the human’s knowledge and the completion of the science and technology, the mankind invoked new logical and computational tools based on the modeling and computers. In this direction, the mathematical operators are some of these tools useful for modeling the natural processes in the world. Over the years, mathematicians have introduced various operators for different models, but since fractional order models are more accurate than those of integer order, new fractional operators have been defined for this goal today.

As we know, the Caputo and Riemann–Liouville fractional operators have been used more than other operators for complicated fractional models (see, for example, [1–17]). Later, the Hadamard and Caputo–Hadamard fractional operators were introduced by some researchers and then different models were studied using these operators (see [18–21]). In 2015, Caputo and Fabrizio [22] presented a new fractional derivative without singular kernel entitled the fractional Caputo–Fabrizio operator; and in the same year, Losada and Nieto [23] investigated some properties of this new fractional operator. Some flexible properties of this nonsingular operator led to numerous published papers on the various fractional models in this regard [24–27].

Following this path, Abdeljawad [28] developed the concepts introduced in [29] and investigated some properties of the well-behaved conformable fractional derivatives. In a paper published in 2017, Jarad et al. [30] wanted to answer the question if one can extend the standard Riemann–Liouville integral of fractional order so that we obtain a unification to other fractional operators, including Riemann–Liouville, Caputo, Hadamard, Caputo–Hadamard, and other derivatives [31]. To reach this goal, the authors introduced novel integration and differentiation operators of fractional order based on conformable operators. Indeed, they defined new functional spaces and established some basic properties of these new combined operators. After that manuscript, few papers have been published so far which rely on these novel operators. For instance, in the following paper for the first time, the authors applied new Caputo and Riemann–Liouville conformable operators in their BVP. Later the new problem involving the conformable differential equation of Caputo type with four-point integral conditions

$$ \textstyle\begin{cases} {}^{CC}\mathcal{D}_{a}^{\upsilon , \varrho } w(s) = \breve{g} (s , w(s)) \quad (a< s < T), \\ w(a) = \mu _{1} w(\xi ) + \mu _{2} , \qquad w(T) = \lambda {}^{RC} \mathcal{I}_{a}^{\upsilon , \beta } w( \sigma ), \end{cases} $$

where \({}^{CC}\mathcal{D}_{a}^{\upsilon , \varrho }\) is the conformable derivative of Caputo type of order \(\varrho \in (1, 2] \) with \(\upsilon \in (0, 1]\), was considered. Above, \({}^{RC}\mathcal{I}_{a}^{\upsilon , \beta }\) is the conformable integral of Riemann–Liouville type of order \(\beta > 0\).

In this manuscript, we intend to study the existence and approximation of solutions for a fractional hybrid multi-term integro-differential equation in the Caputo conformable setting. It is notable that the main motivation for this work is taken from a valuable paper published by Somjaiwang and Ngiamsunthorn in 2016 [32]. They formulated a fractional hybrid IVP involving the Caputo derivative as follows:

$$ \textstyle\begin{cases} \frac{d^{\varrho }}{ds^{\varrho }} [ w(s) - \tilde{g} (s, w(s)) ] = \tilde{h} (s , w(s)), \\ w(s_{0} ) = w_{0} \in \mathbb{R}^{+} , \end{cases} $$
(1)

where \(\frac{d^{\varrho }}{ds^{\varrho }} \) is the Caputo derivative with respect to \(s\in \mathfrak{J} = [s_{0} , s_{0} + k ] \) of fractional order \(\varrho \in (0, 1] \) with \(s_{0} \geq 0 \) and \(k > 0\). The authors dealt with the existence of mild solutions for this hybrid IVP and also they obtained an approximation of solutions by the help of an iterative sequence [32].

By extending the hybrid initial problem mentioned in [32] to the newly defined fractional operator introduced by [30], we intend to investigate the existence and approximation of solutions for the following Caputo conformable fractional hybrid initial value problem:

$$ \textstyle\begin{cases} {}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } [{{}^{CC} \mathcal{D}_{s_{0}}^{\upsilon , \alpha ^{*}}}w(s) - \hat{\varphi } (s, w(s)) ] = {{}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \theta ^{*}}} \hat{\sigma } (s , w(s), {{}^{RC}\mathcal{I}_{s_{0}}^{ \upsilon , \eta ^{*}} w(s)} ), \\ w(s_{0}) = w_{0}, \qquad {{}^{CC}\mathcal{D}_{s_{0}}^{ \upsilon , \alpha ^{*}}w(s_{0})=\hat{\varphi } (s_{0}, w(s_{0}))}, \end{cases} $$
(2)

where \(0<\varrho \), \(\alpha ^{*} < 1\), \({\theta ^{*} , \eta ^{*} > 0}\), \({}^{CC}\mathcal{D}_{s_{0}}^{\beta ^{*} , \varrho }\) denotes the Caputo conformable derivative of fractional order \(\beta ^{*}\) and \({}^{RC} \mathcal{I}_{s_{0}}^{\gamma ^{*}, \varrho }\) denotes the Riemann–Liouville conformable integral of the fractional order \(\gamma ^{*}\) with \(\upsilon \in (0, 1] \) and \(s\in \mathfrak{J} = [s_{0} , s_{0} + k ] \) so that \(s_{0} \geq 0 \) and \(k > 0\). Also, \(\hat{\varphi } : \mathfrak{J} \times \mathbb{R} \to \mathbb{R} \) and \(\hat{\sigma } : \mathfrak{J} \times \mathbb{R} {\times \mathbb{R}} \to \mathbb{R} \) are continuous functions. Notice that our proposed hybrid initial problem is an extended version of the aforementioned hybrid problem (1). Also, it is necessary to mention that we apply the same techniques used in the paper published by Somjaiwang and Ngiamsunthorn [32] but for a new structure of the multi-term integro-differential equation equipped with newly-defined Caputo and Riemann–Liouville conformable derivative operator given by (2). In other words, in the current research work, we discuss two results on the existence and approximation of solutions simultaneously. To reach this goal, we first construct a successive sequence which approximates solutions and then derive the existence criteria by applying a theorem demonstrated by Dhage et al. [33] which guarantees the existence of such solutions.

2 Preliminaries

In the current section, we state some fundamental and auxiliary concepts. According to existing definitions in the literature, the concept of the Riemann–Liouville integral of order \(\varrho >0\) for a function \(w : [0, + \infty ) \to \mathbb{R}\) is given by \({}^{R}\mathcal{I}_{0}^{ \varrho } w(s) = \int _{0}^{s} \frac{(s - r )^{ \varrho -1 }}{\Gamma ( \varrho )} w(r) \,\mathrm{d}r \) provided that the value of the integral is finite (see [34, 35]). Now, assume that \(\varrho \in (n-1 , n)\) so that \(n = [ \varrho ] +1\). For a function \(w\in \mathcal{AC}^{(n)}_{\mathbb{R}}([0, + \infty ))\), the fractional derivative of Caputo type is given by

$$ {}^{C}\mathcal{D}_{0}^{ \varrho } w(s) = \int _{0}^{s} \frac{(s - r)^{n- \varrho -1}}{\Gamma (n- \varrho )} w^{(n)}(r) \,\mathrm{d} r $$

so that the RHS integral is finite-valued (see [34, 35]). The left conformable derivative at the initial point \(s_{0}\) for a function \(w: [s_{0}, \infty ) \to \mathbb{R}\) with \(\upsilon \in (0,1]\) is defined as follows:

$$ \mathcal{D}_{s_{0}}^{\upsilon }w(s) = \lim_{\lambda \to 0} \frac{w(s+ \lambda (s-s_{0})^{ 1- \upsilon }) - w(s)}{\lambda } $$

so that the limit exists [29]. Notice that \(\mathcal{D}_{s_{0}}^{\upsilon }w(s_{0}) = \lim_{s\to {s_{0}}^{+}} \mathcal{D}_{s_{0}}^{\upsilon }w(s) \) whenever \(\mathcal{D}_{s_{0}}^{\upsilon }w(s)\) exists on \((s_{0},b)\). Moreover, if the function w is differentiable, then \(\mathcal{D}_{s_{0}}^{\upsilon }w(s) = (s-s_{0})^{1-\upsilon } w'(s)\). In this direction, the notion of the left conformable integral of w with \(\upsilon \in (0, 1]\) is defined by \(\mathcal{I}_{s_{0}}^{\upsilon }w(s) = \int _{s_{0}}^{s} w(r) \frac{\mathrm{d}r}{(r-s_{0})^{1-\upsilon }}\) if the integral is finite-valued [29]. In 2017, Jarad et al. [30] generalized the above notions of conformable operators to arbitrary orders in the Caputo and Riemann–Liouville settings. For more information, assume that \(\varrho \in \mathbb{C}\) with \(\operatorname{Re}(\varrho ) \geq 0\). Then the Riemann–Liouville fractional conformable integral of a function w of order ϱ with \(\upsilon \in (0,1]\) is defined by

$$ {}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \varrho } w (s) = \frac{1}{\Gamma ( \varrho )} \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho -1} w(r) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\varrho } } $$

if the value of the integral exists [30]. One can easily observe that if \(s_{0}=0\) and \(\upsilon =1\), then \({}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \varrho } w (s)\) reduces to the usual Riemann–Liouville integral \({}^{R}\mathcal{I}_{0}^{ \varrho } w (s)\). On the other hand, the Riemann–Liouville conformable derivative of a function w of order ϱ with \(\upsilon \in (0,1]\) is given as follows:

$$\begin{aligned} {}^{RC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } w (s) &= \mathcal{D}_{s_{0}}^{ \upsilon , n} \bigl( {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , n- \varrho } w \bigr) (s) \\ &= \frac{\mathcal{D}_{s_{0}}^{\upsilon , n}}{\Gamma ( n-\varrho )} \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{n- \varrho -1} w(r) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\varrho } } \end{aligned}$$

so that \(n = [ \operatorname{Re}(\varrho )] +1\) and \(\mathcal{D}_{s_{0}}^{\upsilon , n} = \overbrace{\mathcal{D}_{s_{0}}^{\upsilon } \mathcal{D}_{s_{0}}^{\upsilon } \cdots \mathcal{D}_{s_{0}}^{\upsilon }}^{n \text{ times}} \) where \(\mathcal{D}_{s_{0}}^{\upsilon }\) denotes the left conformable derivative with \(\upsilon \in (0,1]\) [30]. In a similar way, it is obvious that if we take \(s_{0}=0\) and \(\upsilon =1\), then \({}^{RC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } w (s)\) reduces to the usual Riemann–Liouville derivative \({}^{R}\mathcal{D}_{0}^{ \varrho } w (s)\). Now, to define a similar concept in the Caputo setting, we construct

$$ \mathcal{L}_{\upsilon }(s_{0}) := \bigl\{ \varphi : [s_{0},b] \to \mathbb{R} : \mathcal{I}_{s_{0}}^{\upsilon } \varphi (s) \text{ exists for any } s\in [s_{0},b] \bigr\} $$

for \(\upsilon \in (0,1]\) and set

$$ \mathbb{I}_{\upsilon }\bigl([s_{0},b]\bigr) := \bigl\{ w: [s_{0},b] \to \mathbb{R} : w(s) = \mathcal{I}_{s_{0}}^{\upsilon } \varphi (s) + w(s_{0}), \text{for some } \varphi \in \mathcal{L}_{\upsilon }(s_{0}) \bigr\} , $$

where \(\mathcal{I}_{s_{0}}^{\upsilon }\varphi (s) = \int _{s_{0}}^{s} \varphi (r) \,\mathrm{d} \upsilon (r, s_{0}) = \int _{s_{0}}^{s} \varphi (r) \frac{\mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \) is the left conformable integral of φ [28]. For \(n\geq 1\), we define

$$ \mathcal{C}_{s_{0}, \upsilon }^{n} \bigl([s_{0},b]\bigr) := \bigl\{ w: [s_{0},b] \to \mathbb{R}: \mathcal{D}_{s_{0}}^{\upsilon , n-1} w \in \mathbb{I}_{\upsilon }\bigl([s_{0},b]\bigr) \bigr\} . $$

Then, the Caputo conformable derivative of a function \(w \in \mathcal{C}_{s_{0}, \upsilon }^{n} ([s_{0},b])\) of order ϱ with \(\upsilon \in (0,1]\) is given by

$$\begin{aligned} {}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } w (s) &= {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , n- \varrho } \bigl( \mathcal{D}_{s_{0}}^{ \upsilon , n } w \bigr) (s) \\ &= \frac{1}{\Gamma ( n-\varrho )} \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{n- \varrho -1} \mathcal{D}_{s_{0}}^{\upsilon , n} w(r) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\varrho } }, \end{aligned}$$

where \(n = [ \operatorname{Re}(\varrho )] + 1\) [30]. Evidently, \({}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } w (s) = {}^{C} \mathcal{D}_{0}^{\varrho } w (s) \) if \(s_{0}=0\) and \(\upsilon =1\). Some important and useful properties of the Caputo and Riemann–Liouville fractional conformable operators can be found in the following lemmas.

Lemma 2.1

([30])

Let \(\operatorname{Re}(\varrho ) > 0 \), \(\operatorname{Re} (\varpi ) > 0\), and \(\operatorname{Re}(\beta ) > 0\). Then for \(\upsilon \in (0,1]\) and for all \(s>s_{0}\), the following statements hold:

  1. (s1)

    \({}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \varrho } ( {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \varpi } w ) (s) = ( {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \varrho + \varpi } w ) (s) \),

  2. (s2)

    \({}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \varrho } (s-s_{0})^{ \upsilon (\beta -1)} (z) = \frac{1}{\upsilon ^{\varrho }} \frac{ \Gamma (\beta ) }{ \Gamma ( \beta + \varrho )} (z-s_{0})^{ \upsilon ( \beta + \varrho -1) } \),

  3. (s3)

    \({}^{RC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } (s-s_{0})^{ \upsilon (\beta -1)} (z) = \upsilon ^{\varrho }\frac{ \Gamma (\beta ) }{ \Gamma ( \beta - \varrho )} (z-s_{0})^{ \upsilon ( \beta - \varrho -1) } \),

  4. (s4)

    \({}^{RC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } ( {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \varpi } w ) (s) = ( {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \varpi - \varrho } w ) (s) \), \((\operatorname{Re}(\varrho ) < \operatorname{Re} (\varpi ) ) \).

Lemma 2.2

([32])

Let \(n-1 < \operatorname{Re}(\varrho ) < n\) and \(w\in \mathcal{C}_{s_{0}, \upsilon }^{n} ([s_{0},b])\). Then for \(\upsilon \in (0,1]\), we have

$$ {}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \varrho } \bigl( {}^{CC} \mathcal{D}_{s_{0}}^{\upsilon , \varrho } w \bigr) (s) = w(s) - \sum_{j=0}^{n-1} \frac{\mathcal{D}_{s_{0}}^{\upsilon , j} w(s_{0})}{ \upsilon ^{j} j!} (s-s_{0})^{j \upsilon } . $$

Considering the above lemmas, it is verified that the general solution of the homogeneous equation \(({}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } w )(s) =0\) is obtained by

$$ w(s) = \sum_{j=0}^{n-1} b_{j} (s-s_{0})^{j\upsilon } = b_{0} + b_{1} (s-s_{0})^{\upsilon }+ b_{2} (s-s_{0})^{2\upsilon } + \cdots + b_{n-1}(s-s_{0})^{ (n-1)\upsilon } , $$

where \(n-1 < \operatorname{Re}(\varrho ) < n\) and \(b_{0} , b_{1} , \dots , b_{n-1} \in \mathbb{R}\). The rest of the present section is devoted to recalling some preliminaries on the partially ordered Banach spaces (see [36–38]).

Assume that \(\mathcal{W} = (\mathcal{W}, \leq , \Vert \cdot \Vert _{\mathcal{W}} )\) is a partially ordered Banach space. The space \(\mathcal{W}\) is called regular if for every nondecreasing convergent sequence \(\{ w_{n} \}_{n\geq 1} \subseteq \mathcal{W}\) such that \(w_{n} \to w^{*}\) as \(n\to \infty \), we have \(w_{n} \leq w^{*}\) for each \(n\in \mathbb{N}\) [33, 38]. We say that the operator \(\mathfrak{P} : \mathcal{W} \to \mathcal{W} \) is nondecreasing if for each \(w_{1} , w_{2} \in \mathcal{W}\) such that \(w_{1} \leq w_{2}\), the inequality \(\mathfrak{P} w_{1} \leq \mathfrak{P}w_{2} \) holds [36]. An operator \(\mathfrak{P} : \mathcal{W} \to \mathcal{W} \) is said to be partially continuous at \(v\in \mathcal{W}\) whenever for each \(\varepsilon >0\), there is \(\delta >0\) such that \(\Vert \mathfrak{P}w - \mathfrak{P} v \Vert _{\mathcal{W}} < \varepsilon \) for any \(w \in \mathcal{W}\) which is comparable to \(v \in \mathcal{W}\) with \(\Vert w-v \Vert _{\mathcal{W}} < \delta \) [37]. Moreover, \(\mathfrak{P}\) has the partial continuity property on \(\mathcal{W}\) if it has the partial continuity property at every \(v \in \mathcal{W}\). Particularly, if \(\mathfrak{P}\) is an operator possessing the partial continuity property on \(\mathcal{W}\), then \(\mathfrak{P}\) is continuous on each chain \(\mathfrak{C}\) belonging to \(\mathcal{W}\) [37]. In the following, we say that \(\mathfrak{P}\) is partially bounded if \(\mathfrak{P}( \mathfrak{C})\) is bounded for each chain \(\mathfrak{C}\) in the space \(\mathcal{W}\) [37]. Besides, \(\mathfrak{P}\) is supposed to be uniformly partially bounded whenever all chains \(\mathfrak{P}( \mathfrak{C})\) belonging to \(\mathcal{W}\) are bounded by the same constant [37].

We say that \(\mathfrak{P} : \mathcal{W} \to \mathcal{W} \) is partially compact if for every chain \(\mathfrak{C}\) in the partially ordered space \(\mathcal{W}\), the subset \(\mathfrak{P}( \mathfrak{C}) \subseteq \mathcal{W}\) is a relatively compact [37]. Furthermore, \(\mathfrak{P}\) is supposed to be partially totally bounded if the subset \(\mathfrak{P}( \mathfrak{C}) \subseteq \mathcal{W}\) is a relatively compact for any totally ordered and bounded subset \(\mathfrak{C} \subseteq \mathcal{W}\) [37]. Therefore, when \(\mathfrak{P}\) is partially totally bounded and partially continuous, we say that \(\mathfrak{P}\) has the partial complete continuity property on the space \(\mathcal{W}\) [37].

Here, consider a nonempty set \(\mathcal{W}\) furnished with an order relation ≤ and a metric d. The order relation ≤ and the metric d are said to be compatible whenever the subsequent property holds: if \(\{ w_{n} \}_{n\geq 1} \) is a monotone sequence belonging to \(\mathcal{W}\) for which a subsequence \(\{ w_{n_{k}} \}_{k\geq 1} \) of \(\{ w_{n} \}_{n\geq 1} \) converges to \(w^{*}\), then we have \(w_{n} \to w^{*}\) by letting \(n\to \infty \) [36]. In the similar manner, let us assume that \((\mathcal{W} , \leq , \Vert \cdot \Vert _{ \mathcal{W} } )\) is a partially ordered normed linear space. In this case, the order relation ≤ and the norm \(\Vert \cdot \Vert _{\mathcal{W}} \) are said to be compatible whenever ≤ and the metric d induced by \(\Vert \cdot \Vert _{\mathcal{W}} \) are compatible [36]. For example, notice that one can prove that the norms and the order relations defined on two spaces \(( \mathbb{R} , \leq , \vert \cdot \vert )\) and \((\mathcal{C}_{\mathbb{R}} (\mathfrak{J}), \leq , \Vert \cdot \Vert )\) are compatible [36].

Let \(\mathfrak{K} : \mathbb{R}^{+} \to \mathbb{R}^{+} \) be a nondecreasing function having the upper semicontinuity property. We say that \(\mathfrak{K}\) is a \(\breve{\mathcal{D}}\)-function if \(\mathfrak{K} (0) = 0\) [36]. An operator \(\mathfrak{P} : \mathcal{W} \to \mathcal{W}\) is said to be partially nonlinear \(\breve{\mathcal{D}}\)-Lipschitz if there exists a \(\breve{\mathcal{D}}\)-function, namely \(\mathfrak{K} : \mathbb{R}^{+} \to \mathbb{R}^{+}\), such that

$$ \Vert \mathfrak{P} w_{1} - \mathfrak{P}w_{2} \Vert _{\mathcal{W}} \leq \mathfrak{K} \bigl( \Vert w_{1} - w_{2} \Vert _{\mathcal{W}} \bigr) $$

for all comparable elements \(w_{1} , w_{2} \in \mathcal{W}\) [37]. If for some \(k>0\) we have \(\mathfrak{K} (z) = kz\), then we say that \(\mathfrak{P}\) is a partially Lipschitz with constant k, where \(z\in \mathbb{R}^{+}\). Moreover, we say that \(\mathfrak{P}\) is a partial contraction with constant k whenever \(k<1\) [37]. Finally, we say that \(\mathfrak{P}\) is a nonlinear \(\breve{\mathcal{D}}\)-contraction whenever \(\mathfrak{P}\) is nonlinear \(\breve{\mathcal{D}}\)-Lipschitz with \(\mathfrak{K} (z) < z\) for each \(z >0\) [37]. The subsequent hybrid theorem is employed to derive the existence and approximation of solutions for our fractional initial problem.

Theorem 2.3

([37])

Suppose that \(( \mathcal{W} ,\leq , \Vert \cdot \Vert _{\mathcal{W}} )\) is a regular partially ordered Banach space furnished with the order relation ≤ and the norm \(\Vert \cdot \Vert _{\mathcal{W}} \) which are compatible. Further, let \(\mathfrak{P}: \mathcal{W} \to \mathcal{W}\) and \(\mathfrak{Q}: \mathcal{W} \to \mathcal{W} \) be two nondecreasing selfmaps having the following properties:

  1. (q1)

    \(\mathfrak{P}\) is a partially nonlinear \(\breve{\mathcal{D}} \)-contraction.

  2. (q2)

    \(\mathfrak{Q}\) is partially continuous and partially compact.

  3. (q3)

    There is an element \(w_{0}\in \mathcal{W} \) satisfying the inequality \(w_{0} \leq \mathfrak{P} w_{0} + \mathfrak{Q} w_{0} \).

Then there is a solution \(w^{*} \in \mathcal{W} \) satisfying the equation \(w=\mathfrak{P}w+\mathfrak{Q}w \). Also, the sequence of successive iterations \(\{ w_{n}\}_{n=0}^{\infty }\) represented by

$$ w_{n+1}= \mathfrak{P} w_{n}+ \mathfrak{Q} w_{n} \quad (n=0,1,2,\dots ) $$
(3)

is a monotone sequence converging to a solution function \(w^{*} \).

3 Main results

After presenting some basic concepts in the two previous sections, we are going to state the desired existence and approximation theorems. To arrive at this goal, we define the supremum norm \(\Vert w \Vert _{\mathcal{W} } = \sup_{ s\in \mathfrak{J} } \vert w(s) \vert \) on the space \(\mathcal{W} = \{ w(s): w(s) \in \mathcal{C}_{ \mathbb{R} }( \mathfrak{J} ) \}\) where \(\mathfrak{J} = [s_{0} , s_{0} + k]\) with \(k>0\). Then \((\mathcal{W}, \Vert \cdot \Vert _{\mathcal{W}} )\) is a Banach space. Moreover, we consider a partial order relation on the Banach space \(\mathcal{W}\). Indeed, for any \(v, w \in \mathcal{W}\), the order relation \(v \leq w \) given by \(v(s) \leq w(s) \) for all \(s\in \mathfrak{J}\) yields a partial ordering in \(\mathcal{W}\). Therefore, an ordered triple \((\mathcal{W}, \leq , \Vert \cdot \Vert _{\mathcal{W}} )\) is a regular partially ordered Banach space [33].

In the following lemma, we introduce an equivalent integral structure for the solution of the Caputo conformable hybrid IVP (2).

Lemma 3.1

Let \(\breve{h} \in \mathcal{W}\). Then \(w_{0}\) is a solution function for the Caputo conformable hybrid differential equation

$$ {}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } \bigl[{{}^{CC} \mathcal{D}_{s_{0}}^{\upsilon , \alpha ^{*}}}w(s) - \hat{\varphi } \bigl(s, w(s)\bigr) \bigr]= \breve{h}(s) \quad (s\in \mathfrak{J}, s_{0}\geq 0) $$
(4)

endowed with initial value conditions \(w(s_{0})=w_{0} \) and \({}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \alpha ^{*}}w(s_{0})= \hat{\varphi } (s_{0}, w(s_{0}))\) if and only if \(w_{0}\) satisfies the integral equation

$$\begin{aligned} w(s)={}&\frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \hat{\varphi } \bigl(r, w(r)\bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }+w_{0} \\ &{}+\frac{1}{\Gamma (\varrho +\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*} - 1 } \breve{h}(r) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }. \end{aligned}$$
(5)

Proof

At the beginning, w is supposed to satisfy the Caputo conformable hybrid equation (4). Clearly, we have \({}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \varrho } [{{}^{CC} \mathcal{D}_{s_{0}}^{\upsilon , \alpha ^{*}}}w(s) - \hat{\varphi } (s, w(s)) ]= \breve{h}(s) \). Now, by taking the ϱth order Riemann–Liouville conformable integral on the last equality, we obtain the following equation:

$$ {{}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \alpha ^{*}}}w(s) - \hat{\varphi } \bigl(s, w(s)\bigr) = \frac{1}{\Gamma (\varrho ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho - 1 } \breve{h}(r) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } + b_{0}, $$
(6)

where we wish to seek the constant \(b_{0} \in \mathbb{R}\). By taking into account the second initial value condition \({}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \alpha ^{*}}w(s_{0})= \hat{\varphi } (s_{0}, w(s_{0}))\), we get \(b_{0} =0 \). In the sequel, by computing the \(\alpha ^{*}\)th order Riemann–Liouville conformable integral on the two sides of (6), we obtain the following equation:

$$\begin{aligned} w(s) = {}&\frac{1}{\Gamma (\varrho +\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*} - 1 } \breve{h}(r) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \\ &{}+\frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \hat{\varphi } \bigl(r, w(r)\bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }+b_{1}, \end{aligned}$$
(7)

where we wish to seek the constant \(b_{1} \in \mathbb{R}\). By taking into account the first initial value condition, we get \(b_{1} = w_{0} \). As a consequence, by substituting the obtained \(b_{1}\) value into (7), we get (5), which shows that the function w satisfies the integral equation (5). In the opposite direction, one can easily check that w is a solution for the Caputo conformable hybrid IVP (4) whenever w satisfies the integral equation (5), and the proof is completed. □

Remark 3.2

In view of Lemma 3.1, the initial value problem (2) is equivalent to the integral equation

$$\begin{aligned} w(s)={}& \frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \hat{\varphi } \bigl(r, w(r)\bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \\ &{}+w_{0}+ \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \\ &{}\times \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \hat{\sigma } \bigl(r , w(r), {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w(r) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }. \end{aligned}$$

Definition 3.3

An element \(u\in \mathcal{W} \) is called a lower solution of the initial problem (2) whenever we have

$$\begin{aligned} \textstyle\begin{cases} {}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \alpha ^{*}}u(s) \leq \hat{\varphi } (s, u(s)) +\frac{1}{\Gamma (\varrho ) } \int _{s_{0}}^{s} ( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } )^{ \varrho - 1 } \breve{h}(r) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }, \\ u(s_{0}) \leq u_{0}, \end{cases}\displaystyle \end{aligned}$$
(8)

where \(\breve{h}(s) = \hat{\sigma } (s , w(s), {}^{RC}\mathcal{I}_{s_{0}}^{ \upsilon , \eta ^{*}} w(s) )\).

This part of paper is devoted to proving the main result on the existence and approximation of solutions for the Caputo conformable hybrid multi-term IVP (2). For this aim, consider the following assumptions:

\((\mathcal{HP}0) \):

The real-valued functions \(\hat{\varphi }:\mathfrak{J}\times \mathbb{R} \to \mathbb{R} \) and \(\hat{ \sigma }:\mathfrak{J}\times \mathbb{R}{\times \mathbb{R}} \to \mathbb{R} \) are continuous.

\((\mathcal{HP}1) \):

φ̂ is nondecreasing with respect to w for each \(s\in \mathfrak{J} \) and \(w\in \mathbb{R} \).

\((\mathcal{HP}2) \):

There is a number \(M_{\hat{\varphi }}>0 \) so that \(0\leq \vert \hat{\varphi }(s,w)\vert \leq M_{\hat{\varphi }} \) for all \(s \in \mathfrak{J} \) and \(w\in \mathbb{R} \).

\((\mathcal{HP}3) \):

There is a \(\breve{\mathcal{D}}\)-contraction \(\mathfrak{K}\) so that \(0\leq \hat{\varphi }(s,w_{1})-\hat{\varphi }(s,w_{2})\leq \mathfrak{K}(w_{1}-w_{2}) \) for \(s\in \mathfrak{J} \) and \(w_{1}, w_{2} \in \mathbb{R} \) with \(w_{2}\leq w_{1} \).

\((\mathcal{HP}4) \):

σ̂ is nondecreasing with respect to \((w_{1},u_{1} )\) and \((w_{2},u_{2} )\) for any \(s\in \mathfrak{J} \) and \((w_{1},u_{1} ), (w_{2},u_{2} ) \in \mathbb{R}^{2} \).

\((\mathcal{HP}5) \):

There is a number \(M_{\hat{ \sigma }}>0 \) such that \(0\leq \vert \hat{ \sigma }(s,w,{v})\vert \leq M_{ \hat{ \sigma }} \) for all \(s \in \mathfrak{J} \) and \({(w,v)\in \mathbb{R}^{2} }\).

\((\mathcal{HP}6) \):

There is a function \(u\in \mathcal{C}_{\mathbb{R}}(\mathfrak{J}) \) so that u is a lower solution for the Caputo conformable hybrid multi-term IVP (2); i.e. an equation (8) holds.

Now, we are ready to demonstrate the main theorem based on above assumptions.

Theorem 3.4

Suppose that all seven assumptions \((\mathcal{HP}0)\)–\((\mathcal{HP}6) \) are valid. Then the Caputo conformable hybrid multi-term initial problem (2) has a mild solution \(w^{*} :\mathfrak{J}\to \mathbb{R} \) and the sequence of successive approximations of \(w_{n}\) (\(n = 0,1, 2,\dots \)) given by

$$\begin{aligned} \textstyle\begin{cases} w_{n+1}(s)= \frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} ( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } )^{ \alpha ^{*} - 1 } \hat{\varphi } (r, w_{n}(r)) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \\ \hphantom{w_{n+1}(s)=}{}+w_{0} + \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \\ \hphantom{w_{n+1}(s)=}{}\times \int _{s_{0}}^{s} ( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } )^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \hat{\sigma } (r , w_{n}(r), {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w_{n}(r) ) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }, \\ w_{0}(s)=u(s), \end{cases}\displaystyle \end{aligned}$$
(9)

is a monotone sequence converging to a solution function \(w^{*} \).

Proof

Assume that \(\mathcal{W} \) is a partially ordered Banach space equipped with supremum norm \(\Vert \cdot \Vert _{ \mathcal{W}} \) and order relation ≤ defined at the beginning of this section. We derive an existence criterion for the solution of the Caputo conformable hybrid multi-term initial problem (2) based on the following operator equation:

$$ w(s)=\mathfrak{P}w(s)+\mathfrak{Q}w(s), $$
(10)

where \(\mathfrak{P}: \mathcal{W} \to \mathcal{W}\) and \(\mathfrak{Q}: \mathcal{W} \to \mathcal{W} \) are two operators given by

$$ {\mathfrak{P}w(s)= \frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \hat{\varphi } \bigl(r, w(r)\bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } } $$

and

$$\begin{aligned} \mathfrak{Q}w(s)={}& \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &{}\times \hat{\sigma } \bigl(r , w(r), {}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w(r) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }+w_{0} \end{aligned}$$

for any \(s\in \mathfrak{J} \). In the following, we intend to prove that the two operators \(\mathfrak{P}\) and \(\mathfrak{Q}\) satisfy all the assumptions of Theorem 2.3. This claim is proved in five steps.

Step I. In this step, we first verify that \(\mathfrak{P}\) and \(\mathfrak{Q}\) are nondecreasing. To do this, for any \(w_{1}, w_{2} \in \mathcal{W} \) with \(w_{2}\leq w_{1} \) and by considering assumption \((\mathcal{HP}1) \), we obtain

$$\begin{aligned} \mathfrak{P}w_{1}(s)&= \frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \hat{\varphi } \bigl(r, w_{1}(r)\bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \\ &\geq \frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \hat{\varphi } \bigl(r, w_{2}(r)\bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \\ &=\mathfrak{P}w_{2}(s). \end{aligned}$$

This inequality implies that the operator \(\mathfrak{P}\) is nondecreasing. In the same manner, in view of assumption \((\mathcal{HP}4) \) and for each \(w_{1}, w_{2} \in \mathcal{W} \) with \(w_{2}\leq w_{1} \), one can write

$$\begin{aligned} & \mathfrak{Q}w_{1}(s)-\mathfrak{Q}w_{2}(s) \\ &\quad ={}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \varrho +\theta ^{*}+\alpha ^{*}} \bigl( \hat{ \sigma } \bigl(s , w_{1}(s), {}^{RC}\mathcal{I}_{s_{0}}^{ \upsilon , \eta ^{*}} w_{1}(s) \bigr)-\hat{\sigma } \bigl(s , w_{2}(s), {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w_{2}(s) \bigr) \bigr) \geq 0. \end{aligned}$$

So \(\mathfrak{Q}w_{2}(s) \leq \mathfrak{Q}w_{1}(s)\), which means that \(\mathfrak{Q} \) is also nondecreasing.

Step II. In this step, we intend to confirm that \(\mathfrak{P}\) satisfies \(\mathrm{(q2)}\) in Theorem 2.3. In other words, we show that \(\mathfrak{P}\) is a partially bounded and also a partially nonlinear \(\breve{\mathcal{D}}\)-contraction on the space \(\mathcal{W}\). To reach this goal, consider an arbitrary element \(w\in \mathcal{W} \). Due to the boundedness of function φ̂ stated in assumption (\(\mathcal{HP}2\)), we have

$$\begin{aligned} \bigl\vert \mathfrak{P}w(s) \bigr\vert &= \biggl\vert \frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \hat{\varphi } \bigl(r, w(r)\bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \biggr\vert \\ &\leq \frac{k^{\alpha ^{*}}M_{\hat{\varphi }}}{\upsilon ^{\alpha ^{*}}\Gamma (\alpha ^{*} +1) } \end{aligned}$$

for any \(s\in \mathfrak{J} \). By taking the supremum norm, we get \(\Vert \mathfrak{P} \Vert _{\mathcal{W}} \leq {\frac{k^{\alpha ^{*}}M_{\hat{\varphi }}}{\upsilon ^{\alpha ^{*}}\Gamma (\alpha ^{*} +1) }} \), which demonstrates that \(\mathfrak{P}\) is bounded on the space \(\mathcal{W,}\) and so by definition \(\mathfrak{P}\) is partially bounded. Furthermore, according to assumption \((\mathcal{HP}3)\), for any \(w_{1} , w_{2} \in \mathcal{W} \) such that \(w_{2} \leq w_{1} \), we obtain

$$ \bigl\vert \mathfrak{P}w_{1}(s)-\mathfrak{P}w_{2}(s) \bigr\vert ={}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \alpha ^{*}} \hat{\varphi } \bigl(r, w_{1}(r)\bigr)- \hat{\varphi } \bigl(r, w_{2}(r)\bigr)\leq \frac{k^{\alpha ^{*}}\mathfrak{K} ( \Vert w_{1}-w_{2} \Vert _{\mathcal{W}})}{\upsilon ^{\alpha ^{*}}\Gamma (\alpha ^{*} +1) } $$

for each \(s\in \mathfrak{J} \), where since \(\mathfrak{K}\) is nondecreasing, so the latter inequality is obtained. Therefore, we get \(\Vert \mathfrak{P}w_{1}(s)-\mathfrak{P}w_{2}(s)\Vert _{ \mathcal{W}} \leq {\frac{k^{\alpha ^{*}}\mathfrak{K} (\Vert w_{1}-w_{2}\Vert _{\mathcal{W}})}{\upsilon ^{\alpha ^{*}}\Gamma (\alpha ^{*} +1) }}\) for all \(w_{1} , w_{2}\in \mathcal{W} \) with \(w_{2}\leq w_{1}\). It follows that \(\mathfrak{P}\) is a partially nonlinear \(\breve{\mathcal{D}}\)-contraction on the space \(\mathcal{W,}\) and so is partially continuous.

Step III. At this moment, we investigate the partial continuity of the operator \(\mathfrak{Q}\) on the space \(\mathcal{W}\). To achieve this purpose, let \(\{w_{n}\}_{n\geq 1} \) be a sequence belonging to the chain \(\mathfrak{C}\) in \(\mathcal{W}\) which converges to w as \(n \to \infty \). From the boundedness of σ̂ based on assumption \((\mathcal{HP}5) \) and also from the continuity of σ̂ based on assumption \((\mathcal{HP}0) \) and by applying the dominated convergence theorem, we reach

$$\begin{aligned} \lim_{n\to \infty }(\mathfrak{Q}w_{n}) (s) ={}& \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &{}\times \lim_{n\to \infty }\hat{\sigma } \bigl(r , w_{n}(r), {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w_{n}(r) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } +\lim_{n\to \infty } (w_{0}) \\ ={}& (\mathfrak{Q}w) (s) \end{aligned}$$

for any \(s\in \mathfrak{J} \). It is observed that the operator sequence \(\mathfrak{Q}w_{n}\) converges to \(\mathfrak{Q}w\) pointwise on the interval \(\mathfrak{J} \) and also this convergence is monotonic due to the monotonicity of the function σ̂. In the next step, we check the equicontinuity of \(\{\mathfrak{Q}w_{n}\}_{n \geq 1} \) in \(\mathcal{W} \). Let \(s_{1}, s_{2}\in \mathfrak{J}=[s_{0}, s_{0} + k] \) be such that \(s_{1}< s_{2} \). Again by assumption \((\mathcal{HP}5)\), we may write

$$\begin{aligned} & \bigl\vert (\mathfrak{Q} w_{n}) (s_{2})-( \mathfrak{Q}w_{n}) (s_{1}) \bigr\vert \\ &\quad = \biggl\vert \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \int _{s_{0}}^{s_{2}} \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &\qquad {}\times \hat{\sigma } \bigl(r , w_{n}(r), {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w_{n}(r) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ &\qquad {}-\frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \int _{s_{0}}^{s_{1}} \biggl( \frac{(s_{1}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &\qquad {}\times \hat{ \sigma }\bigl(r , w_{n}(r), {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w_{n}(r) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ &\quad \leq \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \int _{s_{1}}^{s_{2}} \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ & \qquad {}\times \bigl\vert \hat{ \sigma }\bigl(r , w_{n}(r), {}^{RC} \mathcal{I}_{s_{0}}^{ \upsilon , \eta ^{*}} w_{n}(r) \bigr) \bigr\vert \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \biggr\vert \\ &\qquad {}+ \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \int _{s_{0}}^{s_{1}} \biggl[ \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &\qquad {}- \biggl( \frac{(s_{1}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \biggr] \\ &\qquad {}\times \big\vert \hat{ \sigma }\bigl(r , w_{n}(r), {}^{RC} \mathcal{I}_{s_{0}}^{ \upsilon , \eta ^{*}} w_{n}(r) \bigr) \big\vert \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ &\quad \leq \frac{M_{\hat{ \sigma }} }{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \int _{s_{1}}^{s_{2}} \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \frac{\mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ &\qquad {}+ \frac{M_{\hat{ \sigma }}}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \times \int _{s_{0}}^{s_{1}} \biggl[ \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &\qquad {}- \biggl( \frac{(s_{1}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \biggr] \frac{\mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ &\quad \leq \frac{M_{\hat{ \sigma }}}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}+1 ) } \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (s_{1}-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ (\varrho +\alpha ^{*}+\theta ^{*}) } \\ &\qquad {}+ \frac{M_{\hat{ \sigma }}}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}+1) } \times \biggl[- \biggl( \frac{(s_{2}-s_{0})^{\upsilon } -(s_{1}-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{\varrho +\alpha ^{*}+\theta ^{*}} \\ &\qquad {}+ \frac{(s_{2}-s_{0})^{\upsilon (\varrho +\alpha ^{*}+\theta ^{*})}- (s_{1}-s_{0})^{\upsilon (\varrho +\alpha ^{*}+\theta ^{*}) }}{ \upsilon ^{ (\varrho +\alpha ^{*}+\theta ^{*})} } \biggr]. \end{aligned}$$

By utilizing the dominated convergence theorem for the limit with respect to the second component, we deduce that the RHS of the above inequalities tends to 0 by letting \(s_{1} \to s_{2}\). Therefore, we find that \(\mathfrak{Q}w_{n} \to \mathfrak{Q}w\) uniformly for all \(n\in \mathbb{N}\). Consequently, the operator \(\mathfrak{Q}\) possesses the partial continuity property on the space \(\mathcal{W}\).

Step IV. Here, we claim that the operator \(\mathfrak{Q}\) has the partial compactness property on the space \(\mathcal{W}\). To see the validity of this claim, let us assume that \(\mathfrak{C} \) is a chain belonging to \(\mathcal{W}\). We need to check the uniform boundedness and equicontinuity of \(\mathfrak{Q}(\mathfrak{C})\) in \(\mathcal{W}\). Let \(v\in \mathfrak{Q}(\mathfrak{C})\) be arbitrary. Then we have \(v=\mathfrak{Q}(w)\) for some \(w\in \mathfrak{C}\). In view of hypothesis \((\mathcal{HP}5) \), one can write

$$\begin{aligned} \bigl\vert v(s) \bigr\vert ={}& \bigl\vert \mathfrak{Q}w(s) \bigr\vert \\ ={}& \biggl\vert \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &{}\times \hat{\sigma } \bigl(r , w(r), {}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w(r) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }+w_{0} \biggr\vert \\ \leq{}& { \vert w_{0} \vert } + \biggl\vert \frac{M_{\hat{ \sigma }}}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \biggr\vert \\ \leq{}& { \vert w_{0} \vert } + \biggl\vert \frac{M_{\hat{ \sigma }}}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}+1 ) } \biggl( \frac{(s-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho + \alpha ^{*}+\theta ^{*} } \biggr\vert \\ \leq{}& { \vert w_{0} \vert } + \frac{M_{\hat{ \sigma }}}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}+1 ) } \biggl( \frac{k^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+ \theta ^{*} }=\mathcal{O}^{*} \end{aligned}$$

for any \(s\in \mathfrak{J} \). Hence, this yields \(\Vert v\Vert _{\mathcal{W} } =\Vert (\mathfrak{Q})w\Vert _{ \mathcal{W} } \leq \mathcal{O}^{*} \) for each \(v \in \mathfrak{Q}(\mathfrak{C})\), which illustrates that \(\mathfrak{Q}(\mathfrak{C})\) is uniformly bounded. In the following, the equicontinuity of \(\mathfrak{Q}(\mathfrak{C}) \) is checked. Let \(w \in \mathfrak{C}\) be arbitrary and take \(s_{1},s_{2} \in \mathfrak{J} \) such that \(s_{1} < s_{2} \). We get

$$\begin{aligned} &\bigl\vert (\mathfrak{Q} w) (s_{2})-(\mathfrak{Q}w) (s_{1}) \bigr\vert \\ &\quad = \biggl\vert \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \int _{s_{0}}^{s_{2}} \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &\qquad {}\times \hat{\sigma } \bigl(r , w(r), {}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w(r) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ &\qquad {}-\frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \int _{s_{0}}^{s_{1}} \biggl( \frac{(s_{1}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &\qquad {}\times \hat{ \sigma }\bigl(r , w(r), {}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w(r) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \biggr\vert \\ &\quad \leq \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \int _{s_{1}}^{s_{2}} \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &\qquad {}\times \bigl\vert \hat{ \sigma }\bigl(r , w(r), {}^{RC} \mathcal{I}_{s_{0}}^{ \upsilon , \eta ^{*}} w(r) \bigr) \bigr\vert \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ &\qquad {}+ \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \int _{s_{0}}^{s_{1}} \biggl[ \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &\qquad {}- \biggl( \frac{(s_{1}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \biggr] \\ &\qquad {}\times \bigl\vert \hat{ \sigma }\bigl(r , w(r), {}^{RC} \mathcal{I}_{s_{0}}^{ \upsilon , \eta ^{*}} w(r) \bigr) \bigr\vert \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ &\quad \leq \frac{M_{\hat{ \sigma }} }{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \int _{s_{1}}^{s_{2}} \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \frac{\mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ & \qquad {}+ \frac{M_{\hat{ \sigma }}}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}) } \\ &\qquad {}\times \int _{s_{0}}^{s_{1}} \biggl[ \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ &\qquad {}- \biggl( \frac{(s_{1}-s_{0})^{\upsilon } - (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \biggr] \frac{\mathrm{d}r}{(r-s_{0})^{1-\upsilon }} \\ &\quad \leq \frac{M_{\hat{ \sigma }}}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}+1 ) } \biggl( \frac{(s_{2}-s_{0})^{\upsilon } - (s_{1}-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ (\varrho +\alpha ^{*}+\theta ^{*}) } \\ &\qquad {}+ \frac{M_{\hat{ \sigma }}}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*}+1) } \\ &\qquad {}\times \biggl[- \biggl( \frac{(s_{2}-s_{0})^{\upsilon } -(s_{1}-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{\varrho +\alpha ^{*}+\theta ^{*}} \\ &\qquad {}+ \frac{(s_{2}-s_{0})^{\upsilon (\varrho +\alpha ^{*}+\theta ^{*})}- (s_{1}-s_{0})^{\upsilon (\varrho +\alpha ^{*}+\theta ^{*}) }}{ \upsilon ^{ (\varrho +\alpha ^{*}+\theta ^{*})} } \biggr]. \end{aligned}$$

It is observed that the RHS of the above inequalities tends to 0 uniformly for \(w\in \mathfrak{C}\) by letting \(s_{1} \to s_{2}\). This shows that \(\mathfrak{Q}(\mathfrak{C})\) is equicontinuous. Hence, it is realized that \(\mathfrak{Q}(\mathfrak{C})\) is relatively compact, and so \(\mathfrak{Q}\) has the partial compactness property in \(\mathcal{W}\).

Step V. In the last part of the proof, we prove that there exists an element of \(\mathcal{W}\) so that condition \((\mathrm{q3})\) of Theorem 2.3 holds. To reach this goal, in view of assumption \((\mathcal{HP}6)\), there is a function \(u\in \mathcal{C}_{\mathbb{R}}(\mathfrak{J}) \) such that u is a lower solution for the Caputo conformable hybrid multi-term IVP (2). In other words, we have

$$\begin{aligned} \textstyle\begin{cases} {}^{CC}\mathcal{D}_{s_{0}}^{\upsilon , \alpha ^{*}}u(s) \leq \hat{\varphi } (s, u(s)) +\frac{1}{\Gamma (\varrho ) } \int _{s_{0}}^{s} ( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } )^{ \varrho - 1 } \breve{h}(r) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }, \\ u(s_{0}) \leq u_{0} \in \mathbb{R}^{+}, \end{cases}\displaystyle \end{aligned}$$

where \(\breve{h}(s) = \hat{\sigma } (s , w(s), {}^{RC}\mathcal{I}_{s_{0}}^{ \upsilon , \eta ^{*}} w(s) )\). By considering Lemma 3.1 and by reformulating a mild solution, we get

$$\begin{aligned} u(s)\leq{}& \frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \hat{\varphi } \bigl(r, u(r)\bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }+w_{0} \\ &{} + \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+ \theta ^{*} - 1 } \\ &{}\times \hat{\sigma } \bigl(s , u(s), {}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} u(s) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \\ ={}& \mathfrak{P}u+\mathfrak{Q}u \end{aligned}$$
(11)

for every \(s\in \mathfrak{J} \). Hence, we find that u satisfies the operator inequality \(u\leq \mathfrak{P}u+\mathfrak{Q}u \) and condition \((\mathrm{q3})\) of Theorem 2.3 is valid.

After five steps, we realize that two operators \(\mathfrak{P}\) and \(\mathfrak{Q}\) satisfy all the conditions of Theorem 2.3. Therefore, the operator equation \(w= \mathfrak{P}w+\mathfrak{Q}w \) has a solution \(w^{*}\). In other words, \(w^{*}\) is a solution for the Caputo conformable hybrid multi-term initial problem (2) and also, by Theorem 2.3, the approximate solutions \(w_{n}\) given by (9) for the Caputo conformable hybrid multi-term initial problem (2) converge to \(w^{*}\) monotonically for all \(n=0, 1,2,\dots \), so finally, the proof is completed. □

4 Numerical example

In the current section, we demonstrate an illustrative numerical example for the proposed Caputo conformable hybrid multi-term initial problem (2). We show that our analytical findings are valid and one can utilize the conditions of Theorem 3.4 to construct a successive sequence for approximating the solution function. We also illustrate these results by plotting the graphs of approximate solutions for different values of noninteger orders.

Example 4.1

According to the proposed Caputo conformable hybrid multi-term initial problem (2), we present the following hybrid multi-term IVP:

$$ \textstyle\begin{cases} {}^{CC}\mathcal{D}_{0.1}^{\upsilon , \varrho } [{{}^{CC} \mathcal{D}_{0.1}^{\upsilon , \alpha ^{*}}}w(s) - \hat{\varphi } (s, w(s)) ] = {{}^{RC}\mathcal{I}_{0.1}^{\upsilon , \theta ^{*}}} \hat{\sigma } (s , w(s), {{}^{RC}\mathcal{I}_{0.1}^{ \upsilon , \eta ^{*}} w(s)} ), \\ w(0.1) = 0.2, \qquad {{}^{CC}\mathcal{D}_{0.1}^{ \upsilon , \alpha ^{*}}w(0.1)=\hat{\varphi } (0.1, w(0.1))}, \end{cases} $$
(12)

where ϱ, \(\alpha ^{*}\), \(\theta ^{*}\), and \(\eta ^{*} \in (0, 1) \), \(\upsilon \in (0, 1] \), \(s_{0} = 0.1\), \(w_{0} =0.2\), and \(s\in \mathfrak{J} = [{0.1} , 1] \) with \(k=0.9\). Moreover, two function \(\hat{\varphi } : \mathfrak{J} \times \mathbb{R} \to \mathbb{R} \) and \(\hat{\sigma } : \mathfrak{J} \times \mathbb{R} \to \mathbb{R} \) defined by

$$ \hat{\varphi }(s, w) = \textstyle\begin{cases} \frac{1}{2} (\frac{w}{w+1} ), & w\geq 0, \\ 0, & w< 0, \end{cases} $$

and

$$\begin{aligned}& \hat{ \sigma }\bigl(s,w,{}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w\bigr) \\& \quad =\frac{1}{8} \biggl(1+\tanh \biggl( \frac{1}{\Gamma (\eta ^{*})} \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{v}-(r-s_{0})^{v}}{v} \biggr)^{\eta ^{*}-1}w(r) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \biggr) \biggr) \end{aligned}$$

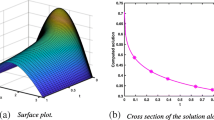
are continuous on \({[0.1,1]\times \mathbb{R}\times \mathbb{R} }\) and so assumption \((\mathcal{HP}0) \) holds. One can see the graph of the functions φ̂ and σ̂ in Figs. 1 and 2. In view of the above graphs, it is obvious that both functions φ̂ and σ̂ are nondecreasing with respect to their components, and this shows that assumptions \((\mathcal{HP}1)\) and \((\mathcal{HP}4)\) are satisfied. On the other hand, the function φ̂ is bounded with upper bound \(M_{\hat{\varphi }}=\frac{1}{2}\), that is, for each \(w \in \mathbb{R}\) we have

$$ 0 \leq \bigl\vert \hat{\varphi }(s,w) \bigr\vert \leq \frac{1}{2} \biggl\vert \frac{w}{w+1} \biggr\vert \leq M_{\hat{\varphi }} = \frac{1}{2}. $$

Besides, the function σ̂ is bounded by \(M_{\hat{ \sigma }}=\frac{1}{4}\), since we have

$$ 0\leq \bigl\vert \hat{ \sigma }\bigl(s,w,{{}^{RC} \mathcal{I}_{s_{0}}^{ \upsilon , \eta ^{*}} w}\bigr) \bigr\vert = \frac{1}{8} \bigl\vert \bigl(1+\tanh { {}^{RC} \mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}}} w\bigr) \bigr\vert \leq M_{\hat{ \sigma }}=\frac{1}{4} $$

for all \(w\in \mathbb{R} \). Therefore, both assumptions \((\mathcal{HP}2)\) and \((\mathcal{HP}5)\) are satisfied. To check assumption \((\mathcal{HP}3)\), we verify that there is a \(\breve{ \mathcal{D}}\)-contraction \(\mathfrak{K} :\mathbb{R}^{+} \to \mathbb{R}^{+} \) given by \(\mathfrak{K}(z) =\frac{1}{2}z\) for any \(z >0\) so that \(0\leq \hat{\varphi }(s,w_{1})-\hat{\varphi }(s,w_{2})\leq \mathfrak{K}(w_{1}-w_{2}) \) for each \(s\in [0.1,1] \) and \(w_{1},w_{2} \in \mathbb{R} \) with \(w_{2} \leq w_{1} \). In the first step, we take \(0 \leq w_{2} \leq w_{1} \). Then we observe that for any \(s\in [{0.1},1] \), the following inequalities hold:

$$\begin{aligned} 0 &\leq \hat{\varphi }\bigl(s,w_{1}(s)\bigr) - \hat{\varphi } \bigl(s,w_{2}(s)\bigr) \\ & = \frac{1}{2}\biggl( \frac{w_{1}(s)}{w_{1}(s)+1}-\frac{w_{2}(s)}{w_{2}(s)+1}\biggr) \\ &\leq \frac{1}{2}\biggl( \frac{w_{1}(s)-w_{2}(s)}{w_{1}(s)w_{2}(s)+w_{1}(s)+w_{2}(s)+1}\biggr) \\ & \leq \frac{1}{2} \bigl\vert w_{1}(s)-w_{2}(s) \bigr\vert \\ &=\mathfrak{K} \bigl(w_{1}(s)-w_{2}(s)\bigr). \end{aligned}$$

In a similar manner, for all \(s\in [{0.1},1] \), one can easily see that the inequality \(0\leq \hat{\varphi }(s,w_{1})-\hat{\varphi }(s,w_{2}) \leq \mathfrak{K}(w_{1}-w_{2}) \) is also valid for \(w_{2} \leq w_{1} < 0\) and \(w_{2} < 0 \leq w_{1} \). Hence assumption \((\mathcal{HP}3)\) is satisfied for the \(\breve{ \mathcal{D}}\)-contraction \(\mathfrak{K}\) in all three cases. Eventually, we check the validity of assumption \((\mathcal{HP}6)\) on the existence of the lower solution for the Caputo conformable hybrid multi-term initial problem formulated by (12). We claim that the constant function \(u(s) = {0} \) is a lower solution for the hybrid multi-term IVP (12) for any \(s\in \mathfrak{J} = [{0.1},1] \). To see this, one can write

$$\begin{aligned} & \frac{1}{\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \hat{\varphi } \bigl(r, w(r)\bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } }+w_{0} \\ &\qquad {} + \frac{1}{\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ & \qquad {}\times \hat{\sigma } \bigl(r , w(r), {}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w(r) \bigr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \\ &\quad = 0.2+ \frac{1}{8\Gamma (\varrho +\alpha ^{*}+\theta ^{*}+1 ) } \biggl( \frac{(s-0.1)^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+ \theta ^{*} } \end{aligned}$$

for any \(s\in \mathfrak{J} = [{0.1},1]\). This implies that

$$\begin{aligned} {0} =u(s)&\leq { 0.2+ \frac{1}{8\Gamma (\varrho +\alpha ^{*}+\theta ^{*}+1 ) } \biggl( \frac{(s-0.008)^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+ \theta ^{*} }} \end{aligned}$$

for each \(s\in \mathfrak{J} = [{0.1},1] \) and so the constant function \(u(s)={0} \) is a lower solution for the hybrid IVP (12). Therefore, assumption \((\mathcal{HP}6)\) holds. Thus, we see that all hypotheses \((\mathcal{HP}0)\)–\((\mathcal{HP}6)\) hold.

Figure 1
figure 1

Graph of the function \(\hat{\varphi } (s, w(s)) \)

Full size image
Figure 2
figure 2

Graph of the function \(\hat{ \sigma }(s,w,{}^{RC}\mathcal{I}_{s_{0}}^{\upsilon , \eta ^{*}} w) \) with \(\upsilon = 1\) and \(\eta ^{*} = 0.99\)

Full size image

Hence, due to Theorem 3.4, we find that the Caputo conformable hybrid multi-term initial value problem (12) has a mild solution \(w^{*} :[{0.1},1] \to \mathbb{R}\) which is a limit function of the monotone convergent sequence \(w_{n}\) (\(n=0,1,2,\dots \)) defined by

$$\begin{aligned} w_{n+1}(s)={}& \frac{1}{2\Gamma (\alpha ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \alpha ^{*} - 1 } \frac{w_{n}(r)}{w_{n}(r)+1} \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \\ &{}+ \frac{1}{8\Gamma (\varrho +\alpha ^{*}+\theta ^{*} ) } \int _{s_{0}}^{s} \biggl( \frac{(s-s_{0})^{\upsilon }- (r-s_{0})^{\upsilon }}{ \upsilon } \biggr)^{ \varrho +\alpha ^{*}+\theta ^{*} - 1 } \\ & {}\times \biggl(1+\tanh \biggl(\frac{1}{\Gamma (\eta )} \int _{s0}^{r} \biggl( \frac{(r-s0)^{v}-(t-s0)^{v}}{v} \biggr)^{1-\eta } \\ &{}\times w_{n}(t)\frac{ \mathrm{d}t}{(t-s_{0})^{1-\upsilon } } \biggr) \biggr) \frac{ \mathrm{d}r}{(r-s_{0})^{1-\upsilon } } \end{aligned}$$
(13)

for each \(s\in \mathfrak{J} = [{0.1},1] \), where \(w_{0}(s)= u(s) = {0} \) for any \(s \in \mathfrak{J} = [{0.1},1] \).

The successive iterations of the sequence \(w_{n}\) to approximate the solution function \(w^{*}\) for the Caputo conformable hybrid multi-term initial value problem (12) are illustrated in Figs. 3 and 4 when the fractional order equals to \(\varrho = 0.2\) with \(\upsilon = 0.2\) and \(\upsilon = 0.8\). In a similar manner, Figs. 5–6 illustrate the successive iterations of the sequence \(w_{n}\) to approximate the solution function \(w^{*}\) for the mentioned hybrid initial problem (12) when the fractional order equals to \(\varrho = 0.8\) with \(\upsilon = 0.3\) and \(\upsilon = 0.7\). Finally, Figs. 7 and 8 illustrate the successive iterations of the sequence \(w_{n}\) to approximate the solution function \(w^{*}\) for the mentioned hybrid multi-term initial problem (12) when the fractional order equals to \(\varrho = 0.9\) with \(\upsilon = 0.1\) and \(\upsilon = 1\), respectively. In this illustration for the iterative sequence \(w_{n}\) formulated by (13), we utilize the trapezoidal rule for an integration with step size 0.009 numerically.

Figure 3
figure 3

Approximating the successive iterations \(w_{n} \) for the solution when \(\varrho = 0.2 \)

Full size image
Figure 4
figure 4

Approximating the successive iterations \(w_{n} \) for the solution when \(\varrho = 0.2 \)

Full size image
Figure 5
figure 5

Approximating the successive iterations \(w_{n} \) for the solution when \(\varrho = 0.8 \)

Full size image
Figure 6
figure 6

Approximating the successive iterations \(w_{n} \) for the solution when \(\varrho = 0.8 \)

Full size image
Figure 7
figure 7

Approximating the successive iterations \(w_{n} \) for the solution when \(\varrho = 0.9 \)

Full size image
Figure 8
figure 8

Approximating the successive iterations \(w_{n} \) for the solution when \(\varrho = 0.9 \)

Full size image

Moreover, since we cannot obtain the exact solution \(w^{*}\) explicitly, we identify the relative error between two iterates \(\Vert w_{n} - w_{n-1} \Vert \) as a stopping factor of the iterations whenever this constant value is less than 0.009. In Table 1, we assemble the relative errors between two successive iterates \(\Vert w_{6} - w_{5} \Vert \) for four different orders \(\varrho = 0.2, 0.5, 0.8\), and \(\varrho = 0.9\), respectively. The obtained results demonstrate that the sequence of successive approximations of solutions \(w_{n}\) for the Caputo conformable hybrid multi-term initial value problem (12) is convergent monotonically.

Table 1 Some values of \(\Vert w_{6} - w_{5}\Vert \) for different ϱ and υ
Full size table

5 Conclusion

It is important that we examine the fractional equations of the function with distinct derivatives numerically from different aspects. In the current manuscript, we derive an existence criterion for a Caputo conformable hybrid multi-term integro-differential equation equipped with initial conditions (2). Note that unlike other published papers in the field of the existence theory, this hybrid problem is considered by a newly defined Caputo fractional conformable derivative for the first time. In this direction, we consider a partially ordered Banach space, and, by applying the lower solution property, the existence and successive approximations of solutions for the hybrid multi-term initial problem (2) are investigated. Eventually, we formulate an illustrative example (12) to support our findings from a numerical point of view. Moreover, we plot the sequence of the obtained approximate solutions for different values of noninteger orders in Figs. 3–8.