Pseudo almost periodic synchronization of Clifford-valued fuzzy cellular neural networks with time-varying delays on time scales

Abstract

At present, the research on discrete-time Clifford-valued neural networks is rarely reported. However, the discrete-time neural networks are an important part of the neural network theory. Because the time scale theory can unify the study of discrete- and continuous-time problems, it is not necessary to separately study continuous- and discrete-time systems. Therefore, to simultaneously study the pseudo almost periodic oscillation and synchronization of continuous- and discrete-time Clifford-valued neural networks, in this paper, we consider a class of Clifford-valued fuzzy cellular neural networks on time scales. Based on the theory of calculus on time scales and the contraction fixed point theorem, we first establish the existence of pseudo almost periodic solutions of neural networks. Then, under the condition that the considered network has pseudo almost periodic solutions, by designing a novel state-feedback controller and using reduction to absurdity, we obtain that the drive-response structure of Clifford-valued fuzzy cellular neural networks on time scales with pseudo almost periodic coefficients can realize the global exponential synchronization. Finally, we give a numerical example to illustrate the feasibility of our results.

1 Introduction

Fuzzy cellular neural networks, introduced into the field of artificial neural networks in 1996 by Yang and Yang [1, 2], are a combination of fuzzy operations (fuzzy AND and fuzzy OR) and cellular neural networks. They combine the advantages of neural network and fuzzy theory and integrate learning, association, recognition, and information processing. Because fuzzy neural networks are based on uncertainty, which is a common problem in the study of brain model, they are closer to human brain than the general neural networks. Therefore the fuzzy cellular neural networks are widely used in the fields such as pattern recognition, computer science, artificial intelligence, optimal control, equation solving, robotics, military science, and so on. Because the application of neural networks in these fields is related to their long-term behaviors and the time delay is inevitable in real neural networks, the dynamics of fuzzy cellular neural networks with various time delays has been extensively studied [3–9].

On the one hand, it is well known that discrete- and continuous-time systems have the same importance in theory and practice, and the discrete-time systems are more convenient for calculation and numerical simulation. Therefore it is necessary to study the discrete-time systems while studying continuous-time systems. Fortunately, studying the neural network systems on time scales can unify the research of discrete- and continuous-time neural networks. So it is necessary and meaningful to study neural network models on time scales [10–16].

On the other hand, Clifford-valued neural network models are a kind of multidimensional neural network models, which are introduced into the study of neural networks in [17, 18]. They include real-valued, complex-valued, and quaternion-valued neural network models as their particular cases. Because of the potential application value of Clifford-valued neural network models in high-dimensional data processing, they have attracted researchers’ attention in recent years [17–23]. However, so far, there are few results on the dynamics of Clifford-valued neural networks [22–27]. In particular, up to date, there are no papers published on the dynamics of Clifford-valued fuzzy cellular neural networks on time scales.

Moreover, we know that periodic, almost periodic, and almost automorphic oscillations are important dynamics of nonautonomous neural networks. Pseudo almost periodicity is an extension of almost periodicity, so it is of great theoretical and practical significance to study the pseudo almost periodic oscillations of neural networks. Therefore many scholars have studied the pseudo almost periodic oscillation of neural networks [28–37]. In addition, synchronization is a common phenomenon in real systems, which shows that many different systems can adjust each other to produce a common dynamic behavior. With the help of synchronization, we can know the behavior of the unknown system through the known one. Therefore, as a powerful tool, it plays an important role in network control and system design. There are many results in the study of synchronization of neural networks [38–49]. However, the results of pseudo almost periodic synchronization of Clifford-valued neural networks on time scales have not been reported.

Based on the above observations and discussion, the primary purpose of this paper is to study the existence of pseudo almost periodic solutions and synchronization for fuzzy cellular neural networks with time-varying delays on time scales. This is the first paper studying the existence of pseudo almost periodic solutions and synchronization of Clifford-valued fuzzy cellular neural networks on time scales.

The remainder of the paper is organized as follows. In Sect. 2, we give some preliminaries and model description. In Sect. 3, we obtain sufficient conditions for the existence of pseudo almost periodic solutions of the proposed networks on time scales. In Sect. 4, we investigate global exponential synchronization. In Sect. 5, we show the effectiveness and feasibility of the developed methods in this paper by a numerical example. In Sect. 6, we draw a brief conclusion.

2 Preliminaries and model description

The real Clifford algebra over $\mathbb{R}^{m}$ is defined as

$$\begin{aligned} \mathcal{A}= \biggl\{ \sum_{A\subseteq \{1,2,\ldots ,m\}}u^{A}e_{A}, u^{A} \in \mathbb{R} \biggr\} , \end{aligned}$$

where $e_{A}=e_{h_{1}}e_{h_{2}}\cdots e_{h_{\nu }}$ with $A=\{h_{1},h_{2},\ldots ,h_{\nu }\}$, $1\leq h_{1}< h_{2}<\cdots <h_{\nu }\leq m$. Moreover, $e_{\emptyset }=e_{0}=1$ and $e_{\{h\}}=e_{h}$, $h=1,2,\ldots ,m$, are called Clifford generators, which satisfy the relations

$$\begin{aligned} \textstyle\begin{cases} e^{2}_{i}=1, & i=1,2,\ldots ,s< m, \\ e_{i}^{2}=-1, & i = s+1, s+2,\ldots ,m, \\ e_{i}e_{j}+e_{j}e_{i}=0, &i\neq j. \end{cases}\displaystyle \end{aligned}$$

Let $Q=\{\emptyset , 1,2,\ldots ,A,\ldots ,12\cdots m\}$. Then it is easy to see that $\mathcal{A}= \{\sum_{A}u^{A}e_{A}, u^{A}\in \mathbb{R} \}$, where $\sum_{A}$ is a shorthand for $\sum_{A\in Q}$. For $u=\sum_{A}u^{A}e_{A}\in \mathcal{A}$ and $v=(v_{1},v_{2},\ldots ,v_{n})^{T}\in \mathcal{A}^{n}$, the norms of u and v are defined as $\|u\|_{\mathcal{A}}=\sqrt{\sum_{A}(u^{A})^{2}}$ and $\|v\|_{\mathcal{A}^{n}}=\max_{1\leq p\leq n}\|v_{p}\|_{ \mathcal{A}}$, respectively; for $v=(v_{1},v_{2},\ldots ,v_{n})^{T}\in \mathcal{A}^{n}$, the norm of v is defined as $\|v\|_{\mathcal{A}^{n}}=\max_{1\leq p\leq n}\|v_{p}\|_{ \mathcal{A}}$. For information on the Clifford algebra, we refer the reader to [50].

Definition 2.1

([8])

For $x,y\in \mathbb{R}$, we denote

$$ x\wedge y=\min \{x,y\} \quad \text{and} \quad x\vee y=\max \{x,y\}. $$

For $x=\sum_{A\in Q}x^{A}e_{A}$, $y=\sum_{A\in Q}y^{A}e_{A} \in \mathcal{A}$, we denote $x\wedge y=\sum_{A\in Q} (x^{A}\wedge y^{A} )e_{A}$ and $x\vee y=\sum_{A\in Q} (x^{A}\vee y^{A} )e_{A}$.

Let $\mathbb{T}$ be a time scale, that is, an arbitrary nonempty closed subset of the real set $\mathbb{R}$ with the topology and ordering inherited from $\mathbb{R}$, let σ and η denote the forward jump operator and the graininess function, respectively, and let $\mathcal{R}$ denote the set of regressive functions on $\mathbb{T}$. We define the set $\mathcal{R}^{+}=\{r\in \mathcal{R}:1+\mu (t)r(t)>0, \forall t\in \mathbb{T}\}$. For the time scale theory, we refer the reader to [51].

Definition 2.2

Let $z=\sum_{A}z^{A}e_{A}:\mathbb{T}\rightarrow \mathcal{A}$, where $z^{A}:\mathbb{T}\rightarrow \mathbb{R}$. The delta derivative of the function z is $z^{\Delta }(t)=\sum_{A\in Q}(z^{A})^{\Delta }(t)e_{A}$, provided that $(z^{A})^{\Delta }(t)$ exists for each $A\in Q$.

Definition 2.3

([52])

A time scale $\mathbb{T}$ is called an almost periodic time scale if

$$\begin{aligned} \Pi :=\{\tau \in \mathbb{R}:t\pm \tau \in \mathbb{T}, \forall t\in \mathbb{T}\} \neq \{0\}. \end{aligned}$$

From now on, we assume that $\mathbb{T}$ is an almost periodic time scale.

Definition 2.4

A function $f \in C(\mathbb{T},\mathcal{A}^{n})$ is called almost periodic if for every $\varepsilon >0$, there exists a constant $l(\varepsilon )>0$ such that each interval of length $l(\varepsilon )$ contains $\tau \in \Pi$ such that

$$\begin{aligned} \bigl\Vert f(t+\tau )-f(t) \bigr\Vert _{\mathcal{A}^{n}}< \varepsilon ,\quad \forall t \in \mathbb{T}. \end{aligned}$$

We denote by $AP(\mathbb{T},\mathcal{A}^{n})$ the set of all almost periodic functions defined on $\mathbb{T}$ and by $BC(\mathbb{T},\mathcal{A}^{n})$ the set of all bounded continuous functions from $\mathbb{T}$ to $\mathcal{A}^{n}$.

Let

$$\begin{aligned} PAP_{0}\bigl(\mathbb{T},\mathcal{A}^{n}\bigr) &= \biggl\{ f \in BC\bigl(\mathbb{T}, \mathcal{A}^{n}\bigr): f \text{ is } \Delta \text{-measurable such that} \\ &\quad \lim_{r\rightarrow +\infty }\frac{1}{2r} \int ^{r}_{-r} \bigl\Vert f(s) \bigr\Vert _{ \mathcal{A}^{n}}\Delta s=0, r\in \mathbb{T} \biggr\} . \end{aligned}$$

Inspired by Definition 3 in [11], we introduce the following definition.

Definition 2.5

A function $f\in BC(\mathbb{T},\mathcal{A}^{n})$ is called pseudo almost periodic if $f=g+h$, where $g\in AP(\mathbb{T},\mathcal{A}^{n})$ and $h\in PAP_{0}(\mathbb{T},\mathcal{A}^{n})$.

We denote by $PAP(\mathbb{T},\mathcal{A}^{n})$ the class of all pseudo almost periodic functions defined on $\mathbb{T}$.

From the above definition, similarly to the proofs of Lemmas 2.5 and 2.6 in [11], it is not difficult to prove the following two lemmas.

Lemma 2.1

If $\alpha \in \mathbb{R}$, $f,g\in PAP(\mathbb{T},\mathcal{A}^{n})$, then $\alpha f, f+g,f\times g\in PAP(\mathbb{T},\mathcal{A}^{n})$.

Lemma 2.2

If $f \in C(\mathcal{A},\mathcal{A}^{n})$ satisfies the Lipschitz condition, $x\in PAP(\mathbb{T},\mathcal{A})$, $\tau \in C^{1}(\mathbb{T},\mathbb{R})\cap AP(\mathbb{T},\Pi )$, and $\inf_{t\in \mathbb{T}}(1-\tau ^{\Delta }(t))>0$, then $f(x(\cdot -\tau (\cdot )))\in PAP(\mathbb{T},\mathcal{A}^{n})$.

The following lemma can be proved by the same proof method as that for Lemma 6 in [53].

Lemma 2.3

Let $a\in AP(\mathbb{T},\mathbb{R}^{+})$ with $-a\in \mathcal{R}^{+}$, $\inf_{t\in \mathbb{T}}a(t)=a^{-}>0$, and $g\in PAP(\mathbb{T},\mathcal{A})$. Then the function $F:t\rightarrow \int _{-\infty }^{t}e_{-a}(t,\sigma (s))g(s)\Delta s$ belongs to $PAP(\mathbb{T},\mathcal{A})$.

Similarly to the proof of Corollary 1 in [1], we can prove the following:

Lemma 2.4

Suppose that $\alpha _{i},\beta _{i}\in C(T,\mathcal{A})$ and $f_{i}\in C(\mathcal{A},\mathcal{A})$, $i=1,2,\ldots ,n$. Then we have

$$\begin{aligned}& \Biggl\Vert \bigwedge_{i=1}^{n}\alpha _{i}f_{i}(x) -\bigwedge_{i=1}^{n} \alpha _{i}f_{i}(y) \Biggr\Vert _{\mathcal{A}} \leq \sum _{i=1}^{n} \Vert \alpha _{i} \Vert _{\mathcal{A}} \bigl\Vert f_{i}(x)-f_{i}(y) \bigr\Vert _{\mathcal{A}},\quad i=1,2,\ldots ,n, \\& \Biggl\Vert \bigvee_{i=1}^{n}\beta _{i}f_{i}(x) -\bigvee_{i=1}^{n} \beta _{i}f_{i}(y) \Biggr\Vert _{\mathcal{A}} \leq \sum _{i=1}^{n} \Vert \beta _{i} \Vert _{\mathcal{A}} \bigl\Vert f_{i}(x)-f_{i}(y) \bigr\Vert _{\mathcal{A}},\quad i=1,2,\ldots ,n. \end{aligned}$$

Similarly to the proof of Lemma 2.2 in [28], we can easily prove the following:

Lemma 2.5

If $\mathcal{F}_{i}\in PAP(T,\mathcal{A})$, $i=1,2,\ldots ,n$, then $\bigwedge_{i=1}^{n}\mathcal{F}_{i}(\cdot )$, $\bigvee_{i=1}^{n}\mathcal{F}_{i}(\cdot )\in PAP(T, \mathcal{A})$.

In the paper, we consider the following Clifford-valued fuzzy cellular neural network with time-varying delays on time scale $\mathbb{T}$:

$$\begin{aligned} x^{\Delta }_{i}(t)&=-a_{i}(t)x_{i}(t)+ \sum_{j=1}^{n}b_{ij}(t)f_{j} \bigl(x_{j}\bigl(t-\eta _{ij}(t)\bigr) \bigr) \\ &\quad{}+\bigwedge_{j=1}^{n}\alpha _{ij}(t)g_{j} \bigl(x_{j}\bigl(t-\tau _{ij}(t)\bigr) \bigr)+\bigvee_{j=1}^{n} \tilde{\alpha }_{ij}(t)\tilde{g}_{j} \bigl(x_{j} \bigl(t-\tilde{\tau }_{ij}(t)\bigr) \bigr) \\ &\quad{}+\sum_{j=1}^{n}d_{ij}(t) \mu _{j}(t) +\bigwedge_{j=1}^{n}T_{ij}(t) \mu _{j}(t) \\ &\quad{}+\bigvee_{j=1}^{n}S_{ij}(t) \mu _{j}(t)+I_{i}(t), \quad i=1,2, \ldots ,n, \end{aligned}$$

(1)

where n is the number of neurons in layers; $x_{i}(t)\in \mathcal{A}$, $\mu _{j}(t)\in \mathcal{A}$, and $I_{i}(t)\in \mathcal{A}$ express the state, input, and bias of the ith neuron, respectively, where $\mathcal{A}$ is a Clifford algebra; $a_{i}(t)>0$ is the rate at which the ith neuron resets its potential to the resting state in isolation when they are disconnected from the network and the external inputs at time t; $\alpha _{ij}(t)\in \mathcal{A}$ represents an element of the fuzzy feedback MIN template; $\tilde{\alpha }_{ij}(t)\in \mathcal{A}$ is an element of the fuzzy feedback MAX template; $T_{ij}(t)\in \mathcal{A}$ and $S_{ij}(t)\in \mathcal{A}$ are fuzzy feed forward MIN template and fuzzy feed forward MAX template, respectively; $b_{ij}(t)\in \mathcal{A}$ is an element of the feedback template; $d_{ij}(t)\in \mathcal{A}$ is the feed forward template; ⋀ and ⋁ denote the fuzzy AND and fuzzy OR operations, respectively; $f_{j}$, $g_{j}$, and $\tilde{g}_{j}:\mathcal{A}\rightarrow \mathcal{A}$ are the activation functions; $\eta _{ij}(t)$, $\tau _{ij}(t)$, and $\tilde{\tau }_{ij}(t)$ correspond to the transmission delays at time t and satisfy $t-\eta _{ij}(t)$, $t-\tau _{ij}(t)$, and $t-\tilde{\tau }_{ij}(t)\in \mathbb{T}$ for $t\in \mathbb{T}$.

Throughout the rest of the paper, we adopt the following notation:

$$\begin{aligned}& a^{-}_{i} =\inf_{t\in \mathbb{T}}a_{i}(t), \qquad b^{+}_{ij}= \sup_{t\in \mathbb{T}} \bigl\Vert b_{ij}(t) \bigr\Vert _{\mathcal{A}},\qquad \alpha ^{+}_{ij}=\sup_{t\in \mathbb{T}} \bigl\Vert \alpha _{ij}(t) \bigr\Vert _{ \mathcal{A}}, \\& \tilde{\alpha }^{+}_{ij} =\sup_{t\in \mathbb{T}} \bigl\Vert \tilde{\alpha }_{ij}(t) \bigr\Vert _{\mathcal{A}},\qquad \eta ^{+}_{ij}=\sup_{t\in \mathbb{T}}\eta _{ij}(t),\qquad \tau ^{+}_{ij}=\sup _{t\in \mathbb{T}}\tau _{ij}(t), \\& \tilde{\tau }^{+}_{ij} =\sup_{t\in \mathbb{T}}\tilde{ \tau }_{ij}(t), \qquad \mathcal{I}=\{1,2,\ldots ,n\},\qquad \zeta =\max _{i,j\in \mathcal{I}} \bigl\{ \eta ^{+}_{ij},\tau ^{+}_{ij},\tilde{\tau }^{+}_{ij} \bigr\} . \end{aligned}$$

The initial values of system (1) are as follows:

$$\begin{aligned} x_{i}(s)=\varphi _{i}(s)\in \mathcal{A},\quad s\in [-\zeta ,0]_{ \mathbb{T}}, \end{aligned}$$

where $\varphi _{i} \in C([-\zeta ,0]_{\mathbb{T}},\mathcal{A})$, $i\in \mathcal{I}$.

To obtain our primary results, we need the following assumptions:

$(S_{1})$:

For $i,j\in \mathcal{I}$, $a_{i}\in AP(\mathbb{T},\mathbb{R}^{+})$ with $-a_{i}\in \mathcal{R}^{+}$, $\eta _{ij},\tau _{ij}, \tilde{\tau }_{ij}\in C^{1}(\mathbb{T}, \mathbb{R}^{+})\cap AP(\mathbb{T},\Pi )$ with $\inf_{t\in \mathbb{R}} \{(1-\eta ^{\Delta }_{ij}(t)),(1- \tau ^{\Delta }_{ij}(t)),(1-\tilde{\tau }^{\Delta }_{ij}(t)) \}>0$, and $b_{ij},\alpha _{ij},\tilde{\alpha }_{ij}, \mu _{j},d_{ij},S_{ij},T_{ij},I_{i}\in PAP(\mathbb{T},\mathcal{A})$.

$(S_{2})$:

For $j\in \mathcal{I}$, $f_{j},g_{j},\tilde{g}_{j}\in C(\mathcal{A},\mathcal{A})$, d there exist positive constants $L^{f}_{j}$, $L^{g}_{j}$, $L^{\tilde{g}}_{j}$ such that for any $u,v\in \mathcal{A}$, $\|f_{j}(u)-f_{j}(v)\|_{\mathcal{A}}\leq L^{f}_{j}\|u-v\|_{ \mathcal{A}}$, $\|g_{j}(u)-g_{j}(v)\|_{\mathcal{A}}\leq L^{g}_{j}\|u-v \|_{\mathcal{A}}$, $\|\tilde{g}_{j}(u)-\tilde{g}_{j}(v)\|_{\mathcal{A}} \leq L^{\tilde{g}}_{j}\|u-v\|_{\mathcal{A}}$.

$(S_{3})$:

$\max_{i\in \mathcal{I}} \{\frac{\mathcal{P}_{i}}{a^{-}_{i}} \}\leq \frac{1}{2} \text{ and } \max_{i\in \mathcal{I}} \{\frac{\mathcal{Q}_{i}}{a^{-}_{i}} \}=:\kappa < 1$, where for $i,j\in \mathcal{I}$,

$$\begin{aligned}& \mathcal{P}_{i} =\sum_{j=1}^{n}b^{+}_{ij} \biggl(L^{f}_{j} + \frac{1}{2} \biggr)+\sum _{j=1}^{n}\alpha ^{+}_{ij} \biggl(L^{g}_{j}+ \frac{1}{2} \biggr) +\sum _{j=1}^{n}\tilde{\alpha }^{+}_{ij} \biggl(L^{ \tilde{g}}_{j} +\frac{1}{2} \biggr), \\& \mathcal{Q}_{i} =\sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} +\sum_{j=1}^{n}\alpha ^{+}_{ij}L^{g}_{j}+ \sum_{j=1}^{n} \tilde{\alpha }^{+}_{ij}L^{\tilde{g}}_{j}. \end{aligned}$$

3 The existence of pseudo almost periodic solutions

In this section, we state and prove sufficient conditions for the existence of pseudo almost periodic solutions of (1).

Let $\mathbf{Y}= PAP(\mathbb{T},\mathcal{A}^{n})$. Then it is a Banach space with the norm $\|f\|_{\mathbf{Y}}=\sup_{t\in \mathbb{T}}\|f(t)\|_{ \mathcal{A}^{n}}$. Take

$$ \mathbf{Y}_{0}= \bigl\{ \varphi \in \mathbf{Y}| \Vert \varphi - \varphi _{0} \Vert _{ \mathbf{Y}}\leq \varpi \bigr\} , $$

where $\varphi _{0}=(\varphi ^{1}_{0},\varphi ^{2}_{0},\ldots ,\varphi ^{n}_{0})^{T}$,

$$\begin{aligned} \varphi ^{i}_{0}(t)&= \int _{-\infty }^{t}e_{-a_{i}}\bigl(t,\sigma (s) \bigr) \Biggl(\sum_{j=1}^{n}d_{ij}(s) \mu _{j}(s) +\bigwedge_{j=1}^{n}T_{ij}(s) \mu _{j}(s) \\ &\quad{}+\bigvee_{j=1}^{n} S_{ij}(s)\mu _{j}(s) +I_{i}(s) \Biggr) \Delta s, \quad i\in \mathcal{I}, \end{aligned}$$

and

$$\begin{aligned} \varpi \geq \Bigl\{ \Vert \varphi _{0} \Vert _{\mathbf{Y}},\max _{j\in \mathcal{I}}\bigl\{ \bigl\Vert f_{j}(0) \bigr\Vert _{\mathcal{A}}\bigr\} , \max_{j\in \mathcal{I}}\bigl\{ \bigl\Vert g_{j}(0) \bigr\Vert _{\mathcal{A}}\bigr\} ,\max_{j\in \mathcal{I}} \bigl\{ \bigl\Vert \tilde{g}_{j}(0) \bigr\Vert _{\mathcal{A}}\bigr\} \Bigr\} . \end{aligned}$$

Theorem 3.1

Let $(S_{1})$–$(S_{3})$ be satisfied. Then system (1) possesses only one pseudo almost periodic solution in $\mathbf{Y}_{0}$.

Proof

Firstly, it is easy to check that if $x\in BC(\mathbb{T},\mathcal{A}^{n})$ is a solution of the integral equation

$$\begin{aligned} x_{i}(t)&= \int _{-\infty }^{t}e_{-a_{i}}\bigl(t,\sigma (s) \bigr) \Biggl(\sum_{j=1}^{n}b_{ij}(s)f_{j} \bigl(x_{j}\bigl(s-\eta _{ij}(s)\bigr) \bigr) \\ &\quad{}+\bigwedge_{j=1}^{n}\alpha _{ij}(s)g_{j} \bigl(x_{j}\bigl(s-\tau _{ij}(s)\bigr) \bigr)+\bigvee_{j=1}^{n} \tilde{\alpha }_{ij}(s)\tilde{g}_{j} \bigl(x_{j} \bigl(s-\tilde{\tau }_{ij}(s)\bigr) \bigr) \\ &\quad{}+\sum_{j=1}^{n}d_{ij}(s) \mu _{j}(s) +\bigwedge_{j=1}^{n}T_{ij}(s) \mu _{j}(s) \\ &\quad{}+\bigvee_{j=1}^{n}S_{ij}(s) \mu _{j}(s)+I_{i}(s) \Biggr) \Delta s,\quad i\in \mathcal{I}, \end{aligned}$$

then x is also a solution of system (1).

Secondly, we define the operator $\Upsilon :\mathbf{Y}\rightarrow BC(\mathbb{T},\mathcal{A}^{n})$ by

$$ \Upsilon \varphi =(\Upsilon _{1}\varphi ,\Upsilon _{2} \varphi , \ldots ,\Upsilon _{n}\varphi )^{T}, $$

where $\varphi \in \mathbf{Y}$,

$$\begin{aligned} (\Upsilon _{i}\varphi ) (t)= \int _{-\infty }^{t}e_{-a_{i}}\bigl(t,\sigma (s) \bigr) \mathcal{W}_{i}(s)\Delta s, \end{aligned}$$

and

$$\begin{aligned} \mathcal{W}_{i}(s)&=\sum_{j=1}^{n}b_{ij}(s)f_{j} \bigl( \varphi _{j}\bigl(s-\eta _{ij}(s)\bigr) \bigr) + \bigwedge_{j=1}^{n} \alpha _{ij}(s)g_{j} \bigl(\varphi _{j}\bigl(s-\tau _{ij}(s)\bigr) \bigr) \\ &\quad{}+\bigvee_{j=1}^{n}\tilde{\alpha }_{ij}(s)\tilde{g}_{j} \bigl( \varphi _{j} \bigl(s-\tilde{\tau }_{ij}(s)\bigr) \bigr) +\sum _{j=1}^{n}d_{ij}(s) \mu _{j}(s) + \bigwedge_{j=1}^{n}T_{ij}(s)\mu _{j}(s) \\ &\quad{}+\bigvee_{j=1}^{n}S_{ij}(s) \mu _{j}(s)+I_{i}(s),\quad i\in \mathcal{I}. \end{aligned}$$

We will show that $\Upsilon :\mathbf{Y}\rightarrow \mathbf{Y}$ is well defined. In fact, by Lemmas 2.1, 2.2, and 2.5 for any $\varphi \in \mathbf{Y}$, we have $\mathcal{W}_{i}(s) \in PAP(\mathbb{T},\mathcal{A})$, $i\in \mathcal{I}$. Furthermore, by Lemma 2.3 we conclude that $\Upsilon _{i}\varphi \in PAP(\mathbb{T},\mathcal{A})$, $i\in \mathcal{I}$. Hence $\Upsilon \varphi \in \mathbf{Y}$.

Thirdly, we will prove that $\Upsilon (\mathbf{Y}_{0})\subset \mathbf{Y}_{0}$. In fact, for every $\varphi \in \mathbf{Y}_{0}$, we have that

$$ \Vert \varphi \Vert _{\mathbf{Y}}\leq \Vert \varphi -\varphi _{0} \Vert _{\mathbf{Y}}+ \Vert \varphi _{0} \Vert _{\mathbf{Y}}\leq 2\varpi , $$

and so we deduce that

$$\begin{aligned} &\sup_{t\in \mathbb{T}} \bigl\Vert (\Upsilon \varphi -\varphi _{0}) (t) \bigr\Vert _{\mathcal{A}^{n}} \\ &\quad =\max_{i\in \mathcal{I}} \Biggl\{ \sup_{t\in \mathbb{T}} \Biggl\Vert \int _{-\infty }^{t}e_{-a_{i}}\bigl(t,\sigma (s) \bigr) \Biggl(\sum_{j=1}^{n}b_{ij}(s)f_{j} \bigl(\varphi _{j}\bigl(s-\eta _{ij}(s)\bigr) \bigr) \\ &\qquad{}+\bigwedge_{j=1}^{n}\alpha _{ij}(s)g_{j} \bigl(\varphi _{j}\bigl(s- \tau _{ij}(s)\bigr) \bigr) +\bigvee_{j=1}^{n} \tilde{\alpha }_{ij}(s) \tilde{g}_{j} \bigl(\varphi _{j}\bigl(s-\tilde{\tau }_{ij}(s)\bigr) \bigr) \Biggr) \Delta s \Biggr\Vert _{\mathcal{A}} \Biggr\} \\ &\quad \leq \max_{i\in \mathcal{I}} \Biggl\{ \sup_{t\in \mathbb{T}} \Biggl[ \int _{-\infty }^{t}e_{-a_{i}}\bigl(t,\sigma (s) \bigr) \Biggl(\sum_{j=1}^{n}b^{+}_{ij} \bigl(L^{f}_{j} \bigl\Vert \varphi _{j} \bigl(s-\eta _{ij}(s)\bigr) \bigr\Vert _{\mathcal{A}} + \bigl\Vert f_{j}( {0}) \bigr\Vert _{\mathcal{A}} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}\alpha ^{+}_{ij} \bigl(L^{g}_{j} \bigl\Vert \varphi _{j}\bigl(s- \tau _{ij}(s)\bigr) \bigr\Vert _{\mathcal{A}} + \bigl\Vert g_{j}({0}) \bigr\Vert _{\mathcal{A}} \bigr) \\ &\qquad{}+\sum_{j=1}^{n}\tilde{\alpha }^{+}_{ij} \bigl(L^{\tilde{g}}_{j} \bigl\Vert \varphi _{j}\bigl(s-\tilde{\tau }_{ij}(s)\bigr) \bigr\Vert _{\mathcal{A}}+ \bigl\Vert \tilde{g}_{j}( {0}) \bigr\Vert _{\mathcal{A}} \bigr) \Biggr)\Delta s \Biggr] \Biggr\} \\ &\quad \leq \max_{i\in \mathcal{I}} \Biggl\{ \frac{2\varpi }{a^{-}_{i}} \Biggl( \sum _{j=1}^{n}b^{+}_{ij} \biggl(L^{f}_{j} +\frac{1}{2} \biggr) + \sum _{j=1}^{n}\alpha ^{+}_{ij} \biggl(L^{g}_{j} +\frac{1}{2} \biggr) +\sum _{j=1}^{n}\tilde{\alpha }^{+}_{ij} \biggl(L^{ \tilde{g}}_{j} +\frac{1}{2} \biggr) \Biggr) \Biggr\} \\ &\quad =\max_{i\in \mathcal{I}} \biggl\{ \frac{2\varpi \mathcal{P}_{i}}{a^{-}_{i}} \biggr\} , \end{aligned}$$

which, combined with condition $(S_{3})$, implies that $\|\Phi \varphi \|_{\mathbf{Y}}\leq \varpi$. Hence $\Upsilon (\mathbf{Y}_{0})\subset \mathbf{Y}_{0}$.

Finally, we will prove that ϒ is a contraction. Noting that, for any $\varphi , \psi \in \mathbf{Y}_{0}$,

$$\begin{aligned} &\sup_{t\in \mathbb{T}} \bigl\Vert (\Upsilon \varphi -\Upsilon \psi ) (t) \bigr\Vert _{\mathcal{A}^{n}} \\ &\quad =\max_{i\in \mathcal{I}} \Biggl\{ \sup_{t\in \mathbb{T}} \Biggl\Vert \int _{-\infty }^{t}e_{-c_{i}}\bigl(t,\sigma (s) \bigr) \Biggl(\sum_{j=1}^{n}b_{ij}(s) \bigl(f_{j}\bigl(\varphi _{j}\bigl(s-\eta _{ij}(s) \bigr)\bigr) \\ &\qquad{}-f_{j}\bigl(\psi _{j}\bigl(s-\eta _{ij}(s)\bigr)\bigr) \bigr)+\bigwedge_{j=1}^{n} \alpha _{ij}(s) \bigl(g_{j}\bigl(\varphi _{j} \bigl(s-\tau _{ij}(s)\bigr)\bigr)-g_{j}\bigl(\psi _{j}\bigl(s- \tau _{ij}(s)\bigr)\bigr) \bigr) \\ &\qquad{}+\bigvee_{j=1}^{n}\tilde{\alpha }_{ij}(s) \bigl(\tilde{g}_{j}\bigl( \varphi _{j} \bigl(s-\tilde{\tau }_{ij}(s)\bigr)\bigr)-\tilde{g}_{j}\bigl( \psi _{j}\bigl(s- \tilde{\tau }_{ij}(s)\bigr)\bigr) \bigr) \Biggr) \Delta s \Biggr\Vert _{\mathcal{A}} \Biggr\} \\ &\quad \leq \max_{i\in \mathcal{I}} \Biggl\{ \frac{1}{a^{-}_{i}} \Biggl(\sum _{j=1}^{n}b^{+}_{ij}L^{f}_{j} +\sum_{j=1}^{n}\alpha ^{+}_{ij}L^{g}_{j}+ \sum_{j=1}^{n}\tilde{\alpha }^{+}_{ij}L^{\tilde{g}}_{j} \Biggr) \Biggr\} \Vert \varphi -\psi \Vert _{\mathbf{Y}} \\ &\quad =\max_{i\in \mathcal{I}} \biggl\{ \frac{\mathcal{Q}_{i}}{a^{-}_{i}} \biggr\} \Vert \varphi -\psi \Vert _{\mathbf{Y}}, \end{aligned}$$

by $(S_{3})$ we arrive at

$$\begin{aligned} \Vert \Phi \varphi -\Phi \psi \Vert _{\mathbf{Y}}\leq \kappa \Vert \varphi -\psi \Vert _{\mathbf{Y}}. \end{aligned}$$

Hence ϒ is a contraction mapping. Consequently, ϒ has a unique fixed point in $\mathbf{Y}_{0}$, that is, system (1) possesses a unique pseudo almost periodic solution in $\mathbf{Y}_{0}$. This completes the proof of Theorem 3.1. □

4 Pseudo almost periodic synchronization

In this section, we take (1) as the driving system to study the global exponential synchronization of the drive-response structure of system (1). For this purpose, we take the following system as the response system:

$$\begin{aligned} y^{\Delta }_{i}(t)&=-a_{i}(t)y_{i}(t)+ \sum_{j=1}^{n}b_{ij}(t)f_{j} \bigl(y_{j}\bigl(t-\eta _{ij}(t)\bigr) \bigr)\bigwedge _{j=1}^{n}\alpha _{ij}(t)g_{j} \bigl(y_{j}\bigl(t-\tau _{ij}(t)\bigr) \bigr) \\ &\quad{}+\bigvee_{j=1}^{n}\tilde{\alpha }_{ij}(t)\tilde{g}_{j} \bigl(y_{j}\bigl(t- \tilde{\tau }_{ij}(t)\bigr) \bigr) +\sum_{j=1}^{n}d_{ij}(t) \mu _{j}(t) +\bigwedge_{j=1}^{n}T_{ij}(t) \mu _{j}(t) \\ &\quad{}+\bigvee_{j=1}^{n}S_{ij}(t) \mu _{j}(t)+I_{i}(t)+\theta _{i}(t), \end{aligned}$$

(2)

where $t\in \mathbb{T}$, $i\in \mathcal{I}$, $y_{i}(t)\in \mathcal{A}$ denotes the state of the response system, $\theta _{i}(t)$ is a state-feedback controller, the remaining notations are the same as those in system (2), and the initial condition is as follows:

$$\begin{aligned} y_{i}(s)=\psi _{i}(s)\in \mathcal{A},\quad s\in [-\zeta ,0]_{ \mathbb{T}}, \end{aligned}$$

where $\psi _{i} \in C([-\zeta ,0]_{\mathbb{T}},\mathcal{A})$, $i\in \mathcal{I}$.

Put $z_{i}(t)=y_{i}(t)-x_{i}(t)$. Subtracting (1) from (2) yields the following error system:

$$\begin{aligned} z^{\Delta }_{i}(t) &=-a_{i}(t)z_{i}(t)+ \sum_{j=1}^{n}b_{ij}(t) \bigl(f_{j}\bigl(y_{j}\bigl(t-\eta _{ij}(t)\bigr) \bigr) -f_{j}\bigl(x_{j}\bigl(t-\eta _{ij}(t) \bigr)\bigr) \bigr) \\ &\quad{}+\bigwedge_{j=1}^{n}\alpha _{ij}(s) \bigl(g_{j}\bigl(y_{j}\bigl(t- \tau _{ij}(t)\bigr)\bigr)-g_{j}\bigl(x_{j}\bigl(t-\tau _{ij}(t)\bigr)\bigr) \bigr) \\ &\quad{}+\bigvee_{j=1}^{n}\tilde{\alpha }_{ij}(t) \bigl(\tilde{g}_{j}\bigl(y_{j}\bigl(t- \tilde{\tau }_{ij}(t)\bigr)\bigr)-\tilde{g}_{j} \bigl(x_{j}\bigl(t-\tilde{\tau }_{ij}(t)\bigr)\bigr) \bigr)+ \theta _{i}(t),\quad i\in \mathcal{I}. \end{aligned}$$

(3)

To achieve the global exponential synchronization of the drive-response systems, we design the following state-feedback controller:

$$\begin{aligned} \theta _{i}(t)&=-c_{i}(t)z_{i}(t)+\bigwedge _{j=1}^{n}\beta _{ij}(t) \bigl(h_{j}\bigl(y_{j}\bigl(t-\tau _{ij}(t)\bigr) \bigr) -h_{j}\bigl(x_{j}\bigl(t-\tau _{ij}(t) \bigr)\bigr) \bigr) \\ &\quad{}+\bigvee_{j=1}^{n}\tilde{\beta }_{ij}(t) \bigl(\tilde{h}_{j}\bigl(y_{j}\bigl(t- \tilde{\tau }_{ij}(t)\bigr)\bigr) -\tilde{h}_{j} \bigl(x_{j}\bigl(t-\tilde{\tau }_{ij}(t)\bigr)\bigr) \bigr), \quad i\in \mathcal{I}. \end{aligned}$$

Definition 4.1

The response system (2) and the drive system (1) are said to be globally exponentially synchronized if for every solution z of the error system (3), there exist positive constants ξ with $\ominus \xi \in \mathcal{R}^{+}$ and $\mathcal{M}>1$ such that

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert _{\mathcal{A}^{n}}\leq \mathcal{M} \Vert \psi - \varphi \Vert _{0}e_{ \ominus \xi }(t,t_{0}), \quad t\in [0,+\infty )_{\mathbb{T}}, \end{aligned}$$

where $t_{0}\in [-\zeta ,0]_{\mathbb{T}}$, $\|\psi -\varphi \|_{0}=\sup_{ s\in [-\zeta ,0]_{\mathbb{T}}}\|\psi (s)-\varphi (s)\|_{ \mathcal{A}^{n}}$, and ξ, M are independent of z.

Theorem 4.1

Let $(S_{1})$–$(S_{3})$ hold. Suppose further that:

$(S_{4})$:

For $i,j\in \mathcal{I}$, $c_{i}\in AP(\mathbb{T},\mathbb{R}^{+})$ with $-(c_{i}+a_{i})\in \mathcal{R}^{+}$, $\beta _{ij}, \tilde{\beta }_{ij}\in PAP(\mathbb{T},\mathcal{A})$.

$(S_{5})$:

For $i,j\in \mathcal{I}$, $h_{j},\tilde{h}_{j}\in C(\mathcal{A},\mathcal{A})$, and there exist positive constant numbers $L^{h}_{j}$, $L^{\tilde{h}}_{j}$ such that for any $u,v\in \mathcal{A}$,

$$\begin{aligned} \bigl\Vert h_{j}(u)-h_{j}(v) \bigr\Vert _{\mathcal{A}}\leq L^{h}_{j} \Vert u-v \Vert _{\mathcal{A}}, \qquad \bigl\Vert \tilde{h}_{j}(u)- \tilde{h}_{j}(v) \bigr\Vert _{\mathcal{A}}\leq L^{ \tilde{h}}_{j} \Vert u-v \Vert _{\mathcal{A}}. \end{aligned}$$

$(S_{6})$:

$\max_{i\in \mathcal{I}} \{ \frac{\tilde{\mathcal{Q}}_{i}}{a^{-}_{i}+c^{-}_{i}} \}< 1$, where $\tilde{\mathcal{Q}}_{i}=\mathcal{Q}_{i}+\sum_{j=1}^{n} \beta ^{+}_{ij}L^{h}_{j} +\sum_{j=1}^{n}\tilde{\beta }^{+}_{ij}L^{ \tilde{h}}_{j}$.

Then the response system (1) and the drive system (2) are globally exponentially synchronized.

Proof

Multiplying (3) by $e_{-(a_{i}+c_{i})}(t_{0},\sigma (t))$ and then integrating it over the interval $[t_{0},t]_{\mathbb{T}}$, where $t_{0}\in [-\zeta ,0]_{\mathbb{T}}$, we get that

$$\begin{aligned} z_{i}(t) &=z_{i}(t_{0})e_{-(a_{i}+c_{i})}(t,t_{0}) + \int _{t_{0}}^{t}e_{-(a_{i}+c_{i})}\bigl(t, \sigma (s) \bigr) \\ &\quad{}\times \Biggl(\sum_{j=1}^{n}b_{ij}(t) \bigl(f_{j}\bigl(y_{j}\bigl(s- \eta _{ij}(s) \bigr)\bigr)-f_{j}\bigl(x_{j}\bigl(s-\eta _{ij}(s) \bigr)\bigr) \bigr) \\ &\quad{}+\bigwedge_{j=1}^{n}\alpha _{ij}(s) \bigl(g_{j}\bigl(y_{j}\bigl(s- \tau _{ij}(s)\bigr)\bigr)-g_{j}\bigl(x_{j}\bigl(s-\tau _{ij}(s)\bigr)\bigr) \bigr) \\ &\quad{}+\bigvee_{j=1}^{n}\tilde{\alpha }_{ij}(s) \bigl(\tilde{g}_{j}\bigl(y_{j}\bigl(s- \tilde{\tau }_{ij}(s)\bigr)\bigr)-\tilde{g}_{j} \bigl(x_{j}\bigl(s-\tilde{\tau }_{ij}(s)\bigr)\bigr) \bigr) \\ &\quad{}+\bigwedge_{j=1}^{n}\beta _{ij}(s) \bigl(h_{j}\bigl(y_{j}\bigl(s-\tau _{ij}(s)\bigr)\bigr)-h_{j}\bigl(x_{j}\bigl(s- \tau _{ij}(s)\bigr)\bigr) \bigr) \\ &\quad{}+\bigvee_{j=1}^{n}\tilde{\beta }_{ij}(s) \bigl(\tilde{h}_{j}\bigl(y_{j}\bigl(s- \tilde{\tau }_{ij}(s)\bigr)\bigr) -\tilde{h}_{j} \bigl(x_{j}\bigl(s-\tilde{\tau }_{ij}(s)\bigr)\bigr) \bigr) \Biggr) \Delta s,\quad i\in \mathcal{I}. \end{aligned}$$

(4)

Set

$$\begin{aligned} \Theta _{i}(\omega )&=a^{-}_{i}+c^{-}_{i}- \omega - \exp \Bigl(\omega \sup_{s\in \mathbb{T}}\mu (s) \Bigr) \Biggl(\sum _{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\omega \eta ^{+}_{ij} \bigr) \\ &\quad{}+\sum_{j=1}^{n} \bigl(\alpha ^{+}_{ij}L^{g}_{j}+\beta ^{+}_{ij}L^{h}_{j} \bigr) \exp \bigl( \omega \tau ^{+}_{ij} \bigr) \\ &\quad{}+\sum_{j=1}^{n} \bigl(\tilde{\alpha }^{+}_{ij}L^{\tilde{g}}_{j} +\tilde{\beta }^{+}_{ij}L^{\tilde{h}}_{j} \bigr) \exp \bigl( \omega \tilde{\tau }^{+}_{ij} \bigr) \Biggr),\quad i\in \mathcal{I}. \end{aligned}$$

Then by ($S_{6}$), for $i\in \mathcal{I}$, we find

$$\begin{aligned} \Theta _{i}(0)=a^{-}_{i}+c^{-}_{i}- \tilde{\mathcal{Q}}_{i}>0,\quad i \in \mathcal{I}. \end{aligned}$$

Because of the continuity of $\Theta _{i}$ and the fact that $\Theta _{i}(\omega ) \rightarrow -\infty$ as $\omega \rightarrow +\infty$, we see that there exist $\theta _{i}$ such that $\Theta _{i}(\theta _{i})=0$ and $\Theta _{i}(\omega )>0$ for $\omega \in (0,\theta _{i})$, $i\in \mathcal{I}$. Obviously, we have $\Theta _{i}(e)\geq 0$, $i\in \mathcal{I}$, where $e=\min_{i\in \mathcal{I}}\{\theta _{i}\}$. So, we can choose a positive constant $0<\xi <\min \{e,\min_{i\in \mathcal{I}}\{a^{-}_{i}+c^{-}_{i} \} \}$ with $\ominus \xi \in \mathcal{R}^{+}$ such that $\Theta _{i}(\xi )>0$, $i\in \mathcal{I}$, which implies that

$$\begin{aligned} &\frac{\exp (\xi \sup_{s\in \mathbb{T}}\mu (s) )}{a^{-}_{i}+c^{-}_{i}-\xi } \Biggl(\sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\xi \eta ^{+}_{ij} \bigr) +\sum _{j=1}^{n} \bigl(\alpha ^{+}_{ij}L^{g}_{j}+ \beta ^{+}_{ij}L^{h}_{j} \bigr) \exp \bigl(\xi \tau ^{+}_{ij} \bigr) \\ &\quad{}+\sum_{j=1}^{n} \bigl(\tilde{\alpha }^{+}_{ij}L^{\tilde{g}}_{j} +\tilde{\beta }^{+}_{ij}L^{\tilde{h}}_{j} \bigr) \exp \bigl( \xi \tilde{\tau }^{+}_{ij} \bigr) \Biggr)< 1,\quad i\in \mathcal{I}. \end{aligned}$$

Taking

$$ \mathcal{M}=\max_{ i\in \mathcal{I}} \biggl\{ \frac{a^{-}_{i}+c^{-}_{i}}{\tilde{\mathcal{Q}}_{i}} \biggr\} , $$

from ($S_{6}$) we have $\mathcal{M}>1$. Thus

$$\begin{aligned} \frac{1}{\mathcal{M}}&< \frac{\exp (\xi \sup_{s\in \mathbb{T}}\mu (s) )}{a^{-}_{i}+c^{-}_{i}-\xi } \Biggl(\sum_{j=1}^{n}b^{+}_{ij}L^{f}_{j} \exp \bigl(\xi \eta ^{+}_{ij} \bigr) \\ &\quad{}+\sum_{j=1}^{n} \bigl(\alpha ^{+}_{ij}L^{g}_{j}+\beta ^{+}_{ij}L^{h}_{j} \bigr) \exp \bigl( \xi \tau ^{+}_{ij} \bigr) +\sum_{j=1}^{n} \bigl( \tilde{\alpha }^{+}_{ij}L^{\tilde{g}}_{j} +\tilde{\beta }^{+}_{ij}L^{ \tilde{h}}_{j} \bigr) \exp \bigl(\xi \tilde{\tau }^{+}_{ij} \bigr) \Biggr). \end{aligned}$$

For $e_{\ominus \xi }(t,t_{0})>1$, where $t\in [-\zeta ,t_{0}]_{\mathbb{T}}$, it is evident that

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert _{\mathcal{A}^{n}}\leq \mathcal{M}e_{\ominus \xi }(t,t_{0}) \Vert \psi -\varphi \Vert _{0},\quad \forall t\in [-\zeta ,t_{0}]_{\mathbb{T}}. \end{aligned}$$

Further, we will prove the following inequality:

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert _{\mathcal{A}^{n}}\leq \mathcal{M}e_{\ominus \xi }(t,t_{0}) \Vert \psi -\varphi \Vert _{0},\quad \forall t\in (t_{0},+\infty )_{ \mathbb{T}}. \end{aligned}$$

(5)

To this end, we first prove that for any $\varsigma >1$,

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert _{\mathcal{A}^{n}}< \varsigma \mathcal{M}e_{\ominus \xi }(t,t_{0}) \Vert \psi -\varphi \Vert _{0},\quad \forall t\in (t_{0},+\infty )_{ \mathbb{T}}, \end{aligned}$$

(6)

which implies that for all $i\in \mathcal{I}$,

$$\begin{aligned} \bigl\Vert z_{i}(t) \bigr\Vert _{\mathcal{A}}< \varsigma \mathcal{M}e_{\ominus \xi }(t,t_{0}) \Vert \psi -\varphi \Vert _{0},\quad \forall t\in (t_{0},+ \infty )_{ \mathbb{T}}. \end{aligned}$$

(7)

Otherwise, if (7) is not true, then there exist $i_{0}\in \mathcal{I}$ and $\tilde{t}\in (t_{0},+\infty )_{\mathbb{T}}$ such that

$$\begin{aligned} \bigl\Vert z_{i_{0}}(\tilde{t}) \bigr\Vert _{\mathcal{A}}\geq \varsigma \mathcal{M} \Vert \psi -\varphi \Vert _{0}e_{\ominus \xi }( \tilde{t},t_{0}) \end{aligned}$$

and

$$\begin{aligned} \bigl\Vert z_{i_{0}}(t) \bigr\Vert _{\mathcal{A}}< \varsigma \mathcal{M} \Vert \psi -\varphi \Vert _{0}e_{\ominus \xi }(t,t_{0}), \quad t\in (t_{0},\tilde{t})_{ \mathbb{T}}. \end{aligned}$$

Therefore there must exist a constant $C\geq 1$ such that

$$\begin{aligned} \bigl\Vert z_{i_{0}}(\tilde{t}) \bigr\Vert _{\mathcal{A}}= C\varsigma \mathcal{M} \Vert \psi - \varphi \Vert _{0}e_{\ominus \xi }(\tilde{t},t_{0}) \end{aligned}$$

(8)

and

$$\begin{aligned} \bigl\Vert z_{i_{0}}(t) \bigr\Vert _{\mathcal{A}}< C\varsigma \mathcal{M} \Vert \psi -\varphi \Vert _{0}e_{\ominus \xi }(t,t_{0}),\quad t\in (t_{0}, \tilde{t})_{ \mathbb{T}}. \end{aligned}$$

(9)

In view of (8), (9), (4), and $\mathcal{M}>1$, we have

$$\begin{aligned} & \bigl\Vert z_{i_{0}}(\tilde{t}) \bigr\Vert _{\mathcal{A}} \\ &\quad = \Biggl\Vert z_{i_{0}}(t_{0})e_{-(a_{i_{0}}+c_{i_{0}})}( \tilde{t},t_{0})+ \int _{t_{0}}^{\tilde{t}}e_{-(a_{i_{0}}+c_{i_{0}})}\bigl(\tilde{t},\sigma (s)\bigr) \\ &\qquad{}\times \Biggl(\sum_{j=1}^{n}b_{i_{0}j}(s) \bigl(f_{j}\bigl(y_{j}\bigl(s- \eta _{i_{0}j}(s) \bigr)\bigr)-f_{j}\bigl(x_{j}\bigl(s-\eta _{i_{0}j}(s) \bigr)\bigr) \bigr) \\ &\qquad{}+\bigwedge_{j=1}^{n}\alpha _{i_{0}j}(s) \bigl(g_{j}\bigl(\varphi _{j}\bigl(s- \tau _{i_{0}j}(s)\bigr)\bigr) -g_{j}\bigl(\psi _{j} \bigl(s-\tau _{i_{0}j}(s)\bigr)\bigr) \bigr) \\ &\qquad{}+\bigvee_{j=1}^{n}\tilde{\alpha }_{i_{0}j}(s) \bigl(\tilde{g}_{j}\bigl( \varphi _{j} \bigl(s-\tilde{\tau }_{i_{0}j}(s)\bigr)\bigr) -\tilde{g}_{j} \bigl(\psi _{j}\bigl(s- \tilde{\tau }_{i_{0}j}(s)\bigr)\bigr) \bigr) \\ &\qquad{}+\bigwedge_{j=1}^{n}\beta _{i_{0}j}(s) \bigl(h_{j}\bigl(\varphi _{j}\bigl(s- \tau _{i_{0}j}(s)\bigr)\bigr) -h_{j}\bigl(\psi _{j} \bigl(s-\tau _{i_{0}j}(s)\bigr)\bigr) \bigr) \\ &\qquad{}+\bigvee_{j=1}^{n}\tilde{\beta }_{i_{0}j}(s) \bigl(\tilde{h}_{j}\bigl( \varphi _{j} \bigl(s-\tilde{\tau }_{i_{0}j}(s)\bigr)\bigr)-\tilde{h}_{j}\bigl( \psi _{j}\bigl(s- \tilde{\tau }_{i_{0}j}(s)\bigr)\bigr) \bigr) \Biggr) \Delta s \Biggr\Vert _{\mathcal{A}} \\ &\quad < \bigl\Vert z_{i_{0}}(t_{0}) \bigr\Vert _{\mathcal{A}}e_{-(a_{i_{0}}+c_{i_{0}})}( \tilde{t},t_{0}) +C\varsigma \mathcal{M} \Vert \psi -\varphi \Vert _{0}e_{ \ominus \xi }( \tilde{t},t_{0}) \\ &\qquad{}\times \int _{t_{0}}^{\tilde{t}}e_{-(a_{i_{0}}+c_{i_{0}})}\bigl(\tilde{t}, \sigma (s)\bigr) e_{\xi }\bigl(\tilde{t},\sigma (s)\bigr) \Biggl(\sum _{j=1}^{n}b^{+}_{i_{0}j}L^{f}_{j} e_{\xi }\bigl(\sigma (s),s-\eta _{i_{0}j}(s)\bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\alpha ^{+}_{i_{0}j}L^{g}_{j}+\beta ^{+}_{i_{0}j}L^{h}_{j} \bigr) e_{\xi }\bigl(\sigma (s),s-\tau _{i_{0}j}(s)\bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\tilde{\alpha }^{+}_{i_{0}j}L^{\tilde{g}}_{j} +\tilde{\beta }^{+}_{i_{0}j}L^{\tilde{h}}_{j} \bigr) e_{\xi }\bigl(\sigma (s),s- \tilde{\tau }_{i_{0}j}(s)\bigr) \Biggr) \Delta s \\ &\quad = \bigl\Vert z_{i_{0}}(t_{0}) \bigr\Vert _{\mathcal{A}}e_{-(a_{i_{0}}+c_{i_{0}})}( \tilde{t},t_{0}) +C\varsigma \mathcal{M} \Vert \psi -\varphi \Vert _{0} e_{ \ominus \xi }( \tilde{t},t_{0}) \\ &\qquad{}\times \int _{t_{0}}^{\tilde{t}}e_{-(a_{i_{0}}+c_{i_{0}})\oplus \xi }\bigl( \tilde{t}, \sigma (s)\bigr) \Biggl(\sum_{j=1}^{n}b^{+}_{i_{0}j}L^{f}_{j} e_{\xi }\bigl(\sigma (s),s-\eta _{i_{0}j}(s)\bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\alpha ^{+}_{i_{0}j}L^{g}_{j}+\beta ^{+}_{i_{0}j}L^{h}_{j} \bigr) e_{\xi }\bigl(\sigma (s),s-\tau _{i_{0}j}(s)\bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\tilde{\alpha }^{+}_{i_{0}j}L^{\tilde{g}}_{j} +\tilde{\beta }^{+}_{i_{0}j}L^{\tilde{h}}_{j} \bigr) e_{\xi }\bigl(\sigma (s),s- \tilde{\tau }_{i_{0}j}(s)\bigr) \Biggr) \Delta s \\ &\quad \leq \bigl\Vert z_{i_{0}}(t_{0}) \bigr\Vert _{\mathcal{A}}e_{-(a_{i_{0}}+c_{i_{0}})}( \tilde{t},t_{0})+C\varsigma \mathcal{M} \Vert \psi -\varphi \Vert _{0} e_{ \ominus \xi }( \tilde{t},t_{0}) \\ &\qquad{}\times \int _{t_{0}}^{\tilde{t}}e_{-(a_{i_{0}}+c_{i_{0}})\oplus \xi }\bigl( \tilde{t}, \sigma (s)\bigr) \Biggl(\sum_{j=1}^{n}b^{+}_{i_{0}j}L^{f}_{j} \exp \Bigl(\xi \Bigl(\eta ^{+}_{i_{0}j}+\sup_{s\in \mathbb{T}} \mu (s)\Bigr) \Bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\alpha ^{+}_{i_{0}j}L^{g}_{j}+\beta ^{+}_{i_{0}j}L^{h}_{j} \bigr) \exp \Bigl( \xi \Bigl(\tau ^{+}_{i_{0}j}+\sup_{s\in \mathbb{T}}\mu (s) \Bigr) \Bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\tilde{\alpha }^{+}_{i_{0}j}L^{\tilde{g}}_{j} +\tilde{\beta }^{+}_{i_{0}j}L^{\tilde{h}}_{j} \bigr)\exp \Bigl( \xi \Bigl( \tilde{\tau }^{+}_{i_{0}j}+\sup_{s\in \mathbb{T}} \mu (s)\Bigr) \Bigr) \Biggr) \Delta s \\ &\quad \leq C\varsigma \mathcal{M} \Vert \psi -\varphi \Vert _{0} \Biggl\{ \frac{e_{-(a_{i_{0}}+c_{i_{0}})\oplus \xi }(\tilde{t},t_{0})}{C\varsigma \mathcal{M}}+ \exp \Bigl(\xi \sup_{s\in \mathbb{T}}\mu (s) \Bigr) \\ &\qquad{}\times \Biggl(\sum_{j=1}^{n}b^{+}_{i_{0}j}L^{f}_{j} \exp \bigl(\xi \eta ^{+}_{i_{0}j} \bigr)+\sum _{j=1}^{n} \bigl(\alpha ^{+}_{i_{0}j}L^{g}_{j}+ \beta ^{+}_{i_{0}j}L^{h}_{j} \bigr) \exp \bigl(\xi \tau ^{+}_{i_{0}j} \bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\tilde{\alpha }^{+}_{i_{0}j}L^{ \tilde{g}}_{j} +\tilde{\beta }^{+}_{i_{0}j}L^{\tilde{h}}_{j} \bigr) \exp \bigl( \xi \tilde{\tau }^{+}_{i_{0}j} \bigr) \Biggr) \\ &\qquad{}\times \int _{t_{0}}^{\tilde{t}}e_{-(a_{i_{0}}+c_{i_{0}})\oplus \xi }\bigl( \tilde{t}, \sigma (s)\bigr)\Delta s \Biggr\} e_{\ominus \xi }(\tilde{t},t_{0}) \\ &\quad \leq \Biggl\{ \frac{e_{-(a_{i_{0}}+c_{i_{0}})\oplus \xi }(\tilde{t},t_{0})}{C\varsigma \mathcal{M}}+ \exp \Bigl(\xi \sup_{s\in \mathbb{T}} \mu (s) \Bigr) \Biggl(\sum_{j=1}^{n}b^{+}_{i_{0}j}L^{f}_{j} \exp \bigl(\xi \eta ^{+}_{i_{0}j} \bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\alpha ^{+}_{i_{0}j}L^{g}_{j}+\beta ^{+}_{i_{0}j}L^{h}_{j} \bigr) \exp \bigl( \xi \tau ^{+}_{i_{0}j} \bigr) +\sum_{j=1}^{n} \bigl(\tilde{\alpha }^{+}_{i_{0}j}L^{\tilde{g}}_{j} +\tilde{\beta }^{+}_{i_{0}j}L^{ \tilde{h}}_{j} \bigr) \exp \bigl(\xi \tilde{\tau }^{+}_{i_{0}j} \bigr) \Biggr) \\ &\qquad{}\times \frac{1-e_{-(a_{i_{0}}+c_{i_{0}})\oplus \xi }(\tilde{t},t_{0})}{a^{-}_{i_{0}}+c^{-}_{i_{0}}-\xi } \Biggr\} C\varsigma \mathcal{M} \Vert \psi - \varphi \Vert _{0}e_{\ominus \xi }( \tilde{t},t_{0}) \\ &\quad < \Biggl\{ \Biggl[\frac{1}{ \mathcal{M}}- \frac{\exp (\xi \sup_{s\in \mathbb{T}}\mu (s) )}{a^{-}_{i_{0}}+c^{-}_{i_{0}}-\xi } \Biggl(\sum _{j=1}^{n}b^{+}_{i_{0}j}L^{f}_{j} \exp \bigl(\xi \eta ^{+}_{i_{0}j} \bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\alpha ^{+}_{i_{0}j}L^{g}_{j}+\beta ^{+}_{i_{0}j}L^{h}_{j} \bigr) \exp \bigl( \xi \tau ^{+}_{i_{0}j} \bigr) +\sum_{j=1}^{n} \bigl(\tilde{\alpha }^{+}_{i_{0}j}L^{\tilde{g}}_{j} +\tilde{\beta }^{+}_{i_{0}j}L^{ \tilde{h}}_{j} \bigr) \exp \bigl(\xi \tilde{\tau }^{+}_{i_{0}j} \bigr) \Biggr) \Biggr] \\ &\qquad{}\times e_{-(a_{i_{0}}+c_{i_{0}})\oplus \xi }(\tilde{t},t_{0})+ \frac{\exp (\xi \sup_{s\in \mathbb{T}}\mu (s) )}{a^{-}_{i_{0}}+c^{-}_{i_{0}}-\xi } \\ &\qquad{}\times \Biggl(\sum_{j=1}^{n}b^{+}_{i_{0}j}L^{f}_{j} \exp \bigl(\xi \eta ^{+}_{i_{0}j} \bigr) +\sum _{j=1}^{n} \bigl(\alpha ^{+}_{i_{0}j}L^{g}_{j}+ \beta ^{+}_{i_{0}j}L^{h}_{j} \bigr) \exp \bigl(\xi \tau ^{+}_{i_{0}j} \bigr) \\ &\qquad{}+\sum_{j=1}^{n} \bigl(\tilde{\alpha }^{+}_{i_{0}j}L^{\tilde{g}}_{j} +\tilde{\beta }^{+}_{i_{0}j}L^{\tilde{h}}_{j} \bigr) \exp \bigl( \xi \tilde{\tau }^{+}_{i_{0}j} \bigr) \Biggr) \Biggr\} C\varsigma \mathcal{M} \Vert \psi -\varphi \Vert _{0}e_{\ominus \xi }( \tilde{t},t_{0}) \\ &\quad < C\varsigma \mathcal{M} \Vert \psi -\varphi \Vert _{0}e_{\ominus \xi }( \tilde{t},t_{0}), \end{aligned}$$

which contradicts (8), and so (7) holds. Letting $\varsigma \rightarrow 1$, we conclude that (5) holds. As a result, the response system (1) and the drive system (2) are globally exponentially synchronized. The proof of Theorem 4.1 is completed. □

5 Examples

In this section, we present an example to illustrate the feasibility and effectiveness of our results obtained in Sect. 4.

Example 5.1

In systems (1) and (2), let $m=3$ and $n=2$ and take the coefficients are follows:

$$\begin{aligned}& a_{1}(t)=0.35+0.3 \vert \cos \sqrt{3}t \vert , \qquad a_{2}(t)=0.4+0.1 \vert \sin 3t \vert , \\& c_{1}(t)=0.6+0.1 \vert \sin \sqrt{5}t \vert ,\qquad c_{2}(t)=0.3+0.2 \vert \cos 5t \vert , \\& \begin{aligned} f_{j}(x)&= \frac{1}{320}e_{0}\cos \sqrt{5}x^{13}+\frac{3}{800}\sin \bigl(x^{12}+x^{123} \bigr)e_{1}+ \frac{1}{530}e_{2}\tanh 4x^{13} \\ &\quad{}+\frac{1}{390}e_{3}\cos \bigl(x^{2}+x^{13} \bigr)+\frac{1}{245}e_{12}\sin ^{2}x^{3}+ \frac{1}{350}\cos \bigl(x^{3}+x^{1} \bigr)e_{13} \\ &\quad{}+\frac{1}{390}e_{23}\tanh x^{12}+ \frac{1}{380}e_{123}\sin \bigl(x^{0}+x^{2}+x^{23} \bigr), \quad j=1,2, \end{aligned} \\& \begin{aligned} g_{j}(x)&=\tilde{g}_{j}(x)=\frac{\sqrt{3}}{480}e_{0} \cos \sqrt{3}x^{3}+ \frac{1}{225} \bigl\vert x^{1}+x^{3} \bigr\vert e_{1}+ \frac{1}{410}e_{2}\tanh x^{123} \\ &\quad{}+\frac{2}{325}e_{3}\cos \bigl(x^{13}+x^{23} \bigr) +\frac{1}{430} \bigl( \bigl\vert x^{13}+1 \bigr\vert - \bigl\vert x^{2}-1 \bigr\vert \bigr)e_{12} \\ &\quad{}+\frac{\sqrt{2}}{570}e_{13}\sin \bigl(x^{2}+x^{13} \bigr) + \frac{1}{485}e_{23}\cos x^{23} \\ &\quad{}+\frac{1}{390}e_{123}\tanh \bigl(x^{1}+x^{12}+x^{13} \bigr),\quad j=1,2, \end{aligned} \\& h_{j}(x)=\tilde{h}_{j}(x)=\frac{\sqrt{3}}{1110}e_{0} \cos \sqrt{5}\bigl(x^{2}+x^{13}\bigr)+ \frac{1}{345} \bigl\vert x^{12}+x^{123} \bigr\vert e_{1} \\& \hphantom{h_{j}(x)=}{}+ \frac{1}{530}e_{2}\tanh x^{2} + \frac{3}{870}e_{3}\sin \bigl(x^{23}+x^{2} \bigr)+ \frac{1}{470}\cos \bigl(x^{12}\bigr)e_{12} \\& \hphantom{h_{j}(x)=}{}+e_{13}\frac{\sqrt{3}}{990}\sin \bigl(x^{0}+x^{12} \bigr) +e_{23} \frac{1}{435}\tanh x^{23} \\& \hphantom{h_{j}(x)=}{}+\frac{1}{340}e_{123}\cos \bigl(x^{0}+x^{3}+x^{123} \bigr),\quad j=1,2, \\& \begin{aligned} I_{1}(t)&=0.4e_{0}\cos \sqrt{5}t+ (0.1+0.5\cos \sqrt{3}t)e_{1} +0.7 e_{2} \sin 4t \\ &\quad{}+0.4 e_{3}\sin \sqrt{5}t +0.9e_{12}\sin 5t + (0.1+0.6\sin \sqrt{7}t)e_{13} \\ &\quad{}+ \biggl(0.6\cos 5t +\frac{3}{10+t^{2}} \biggr)e_{23}+0.4 e_{123}\cos 3t, \end{aligned} \\& \begin{aligned} I_{2}(t)&=0.7e_{0}\sin \sqrt{3}t+0.6e_{1}\cos 3t+0.8e_{2}\sin 6t \\ &\quad{}+0.8e_{3}\cos \sqrt{3}t +0.5e_{12}\sin 3t +0.7e_{13}\cos \sqrt{5}t \\ &\quad{}+0.6e_{23}\sin 3t +0.9e_{123}\cos 5t+ \frac{4}{20+t^{2}}, \end{aligned} \\& b_{11}(t)=0.03e_{0}\sin 5t+0.01 e_{3}\cos 2t +0.01 e_{23} \sin 5t+ 0.03 e_{123}\cos ^{2} 7t, \\& b_{12}(t)=0.04e_{0}\cos 6t+0.02 e_{2}\sin ^{2} 4t +0.01 e_{3} \sin 3t+ 0.03 e_{12}\cos 6t, \\& b_{21}(t)=0.025e_{2}\sin 2t+0.01 e_{3}\cos 3t +0.02 e_{13} \cos 6t+ 0.03 e_{23}\sin ^{2} 7t, \\& b_{22}(t)=0.04e_{3}\cos 5t+0.02 e_{12}\sin 7t +0.02 e_{13} \cos ^{2} 6t+ 0.03 e_{23}\cos 6t, \\& \tilde{b}_{11}(t)=0.02e_{0}\cos t+0.01 e_{3} \cos 2t +0.01 e_{23} \sin 4t+ 0.03 e_{123}\sin ^{2} 5t, \\& \tilde{b}_{12}(t)=0.02e_{0}\sin 3t+0.02 e_{2} \cos ^{2} 4t +0.01 e_{3} \cos 3t+ 0.04 e_{12}\cos 3t, \\& \tilde{b}_{21}(t)=0.03e_{2}\sin 5t+0.01 e_{3} \cos 3t +0.035 e_{13} \cos 4t+ 0.02 e_{23}\sin ^{2} 7t, \\& \tilde{b}_{22}(t)=0.025e_{3}\sin 3t+0.01 e_{12} \sin ^{2} 5t +0.04 e_{13} \cos 3t+ 0.03 e_{23}\cos 2t, \\& \begin{aligned} \alpha _{11}(t)&=\tilde{\alpha }_{11}(t)=0.01e_{3} \cos 5t+0.02 e_{12} \sin 3t \\ &\quad{}+0.02 e_{13}\sin ^{2} 6t+ 0.01 e_{23}\sin 4t, \end{aligned} \\& \begin{aligned} \alpha _{12}(t)&=\tilde{\alpha }_{12}(t)=0.02e_{2} \cos 4t+0.04 e_{3} \sin 5t \\ &\quad{}+0.02 e_{12}\cos 4t+ 0.04 e_{123}\cos 3t, \end{aligned} \\& \begin{aligned} \alpha _{21}(t)&=\tilde{\alpha }_{21}(t)=0.03e_{1} \sin 3t+0.02 e_{2} \cos 4t \\ &\quad{}+0.02 e_{3}\sin 5t+ 0.01 e_{12}\cos ^{2} 2t, \end{aligned} \\& \begin{aligned} \alpha _{22}(t)&=\tilde{\alpha }_{22}(t)=0.05e_{0} \sin 4t+0.03 e_{1} \cos 5t \\ &\quad{}+0.02 e_{2}\cos 5t+ 0.03 e_{13}\sin ^{2} 4t, \end{aligned} \\& \begin{aligned} \beta _{11}(t)&=\tilde{\beta }_{11}(t)=0.03e_{0} \sin 2t+0.01 e_{1} \cos 3t \\ &\quad{}+0.02 e_{2}\cos \sqrt{5}t+0.02e_{123}\cos 3t, \end{aligned} \\& \begin{aligned} \beta _{12}(t)&=\tilde{\beta }_{12}(t)=0.02e_{0} \cos 4t+0.03 e_{1} \sin 5t \\ &\quad{}+0.04 e_{2}\cos \sqrt{6}t+0.01e_{23}\sin 3t, \end{aligned} \\& \begin{aligned} \beta _{21}(t)&=\tilde{\beta }_{21}(t)=0.03e_{0} \sin t+0.01 e_{1}\sin t \\ &\quad{}+0.02 e_{2}\sin \sqrt{3}t+0.02e_{12}\cos 4t, \end{aligned} \\& \begin{aligned} \beta _{22}(t)&=\tilde{\beta }_{22}(t)=0.015e_{1} \cos 5t+0.02 e_{2} \cos 3t \\ &\quad{}+0.01 e_{12}\sin \sqrt{6}t+0.02e_{123}\cos 5t, \end{aligned} \\& \begin{aligned} d_{ij}(t)&=0.3e_{0}\sin 2\sqrt{5}t+0.3 e_{1}\cos 2\sqrt{5}t \\ &\quad{}+0.2e_{12}\sin 2t+0.1 e_{23}\sin \sqrt{2}t,\quad i,j=1,2, \end{aligned} \\& \begin{aligned} T_{ij}(t)&=(0.2+0.1\cos 2t)e_{0}+0.4 e_{12}\sin ^{2} 3t \\ &\quad{}+0.6 e_{23}\sin 5t+0.5 e_{123}\cos 4t,\quad i,j=1,2, \end{aligned} \\& \begin{aligned} S_{ij}(t)&= \biggl(0.5\cos 6t+\frac{3}{16+t^{2}} \biggr)e_{0}+0.4 e_{1} \sin 2t \\ &\quad{}+0.3 e_{2}\sin 5t+0.4 e_{12}\cos t, \quad i,j=1,2, \end{aligned} \\& \begin{aligned} \mu _{j}(t)&=0.2e_{2}\cos 2t+0.2 e_{3}\cos ^{2} t+0.2 e_{23}\cos 3t \\ &\quad{}+ \biggl(0.8\sin \sqrt{3}t +\frac{2}{30+t^{2}} \biggr)e_{123}, \quad j=1,2. \end{aligned} \end{aligned}$$

If $\mathbb{T}=\mathbb{R}$, then we take

$$\begin{aligned} \eta _{ij}(t)=0.4 \vert \cos 3t \vert ,\qquad \tau _{ij}(t)=0.7 \vert \cos 6t \vert ,\qquad \tilde{\tau }_{ij}(t)=0.9 \vert \sin 3t \vert , \quad i,j=1,2, \end{aligned}$$

and if $\mathbb{T}=\mathbb{Z}$, then we take

$$\begin{aligned}& \eta _{ij}(t) =3 \biggl\vert \sin \biggl(3\pi t+\frac{\pi }{2} \biggr) \biggr\vert ,\qquad \tau _{ij}(t)=2e^{-5 \vert \cos (\pi t+\frac{\pi }{2}) \vert }, \\& \tilde{\tau }_{ij}(t) =4 \vert \cos 4\pi t \vert ,\quad i,j=1,2. \end{aligned}$$

Obviously, $(S_{1})$ and $(S_{4})$ hold. By calculating we have $L_{j}^{f}=\frac{1}{265}$, $L_{j}^{g}=L^{\tilde{g}}_{j}=\frac{3}{480}$, $L_{j}^{h}=L^{ \tilde{h}}_{j}=\frac{\sqrt{15}}{1110}$, $j=1,2$; $a^{-}_{1}=0.35$, $a^{-}_{2}=0.4$, $c^{-}_{1}=0.6$, $c^{-}_{2}=0.3$, $b_{11}^{+}= \tilde{b}_{11}^{+}=b_{21}^{+}=\tilde{b}_{12}^{+}=0.03$, $b_{12}^{+}=b_{22}^{+}= \tilde{b}_{22}^{+}=0.04$, $\tilde{b}_{21}^{+}=0.035$, $\alpha _{11}^{+}= \tilde{\alpha }_{11}^{+}=\beta _{22}^{+}=\tilde{\beta }_{22}^{+}=0.02$, $\alpha _{12}^{+}=\tilde{\alpha }_{12}^{+}=\beta _{12}^{+}= \tilde{\beta }_{12}^{+}=0.04$, $\alpha _{21}^{+}=\tilde{\alpha }_{21}^{+}= \beta _{11}^{+}=\tilde{\beta }_{11}^{+}=\beta _{21}^{+}=\tilde{\beta }_{21}^{+}=0.03$, $\alpha _{22}^{+}=\tilde{\alpha }_{22}^{+}=0.05$;

$$\begin{aligned}& \mathcal{P}_{1}\approx 0.0963,\qquad \mathcal{P}_{2} \approx 0.1165,\qquad \mathcal{Q}_{1}\approx 0.0013, \\& \mathcal{Q}_{2}\approx 0.0015, \qquad \tilde{\mathcal{Q}}_{1} \approx 0.00179, \qquad \tilde{\mathcal{Q}}_{2}\approx 0.00185, \\& \max \biggl\{ \frac{\mathcal{P}_{1}}{a^{-}_{1}}, \frac{\mathcal{P}_{2}}{a^{-}_{2}} \biggr\} \approx \max \{0.2751,0.2913 \} =0.2913< \frac{1}{2}, \\& \max \biggl\{ \frac{\mathcal{Q}_{1}}{a^{-}_{1}}, \frac{\mathcal{Q}_{2}}{a^{-}_{2}} \biggr\} \approx \max \{0.0037,0.0038 \} =0.0038 =\kappa < 1, \end{aligned}$$

and

$$\begin{aligned} \max \biggl\{ \frac{\tilde{\mathcal{Q}}_{1}}{a^{-}_{1}+c^{-}_{1}}, \frac{\tilde{\mathcal{Q}}_{2}}{a^{-}_{2}+c^{-}_{2}} \biggr\} \approx \max \{0.0019,0.0026\} =0.0026< 1. \end{aligned}$$

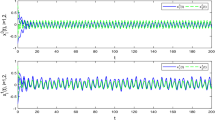
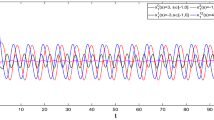
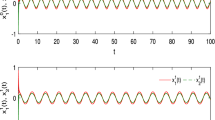
Hence, whether $\mathbb{T}=\mathbb{R}$ or $\mathbb{T}=\mathbb{Z}$, all the assumptions of Theorem 4.1 are satisfied. So by Theorem 4.1 systems (1) and (2) are globally exponentially synchronized about the pseudo almost periodic solution (see Figs. 1–10).

Figure 1

$\mathbb{T}=\mathbb{R}$. Transient states of $x^{0}(t)$, $x^{1}(t)$, $x^{2}(t)$ and $x^{3}(t)$

Figures 1 and 3 have the same initial values

$$\begin{aligned} &\bigl(x_{1}^{0}(0),x_{2}^{0}(0) \bigr)^{T} =\bigl(y_{1}^{0}(0),y_{2}^{0}(0) \bigr)^{T} =(0.2,-0.1)^{T}, (1,-0.9)^{T}, \\ &\bigl(x_{1}^{1}(0),x_{2}^{1}(0) \bigr)^{T} =\bigl(y_{1}^{1}(0),y_{2}^{1}(0) \bigr)^{T}=(0.3,-0.4)^{T},(0.9,-0.7)^{T}, \\ &\bigl(x_{1}^{2}(0),x_{2}^{2}(0) \bigr)^{T} =\bigl(y_{1}^{2}(0),y_{2}^{2}(0) \bigr)^{T}=(0.1,0.4)^{T}, (-0.5,-0.8)^{T}, \\ &\bigl(x_{1}^{3}(0),x_{2}^{3}(0) \bigr)^{T} =\bigl(y_{1}^{3}(0),y_{2}^{3}(0) \bigr)^{T}=(0.3,-0.2)^{T}, (-0.9,0.7)^{T}. \end{aligned}$$

Figures 2 and 4 have the same initial values

$$\begin{aligned} &\bigl(x_{1}^{12}(0),x_{2}^{12}(0) \bigr)^{T} = \bigl(y_{1}^{12}(0),y_{2}^{12}(0) \bigr)^{T}=(-0.4,0.2)^{T}, (1,-0.8)^{T}, \\ &\bigl(x_{1}^{13}(0),x_{2}^{13}(0) \bigr)^{T} = \bigl(y_{1}^{13}(0),y_{2}^{13}(0) \bigr)^{T}=(-0.1,0.3)^{T}, (-0.6,0.9)^{T}, \\ &\bigl(x_{1}^{23}(0),x_{2}^{23}(0) \bigr)^{T} = \bigl(y_{1}^{23}(0),y_{2}^{23}(0) \bigr)^{T}=(-0.2,0.5)^{T}, (0.7,-0.8)^{T}, \\ &\bigl(x_{1}^{123}(0),x_{2}^{123}(0) \bigr)^{T} = \bigl(y_{1}^{123}(0),y_{2}^{123}(0) \bigr)^{T}=(-0.3,0.4)^{T}, (0.9,-0.6)^{T}. \end{aligned}$$

Figure 2

$\mathbb{T}=\mathbb{R}$. Transient states of $x^{12}(t)$, $x^{13}(t)$, $x^{23}(t)$, and $x^{123}(t)$

Figure 3

$\mathbb{T}=\mathbb{R}$. Transient states of $y^{0}(t)$, $y^{1}(t)$, $y^{2}(t)$, and $y^{3}(t)$

Figure 4

$\mathbb{T}=\mathbb{R}$. Transient states of $y^{12}(t)$, $y^{13}(t)$, $y^{23}(t)$, and $y^{123}(t)$

Figure 5 has two different initial values.

Figure 5

$\mathbb{T}=\mathbb{R}$. Synchronization errors $z(t)=y(t)-x(t)$

Figures 6 and 8 have the same initial values

$$\begin{aligned} &\bigl(x_{1}^{0}(0),x_{2}^{0}(0) \bigr)^{T} = \bigl(y_{1}^{0}(0),y_{2}^{0}(0) \bigr)^{T}=(0.5,-0.5)^{T}, (-1,1)^{T}, \\ &\bigl(x_{1}^{1}(0),x_{2}^{1}(0) \bigr)^{T} = \bigl(y_{1}^{1}(0),y_{2}^{1}(0) \bigr)^{T}=(-0.7,0.6)^{T},(-1.2,1.5)^{T}, \\ &\bigl(x_{1}^{2}(0),x_{2}^{2}(0) \bigr)^{T} = \bigl(y_{1}^{2}(0),y_{2}^{2}(0) \bigr)^{T}=(-0.8,0.5)^{T}, (1,-1.4)^{T}, \\ &\bigl(x_{1}^{3}(0),x_{2}^{3}(0) \bigr)^{T} = \bigl(y_{1}^{3}(0),y_{2}^{3}(0) \bigr)^{T}=(1.5,1)^{T}, (-0.6,-1)^{T}. \end{aligned}$$

Figures 7 and 9 have the same initial values

$$\begin{aligned} &\bigl(x_{1}^{12}(0),x_{2}^{12}(0) \bigr)^{T} = \bigl(y_{1}^{12}(0),y_{2}^{12}(0) \bigr)^{T}=(-1,0.8)^{T}, (1.5,-1.5)^{T}, \\ &\bigl(x_{1}^{13}(0),x_{2}^{13}(0) \bigr)^{T} = \bigl(y_{1}^{13}(0),y_{2}^{13}(0) \bigr)^{T}=(1,-1.2)^{T}, (-0.7,0.5)^{T}, \\ &\bigl(x_{1}^{23}(0),x_{2}^{23}(0) \bigr)^{T} = \bigl(y_{1}^{23}(0),y_{2}^{23}(0) \bigr)^{T}=(0.5,-1)^{T}, (-1.5,1.3)^{T}, \\ &\bigl(x_{1}^{123}(0),x_{2}^{123}(0) \bigr)^{T} = \bigl(y_{1}^{123}(0),y_{2}^{123}(0) \bigr)^{T}=(-1,-0.5)^{T}, (0.9,1.5)^{T}. \end{aligned}$$

Figure 6

$\mathbb{T}=\mathbb{Z}$. Transient states of $x^{0}(n)$, $x^{1}(n)$, $x^{2}(n)$ and $x^{3}(n)$

Figure 7

$\mathbb{T}=\mathbb{Z}$. Transient states of $x^{12}(n)$, $x^{13}(n)$, $x^{23}(n)$, and $x^{123}(n)$

Figure 8

$\mathbb{T}=\mathbb{Z}$. Transient states of $y^{0}(n)$, $y^{1}(n)$, $y^{2}(n)$, and $y^{3}(n)$

Figure 9

$\mathbb{T}=\mathbb{Z}$. Transient states of $y^{12}(n)$, $y^{13}(n)$, $y^{23}(n)$, and $y^{123}(n)$

Figure 10 has two different initial values.

Figure 10

$\mathbb{T}=\mathbb{Z}$. Synchronization errors $z(n)=y(n)-x(n)$

6 Conclusion

In this paper, we study pseudo almost periodic synchronization of Clifford-valued fuzzy cellular neural networks with time-varying delays on time scales by a direct method. That is to say, we do not decompose the Clifford-valued systems into real-valued systems, but directly study the Clifford systems. This is the first paper to study the pseudo almost periodic synchronization of Clifford-valued neural networks on time scales. The results of this paper are brand-new, and the proposed approach can be used to study the periodic, almost periodic, and almost automorphic synchronization for other types of neural networks on time scales. Studying the dynamics of Clifford-valued neural networks on time scales can not only unify the research of discrete- and continuous-time neural networks, but also unify the research of real-valued, complex-valued, and quaternion-valued neural networks.