Identifying the space source term problem for time-space-fractional diffusion equation

Abstract

In this paper, we consider an inverse source problem for the time-space-fractional diffusion equation. Here, in the sense of Hadamard, we prove that the problem is severely ill-posed. By applying the quasi-reversibility regularization method, we propose by this method to solve the problem (1.1). After that, we give an error estimate between the sought solution and regularized solution under a prior parameter choice rule and a posterior parameter choice rule, respectively. Finally, we present a numerical example to find that the proposed method works well.

1 Introduction

Let T be a given positive number, Ω a bounded domain in $\mathbb{R}^{n}$ ($n \ge1$) with a smooth boundary ∂Ω. In this work, we consider the inverse source problem of the time-fractional diffusion equation as follows:

$$\begin{aligned} \textstyle\begin{cases} D_{t}^{\beta}u(x,t) = -\mathcal{L}^{\gamma} u(x,t) + \varphi(t)f(x),\quad (x,t) \in{ \Omega} \times(0,T), \\ u(x,t) = 0,\quad x \in\partial{ \Omega}, t \in(0,T], \\ u(x,0) = g(x),\quad x \in{\Omega}, \\ u(x,T) = \ell(x),\quad x \in\Omega, \end{cases}\displaystyle \end{aligned}$$

(1.1)

where $D_{t}^{\beta}u(x,t)$ is the Caputo fractional derivative of order β defined as [1] in the following form:

$$\begin{aligned} D_{t}^{\beta}u(x,t) = \frac{\partial^{\beta} u }{\partial t^{\beta }} := \frac{1}{\Gamma(1-\beta)} \int_{0}^{t} \frac {u_{s}(x,s)}{(t-s)^{\beta }} \,ds,\quad 0 < \beta< 1, \end{aligned}$$

(1.2)

where $\Gamma(\cdot)$ is the Gamma function. In fact $(g,\ell,\varphi)$ is noised by observation data $(g^{\varepsilon}, \ell^{\varepsilon}, \varphi^{\varepsilon} )$ where the order of ε is the noise level. We have

$$\begin{aligned} \bigl\Vert g - g^{\varepsilon} \bigr\Vert _{L^{2}(\Omega)} \le\varepsilon,\qquad \bigl\Vert \ell- \ell ^{\varepsilon} \bigr\Vert _{L^{2}(\Omega)} \le\varepsilon,\quad \text{and} \quad\bigl\Vert \varphi- \varphi^{\varepsilon} \bigr\Vert _{L^{\infty}(\Omega )} \le \varepsilon. \end{aligned}$$

(1.3)

In all functions $g(x)$, $\ell(x)$, and $\varphi(t)$ are given data. It is well known that, if ε is small enough, the sought solution $f(x)$ may have a large error. It is known that the inverse source problem mentioned above is ill-posed. In general, the definition of the ill-posed problem was introduced in [2]. Therefore, regularization is needed.

As is well known, in the last few decades, the fractional calculation is a concept that has a great influence on the mathematical background and its application in modeling real problems. Fractional calculus has many applications in mechanics, physics and engineering science, etc. We present to the reader much of the published work on these issues, such as [3–21] and the references cited therein. This makes it attractive to study this model. The space source term problem for the time-fractional partial differential equations has attracted a lot of attention, and much work has been completed to study many aspects of this problem, specifically as follows.

In 2009, Cheng, Yamamoto et al. considered the problem (1.1) with $\varphi(t)f(x) = 0$, the operator $\mathcal{L}= \frac{\partial }{\partial x} (p(x) \frac{\partial u}{\partial x} )$ and the homogeneous Neumann boundary condition; see [22].

In 2016, the homogeneous problem, i.e, $\varphi(t)f(x) = 0$, in Eq. (1.1) has been considered by Dou and Hon; see [23]. They used the Tikhonov regularization method to solve this problem (1.1) based on the kernel-based approximation technique.

In 2019, the authors Yan, Xiong and Wei proposed a conjugate gradient algorithm to solve the Tikhonov regularization problem for the case $\gamma=1$.

In the case $f(x) =1$, in 2014, Fan Yang and his group considered the Fourier transform and the quasi-reversibility regularization method; see [24]. Recently, the simple source problem, i.e, $\varphi(t) = 1$ and $\gamma=1$ in Eq. (1.1) has been considered by Fan Yang, Zhang and Li, see [20, 21, 25–27]; the authors used the Landweber iterative regularization, Truncation regularization and Tikhonov regularization methods solve this problem and achieved the results of convergence results to the order of $\epsilon^{\frac {p}{p+1}}$ for $0< p<2$ and $\epsilon^{\frac{1}{2}}$ for $p>2$, respectively.

The problem (1.1) with discrete random noise has been studied by Tuan et al, they used the filter regularization and trigonometric methods to solve this problem (1.1); see [28–30]. According to our searching, the results about applying the quasi-reversibility regularization method to solve the inverse source problem for the time-space-fractional diffusion equation is still limited. To the best of our knowledge, this is one of the first results of this type of problem. In particular, one addressed the case where $\mathcal{L}^{\gamma}$ and the right-hand side $\varphi(t)f(x)$ are represented in a general form. Motivated by all the above reasons, we consider the quasi-reversibility regularization method to solve the problem (1.1). The present paper aims to use the quasi-reversibility regularization method (QR method) to solve the problem (1.1).

The outline of the paper is as follows. In Sect. 2, we show some basic concepts, the function setting, the definitions, and the ill-posed problem are presented in Sect. 2. In Sect. 3, we construct the structure for the regularized problem (in Sect. 3.1), and the convergent rate between the sought solution and the regularized solution under a prior parameter choice rule (in Sect. 3.2), and a posterior parameter choice rule (in Sect. 3.3). A numerical example is presented in Sect. 4.

2 Preliminary results

The eigenvalues of the operator $\mathcal{L}^{\gamma}$ is introduced in [31]. Let us recall that the spectral problem

$$\begin{aligned} \textstyle\begin{cases} \mathcal{L}^{\gamma} \mathrm{e}_{k}(x) = -\lambda_{k}^{\gamma} \mathrm {e}_{k}(x), \quad x \in{ \Omega}, \\ \mathrm{e}_{k}(x) = 0,\quad x \in\partial{ \Omega}, \end{cases}\displaystyle \end{aligned}$$

(2.1)

admits a family of eigenvalues

$$\begin{aligned} 0 < \lambda_{1}^{\gamma} \leq\lambda_{2}^{\gamma} \leq\lambda _{3}^{\gamma} \leq\cdots\leq \lambda_{k}^{\gamma} \cdots\to \infty. \end{aligned}$$

Defining

$$\begin{aligned} \mathcal{D}^{\zeta}(\Omega) = \Biggl\{ v \in L^{2}(\Omega) : \sum_{k=1}^{\infty} \lambda_{k}^{2\zeta} \bigl\vert \langle v,\mathrm {e}_{k} \rangle \bigr\vert ^{2} < + \infty \Biggr\} , \end{aligned}$$

(2.2)

where $\langle\cdot\rangle$ is the inner product in $L^{2}(\Omega)$, then $\mathcal{D}^{\zeta}(\Omega)$ is a Hilbert space equipped with the norm

$$\begin{aligned} \Vert v \Vert _{\mathcal{D}^{\zeta}(\Omega)} = \Biggl( \sum _{k=1}^{\infty} \lambda _{k}^{2 \zeta} \bigl\vert \langle v,\mathrm{e}_{k} \rangle \bigr\vert ^{2} \Biggr)^{\frac{1}{2}}. \end{aligned}$$

(2.3)

Definition 2.1

(see [1])

The Mittag-Leffler function is

$$\begin{aligned} E_{\beta,\gamma}(z) = \sum_{i=0}^{\infty} \frac{z^{i}}{ \Gamma (\beta i + \gamma) },\quad z \in\mathbb{C}, \end{aligned}$$

where $\beta> 0$ and $\gamma\in\mathbb{R}$ are arbitrary constant.

Lemma 2.2

(see [1])

Let $0 < \beta_{0} < \beta_{1} < 1$. Then there exist positive constants $\mathcal{A}$, $\mathcal{B}$, $\mathcal{C}$ depending only on $\beta_{0}$, $\beta_{1}$ such that, for all $\beta\in[\beta _{0}, \beta_{1}]$,

$$\begin{aligned} \frac{\mathcal{A}}{1+z} \le E_{\beta,1}(-z) \le\frac{\mathcal {B}}{1+z},\qquad E_{\beta,\kappa}(-z) \le\frac{\mathcal{C}}{1+z}, \quad\textit{for all } z \ge0, \kappa\in\mathbb{R}. \end{aligned}$$

(2.4)

Lemma 2.3

([32])

The following equality holds for $\lambda> 0$, $\alpha> 0$ and $m \in\mathbb{N:}$

$$ \frac{d^{m}}{dt^{m}}E_{\alpha,1}\bigl(-\lambda t^{\alpha}\bigr) = -\lambda t^{\alpha-m} E_{\alpha, \alpha- m + 1} \bigl(-\lambda t^{\alpha}\bigr),\quad t > 0 . $$

(2.5)

Lemma 2.4

([33])

For $0 < \beta< 1$, $\omega> 0$, we get $0 \leq E_{\beta,1}(-\omega) < 1$. Therefore, $E_{\beta,1}(-\omega)$ is completely monotonic, that is,

$$\begin{aligned} (-1)^{c} \frac{d^{c}}{d\omega^{c}} E_{\beta,1}(-\omega) \geq0,\quad \omega \geq0. \end{aligned}$$

Lemma 2.5

Let $\beta> 0$, $\gamma\in \mathbb {R}$, then we get

$$\begin{aligned} E_{\beta, \gamma}(z) = zE_{\beta,\beta+\gamma}(z) + \frac {1}{\Gamma (\gamma)},\quad z \in \mathbb {C}. \end{aligned}$$

(2.6)

Lemma 2.6

For $\lambda_{k} > 0$, $\beta> 0$, and positive integer $k \in \mathbb {N}$, we have

$$\begin{aligned} \frac{d}{dt} \bigl(tE_{\beta,2}\bigl(\lambda_{k}t^{\beta} \bigr) \bigr) = E_{\beta ,1}\bigl(-\lambda_{k}t^{\beta} \bigr), \frac{d}{dt} \bigl(E_{\beta,1}\bigl(-\lambda _{k}t^{\beta}\bigr) \bigr) = -\lambda_{k}t^{\beta-1}E_{\beta,\beta } \bigl(-\lambda _{i}t^{\beta}\bigr). \end{aligned}$$

(2.7)

Lemma 2.7

For any $\lambda_{k}^{\gamma}$ satisfying $\lambda_{k}^{\gamma} \ge {\lambda_{1}^{\gamma}} > 0$, $\mathcal{A}$, $\mathcal{B}$ are positive constants satisfying

$$\begin{aligned} \frac{\mathcal{A}_{**}}{\lambda_{k}^{\gamma} T^{\beta}} \le \bigl\vert E_{\beta,\beta+1} \bigl( - \lambda_{k}^{\gamma} T^{\beta} \bigr) \bigr\vert \le\frac{1}{\lambda_{k}^{\gamma} T^{\beta}}, \end{aligned}$$

(2.8)

where $\mathcal{A}_{**} =1 - E_{\beta,1}(-\lambda_{1}^{\gamma }T^{\beta })$.

Proof

By [33], it is easy to get the above conclusion. □

Lemma 2.8

([32])

Let $E_{\beta,\beta} (-\eta) \ge0$, $0 < \beta< 1$, we have

$$ \begin{aligned}[b] \int_{0}^{\mathcal{M}} \bigl\vert \tau^{\beta- 1} E_{\beta,\beta} \bigl(-\lambda_{k}^{\gamma} \tau^{\beta}\bigr) \bigr\vert \,d\tau &= - \frac{1}{ \lambda_{k}^{\gamma} } \int_{0}^{\mathcal{M}} \frac {d}{d\tau} E_{\beta,1}\bigl(-\lambda_{k}^{\gamma} \tau^{\beta} \bigr) \,d\tau\\&= \frac {1}{\lambda_{k}^{\gamma} } \bigl( 1 - E_{\beta,1}\bigl(-\lambda_{k}^{\gamma} \mathcal{M}^{\beta} \bigr) \bigr) . \end{aligned} $$

(2.9)

Lemma 2.9

Assume that $\varphi_{0} \le|\varphi_{\varepsilon}(t)| \le\varphi _{1}$, $\mathrm{\forall t \in[0,T]}$, by choosing $\varepsilon\in (0, \frac{\varphi_{0}}{4} )$, then we know

$$\begin{aligned} \frac{\varphi_{0}}{4} \le \bigl\vert \varphi(t) \bigr\vert \le\mathcal {P}(\varphi _{0},\varphi_{1}). \end{aligned}$$

(2.10)

Proof

First of all, we have

$$\begin{aligned} \bigl\vert \varphi_{\varepsilon}(t) \bigr\vert &\le \bigl\vert \varphi(t) \bigr\vert + \bigl\vert \varphi^{\varepsilon}(t) - \varphi(t) \bigr\vert \le \bigl\vert \varphi (t) \bigr\vert + \sup _{t \in[0,T]} \bigl\vert \varphi_{\varepsilon}(t) - \varphi(t) \bigr\vert \\ &\le \bigl\vert \varphi(t) \bigr\vert + \Vert \varphi_{\varepsilon} - \varphi \Vert _{L^{\infty}(0,T)} \le \bigl\vert \varphi(t) \bigr\vert + \varepsilon. \end{aligned}$$

(2.11)

From (2.11), we know that

$$\begin{aligned} \bigl\vert \varphi(t) \bigr\vert \ge \bigl\vert \varphi_{\varepsilon}(t) \bigr\vert - \varepsilon\ge\varphi_{0} - \varepsilon\ge\frac{\varphi_{0}}{4}, \quad\text{and}\quad \bigl\vert \varphi(t) \bigr\vert \le\varphi_{1} + \varepsilon< \varphi _{1} + \frac{\varphi_{0}}{4}. \end{aligned}$$

(2.12)

Denoting $\mathcal{P}(\varphi_{0},\varphi_{1}) = \varphi_{1} + \frac {\varphi _{0}}{4}$, combining with (2.12) leads to (2.10). □

Lemma 2.10

Let $\varphi: [0,T] \to\mathbb{R}^{+}$ be a continuous function such that $\frac{\varphi_{0}}{4} \le |\varphi(t) | \le\mathcal {P}(\varphi_{0},\varphi_{1})$. Then we have

$$ \frac{ \varphi_{0} (1 - E_{\beta,1}(- \lambda_{1}^{\gamma} T^{\beta}) ) }{4\lambda_{k}^{\gamma} } \le \int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta,\beta}\bigl(-\lambda _{k}^{\gamma }(T- \tau)^{\beta}\bigr) \varphi(\tau)\,d\tau \le\frac{\mathcal{P}(\varphi_{0},\varphi_{1})}{ \lambda_{k}^{\gamma}}, $$

(2.13)

and using Lemmas 2.5and 2.6we get

$$\begin{aligned} \int_{0}^{T} (T-\tau)^{\beta-1}E_{\beta,\beta} \bigl(-\lambda _{k}^{\gamma}(T-\tau)^{\beta} \bigr) \, d\tau = T^{\beta} E_{\beta ,\beta +1}\bigl(-\lambda_{k}^{\gamma}T^{\beta} \bigr). \end{aligned}$$

(2.14)

Theorem 2.11

Let $g, f \in L^{2}(\Omega)$ and $\varphi\in L^{\infty}(0,T)$, then there exists a unique weak solution $u \in C([0,T];L^{2}(\Omega)) \cup C([0,T];\mathcal{D}^{\zeta}(\Omega))$ for (1.1) given by

$$\begin{aligned} u(x,t) &= \sum_{k=1}^{\infty} \biggl[\bigl\langle g(x),\mathrm {e}_{k}(x)\bigr\rangle E_{\beta,1}\bigl(- \lambda^{\gamma}_{k}t^{\beta}\bigr) \\ &\quad+\bigl\langle f(x),\mathrm{e}_{k}(x) \bigr\rangle \int_{0}^{t} (t-\tau)^{\beta-1} E_{\beta,\beta}\bigl(-\lambda_{k}^{\gamma}(t- \tau)^{\beta}\bigr) \varphi (\tau)\,d\tau \biggr] \mathrm{e}_{k}(x). \end{aligned}$$

(2.15)

From (2.15), letting $t = T$, we obtain

$$\begin{aligned} \bigl\langle \ell(x),\mathrm{e}_{k}(x) \bigr\rangle &=\bigl\langle g(x),\mathrm {e}_{k}(x)\bigr\rangle E_{\beta,1}\bigl(-\lambda^{\gamma}_{k}T^{\beta} \bigr) \\ &\quad+\bigl\langle f(x),\mathrm{e}_{k}(x) \bigr\rangle \int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta,\beta}\bigl(-\lambda_{k}^{\gamma}(T- \tau)^{\beta}\bigr) \varphi (\tau)\,d\tau. \end{aligned}$$

(2.16)

By a simple transformation we can see that

$$\begin{aligned} \bigl\langle f(x),\mathrm{e}_{k}(x) \bigr\rangle = \frac{ \langle\ell(x),\mathrm {e}_{k}(x) \rangle - \langle g(x),\mathrm{e}_{k}(x)\rangle E_{\beta ,1}(-\lambda _{k}^{\gamma} T^{\beta}) }{\int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta ,\beta }(-\lambda_{k}^{\gamma}(T-\tau)^{\beta}) \varphi(\tau)\,d\tau}. \end{aligned}$$

(2.17)

This implies that

$$\begin{aligned} f(x) = \sum_{k=1}^{\infty} \frac{ [ \langle\ell(x),\mathrm{e}_{k}(x) \rangle - \langle g(x),\mathrm{e}_{k}(x) \rangle ]E_{\beta,1}(-\lambda _{k}^{\gamma} T^{\beta}) }{\int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta ,\beta }(-\lambda_{k}^{\gamma}(T-\tau)^{\beta}) \varphi(\tau)\,d\tau} \mathrm {e}_{k}(x) . \end{aligned}$$

(2.18)

2.1 The ill-posedness of inverse source problem (1.1)

Theorem 2.12

The inverse source problem is not well-posed.

Proof

Denote $\|\varphi\|_{L^{\infty}(0,T)} = \mathcal{P}(\varphi _{0},\varphi _{1})$. A linear operator is defined $\mathcal{R}:L^{2}(\Omega) \to L^{2}(\Omega)$ as follows:

$$\begin{aligned} \mathcal{R}f(x) &= \sum_{k=1}^{\infty} \biggl[ \int_{0}^{T} (T-\tau )^{\beta-1} E_{\beta,\beta}\bigl(-\lambda_{k}^{\gamma}(T- \tau)^{\beta}\bigr) \varphi(\tau)\,d\tau \biggr] \bigl\langle f(x),{\mathrm {e}}_{k}(x) \bigr\rangle {\mathrm {e}}_{k}(x) \\ &= \int_{\Omega}k(x,\xi)f(\xi)\,d\xi \\&= \sum _{k=1}^{\infty} \bigl[ \bigl\langle \ell (x), \mathrm{e}_{k}(x)\bigr\rangle - \bigl\langle g(x),\mathrm{e}_{k}(x) \bigr\rangle E_{\beta ,1}\bigl(-\lambda_{k}^{\gamma}T^{\beta} \bigr) \bigr]\mathrm{e}_{k}(x), \end{aligned}$$

(2.19)

the integral kernel is

$$\begin{aligned} k(x,\xi) = \sum_{k=1}^{\infty} \biggl( \int_{0}^{T} (T-\tau )^{\beta-1} E_{\beta,\beta}\bigl(-\lambda_{k}^{\gamma}(T- \tau)^{\beta}\bigr) \varphi(\tau)\,d\tau \biggr) {\mathrm {e}}_{k}(x){\mathrm {e}}_{k}(\xi) . \end{aligned}$$

(2.20)

Because of $k(x,\xi) = k(\xi,x)$, we can see that $\mathcal{R}$ is self-adjoint operator. Next, we are going to prove its compactness. Let us define $\mathcal{R}_{M}$ as follows:

$$\begin{aligned} \mathcal{R}_{M}f(x) = \sum _{k=1}^{M} \biggl( \int_{0}^{T} (T-\tau )^{\beta-1}E_{\beta,\beta} \bigl(-\lambda_{k}^{\gamma}(T-\tau)^{\beta}\bigr) \varphi(\tau)\,d\tau \biggr) \bigl\langle f(x),\textit{e}_{k}(x) \bigr\rangle \textit{e}_{k}(x). \end{aligned}$$

(2.21)

We check that $\mathcal{R}_{M}$ is a finite rank operator. From (2.19) and (2.21) we have

$$\begin{aligned} & \Vert \mathcal{R}_{M}f - \mathcal{R}f \Vert _{L^{2}(\Omega)}^{2} \\ &\quad= \sum_{k=M+1}^{\infty} \biggl( \int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta,\beta}\bigl(-\lambda_{k}^{\gamma}(T- \tau)^{\beta}\bigr) \varphi (\tau )\,d\tau \biggr)^{2} \bigl\vert \bigl\langle f(x),{\mathrm {e}}_{k}(x) \bigr\rangle \bigr\vert ^{2} \\ &\quad= \bigl[\mathcal{P}(\varphi_{0}, \varphi_{1}) \bigr]^{2} \sum_{k=M+1}^{\infty} \frac{1}{\lambda_{k}^{2\gamma}} \bigl\vert \bigl\langle f(x),{\mathrm {e}}_{k}(x) \bigr\rangle \bigr\vert ^{2} \\ &\quad\le\frac{ [\mathcal{P}(\varphi_{0},\varphi_{1}) ]^{2}}{ \lambda _{M}^{2\gamma}} \sum_{k=M+1}^{\infty} \bigl\vert \bigl\langle f(x),{\mathrm {e}}_{k}(x) \bigr\rangle \bigr\vert ^{2}. \end{aligned}$$

(2.22)

This implies that

$$\begin{aligned} \Vert \mathcal{R}_{M}f - \mathcal{R} f \Vert _{L^{2}(\Omega)} \le \frac{ [\mathcal{P}(\varphi_{0},\varphi_{1}) ]}{\lambda _{M}^{\gamma }} \Vert f \Vert _{L^{2}(\Omega)}. \end{aligned}$$

(2.23)

Therefore, $\|\mathcal{R}_{M} - \mathcal{R}\|_{L^{2}(\Omega)} \to0$ in the sense of operator norm in $L(L^{2}(\Omega);L^{2}(\Omega))$ as $M \to\infty$. We know that $\mathcal{R}$ is a compact operator. Next, the linear self-adjoint compact operator $\mathcal{R}$ is

$$\begin{aligned} \Theta_{k} = \int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta,\beta }\bigl(-\lambda _{k}^{\gamma} (T- \tau)^{\beta}\bigr) \varphi(\tau)\,d\tau, \end{aligned}$$

(2.24)

and the corresponding eigenvectors are ${\mathrm {e}}_{k}$ which is known as an orthonormal basis in $L^{2}(\Omega)$. From (2.19), the inverse source problem can be formulated as an operator equation,

$$\begin{aligned} \mathcal{R}f(x)=\ell(x) - \sum_{k=1}^{\infty} \bigl\langle g(x),\mathrm {e}_{k}(x) \bigr\rangle E_{\beta,1}\bigl(- \lambda_{k}^{\gamma}\bigr)\mathrm{e}_{k}(x), \end{aligned}$$

(2.25)

and by Kirsch ([2]), we conclude that the problem (1.1) is ill-posed. We present an example. Fix β and choose

$$\begin{aligned} \ell_{m}(x) = \frac{\mathrm{e}_{m}(x) }{\sqrt{\lambda_{m}}},\qquad g_{m} = \frac {\mathrm{e}_{m}(x)}{\sqrt{\lambda_{m}}} . \end{aligned}$$

(2.26)

Because of (2.18) and combining (2.26), the source term $f^{m}$ is

$$\begin{aligned} f_{m}(x) &= \sum_{k=1}^{\infty} \frac{ \langle\frac{\mathrm{e}_{m}(x) }{\sqrt{\lambda_{m}}},\mathrm{e}_{k}(x) \rangle - E_{\beta,1}(-\lambda _{k}^{\gamma} T^{\beta}) \langle\frac{\mathrm{e}_{m}(x)}{\sqrt{\lambda_{m}} },\mathrm{e}_{k}(x) \rangle}{ \int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta ,\beta}(-\lambda_{k}^{\gamma}(T-\tau)^{\beta}) \varphi(\tau)\,d\tau} \mathrm{e}_{k}(x) \\ &= \frac{\mathrm{e}_{m}(x)}{\sqrt {\lambda _{m}}} \frac{ (1 - E_{\beta,1}(-\lambda_{m}^{\gamma} T^{\beta}) ) }{ \int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta,\beta}(-\lambda _{m}^{\gamma }(T-\tau)^{\beta}) \varphi(\tau)\,d\tau} . \end{aligned}$$

(2.27)

If we have input data $\ell,g=0$, then the source term $f=0$. An error in $L^{2}(\Omega)$ norm between $(\ell,g)$ and $(\ell _{m},g_{m})$ is

$$\begin{aligned} \Vert \ell_{m}-\ell \Vert _{L^{2}( \Omega)} = \frac{1}{\sqrt{\lambda_{m}} },\qquad \Vert g_{m}-g \Vert _{L^{2}(\Omega)} = \frac{1}{\sqrt{\lambda_{m}} } . \end{aligned}$$

(2.28)

Therefore,

$$\begin{aligned} &\lim_{m \to+\infty} \bigl\Vert h^{m}-h \bigr\Vert _{L^{2}({ \Omega})} = \lim_{m \to +\infty } \frac{1}{\sqrt{\lambda_{m}} } \to0, \\ &\lim_{m \to+\infty} \bigl\Vert g^{m}-g \bigr\Vert _{L^{2}({ \Omega})} = \lim_{m \to +\infty } \frac{1}{\sqrt{\lambda_{m}} } \to0. \end{aligned}$$

(2.29)

The error $\|f_{m}-f\|_{L^{2}({\Omega})}$ is

$$\begin{aligned} \Vert f_{m}-f \Vert _{L^{2}({\Omega})} &= \frac{ ( 1 - E_{\beta,1}(-\lambda _{m}^{\gamma} T^{\beta}) ) }{\mathcal{P}(\varphi_{0},\varphi _{1}) } \frac{\lambda_{m}^{\gamma}}{\sqrt{\lambda_{m}}}. \end{aligned}$$

(2.30)

From (2.30), we obtain

$$\begin{aligned} \Vert f_{m}-f \Vert _{L^{2}( \Omega)} \ge \bigl[\mathcal{P}(\varphi_{0},\varphi _{1}) \bigr]^{-1} \lambda_{m}^{\gamma-\frac{1}{2}} \bigl( 1 - E_{\beta ,1}\bigl(-\lambda_{m}^{\gamma} T^{\beta}\bigr) \bigr) . \end{aligned}$$

(2.31)

From (2.31), by choosing $\gamma> \frac{1}{2}$,

$$\begin{aligned} \lim_{m \to+\infty} \Vert f_{m}-f \Vert _{L^{2}( \Omega)} &> \lim_{m \to +\infty} \bigl[\mathcal{P}( \varphi_{0},\varphi_{1})\bigr]^{-1} \lambda _{m}^{\gamma -\frac{1}{2}} \biggl( 1 - \frac{\mathcal {A}}{\lambda_{m}^{\gamma} T^{\beta }} \biggr) =+ \infty. \end{aligned}$$

(2.32)

Combining (2.29) and (2.32), we conclude that the inverse source problem is not well-posed. □

2.2 Conditional stability of source term f

Theorem 2.13

Suppose that $\|f\|_{H^{\gamma j}(\Omega)} \le\mathcal{M}_{1}$ for $\mathcal{M}_{1}>0$, then

$$\begin{aligned} \Vert f \Vert _{L^{2}( \Omega)} \le\overline{C} \mathcal{M}_{1}^{\frac{1}{j+1}} \biggl(2 \Vert \ell \Vert _{L^{2}(\Omega)}^{2} + 2 \Vert g \Vert _{L^{2}(\Omega )}^{2} \frac {\mathcal{B}^{2}}{\lambda_{1}^{2\gamma}T^{2\beta}} \biggr)^{\frac {j}{2(j+1)}}, \end{aligned}$$

(2.33)

in which $\overline{C} = (\frac{4}{\varphi_{0}\mathcal{A}_{**}} )^{\frac{j}{j+1}}$.

Proof

From (2.18) and the Hölder inequality, we get

$$\begin{aligned} \Vert f \Vert ^{2}_{L^{2}(\Omega)}& = \sum _{k=1}^{\infty} \biggl( \frac{ [ \langle\ell(\cdot),\mathrm{e}_{k}(\cdot) \rangle - \langle g(\cdot ),\mathrm {e}_{k}(\cdot) \rangle E_{\beta,1}(-\lambda_{k}^{\gamma} T^{\beta}) ] }{\int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta,\beta}(-\lambda _{k}^{\gamma }(T-\tau)^{\beta}) \varphi(\tau)\,d\tau} \biggr)^{2} \\ &\leq \Biggl(\sum_{k=1}^{\infty} \frac{ [ \langle\ell(\cdot ),\mathrm {e}_{k}(\cdot) \rangle - \langle g(\cdot),\mathrm{e}_{k}(\cdot) \rangle E_{\beta ,1}(-\lambda_{k}^{\gamma} T^{\beta}) ]^{2} }{ \vert \int_{0}^{T} (T-\tau )^{\beta-1} E_{\beta,\beta}(-\lambda_{k}^{\gamma}(T-\tau)^{\beta}) \varphi (\tau)\,d\tau \vert ^{2j+2} } \Biggr)^{\frac{1}{j+1}} \\ &\quad\times \Biggl(\sum_{k=1}^{\infty} \bigl[ \langle\ell(\cdot),\mathrm {e}_{k}(\cdot) \rangle - \langle g(\cdot), \mathrm{e}_{k}(\cdot)\rangle E_{\beta ,1}\bigl(-\lambda _{k}^{\gamma} T^{\beta}\bigr) \bigr]^{2} \Biggr)^{\frac{j}{j+1}} \\ &\leq(\mathbb{L}_{1})^{\frac{1}{j+1}} \times(\mathbb {L}_{2})^{\frac{j}{j+1}}. \end{aligned}$$

(2.34)

Step 1: For an estimate of $(\mathbb{L}_{1})$, applying Lemma 2.7, it gives

$$\begin{aligned} \begin{aligned}[b](\mathbb{L}_{1} )^{\frac{1}{j+1}} &\leq \Biggl( \sum_{k=1}^{\infty} \frac{ \vert \langle f(\cdot), \mathrm{e}_{k}(\cdot ) \rangle \vert ^{2}}{ \vert \int_{0}^{T} (T-\tau)^{\beta-1} E_{\beta,\beta }(-\lambda _{k}^{\gamma}(T-\tau)^{\beta}) \varphi(\tau)\,d\tau \vert ^{2j} } \Biggr)^{\frac{1}{j+1}} \\ &\leq \biggl(\frac{4}{\varphi_{0}} \biggr)^{\frac{2j}{j+1}} \Biggl( \sum _{k=1}^{\infty} \frac{ \vert \langle f(\cdot), \mathrm{e}_{k}(\cdot ) \rangle \vert ^{2}}{ \vert T^{\beta} E_{\beta,\beta+1}(-\lambda_{k}^{\gamma }T^{\beta }) \vert ^{2j} } \Biggr)^{\frac{1}{j+1}} \\ &\leq \biggl(\frac{4}{\varphi_{0}\mathcal{A}_{**}} \biggr)^{\frac {2j}{j+1}} \Biggl( \sum _{k=1}^{\infty} \lambda_{k}^{2\gamma j} \bigl\vert \bigl\langle f(\cdot), \mathrm{e}_{k}(\cdot) \bigr\rangle \bigr\vert ^{2} \Biggr)^{\frac{1}{j+1}} \leq \biggl(\frac{4}{\varphi_{0}\mathcal{A}_{**}} \biggr)^{\frac{2j}{j+1}} M_{1}^{\frac{2}{j+1}}.\end{aligned} \end{aligned}$$

(2.35)

Step 2: For an estimate of $(\mathbb{L}_{2})$, it gives

$$\begin{aligned} (\mathbb{L}_{2} )^{\frac{j}{j+1}} &\leq \Biggl( \sum_{k=1}^{\infty }2 \bigl\vert \bigl\langle \ell( \cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle \bigr\vert ^{2} + 2 \bigl\vert \bigl\langle g(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle \bigr\vert ^{2} \frac {\mathcal {B}^{2}}{\lambda_{k}^{2\gamma}T^{2\beta}} \Biggr)^{\frac{j}{j+1}} \\ &\leq \biggl(2 \Vert \ell \Vert _{L^{2}(\Omega)}^{2} + 2 \Vert g \Vert _{L^{2}(\Omega )}^{2}\frac{\mathcal{B}^{2}}{\lambda_{1}^{2\gamma}T^{2\beta}} \biggr)^{\frac{j}{j+1}}. \end{aligned}$$

(2.36)

Combining (2.35) and (2.36), we conclude that

$$\begin{aligned} \Vert f \Vert ^{2}_{L^{2}(\Omega)} \leq \biggl( \frac{4}{\varphi_{0}\mathcal {A}_{**}} \biggr)^{\frac{2j}{j+1}} M_{1}^{\frac{2}{j+1}} \biggl(2 \Vert \ell \Vert _{L^{2}(\Omega)}^{2} + 2 \Vert g \Vert _{L^{2}(\Omega)}^{2}\frac{\mathcal {B}^{2}}{\lambda_{1}^{2\gamma}T^{2\beta}} \biggr)^{\frac{j}{j+1}} . \end{aligned}$$

(2.37)

 □

3 Quasi-reversibility method

In this section, the quasi-reversibility method is used to investigate problem (1.1), and give information for convergence of the two estimates under a prior parameter choice rule and a posterior parameter choice rule, respectively.

3.1 Construction of a regularization method

We employ the QR method to established a regularized problem, namely

$$\begin{aligned} \textstyle\begin{cases} D_{t}^{\beta}u_{\varepsilon}(x,t) = \alpha(\varepsilon) \bigl(-\mathcal {L}^{\gamma}\bigr) u_{\varepsilon}(x,t) + \varphi_{\varepsilon }(t)f_{\varepsilon}(x) + \alpha(\varepsilon) (-\mathcal{L})^{\gamma} f_{\varepsilon}(x) \varphi_{\varepsilon}(t) , \\ \quad(x,t) \in { \Omega} \times(0,T), \\ u_{\varepsilon}(x,t) = 0, \quad x \in\partial{ \Omega}, t \in(0,T], \\ u_{\varepsilon}(x,0) = g_{\varepsilon}(x),\quad x \in{\Omega}, \\ u_{\varepsilon}(x,T) = \ell_{\varepsilon}(x),\quad x \in\Omega, \end{cases}\displaystyle \end{aligned}$$

(3.1)

where $g_{\varepsilon}, \ell_{\varepsilon}$ are perturbed initial data and final data satisfying

$$\begin{aligned} \Vert g_{\varepsilon}-g \Vert _{L^{2}(\Omega)} \leq \varepsilon,\qquad \Vert \ell _{\varepsilon}-\ell \Vert _{L^{2}(\Omega)} \leq \varepsilon, \end{aligned}$$

(3.2)

and $\alpha(\varepsilon)$ is a regularization parameter. We can assert that

$$\begin{aligned} f_{\varepsilon,\alpha(\varepsilon)}(x) = \sum_{k=1}^{\infty} \frac { [ \langle\ell_{\varepsilon}(x),\mathrm{e}_{k}(x) \rangle - \langle g_{\varepsilon}(x),\mathrm{e}_{k}(x) \rangle E_{\beta,1}(-\lambda _{k}^{\gamma}T^{\beta}) ]\mathrm{e}_{k}(x) }{ (1+\alpha (\varepsilon)\lambda_{k}^{\gamma} ) \int_{0}^{T} (T-\tau )^{\beta -1}E_{\beta,\beta}(-\lambda_{k}^{\gamma}(T-\tau)^{\beta}) \varphi _{\varepsilon}(\tau) \, d\tau } . \end{aligned}$$

(3.3)

From now on, for brevity, we denote

$$\begin{aligned} &\mathcal{C}_{\gamma,\beta}(\ell_{\varepsilon},g_{\varepsilon }, \lambda _{k},T)= \bigl[ \bigl\langle \ell_{\varepsilon}(x), \mathrm{e}_{k}(x) \bigr\rangle - \bigl\langle g_{\varepsilon}(x),\mathrm{e}_{k}(x) \bigr\rangle E_{\beta ,1}\bigl(-\lambda _{k}^{\gamma}T^{\beta} \bigr) \bigr], \\ &{\mathcal{D}_{\gamma,\beta}(\varphi_{\varepsilon},\lambda _{k},T,\tau) }= (T-\tau)^{\beta-1}E_{\beta,\beta} \bigl(-\lambda_{k}^{\gamma }(T-\tau )^{\beta}\bigr) \varphi_{\varepsilon}(\tau). \end{aligned}$$

(3.4)

With (3.4), (3.3) becomes

$$\begin{aligned} f_{\varepsilon,\alpha(\varepsilon)}(x) = \sum_{k=1}^{\infty} \frac{ \mathcal{C}_{\gamma,\beta}(\ell_{\varepsilon},g_{\varepsilon },\lambda _{k},T) }{ (1+\alpha(\varepsilon)\lambda_{k}^{\gamma} ) \int _{0}^{T} \mathcal{D}_{\gamma,\beta}(\varphi_{\varepsilon},\lambda _{k},T,\tau)\, d\tau}\mathrm{e}_{k}(x) \end{aligned}$$

(3.5)

and

$$\begin{aligned} f_{\alpha(\varepsilon)}(x) = \sum_{k=1}^{\infty} \frac{\mathcal {C}_{\gamma,\beta}(\ell,g,\lambda_{k},T)}{ (1+\alpha (\varepsilon )\lambda_{k}^{\gamma} ) \int_{0}^{T} \mathcal{D}_{\gamma,\beta }(\varphi,\lambda_{k},T,\tau)\, d\tau }\mathrm{e}_{k}(x) . \end{aligned}$$

(3.6)

3.2 A prior parameter choice

Afterwards, $\|f(\cdot)-f_{\varepsilon,\alpha(\varepsilon )}(\cdot ) \|_{L^{2}(\Omega)}$ is shown under a suitable choice for the regularization parameter. To do this, we introduced the following lemma.

Lemma 3.1

For α, γ, $\lambda_{1}$ are positive constants. The function $\mathcal{G}$ is given by

$$\begin{aligned} \mathcal{G}(s) = \frac{\alpha s^{\gamma-\gamma j} }{ 1 + \alpha s^{\gamma} } , \quad z>0, \end{aligned}$$

then

$$\begin{aligned} \mathcal{G}(s) \le \textstyle\begin{cases} j^{j} (1-j)^{1-j}\alpha^{j}& \textit{if } 0 < j < 1, \\ \frac{1}{\lambda_{1}^{\gamma(j-1)}} \alpha &\textit{if } j \ge 1 , s \ge \lambda_{1}. \end{cases}\displaystyle \end{aligned}$$

(3.7)

Proof

(1) If $j \geq1$ then from $s \ge\lambda_{1}$, we get

$$\begin{aligned} \mathcal{G}(s) =\frac{\alpha s^{\gamma-\gamma j}}{1+ \alpha s^{\gamma }} = \frac{\alpha}{ ( 1 + \alpha s^{\gamma} )s^{\gamma j - \gamma} } \le \frac{\alpha}{s^{\gamma j-\gamma}} \le\frac{\alpha}{ \lambda_{1}^{\gamma(j-1)} } . \end{aligned}$$

(2) If $0 < j < 1$ then it can be seen that $\lim_{s \to0} \mathcal{G}(s) = \lim_{s \to+ \infty}\mathcal {G}(s) = 0$. We have $\mathcal{G}^{\prime}(s) = \frac{\alpha\gamma s^{\gamma-\gamma j-1} [ 1 - j - \alpha s^{\gamma} j ]}{ (1+ \alpha s^{\gamma } )^{2}}$. Solving $\mathcal{G}^{\prime}(s) = 0$, we can see that $s_{0} = (\frac{1-j}{j} )^{\frac{1}{\gamma}} \alpha^{-\frac{1}{\gamma }}$. Therefore,

$$\begin{aligned} \mathcal{G}(s) \le\mathcal{G}(s_{0}) = j^{j} (1-j)^{1-j}\alpha^{j} . \end{aligned}$$

This is precisely the assertion of the lemma. □

Theorem 3.2

Let f be as (2.18) and the noise assumption (2.13) hold. We obtain the following two cases.

• If $0 < j < 1$, by choosing $\alpha(\varepsilon) = (\frac {\varepsilon}{\mathcal{M}_{1}} )^{\frac{1}{j+1}}$, we have

  $$\begin{aligned} \bigl\Vert f(\cdot) - f_{\varepsilon,\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \leq\varepsilon^{\frac{j}{j+1}} \bigl(\mathcal {H} ( \mathcal{B},\gamma, \lambda_{1},\varphi_{0},f ) + j^{j} (1-j)^{1-j} \mathcal{M}_{1}^{\frac{j}{j+1}} \bigr). \end{aligned}$$

  (3.8)

• If $j > 1$, by choosing $\alpha(\varepsilon) = (\frac {\varepsilon}{\mathcal{M}_{1}} )^{\frac{1}{2}}$, we have

  $$\begin{aligned} \bigl\Vert f(\cdot) - f_{\varepsilon,\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \leq\varepsilon^{\frac{1}{2}} \biggl(\mathcal {H} ( \mathcal{B},\gamma, \lambda_{1},\varphi_{0},f ) + \frac {1}{\lambda _{1}^{\gamma(j-1)}} \mathcal{M}_{1}^{\frac{1}{2}} \biggr). \end{aligned}$$

  (3.9)

Proof

By the triangle inequality, we know

$$\begin{aligned} \bigl\Vert f(\cdot) -f_{\varepsilon, \alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}( \Omega)} \le \bigl\Vert f_{\alpha(\varepsilon)} (\cdot) -f_{\varepsilon, \alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} + \bigl\Vert f( \cdot) -f_{\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}( \Omega)}. \end{aligned}$$

(3.10)

The proof falls naturally into two steps.

Step 1: Estimation for $\|f_{\alpha(\varepsilon)}(\cdot) -f_{\varepsilon, \alpha(\varepsilon)}(\cdot) \|_{L^{2}(\Omega)}$, we receive

$$\begin{aligned} &f_{\alpha(\varepsilon)}(x)- f_{\varepsilon,\alpha(\varepsilon )}(x) \\&\quad = \overbrace{ \sum_{k=1}^{\infty} \frac{ \mathcal{C}_{\gamma,\beta } (\ell_{\varepsilon}(x)-\ell(x),g_{\varepsilon}(x)-g(x),\lambda _{k},T ) }{ (1 + \alpha(\varepsilon)\lambda_{k}^{\gamma} ) \int _{0}^{T}\mathcal{D}_{\gamma,\beta}(\varphi_{\varepsilon},\lambda _{k},T,\tau)\, d\tau }}^{\widetilde{E}_{1}} \\ &\qquad+\overbrace{\sum_{k=1}^{\infty} \frac{ \mathcal{C}_{\gamma,\beta }(\ell ,g,\lambda_{k},T)) \mathrm{e}_{k}(x) }{ (1 + \alpha(\varepsilon )\lambda_{k}^{\gamma} ) \int_{0}^{T}\mathcal{D}_{\gamma,\beta }(\varphi,\lambda_{k},T,\tau)\, d\tau } \frac{\int_{0}^{T} \mathcal {D}_{\gamma,\beta}(\varphi_{\varepsilon}-\varphi,\lambda _{k},T,\tau )\, d\tau }{\int_{0}^{T}\mathcal{D}_{\gamma,\beta}(\varphi _{\varepsilon },\lambda_{k},T,)\,d\tau}}^{\widetilde{E}_{2}} . \end{aligned}$$

(3.11)

From (3.11), using the Lemma 2.10, we have an estimate of $\|\widetilde{E}_{1}\|_{L^{2}(\Omega)}$:

$$\begin{aligned} \Vert \widetilde{E}_{1} \Vert ^{2}_{L^{2}(\Omega)} &= \sum_{k=1}^{\infty} \frac{ [\mathcal{C}_{\gamma,\beta} (\ell_{\varepsilon}(x)-\ell (x),g_{\varepsilon}(x)-g(x),\lambda_{k},T ) ]^{2} }{ (1 + \lambda_{k}^{\gamma}\alpha(\varepsilon) )^{2} \vert \int _{0}^{T}\mathcal{D}_{\gamma,\beta}(\varphi_{\varepsilon},\lambda _{k},T,\tau)\,d\tau \vert ^{2} } \\ &\leq\sum_{k=1}^{\infty} \frac{4\varepsilon^{2} \vert \max \{ 1,\frac{\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta} } \} \vert ^{2} }{ (1 + \alpha(\varepsilon) \lambda_{k}^{\gamma} )^{2}} \frac {T^{2\beta} \lambda_{k}^{2\gamma}}{\varphi_{0}^{2} [1 - E_{\beta ,1}(-\lambda_{1}^{\gamma}T^{\beta}) ]^{2} } \\ &\leq\frac{\varepsilon^{2}}{[\alpha(\varepsilon)]^{2}} \frac{4 \vert \max \{1,\frac{\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta} } \} \vert ^{2} T^{2\beta} }{\varphi_{0}^{2} [1 - E_{\beta ,1}(-\lambda _{1}^{\gamma}T^{\beta}) ]^{2}} . \end{aligned}$$

(3.12)

Next, using the condition of f in Theorem 2.13, we have the estimate for $\|\widetilde{E}_{2}\|_{L^{2}(\Omega)}$ as follows:

$$\begin{aligned} \Vert \widetilde{E}_{2} \Vert ^{2}_{L^{2}(\Omega)} &\leq\frac{\varepsilon ^{2}}{\varphi_{0}^{2}} \sum _{k=1}^{\infty} \frac{ \vert \langle f(\cdot),\mathrm{e}_{k}(\cdot) \rangle \vert ^{2}}{ (1+\alpha(\varepsilon )\lambda _{k}^{\gamma} )^{2}} \leq \frac{\varepsilon^{2}}{[\alpha (\varepsilon )]^{2}} \frac{1}{\varphi_{0}^{2}\lambda_{1}^{2\gamma}} \sum_{k=1}^{\infty} \bigl\vert \bigl\langle f(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle \bigr\vert ^{2} \\ &\leq\frac{\varepsilon^{2}}{[\alpha(\varepsilon)]^{2}} \frac{ \Vert f \Vert ^{2}_{L^{2}(\Omega)}}{\varphi_{0}^{2}\lambda_{1}^{2\gamma}} . \end{aligned}$$

(3.13)

Combining (3.12) and (3.13), one has

$$\begin{aligned} \bigl\Vert f_{\alpha(\varepsilon)}(\cdot)- f_{\varepsilon,\alpha (\varepsilon )}( \cdot) \bigr\Vert _{L^{2}(\Omega)} \leq\frac{\varepsilon}{[\alpha (\varepsilon)]} \biggl( \frac{2 \vert \max \{1,\frac{\mathcal {B}}{\lambda_{1}^{\gamma}T^{\beta} } \} \vert T^{\beta} }{\varphi_{0} [1 - E_{\beta,1}(-\lambda_{1}^{\gamma}T^{\beta}) ]} + \frac{ \Vert f \Vert _{L^{2}(\Omega)}}{\varphi_{0}\lambda_{1}^{\gamma}} \biggr). \end{aligned}$$

(3.14)

Step 2: For an estimation for $\|f(\cdot) -f_{ \alpha (\varepsilon)}(\cdot) \|_{L^{2}(\Omega)}$, we have

$$\begin{aligned} f(x) - f_{\alpha(\varepsilon)}(x) = \sum _{k=1}^{\infty} \biggl(1 - \frac{1}{1+\alpha(\varepsilon)\lambda_{k}^{\gamma}} \biggr) \frac {\mathcal {C}_{\gamma,\beta}(\ell,g,\lambda_{k},T)}{\int_{0}^{T}\mathcal {D}_{\gamma,\beta}(\varphi,\lambda_{k},T,\tau)\, d\tau }\mathrm{e}_{k}(x). \end{aligned}$$

(3.15)

From (3.15), we get

$$\begin{aligned} \bigl\Vert f(\cdot) - f_{\alpha(\varepsilon)}(\cdot) \bigr\Vert ^{2}_{L^{2}(\Omega )} &= \sum_{k=1}^{\infty} \biggl(\frac{\alpha(\varepsilon) \lambda _{k}^{\gamma(1-j)}}{1+ \alpha(\varepsilon) \lambda_{k}^{\gamma} } \biggr)^{2} \bigl\vert \lambda_{k}^{\gamma j} \bigl\langle f(\cdot),\mathrm {e}_{k}( \cdot) \bigr\rangle \bigr\vert ^{2} \\ &\leq\sup_{k \in \mathbb {N}} \biggl(\frac{\alpha(\varepsilon) \lambda _{k}^{\gamma(1-j)}}{1+\alpha(\varepsilon) \lambda_{k}^{\gamma}} \biggr)^{2} \mathcal{M}_{1}^{2} \leq\sup _{k \in \mathbb {N}} \mathcal{G}(\lambda _{k}) \mathcal{M}_{1}^{2}. \end{aligned}$$

(3.16)

Combining with Lemma 3.1, it gives

$$\begin{aligned} \sup_{k \in \mathbb {N}}\mathcal{G}( \lambda_{k}) = \sup_{k \in \mathbb {N}} \biggl( \frac {\alpha(\varepsilon) \lambda_{k}^{\gamma(1-j)}}{1+\alpha (\varepsilon) \lambda_{k}^{\gamma}} \biggr) \leq \textstyle\begin{cases} j^{j} (1-j)^{1-j}[\alpha(\varepsilon) ]^{j} &\text{if }0 < j < 1, \\ \frac{1}{\lambda_{1}^{\gamma(j-1)}} \alpha(\varepsilon) & \text{if }j \ge1 , \lambda_{k} \ge\lambda_{1}. \end{cases}\displaystyle \end{aligned}$$

(3.17)

Therefore, combining (3.16) and (3.17), we can find that

$$\begin{aligned} \bigl\Vert f(\cdot)- f_{\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \leq \textstyle\begin{cases} j^{j} (1-j)^{1-j}[\alpha(\varepsilon)]^{j} \mathcal{M}_{1} & \text{if }0 < j < 1, \\ \frac{1}{\lambda_{1}^{\gamma(j-1)}} [\alpha(\varepsilon)]\mathcal {M}_{1} & \text{if }j \ge1 , \lambda_{k} \ge \lambda_{1}. \end{cases}\displaystyle \end{aligned}$$

(3.18)

Choose the regularization parameter as follows:

$$\begin{aligned} \alpha(\varepsilon) = \textstyle\begin{cases} (\frac{\varepsilon}{\mathcal {M}_{1}} )^{\frac{1}{j+1}} & \text{if }0 < j < 1, \\ (\frac{\varepsilon}{\mathcal {M}_{1}} )^{\frac{1}{2}}& \text{if }j \ge1 , \lambda_{k} \ge\lambda_{1}. \end{cases}\displaystyle \end{aligned}$$

(3.19)

Finally, from (3.14), (3.18) and (3.19), we conclude the following.

• If $0 < j < 1$ then

  $$\begin{aligned} \bigl\Vert f(\cdot) - f_{\varepsilon,\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \leq\varepsilon^{\frac{j}{j+1}} \bigl(\mathcal {H} ( \mathcal{B},\gamma, \lambda_{1},\varphi_{0},f ){ \mathcal {M}_{1}^{\frac {1}{1+j}}} + j^{j} (1-j)^{1-j} \mathcal{M}_{1}^{\frac{j}{j+1}} \bigr). \end{aligned}$$

  (3.20)

• If $j \geq1$ then

  $$\begin{aligned} \bigl\Vert f(\cdot) - f_{\varepsilon,\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \leq\varepsilon^{\frac{1}{2}} \biggl(\mathcal {H} ( \mathcal{B},\gamma, \lambda_{1},\varphi_{0},f ) + \frac {1}{\lambda _{1}^{\gamma(j-1)}} \mathcal{M}_{1}^{\frac{1}{2}} \biggr), \end{aligned}$$

  (3.21)

where $\mathcal{H} (\mathcal{B},\gamma, \lambda_{1},\varphi _{0},f ) = ( \frac{2 |\max \{1,\frac{\mathcal{B}}{\lambda _{1}^{\gamma}T^{\beta} } \} | T^{\beta} }{\varphi_{0} [1 - E_{\beta,1}(-\lambda_{1}^{\gamma}T^{\beta}) ]} + \frac{\|f\| _{L^{2}(\Omega)}}{\varphi_{0}\lambda_{1}^{\gamma}} )$. □

3.3 A posterior parameter choice

In this subsection, a posterior regularization parameter choice rule is considered. By the Morozov discrepancy principle here we find ζ such that

$$\begin{aligned} \begin{aligned}[b] \mathcal{R}\bigl(\alpha(\varepsilon)\bigr) &= \bigl\| \alpha( \varepsilon ) \bigl(-\mathcal{L}^{\gamma}\bigr) \bigl(1 - \alpha( \varepsilon) \mathcal {L}^{\gamma} \bigr)^{-1} \bigl(f_{\varepsilon, \alpha(\varepsilon)} - \bigl\langle \ell_{\varepsilon}(\cdot),\mathrm{e}_{k}( \cdot) \bigr\rangle \\ & \quad+ \bigl\langle g_{\varepsilon}(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle E_{\beta ,1}\bigl(-\lambda_{k}^{\gamma}T^{\beta} \bigr) \bigr) ) \bigr\| _{L^{2}(\Omega)} \\&= \zeta\varepsilon,\end{aligned} \end{aligned}$$

(3.22)

see [2], where $\zeta> 1$ is a constant. We know there exists an unique solution for (3.22) if $[ \langle\ell_{\varepsilon}(x),\mathrm{e}_{k}(x) \rangle - \langle g_{\varepsilon }(x),\mathrm{e}_{k}(x) \rangle E_{\beta,1}(-\lambda_{k}^{\gamma }T^{\beta }) ] > \zeta\varepsilon$.

Lemma 3.3

We need the following auxiliary result.

• (a) $\mathcal{R}(\alpha(\varepsilon))$ is a continuous function.

• (b) $\lim_{\alpha(\varepsilon) \to0^{+}}\mathcal{R}(\alpha (\varepsilon)) = 0$.

• (c) $\lim_{\alpha(\varepsilon) \to+\infty}\mathcal {R}(\alpha (\varepsilon)) = \| \langle\ell_{\varepsilon}(x),\mathrm {e}_{k}(x) \rangle - \langle g_{\varepsilon}(x),\mathrm{e}_{k}(x) \rangle E_{\beta ,1}(-\lambda _{k}^{\gamma}T^{\beta}) \|_{L^{2}(\Omega)}$.

• (d) $\mathcal{R}(\alpha(\varepsilon))$ is a strictly increasing function.

Proof

Our proof starts with the observation that

$$\begin{aligned} \mathcal{R}\bigl(\alpha(\varepsilon)\bigr) = \Biggl( \sum _{k=1}^{\infty} \biggl(\frac{\alpha(\varepsilon) \lambda_{k}^{\gamma}}{1 + \alpha (\varepsilon ) \lambda_{k}^{\gamma} } \biggr)^{4} \bigl[ \bigl\langle \ell_{\varepsilon }(x),\mathrm{e}_{k}(x) \bigr\rangle - \bigl\langle g_{\varepsilon}(x),\mathrm {e}_{k}(x) \bigr\rangle E_{\beta,1} \bigl(-\lambda_{k}^{\gamma}T^{\beta}\bigr) \bigr]^{2} \Biggr)^{\frac{1}{2}}. \end{aligned}$$

(3.23)

In this section, for brevity, by we put

$$\bigl[ \bigl\langle \ell_{\varepsilon }(x),\mathrm{e}_{k}(x) \bigr\rangle - \bigl\langle g_{\varepsilon}(x),\mathrm {e}_{k}(x)\bigr\rangle E_{\beta,1}\bigl(-\lambda_{k}^{\gamma}T^{\beta}\bigr) \bigr] = \bigl\langle \chi_{\varepsilon}(x),\mathrm{e}_{k}(x) \bigr\rangle .$$

• From (3.23), we have

  $$\begin{aligned} \bigl[\mathcal{R}\bigl(\alpha(\varepsilon)\bigr) \bigr]^{2} = \sum_{k=1}^{\infty} \biggl(\frac{\alpha(\varepsilon) \lambda_{k}^{\gamma}}{1 + \alpha (\varepsilon) \lambda_{k}^{\gamma} } \biggr)^{4} \bigl\vert \langle\chi ,\mathrm {e}_{k} \rangle \bigr\vert ^{2} . \end{aligned}$$

  (3.24)

  We directly verify the continuity of $\mathcal{R}$ and $\mathcal {R}(\alpha(\varepsilon))$ for all $\alpha(\varepsilon) > 0$.

• Assume that θ be a positive number. From

  $$\Vert \chi_{\varepsilon} \Vert _{L^{2}(\Omega)}^{2} = \sum _{k=1}^{\infty} \bigl\vert \bigl\langle \ell_{\varepsilon}(\cdot) - \langle g_{\varepsilon},\mathrm {e}_{k} \rangle E_{\beta,1}\bigl(-\lambda_{k}^{\gamma}T^{\beta} \bigr),\mathrm {e}_{k}(x) \bigr\rangle \bigr\vert ^{2}, $$

  there exists a positive number $m_{\theta}$ such that $\sum_{k=m_{\theta}+1}^{\infty} | \langle\chi_{\varepsilon},\mathrm {e}_{k} \rangle|^{2} < \frac{\theta^{2}}{2} \cdot$ For $0 < \alpha (\varepsilon) < \frac{\theta^{\frac{1}{2}}}{\sqrt[4]{2}} [\lambda _{m_{\theta}}^{\gamma}\|\chi_{\varepsilon}^{\frac{1}{2}} \| _{L^{2}(\Omega)} ]^{-1}$, we have

  $$\begin{aligned} \bigl[\mathcal{R}\bigl(\alpha(\varepsilon)\bigr) \bigr]^{2} &\leq \sum_{k=1}^{m_{\theta}} \biggl( \frac{\alpha(\varepsilon) \lambda _{k}^{\gamma }}{1 + \alpha(\varepsilon) \lambda_{k}^{\gamma} } \biggr)^{4} \bigl\vert \bigl\langle \chi_{\varepsilon}(x), \mathrm{e}_{k}(x) \bigr\rangle \bigr\vert ^{2} +\sum _{k=m_{\theta}+1}^{\infty} \bigl\vert \langle\chi_{\varepsilon},\mathrm {e}_{k} \rangle \bigr\vert ^{2} \\ &\leq\sum_{k=1}^{m_{\theta}} \bigl[\alpha( \varepsilon)\bigr]^{4} \lambda _{k}^{4\gamma} \bigl\vert \langle\chi_{\varepsilon},\mathrm{e}_{k} \rangle \bigr\vert ^{2} + \frac{\theta^{2}}{2} = \bigl[\alpha(\varepsilon) \bigr]^{4} \lambda ^{4\gamma}_{m_{\theta}} \Vert \chi_{\varepsilon} \Vert ^{2} + \frac {\theta ^{2}}{2} \le \theta^{2}. \end{aligned}$$

• From (3.24), we can see that $\mathcal{R}(\alpha(\varepsilon)) \leq | \langle\ell _{\varepsilon }(\cdot),\mathrm{e}_{k}(\cdot) \rangle - \langle g_{\varepsilon}(\cdot ),\mathrm{e}_{k}(\cdot) \rangle E_{\beta,1}(-\lambda_{k}^{\gamma }T^{\beta }),\mathrm{e}_{k}(x) \rangle |^{2}$, one has

  $$\begin{aligned} \bigl[\mathcal{R}\bigl(\alpha(\varepsilon)\bigr) \bigr]^{2} &= \sum _{k=1}^{\infty} \frac{ \vert \langle\chi_{\varepsilon},\mathrm{e}_{k} \rangle \vert ^{2}}{ (1 + \frac{1}{\alpha(\varepsilon)\lambda_{k}^{\gamma}} )^{2}} \geq \biggl\Vert \frac{\chi_{\varepsilon}}{1 + \frac{1}{\alpha(\varepsilon )\lambda_{1}^{\gamma}} } \biggr\Vert _{L^{2}(\Omega)}. \end{aligned}$$

  Hence, $\|\chi_{\varepsilon}\|_{L^{2}(\Omega)} \geq\mathcal {R}(\alpha (\varepsilon)) \geq\frac{\chi_{\varepsilon}}{1 + \frac{1}{\alpha (\varepsilon)\lambda_{1}^{\gamma}}}$ which implies that $\lim_{\alpha (\varepsilon) \to+\infty} \mathcal{R}(\alpha(\varepsilon)) = \| \chi _{\varepsilon}\|_{L^{2}(\Omega)}$.

• For $0 < \alpha_{1}(\varepsilon) < \alpha_{2}(\varepsilon)$, we get $\frac{\alpha_{1}(\varepsilon) \lambda_{k}^{\gamma}}{1 + \alpha _{1}(\varepsilon) \lambda_{k}^{\gamma} } < \frac{\alpha _{2}(\varepsilon ) \lambda_{k}^{\gamma}}{1 + \alpha_{2}(\varepsilon) \lambda _{k}^{\gamma } } \cdot$ From $\|\chi_{\varepsilon}\|_{L^{2}(\Omega)}>0$, there exists a positive integer $k_{0}$ such that $| \langle\chi _{\varepsilon},\mathrm{e}_{k_{0}} \rangle |^{2} > 0$. Then $\mathcal {R}(\alpha_{1}(\varepsilon)) < \mathcal{R}(\alpha_{2}(\varepsilon))$, We can conclude that this is a strictly increasing function. The lemma is proved.

 □

Lemma 3.4

For α, γ, $\lambda_{1}$ are positive constants. The function $\widetilde{\mathcal{H}}$ is given by

$$\begin{aligned} \widetilde{\mathcal{H}}(s) = \frac{\alpha s^{\gamma- \frac{\gamma }{2}(j+1)}}{1+\alpha s^{\gamma}} ,\quad s>0. \end{aligned}$$

(3.25)

Then

$$\begin{aligned} \widetilde{\mathcal{H}}(s) \le \textstyle\begin{cases} 2^{-1}(1-j)^{\frac{1}{2}(1-j)} (1+j)^{\frac{1}{2}(1+j)} \alpha ^{\frac {1}{2}(1+j)} &\textit{if } 0 < j < 1, \\ \frac{1}{\lambda_{1}^{\frac{\gamma}{2}(j-1)}} \alpha & \textit{if } j \ge1 , s \ge \lambda_{1}. \end{cases}\displaystyle \end{aligned}$$

(3.26)

Proof

(1) If $j \geq1$, then from $s \ge\lambda_{1}$, we get

$$\begin{aligned} \widetilde{\mathcal{H}}(s) =\frac{\alpha s^{\gamma-\frac{\gamma }{2}(j+1)}}{1+ \alpha s^{\gamma}} = \frac{\alpha}{ ( 1 + \alpha s^{\gamma} )s^{\frac{\gamma}{2}(j+1)-\gamma} } \le \frac {\alpha }{s^{\frac{\gamma}{2}(j+1)-\gamma}} \le\frac{\alpha}{\lambda _{1}^{\frac {\gamma}{2}(j-1)}} . \end{aligned}$$

(3.27)

(2) If $0 < j < 1$, then it can be seen that $\lim_{s \to0} \widetilde{\mathcal{H}}(s) = \lim_{s \to+ \infty }\widetilde{\mathcal{H}}(s) = 0$. Afterward, we have $\widetilde{\mathcal{H}}^{\prime}(s) = \frac{ \frac{\alpha\gamma}{2} s^{\frac{\gamma}{2}-\frac{\gamma j}{2}-1} [(1-j)-\alpha (1+j)s^{\gamma} ]}{ (1+ \alpha s^{\gamma} )^{2}}$. Solving $\widetilde{\mathcal{H}}^{\prime}(s) = 0$, we know that $s_{0} = (\frac{1-j}{1+j} )^{\frac{1}{\gamma}} \alpha ^{-\frac {1}{\gamma}}$. Hence, we can assert that

$$\begin{aligned} \widetilde{\mathcal{H}}(s) \le\widetilde{\mathcal{H}}(s_{0}) = 2^{-1} (1-j)^{\frac{1}{2}(1-j)} (1+j)^{\frac{1}{2}(1+j)} \alpha^{\frac{1}{2}(1+j)}. \end{aligned}$$

(3.28)

This completes the proof. □

Lemma 3.5

Let $\alpha(\varepsilon)$ be the solution of (3.23), it gives

$$\begin{aligned} \frac{1}{\alpha(\varepsilon)} \le \textstyle\begin{cases} \frac{ ([2\sqrt{2}]^{-1}\mathcal{V}_{1}(\varphi_{0},\varphi _{1},j) )^{\frac{1}{j+1}} }{ (\zeta^{2} - 4 \vert \max \{ 1,\frac {\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \} \vert ^{2} )^{\frac {1}{2(j+1)}}} \frac{\mathcal{M}_{1}^{\frac{1}{j+1}}}{\varepsilon ^{\frac {1}{j+1}}}, &0 < j < 1, \\ \frac{ (\sqrt{2}\mathcal{V}_{2}(\varphi_{0},\varphi_{1},\gamma ,j,\lambda_{1}) )^{\frac{1}{2}}}{ (\zeta^{2} - 4 \vert \max \{ 1,\frac{\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \} \vert ^{2} )^{\frac{1}{4}}} \frac{\mathcal{M}_{1}^{\frac{1}{2}}}{\varepsilon ^{\frac {1}{2}}}, & j \ge1, \end{cases}\displaystyle \end{aligned}$$

(3.29)

which gives the required results.

Proof

Step 1: Using the inequality $(a+b)^{2} \leq2a^{2} + 2b^{2}$, we have $[ \langle\ell_{\varepsilon}(\cdot),\mathrm {e}_{k}(\cdot) \rangle - \langle g_{\varepsilon}(\cdot),\mathrm {e}_{k}(\cdot ) \rangle E_{\beta,1}(-\lambda_{k}^{\gamma}T^{\beta}) ]^{2}$ as follows:

$$\begin{aligned} & \bigl[\bigl\langle \ell_{\varepsilon}(\cdot),\mathrm{e}_{k}( \cdot) \bigr\rangle - \bigl\langle g_{\varepsilon}(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle E_{\beta ,1}\bigl(-\lambda _{k}^{\gamma}T^{\beta} \bigr) \bigr]^{2} \\ &\quad\leq2 \bigl[ \bigl\langle \ell _{\varepsilon}(\cdot) - \ell(\cdot),\mathrm{e}_{k}( \cdot) \bigr\rangle + \bigl\langle g_{\varepsilon}(\cdot) - g(\cdot),\mathrm{e}_{k}( \cdot) \bigr\rangle E_{\beta ,1}\bigl(-\lambda_{k}^{\gamma}T^{\beta} \bigr) \bigr]^{2} \\ &\qquad+ 2 \bigl[ \bigl\langle \ell(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle -\bigl\langle g(\cdot), \mathrm {e}_{k}(\cdot) \bigr\rangle E_{\beta,1}\bigl(- \lambda_{k}^{\gamma}T^{\beta}\bigr) \bigr]^{2} \\ &\quad\leq4 \varepsilon^{2} \biggl\vert \max \biggl\{ 1, \frac{\mathcal {B}}{\lambda _{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert ^{2} + 2 \bigl[ \bigl\langle \ell( \cdot ),\mathrm {e}_{k}(\cdot) \bigr\rangle -\bigl\langle g(\cdot),\mathrm{e}_{k}( \cdot) \bigr\rangle E_{\beta ,1}\bigl(-\lambda_{k}^{\gamma}T^{\beta} \bigr) \bigr]^{2}. \end{aligned}$$

(3.30)

Next, from (3.30), applying Eqs. (2.18) and (2.14), we know that

$$\begin{aligned} & \bigl\langle \ell(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle -\bigl\langle g(\cdot ),\mathrm {e}_{k}(\cdot) \bigr\rangle E_{\beta,1}\bigl(- \lambda_{k}^{\gamma}T^{\beta}\bigr) \\ &\quad= \bigl\langle f(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle \int_{0}^{T} (T-\tau )^{\beta-1} E_{\beta,\beta}\bigl(-\lambda_{k}^{\gamma}(T- \tau)^{\beta}\bigr) \varphi (\tau)\,d\tau \\ &\quad\leq \bigl\langle f(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle \mathcal {P}(\varphi _{0},\varphi_{1})\frac{T^{\beta}}{\lambda_{k}^{\gamma}} E_{\beta ,\beta +1}\bigl(-\lambda_{k}^{\gamma}T^{\beta} \bigr). \end{aligned}$$

(3.31)

Combining (3.30) and (3.31), it gives

$$\begin{aligned} &\bigl[ \bigl\langle \ell_{\varepsilon}(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle - \bigl\langle g_{\varepsilon}(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle E_{\beta ,1}\bigl(-\lambda _{k}^{\gamma}T^{\beta} \bigr) \bigr]^{2} \\&\quad\leq4 \varepsilon^{2} \biggl\vert \max \biggl\{ 1,\frac{\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert ^{2} \\ &\qquad+ 2 \bigl\vert \bigl\langle f(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle \bigr\vert ^{2} \bigl[\mathcal{P}(\varphi_{0}, \varphi_{1}) \bigr]^{2} \bigl[T^{\beta} E_{\beta ,\beta+1}\bigl(-\lambda_{k}^{\gamma}T^{\beta} \bigr) \bigr]^{2}. \end{aligned}$$

(3.32)

Step 2:

$$\begin{aligned} \zeta^{2} \varepsilon^{2}& = \sum _{k=1}^{\infty} \biggl(\frac {\alpha (\varepsilon) \lambda_{k}^{\gamma}}{1 + \alpha(\varepsilon) \lambda _{k}^{\gamma} } \biggr)^{4} \bigl[ \bigl\langle \ell_{\varepsilon}(\cdot ),\mathrm {e}_{k}(\cdot) \bigr\rangle - \bigl\langle g_{\varepsilon}(\cdot),\mathrm {e}_{k}(\cdot ) \bigr\rangle E_{\beta,1}\bigl(-\lambda_{k}^{\gamma}T^{\beta} \bigr) \bigr]^{2} \\ &\le4 \varepsilon^{2} \biggl\vert \max \biggl\{ 1, \frac{\mathcal {B}}{\lambda _{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert ^{2} + 2 \sum _{k=1}^{\infty} \biggl(\frac{\alpha(\varepsilon) \lambda_{k}^{\gamma}}{1 + \alpha (\varepsilon ) \lambda_{k}^{\gamma} } \biggr)^{4} \frac{ [\mathcal {P}(\varphi _{0},\varphi_{1}) ]^{2} }{\lambda_{k}^{2\gamma(j+1)}} \bigl\vert \lambda _{k}^{2\gamma j} \bigl\langle f(\cdot),\mathrm{e}_{k}(\cdot) \bigr\rangle \bigr\vert ^{2} \\ &\le4 \varepsilon^{2} \biggl\vert \max \biggl\{ 1, \frac{\mathcal {B}}{\lambda _{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert ^{2} + 2 \sum _{k=1}^{\infty} \biggl(\frac{\alpha(\varepsilon) \lambda_{k}^{\gamma- \frac{\gamma }{2}(j+1)}}{1+\alpha(\varepsilon) \lambda_{k}^{\gamma}} \biggr)^{4} \bigl[\mathcal{P}(\varphi_{0}, \varphi_{1}) \bigr]^{2}\mathcal{M}_{1}^{2}. \end{aligned}$$

(3.33)

From (3.33), using Lemma 3.4, we have

$$\begin{aligned} &\sup_{k \in \mathbb {N}} \biggl(\frac{\alpha(\varepsilon) \lambda _{k}^{\gamma- \frac{\gamma}{2}(j+1)}}{1+\alpha(\varepsilon) \lambda_{k}^{\gamma}} \biggr)^{4} \\ &\quad\leq \textstyle\begin{cases} \frac{1}{16}(1-j)^{2(1-j)} (1+j)^{2(1+j)} [\alpha(\varepsilon )]^{2(1+j)} & \text{if }0 < j < 1, \\ \frac{1}{\lambda_{1}^{2\gamma(j-1)}} [\alpha(\varepsilon)]^{4}& \text{if }j \ge1 , \lambda_{k} \ge\lambda_{1}. \end{cases}\displaystyle \end{aligned}$$

Here, put

$$\begin{aligned} &\mathcal{V}^{2}_{1}( \varphi_{0},\varphi_{1},j) = \frac{1}{16} (1-j)^{2(1-j)} (1+j)^{2(1+j)} \bigl[\mathcal{P}( \varphi_{0},\varphi _{1}) \bigr]^{2}, \\ &\mathcal{V}^{2}_{2}(\varphi_{0}, \varphi_{1},\gamma,j,\lambda_{1}) = \frac{1}{\lambda_{1}^{2\gamma(j-1)}} \bigl[\mathcal{P}(\varphi _{0},\varphi _{1}) \bigr]^{2}. \end{aligned}$$

(3.34)

Therefore, combining (3.33) to (3.34), we know that

$$\begin{aligned} \zeta^{2} \varepsilon^{2} &\le4 \varepsilon^{2} \biggl\vert \max \biggl\{ 1,\frac {\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert ^{2} + \textstyle\begin{cases} \frac{1}{8}\mathcal{V}^{2}_{1}( \varphi_{0},\varphi_{1},j)\mathcal {M}_{1}^{2} [\alpha(\varepsilon)^{2(1+j)}], &0 < j < 1, \\ 2\mathcal{V}^{2}_{2}(\varphi_{0}, \varphi_{1},\gamma,j,\lambda_{1}) \mathcal{M}^{2}_{1} [\alpha(\varepsilon)]^{4},& j \ge1. \end{cases}\displaystyle \end{aligned}$$

(3.35)

From (3.35), it is very easy to see that

$$\begin{aligned} \biggl(\zeta^{2} - 4 \biggl\vert \max \biggl\{ 1, \frac{\mathcal{B}}{\lambda _{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert ^{2} \biggr) \varepsilon^{2} \le \textstyle\begin{cases} \frac{1}{8}\mathcal{V}^{2}_{1}( \varphi_{0},\varphi_{1},j)\mathcal {M}_{1}^{2} [\alpha(\varepsilon)^{2(1+j)}],& 0 < j < 1, \\ 2\mathcal{V}^{2}_{2}(\varphi_{0}, \varphi_{1},\gamma,j,\lambda_{1}) \mathcal{M}^{2}_{1} [\alpha(\varepsilon)]^{4},& j \ge1. \end{cases}\displaystyle \end{aligned}$$

(3.36)

Therefore, we conclude that

$$\begin{aligned} \frac{1}{\alpha(\varepsilon)} \le \textstyle\begin{cases} \frac{ ([2\sqrt{2}]^{-1}\mathcal{V}_{1}(\varphi_{0},\varphi _{1},j) )^{\frac{1}{j+1}} }{ (\zeta^{2} - 4 \vert \max \{ 1,\frac {\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \} \vert ^{2} )^{\frac {1}{2(j+1)}}} \frac{\mathcal{M}_{1}^{\frac{1}{j+1}}}{\varepsilon ^{\frac {1}{j+1}}}, &0 < j < 1, \\ \frac{ (\sqrt{2}\mathcal{V}_{2}(\varphi_{0},\varphi_{1},\gamma ,j,\lambda_{1}) )^{\frac{1}{2}}}{ (\zeta^{2} - 4 \vert \max \{ 1,\frac{\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \} \vert ^{2} )^{\frac{1}{4}}} \frac{\mathcal{M}_{1}^{\frac{1}{2}}}{\varepsilon ^{\frac {1}{2}}}, & j \ge1, \end{cases}\displaystyle \end{aligned}$$

(3.37)

which gives the required results. □

Theorem 3.6

Assume that $f(x)$ is defined in (2.18) and the quasi-reversibility solution $f_{\varepsilon, \alpha(\varepsilon)}$ be given by (3.5). In this theorem, we suppose that $f(x)$ satisfy a prior bounded condition (2.33), and the condition (3.2) holds. There exists $\zeta> 1$ such that $[ \langle\ell_{\varepsilon}(\cdot),\mathrm {e}_{k}(\cdot ) \rangle - \langle g_{\varepsilon}(\cdot),\mathrm{e}_{k}(\cdot) \rangle E_{\beta ,1}(-\lambda_{k}^{\gamma}T^{\beta}) ] > \zeta\varepsilon> 0$. Then we have the following.

• If $0 < j < 1$, it gives

  $$\begin{aligned} \bigl\Vert f(\cdot)-f_{\varepsilon,\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \textit{ is of order } \varepsilon^{\frac{j}{j+1}}. \end{aligned}$$

  (3.38)

• If $j \ge1$, it gives

  $$\begin{aligned} \bigl\Vert f(\cdot)-f_{\varepsilon,\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \textit{ is of order } \varepsilon^{\frac{1}{2}}. \end{aligned}$$

  (3.39)

Proof

Applying the triangle inequality, we get

$$\begin{aligned} & \bigl\Vert f(\cdot)-f_{\varepsilon,\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \\ &\quad\le\underbrace{ \bigl\Vert f(\cdot )-f_{\alpha (\varepsilon)}(\cdot) \bigr\Vert _{L^{2}( \Omega)}}_{\text{Lemma 3.5}} + \bigl\Vert f_{\alpha (\varepsilon)}( \cdot)-f_{\varepsilon,\alpha(\varepsilon)}(\cdot ) \bigr\Vert _{L^{2}( \Omega)}. \end{aligned}$$

(3.40)

Lemma 3.7

Assume that $\|f\|_{H^{\gamma j}(\Omega)} \leq\mathcal{M}_{1}$, we see that $\|f(\cdot)-f_{\alpha(\varepsilon)}(\cdot)\|_{L^{2}( \Omega )}$ is estimated as follows:

$$\begin{aligned} \bigl\Vert f(\cdot)-f_{\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega )} \leq \varepsilon^{\frac{j}{j+1}}\mathcal{M}_{1}^{\frac{1}{j+1}} \biggl(2 \biggl\vert \max \biggl\{ 1,\frac{\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert + \zeta \biggr)^{\frac{j}{j+1}} \mathcal{A}_{**}^{-\frac {j}{j+1}} . \end{aligned}$$

Using the Hölder inequality with $0 < j < 1$, we get

$$\begin{aligned} \begin{aligned}[b]& \bigl\Vert f(\cdot)-f_{\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \\ &\quad\leq \Biggl\Vert \sum_{k=1}^{\infty} \frac{\alpha(\varepsilon) \lambda _{k}^{\gamma} }{1 + \alpha(\varepsilon) \lambda_{k}^{\gamma} } \frac {C_{\gamma,\beta}(\ell,g,\lambda_{k},T) }{\int_{0}^{T} \mathcal {D}_{\gamma,\beta}(\varphi,\lambda_{k},T,\tau)\, d\tau } \mathrm{e}_{k}(x) \Biggr\Vert _{L^{2}(\Omega)} \\ &\quad= \Biggl\Vert \sum_{k=1}^{\infty} \biggl( \frac{\alpha(\varepsilon) \lambda _{k}^{\gamma} \int_{0}^{T} \mathcal{D}_{\gamma,\beta}(\varphi ,\lambda _{k},T,\tau)\, d\tau }{1+\alpha(\varepsilon) \lambda_{k}^{\gamma} } \biggr)^{j} \biggl( \frac{\alpha(\varepsilon) \lambda_{k}^{\gamma} }{1 + \alpha (\varepsilon) \lambda_{k}^{\gamma} } \biggr)^{1-j} \frac{ \langle f(\cdot ),\mathrm{e}_{k}(\cdot) \rangle }{ (\int_{0}^{T} \mathcal {D}_{\gamma ,\beta}(\varphi,\lambda_{k},T,\tau)\, d\tau )^{j}} \Biggr\Vert _{L^{2}(\Omega )} \\ &\quad\leq\underbrace{ \Biggl\Vert \sum_{k=1}^{\infty} \biggl( \frac{\alpha (\varepsilon)\lambda_{k}^{\gamma} \int_{0}^{T} \mathcal{D}_{\gamma ,\beta}(\varphi,\lambda_{k},T,\tau)\, d\tau }{1 + \alpha(\varepsilon) \lambda_{k}^{\gamma}} \biggr)^{j+1} \biggl( \frac{\alpha(\varepsilon) \lambda_{k}^{\gamma}}{1+ \alpha(\varepsilon) \lambda_{k}^{\gamma }} \biggr)^{1-j} \frac{\langle f(\cdot),\mathrm{e}_{k}(\cdot) \rangle}{ ( \int _{0}^{T} \mathcal{D}_{\gamma,\beta}(\varphi,\lambda_{k},T,\tau )\, d\tau )^{j}} \mathrm{e}_{k}(x) \Biggr\Vert ^{\frac{j}{j+1}}_{L^{2}(\Omega )}}_{\mathcal{N}_{1}}\hspace{-24pt} \\ &\qquad\times\underbrace{ \Biggl\Vert \sum_{k=1}^{\infty} \biggl( \frac {\alpha (\varepsilon) \lambda_{k}^{\gamma}}{1+\alpha(\varepsilon)\lambda _{k}^{\gamma}} \biggr)^{1-j} \frac{\langle f(\cdot),\mathrm {e}_{k}(\cdot ) \rangle}{ ( \int_{0}^{T} \mathcal{D}_{\gamma,\beta}(\varphi ,\lambda _{k},T,\tau)\, d\tau )^{j}} \mathrm{e}_{k}(x) \Biggr\Vert ^{\frac{1}{j+1}} }_{\mathcal{N}_{2}}.\end{aligned} \end{aligned}$$

(3.41)

From (3.41), we have estimates through two steps.

Claim 1

From (3.22) and (3.30), we can find that estimation for $\mathcal{N}_{1}$ as follows:

$$\begin{aligned} \mathcal{N}_{1} &\leq \Biggl\Vert \sum _{k=1}^{\infty} \biggl( \frac {\alpha (\varepsilon)\lambda_{k}^{\gamma} }{1 + \alpha(\varepsilon) \lambda _{k}^{\gamma}} \biggr)^{2} \int_{0}^{T} \mathcal{D}_{\gamma,\beta }( \varphi,\lambda_{k},T,\tau)\, d\tau \bigl\langle f(\cdot),\mathrm {e}_{k}(\cdot ) \bigr\rangle \mathrm{e}_{k}(x) \Biggr\Vert ^{\frac{j}{j+1}}_{L^{2}(\Omega)} \\ &\leq \Biggl\Vert \sum_{k=1}^{\infty} \biggl(\frac{\alpha(\varepsilon )\lambda_{k}^{\gamma} }{1 + \alpha(\varepsilon) \lambda _{k}^{\gamma}} \biggr)^{2} \mathcal{C}_{\gamma,\beta}( \ell,g,\lambda_{k},T) \mathrm {e}_{k}(x) \Biggr\Vert ^{\frac{j}{j+1}}_{L^{2}(\Omega)} \\ &\leq \Biggl( \Biggl\Vert \sum_{k=1}^{\infty} \biggl( \frac{\alpha (\varepsilon )\lambda_{k}^{\gamma} }{1 + \alpha(\varepsilon) \lambda _{k}^{\gamma}} \biggr)^{2} \bigl[ \mathcal{C}_{\gamma,\beta}(\ell,g,\lambda_{k},T) - \mathcal{C}_{\gamma,\beta}(\ell_{\varepsilon},g_{\varepsilon },\lambda _{k},T) \bigr]\mathrm{e}_{k}(x) \Biggr\Vert _{L^{2}(\Omega)} \\ &\quad+ \Biggl\Vert \sum_{k=1}^{\infty} \biggl( \frac{\alpha(\varepsilon )\lambda _{k}^{\gamma} }{1 + \alpha(\varepsilon) \lambda_{k}^{\gamma}} \biggr)^{2} \mathcal{C}_{\gamma,\beta}( \ell_{\varepsilon},g_{\varepsilon },\lambda _{k},T) \mathrm{e}_{k}(x) \Biggr\Vert _{L^{2}(\Omega)} \Biggr)^{\frac {j}{j+1}} \\ &\leq \biggl( 2\varepsilon \biggl\vert \max \biggl\{ 1,\frac{\mathcal {B}}{\lambda _{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert + \zeta\varepsilon \biggr)^{\frac {j}{j+1}} = \varepsilon^{\frac{j}{j+1}} \biggl(2 \biggl\vert \max \biggl\{ 1, \frac {\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert + \zeta \biggr)^{\frac{j}{j+1}}. \end{aligned}$$

(3.42)

Claim 2

Using Lemma 2.7then we get an estimate of $\mathcal{N}_{2}$ as follows:

$$\begin{aligned} \mathcal{N}_{2} &\leq \Biggl\Vert \sum _{k=1}^{\infty} \biggl( \frac {\alpha (\varepsilon) \lambda_{k}^{\gamma}}{1+\alpha(\varepsilon)\lambda _{k}^{\gamma}} \biggr)^{1-j} \frac{\langle f(\cdot),\mathrm {e}_{k}(\cdot ) \rangle}{ ( \int_{0}^{T} \mathcal{D}_{\gamma,\beta}(\varphi ,\lambda _{k},T,\tau)\, d\tau )^{j}} \mathrm{e}_{k}(x) \Biggr\Vert ^{\frac {1}{j+1}}_{L^{2}(\Omega)} \\ &\leq \Biggl\Vert \sum_{k=1}^{\infty} \frac{\langle f(\cdot),\mathrm {e}_{k}(\cdot) \rangle}{ ( \int_{0}^{T} \mathcal{D}_{\gamma ,\beta }(\varphi,\lambda_{k},T,\tau)\, d\tau )^{j}} \mathrm{e}_{k}(x) \Biggr\Vert ^{\frac{1}{j+1}}_{L^{2}(\Omega)} \\ &\leq \Biggl\Vert \sum_{k=1}^{\infty} \frac{\lambda_{k}^{\gamma j} \vert \langle f(\cdot),\mathrm{e}_{k}(\cdot) \langle \vert \mathrm{e}_{k}(x)}{ \mathcal{A}_{**}^{j}} \Biggr\Vert ^{\frac{1}{j+1}}_{L^{2}(\Omega)} \leq \mathcal{A}_{**}^{-\frac{j}{j+1}} \mathcal{M}_{1}^{\frac{1}{j+1}}. \end{aligned}$$

(3.43)

Combining (3.41) to (3.43), we can conclude that

$$\begin{aligned} \bigl\Vert f(\cdot)-f_{\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega )} \leq \varepsilon^{\frac{j}{j+1}}\mathcal{M}_{1}^{\frac{1}{j+1}} \biggl(2 \biggl\vert \max \biggl\{ 1,\frac{\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \biggr\} \biggr\vert + \zeta \biggr)^{\frac{j}{j+1}} \mathcal{A}_{**}^{-\frac {j}{j+1}} . \end{aligned}$$

(3.44)

Now, we give the bound for the first term. Similar to (3.14), we recall that

$$\begin{aligned} \bigl\Vert f_{\alpha(\varepsilon)}(\cdot)- f_{\varepsilon,\alpha (\varepsilon )}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \leq\frac{\varepsilon}{[\alpha (\varepsilon)]} \biggl( \frac{2 \vert \max \{1,\frac{\mathcal {B}}{\lambda_{1}^{\gamma}T^{\beta} } \} \vert T^{\beta} }{\varphi_{0} [1 - E_{\beta,1}(-\lambda_{1}^{\gamma}T^{\beta}) ]} + \frac{ \Vert f \Vert _{L^{2}(\Omega)}}{\varphi_{0}\lambda_{1}^{\gamma}} \biggr). \end{aligned}$$

(3.45)

• If $0 < j < 1$ then

  $$\begin{aligned} \bigl\Vert f_{\alpha(\varepsilon)}(\cdot)- f_{\varepsilon,\alpha (\varepsilon )}( \cdot) \bigr\Vert _{L^{2}(\Omega)} \leq\varepsilon^{\frac{j}{j+1}} \mathcal{M}_{1}^{\frac{1}{j+1}} \mathcal{Z}_{\gamma,\beta }( \mathcal {V}_{1},\zeta,f,\lambda_{1},j). \end{aligned}$$

  (3.46)

• If $j \geq1$ then

  $$\begin{aligned} \bigl\Vert f_{\alpha(\varepsilon)}(\cdot)- f_{\varepsilon,\alpha (\varepsilon )}( \cdot) \bigr\Vert _{L^{2}(\Omega)} \leq\varepsilon^{\frac{1}{2}} \mathcal {M}_{1}^{\frac{1}{2}} \mathcal{Z}_{\gamma,\beta}(\mathcal {V}_{2},\zeta ,f,\lambda_{1},1), \end{aligned}$$

  (3.47)

in which

$$\begin{aligned} &\mathcal{Z}_{\gamma,\beta}(\mathcal{V}_{1},\zeta,f, \lambda_{1},j) \\ &\quad= \biggl[ \frac{ ([2\sqrt{2}]^{-1}\mathcal{V}_{1}(\varphi _{0},\varphi_{1},j) )^{\frac{1}{j+1}} }{ (\zeta^{2} - 4 \vert \max \{1,\frac{\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \} \vert ^{2} )^{\frac{1}{2(j+1)}}} \biggl( \frac{2 \vert \max \{ 1,\frac {\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta} } \} \vert T^{\beta} }{\varphi_{0} [1 - E_{\beta,1}(-\lambda_{1}^{\gamma}T^{\beta }) ]} + \frac{ \Vert f \Vert _{L^{2}(\Omega)}}{\varphi_{0}\lambda_{1}^{\gamma}} \biggr) \biggr], \\ &\mathcal{Z}_{\gamma,\beta}(\mathcal{V}_{2},\zeta,f, \lambda_{1},1) \\ &\quad= \biggl[ \frac{ (\sqrt{2}\mathcal{V}_{2}(\varphi_{0},\varphi _{1},\gamma,j) )^{\frac{1}{2}} }{ (\zeta^{2} - 4 \vert \max \{ 1,\frac{\mathcal{B}}{\lambda_{1}^{\gamma}T^{\beta}} \} \vert ^{2} )^{\frac{1}{4}}} \biggl( \frac{2 \vert \max \{1,\frac{\mathcal {B}}{\lambda_{1}^{\gamma}T^{\beta} } \} \vert T^{\beta} }{\varphi_{0} [1 - E_{\beta,1}(-\lambda_{1}^{\gamma}T^{\beta}) ]} + \frac{ \Vert f \Vert _{L^{2}(\Omega)}}{\varphi_{0}\lambda_{1}^{\gamma}} \biggr) \biggr]. \end{aligned}$$

(3.48)

• If $0 < j < 1$, combining (3.44) and (3.46), then we have the following estimate:

  $$\begin{aligned} \bigl\Vert f(\cdot)-f_{\varepsilon,\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \text{ is of order } \varepsilon^{\frac{j}{j+1}}. \end{aligned}$$

  (3.49)

• If $j \geq1$, combining (3.44) and (3.47), then we have the following estimate:

  $$\begin{aligned} \bigl\Vert f(\cdot)-f_{\varepsilon,\alpha(\varepsilon)}(\cdot) \bigr\Vert _{L^{2}(\Omega)} \text{ is of order } \varepsilon^{\frac{1}{2}}. \end{aligned}$$

  (3.50)

 □

4 Simulation

In this example, we consider the assumptions $T = 1$, $\lambda _{k}^{\gamma} = k^{2\gamma}$, $\mathrm{e}_{k}(x) = \sqrt{\frac {2}{\pi}} \sin(kx)$ and choose

$$\begin{aligned} \ell(x) = \sin(x),\qquad g(x) = \sin(2x) + \sin(4x). \end{aligned}$$

In here, we choose the φ function as follows:

$$\begin{aligned} \varphi(t) = - t^{2} + 2t + \frac{2t^{1-\beta}}{\Gamma(2-\beta)} - \frac {2t^{2-\beta}}{\Gamma(3-\beta)} . \end{aligned}$$

(4.1)

We use the fact that we have

$$\begin{aligned} \int_{0}^{1} \tau^{\beta-1}E_{\beta,\beta} \bigl(\lambda\tau^{\beta}\bigr) (1-\tau)^{\kappa-1} \, d\tau = \Gamma( \beta) E_{\beta,\beta+\kappa }(\lambda ),\quad \forall\kappa> 0. \end{aligned}$$

(4.2)

From (4.1) and (4.2), we know that

$$\begin{aligned} \int_{0}^{1} \tau^{\beta-1}E_{\beta,\beta} \bigl(-\lambda_{k}^{\gamma} \tau ^{\beta}\bigr) \varphi(\tau) \, d\tau &= 2 E_{\beta,3}\bigl(-\lambda _{k}^{\gamma} \bigr) + \Gamma(3)E_{\beta,\beta+3}\bigl(-\lambda_{k}^{\gamma} \bigr) \\ &\quad- 2E_{\beta,2}\bigl(-\lambda_{k}^{\gamma}\bigr) - 2\Gamma(2) E_{\beta,\beta +2}\bigl(-\lambda_{k}^{\gamma} \bigr). \end{aligned}$$

(4.3)

Here, the prior parameter choice rule $\alpha_{\mathrm{pri}} = (\frac {\varepsilon}{M_{1}} )^{\frac{1}{2}}$, and $\alpha_{\mathrm{pos}}$ is chosen by the formula in Lemma 3.5 with $j=1$ and $\zeta=1.95$. We see that $M_{1}$ plays a role as a prior condition computed by $\|f\| _{\mathcal {H}^{\gamma j }(0,\pi)}$. From (2.18), one has

$$\begin{aligned} f(x) = \sqrt{\frac{2}{\pi}} \sum_{k=1}^{N} \frac{ [\ell_{k} - g_{k}E_{\beta,1}(-\lambda_{k}^{\gamma} T^{\beta}) ] \sin(kx) }{\int _{0}^{T} (T-\tau)^{\beta-1} E_{\beta,\beta}(-\lambda_{k}^{\gamma }(T-\tau )^{\beta}) \varphi(\tau)\,d\tau}. \end{aligned}$$

(4.4)

From (3.3), we by definition compute the regularized solution by a quasi-reversibility method:

$$\begin{aligned} f_{\varepsilon,\alpha(\varepsilon)}(x) = \sqrt{\frac{2}{\pi}} \sum _{k=1}^{N}\frac{ [ \ell_{\varepsilon,k} - g_{\varepsilon,k} E_{\beta ,1}(-\lambda_{k}^{\gamma}T^{\beta}) ] \sin(kx) }{ (1+\alpha (\varepsilon)\lambda_{k}^{\gamma} ) \int_{0}^{T} (T-\tau )^{\beta -1}E_{\beta,\beta}(-\lambda_{k}^{\gamma}(T-\tau)^{\beta}) \varphi _{\varepsilon}(\tau) \, d\tau } . \end{aligned}$$

(4.5)

• Suppose that the interval $[a,b]$ is split up into n sub-intervals, with n being an even number. Then the Simpson rule is given by

  $$\begin{aligned} \int_{a}^{b}\varphi(z)\, dz&\approx{ \frac{h}{3}}\sum_{j=1}^{n/2}{ \bigl[}\varphi(z_{2j-2})+4\varphi(z_{2j-1})+\varphi (z_{2j}){ \bigr]} \\ &={\frac{h}{3}} { \Biggl[} \varphi(z_{0})+2\sum _{j=1}^{n/2-1}\varphi (z_{2j})+4 \sum_{j=1}^{n/2}\varphi(z_{2j-1})+ \varphi(z_{n}){ \Biggr]}, \end{aligned}$$

  (4.6)

  where $z_{j}=a+jh$ for $j=0,1,\ldots,n-1,n$ with $h=\frac{b-a}{n}$, in particular, $z_{0}=a$ and $z_{n}=b$.

• Use a finite difference method to discretize the time and spatial variable for $(x,t) \in(0,\pi) \times(0,1)$ as follows:

  $$\begin{aligned} &x_{i} = (i-1) \Delta x,\qquad t_{j} = (j-1) \Delta t, \\ &1\le i \le N+1,\qquad 1\le j \le M+1,\qquad \Delta x = \frac{\pi}{N+1} , \qquad\Delta t = \frac{1}{M+1}. \end{aligned}$$

• Instead of getting accurate data $(\ell_{\varepsilon },g_{\varepsilon},\varphi_{\varepsilon})$, we get approximated data of $(\ell,g,\varphi)$, i.e., the input data $(\ell,g,\varphi)$ is noised by observation data $(\ell_{\varepsilon}, g_{\varepsilon}, \varphi _{\varepsilon} )$ with order ε which satisfies

  $$\begin{aligned} \begin{gathered} \ell_{\varepsilon} = \ell+ \varepsilon\bigl(2\operatorname{rand}(\cdot)-1\bigr),\qquad g_{\varepsilon} = g + \varepsilon\bigl(2\operatorname{rand}(\cdot)-1\bigr),\\ \varphi _{\varepsilon} = \varphi+ \varepsilon\bigl(2\operatorname{rand}(\cdot)-1\bigr).\end{gathered} \end{aligned}$$

• Next, the relative error estimation is defined by

  $$\begin{aligned} \mathit{Error} = \frac{ \sqrt{ \sum_{k=1}^{N+1} \vert f_{\varepsilon, \alpha (\varepsilon)}(x_{k}) - f(x_{k}) \vert _{L^{2}(\Omega)}^{2} } }{ \sqrt{ \sum_{k=1}^{N+1} \vert f(x_{k}) \vert _{L^{2}(\Omega)}^{2} } } . \end{aligned}$$

  (4.7)

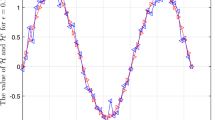
In Fig. 1, we show the convergent estimate between exact solution and its approximation by the quasi-reversibility method under a prior parameter choice rule and under a posterior parameter choice rule. In Fig. 2, we show the convergent estimate between the sought solution and its approximation by QRM and the corresponding errors with $\varepsilon= 0.2$. Similarly, in Fig. 3 and in Fig. 4, we show the comparison in the cases $\varepsilon = 0.02$ and $\varepsilon= 0.0125$. While drawing these figures, we choose values $\beta= 0.5$, $\gamma=0.5$ and $j=1$. In the tables of errors that we calculated in this numerical example, we present the error estimation for both a prior and a posterior parameter choice rule, respectively. In Table 1, we give the comparison of the convergent rate between the sought solution and the regularized solutions. Next, in Table 2, we fixed $\varepsilon=0.034$. In the first column, with $\beta_{p+1} = \beta_{p} + 0.11$, $p=\overline{1,8}$ with $\beta_{1}=0.11$. Using Eq. (4.7), we show the error estimate between the sought solution and its approximation with $\beta=0.3$, in the second column and the third column. Similarly for $\beta=0.5$ and $\beta=0.7$. According to the observations on the tables, we can conclude that the convergent results are appropriate. It is clear that in Tables 1 and 2 the convergence levels of these two methods are still equivalent.

Figure 1

Graph of the regularized, exact solutions under a prior parameter choice rule and under a posterior parameter choice rule at $\beta= \gamma= 0.5$, ${\varepsilon=0.2}$, $\varepsilon=0.02$ and $\varepsilon=0.0125$

Figure 2

A comparison between the regularized solutions and the sought solution (left), and graph of the error estimate (right) at $\varepsilon =0.2$ with ${\beta= \gamma= 0.5}$

Figure 3

A comparison between the regularized solutions and exact solution (left), and graph of the error estimate (right) at $\varepsilon =0.02$ with $\beta= \gamma= 0.5$

Figure 4

A comparison between the regularized solutions and sought solution (left), and graph of the error estimate (right) at $\varepsilon =0.0125$ with ${\beta= \gamma= 0.5}$

Table 1 The error between the regularized solutions and sought solution at $\beta= 0.5$, $\gamma= 0.5$

Table 2 The error between the regularized solutions and the sought solution at $\varepsilon= 0.034$

5 Conclusions

In this work, we use the QR method to regularize the inverse problem to determine an unknown source term of a space-time-fractional diffusion equation. We showed that the problem (1.1) is ill-posed in the sense of Hadamard. Next, we give the results for the convergent estimate between the regularized solution and the sought solution under a prior and a posterior parameter choice rule. We illustrate our theoretical results by a numerical example. In future work, we will be interested in the case of the source function being a function of the general form $f(x, t)$, and this is still an open problem and will show more difficulty.