1 Introduction

The pandemic virus AH1N1/09 that was identified in April 2009 is a flu virus of swine, avian, and human origin. This virus first was identified in Mexico and the USA and then spread to the rest of the world so that the WHO declared the new influenza A(H1N1) a pandemic on June 11, 2009 [1]. Through effective contacts of susceptible people with infectious people, the virus AH1N1 transmits. In the USA, approximately 36,000 people die from seasonal influenza or flu-related causes every year. Due to the importance of vaccination in epidemics, many attempts were made to find the vaccine of this disease until the first effective vaccine was found in the United States in October 2009 [2].

To investigate the dynamic behavior of epidemic diseases, mathematical models have an important role. There are several mathematical models such as SI, SIR, SIS, SIRS, and SEIR [3]. To study the dynamics of H1N1 influenza virus transmission, several mathematical models have been presented. The SIR model has been presented in the approach of Ebenezer [4], Hattaf et al. [5]. El-Shahed and his colleagues used the SIRC model [6] to investigate this disease transmission. Karim and Razali examined the spread of influenza in Malaysia using the SEIRS model [7]. Altaf Khan and his colleagues [8] and Gonzalez-Parra [9] also studied the spread of influenza using the mathematical SEIR model, which is one of the good models in the study of the spread of diseases. With the spread of influenza, Tan et al. used the SEIARC model [10], which has two groups more than the SEIR model and includes more details, to analyze the spread of the disease in Guangdong province. The study of diseases dynamics is a dominating theme for many biologists and mathematicians (see, for example, [11–21]).

It has been studied by many researchers that fractional extensions of mathematical models of integer order represent the natural fact in a very systematic way such as in the approach of Akbari et al. [22], Baleanu et al. [23–25], Kumar et al. [26], Singh et al. [27]. With the expansion of the application of fractional derivatives, methods for solving fractional mathematical systems have been considered by many researchers (see, for example, [28–35]). Also, the study of the mathematical model of phenomena with fractional order derivatives and their optimal control has been the subject of research by many researchers (see, for example, [36–40]). In recent years, many papers have been published on the subject of Caputo–Fabrizio fractional derivative (see, for example, [41–48]).

Given that research conducted in the recent decade shows that fractional-order derivatives work better in modeling real phenomena than integer-order derivatives and include the system of internal memory, in this paper, we study the mathematical model for AH1N1/09 influenza transmission [9] by using the Caputo–Fabrizio fractional derivative. In order to examine the difference between the results of the model with the fractional and integer order, in the numerical part, we also obtain the results with the integer derivative and compare them. We obtain the reproduction number and equilibrium points of the system, and in the numerical simulation we examine the behavior of the system at equilibrium points. In the integer-order derivative, the least change in the order is a unit and the effect of small changes in the derivative order in the results cannot be examined. In this work, we obtain the results of the fractional-order model for different values of derivative order and investigate the effect of derivation order on the results.

The structure of the paper is as follows. In Sect. 2 some basic definitions and concepts of fractional calculus are recalled. The SEIR model of fractional order for AH1N1/09 influenza transmission is presented in Sect. 3. In Sect. 4, the equilibrium points and the reproduction number are calculated and the stability of the equilibrium points is investigated. The existence of solution for the system is proved in Sect. 5. In Sect. 6, a numerical method for solving the model is described and a numerical simulation is presented.

2 Preliminaries

In this section, we recall some of the fundamental concepts of fractional differential calculus, which are found in many books and papers.

Definition 1

([49])

For an integrable function g, the Caputo derivative of fractional order \(\nu \in (0,1)\) is given by

$$ {}^{C}D^{\nu }g(t)=\frac{1}{\varGamma (m-\nu )} \int _{0}^{t} \frac{g^{(m)}(\upsilon )}{(t-\upsilon )^{\nu -m+1}} \,d\upsilon,\quad m=[\nu ]+1. $$

Also, the corresponding fractional integral of order ν with \(\operatorname{Re} (\nu ) > 0\) is given by

$$ {}^{C}I^{\nu } g(t)= \frac{1}{\varGamma (\nu )} \int _{0}^{t} (t-\upsilon )^{\nu -1}g(\upsilon ) \,d\upsilon. $$

Definition 2

([41, 50])

For \(g\in H^{1}(c,d)\) and \(d>c\), the Caputo–Fabrizio derivative of fractional order \(\nu \in (0,1)\) for g is given by

$$ {}^{CF}D^{\nu } g(t)=\frac{M(\nu )}{(1-\nu )} \int _{c}^{t} \exp \biggl(\frac{-\nu }{1-\nu }(t- \upsilon ) \biggr)g'(\upsilon )\,d\upsilon, $$

where \(t\geq 0\), \(M(\nu )\) is a normalization function that depends on ν and \(M(0)=M(1)=1\). If \(g \notin H^{1}(c,d)\) and \(0<\nu <1\), this derivative for \(g\in L^{1}(-\infty,d)\) is given by

$$ {}^{CF}D^{\nu } g(t)=\frac{\nu M(\nu )}{(1-\nu )} \int _{- \infty }^{d} \bigl(g(t)-g(\upsilon ) \bigr)\exp \biggl(\frac{-\nu }{1-\nu }(t-\upsilon ) \biggr)\,d \upsilon. $$

Also, the corresponding CF fractional integral is presented by

$$ {}^{CF}I^{\nu } g(t)=\frac{2(1-\nu )}{(2-\nu )M(\nu )} g(t)+ \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} g(\upsilon )\,d \upsilon. $$

The Laplace transform is one of the important tools in solving differential equations that are defined below for two kinds of fractional derivative.

Definition 3

([49])

The Laplace transform of Caputo fractional differential operator of order ν is given by

$$ L \bigl[{}^{C} D^{\nu }g(t) \bigr](s)=s^{\nu }L{g(t)}- \sum_{i=0}^{m-1}s^{\nu -i-1}g^{(i)}(0), \quad m-1 < \nu \leq m\in N, $$

which can also be obtained in the form

$$ L \bigl[{}^{C} D^{\nu }g(t) \bigr]= \frac{s^{m} L[g(t)]-s^{m-1}g(0)-s^{m-1}g^{\prime }(0)-\cdots-g^{(m-1)}}{s^{m-\nu }}. $$

Definition 4

([41])

The Laplace transform of the Caputo–Fabrizio derivative is defined by

$$ L \bigl[{}^{CF} D^{(\alpha )}f(t) \bigr](s)=\frac{M(\alpha )(2-\alpha )}{2(s+\alpha (1-s))} \bigl(sL \bigl[f(t) \bigr]-f(0) \bigr). $$

Since \(M(\alpha )=\frac{2}{2-\alpha }\) for \(0<\alpha <1\), we get

$$ L \bigl[{}^{CF} D^{(\alpha )}f(t) \bigr](s)=\frac{sL[f(t)]-f(0)}{(s+\alpha (1-s))}. $$

Definition 5

([51])

Let \((X,d)\) be a metric space, a map \(g:X\to X\) is called a Picard operator whenever there exists \(x^{*}\in X\) such that \(Fix(g)=\{x^{*}\}\) and the sequence \((g^{n}(x_{0}))_{n\in N}\) converges to \(x^{*}\) for all \(x_{0}\in X\).

3 Mathematical model of the AH1N1/09 influenza transmission

With the global outbreak of influenza AH1N1 virus in 2009, which killed more than 14,000 people worldwide, various mathematical models have been developed to study and simulate the spread of the virus. One of these models that have good results in epidemic diseases is the SEIR model, which has been modeled and studied by Gilberto González-Parra and his colleagues with the integer-order derivative [9]. Considering the good results of fractional derivative order in modeling real phenomena in recent years, in this work we investigate the SEIR model of AH1N1/09 influenza virus transmission with Caputo–Fabrizio fractional-order derivative.

In this model, the total population \(N(t)\) is divided into four categories: the susceptible individuals \(S(t)\), the exposed individuals \(E(t)\), the infectious individuals \(I(t)\), and the individuals who have recovered \(R(t)\). The desired SEIR model is as follows:

$$ \textstyle\begin{cases} \frac{dS}{dt}=\kappa -\beta S(t)I(t)-m S(t), \\ \frac{dE}{dt}=\beta S(t)I(t)-(m+\delta )E(t), \\ \frac{dI}{dt}=\delta E(t)-(m+\mu )I(t), \\ \frac{dR}{dt}=\mu I(t)-m R(t), \end{cases} $$

where κ: the birth rate of people, m: the death rate of people, β: the transmission rate of infection from I to S, δ: the transmission rate of people from E to I, μ: the recovery rate of infected people, with initial conditions \(S(0)=S_{0}>0, E(0)=E_{0}> 0, I(0)=I_{0} > 0, R(0)=R_{0}\geq 0\).

In this section, we moderate the system by substituting the time derivative by the Caputo–Fabrizio fractional derivative. With this change, the right- and left-hand sides will not have the same dimension. To solve this problem, we use an auxiliary parameter θ, having the dimension of sec., to change the fractional operator so that the sides have the same dimension [52]. According to the explanation presented, the fractional model of the H1N1/09 influenza transmission for \(t\geq 0\) and \(\nu \in (0,1)\) is given as follows:

$$ \textstyle\begin{cases} \eta ^{\nu -1} {}^{CF} {D}^{\nu }_{t} S(t)=\kappa -\beta S(t)I(t)-m S(t), \\ \eta ^{\nu -1} {}^{CF} {D}^{\nu }_{t}E(t)=\beta S(t)I(t)-(m+\delta )E(t), \\ \eta ^{\nu -1} {}^{CF} {D}^{\nu }_{t} I(t)=\delta E(t)-(m+\mu )I(t), \\ \eta ^{\nu -1} {}^{CF} {D}^{\nu }_{t} R(t)=\mu I(t)-m R(t), \end{cases} $$
(1)

where the initial conditions are \(S(0)=S_{0}>0, E(0)=E_{0}> 0, I(0)=I_{0} > 0, R(0)=R_{0}\geq 0\).

4 Equilibrium points

To determine the equilibrium points of fractional order system (1), we solve the following equations:

$$ {}^{CF} {D}^{\nu }S(t)={}^{CF} {D}^{\nu }E(t)={}^{CF} {D}^{\nu }I(t)={}^{CF} {D}^{\nu }R(t)=0. $$

By solving the algebraic equations, we obtain equilibrium points of system (1). The disease-free equilibrium point is obtained as \(E_{0}=(\frac{\kappa }{m},0,0,0)\), and if \(R_{0}> 1\) then the system has the endemic equilibrium point \(E_{1}=(S^{*},E^{*},I^{*},R^{*})\) so that

$$\begin{aligned} &S^{*}=\frac{\delta (m+\mu )+m^{2}+m\mu }{\beta \delta }, \\ &E^{*}= \frac{\beta \delta \kappa -\delta m^{2}-\delta m\mu -m^{3}-m^{2}\mu }{\delta \beta (m+\delta )}, \\ &I^{*}= \frac{\beta \delta \kappa -\delta m^{2}-\delta m\mu -m^{3}-m^{2}\mu }{\beta (\delta m+\delta \mu +m^{2}+m\mu )} , \\ &R^{*}= \frac{\mu (\beta \delta \kappa -\delta m^{2}-\delta m\mu -m^{3}-m^{2}\mu )}{\beta m(\delta m+\delta \mu +m^{2}+m\mu )}. \end{aligned}$$

Also, \(R_{0}\) is the basic reproduction number and is obtained using the next generation method [53]. To find \(R_{0}\), we first consider the system as follows:

$$ {}^{C} {D}^{\nu }\varPsi (t)=F \bigl(\varPsi (t) \bigr)-V \bigl( \varPsi (t) \bigr), $$

where

$$ F \bigl(\varPsi (t) \bigr)=\eta ^{1-\nu } \begin{bmatrix} \beta S(t)I(t) \\ 0 \end{bmatrix} $$

and

$$ V \bigl(\varPsi (t) \bigr)=\eta ^{1-\nu } \begin{bmatrix} (m+\delta )E(t) \\ -\delta E(t)+(m+\mu )I(t) \end{bmatrix}. $$

At \(E^{0}\), the Jacobian matrix for F and V is obtained as follows:

$$ J_{F}(E_{0})=\eta ^{1-\nu } \begin{bmatrix} 0 & \beta \frac{\kappa }{m} \\ 0& 0 \end{bmatrix} ,\qquad J_{v}(E_{0})= \eta ^{1-\nu } \begin{bmatrix} m+\delta & 0 \\ -\delta & m+\mu \end{bmatrix} . $$

\(FV^{-1}\) is the next generation matrix for system (1), and the basic reproduction number is obtained from \(R_{0}=\rho (FV^{-1})\). So we obtain the reproduction as \(R_{0}=\frac{\beta \delta \kappa }{m}\). This basic reproduction number \(R_{0}\) is an epidemiologic metric used to describe the contagiousness or transmissibility of infectious agents.

4.1 Stability of equilibrium point

To investigate the stability of an equilibrium point, first consider the fractional-order linear system

$$ {}^{CF}{D}^{\nu }_{t}y(t)=T y(t), $$
(2)

where \(y(t)\in R^{n}, T\in R^{n\times n}, 0<\nu <1\).

Definition 6

([54])

For system (2) with Caputo–Fabrizio fractional derivative, the characteristic equation is given by

$$ \det \bigl(s \bigl(I-(1-\nu )T \bigr)-\nu T \bigr)=0. $$
(3)

Theorem 7

([54])

If \((I-(1-\nu )T)\)is invertible, then system (2) is asymptotically stable if and only if the roots to the characteristic equation of system (3) have negative real parts.

The Jacobian matrix associated with system (2) is given as follows:

$$ J=\eta ^{1-\nu } \begin{bmatrix} -(\beta I+m) & 0 & -\beta S & 0 \\ \beta I & -(m+\delta ) & \beta S &0 \\ 0 & \delta & -(m+\mu ) & 0 \\ 0 & 0 & \mu & -m \end{bmatrix}. $$

Then the Jacobian matrix at \(E_{0}\) is

$$ J(E_{0})=\eta ^{1-\nu } \begin{bmatrix} -m & 0 & -\beta \frac{\kappa }{m} & 0 \\ 0 & -(m+\delta ) & \beta \frac{\kappa }{m} &0 \\ 0 & \delta & -(m+\mu ) & 0 \\ 0 & 0 & \mu & -m \end{bmatrix}. $$

The characteristic equation of \(J(E_{0})\) is

$$\begin{aligned} &\bigl[s \bigl(1+m(1-\nu ) \bigr)+m\nu \bigr]^{2} \bigl[s \bigl(1+(1- \nu ) (m+\delta ) \bigr)+\nu (m+\delta ) \bigr]\\ &\quad{}\times \bigl[s \bigl(1+(1- \nu ) (m+\mu ) \bigr)+\nu (m+\mu ) \bigr]=0. \end{aligned}$$

By computing the roots of the above equation, we obtain

$$\begin{aligned} &s_{1}=s_{2}=\frac{-m\nu }{1+m(1-\nu )}, \\ &s_{3}=\frac{-\nu (m+\delta )}{1+(1-\nu )(m+\delta )}, \\ &s_{4}=\frac{-\nu (m+\mu )}{1+(1-\nu )(m+\mu )}. \end{aligned}$$

Since all of the parameters are positive and \(0 < \nu <1\), then the roots of characteristic equation are negative. Thus by using Theorem 7, the disease-free equilibrium point \(E_{0}\) of model (1) is asymptotically stable.

5 Existence of solution

The system of differential equations for the AH1N1 disease model (1) using the Caputo–Fabrizio fractional-order derivative is considered as follows:

$$ \textstyle\begin{cases} {}^{CF} {D}^{\nu }_{t} S(t)=\eta ^{1-\nu } [ \kappa -\beta S(t)I(t)-m S(t)], \\ {}^{CF} {D}^{\nu }_{t}E(t)=\eta ^{1-\nu } [\beta S(t)I(t)-(m+\delta )E(t)], \\ {}^{CF} {D}^{\nu }_{t} I(t)=\eta ^{1-\nu } [\delta E(t)-(m+\mu )I(t)], \\ {}^{CF} {D}^{\nu }_{t} R(t)=\eta ^{1-\nu } [\mu I(t)-m R(t)]. \end{cases} $$
(4)

Applying the Losada and Nieto integral operator [41] on both sides of equations (4), we obtain

$$ \begin{aligned} S(t)-u_{1}(t) ={}&\eta ^{1-\nu } \biggl[ \frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\{ \kappa -\beta S(t)I(t)-m S(t) \bigr\} \\ &{} +\frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl[ \kappa -\beta S(\tau )I(\tau )-m S(\tau ) \bigr]\,d\tau \biggr], \\ E(t)-u_{2}(t) ={}&\eta ^{1-\nu } \biggl[\frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\{ \beta S(t)I(t)-(m+\delta )E(t) \bigr\} \\ &{} +\frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl[ \beta S(\tau )I(\tau )-(m+ \delta )E(\tau ) \bigr]\,d\tau \biggr], \\ I(t)-u_{3}(t) ={}&\eta ^{1-\nu } \biggl[\frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\{ \delta E(t)-(m+\mu )I(t) \bigr\} \\ & {}+ \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl[ \delta E(\tau )-(m+\mu )I(\tau ) \bigr]\,d\tau \biggr], \\ R(t)-u_{4}(t) ={}&\eta ^{1-\nu } \biggl[\frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\{ \mu I(t)-m R(t) \bigr\} \\ &{} + \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl[\mu I( \tau )-m R(\tau ) \bigr] \,d\tau \biggr]. \end{aligned} $$
(5)

We present the differential equations (5) as follows:

$$\begin{aligned} &S_{0}(t)=u_{1}(t),\qquad E_{0}(t)=u_{2}(t), \\ &I_{0}(t)=u_{3}(t),\qquad R_{0}(t)=u_{4}(t), \\ &S_{n+1}(t)=\eta ^{1-\nu } \biggl[\frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\{ \kappa - \beta S(t)I(t)-m S(t) \bigr\} \\ &\phantom{S_{n+1}(t)=}{}+\frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl[\kappa - \beta S(\tau )I(\tau )-m S(\tau ) \bigr]\,d\tau \biggr], \\ &E_{n+1}(t))=\eta ^{1-\nu } \biggl[\frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\{ \beta S(t)I(t)-(m+ \delta )E(t) \bigr\} \\ &\phantom{E_{n+1}(t))=}{}+\frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl[\beta S( \tau )I(\tau )-(m+ \delta )E(\tau ) \bigr]\,d\tau \biggr], \\ &I_{n+1}(t)=\eta ^{1-\nu } \biggl[\frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\{ \delta E(t)-(m+ \mu )I(t) \bigr\} \\ &\phantom{I_{n+1}(t)=}{}+ \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl[\delta E( \tau )-(m+\mu )I(\tau ) \bigr]\,d\tau \biggr], \\ &R_{n+1}(t)=\eta ^{1-\nu } \biggl[\frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\{ \mu I(t)-m R(t) \bigr\} \\ &\phantom{R_{n+1}(t)=}{}+ \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl[\mu I( \tau )-m R(\tau ) \bigr] \,d\tau \biggr]. \end{aligned}$$

By taking the limit from above Picard’s repetitive series when n tends to ∞, we obtain the solution of the equation as follows:

$$ \textstyle\begin{cases} \lim_{n\rightarrow \infty } S_{n}(t)=S(t), \\ \lim_{n\rightarrow \infty } E_{n}(t)=E(t), \\ \lim_{n\rightarrow \infty } I_{n}(t)=I(t), \\ \lim_{n\rightarrow \infty } R_{n}(t)=R(t). \end{cases} $$
(6)

5.1 Existence of solution by the Picard–Lindelof approach

Using the Picard–Lindelof approach and the Banach fixed point theorem, we prove the existence of solution. We define the following operators:

$$ \textstyle\begin{cases} h_{1}(t,S)=\eta ^{1-\nu } [\kappa -\beta S(t)I(t)-m S(t)], \\ h_{2}(t,E)=\eta ^{1-\nu } [\beta S(t)I(t)-(m+\delta )E(t)], \\ h_{3}(t,I)=\eta ^{1-\nu } [\delta E(t)-(m+\mu )I(t)], \\ h_{4}(t,R)=\eta ^{1-\nu } [\mu I(t)-m R(t)]. \end{cases} $$

Let \(L_{1}=\sup_{C[a,c_{1}]} \Vert h_{1}(t,S) \Vert \), \(L_{2}=\sup_{C[a,c_{2}]} \Vert h_{2}(t,E) \Vert \), \(L_{3}=\sup_{C[a,c_{3}]} \Vert h_{3}(t,I) \Vert \), and \(L_{4}=\sup_{C[a,c_{4}]} \Vert h_{4}(t,R) \Vert \), where

$$ \textstyle\begin{cases} C[a,c_{1}]= \vert t-a,t+a \vert \times \vert S-c_{1}, S+c_{1} \vert =A \times C_{1}, \\ C[a,c_{2}]= \vert t-a,t+a \vert \times \vert E-c_{2}, E+c_{2} \vert =A \times C_{2}, \\ C[a,c_{3}]= \vert t-a,t+a \vert \times \vert I-c_{3}, I+c_{3} \vert =A \times C_{3}, \\ C[a,c_{4}]= \vert t-a,t+a \vert \times \vert R-c_{4}, R+c_{4} \vert =A \times C_{4}. \end{cases} $$

Now, we assume a uniform norm on \(C[a,c_{i}], (i=1,2,3,4)\) as follows:

$$ \bigl\Vert Y(t) \bigr\Vert _{\infty }=\sup_{t\in [t-a,t+a]} \bigl\vert Y(t) \bigr\vert . $$

Consider the Picard operator

$$ \varTheta: C(A,C_{1},C_{2},C_{3},C_{4}) \rightarrow C(A,C_{1},C_{2},C_{3},C_{4}) $$

given as follows:

$$ \varTheta \bigl(Y(t) \bigr)=Y_{0}(t)+\frac{2(1-\nu )}{2-\nu )M(\nu )}H \bigl(t,Y(t) \bigr)+ \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} H \bigl(\tau,Y( \tau ) \bigr) \,d\tau $$

so that \(Y(t)=\{S(t),E(t),I(t),R(t)\},Y_{0}(t)=\{S(0),E(0),I(0),R(0)\}\) and

$$ H \bigl(t,Y(t) \bigr)= \bigl\{ h_{1}(t,S), h_{2}(t,E), h_{3}(t,I), h_{4}(t,R) \bigr\} . $$

We assume that the solutions of system (1) are bounded within a time period,

$$ \bigl\Vert Y(t) \bigr\Vert _{\infty } \leq \max \{c_{1},c_{2},c_{3},c_{4} \}=C. $$

Let \(L=\max \{L_{1},L_{2},L_{3},L_{4}\}\) and there exist \(t_{0}\) so that \(t_{0}\geq t\), then

$$\begin{aligned} & \bigl\Vert \varTheta Y(t)-Y_{0}(t) \bigr\Vert \\ & \quad= \biggl\Vert \frac{2(1-\nu )}{(2-\nu ) M(\nu )}H \bigl(t,Y(t) \bigr)+ \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} H \bigl(\tau,Y(\tau ) \bigr)\,d\tau \biggr\Vert , \\ &\quad\leq \frac{2(1-\nu )}{(2-\nu ) M(\nu )} \bigl\Vert H(t,Y) \bigr\Vert + \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl\Vert H(\tau,Y) \bigr\Vert \,d\tau, \\ &\quad\leq \biggl(\frac{2(1-\nu )}{(2-\nu )M(\nu )} + \frac{2\nu t}{(2-\nu )M(\nu )} \biggr)L \\ &\quad\leq \biggl(\frac{2(1-\nu )}{(2-\nu )M(\nu )} + \frac{2\nu t_{0}}{(2-\nu )M(\nu )} \biggr)L\leq \gamma L \leq C, \end{aligned}$$

where we demand that

$$ \gamma < \frac{C}{L}. $$

Also we evaluate the following equality:

$$ \Vert \varTheta Y_{1}-\varTheta Y_{2} \Vert =\sup _{t\in A} \bigl\vert Y_{1}(t)-Y_{2}(t) \bigr\vert . $$

By our Picard’s operator, we obtain

$$\begin{aligned} \Vert \varTheta Y_{1}-\varTheta Y_{2} \Vert ={}& \biggl\Vert \frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\{ H(t,Y_{1}(t)-H(t,Y_{2}(t) \bigr\} \\ &{} + \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl\{ H(\tau,Y_{1}(\tau )-H(\tau,Y_{2}(\tau ) \bigr\} \,d\tau \biggr\Vert , \\ \leq {}&\frac{2(1-\nu )}{(2-\nu )M(\nu )} \bigl\Vert H(t,Y_{1}(t)-H(t,Y_{2}(t) \bigr\Vert \\ &{} + \frac{2\nu }{(2-\nu )M(\nu )} \int _{0}^{t} \bigl\Vert H(\tau,Y_{1}( \tau )-H( \tau,Y_{2}(\tau ) \bigr\Vert \,d\tau, \\ \leq{} &\frac{2(1-\nu )}{(2-\nu )M(\nu )}\rho \bigl\Vert Y_{1}(t)-Y_{2}(t) \bigr\Vert \\ &{}+\frac{2\nu \rho }{(2-\nu ) M(\nu )} \int _{0}^{t} \bigl\Vert Y_{1}( \tau )-Y_{2}(\tau ) \bigr\Vert \,d\tau, \\ \leq{}& \biggl(\frac{2(1-\nu ) \lambda }{(2-\nu )M(\nu )} + \frac{2\nu \rho t_{0}}{(2-\nu )M(\nu )} \biggr) \bigl\Vert Y_{1}(t)-Y_{2}(t) \bigr\Vert \\ \leq{} &\gamma \rho \bigl\Vert Y_{1}(t)-Y_{2}(t) \bigr\Vert \end{aligned}$$

with \(\rho <1\). Since H is a contraction, then \(\gamma \rho <1\), this proves that Θ is a contraction and completes the proof.

6 Numerical results

Using the fractional Euler method for Caputo–Fabrizio derivative, we present the approximate solutions for a fractional-order SEIR model of the AH1N1/09 influenza transmission model.

6.1 Numerical method

We consider system (1) in a compact form as follows:

$$ \eta ^{\nu -1} {}^{C} {D}^{\nu }_{t} w(t)=g \bigl(t,w(t) \bigr),\qquad w(0)=w_{0},\quad 0\leq t \leq T< \infty, $$
(7)

where \(w=(S,E,I,R)\in R^{4}_{+}\), \(w_{0}=(S_{0},E_{0},I_{0},R_{0})\) is the initial vector, and \(g(t)\in R\) is a continuous vector function satisfying the Lipschitz condition

$$ \bigl\Vert g \bigl(w_{1}(t) \bigr)-g \bigl(w_{2}(t) \bigr) \bigr\Vert \leq k \bigl\Vert w_{1}(t)-w_{2}(t) \bigr\Vert ,\quad k> 0. $$

Applying a fractional integral operator corresponding to Caputo derivative to equation (7), we obtain

$$ w(t)=\eta ^{1-\nu } \bigl[w_{0}+I^{\nu } g \bigl(w(t) \bigr) \bigr],\quad 0\leq t \leq T< \infty. $$

Set \(h=\frac{T-0}{N}\) and \(t_{n}=nh\), where \(t\in [0,T]\) and N is a natural number and \(n=0,1,2,\ldots,N\). Let \(w_{n}\) be the approximation of \(w(t)\) at \(t=t_{n}\). Using the fractional Euler method [55, 56], we get

$$ w_{n+1}=\eta ^{1-\nu } \Biggl[w_{0}+(1- \nu )g(t_{n+1},w_{n+1})+\nu h \sum _{j=0}^{n}g(t_{j},w_{j}) \Biggr],\quad n=0,1,2,\ldots,N-1, $$
(8)

the stability analysis of the obtained scheme has been proved in Theorem (3.1) in [55].

Thus, the solution of system (1) is written as follows:

$$\begin{aligned} &S_{n+1}=\eta ^{1-\nu } \Biggl[S_{0}+(1-\nu )f_{1}(t_{n+1},w_{n+1})+\nu h\sum _{j=0}^{n}f_{1}(t_{j},w_{j}) \Biggr], \\ &E_{n+1}=\eta ^{1-\nu } \Biggl[E_{0}+(1-\nu )f_{2}(t_{n+1},w_{n+1})+\nu h\sum _{j=0}^{n}f_{2}(t_{j},w_{j}) \Biggr], \\ &I_{n+1}=\eta ^{1-\nu } \Biggl[I_{0}+(1-\nu )f_{3}(t_{n+1},w_{n+1})+\nu h\sum _{j=0}^{n}f_{3}(t_{j},w_{j}) \Biggr], \\ &R_{n+1}=\eta ^{1-\nu } \Biggl[R_{0}+(1-\nu )f_{4}(t_{n+1},w_{n+1})+\nu h\sum _{j=0}^{n}f_{4}(t_{j},w_{j}) \Biggr], \end{aligned}$$

where \(f_{1}(t,w(t))=\kappa -\beta S(t)I(t)-m S(t)\), \(f_{2}(t,w(t))= \beta S(t)I(t)-(m+\delta )E(t)\), \(f_{3}(t,w(t))=\delta E(t)-(m+\mu )I(t)\), \(f_{4}(t,w(t))=\mu I(t)-m R(t)\).

6.2 Numerical simulation

To check the behavior of the model, we use the parameters obtained by Gonzalez-Parra et al. [9]. The reported incubation period for the AH1N1/09 virus is \(2--10\) days. So the assumed mean time in \(E(t)\) is \(\delta =\frac{1}{5}\ \mathrm{days}^{-1}\). The reported infectious period is 4–7 days, so it has been assumed \(\mu =\frac{1}{7}\). Since the used time period is short, then the population size is assumed to be constant, and thus \(\kappa =m=\frac{0.015}{52}\ \mathrm{days}^{-1}\). Also, by fitting the data technique and confirmed cases of pandemic AH1N1/09 influenza for Bogota D.C, it is obtained \(\beta =3.58\). Also, the initial conditions are \(S(0)=1-0.001, E(0)=0, I(0)=0.001, R(0)=0\).

In this simulation, the reproduction number is \(R_{0}=0.716\) and the endemic equilibrium point is

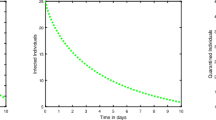
$$ E_{1}= \bigl(S^{*},E^{*},I^{*},R^{*} \bigr)=(0.04004248, 0.00138256, 0.00193168, 0.95664328). $$

In Fig. 1, the answers of the fractional-order model for AH1N1 influenza with \(\nu =0.98\) are plotted. In this simulation, the value of \(R_{0}\) is equal to 0.716 which is smaller than 1 and, as you can see, the spread of the disease is controlled and the number of infected people is reduced to zero. We also see that each of the functions tends to its equilibrium point and the system in equilibrium points becomes stable. In Figs. 2 and 3, we have plotted the results of model (1) for different fractional orders \(\nu =1,0.95,0.9,0.85,0.8\). Given that disease propagation models are usually used in predicting disease progression and making controlling decisions, it is important to determine the exact order of derivation of the model, as shown in Fig. 3, while in model 1 after the disease is controlled for 60 days. But in the model, with the order of 0.9 or 0.8 the disease still persists and it takes several days to be controlled. The results of the AH1N1 influenza transmission model (1) are plotted for fractional-order Caputo–Fabrizio derivatives \(\nu =0.94\) and integer-order derivative \(\nu =1\) in Figs. 4–5. Comparison of the graphs shows that the resulting values are different, but the behavior of the functions derived from both types of derivatives is the same.

Figure 1
figure 1

Dynamics of \(S(t)\), \(E(t)\), \(I(t)\), \(R(t)\) for \(\nu =0.98\)

Full size image
Figure 2
figure 2

Dynamics of \(S(t)\) and \(E(t)\) for different values of \(\nu =1, 0.95, 0.9, 0.85, 0.8\)

Full size image
Figure 3
figure 3

Dynamics of \(S(t)\) and \(E(t)\) for different values of \(\nu =1, 0.95, 0.9, 0.85, 0.8\)

Full size image
Figure 4
figure 4

Plots of \(S(t)\) and \(R(t)\) for integer order \(\nu =1\) and fractional order \(\nu =0.94\)

Full size image
Figure 5
figure 5

Plots of \(E(t)\) and \(I(t)\) for integer order \(\nu =1\) and fractional order \(\nu =0.94\)

Full size image

7 Conclusion

In this work, the SEIR epidemic model for the transmission of AH1N1 influenza using the Caputo–Fabrizio fractional-order derivative has been presented. The reproduction number of the system and equilibrium points have been calculated and the stability of a disease-free equilibrium point has been investigated. The existence of solution for the model by using fixed point theory has been proved. Using the fractional Euler method, an approximate answer to the model has been calculated. Also, with a numerical simulation, the values of reproduction number and equilibrium points are calculated, and the results show that the system is stable at equilibrium points and each of the obtained functions converges to its equilibrium point. According to the obtained reproduction number \(R_{0}=0.716 <1\), the epidemic has been controlled and the number of infected people has reduced to zero. To investigate the effect of derivative order on the model results, the functions obtained from the model are plotted for different degrees of fraction, and the results show that the general behavior of the functions is the same in small changes of derivative order but the numerical results are different. In future studies, the effect of each of the coefficients in Model 1 on the disease transmission process can be investigated. Also, research can be done to optimally control the disease spread model and the effect of drugs and vaccination on the current model.