1 Introduction

Lately, fractional calculus has been in the limelight because of its nature of hereditariness and memory [1–3]. By making a comparison between fractional calculus and conventional integer-order one, we can make a discovery that fractional modeling can better tally with the real world. In point of fact, differential equations on the basis of fractional calculus have been in the wide-ranging application in the scope of engineering system [4, 5], financial system [6–8], neural network [9–11], and so on. In fact, the behavior of animals is also under the influence of their experiences or memory [12, 13]. Therefore, the impact of memory is reflected once the biological system is equipped with fractional derivative [14–17]. Furthermore, the biological process is in relation to the entire time information of the system in the light of the traits of the fractional derivative, whereas the classic integer-order derivative places a high value on the information at a given time [18, 19]. Insomuch as fractional-order differential system is in possession of more advantages than integer-order one, the indagation of fractional order prey-predator system has drawn great attention from many researchers (see [20, 21] and the references therein).

In the real ecosystem, diffusion between two disparate biotopes is widely in existence and of immense significance in the protection of animals on the brink of extinction. Plenteous outstanding works have probed into the impact of the dispersal process on the dynamic behaviors of Lotka–Volterra models [19, 22–24]. Furthermore, time delay is indispensable in the real world. It is well known that discrete delay is related to the evaluation of the population a certain number of time units ago [25, 26], and the use of a distributed delay can be viewed as allowing for stochastic effects [27]. Equations with time delay are also common in other fields, especially in control theory [28]. Another significant cause for incorporating time delay is to describe the maturation time which is shown in Nicholson’s blowflies model [29]. It is uncontroverted that gestation delay is immanent since it is the duration of τ time units that the predators need to increase their population after killing prey, and taking time delay into account is essential [30–33] in the predator-prey model. Nevertheless, the underlying system may undergo Hopf bifurcation or even chaos if we draw into gestation delay, which may be baneful to biological systems [34, 35].

Fortunately, bifurcation control is a valid tool for the amelioration of the stability of delayed prey-predator systems [36, 37]. The dominant job in respect of bifurcation control is to hatch up a controller to modify the bifurcation dynamical behaviors in existence, therefore procure some expectant dynamical properties for a specific complex system [38]. The delayed feedback control strategy is considered as a useful tool to suppress bifurcation dynamics on account of its forte that the equilibrium points of the original system are unchangeable, and there is a large number of excellent results on it [39–44]. In [42], the bifurcation inception of a delayed prey-predator was efficaciously postponed by designing a linear delayed feedback control tool. In [43], the authors took account of an extended delay feedback controller and discovered that chaos is scarcely observed under the large extended feedback delay. In [44], the authors worked out an extended delayed feedback scheme for a fractional Lotka–Volterra system and found that the Hopf bifurcation of an uncontrolled system can be effectively suppressed by tinkering up extended feedback delay and fractional order. Up to this date, there are few outcomes on bifurcation control for fractional predator-prey systems with dispersal and gestation delay based on extended delayed feedback tool.

Propelled by the aforesaid discussions, we shall conduct fractional modeling and theoretical analysis for a predator-prey model with dispersal and gestation delay by utilizing an extended feedback scheme in this paper. The luminescent spot of this paper reads as follows: (1) The generalization of delayed feedback control strategy is devised to address the bifurcation control problem in a fractional delayed predator-prey model with dispersal. (2) The contributions of dispersal rates on the uncontrolled system are discussed. (3) The joint effects of feedback gain and feedback delay on the controlled system are investigated. (4) The bifurcation value can be apparently very large if we single out opposite feedback gain and extended feedback delay.

The structure of this paper is arranged as follows. Some basic definitions with regard to fractional calculus are procured in Sect. 2. The mathematical model is formulated in Sect. 3. The predominant results are presented in Sect. 4. The veracity and excellent feature of the proposed control plot are conformed by the aid of simulations in Sect. 5. Finally, to generalize our work, a conclusion is given.

2 Basic definition

The basic definitions about fractional-order integral, Caputo derivative, and the equilibrium of fractional-order system are shown in this section. This paper is based upon the Caputo derivative.

Definition 2.1

([14])

Define the fractional-order integral for a function \(f(x)\)

$$ _{C}I^{-\kappa }_{t_{0},t}f(t)=\frac{1}{\varGamma (\kappa )} \int _{t_{0}}^{t}(t- \vartheta )^{\kappa -1}f( \vartheta )\,\mathrm{d}\vartheta, $$

where \(\kappa >0\) is the noninteger order, \(\varGamma (s)=\int _{0}^{ \infty }t^{s-1}{\mathrm{e}}^{-t}{\,\mathrm{d}}s\).

Definition 2.2

([14])

Define the Caputo fractional-order derivative

$$ _{C}D^{\kappa }_{t_{0},t}f(t)=\frac{1}{\varGamma (m-\kappa )} \int _{t_{0}}^{t}(t- \vartheta )^{m-\kappa -1}f^{(m)}( \vartheta )\,\mathrm{d}\vartheta, $$

where \(m-1\leq \kappa < m\in Z^{+}\).

Especially, when \(0<\kappa \leq 1\), \({}_{C}D^{\kappa }_{t_{0},t}f(t)=\frac{1}{\varGamma (m-\kappa )}\int _{t_{0}}^{t}(t- \vartheta )^{\kappa }f'(\vartheta )\,\mathrm{d}\vartheta \).

For the sake of simplicity, \(D^{\kappa }f(t)\) stands for \({}_{C}D^{\kappa }_{0,t}f(t)\) and suppose \(0<\kappa \leq 1\). Based on [15], the definition of equilibrium points for the n-dimension fractional-order equations is presented.

Definition 2.3

For the following system

$$ D^{\kappa }x_{i}(t)=f_{i}\bigl(x_{i}(t) \bigr),\quad i=1,2,\ldots, n, $$

where \(x_{i}(t)=(x_{1}(t),x_{2}(t),\ldots,x_{n}(t)), f_{i}(t)=(f_{1}(t),f_{2}(t), \ldots,f_{n}(t))\). The equilibria are defined by \(f_{i}(x_{i}^{*})=0\), and the equilibria can be obtained \((x_{1}^{*},x_{2}^{*},\ldots,x_{n}^{*})\).

3 Model formulation

Kuang and Takeuchi put forward the following predator-prey model of prey dispersal [22]:

$$ \textstyle\begin{cases} \dot{P}_{1}(t)=P_{1}(t)(r_{1}-k_{1}P_{1}(t)-\alpha _{1}N(t))+ \varepsilon (P_{2}(t)-P_{1}(t)), \\ \dot{P}_{2}(t)=P_{2}(t)(r_{2}-k_{2}P_{2}(t)-\alpha _{2}N(t))+ \varepsilon (P_{1}(t)-P_{2}(t)), \\ \dot{N}(t)=N(t)(-s-\delta N(t)+c_{1}P_{1}(t)+c_{2}P_{2}(t)), \end{cases} $$
(1)

where \(P_{i}(t)\) represents the density of prey in the ith patch at time t, \(i=1,2\). \(N(t)\) stands for the density of predator at time t. ε is the dispersal rate. The authors found that if \(\alpha _{2}=c_{2}=0\), system (1) has a global stable equilibrium if it exists.

Having noted that to explore the information of equilibrium for system (1) is an arduous task, Zheng and Song consider the following Lotka–Volterra model with gestation delay and different dispersal rates [30]:

$$ \textstyle\begin{cases} \dot{P}_{1}(t)=r_{1}P_{1}(t)(1-P_{1}(t)-N(t))+D_{1}(P_{2}(t)-P_{1}(t)), \\ \dot{P}_{2}(t)=r_{2}P_{2}(t)(1-P_{2}(t)-N(t))+D_{2}(P_{1}(t)-P_{2}(t)), \\ \dot{N}(t)=-r_{3}N(t)+c_{1} P_{1}(t-\tau )N(t-\tau )+c_{2} P_{2}(t-\tau )N(t-\tau ), \end{cases} $$
(2)

where τ is gestation delay. Zheng and Song discovered that the introduction of gestation delay makes system (2) undergo Hopf bifurcation under certain conditions.

The influence of memory is considered by integrating system (2) with the Caputo fractional derivative and ultimately the model can be obtained:

$$\begin{aligned} \textstyle\begin{cases} D^{\kappa _{1}}P_{1}(t)=r_{1}P_{1}(t)(1-P_{1}(t)-N(t))+D_{1}(P_{2}(t)-P_{1}(t)), \\ D^{\kappa _{2}}P_{2}(t)=r_{2}P_{2}(t)(1-P_{2}(t)-N(t))+D_{2}(P_{1}(t)-P_{2}(t)), \\ D^{\kappa _{3}}N(t)=-r_{3}N(t)+c_{1} P_{1}(t-\tau )N(t- \tau )+c_{2} P_{2}(t-\tau )N(t-\tau ), \end{cases}\displaystyle \end{aligned}$$
(3)

where \(\kappa _{i}\in (0,1]\) is fractional order.

To postpone the onset of bifurcation value, an extended delayed feedback controller is introduced.

$$\begin{aligned} \textstyle\begin{cases} D^{\kappa _{1}}P_{1}(t)=r_{1}P_{1}(t)(1-P_{1}(t)-N(t))+D_{1}(P_{2}(t)-P_{1}(t)), \\ D^{\kappa _{2}}P_{2}(t)=r_{2}P_{2}(t)(1-P_{2}(t)-N(t))+D_{2}(P_{1}(t)-P_{2}(t)), \\ D^{\kappa _{3}}N(t)=-r_{3}N(t)+c_{1} P_{1}(t-\tau )N(t- \tau )+c_{2} P_{2}(t-\tau )N(t-\tau ) \\ \phantom{D^{\kappa _{3}}N(t)=}{} +k(N(t)-N(t-\sigma )). \end{cases}\displaystyle \end{aligned}$$
(4)

Remark 1

\(k<0\) is the feedback gain and \(\sigma >0\) is the extended feedback delay. The introduction of such a controller can make sure that the original equilibria are preserved and the control of feedback strategy will vanish once the steady state is reached and stabilization is achieved [39, 41]. In the field of ecological control, with the aim of enhancing the stability performance, we may harvest or release predator on the basis of past data(the time unit is σ) [42, 44].

4 Major results

4.1 Delay-stimulated bifurcation conditions of uncontrolled system (3)

In this subsection, the criteria of Hopf bifurcation with respect to system (3) are explored by selecting gestation delay as a bifurcation parameter.

By virtue of the ecological balance, we just consider the equilibrium point of three species coexistence. The positive equilibrium \(E^{\dagger }(P_{1}^{*},P_{2}^{*},N^{*})\) can be obtained, where \(P_{1}^{*}=P_{2}^{*}= \frac{r_{3}}{c_{1}+c_{2}}\) and \(N^{*}=\frac{c_{1}+c_{2}-r_{3}}{c_{1}+c_{2}}\) if \(c_{1}+c_{2}-r_{3}>0\).

The linear transformation of system (3) is firstly performed in order to acquire the main results. Taking advantage of the transformation \(x_{1}(t)=P_{1}(t)-P_{1}^{*}, x_{2}(t)=P_{2}(t)-P_{2}^{*}, y(t)=N(t)-N^{*}\), then system (3) can be obtained as follows:

$$\begin{aligned} \textstyle\begin{cases} D^{\kappa _{1}}x_{1}(t)=(-D_{1}-r_{1}P_{1}^{*})x_{1}(t)+D_{1}x_{2}(t)-r_{1}P_{1}^{*}y(t)-r_{1}x_{1}^{2}(t)-r_{1}x_{1}(t)y(t), \\ D^{\kappa _{2}}x_{2}(t)=D_{2}x_{1}(t)-(D_{2}+r_{2}P_{2}^{*})x_{2}(t)-r_{2}P_{2}^{*}y(t)-r_{2}x_{2}^{2}(t)-r_{2}x_{2}(t)y(t), \\ D^{\kappa _{3}}y(t)=c_{1}N^{*}x_{1}(t-\tau )+c_{2}N^{*}x_{2}(t- \tau )-r_{3}[y(t)-y(t-\tau )] \\ \phantom{D^{\kappa _{3}}y(t)=}{} +c_{1}x_{1}(t-\tau )y(t-\tau )+c_{2}x_{2}(t-\tau )y(t- \tau ). \end{cases}\displaystyle \end{aligned}$$
(5)

From system (5), one can get

$$\begin{aligned} \textstyle\begin{cases} D^{\kappa _{1}}x_{1}=q_{11}x_{1}(t)+q_{12}x_{2}(t)+q_{13} y(t), \\ D^{\kappa _{2}}x_{2}=q_{21}x_{1}(t)+q_{22}x_{2}(t)+q_{23} y(t), \\ D^{\kappa _{3}}y=q_{31}x_{1}(t-\tau )+q_{32}x_{2}(t- \tau )+q_{33} [y(t)-y(t-\tau )], \end{cases}\displaystyle \end{aligned}$$
(6)

where

$$\begin{aligned} &q_{11}=-D_{1}-r_{1}P_{1}^{*},\qquad q_{12}=D_{1}, \qquad q_{13}=-r_{1} P_{1}^{*}, \\ &q_{21}=D_{2}, \qquad q_{22}=-D_{2}-r_{2}P_{2}^{*},\qquad q_{23}=-r_{2} P_{2}^{*}, \\ &q_{31}=c_{1} N^{*},\qquad q_{32}=c_{2} N^{*}, \qquad q_{33}=-r_{3}. \end{aligned}$$

The characteristic equation of system (6) can be acquired

$$ \begin{vmatrix} s^{\kappa _{1}}-q_{11} &-q_{12}&-q_{13} \\ -q_{21} & s^{\kappa _{2}}-q_{22}&-q_{23} \\ -q_{31}{\mathrm{e}}^{-s \tau } &-q_{32}{ \mathrm{e}}^{-s \tau } & s^{\kappa _{3}}-q_{33} \bigl(1-\mathrm{e}^{-s \tau }\bigr) \end{vmatrix}=0. $$
(7)

Equation (7) can be rewritten as

$$ \hbar _{1}( s)+\hbar _{2} ( s) \mathrm{e}^{- s\tau }=0, $$
(8)

where

$$\begin{aligned} \hbar _{1}(s)={}&s ^{\kappa _{1}+\kappa _{2}+\kappa _{3}}-q_{33}s^{ \kappa _{1}+\kappa _{2}}-q_{22}s ^{\kappa _{1}+\kappa _{3}}-q_{11}s^{ \kappa _{2}+\kappa _{3}}+q_{22}q_{33}s^{\kappa _{1}}+q_{11}q_{33}s ^{ \kappa _{2}}+q_{11}q_{22}s ^{\kappa _{3}} \\ &{} -q_{12}q_{21}s^{\kappa _{3}} -q_{11}q_{22}q_{33}+q_{12}q_{21}q_{33}, \\ \hbar _{2}(s)={}&q_{33}s^{\kappa _{1}+\kappa _{2}}-(q_{22}q_{33}+q_{23}q_{32})s^{ \kappa _{1}}-(q_{11}q_{33}+q_{13}q_{31})s^{\kappa _{2}}+q_{11}q_{22}q_{33}+q_{11}q_{23}q_{32} \\ & {}+q_{13}q_{22}q_{31}-(q_{12} q_{21}q_{33}+q_{12}q_{31}q_{23}+q_{13}q_{21}q_{32}). \end{aligned}$$

If \(s=w(\cos \frac{\pi }{2}+i \sin \frac{\pi }{2})\), \(w>0\) is a root of Eq. (8), then

$$\begin{aligned} \textstyle\begin{cases} B_{2} \cos w\tau +Q_{2} \sin w\tau =-B_{1}, \\ Q_{2}\cos w\tau -B_{2} \sin w\tau =-Q_{1}, \end{cases}\displaystyle \end{aligned}$$
(9)

where \(B_{i},Q_{i}\) are the real and imaginary parts of \(\hbar _{i}(s)\).

Equation (9) connotes that

$$\begin{aligned} \textstyle\begin{cases} \cos w\tau =- \frac{B_{1}B_{2}+Q_{1}Q_{2}}{B_{2}^{2}+Q_{2}^{2}}=G_{1}(w), \\ \sin w\tau = \frac{B_{2}Q_{1}-B_{1}Q_{2}}{B_{2}^{2}+Q_{2}^{2}}=G_{2}(w). \end{cases}\displaystyle \end{aligned}$$
(10)

It is unambiguous that

$$ G_{1}^{2}(w)+G_{2}^{2}(w)=1. $$
(11)

From \(\cos w\tau =G_{1}(w)\), we have

$$ \tau ^{(p)}=\frac{1}{w}\bigl[\mathrm{arc} \cos G_{1}(w)+2p\pi \bigr],\quad p=0,1,2,\ldots. $$
(12)

We hypothesize that Eq. (11) has not less than one nonnegative real root. The bifurcation value can be defined as

$$ \tau _{0}=\min \bigl\{ \tau ^{(p)}\bigr\} , \quad p=0,1,2,\ldots, $$
(13)

where \(\tau ^{(p)}\) is defined by (12).

To present primary results, the following assumption is indispensable:

  1. (A1)

    \(\frac{R_{1}T_{1}+R_{2}T_{2}}{T_{1}^{2}+T_{2}^{2}}\neq 0\), where \(R_{i},T_{i}, i=1,2\), are given in Eq. (15), respectively.

Lemma 4.1

Let\(s (\tau )=\varLambda (\tau )+iw(\tau )\)be the root of Eq. (8) near\(\tau =\tau _{j}\)satisfying\(\varLambda (\tau _{j})=0,w(\tau _{j})=w_{0}\)and (A1) holds, then the transversality condition is apparent

$$ \operatorname{Re} \biggl[\frac{\mathrm{d}s}{\mathrm{d}\tau } \biggr]\bigg|_{( \tau =\tau _{0},w=w_{0})}\neq 0. $$

Proof

Differentiating Eq. (8) with regard to τ, an uncomplicated calculation gives that

$$ \hbar ^{\prime }_{1}(s)\frac{\mathrm{d}s}{\mathrm{d}\tau }+\hbar ^{\prime }_{2}(s){ \mathrm{e}}^{-s \tau }\frac{\mathrm{d}s}{\mathrm{d}\tau }+ \hbar _{2}(s)\mathrm{e}^{-s \tau } \biggl(-\tau \frac{\mathrm{d}s}{\mathrm{d}\tau }-s \biggr)=0, $$

where \(\hbar ^{\prime }_{i}(s)\) are the derivatives of \(\hbar _{i}(s)\ (i=1,2)\). Hence

$$ \frac{\mathrm{d}s}{\mathrm{d}\tau }=\frac{R(s)}{T(s)}, $$
(14)

where

$$\begin{aligned} T(s)={}&(\kappa _{1}+\kappa _{2}+ \kappa _{3})s ^{\kappa _{1}+ \kappa _{2}+\kappa _{3}-1}-q_{33}(\kappa _{1}+ \kappa _{2})s ^{\kappa _{1}+ \kappa _{2}-1}-q_{22}(\kappa _{1}+ \kappa _{3})s ^{\kappa _{1}+\kappa _{3}-1} \\ &{}-q_{11}(\kappa _{2}+\kappa _{3})s^{\kappa _{2}+\kappa _{3}-1}+q_{22}q_{33} \kappa _{1}s^{\kappa _{1}-1}+q_{11}q_{33}\kappa _{2}s^{\kappa _{2}-1}+q_{11}q_{22} \kappa _{3}s^{\kappa _{3}-1} \\ &{}-q_{12}q_{21}\kappa _{3}s^{\kappa _{3}-1}+ \bigl[q_{33}(\kappa _{1}+ \kappa _{2})s^{\kappa _{1}+\kappa _{2}-1}-(q_{22}q_{33}+q_{23}q_{32}) \kappa _{1}s^{\kappa _{1}-1} \\ &{}-(q_{11}q_{33}+q_{13}q_{31})\kappa _{2}s^{\kappa _{2}-1} \bigr]{\mathrm{e}}^{-s \tau }- \bigl[q_{33}s ^{\kappa _{1}+\kappa _{2}}-(q_{22}q_{33}+q_{23}q_{32})s ^{\kappa _{1}} \\ &{}-(q_{11}q_{33}+q_{13}q_{31})s ^{\kappa _{2}}+q_{11}q_{22}q_{33}+q_{11}q_{23}q_{32}+q_{13}q_{22}q_{31}-(q_{12}q_{21}q_{33} \\ &{}+q_{12}q_{31}q_{23}+q_{13}q_{21}q_{32}) \bigr]\tau {\mathrm{e}}^{-s \tau }, \\ R(s)={}& \bigl[q_{33}s ^{\kappa _{1}+\kappa _{2}}-(q_{22}q_{33}+q_{23}q_{32})s ^{\kappa _{1}}-(q_{11}q_{33}+q_{13}q_{31})s^{\kappa _{2}}+q_{11}q_{22}q_{33}+q_{11}q_{23}q_{32} \\ &{}+q_{13}q_{22}q_{31}-(q_{12}q_{21}q_{33}+q_{12}q_{31}q_{23}+q_{13}q_{21}q_{32}) \bigr]s \mathrm{e}^{-s \tau }. \end{aligned}$$

By simple computation, it can be derived from Eq. (14) that

$$ \operatorname{Re}\biggl[\frac{\mathrm{d}s}{\mathrm{d}\tau }\biggr]\bigg|_{(\tau = \tau _{0},w=w_{0})}= \frac{R_{1}T_{1}+R_{2}T_{2}}{T_{1}^{2}+T_{2}^{2}} \neq 0, $$
(15)

where the real and imaginary parts of \(R(s)\) are \(R_{1}, R_{2}\), the real and imaginary parts of \(T(s)\) are \(T_{1}, T_{2}\).

Assumption (A1) indicates that the transversality condition is matched. □

To explore the stability of system (3) when \(\tau =0\), the following assumption is essential:

  1. (A2)

    \(c_{1}+c_{2}>r_{3}\) and \(D_{i}\geq c_{i}\ (i=1,2)\).

Lemma 4.2

If (A2) meets, \(E^{\dagger }\)of uncontrolled system (3) is asymptotically stable when\(\tau =0\).

Proof

If there is no delay and \(\kappa _{1}=\kappa _{2}=\kappa _{3}=1\), Eq. (8) develops into

$$ s^{3}+\rho _{0}s^{2}+\rho _{1}s+\rho _{2}=0, $$
(16)

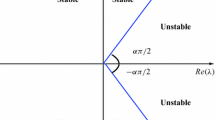
where \(\rho _{0}=D_{1}+D_{2}+r_{1}P^{*}_{1}+r_{2}P^{*}_{2}>0\), \(\rho _{1}=(r_{1}D_{2}+r_{2}D_{1})P^{*}_{1}+r_{1}r_{2}{P^{*}_{1}}^{2}+(r_{1}c_{1}+r_{2}c_{2})P^{*}_{1}N^{*}>0\) and \(\rho _{2}=(c_{1}+c_{2})(r_{1}r_{2}P^{*}_{1}+r_{1}D_{2}+r_{2}D_{1})P^{*}_{1}N^{*}>0\). When assumption (A2) holds, the eigenvalues of characteristic Eq. (16) are negative real parts on the principle of Routh–Hurwitz criterion. Obviously, condition (A2) is just sufficient for conformation of \(\mid \arg (s)\mid > \kappa _{i}\frac{\pi }{2}, i=1,2,3\) [41, 45]. Therefore, \(E^{\dagger }\) of system (3) is asymptotically stable. □

In view of Lemmas 4.1–4.2, the following theorem is derived.

Theorem 4.3

Hypothesize that (A1)–(A2) are met, then

  1. (i)

    The positive equilibrium\(E^{\dagger }\)of uncontrolled system (3) is asymptotically stable if\(\tau \in [0,\tau _{0})\);

  2. (ii)

    System (3) undergoes a Hopf bifurcation when\(\tau =\tau _{0}\).

4.2 Dynamical behaviors of controlled system (4)

In this subsection, the problem of bifurcation control for system (3) is explored by designing an extended delay feedback controller.

System (4) possesses a three-species equilibrium \(E^{\dagger }(P_{1}^{*},P_{2}^{*},N^{*})\). The transformation \(v_{1}(t)=P_{1}(t)-P_{1}^{*}, v_{2}(t)=P_{2}(t)-P_{2}^{*}, v_{3}(t)=N(t)-N^{*}\) is carried out, then the linear equation of system (4) is

$$\begin{aligned} \textstyle\begin{cases} D^{\kappa _{1}}v_{1}=a_{11}v_{1}(t)+a_{12}v_{2}(t)+a_{13} v_{3}(t), \\ D^{\kappa _{2}}v_{2}=a_{21}v_{1}(t)+a_{22}v_{2}(t)+a_{23} v_{3}(t), \\ D^{\kappa _{3}}v_{3}=a_{31}v_{1}(t-\tau )+a_{32}v_{2}(t- \tau )+a_{33} [v_{3}(t)-v_{3}(t-\tau )] \\ \phantom{D^{\kappa _{3}}v_{3}=}{}+k(v_{3}(t)-v_{3}(t-\sigma )), \end{cases}\displaystyle \end{aligned}$$
(17)

where

$$\begin{aligned} &a_{11}=-D_{1}-r_{1}P_{1}^{*},\qquad a_{12}=D_{1},\qquad a_{13}=-r_{1} P_{1}^{*}, \\ &a_{21}=D_{2}, \qquad a_{22}=-D_{2}-r_{2}P_{2}^{*},\qquad a_{23}=-r_{2} P_{2}^{*}, \\ &a_{31}=c_{1} N^{*}, \qquad a_{32}=c_{2} N^{*}, \qquad a_{33}=-r_{3}. \end{aligned}$$

The relevant characteristic equation for system (17) can be shown as follows:

$$ \begin{vmatrix} s^{\kappa _{1}}-a_{11} &-a_{12}&-a_{13} \\ -a_{21} & s^{\kappa _{2}}-a_{22}&-a_{23} \\ -a_{31}{\mathrm{e}}^{-s \tau } &-a_{32}{ \mathrm{e}}^{-s \tau } & s^{\kappa _{3}}-a_{33} \bigl(1-\mathrm{e}^{-s \tau }\bigr)-k\bigl(1-\mathrm{e}^{-s \sigma }\bigr) \end{vmatrix}=0. $$
(18)

That is,

$$ \varXi _{1}( s)+\varXi _{2} ( s) \mathrm{e}^{- s\tau }=0, $$
(19)

where

$$\begin{aligned} \varXi _{1}(s)={}&s ^{\kappa _{1}+\kappa _{2}+\kappa _{3}}-a_{33}s^{ \kappa _{1}+\kappa _{2}}-a_{22}s ^{\kappa _{1}+\kappa _{3}}-a_{11}s^{ \kappa _{2}+\kappa _{3}}+a_{22}a_{33}s^{\kappa _{1}}+a_{11}a_{33}s ^{ \kappa _{2}}+a_{11}a_{22}s ^{\kappa _{3}} \\ &{} -a_{12}a_{21}s^{\kappa _{3}} -a_{11}a_{22}a_{33}+a_{12}a_{21}a_{33}+k \bigl({ \mathrm{e}}^{-s \sigma }-1\bigr)\\ &{}\times\bigl[s^{\kappa _{1}+\kappa _{2}}-a_{22}s ^{\kappa _{1}} -a_{11}s ^{\kappa _{2}}+a_{11}a_{22} -a_{12}a_{21}\bigr], \\ \varXi _{2}(s)={}&a_{33}s^{\kappa _{1}+\kappa _{2}}-(a_{22}a_{33}+a_{23}a_{32})s^{ \kappa _{1}}-(a_{11}a_{33}+a_{13}a_{31})s^{\kappa _{2}}+a_{11}a_{22}a_{33}+a_{11}a_{23}a_{32} \\ &{} +a_{13}a_{22}a_{31}-(a_{12} a_{21}a_{33}+a_{12}a_{31}a_{23}+a_{13}a_{21}a_{32}). \end{aligned}$$

On condition that \(s=\overline{w}(\cos \frac{\pi }{2}+i \sin \frac{\pi }{2})\) is a root of Eq. (19), \(\overline{w}>0\), we have

$$\begin{aligned} \textstyle\begin{cases} \varOmega _{2} \cos \overline{w}\tau + \varTheta _{2} \sin \overline{w}\tau =-\varOmega _{1}, \\ \varTheta _{2}\cos \overline{w}\tau -\varOmega _{2} \sin \overline{w}\tau =-\varTheta _{1}, \end{cases}\displaystyle \end{aligned}$$
(20)

where \(\varOmega _{i},\varTheta _{i}\) are the real and imaginary parts of \(\varXi _{i}(s)\).

Implementing Eq. (20), an easy calculation gives

$$\begin{aligned} \textstyle\begin{cases} \cos \overline{w}\tau =- \frac{\varOmega _{1}\varOmega _{2}+\varTheta _{1}\varTheta _{2}}{\varOmega _{2}^{2}+\varTheta _{2}^{2}}=f_{1}( \overline{w}), \\ \sin \overline{w}\tau = \frac{\varOmega _{2}\varTheta _{1}-\varOmega _{1}\varTheta _{2}}{\varOmega _{2}^{2}+\varTheta _{2}^{2}}=f_{2}( \overline{w}). \end{cases}\displaystyle \end{aligned}$$
(21)

According to Eq. (21), it is obvious that

$$ f_{1}^{2}(\overline{w})+f_{2}^{2}( \overline{w})=1. $$
(22)

Similarly, we can obtain

$$ \tau ^{(j)}=\frac{1}{\overline{w}}\bigl[\mathrm{arc} \cos f_{1}( \overline{w})+2j\pi \bigr],\quad j=0,1,2,\ldots. $$
(23)

Provided that Eq. (22) has not less than one real root, define the bifurcation value

$$ \tau ^{*}_{0}=\min \bigl\{ \tau ^{(j)}\bigr\} ,\quad j=0,1,2,\ldots, $$
(24)

where \(\tau ^{(j)}\) is defined by (23).

In the following, we will make a study of the stability of system (4) if \(\tau =0\). The characteristic equation (19) turns into

$$ \varUpsilon _{1} (s)+\varUpsilon _{2} (s) \mathrm{e}^{- s\sigma }=0, $$
(25)

where

$$\begin{aligned} \varUpsilon _{1}(s)={}&s^{\kappa _{1}+\kappa _{2}+\kappa _{3}}-ks^{\kappa _{1}+ \kappa _{2}}-a_{22}s^{\kappa _{1}+\kappa _{3}}-a_{11}s^{\kappa _{2}+ \kappa _{3}}+(ka_{22}-a_{23}a_{32})s^{\kappa _{1}}+(ka_{11} \\ &{} -a_{13}a_{31})s^{\kappa _{2}}+(a_{11}a_{22}-a_{12}a_{21})s^{ \kappa _{3}}-k(a_{11}a_{22}-a_{12}a_{21})+a_{11}a_{23}a_{32} \\ &{} +a_{13}a_{22}a_{31}-a_{12}a_{23}a_{31}-a_{13}a_{21}a_{32}, \\ \varUpsilon _{2}(s)={}&k\bigl(s^{\kappa _{1}+\kappa _{2}}-a_{22}s^{\kappa _{1}}-a_{11}s^{ \kappa _{2}}+a_{11}a_{22} \bigr). \end{aligned}$$

Let \(s=w^{*}(\cos \frac{\pi }{2}+i \sin \frac{\pi }{2})\) be a root of Eq. (25), \(w^{*}>0\). By substituting it into Eq. (25) and separating the imaginary part and the real part, it leads to

$$\begin{aligned} \textstyle\begin{cases} E_{2} \cos w^{*}\sigma +F_{2} \sin w^{*} \sigma =-E_{1}, \\ F_{2}\cos w^{*}\sigma -E_{2} \sin w^{*}\sigma =-F_{1}, \end{cases}\displaystyle \end{aligned}$$
(26)

where \(E_{i},F_{i}\) are the real and imaginary parts of \(\varUpsilon _{i}(s)\).

From Eq. (26), an easy calculation gives

$$\begin{aligned} \textstyle\begin{cases} \cos w^{*}\sigma =- \frac{E_{1}E_{2}+F_{1}F_{2}}{E_{2}^{2}+F_{2}^{2}}=g_{1}(w^{*}), \\ \sin w^{*}\sigma = \frac{E_{2}F_{1}-E_{1}F_{2}}{E_{2}^{2}+F_{2}^{2}}=g_{2}(w^{*}). \end{cases}\displaystyle \end{aligned}$$
(27)

It is clear that

$$ g_{1}^{2}\bigl(w^{*} \bigr)+g_{2}^{2}\bigl(w^{*}\bigr)=1. $$
(28)

Hence, it derives from \(\cos w^{*}\sigma =g_{1}(w^{*})\) that

$$ \sigma ^{(p)}=\frac{1}{w^{*}}\bigl[\mathrm{arc} \cos g_{1}\bigl(w^{*}\bigr)+2p\pi \bigr], \quad p=0,1,2, \ldots. $$
(29)

Assume that Eq. (28) has not less than one nonnegative real root. Define the bifurcation value

$$ \sigma _{0}=\min \bigl\{ \sigma ^{(p)}\bigr\} , \quad p=0,1,2,\ldots, $$
(30)

where \(\sigma ^{(p)}\) is defined by (29).

Making an assay of the above outcome and based on the stability results in references [26, 44, 46], the following lemma can be obtained.

Lemma 4.4

For system (4), if (A2) holds, the following results can be derived:

  1. (1)

    If\(\tau =\sigma =0\)or\(\tau =0\)and Eq. (28) has no nonnegative real root, then\(E^{\dagger }\)of system (4) is asymptotically stable;

  2. (2)

    If\(\tau =0, \sigma \in [0,\sigma _{0})\), then\(E^{\dagger }\)of system (4) is locally stable.

To obtain the main conclusions, it is essential to give the following assumption:

  1. (A3)

    \(\frac{\mathfrak{R}_{1}\mathfrak{T}_{1}+\mathfrak{R}_{2}\mathfrak{T}_{2}}{\mathfrak{T}_{1}^{2}+\mathfrak{T}_{2}^{2}} \neq 0\), where \(\mathfrak{R}_{i},\mathfrak{T}_{i}, i=1,2\), are defined in Eq. (33), respectively.

Lemma 4.5

If\(s (\tau )=\varGamma (\tau )+iw(\tau )\)is the root of Eq. (19) near\(\tau =\tau _{j}\)meeting\(\varGamma (\tau _{j})=0,w(\tau _{j})=\overline{w}_{0}\), then the transversality condition holds

$$ \operatorname{Re} \biggl[\frac{\mathrm{d}s}{\mathrm{d}\tau } \biggr]\bigg|_{( \tau =\tau ^{*}_{0},w=\overline{w}_{0})}\neq 0. $$

Proof

Differentiating Eq. (19) with regard to τ, a simple calculation gives that

$$ \varXi ^{\prime }_{1}(s)\frac{\mathrm{d}s}{\mathrm{d}\tau }+\varXi ^{\prime }_{2}(s){ \mathrm{e}}^{-s \tau }\frac{\mathrm{d}s}{\mathrm{d}\tau }+ \varXi _{2}(s)\mathrm{e}^{-s \tau } \biggl(-\tau \frac{\mathrm{d}s}{\mathrm{d}\tau }-s \biggr)=0, $$

where \(\varXi ^{\prime }_{i}(s)\) are the derivatives of \(\varXi _{i}(s)\ (i=1,2)\). Hence

$$ \frac{\mathrm{d}s}{\mathrm{d}\tau }= \frac{\mathfrak{R}(s)}{\mathfrak{T}(s)}. $$
(31)

By careful computation, Eq. (31) implies that

$$ \operatorname{Re}\biggl[\frac{\mathrm{d}s}{\mathrm{d}\tau }\biggr]\bigg|_{(\tau = \tau ^{*}_{0},w=\overline{w}_{0})}= \frac{\mathfrak{R}_{1}\mathfrak{T}_{1}+\mathfrak{R}_{2}\mathfrak{T}_{2}}{\mathfrak{T}_{1}^{2}+\mathfrak{T}_{2}^{2}} \neq 0, $$
(32)

where

$$ \begin{aligned} &\mathfrak{R}_{1}=w( \mathrm{Re} \varXi _{2} \sin w\tau - \mathrm{Im} \varXi _{2} \cos w\tau ), \\ &\mathfrak{R}_{2}=w(\mathrm{Re} \varXi _{2} \cos w\tau + \mathrm{Im} \varXi _{2} \sin w\tau ), \\ &\mathfrak{T}_{1}=\mathrm{Re} \varXi '_{1} + \mathrm{Re} \varXi '_{2} \cos w\tau +{ \mathrm{Im}} \varXi '_{2} \sin w\tau +\tau (\mathrm{Re} \varXi _{2} \cos w\tau +{ \mathrm{Im}} \varXi _{2} \sin w\tau ), \\ &\mathfrak{T}_{2}=\mathrm{Im} \varXi '_{1} + \mathrm{Im}\varXi '_{2} \cos w\tau -{ \mathrm{Re}} \varXi '_{2} \sin w\tau +\tau (\mathrm{Im} \varXi _{2} \cos w\tau -{ \mathrm{Re}} \varXi _{2} \sin w\tau ). \end{aligned} $$
(33)

Ostensibly, assumption (A3) indicates that the transversality condition is matched. □

In terms of the previous analysis, the following theorem can be obtained.

Theorem 4.6

On the assumption that (A2), (A3) hold, for controlled model (4), the following results can be derived:

  1. (1)

    If\(\tau =\sigma =0\), then\(E^{\dagger }\)of controlled system (4) is asymptotically stable.

  2. (2)

    Ifσmeets the conditions of Theorem 4.4, then controlled model (4) exhibits a Hopf bifurcation when\(\tau =\tau ^{*}_{0}\).

Remark 2

Compared with [19, 21], we construct the model with incommensurate fractional order since the memory related to various states can be not the same [47].

Remark 3

If \(k=0\) and \(\sigma =0\), system (4) degenerates into the uncontrolled one (3). The controller designed in this paper has an excellent feature as distinguished from the conventional delayed feedback controller in [41, 42], since the choice of feedback delay is agile.

Remark 4

In contrast to results in [33], we assume that the dispersal coefficients are different and the joint effects of dispersal rates on the bifurcation value are discussed by simulations.

Remark 5

The extended delayed feedback strategy was firstly put forward to postpone the inception of the delayed Lotka–Volterra system by changing fractional-order and feedback delay [44]. Nevertheless, the effects of feedback gain on the bifurcation value were not discussed. In this paper, the joint influence of feedback gain and extended feedback delay on the bifurcation point is under consideration.

5 Numerical simulations

Two numerical cases are implemented to validate the exactitude of our work in this section.

5.1 Simulation 1

Time delay is chosen to investigate the stability and bifurcation of (3). We suppose that \(r_{1}=0.7, r_{2}=0.9, c_{1}=0.6, c_{2}=0.4, r_{3}=0.2, D_{1}=0.7, D_{2}=0.8\), then system (3) can be written as

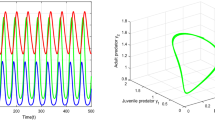
$$ \textstyle\begin{cases} D^{\kappa _{1}}P_{1}(t)=0.7P_{1}(t)(1-P_{1}(t)-N(t))+0.7(P_{2}(t)-P_{1}(t)), \\ D^{\kappa _{2}}P_{2}(t)=0.9P_{2}(t)(1-P_{2}(t)-N(t))+0.8(P_{1}(t)-P_{2}(t)), \\ D^{\kappa _{3}}N(t)=-0.2N(t)+0.6 P_{1}(t-\tau )N(t- \tau )+0.4 P_{2}(t-\tau )N(t-\tau ). \end{cases} $$
(34)

When \(\kappa _{1}=1,\kappa _{2}=1,\kappa _{3}=1\), it is not hard to find that the positive equilibrium point \(E^{\dagger }(P_{1}^{*},P_{2}^{*},N^{*})=(0.2,0.2,0.8)\). The critical \(w_{0}^{I}=0.2794\) and the bifurcation value \(\tau _{0}^{I}=2.1571\) can be calculated. When \(\kappa _{1}=0.97,\kappa _{2}=0.98,\kappa _{3}=0.99\), we can get \(w_{0}=0.2670, \tau _{0}=2.5675\), which indicates that the stability zone is expanded. We can obtain that \(E^{\dagger }\) is asymptotically stable when \(\tau =2<\tau _{0}\), which is shown in Fig. 1, while \(E^{\dagger }\) is unstable when \(\tau =2.7>\tau _{0}\), as is displayed in Fig. 2, initial point: \(E_{0}(P_{1}(0),P_{2}(0),N(0))=(0.17,0.53,0.49)\) according to Theorem 4.3. Next, we will explore the impact of dispersal rates \(D_{1}, D_{2}\) on the bifurcation value \(\tau _{0}\). We first assume that \(D_{1}=0.7\) or \(D_{2}=0.8\) is fixed and let another vary, which is demonstrated in Fig. 3. Furthermore, the joint effects of dispersal rates \(D_{1}, D_{2}\) are discussed, which is shown in Fig. 4. The results state clearly that if \(D_{2}\) is big and \(D_{1}\) is small, \(\tau _{0}\) is big.

Figure 1
figure 1

\(E^{\dagger }\) of system (34) is stable by choosing \(\tau =2.0<\tau _{0}=2.5302\)

Full size image
Figure 2
figure 2

\(E^{\dagger }\) of system (34) is unstable by choosing \(\tau =2.7>\tau _{0}=2.5302\)

Full size image
Figure 3
figure 3

The impact of dispersal rate \(D_{1}\) or \(D_{2}\) on \(\tau _{0}\)

Full size image
Figure 4
figure 4

The joint effects of dispersal rates \(D_{1}, D_{2}\) on \(\tau _{0}\)

Full size image

5.2 Simulation 2

To suppress the Hopf bifurcation of uncontrolled system (34), an extended feedback controller is introduced. Assume that \(k \in [-1,-0.1]\) and \(\sigma \in (0,5]\), then the system is given by

$$\begin{aligned} \textstyle\begin{cases} D^{0.97}P_{1}(t)=0.7P_{1}(t)(1-P_{1}(t)-N(t))+0.7(P_{2}(t)-P_{1}(t)), \\ D^{0.98}P_{2}(t)=0.9P_{2}(t)(1-P_{2}(t)-N(t))+0.8(P_{1}(t)-P_{2}(t)), \\ D^{0.99}N(t)=-0.2N(t)+0.6 P_{1}(t-\tau )N(t-\tau )+0.4 P_{2}(t- \tau )N(t-\tau ) \\ \phantom{D^{0.99}N(t)=}{} +k(N(t)-N(t-\sigma )). \end{cases}\displaystyle \end{aligned}$$
(35)

It is obvious that system (34) is unstable if \(\tau =8\). To postpone the bifurcation onset of system (34), we choose \(k=-0.7, \sigma =4\) and obtain \(\overline{w}_{0}=0.1077\) and \(\tau ^{*}_{0}=11.8375\), which means that stability performance of system (34) is ameliorated, which is shown in Fig. 5. Next, we made efforts to probe into the impact of σ and k on the bifurcation value. We first assume that \(k=-0.7\) or \(\sigma =4\) is established, and let another change, which is demonstrated in Figs. 6–7. Moreover, the joint effects of feedback gain k and feedback delay σ are studied, which is shown in Fig. 8. By careful computation, we find that when k decreases or σ increases, Hopf bifurcation engenders behind of time. Figures 9–10 validate the rightness of the theory.

Figure 5
figure 5

\(E^{\dagger }\) of system (35) is stable when \(\tau =8, k=-0.7,\sigma =4\)

Full size image
Figure 6
figure 6

The influence of feedback gain k on \(\tau ^{*}_{0}\)

Full size image
Figure 7
figure 7

The impact of feedback delay σ on \(\tau ^{*}_{0}\)

Full size image
Figure 8
figure 8

The joint effects of \(\sigma, k\) on \(\tau ^{*}_{0}\)

Full size image
Figure 9
figure 9

The contribution of feedback gain k on system (35)

Full size image
Figure 10
figure 10

The effects of feedback delay σ on system (35)

Full size image

6 Conclusion

Fractional modeling and Hopf bifurcation control for a predator-prey system with prey dispersal have been studied at length in this paper. Delay-stirred bifurcation conditions are procured for the uncontrolled system. The contributions of dispersal coefficients on the bifurcation value for the uncontrolled system are also discussed. Then the problem of bifurcation control has been investigated in detail by devising an extended delay feedback controller. The results state clearly that feedback gain and feedback delay exert a prominent influence on the bifurcation value, which implies that the stability performance of the uncontrolled system can be saliently meliorated by carefully picking feedback gain and feedback delay if other coefficients are selected. As one generalization of conventional feedback control, the controller conceived in this paper gets the advantage over traditional ones since the alternative of feedback delay is agile. Finally, the results achieved in this paper have been well checked through simulations. From the perspective of biology, gestation delay can induce population oscillations of predator and prey, which means that the population of species may be at an unreasonable level. With respect to the control of a biological system, the extended delay feedback controller indicates that we release or capture predator based on past data(the time unit is σ). When the density of predator in the past is higher than that in the present, we reduce the growth rate of predator; conversely, we increase the growth rate of predator. Our results show that by increasing harvest or release intensity(smaller feedback gain k) and monitoring time(larger feedback delay σ) of predator, the population of predators and prey will tend to a constant state of peaceful coexistence, and they can survive together in the same environment. Our future work will show solicitude for the following two aspects: (1) The dispersal delay will be introduced. (2) Taking into control cost accounts, the optimization problem for delayed fractional order predator-prey model will be considered and the optimal feedback gain and feedback delay will be explored.