1 Introduction

In the last few decades, applied scientists have outstretched new models that include fractional derivatives, fractional differential equations (FDEs). The classical and modern dynamical systems modeled by FDEs in physics, engineering, signal processing, fluid mechanics, and bioengineering, manufacturing, systems engineering, and project management can be observed in the recently published book [1]. They indicated that non-integer order derivatives are very appropriate for the explanation of properties of various real materials. Also, it has been exhibited that new order-fractional models are more sufficient than previously applied order-integer ones. In [2–6], the existence and uniqueness of solutions to FDEs have been given. Besides, the authors of [7–13] have published some new results of fractional operators and their applications. In general, it is impossible to gain analytic solutions of FDEs. Therefore, we have to trust in linearization/discretization and numerical integration to attain approximate solutions, see, e.g., [6, 14–17]. Moreover, the applications of series solutions for solving some types of FDEs can be observed in [18–20].

The differentiation matrices have been extended in the last few decades. It has been demonstrated that they are a useful tool in numerical integrations [21, 22]. Those could approximate derivatives by differentiating trial or cardinal basis functions through collocation points. It is noted that these matrices are both dense and very sensitive to rounding errors.

The explicit formulas for the order-integer derivatives of Legendre approximation already exist. Moreover, the authors of [17] proposed a fractional operational matrix based on the shifted Legendre polynomials on the interval \([0,1]\). In this article, we present a numerical algorithm for computing Legendre spectral differentiation matrices of order-fractional α (LFDMs) on the interval \([0,T]\). This algorithm is based on a homogeneous three-term recurrence relation similar to the Legendre recurrence formula and is numerically stable. The proposed LFDMs are then utilized to numerically differentiate.

2 Preliminaries and definitions

First here we give some basic definitions and properties of the fractional calculus theory, the details of which can be found in [6, 23].

The Riemann–Liouville fractional integral operator of order \(\alpha\geq0\), of a function \(f(x)\) is defined as follows:

$$ D^{-\alpha}f(x)=\frac{1}{\varGamma(\alpha)} \int_{a}^{x} (x-t )^{\alpha-1} f(t)\, \mathrm{d}t,\quad x \in[a,b]. $$
(1)

Properties of the fractional integral operator can be found in [6].

The fractional derivative of \(f(x)\) in the Caputo sense is defined as follows:

$$ D^{\alpha}f(x)=\frac{1}{\varGamma(m-\alpha)} \int_{a}^{x} (x-t )^{m-\alpha-1} f^{(m)}(t)\,\mathrm{d}t, \quad x \in[a,b], $$
(2)

for \(m-1<\alpha\leq m\).

Also, we require here four of its main properties [6]:

$$\begin{aligned}& D^{\alpha}c=0,\quad c \text{ is a constant}, \end{aligned}$$
(3)
$$\begin{aligned}& D^{\alpha}x^{\beta}=0\quad \text{for } \beta\in \{0,1,\ldots\} \text{ and } \beta< \lceil\alpha\rceil, \end{aligned}$$
(4)
$$\begin{aligned}& D^{\alpha}x^{\beta}= \frac{\varGamma(\beta+1)}{\varGamma(\beta+1-\alpha)}x^{\beta-\alpha} \quad \text{for } \beta\in\{0,1,\ldots\} \text{ and } \beta\geq \lceil\alpha \rceil, \end{aligned}$$
(5)
$$\begin{aligned}& D^{\alpha} \bigl(\lambda f(x)+\mu g(x) \bigr)=\lambda D^{\alpha}f(x)+ \mu D^{\alpha}g(x), \end{aligned}$$
(6)

where \(\lceil\alpha\rceil\) denotes the ceiling function, the smallest integer greater than or equal to α, and λ and μ are constants.

The standard Legendre polynomials (LPs) are determined by the following three-term recurrence formula:

$$ L_{i+1}(x)=\frac{2i+1}{i+1} x L_{i}(x)-\frac{i}{i+1}L_{i-1}(x),\quad i\geq1, \quad x \in[-1,1], $$
(7)

where \(L_{0}(x)=1\) and \(L_{1}(x)=x\). Here we define the shifted Legendre polynomials \(P_{i}(x)=L_{i}(\frac{2}{T}x-1)\) on the interval \([0,T]\). Until further notice \(x\in[0,T]\) and \(x=\frac{2}{T}x-1\) (for simplicity of statements). The general form of the shifted LP of order i is given by the sum:

$$ P_{i}(x)=\sum_{k=0}^{\lfloor i/2\rfloor} \frac{(-1)^{k} (2i-2k)!}{2^{i} k! (i-k)! (i-2k)!} x^{i-2k},\quad i>0, $$
(8)

where \(\lfloor i/2\rfloor\) denotes the floor function, the largest integer less than or equal to \(i/2\).

Let \(\varLambda=(0,T)\). The set of shifted LPs is the \(L^{2}(\varLambda)\)-orthogonal system in Λ, i.e.,

$$ \int_{\varLambda} P_{i}(x)P_{j}(x)\, \mathrm{d}x= \biggl(\frac{2i+1}{T} \biggr)^{-1} \delta_{ij}, $$
(9)

where \(\delta_{ij}\) is the Kronecker symbol. Thus, for any \(v\in L^{2}(\varLambda)\), we have that

$$ v(x)=\sum_{n=0}^{\infty} \widehat{v}_{n} P_{n}(x),\quad \widehat{v}_{n}= \frac{2n+1}{T} \int_{\varLambda} v(x) P_{n}(x) \,\mathrm{d}x. $$
(10)

Here, the set of all algebraic polynomials of degree at most N, i.e., \(\pi_{N}(\varLambda)=\operatorname{span}\{P_{0},\ldots, P_{N}\}\), is denoted by \(\pi_{N}\). We consider the orthogonal projection \(\mathbf{P}_{N}:L^{2}(\varLambda)\rightarrow\pi_{N}\). For any \(v\in L^{2}(\varLambda)\), it is defined by [24]

$$ (v-\mathbf{P}_{N}v,\phi)=0 \quad \text{for any } \phi \in\pi_{N} $$
(11)

or, equivalently,

$$ \mathbf{P}_{N}v(x)=\sum _{n=0}^{N} \widehat{v}_{n} P_{n}(x). $$
(12)

A complete proof on estimating the difference between v and \(\mathbf{P}_{N}v\) is given by Guo [24]. Now from (12) we have

$$ v(x)=\sum_{k=0}^{N-1} \widehat{v}_{k}P_{k}(x)=V^{T} \varPhi(x), $$
(13)

where the shifted Legendre coefficient vector V and the shifted LP vector \(\varPhi(x)\) are given by \([\widehat{v}_{0},\ldots,\widehat{v}_{N-1}]\) and \([P_{0}(x),\ldots,P_{N-1}(x)]\), respectively. We can express by \(\frac{\mathrm{d}\varPhi(x)}{\mathrm{d}x}=D\varPhi\) the derivative of the vector \(\varPhi(x)\), where D is the \(N\times N\) sparse first order Legendre spectral differentiation matrix. The coefficients of the matrix D are given by

$$ D_{i+1,j+1}=\frac{2(2i+1)}{T},\quad i=0,1,\ldots,N-2, \quad j=i+1,i+3,\ldots,N-1. $$
(14)

3 Legendre fractional differentiation matrices

First of all, we require a set of N collocation points \(x_{0},\ldots,x_{N-1}\in[0,T]\) for computing LFDMs. In this work, we consider the Legendre–Gauss–Lobbato nodes (LGL) \(x_{k}\), \(k=0,1,\ldots,N-1\). In this case, \(x_{0}=-1\), \(x_{N-1}=1\), and \(x_{k}\), \(1\leq k \leq N-2\) are the roots of the first derivative of the standard LP of \((N-1)\) order. Since any interval \([a,b]\) may be scaled into \([-1,1]\), therefore we can obtain the LGL nodes on the desired interval.

Assume that we have the value \(v=(v(x_{0}),\ldots,v(x_{N-1}))\) and we want to approximate derivatives of order α at those points, i.e., \(v^{(\alpha)}=(v^{(\alpha)}(x_{0}),\ldots,v^{(\alpha)}(x_{N-1}))\). One scheme is to use the polynomial interpolation at the grid points \(x_{k}\) and then analytically differentiate it and evaluate these derivatives at the same points. The other scheme is to replace polynomials by linear combinations of shifted LPs. In either case, then there is a matrix \(D^{\alpha}\) such that

$$ v^{(\alpha)}=\frac{\mathrm{d}^{\alpha}v}{\mathrm{d}x^{\alpha}}=D^{ \alpha}v. $$
(15)

The concept of a collocation derivative operator based on trial basis functions is associated with a finite expansion such as

$$ v(x)\approx v_{N-1}(x)=\sum _{j=0}^{N-1}\widehat{v}_{j} \phi_{j}(x), $$
(16)

where the functions \(\phi_{j}(x)\) form a complete set of the approximating space \(\pi_{N-1}\). Here we consider \(v:[0,T]\rightarrow\mathbb{R}\) and \(\phi_{j}(x)=P_{j}(x)\), \(j=0,1,\ldots,N-1\), i.e., the shifted LPs on the interval \([0,T]\). As a result, the function \(v(x)\) can be represented in the spectral form

$$ v(x)=\sum_{k=0}^{N-1} \widehat{v}_{k}P_{k}(x),\quad x\in[0,T]. $$
(17)

Now, using Eqs. (3)–(6) in Eq. (8), we have

$$ P_{k}^{(\alpha)}(x)=0,\quad k=0,1,\ldots,\lceil \alpha\rceil-1. $$
(18)

Also, applying the above-mentioned spectral differentiation matric D, we get

$$ v '(x)=\sum_{k=0}^{N-1} \widehat{v}_{k} P'_{k}(x)=\sum _{k=0}^{N-1}( \widehat{Dv})_{k} P_{k}(x). $$
(19)

First, let us consider \(\alpha\in(0,1)\). Substituting (19) into (2), according to (6), we get

$$ D^{\alpha}v(x)=\frac{1}{\varGamma(1-\alpha)}\sum _{k=0}^{N-1}( \widehat{Dv})_{k} J_{k}(x),\quad x\in[0,T], $$
(20)

where

$$ J_{k}(x)= \int_{0}^{x}(x-t)^{-\alpha}P_{k}(t) \,\mathrm{d}t, \quad x \in[0,T]. $$
(21)

In a similar way to [25], substituting N values of \(x_{k}\), \(k=0,1,\ldots,N-1\), into (20), we can obtain the fractional derivative formulation as follows:

$$ D^{\alpha}v(x)=\frac{1}{\varGamma(1-\alpha)}JDP^{-1}v(x), $$
(22)

where D is as noted in (14) and P is the following matrix of the values of LPs \(P_{k}\), \(k=0,1,\ldots,N-1\), at the vector \(\mathbf{x}\in[0,T]\):

$$ P=\bigl[P_{0}(\eta),\ldots,P_{N-1}( \eta)\bigr], \quad \eta= \frac{2\mathbf{x}}{T}-1, \quad -1 \leq\eta\leq1, $$
(23)

which can be easily calculated based upon the recurrence formula of the standard LPs.

The remaining problem is the estimation of \(J_{k}(x_{i})\) for \(i,k=0,1,\ldots,N-1\). This can be done using a homogeneous linear recurrence relation, as we shall illustrate in the following theorem. Deriving this recurrence relation is based on the properties of LPs.

Theorem 1

The sequence\(J_{k}(x)\), \(k=0,1,\ldots,N-1\), for\(x\in[0,T]\)satisfies the following linear, homogeneous, three-term recurrence relation:

$$ \biggl[1+\frac{1-\alpha}{k+1} \biggr]J_{k+1}(x)= \frac{2k+1}{k+1} x J_{k}(x)- \biggl[\frac{k}{k+1}- \frac{1-\alpha}{k+1} \biggr]J_{k-1}(x),\quad k \geq2, $$
(24)

with starting values

$$\begin{aligned}& J_{0}(x)=\frac{x^{1-\alpha}}{1-\alpha},\qquad J_{1}(x)= \frac{px^{2-\alpha}}{(2-\alpha)(1-\alpha)}+ \frac{qx^{1-\alpha}}{1-\alpha}, \end{aligned}$$
(25)
$$\begin{aligned}& J_{2}(x)= \frac{3p^{2}x^{3-\alpha}}{(3-\alpha)(2-\alpha)(1-\alpha)}+ \frac{3pqx^{2-\alpha}}{(2-\alpha)(1-\alpha)}+\frac{1}{2} \frac{(3q^{2}-1) x^{1-\alpha}}{1-\alpha}, \end{aligned}$$
(26)

where\(p=\frac{2}{T}\)and\(q=-1\).

Proof

Let

$$ I= \int_{0}^{x}(x-t)^{-\alpha} \bigl(1-t^{2}\bigr)P'_{k}(t)\, \mathrm{d}t. $$
(27)

Using the identity

$$ \bigl(1-x^{2}\bigr)P'_{k}(x)= \frac{k(k+1)}{2k+1} \bigl[P_{k-1}(x)-P_{k+1}(x) \bigr], $$
(28)

we can write (27) in the form

$$ I=\frac{k(k+1)}{2k+1} \bigl[J_{k-1}(x)-J_{k+1}(x) \bigr]. $$
(29)

On the other hand, by means of the following properties of the Legendre polynomials

$$ P_{k+1}(x)=\frac{2k+1}{k+1} x P_{k}(x)-\frac{k}{k+1}P_{k-1}(x),\qquad (2k+1)P_{k}(x)=P'_{k+1}(x)-P'_{k-1}(x), $$
(30)

and by integration by parts of equation (27), we gain

$$ I=-\frac{k(k+1)}{1-\alpha}xJ_{k}(x)+ \frac{k(k+1)^{2}}{(2k+1)(1-\alpha)}J_{k+1}(x)+ \frac{k^{2}(k+1)}{(2k+1)(1-\alpha)}J_{k-1}(x). $$
(31)

Now, equating (29) and (31) yields the desired recurrence relation (24). The starting values can be readily calculated directly. □

In view of (22), LFDM in a physical form is given by

$$ \mathbf{D}_{p}^{\alpha}= \frac{1}{\varGamma(1-\alpha)}JDP^{-1},\quad \alpha\in(0,1), $$
(32)

and also, for a spectral form, we have

$$ \mathbf{D}_{s}^{\alpha}= \frac{1}{\varGamma(1-\alpha)}P^{-1}JD, \quad \alpha\in(0,1). $$
(33)

For the case \(\alpha>1\), LFDMs will be

$$ \mathbf{D}_{p}^{\alpha}= \frac{1}{\varGamma(1-\beta)}JD^{(r+1)}P^{-1},\qquad \mathbf{D}_{s}^{\alpha}= \frac{1}{\varGamma(1-\beta)}P^{-1}JD^{(r+1)}, \quad 0< \beta< 1, $$
(34)

where \(r=\lfloor\alpha\rfloor\) and \(\beta=\alpha-\lfloor\alpha\rfloor\).

Note that the Legendre fractional integration matrices can be derived in an analogous way. So, for \(\alpha\geq0\), the fractional integration matrices in physical and spectral forms will respectively be as follows:

$$ \mathbf{I}_{p}^{\alpha}= \frac{1}{\varGamma(\alpha)}JP^{-1} \quad \text{and}\quad \mathbf{I}_{s}^{\alpha}= \frac{1}{\varGamma(\alpha)}P^{-1}J, $$
(35)

where the matrix J can be computed from (24)–(26) with \(\alpha\rightarrow1-\alpha\).

4 Application of LFDMs

Here the results of two numerical tests are given by using Matlab 7 in double precision.

The fractional differentiation of the functions \((x+1)^{3}\) and \(e^{x}\) was selected to verify the correctness of LFDMs. That is because the fractional differentiation of those functions is given by [15]

$$ D^{\alpha}\bigl[(x+1)^{3}\bigr]= \frac{6x^{\lceil\alpha\rceil-\alpha}}{\varGamma(4-\lceil\alpha \rceil)\varGamma(\lceil\alpha\rceil-\alpha+1)} \,{}_{2}F_{1}\bigl(1, \lceil\alpha \rceil-3;\lceil\alpha\rceil-\alpha+1;-x\bigr) $$
(36)

and

$$ D^{\alpha}\bigl[e^{x}\bigr]=x^{\lceil\alpha\rceil-\alpha}E_{1,\lceil \alpha\rceil-\alpha+1}(x), $$
(37)

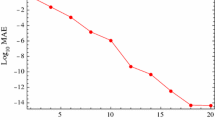
which is used to compare the outputs gained by the above-mentioned method. In the above expressions \(E_{n_{1},n_{2}}\) and \({}_{2}F_{1}\) are respectively the two-parameter Mittag-Leffler function and Gauss’s hypergeometric function. When \(\alpha=0.5, 1.5\) and \(T=1\), the absolute errors (\(\| \mathbf{D}_{p}^{\alpha}v(x)-D^{\alpha}v(x)\|_{\infty}\)) for the fractional differentiation are separately shown in Figs. 1 and 2.

Figure 1
figure 1

Accuracy of the 0.5-order Legendre spectral derivative for two functions \((x+1)^{3}\) and \(e^{x}\)

Full size image
Figure 2
figure 2

Accuracy of the 1.5-order Legendre spectral derivative for two functions \((x+1)^{3}\) and \(e^{x}\)

Full size image

Now we consider the following two examples of the fractional differentiation [26]:

$$ D^{\alpha}\bigl[(x+1)^{\alpha-1}\bigr]=- \frac{x^{1-\alpha}}{(x+1)\varGamma(1-\alpha)}, $$
(38)

and

$$ D^{\alpha}\bigl[J_{0}(2\sqrt{x}) \bigr]=x^{-\alpha/2}J_{-\alpha}(2\sqrt{x})- \frac{x^{-\alpha}}{\varGamma(1-\alpha)}, $$
(39)

where \(\alpha\in(0,1]\) and \(J_{\nu}(\cdot)\) is a Bessel function of the first kind. As before, the numerical results of the fractional differentiation for different values of α are reported in Table 1.

Table 1 Accuracy of Legendre spectral derivative of the different orders for two functions \((x+1)^{\alpha-1}\) and \(J_{0}(2\sqrt{x})\)
Full size table

5 Conclusion

Based on the shifted Legendre polynomials, we proposed an easy procedure for calculating spectral integration/differentiation matrices of the arbitrary order α. The developed algorithm is based on a three-term recurrence relation, which is numerically stable. In order to demonstrate the efficiency of the presented results, four examples of numerical differentiations were given, and the present method performed excellently. Besides, the promising results obtained in the present paper can further be used for solving fractional order problems.