Abstract
This paper studies the global stability of two discrete-time HIV infection models. The models integrate (i) latently infected cells, (ii) long-lived chronically infected cells and (iii) short-lived infected cells. The second model generalizes the first one by assuming that the incidence rate of infection as well as the production and removal rates of the HIV particles and cells are modeled by general nonlinear functions. We discretize the continuous-time models by using a nonstandard finite difference scheme. The positivity and boundedness of solutions are established. The basic reproduction number is derived. By using the Lyapunov method, we prove the global stability of the models. Numerical simulations are presented to illustrate our theoretical results.
Similar content being viewed by others
1 Introduction
Modeling and analysis of within-host human immunodeficiency virus (HIV) dynamics have received considerable attention from biologists and mathematicians during the last decades (see, e.g., [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]). The main target of the HIV is the CD4+ T cell. HIV causes the deadly disease acquired immunodeficiency syndrome (AIDS). Mathematical models of HIV dynamics are useful for describing the interaction between the host cells and HIV [2]. The basic HIV dynamics model which describes the interaction between the HIV (p), uninfected CD4+ T cells (s) and infected CD4+ T cells (z) has been proposed by Nowak and Bangham [1]. Callaway and Perelson [3] have extended the basic HIV dynamics model by taking into consideration three classes of infected cells: (i) latently infected cells (w) which cannot generate HIV particles, (ii) short-lived infected cells (z) which live for short time and generate large numbers of HIV particles, and (iii) long-lived chronically infected cells (u) which live for long time and generate small numbers of HIV particles:
where \(\bar{k}=\bar{k}_{1}+\bar{k}_{2}+\bar{k}_{3}\) represents the incidence rate constant. β represents the rate at which new CD4+ T cells are created from sources. δ is the death rate constant of the uninfected CD4+ T cells. The parameters α, d, a and c denote the death rate constants of the latently infected cells, short-lived infected cells, long-lived chronically infected cells and free HIV particles, respectively. The parameters \(N_{z}\) and \(N_{u}\) represent the average number of HIV particles produced in the lifetime of the short-lived infected cells and long-lived chronically infected cells, respectively. The term mw is the activation rate of the latently infected cells, and ϵ represents the drug efficacy, where \(0\leq \epsilon \leq 1\). This model has been extended in [10] by considering time delay. Several authors have devoted their efforts in studying the global stability of mathematical models in virology (see, e.g., [7, 16,17,18,19,20,21,22] and [24,25,26,27,28,29,30]) and epidemiology (see, e.g., [31, 32]).
Most of the HIV dynamics models presented in the literature are given by systems of nonlinear differential equations. Therefore, the exact analytical solutions of these continuous-time models are unknown. It is important to note that scientists often collect the data and analyze the results at discrete times. Further, the use of digital computers in performing numerical simulations of nonlinear systems necessitated the investigation of the discrete-time models. Consequently, a discretization can be used to obtain a discrete-time model which is an approximation of the exact solution. However, how to select a proper discrete method so that the global properties of solutions of the corresponding continuous-time models can be efficiently preserved is still an open problem [33]. The mixed Euler method which is a mixture of both forward and backward Euler methods has been used for within-host virus dynamics governed by ordinary differential equations (ODEs) in [34, 35], for delayed virus dynamics models governed by delay differential equations (DDEs) in [36]. The mixed Euler method has been utilized for virus dynamics models with diffusion governed by partial differential equations (PDEs) in [37] and delayed partial differential equations (DPDEs) in [38]. It has been proven that the mixed Euler method can preserve the positivity and boundedness of solutions, moreover, it can preserve the global stability of equilibria of the corresponding continuous-time system with no restriction on the space and time step sizes [38].
Mickens [39] has introduced nonstandard finite difference (NSFD) scheme for solving differential equations. It has been proven that NSFD can preserve the main properties of several types of continuous-time models. The main advantage of NSFD approach is that the essential qualitative features of the mathematical model such as equilibria, positivity, boundedness and global behaviors of solutions are preserved independently of the chosen step-size [40]. On the other hand, even though there exist some general methods for construction of NSFD schemes for certain systems of ordinary differential equations (see, e.g., [41, 42]), there is no universal NSFD scheme suitable for every mathematical model. Therefore every model requires the construction of an individual numerical scheme in order to obtain the correct qualitative results. NSFD has been widely employed in the study of different epidemic models (see, e.g., [33] and [43,44,45,46]). NSFD has been used for within-host virus dynamics models governed by
-
ODEs: Virus dynamics models governed by ODEs have been studied by considering Holling type-II infection function in [47] and CTL immune response in [40] and [48].
-
DDEs: Delayed virus dynamics models given by DDEs has been studied by [49].
-
PDEs: Virus dynamics models with diffusion given by PDEs have been studied by considering: general infection function [50], both virus-to-cell and cell-to-cell transmissions in [51] and latently infected cells in [52]. Diffusive HBV infection model with HBV DNA-containing capsids has been studied in [53].
-
DPDEs: Delayed virus dynamics models with diffusion have been studied by considering general nonlinear incidence rate in [54]. The HBV model presented in [53] has been extended by incoporating time delay in [55] and [56].
All the above-mentioned discrete-time virus dynamics models have considered one or two classes of infected cells. In this paper, our target is to study two discrete time HIV infection models with three categories of infected cells, latently infected cells, short-lived infected cells and long-lived chronically infected cells. The first model is obtained by discretizing system (1)–(5) using NSFD. The second model extends the first one by considering that the incidence rate of infection as well as the production and removal rates of the HIV particles and cells are modeled by general nonlinear functions. Positivity and boundedness properties of the solutions are proven. Further, global stability of the equilibria is established by constructing Lyapunov functions and by applying LaSalle’s invariance principle.
2 Discrete-time model
Discretizing system (1)–(5) using the NSFD method [39] we obtain
where, \(k=k_{1}+k_{2}+k_{3}\), \(k_{i}= ( 1-\epsilon ) \bar{k}_{i}\), \(i=1,2,3\) and \(n\in \mathbb{N}=\{0,1,2,\ldots\}\). We consider the initial conditions:
2.1 Preliminaries
Let us consider the region
where \(N_{1}=\frac{\beta }{\xi }\), \(N_{2}=\frac{ ( N_{z}d+N_{u}a ) }{c}N_{1}\) and \(\xi =\min \{ \delta , \alpha ,d,a \} \).
Lemma 1
Any solution \((s_{n},w_{n},z_{n},u_{n},p_{n})\) of model (6)–(10) with initial conditions (11) is positive and ultimately bounded.
Proof
Since all parameters in (6)–(10) are positive, by induction we get \(s_{n}>0\), \(w_{n}>0\), \(z_{n}>0\), \(u_{n}>0\) and \(p_{n}>0\) for all \(n\in \mathbb{N}\).
Define a sequence \(M_{n}\):
Then
Hence
According Lemma 2.2 in [34] we obtain
Consequently, \(\lim_{n\rightarrow \infty }\sup M_{n}\leq N _{1}\), \(\lim_{n\rightarrow \infty }\sup s_{n}\leq N_{1}\), \(\lim_{n\rightarrow \infty }\sup w_{n}\leq N_{1}\), \(\lim_{n\rightarrow \infty }\sup z_{n}\leq N_{1}\), \(\lim_{n\rightarrow \infty }\sup u_{n}\leq N_{1}\). We have
Hence
By induction we get
Consequently, \(\lim_{n\rightarrow \infty }\sup p_{n}\leq N _{2}\). Therefore, the solution \((s_{n},w_{n},z_{n},u_{n},p_{n})\) converges to \(\varGamma _{1}\) as \(n\rightarrow \infty \). □
System (6)–(10) has two equilibria,
-
(i)
HIV-free equilibrium \(Q^{0}(s^{0},0,0,0,0)\) where \(s^{0}=\beta / \delta \).
-
(ii)
persistent HIV equilibrium \(Q^{\ast }(s^{\ast },w^{\ast },z^{ \ast },u^{\ast },p^{\ast })\), where
$$\begin{aligned} &s^{\ast } =\frac{s^{0}}{\mathcal{R}_{0}},\qquad w^{\ast }=\frac{k _{1}\beta }{ ( \alpha +m ) k\mathcal{R}_{0}}( \mathcal{R} _{0}-1), \\ & z^{\ast }=\frac{\beta ( mk_{1}+ ( \alpha +m ) k_{2} ) }{dk ( \alpha +m ) \mathcal{R}_{0}}(\mathcal{R}_{0}-1), \\ & u^{\ast } =\frac{\beta k_{3}}{ak\mathcal{R}_{0}}( \mathcal{R}_{0}-1),\qquad p^{\ast }=\frac{\delta }{k}( \mathcal{R}_{0}-1). \end{aligned}$$
Clearly, \(Q^{\ast }\) exists only when \(\mathcal{R}_{0}>1\), where \(\mathcal{R}_{0}\) is basic reproduction number and is given by
where
2.2 Global stability
We define the function \(G(x)\geq 0\) as \(G(x)=x-\ln x-1\). Hence,
Theorem 1
If \(\mathcal{R}_{0}\leq 1\), then \(Q^{0}\) is globally asymptotically stable.
Proof
Construct a discrete Lyapunov function:
where \(\eta _{i}>0\), \(i=1,2,3,4\) to be determined below.
Hence, \(L_{n}>0\) for all \(s_{n}>0\), \(w_{n}>0\), \(z_{n}>0\), \(u_{n}>0\) and \(p_{n}>0\). In addition, \(L_{n}=0\) if and only if \(s_{n}=s^{0}\), \(w_{n}=0\), \(z_{n}=0\), \(u_{n}=0\) and \(p_{n}=0\). Computing the difference \(\Delta L_{n}=L_{n+1}-L_{n}\):
where \(\eta _{i}\), \(i=1,2,3,4\) will be chosen below. Using inequality (18), we have
Let \(\eta _{i}\), \(i=1,2,3,4\), be chosen so that
The solution of system (19) is given by
and will be used throughout the paper. Then
Hence, for \(R_{0}\leq 1\), we have \(\Delta L_{n} \leq 0\) for all \(n\geq 0\), hence \(L_{n}\) is a non-increasing sequence. Then there exists a constant L̃ such that \(\lim_{n\rightarrow \infty }L_{n}=\widetilde{L}\) which implies that \(\lim_{n \rightarrow \infty }\Delta L_{n}=\lim_{n\rightarrow \infty }(L_{n+1}-L_{n})=0\). From equality (10) and \(\lim_{n \rightarrow \infty }\Delta L_{n}=0\) we have \(\lim_{n \rightarrow \infty }s_{n}=s^{0}\) and \(\lim_{n \rightarrow \infty }(R_{0}-1)p_{n}=0\). For the case \(\mathcal{R}_{0}<1\), we have \(\lim_{n\rightarrow \infty }s _{n+1}=s^{0}\) and \(\lim_{n\rightarrow \infty }p_{n}=0\). From Eqs. (7)–(10), we obtain \(\lim_{n\rightarrow \infty }w_{n}=0\), \(\lim_{n\rightarrow \infty }z_{n}=0\) and \(\lim_{n\rightarrow \infty }u_{n}=0\). For the case \(\mathcal{R}_{0}=1\), we have \(\lim_{n\rightarrow \infty }s _{n+1}=s^{0}\). From Eqs. (7)–(10), we obtain \(\lim_{n \rightarrow \infty }p_{n}=0\), \(\lim_{n\rightarrow \infty }u_{n}=0\), \(\lim_{n\rightarrow \infty }z_{n}=0\) and \(\lim_{n\rightarrow \infty }w_{n}=0\). Hence, in the case \(\mathcal{R}_{0}\leq 1\), the HIV-free equilibrium \(Q^{0}\) is globally asymptotically stable. □
Theorem 2
If \(\mathcal{R}_{0}>1\), then \(Q^{\ast }\) is globally asymptotically stable.
Proof
Define
where \(\eta _{i}\), \(i=1,2,3,4\) are given by Eq. (20).
Clearly, \(U_{n}(s_{n},w_{n},z_{n},u_{n},p_{n})>0\) for all \(s_{n},w _{n},z_{n},u_{n},p_{n}>0\) and \(U_{n}(s^{\ast },w^{\ast },z^{\ast },u ^{\ast },p^{\ast })=0\). Computing \(\Delta U_{n}=U_{n+1}-U_{n}\):
Using inequality (18), we get
Since \(\beta =\delta s^{\ast }+ks^{\ast }p^{\ast }\),
Using the conditions of \(Q^{\ast }\)
we get
and
Thus, \(U_{n}\) is a non-increasing sequence and there exists a constant Ũ such that \(\lim_{n \rightarrow \infty }U_{n}=\widetilde{U}\). Therefore, \(\lim_{n \rightarrow \infty }\Delta U_{n}=0\), which implies \(\lim_{n \rightarrow \infty }s_{n}=s^{\ast }\), \(\lim_{n\rightarrow \infty }w_{n}=w^{\ast }\), \(\lim_{n\rightarrow \infty }z_{n}=z^{\ast }\), \(\lim_{n\rightarrow \infty }u_{n}=u^{\ast }\) and \(\lim_{n\rightarrow \infty }p_{n}=p^{\ast }\). □
3 General model
In this section, we propose a general nonlinear HIV model:
where π, f and \(g_{i}\), \(i=1,\ldots,4\) are general functions and are assumed to satisfy the following conditions [24]:
- (A1):
-
-
(i)
there exists \(s^{0}\) such that \(\pi ( s^{0} ) =0\), \(\pi ( s ) >0\) for \(s\in [ 0,s ^{0} ) \),
-
(ii)
\(\pi ^{\prime } ( s ) <0\) for all \(s>0\),
-
(iii)
there are \(b>0\) and \(\bar{b}>0\) such that \(\pi ( s ) \leq b-\bar{b}s\) for all \(s\geq 0\).
-
(i)
- (A2):
-
-
(i)
\(f(s,p)>0\), and \(f(0,p)=f(s,0)=0\) for all \(s>0\), \(p>0\),
-
(ii)
\(\frac{\partial f(s,p)}{\partial s}>0\), \(\frac{\partial f(s,p)}{ \partial p}>0\), \(\frac{\partial f(s,0)}{\partial p}>0\) for all \(s>0\), \(p>0\),
-
(iii)
\(\frac{d}{ds} ( \frac{\partial f(s,0)}{\partial p} ) >0\) for all \(s>0\).
-
(i)
- (A3):
-
-
(i)
\(g_{j}(\rho )>0\) for \(\rho >0\), \(g_{j}(0)=0\), \(j=1,\ldots,4\),
-
(ii)
\(g_{j}^{\prime }(\rho )>0\) for \(\rho >0\), \(j=1,2,3\) and \(g_{4}^{\prime }(\rho )>0\) for \(\rho \geq 0\),
-
(iii)
there are \(\upsilon _{j}>0\), \(j=1,\ldots,4\) such that \(g_{j}(\rho ) \geq \upsilon _{j}\rho \) for \(\rho \geq 0\).
-
(i)
- (A4):
-
\(\frac{f(s,p)}{g_{4} ( p ) }\) is decreasing with respect to p for all \(p>0\).
Using the NSFD method we get
3.1 Preliminaries
Let us consider the region
where \(\bar{N}_{1}=\frac{b}{\sigma }\), \(\bar{N}_{2}=\frac{( N_{z}dg_{2}(\bar{N}_{1})+N_{u}ag_{3}(\bar{N}_{1})) }{c\upsilon _{3}}\) and \(\sigma =\min \{ \bar{b},\alpha \upsilon _{1},d\upsilon _{2},a\upsilon _{3} \} \).
Lemma 2
Any solution \((s_{n},w_{n},z_{n},u_{n},p_{n})\) of model (27)–(31) with initial conditions (11) is positive and ultimately bounded.
Proof
When \(n=0\) we prove that \((s_{1},w_{1},z_{1},u_{1},p _{1})\) exists and is positive. From Eq. (27) we have
Let \(\varphi _{1}(s)\) be defined by
According to (A1)–(A2) \(\varphi _{1}\) is a strictly increasing function of s. In addition
Hence, there exists a unique \(s_{1}\in (0,\infty )\) such that \(\varphi _{1}(s_{1})=0\).
From Eqs. (28) we have
Let \(\varphi _{2}(w)\) be defined:
Based on (A1)–(A3) \(\varphi _{2}\) is a strictly increasing function of w
Hence, there exists a unique \(w_{1}\in (0,\infty )\) such that \(\varphi _{2}(w_{1})=0\).
From Eqs. (29) we have
Let \(\varphi _{3}(z)\) be defined by
Based on (A1)–(A3) \(\varphi _{3}\) is a strictly increasing function of z
Hence, there exists a unique \(z_{1}\in (0,\infty )\) such that \(\varphi _{3}(z_{1})=0\).
Similarly, one can easily show from Eqs. (30)–(31) that \(u_{1}\in (0,\infty )\) and \(p_{1}\in (0,\infty )\).
Therefore, by using the induction, we obtain \(s_{n}>0\), \(w_{n}>0\), \(z_{n}>0\), \(u_{n}>0\) and \(p_{n}>0\) for all \(n\geq 0\).
Define a sequence \(M_{n}\):
Then
Hence
According Lemma 2.2 in [34] we obtain
Consequently, \(\lim_{n\rightarrow \infty }\sup M_{n}\leq \bar{N}_{1}\), \(\lim_{n\rightarrow \infty }\sup s_{n}\leq \bar{N}_{1}\), \(\lim_{n\rightarrow \infty }\sup w_{n}\leq \bar{N}_{1}\), \(\lim_{n\rightarrow \infty }\sup z_{n}\leq \bar{N}_{1}\), \(\lim_{n\rightarrow \infty }\sup u_{n}\leq \bar{N}_{1}\). Moreover,
Hence
By induction we get
Consequently, \(\lim_{n\rightarrow \infty }\sup p_{n}\leq \bar{N}_{2}\). Therefore, the solution \((s_{n},w_{n},z_{n},u_{n},p_{n})\) converges to \(\bar{\varGamma }_{1}\) as \(n\rightarrow \infty \). □
Lemma 3
For model (27)–(31) let (A1)–(A3) hold true, then there exists a threshold parameter \(\mathcal{R}_{0}>0\) such that
-
(i)
if \(\mathcal{R}_{0}\leq 1\), then there exists only an HIV-free equilibrium \(Q^{0}\),
-
(ii)
if \(\mathcal{R}_{0}>1\), then there exist two equilibria, \(Q^{0}\) and a persistent HIV equilibrium \(Q^{\ast }\).
Proof
Let \(Q(s,w,z,u,p)\) be any equilibrium of model (27)–(31) satisfying
Let us define
Obviously, \(\theta ( s )\), \(\psi ( s )\), \(\mu ( s )\), \(\ell ( s ) >0\) for \(s\in [ 0,s^{0} ) \) and \(\theta ( s^{0} ) =\psi ( s ^{0} ) =\mu ( s^{0} ) =\ell ( s^{0} ) =0\). From Eqs. (32), (37) and (38) we obtain
Equation (38) admits a solution \(s=s^{0}\) which yields the HIV-free equilibrium \(Q^{0}(s^{0},0,0, 0,0)\). Let
From Assumptions (A2) and (A3) \(\varPsi ( 0 ) =-g_{4} ( \ell ( 0 ) ) <0\) and \(\varPsi ( s^{0} ) =0\). Moreover,
We note from Assumption (A2) that \(\frac{\partial f ( s^{0},0 ) }{\partial s}=0\). Then
From Eq. (38), we get
Therefore, from Assumption (A1), we have \(\pi ^{\prime } ( s^{0} ) <0\). Therefore, if \(\frac{\gamma }{g_{4}^{\prime } ( 0 ) }\frac{\partial f ( s^{0},0 ) }{\partial p}>1\), then \(\varPsi ^{\prime } ( s^{0} ) <0\) and there exists \(s^{\ast }\in ( 0,s^{0} ) \) such that \(\varPsi ( s^{ \ast } ) =0\). Assumptions (A1)–(A3) imply that
It means that a persistent-HIV equilibrium \(Q^{\ast } ( s^{ \ast },w^{\ast },z^{\ast },u^{\ast },p^{\ast } ) \) exists when \(\frac{\gamma }{g_{4}^{\prime } ( 0 ) } \frac{\partial f ( s^{0},0 ) }{\partial p}>1\).
Hence, we can define the basic reproduction number of system (27)–(31):
This shows that if \(\mathcal{R}_{0}>1\), then there exists a persistent-HIV equilibrium \(Q^{\ast } ( s^{\ast },w^{\ast },z ^{\ast }, u^{\ast },p^{\ast } ) \). □
3.2 Global stability
Theorem 3
Suppose that \(\mathcal{R}_{0}\leq 1\), then \(Q^{0}\) of system (27)–(31) is globally asymptotically stable.
Proof
Define
Hence, \(L_{n}>0\) for all \(s_{n}\), \(w_{n}\), \(z_{n}\), \(u_{n}\), \(p_{n}>0\) and \(L_{n}=0\) if and only if \(s_{n}=s^{0}\), \(w_{n}=0\), \(z_{n}=0\), \(u_{n}=0\) and \(p_{n}=0\). Computing the difference \(\Delta L_{n}=L_{n+1}-L_{n}\):
Using Lemma 2.1 [35], we get
Hence
Using \(\pi ( s^{0} ) =0\), we obtain
From Assumption (A4) we have
Then we get
From Assumptions (A1) and (A2) we have
Hence, for \(R_{0}\leq 1\), we have \(\Delta L_{n} \leq 0\) for all \(n\geq 0\), hence \(L_{n}\) is a non-increasing sequence. Then there exists a constant L̃ such that \(\lim_{n\rightarrow \infty }L_{n}=\widetilde{L}\), and then \(\lim_{n\rightarrow \infty }\Delta L_{n}=0\) which implies that \(\lim_{n \rightarrow \infty }s_{n}=s^{0}\) and \(\lim_{n \rightarrow \infty }(R_{0}-1)p_{n}=0\). We discuss two cases:
-
If \(\mathcal{R}_{0}<1\), then \(\lim_{n\rightarrow \infty }p_{n}=0\), then we get from Eqs. (28)–(30) \(\lim_{n\rightarrow \infty }w_{n}=0\), \(\lim_{n\rightarrow \infty }z_{n}=0\) and \(\lim_{n\rightarrow \infty }u _{n}=0\).
-
If \(\mathcal{R}_{0}=1\). By using \(\lim_{n\rightarrow \infty }s_{n}=s^{0}\) and from Eq. (27), we obtain \(f(s^{0},p_{n})=0\). Because \(s^{0}>0\), we have \(f(s^{0},p_{n})>f(0,p _{n})=0\) (use Assumption (A1)). Thus, \(\lim_{n\rightarrow \infty }p_{n}=0\).
By the aforementioned discussion, we deduce that the largest compact invariant set in \(\{ (s_{n},w_{n},z_{n},u_{n},p_{n})|(\Delta L _{n})=0 \} \) is the just the singleton \(Q^{0}\).
Therefore, \(Q^{0}\) is globally asymptotically stable by the LaSalle invariance principle [57, 58]. □
Remark 1
Assumptions (A2)–(A4) imply that
which yields
Theorem 4
Suppose that \(\mathcal{R}_{0}>1\), then \(Q^{\ast }\) of system (27)–(31) is globally asymptotically stable.
Proof
Consider
Clearly, \(U_{n}(s_{n},w_{n},z_{n},u_{n},p_{n})>0\) for all \(s_{n},w _{n},z_{n},u_{n},p_{n}>0\) and \(U_{n}(s^{\ast },w^{\ast },z^{\ast },u ^{\ast },p^{\ast })=0\). Computing \(\Delta U_{n}=U_{n+1}-U_{n}\):
From Lemma 2.1 [35], we have
Then
Using the conditions of \(Q^{\ast }\)
we get
and
Assumptions (A1), (A2) and (A4) imply that
Based on the Remark 1, we have
Thus, \(U_{n}\) is a non-increasing sequence and there exists a constant Ũ such that \(\lim_{n \rightarrow \infty }U_{n}=\widetilde{U}\). Therefore, \(\lim_{n \rightarrow \infty }\Delta U_{n}=0\), which implies \(\lim_{n \rightarrow \infty }s_{n}=s^{\ast }\), \(\lim_{n\rightarrow \infty }w_{n}=w^{\ast }\), \(\lim_{n\rightarrow \infty }z_{n}=z^{\ast }\), \(\lim_{n\rightarrow \infty }u_{n}=u^{\ast }\) and \(\lim_{n\rightarrow \infty }p_{n}=p^{\ast }\). □
3.3 Numerical simulations
We perform our simulation by choosing the functions
where \(\lambda >0\) and \(\theta >0\). Therefore, system (27)–(31) becomes
For this system, the basic reproduction number is given by
We verify the assumptions (A1)–(A4). Clearly, \(\pi ( 0 ) =\beta >0\), \(\pi ( s^{0} ) =0\) and \(\pi ^{\prime } ( s ) =-\delta <0\). It follows that, \(\pi ( s ) >0\) for all \(s\in [ 0,s^{0} ) \). Moreover, (A1)(iii) is satisfied with \(b=\beta \) and \(\bar{b}=\delta \). Thus, (A1) is satisfied. We also have
Therefore, Assumption (A2) is satisfied. Moreover, we have \(g_{j} ( \rho ) =\rho >0\) for all \(\rho >0\) and \(g_{j} ( 0 ) =0\), \(j=1,\ldots,4\). We also have, \(g_{j}^{\prime } ( \rho ) =1>0\), \(j=1,2,3\) for all \(\rho >0\) and \(g_{4}^{\prime } ( \rho ) =1>0\) for \(\rho \geq 0\).
Then Assumption (A3) is satisfied, where \(\upsilon _{j}=1\), \(j=1,2,3\). Finally, we have
Therefore, Assumption (A4) holds true and hence Theorems 3 and 4 are applicable.
The numerical simulations for system (41)–(45) will be conducted using the following data: \(\beta =10\), \(\delta =0.01\), \(\alpha =0.1\), \(m=0.2\), \(d=0.2\), \(a=0.1\), \(c=6\), \(\lambda =1\), \(\theta =1\) and \(\bar{k}_{i}=0.02\) (\(i=1,2,3\)). The other parameters will be chosen below.
Let us consider the initial values
-
IV1:
\(s(0)=900\), \(w(0)=7\), \(z(0)=15\), \(u(0)=20\), \(p(0)=60\),
-
IV2:
\(s(0)=700\), \(w(0)=4\), \(z(0)=10\), \(u(0)=12\), \(p(0)=45\),
-
IV3:
\(s(0)=500\), \(w(0)=2\), \(z(0)=5\), \(u(0)=6\), \(p(0)=30\).
Case (1) Effect of \(N_{z}\), \(N_{u}\) of stability of equilibria:
We choose \(\epsilon =0\) and \(N_{z}\), \(N_{u}\) are varied:
-
(i)
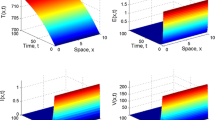
\(N_{z}=100\), \(N_{u}=50\). This yields \(\mathcal{R}_{0}=0.7215<1\). Figure 1 shows that, the concentration of uninfected cells increases and tends to the value \(s^{0}=1000\). In addition, the concentrations of latent infected cells, long-lived infected cells, short-lived infected cells and free HIV particles decrease and tend to zero for the initial values IV1–IV3. This shows that \(Q^{0}\) is globally asymptotically stable and Theorem 3 is valid.
-
(ii)
\(N_{z}=200\), \(N_{u}=100\). With these values we obtain \(\mathcal{R}_{0}=1.4430>1\). Figure 1 shows that for the initial values IV1–IV3, the solutions of the system tend to the equilibrium \(Q^{\ast }=(352.8108,7.1910,17.9775,21.5730,155.8047)\). Therefore, \(Q^{\ast }\) exists and it is globally asymptotically stable. This validates the result of Theorem 4.
Case(2) Effect of the drug efficacy ϵ on the HIV dynamics:
For this case, we take IV2 and choose the values \(N_{z}=200\), \(N_{u}=100\) and ϵ is varied. Figure 2 shows the effect of drug efficacy ϵ on the stability of the system. We observe that, as ϵ is increased, the infection rate is decreased, and then, the concentration of the uninfected cells are increased, while the concentrations of the latent infected cells, long-lived infected cells, short-lived infected cells and free HIV particles are decreased.
References
Nowak, M.A., Bangham, C.R.M.: Population dynamics of immune responses to persistent viruses. Science 272, 74–79 (1996)
Perelson, A.S., Nelson, P.W.: Mathematical analysis of HIV-1 dynamics in vivo. SIAM Rev. 41, 3–44 (1999)
Callaway, D.S., Perelson, A.S.: HIV-1 infection and low steady state viral loads. Bull. Math. Biol. 64, 29–64 (2002)
Wang, J., Teng, Z., Miao, H.: Global dynamics for discrete-time analog of viral infection model with nonlinear incidence and CTL immune response. Adv. Differ. Equ. 2016, 143 (2016)
Culshaw, R.V., Ruan, S.: A delay-differential equation model of HIV infection of CD4+T-cells. Math. Biosci. 165, 27–39 (2000)
Culshaw, R.V., Ruan, S., Webb, G.: A mathematical model of cell-to-cell spread of HIV-1 that includes a time delay. J. Math. Biol. 46, 425–444 (2003)
Wang, L., Li, M.Y.: Mathematical analysis of the global dynamics of a model for HIV infection of CD4+T cells. Math. Biosci. 200, 44–57 (2006)
Zhao, Y., Dimitrov, D.T., Liu, H., Kuang, Y.: Mathematical insights in evaluating state dependent effectiveness of HIV prevention interventions. Bull. Math. Biol. 75(4), 649–675 (2013)
Nelson, P.W., Murray, J.D., Perelson, A.S.: A model of HIV-1 pathogenesis that includes an intracellular delay. Math. Biosci. 163(2), 201–215 (2000)
Elaiw, A.M., Elnahary, E.K., Raezah, A.A.: Effect of cellular reservoirs and delays on the global dynamics of HIV. Adv. Differ. Equ. 2018, 85 (2018)
Elaiw, A.M., Raezah, A.A., Azoz, S.A.: Stability of delayed HIV dynamics models with two latent reservoirs and immune impairment. Adv. Differ. Equ. 2018, 414 (2018)
Elaiw, A.M., AlShamrani, N.H.: Stability of a general delay-distributed virus dynamics model with multi-staged infected progression and immune response. Math. Methods Appl. Sci. 40(3), 699–719 (2017)
Gibelli, L., Elaiw, A.M., Alghamdi, M.A., Althiabi, A.M.: Heterogeneous population dynamics of active particles: progression, mutations, and selection dynamics. Math. Models Methods Appl. Sci. 27, 617–640 (2017)
Li, M.Y., Wang, L.: Backward bifurcation in a mathematical model for HIV infection in vivo with anti-retroviral treatment. Nonlinear Anal., Real World Appl. 17, 147–160 (2014)
Li, B., Chen, Y., Lu, X., Liu, S.: A delayed HIV-1 model with virus waning term. Math. Biosci. Eng. 13, 135–157 (2016)
Elaiw, A.M.: Global properties of a class of HIV models. Nonlinear Anal., Real World Appl. 11, 2253–2263 (2010)
Elaiw, A.M.: Global properties of a class of virus infection models with multitarget cells. Nonlinear Dyn. 69(1–2), 423–435 (2012)
Elaiw, A.M., Almuallem, N.A.: Global properties of delayed-HIV dynamics models with differential drug efficacy in cocirculating target cells. Appl. Math. Comput. 265, 1067–1089 (2015)
Elaiw, A.M., Almuallem, N.A.: Global dynamics of delay-distributed HIV infection models with differential drug efficacy in cocirculating target cells. Math. Methods Appl. Sci. 39, 4–31 (2016)
Elaiw, A.M., Hassanien, I.A., Azoz, S.A.: Global stability of HIV infection models with intracellular delays. J. Korean Math. Soc. 49(4), 779–794 (2012)
Elaiw, A.M., Azoz, S.A.: Global properties of a class of HIV infection models with Beddington-DeAngelis functional response. Math. Methods Appl. Sci. 36, 383–394 (2013)
Elaiw, A.M.: Global dynamics of an HIV infection model with two classes of target cells and distributed delays. Discrete Dyn. Nat. Soc. 2012, Article ID 253703 (2012)
Pinto, C.M.A., Carvalho, A.R.M.: A latency fractional order model for HIV dynamics. J. Comput. Appl. Math. 312, 240–256 (2017)
Huang, G., Takeuchi, Y., Ma, W.: Lyapunov functionals for delay differential equations model of viral infections. SIAM J. Appl. Math. 70(7), 2693–2708 (2010)
Shu, H., Wang, L., Watmough, J.: Global stability of a nonlinear viral infection model with infinitely distributed intracellular delays and CTL immune responses. SIAM J. Appl. Math. 73(3), 1280–1302 (2013)
Elaiw, A.M., AlShamrani, N.H.: Global stability of humoral immunity virus dynamics models with nonlinear infection rate and removal. Nonlinear Anal., Real World Appl. 26, 161–190 (2015)
Elaiw, A.M., AlShamrani, N.H.: Stability of an adaptive immunity pathogen dynamics model with latency and multiple delays. Math. Methods Appl. Sci. 36, 125–142 (2018)
Hobiny, A.D., Elaiw, A.M., Almatrafi, A.: Stability of delayed pathogen dynamics models with latency and two routes of infection. Adv. Differ. Equ. 2018, 276 (2018)
Elaiw, A.M., AlShamrani, N.H.: Global properties of nonlinear humoral immunity viral infection models. Int. J. Biomath. 8(5), Article ID 1550058 (2015)
Elaiw, A.M., Raezah, A.A.: Stability of general virus dynamics models with both cellular and viral infections and delays. Math. Methods Appl. Sci. 40(16), 5863–5880 (2017)
Cao, J., Wang, Y., Alofi, A., Al-Mazrooei, A., Elaiw, A.M.: Global stability of an epidemic model with carrier state in heterogeneous networks. IMA J. Appl. Math. 80(4), 1025–1048 (2015)
Wang, Y., Cao, J.: Global stability of general cholera models with nonlinear incidence and removal rates. J. Franklin Inst. 352, 2464–2485 (2015)
Enatsu, Y., Nakata, Y., Muroya, Y., Izzo, G., Vecchio, A.: Global dynamics of difference equations for SIR epidemic models with a class of nonlinear incidence rates. J. Differ. Equ. Appl. 18, 1163–1181 (2012)
Shi, P., Dong, L.: Dynamical behaviors of a discrete HIV-1 virus model with bilinear infective rate. Math. Methods Appl. Sci. 37, 2271–2280 (2014)
Hattaf, K., Yousfi, N.: Global properties of a discrete viral infection model with general incidence rate. Math. Methods Appl. Sci. 39, 998–1004 (2016)
Hattaf, K., Yousfi, N.: A numerical method for a delayed viral infection model with general incidence rate. J. King Saud Univ., Sci. 28, 368–374 (2016)
Qin, W., Wang, L., Ding, X.: A non-standard finite difference method for a hepatitis B virus infection model with spatial diffusion. J. Differ. Equ. Appl. 20, 1641–1651 (2014)
Hattaf, K., Yousfi, N.: A numerical method for delayed partial differential equations describing infectious diseases. Comput. Math. Appl. 72(11), 2741–2750 (2016)
Mickens, R.E.: Nonstandard Finite Difference Models of Differential Equations. World Scientific, Singapore (1994)
Korpusik, A.: A nonstandard finite difference scheme for a basic model of cellular immune response to viral infection. Commun. Nonlinear Sci. Numer. Simul. 43, 369–384 (2017)
Anguelov, R., Dumont, Y., Lubuma, J.M.-S., Shillo, M.: Dynamically consistent nonstandard finite difference schemes for epidemiological models. J. Comput. Appl. Math. 255, 161–182 (2014)
Wood, D.T., Dimitrov, D.T., Kojouharov, H.V.: A nonstandard finite difference method for n-dimensional productive-destructive systems. J. Differ. Equ. Appl. 21(3), 240–254 (2015)
Ding, D., Ding, X.: Dynamic consistent non-standard numerical scheme for a dengue disease transmission model. J. Differ. Equ. Appl. 20, 492–505 (2014)
Ding, D., Qin, W., Ding, X.: Lyapunov functions and global stability for a discretized multi-group SIR epidemic model. Discrete Contin. Dyn. Syst., Ser. B 20, 1971–1981 (2015)
Liu, J., Peng, B., Zhang, T.: Effect of discretization on dynamical behavior of SEIR and SIR models with nonlinear incidence. Appl. Math. Lett. 39, 60–66 (2015)
Teng, Z., Wang, L., Nie, L.: Global attractivity for a class of delayed discrete SIRS epidemic models with general nonlinear incidence. Math. Methods Appl. Sci. 38, 4741–4759 (2015)
Yang, Y., Xinsheng, M., Yahui, L.: Global stability of a discrete virus dynamics model with Holling type-II infection function. Math. Methods Appl. Sci. 39, 2078–2082 (2016)
Wang, J., Teng, Z., Miao, H.: Global dynamics for discrete-time analog of viral infection model with nonlinear incidence and CTL immune response. Adv. Differ. Equ. 2016, Article ID 143 (2016). https://doi.org/10.1186/s13662-016-0862-y
Zhou, J., Yang, Y.: Global dynamics of a discrete viral infection model with time delay, virus-to-cell and cell-to-cell transmissions. J. Differ. Equ. Appl. 23(11), 1853–1868 (2017). https://doi.org/10.1080/10236198.2017.1371144
Yang, Y., Zhou, J.: Global stability of a discrete virus dynamics model with diffusion and general infection function. Int. J. Comput. Math. 96, 1752–1762 (2019)
Yang, Y., Zhou, J., Ma, X., Zhang, T.: Nonstandard finite difference scheme for a diffusive within-host virus dynamics model both virus-to-cell and cell-to-cell transmissions. Comput. Math. Appl. 72, 1013–1020 (2016)
Xu, J., Hou, J., Geng, Y., Zhang, S.: Dynamic consistent NSFD scheme for a viral infection model with cellular infection and general nonlinear incidence. Adv. Differ. Equ. 2018, 108 (2018)
Manna, K., Chakrabarty, S.P.: Global stability and a non-standard finite difference scheme for a diffusion driven HBV model with capsids. J. Differ. Equ. Appl. 21(10), 918–933 (2015)
Xu, J., Geng, Y., Hou, J.: A nonstandard finite difference scheme for a delayed and diffusive viral infection model with general nonlinear incidence rate. Comput. Math. Appl. 74, 1782–1798 (2017)
Manna, K.: A non-standard finite difference scheme for a diffusive HBV infection model with capsids and time delay. J. Differ. Equ. Appl. 23(11), 1901–1911 (2017)
Geng, Y., Xu, J., Hou, J.: Discretization and dynamic consistency of a delayed and diffusive viral infection model. Appl. Comput. Math. 316, 282–295 (2018)
Elaydi, S.: An Introduction to Difference Equations, 3rd edn. Springer, New York (2005)
Lasalle, J.P.: The Stability and Control of Discrete Processes. Springer, New York (1986)
Acknowledgements
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, under grant No. (DF-006-130-1441). The authors, therefore, gratefully acknowledge DSR technical and financial support.
Availability of data and materials
Not applicable.
Funding
Not applicable.
Author information
Authors and Affiliations
Contributions
All authors contributed equally to the writing of this paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Elaiw, A.M., Alshaikh, M.A. Stability of discrete-time HIV dynamics models with three categories of infected CD4+ T-cells. Adv Differ Equ 2019, 407 (2019). https://doi.org/10.1186/s13662-019-2338-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2338-3