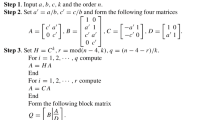1 Introduction

Tridiagonal matrices appear not only in pure linear algebra, but also in many practical applications, such as computer graphics [1], image denoising [2], and partial differential equations [3,4,5,6]. As an example, Holmgren and Otto [7] considered the one-dimensional linear hyperbolic equation

$$ \frac{\partial u(x,t)}{\partial t}+v \frac{\partial u(x,t)}{\partial x}=g $$

to study certain matrices occurring in discretized partial differential equations, where \(0 < x \leq 1\), \(t> 0\), \(u(0, t) = f(- at)\), \(u(x, 0) = f(x)\), \(g = (v - a)f'\), v and a are positive constants, and f is a scalar function with derivative \(f'\). Let k and h denote the time and spatial steps, respectively. Consider the linear hyperbolic equation discretized based on trapezoidal rule in time and center difference in space, respectively. Its coefficient matrix is a tridiagonal matrix with perturbed last row [8]:

$$\begin{aligned} \mathfrak{T}= \begin{pmatrix} 4 &\alpha & 0 &\cdots &\cdots &0 \\ -\alpha &\ddots &\ddots &\ddots & &\vdots \\ 0 &\ddots &\ddots &\ddots &\ddots &\vdots \\ \vdots &\ddots &\ddots &\ddots &\ddots &0 \\ \vdots & &\ddots &-\alpha &4 &\alpha \\ 0 &\cdots &\cdots &0 &-2\alpha &4+2\alpha \end{pmatrix}_{n\times n}, \end{aligned}$$

where \(\alpha =vk/h\). On the other hand, some parallel computing algorithms are also designed for solving tridiagonal systems on graphics processing unit (GPU), which are parallel cyclic reduction [9] and partition methods [10]. Recently, Yang et al. [11] presented a parallel solving method that mixes direct and iterative methods for block-tridiagonal equations on CPU-GPU heterogeneous computing systems, whereas Myllykoski et al. [12] proposed a generalized graphics processing unit implementation of partial solution variant of the cyclic reduction (PSCR) method to solve certain types of separable block tridiagonal linear systems. Compared to an equivalent CPU implementation that utilizes a single CPU core, PSCR method indicated up to 24-fold speedups.

Many studies have been conducted for tridiagonal matrices [13,14,15,16,17,18,19]. Typical results for their inverses include Usmani’s algorithm [20] based on rudimentary matrix analysis, El-Mikkawy and Atlan’s two symbolic algorithms [21, 22] based on the Doolittle LU factorization of the k-tridiagonal matrix, Jia et al.’s algorithms [23, 24] based on block diagonalization technique, and so on. There are also some studies on the solution of periodic tridiagonal linear systems [25,26,27]. Tim and Emrah [28] used backward continued fractions to derive the LU factorization of periodic tridiagonal matrix and then derived an explicit formula for its inverse. Dow [29] discussed some special Toeplitz matrices including periodic tridiagonal Toeplitz matrices, whereas Shehawey [30] generalized Huang and McColl’s [31] work and put forward the inverse formula for periodic tridiagonal Toeplitz matrices.

The main research object of this paper is an \(n\times n\) matrix \(A=(a_{i,j})^{n}_{i,j=1}\), which is called a periodic tridiagonal Toeplitz matrix with perturbed corners of type I and defined as follows:

$$\begin{aligned} &A= \begin{pmatrix} \alpha _{1} &2\xi &0&\cdots &0&\gamma _{1} \\ \xi &-3\xi & 2\xi &\ddots & &0 \\ 0&\xi &\ddots &\ddots &\ddots &\vdots \\ \vdots & \ddots &\ddots & \ddots & 2\xi &0 \\ 0&& \ddots &\xi &-3\xi & 2\xi \\ \alpha _{n}&0 &\cdots & 0 & \xi & \gamma _{n} \end{pmatrix}_{n\times n}, \end{aligned}$$
(1)

where \(\alpha _{1}\), \(\alpha _{n}\), \(\gamma _{1}\), \(\gamma _{n}\), ξ are complex numbers with \(\xi \neq 0\). Let \(\hat{I}_{n}\) be the \(n\times n\) “reverse unit matrix”, which has ones along the secondary diagonal and zeros elsewhere. Let A be defined as a periodic tridiagonal Toeplitz matrix with perturbed corners of type I. A matrix of the form \(B:=\hat{I}_{n}{A}\hat{I}_{n}\) is called a periodic tridiagonal Toeplitz matrix with perturbed corners of type II. In this case, we say that B is induced by A. It is readily seen that A is a periodic tridiagonal Toeplitz matrix with perturbed corners of type I if and only if its transpose \(A^{T}\) is a periodic tridiagonal Toeplitz matrix with perturbed corners of type II.

Besides, the following Fermat sequence \(\{\mathbb{F}_{n}\}\) [32] plays a very important role in our main results:

$$\begin{aligned} &\mathbb{F} _{n+1} =3\mathbb{F}_{n}- 2 \mathbb{F}_{n-1}, \quad \text{where } \mathbb{F}_{0}=2, \mathbb{F}_{1}=3, n \geq 1; \end{aligned}$$
(2)
$$\begin{aligned} &\mathbb{F}_{-(n+1)} =\frac{3}{2}\mathbb{F}_{-n} - \frac{1}{2} \mathbb{F}_{-(n-1)}, \quad \text{where } \mathbb{F}_{0}=2, \mathbb{F}_{-1}=\frac{3}{2}, n \geq 1. \end{aligned}$$
(3)

It is known that the nth Fermat number has the Binet formula \(\mathbb{F}_{n}=2^{n}+1\).

The next section presents the main results of the paper. We present detailed derivations of the determinants and inverses of periodic tridiagonal Toeplitz matrices with perturbed corners. Our approach includes a clever use of matrix decomposition with the Sherman–Morrison–Woodbury formula [33]. In the last section, we compare the CPU times for the determinants and inverses of periodic tridiagonal Toeplitz matrices with perturbed corners between different algorithms.

2 Determinants and inverses

In this section, we derive explicit formulas for the determinants and inverses of a periodic tridiagonal Toeplitz matrix with perturbed corners. Main effort is made for working out those for periodic tridiagonal Toeplitz matrix with perturbed corners of type I, since the results for type II matrices would follow immediately.

Theorem 1

Let \(A=(a_{i,j})^{n}_{i,j=1}\) (\(n\geq 3\)) be given as in (1). Then

$$\begin{aligned} \det A={} &(-\xi )^{n-2} \bigl\{ 4(\mathbb{F}_{n-3}-2)\xi ^{2}+ \bigl[2( \mathbb{F}_{n-2}-2) (\alpha _{1}+ \gamma _{n})-(\mathbb{F}_{n-1}-1)\alpha _{n} \\ &{}-\gamma _{1} \bigr]\xi +(\mathbb{F}_{n-1}-2) (\alpha _{1}\gamma _{n}- \alpha _{n}\gamma _{1}) \bigr\} , \end{aligned}$$
(4)

where \(\mathbb{F}_{i}\) (\(i=n-3,n-2,n-1\)) is the ith Fermat number.

Proof

Define the circulant matrix

$$\begin{aligned} &\rho =(\rho _{i,j})^{n}_{i,j=1}, \end{aligned}$$
(5)

where

$$\begin{aligned} &\rho _{i,j}= \textstyle\begin{cases} 1, & i=n,j=1, \\ 1, & j=i+1, \\ 0 & \text{otherwise}. \end{cases}\displaystyle \end{aligned}$$

Clearly, ρ is invertible, and

$$\begin{aligned} &\det \rho =(-1)^{n-3}. \end{aligned}$$
(6)

Multiply A by ρ from right and then partition Aρ into four blocks:

figure a

Since \(A_{22}\) is upper triangular, the determinant of \(A_{22}\) is

$$\begin{aligned} & \det A_{22}=\xi ^{n-2}. \end{aligned}$$
(8)

Besides, \(\xi \ne 0\), so \(A_{22}\) is invertible. It is known (see, e.g., [34, Lemma 2.5]) that \(A^{-1}_{22}=(\ddot{a}_{i,j})^{n-2} _{i,j=1}\) where

$$\begin{aligned} \ddot{a}_{i,j}={}& \textstyle\begin{cases} \frac{\mathbb{F}_{j-i+1}-2}{\xi }, &i\leq j, \\ 0, &i>j, \end{cases}\displaystyle \end{aligned}$$

and \(\mathbb{F}_{i}\) is the ith Fermat number.

Next, taking the determinants for both sides of (7), by [35, p. 10] we get

$$\begin{aligned} \det (A\rho ) &=\det A_{22}\det \bigl( A_{11}-A_{12} A_{22}^{-1}A_{21} \bigr). \end{aligned}$$
(9)

Therefore

$$\begin{aligned} & \det A=\frac{\det A_{22}\det (A_{11}-A_{12}A_{22}^{-1}A_{21})}{ \det \rho }. \end{aligned}$$
(10)

To find detA, we need to evaluate the determinant of \((A_{11}-A _{12}A_{22}^{-1}A_{21})\). From (7) we have

$$\begin{aligned} &A_{11}- A_{12}A_{22}^{-1}A_{21} \\ &\quad = \begin{pmatrix} \gamma _{1} -2(\mathbb{F}_{n-2}-2)\gamma _{n}-4(\mathbb{F}_{n-3}-2) \xi & \alpha _{1}-2(\mathbb{F}_{n-2}-2)\alpha _{n} \\ (\mathbb{F}_{n-1}-2)\gamma _{n} +2(\mathbb{F}_{n-2}-2)\xi &( \mathbb{F}_{n-1}-2)\alpha _{n}+\xi \end{pmatrix}, \end{aligned}$$

and so

$$\begin{aligned} \det \bigl(A_{11}-A_{12}A_{22}^{-1}A_{21} \bigr)={} &4(2-\mathbb{F}_{n-3}) \xi ^{2}- \bigl[2( \mathbb{F}_{n-2}-2) (\alpha _{1}+\gamma _{n})-( \mathbb{F} _{n-1} \\ &{}-1)\alpha _{n}-\gamma _{1} \bigr]\xi -( \mathbb{F}_{n-1}-2) (\alpha _{1} \gamma _{n}-\alpha _{n}\gamma _{1}) \}. \end{aligned}$$
(11)

Finally, applying (6), (8), and (11) to (10), we get the determinant of A, which completes the proof. □

Theorem 2

Let \(A=(a_{i,j})^{n}_{i,j=1}\) (\(n\geq 3\)) be given as in (1) and assume A to be nonsingular. Then \(A^{-1} =(\breve{a}_{i,j})^{n}_{i,j=1}\), where

$$\begin{aligned}& \breve{a}_{i,j}= \textstyle\begin{cases} \frac{2(\mathbb{F}_{n-2}-2)\xi +(\mathbb{F}_{n-1}-2)\gamma _{n}}{ \psi }, & i=1,j=1, \\ \frac{4(\mathbb{F}_{n-3}-2)\xi -\gamma _{1}+2(\mathbb{F}_{n-2}-2) \gamma _{n}}{\psi }, & i=1,j=2, \\ \frac{2(\mathbb{F}_{n-3}-2)\xi -(\mathbb{F}_{n-2}-1)\alpha _{n}+( \mathbb{F}_{n-2}-2)\gamma _{n}}{\psi }, & i=2,j=1, \\ \frac{2(\mathbb{F}_{n-3}-2)\alpha _{1}\xi +(\mathbb{F}_{n-2}-2)(\alpha _{1}\gamma _{n}-\alpha _{n}\gamma _{1})}{-\psi \xi }, & i=2,j=2, \\ 3\breve{a}_{2,2}-2\breve{a}_{2,1}+\frac{1}{\xi }, & i=2,j=3, \\ \frac{3}{2}\breve{a}_{2,2}-\frac{1}{2}\breve{a}_{1,2}+\frac{1}{2 \xi }, & i=3,j=2, \\ 3\breve{a}_{i,j-1}-2\breve{a}_{i,j-2}, & \textstyle\begin{cases} i\in {\{1,2\}},i+2\leq j\leq n, \\ 3\leq j \leq i\leq n, \end{cases}\displaystyle \\ \frac{3}{2}\breve{a}_{i-1,j}-\frac{1}{2} \breve{a}_{i-2,j},& \textstyle\begin{cases} j\in {\{1,2\}},j+2\leq i\leq n, \\ 3\leq i< j\leq n, \end{cases}\displaystyle \end{cases}\displaystyle \end{aligned}$$
(12)
$$\begin{aligned}& \begin{aligned}[b] \psi ={}& 4(\mathbb{F}_{n-3}-2)\xi ^{2}+ \bigl[2(\mathbb{F}_{n-2}-2) ( \alpha _{1}+\gamma _{n})-(\mathbb{F}_{n-1}-1)\alpha _{n}-\gamma _{1} \bigr]\xi \\ &{}+(\mathbb{F}_{n-1}-2) (\alpha _{1}\gamma _{n}- \alpha _{n}\gamma _{1}), \end{aligned} \end{aligned}$$
(13)

and \(\mathbb{F}_{i}\) (\(i=n-3,n-2,n-1\)) is the ith Fermat number.

Proof

Let \(A^{-1} =(\breve{a}_{i,j})^{n}_{i,j=1}\), and let \(I_{n}=(e_{i,j})^{n} _{i,j=1}\) be the identity matrix, that is,

$$\begin{aligned} e_{i,j}= \textstyle\begin{cases} 1,& i= j, \\ 0&\text{otherwise}. \end{cases}\displaystyle \end{aligned}$$
(14)

For a nonsingular A,

$$ A^{-1}A=AA^{-1}=I_{n}. $$
(15)

According to (15), we get

$$\begin{aligned}& e_{i,j} =2\breve{a}_{i,j-1}\xi -3\breve{a}_{i,j}\xi + \breve{a}_{i,j+1} \xi ,\quad 1\leq i\leq n, 2\leq j\leq n-1, \end{aligned}$$
(16)
$$\begin{aligned}& e_{i,j} =\breve{a}_{i-1,j}\xi -3\breve{a}_{i,j}\xi +2 \breve{a}_{i+1,j} \xi ,\quad 3\leq i\leq n-2, 1\leq j\leq n. \end{aligned}$$
(17)

Based on (14), from (16) we get that

$$\begin{aligned} &\breve{a}_{i,j}=3\breve{a}_{i,j-1}-2 \breve{a}_{i,j-2}, \quad \textstyle\begin{cases} i\in {\{1,2\}},i+2\leq j\leq n,\\ 3\leq j \leq i\leq n, \end{cases}\displaystyle \end{aligned}$$
(18)

and \(\breve{a}_{2,3}=3\breve{a}_{2,2}-2\breve{a}_{2,1}+\frac{1}{ \xi }\).

Similarly, from (17) we get that

$$\begin{aligned} &\breve{a}_{i,j}=\frac{3\breve{a}_{i-1,j}}{2}- \frac{\breve{a}_{i-2,j}}{2}, \quad \textstyle\begin{cases} j\in {\{1,2\}},j+2\leq i\leq n, \\ 3\leq i< j\leq n, \end{cases}\displaystyle \end{aligned}$$
(19)

and \(\breve{a}_{3,2}=\frac{3\breve{a}_{2,2}}{2}- \frac{\breve{a}_{2,1}}{2}+\frac{1}{2\xi }\).

Therefore, based on the previous analysis, we need to determine four initial values, that is, \(\breve{a}_{i,j}\) (\(i,j\in \{1,2\}\)), for the recurrence relations (18) and (19) to compute the inverse of A. The rest of the proof is devoted to evaluating these particular entries of \(A^{-1}\).

We decompose A as follows:

$$\begin{aligned} A=\xi \mathfrak{F}+\mu \nu , \end{aligned}$$
(20)

where \(\mathfrak{F}= ((f_{ij})^{n}_{i,j=1} )^{-1}\), \(\mu = (\mu _{1}^{T},\mu _{2}^{T} )\), ν= ( ν 1 ν 2 ) with

$$\begin{aligned} &f_{ij}= \textstyle\begin{cases} \mathbb{F}_{j-i+1},&1\leq i\leq j\leq n, \\ 2\mathbb{F}_{j-i-1}&\text{otherwise}, \end{cases}\displaystyle \\ &\mu _{1}= \biggl(\alpha _{1}+ \frac{\mathbb{F}_{n+1}-3}{\mathbb{F}_{n+1}-2}\xi ,0, \ldots,0,\alpha _{n}+\frac{2\xi }{\mathbb{F}_{n+1}-2} \biggr)_{1\times n}, \\ &\mu _{2}= \biggl(\gamma _{1}+\frac{\mathbb{F}_{n}-1}{\mathbb{F}_{n+1}-2} \xi ,0, \ldots,0,\gamma _{n}+ \frac{\mathbb{F}_{n+1}-3}{\mathbb{F}_{n+1}-2}\xi \biggr)_{1\times n}, \\ &\nu _{1}= (1,0,\ldots,0 )_{1\times n}, \qquad \nu _{2}= (0,\ldots,0,1 )_{1\times n}, \end{aligned}$$

and \(\mathbb{F}_{i}\) is the ith Fermat number as before.

Applying the Sherman–Morrison–Woodbury formula (see, e.g. [33, p. 50]) to (20) gives

$$\begin{aligned} A^{-1}=(\xi \mathfrak{F}+\mu \nu )^{-1}= \frac{1}{\xi } \mathfrak{F} ^{-1}-\frac{1}{\xi ^{2}} \mathfrak{F}^{-1}\mu \biggl(I_{n}+\frac{1}{\xi } \nu \mathfrak{F}^{-1}\mu \biggr)^{-1}\nu \mathfrak{F}^{-1}. \end{aligned}$$
(21)

Now we compute each component on the right-hand side of (21). Multiplying \(\mathfrak{F}^{-1}\) by ν and μ from left and right, respectively, we have

$$\begin{aligned}& \nu \mathfrak{F}^{-1}= \begin{pmatrix} \tau _{1} \\ \tau _{2} \end{pmatrix}, \end{aligned}$$
(22)
$$\begin{aligned}& \mathfrak{F}^{-1}\mu = \begin{pmatrix} \ell _{1}&\ell _{2} \end{pmatrix}, \end{aligned}$$
(23)

where \(\tau _{1}\) and \(\tau _{2}\) are row vectors, and \(\ell _{1}\) and \(\ell _{2}\) are column vectors,

$$\begin{aligned} &\tau _{1}=(\mathbb{F}_{j})^{n}_{j=1}, \qquad \tau _{2}=(2\mathbb{F}_{j-n-1})^{n} _{j=1}, \\ &\ell _{1}= (\mathbb{F}_{n-i+1}\alpha _{n}+2 \mathbb{F}_{-i}\alpha _{1}+2\mathbb{F}_{1-i}\xi )^{n}_{i=1}, \\ &\ell _{2}= (\mathbb{F}_{n-i+1}\gamma _{n}+2 \mathbb{F}_{-i}\gamma _{1}+2\mathbb{F}_{n-i}\xi )^{n}_{i=1}. \end{aligned}$$

Then multiplying (23) by \(\frac{\nu }{\xi }\) from the left, further adding \(I_{n}\), and computing the inverse of the matrix, we have

$$\begin{aligned} & \biggl(I_{n}+\frac{1}{\xi } \nu \mathfrak{F}^{-1}\mu \biggr)^{-1} \\ &\quad = \frac{\xi }{\sigma } \begin{pmatrix} 2\mathbb{F}_{-n}\gamma _{1}+3\gamma _{n}+5\xi &-3\gamma _{1}-\mathbb{F} _{n}\gamma _{n}-2\mathbb{F}_{n-1}\xi \\ -2\mathbb{F}_{-n}\alpha _{1}-3\alpha _{n} - 2\mathbb{F}_{1-n}\xi &3 \alpha _{1}+\mathbb{F}_{n}\alpha _{n}+5\xi \end{pmatrix}, \end{aligned}$$

where

$$\begin{aligned} \sigma &= -\frac{\mathbb{F}_{n+1}-2}{\mathbb{F}_{n-1}-1} \bigl\{ 4( \mathbb{F}_{n-3}-2)\xi ^{2}+\bigl[2(\mathbb{F}_{n-2}-2) (\alpha _{1}+\gamma _{n})-(\mathbb{F}_{n-1}-1)\alpha _{n} \\ &\quad{} -\gamma _{1}\bigr]\xi +(\mathbb{F}_{n-1}-2) (\alpha _{1}\gamma _{n}-\alpha _{n}\gamma _{1}) \bigr\} . \end{aligned}$$

Multiplying the pervious formula \((I_{n}+\frac{1}{\xi } \nu \mathfrak{F}^{-1}\mu )^{-1}\) by \(\mathfrak{F}^{-1}\mu \) from the left and by \(\nu \mathfrak{F}^{-1}\) from the right, respectively, yields

$$\begin{aligned} &\mathfrak{F}^{-1}\mu \biggl(I_{n}+ \frac{1}{\xi }\nu \mathfrak{F}^{-1} \mu \biggr)^{-1}\nu \mathfrak{F}^{-1}=(k_{ij})^{n}_{i,j=1}, \end{aligned}$$
(24)

where

$$\begin{aligned}& k_{ij}= \frac{\xi }{\psi } \bigl[4\theta _{1}\xi ^{2}+ (\theta _{2} \alpha _{1}-\theta _{3}\alpha _{n}+\theta _{4}\gamma _{1}+ \theta _{5}\gamma _{n} )\xi +\theta _{6}(\alpha _{1}\gamma _{n}-\alpha _{n}\gamma _{1}) \bigr], \\& \theta _{1}= (\mathbb{F}_{n-i}-2) (\mathbb{F}_{j-2}-2)-( \mathbb{F}_{j-i}-1) ( \mathbb{F}_{i-1}-2) (\mathbb{F}_{n-1-j}-2), \\& \begin{aligned} \theta _{2}&= \frac{(\mathbb{F}_{n}-2)[2(\mathbb{F}_{n-i}-2)( \mathbb{F}_{j}-2)-(\mathbb{F}_{j-i+1}-1)(\mathbb{F}_{i-1}-2)( \mathbb{F}_{n+1-j}-2)]}{\mathbb{F}_{n+1}-2} \\ &\quad{} -\frac{3(\mathbb{F}_{n-i}-1)(\mathbb{F}_{i}-2)(\mathbb{F}_{j}-2)}{ \mathbb{F}_{n+1}-2}, \end{aligned} \\& \theta _{3}= (\mathbb{F}_{n-1}-1) (\mathbb{F}_{j-i+1}-2), \\& \theta _{4}= 2(\mathbb{F}_{j-i-1}-2), \\& \begin{aligned} \theta _{5}&= \frac{(\mathbb{F}_{n}-2)[2(\mathbb{F}_{n-i}-2)( \mathbb{F}_{j}-2)-(\mathbb{F}_{j-i+1}-1)(\mathbb{F}_{i-1}-2)( \mathbb{F}_{n+1-j}-2)]}{\mathbb{F}_{n+1}-2} \\ &\quad{} -\frac{3(\mathbb{F}_{j-1}-1)(\mathbb{F}_{n+1-i}-2)(\mathbb{F}_{n+1-j}-2)}{ \mathbb{F}_{n+1}-2}, \end{aligned} \\& \theta _{6}= (\mathbb{F}_{n-i}-2) (\mathbb{F}_{j}-2)-( \mathbb{F}_{j-i}-1) ( \mathbb{F}_{i-1}-2) (\mathbb{F}_{n+1-j}-2), \\& \begin{aligned} \psi &= 4(\mathbb{F}_{n-3}-2)\xi ^{2}+\bigl[2( \mathbb{F}_{n-2}-2) (\alpha _{1}+\gamma _{n})-( \mathbb{F}_{n-1}-1)\alpha _{n}-\gamma _{1}\bigr]\xi \\ &\quad{} +(\mathbb{F}_{n-1}-2) (\alpha _{1}\gamma _{n}-\alpha _{n}\gamma _{1}). \end{aligned} \end{aligned}$$

From (21) and (24) we have

$$\begin{aligned} (\breve{a}_{i,j})^{n}_{i,j=1} &= \frac{1}{\xi }\mathfrak{F}^{-1}-\frac{1}{ \xi ^{2}}(k_{ij})^{n}_{i,j=1}, \end{aligned}$$
(25)

where

$$\begin{aligned}& \breve{a}_{i,j}= \frac{\mathbb{F}_{j-i+1}}{ \xi }-\frac{k_{i,j}}{\xi ^{2}},\quad 1\leq i \leq j\leq n, \end{aligned}$$
(26)
$$\begin{aligned}& \breve{a}_{i,j}= \frac{2\mathbb{F}_{j-i-1}}{ \xi }-\frac{k_{i,j}}{ \xi ^{2}},\quad 1\leq j< i \leq n. \end{aligned}$$
(27)

By (26) we compute

$$\begin{aligned} &\breve{a}_{1,1}=\frac{2(\mathbb{F}_{n-2}-2)\xi +(\mathbb{F}_{n-1}-2) \gamma _{n}}{\psi }, \\ &\breve{a}_{1,2}=\frac{4(\mathbb{F}_{n-3}-2)\xi -\gamma _{1}+2( \mathbb{F}_{n-2}-2)\gamma _{n}}{\psi }, \\ &\breve{a}_{2,2}=\frac{2(\mathbb{F}_{n-3}-2)\alpha _{1}\xi +( \mathbb{F}_{n-2}-2)(\alpha _{1}\gamma _{n}-\alpha _{n}\gamma _{1})}{- \psi \xi }. \end{aligned}$$

By (27) we compute

$$\begin{aligned} &\breve{a}_{2,1}=\frac{2(\mathbb{F}_{n-3}-2)\xi -(\mathbb{F}_{n-2}-1) \alpha _{n}+(\mathbb{F}_{n-2}-2)\gamma _{n}}{\psi }. \end{aligned}$$

This completes the proof. □

Remark 1

Formulas (26) and (27) would give an analytic formula for \(A^{-1}\). However, there is a big advantage of (12) from computational consideration, as we shall see from Sect. 3.

The next two theorems are parallel results of type I matrices.

Theorem 3

Let A be given as in (1), and let B be a periodic tridiagonal Toeplitz matrix with perturbed corners of type II, which is induced by A. Then

$$\begin{aligned} \det B={} &(-\xi )^{n-2} \bigl\{ 4(\mathbb{F}_{n-3}-2)\xi ^{2}+ \bigl[2( \mathbb{F}_{n-2}-2) (\alpha _{1}+ \gamma _{n})-(\mathbb{F}_{n-1}-1)\alpha _{n} \\ &{}-\gamma _{1} \bigr]\xi +(\mathbb{F}_{n-1}-2) (\alpha _{1}\gamma _{n}- \alpha _{n}\gamma _{1}) \bigr\} , \end{aligned}$$

where \(\mathbb{F}_{i}\) (\(i=n-3,n-2,n-1\)) is the ith Fermat number.

Proof

Since \(\det B=\det \hat{I}_{n}\det A \det \hat{I}_{n}\), we obtain this conclusion by using Theorem 1 and \(\det \hat{I}_{n}=(-1)^{ \frac{n(n-1)}{2}}\). □

Theorem 4

Let A be given as in (1), and let B be a periodic tridiagonal Toeplitz matrix with perturbed corners of type II, which is induced by A. Then

$$ B^{-1} =(\breve{a}_{n+1-i,n+1-j})^{n}_{i,j=1}, $$

where \(\breve{a}_{i,j}\) is as in (12).

Proof

It follows immediately from \({B}^{-1}= \hat{I}^{-1}_{n}{A}^{-1} \hat{I}^{-1}_{n}= \hat{I}_{n}{A}^{-1}\hat{I}_{n}\) and Theorem 2. □

3 Numerical experiments

In this section, we give two algorithms for finding the determinant and inverse of a periodic tridiagonal Toeplitz matrix with perturbed corners of type I, which is called A. Besides, we make some analysis of these algorithms to illustrate our theoretical results.

Firstly, based on Theorem 1, we give an algorithm for computing determinant of A:

Algorithm 1

Step 1::

Input \(\alpha _{1}\), \(\alpha _{n}\), \(\gamma _{1}\), \(\gamma _{n}\), ξ, order n and generate Fermat numbers \(\mathbb{F}_{i}\) (\(i=n-3,n-2,n-1\)) by (2).

Step 2::

Calculate and output the determinant of A by (4).

Based on Algorithm 1, we make a comparison of the total number of operations for determinant of A between LU decomposition and Algorithm 1 in Table 1. Specifically, we get that the total number of operations for the determinant of A is \(2n+24\). Moreover, this number can be reduced to \(O(\log n)\) (see [36], pp. 226–227).

Table 1 Comparison of the total number operations for determinant of A
Full size table

Next, based on Theorem 2, we give an algorithm for computing inverse of A:

Algorithm 2

Step 1::

Input \(\alpha _{1}\), \(\alpha _{n}\), \(\gamma _{1}\), \(\gamma _{n}\), ξ, order n and generate Fermat numbers \(\mathbb{F}_{i}\) (\(i=n-3,n-2,n-1\)) by (2).

Step 2::

Calculate ψ by (13), four initial values \(\breve{a}_{1,1}\), \(\breve{a}_{1,2}\), \(\breve{a}_{2,1}\), and \(\breve{a} _{2,2}\) by (12).

Step 3::

Calculate the remaining elements of the inverse:

$$\begin{aligned}& \breve{a}_{2,3} =3\breve{a}_{2,2}-2\breve{a}_{2,1}+ \frac{1}{\xi }, \\& \breve{a}_{3,2} =\frac{3}{2}\breve{a}_{2,2}- \frac{1}{2}\breve{a}_{2,1}+\frac{1}{2 \xi }, \\& \breve{a}_{i,j} =3\breve{a}_{i,j-1}-2\breve{a}_{i,j-2}, \quad i\in {\{1,2\}}, i+2\leq j\leq n, \\& \breve{a}_{i,j} =\frac{3}{2}\breve{a}_{i-1,j}- \frac{1}{2}\breve{a} _{i-2,j}, \quad j\in {\{1,2\}}, j+2\leq i\leq n, \\& \breve{a}_{i,j} =3\breve{a}_{i,j-1}-2\breve{a}_{i,j-2}, \quad 3\leq j \leq i\leq n, \\& \breve{a}_{i,j} =\frac{3}{2}\breve{a}_{i-1,j}- \frac{1}{2}\breve{a} _{i-2,j},\quad 3\leq i< j\leq n. \end{aligned}$$
Step 4::

Output the inverse \(A^{-1}=(\breve{a}_{i,j})^{n}_{i,j=1}\).

To test the effectiveness of Algorithm 2, we compare the total number of operations for the inverse of A between LU decomposition and Algorithm 2 in Table 2. The total number operation of LU decomposition is \(\frac{ n^{3}}{2}+n^{2}+\frac{ 43n}{2}-30\), whereas that of Algorithm 2 is \(\frac{ 7n^{2}}{2}-\frac{ 11n}{2}+63\).

Table 2 Comparison of the total number of operations for the inverse of A
Full size table

4 Conclusions

In this paper, we present explicit formulas for the determinants and inverses of periodic tridiagonal Toeplitz matrices with perturbed corners. The representation of the determinant in the form of products of the Fermat number and some initial values from matrix transformations. For the inverse, our main approach includes a clever use of matrix decomposition with the Sherman–Morrison–Woodbury formula. To test the effectiveness of our method, we propose two algorithms for finding the determinant and inverse of periodic tridiagonal Toeplitz matrices with perturbed corners and compare the total number of operations for two basic quantities between different algorithms. After comparison, we draw a conclusion that our algorithms are superior to other algorithms to some extent.