1 Introduction

The classic neoclassical growth model with time delay can be described as follows:

$$ y'(t)=-\alpha y(t)+\beta y^{\gamma }(t-\tau )e^{-\delta y(t-\tau )}, $$
(1.1)

with the initial conditions

$$ y(s)=\varphi (s) \quad \text{for } s\in [-\tau ,0],\varphi \in C\bigl([-\tau ,0],R^{+}\bigr), \varphi (0)>0. $$
(1.2)

Here, \(R^{+}=[0,+\infty )\), y is the capital per labor, τ is the delay in the production process, \(\alpha =n+s\mu \) with μ being the depreciation ratio of capital, n is the growth rate of labor, and \(s\in (0,1)\) is the average propensity to save. Moreover, the other positive parameters β, γ, and δ possess obvious economic meanings. For more details on the background of model (1.1), one can refer to the literature [1, 2].

It is easy to see that model (1.1), a determinate delay differential equation, was first presented by Matsumoto and Szidarovszky [1, 3] who created the economic model based on the work of Day [4,5,6], Solow [7], Swan [8], Puu [9], and Bischi et al. [10]. Furthermore, delay differential neoclassical growth model with variable coefficients and delays is also examined in [11,12,13,14,15,16].

Nevertheless, environmental noises often interfere in the delay differential neoclassical growth model. Indeed, May [17] have pointed out that in the population model, because of environmental noises, many parameters involved with the system, such as growth rates, environmental capacity, competition coefficient, and so on, exhibit random fluctuation to some degree. Since the neoclassical growth model is always affected by environmental noises, the stochastic model is more suitable in the real world. However, to the best of our knowledge, almost no one considered the stochastic delay differential neoclassical growth model except Shaikhet [18], who has studied the stability of equilibriums of stochastically perturbed delay differential neoclassical growth model.

Suppose that environmental noises disturb the parameter α, the stochastically perturbed model is described by the stochastic delay differential equation

$$ dy(t)=\bigl[-\alpha y(t)+\beta y^{\gamma }(t-\tau )e^{-\delta y(t-\tau )}\bigr] \,dt+ \sigma y(t)\,dB(t), $$
(1.3)

where \(B(t)\) is a one-dimensional Brownian motion with \(B(0)=0\) defined on a complete probability space \((\varOmega ,\{\mathcal{F}_{t}\}_{t \geq 0},\mathcal{P})\), \(\sigma ^{2}\) denotes the intensity of the noise.

This paper has two purposes. One is to find the criteria to guarantee the unique global positive solution, and the other is to estimate the ultimate boundedness and the sample Lyapunov exponent of (1.3).

Let us quickly sketch the structure of the paper. In Sect. 2, we obtain a simple condition that ensures the global positive solution of (1.3) exists uniquely almost surely. Next, we estimate its the ultimate boundedness in mean and the sample Lyapunov exponent in Sect. 3. In Sect. 4, we present a test example with numerical simulation to support the main results. Finally, we conclude and expect our results in the last section.

2 Preliminary results

In this section, some basic definitions and lemmas are provided in order to prove the main result in the next section.

Definition 2.1

(See [19])

If there is independent of initial conditions (1.2) \(L>0\) satisfying

$$ \limsup_{t\rightarrow \infty }E \bigl\vert y(t) \bigr\vert \leq L, $$

then equation (1.3) is said to be ultimately bounded in mean.

Lemma 2.1

If \(\alpha >\frac{\sigma ^{2}}{2}\), then for any \(y\in R\),

$$\begin{aligned}& -\bigl(2\alpha -\sigma ^{2}\bigr)y^{2}+2 \frac{\beta \gamma ^{\gamma }}{ \delta ^{\gamma }e^{\gamma }}y\leq K\bigl(1+y^{2}\bigr), \end{aligned}$$
(2.1)
$$\begin{aligned}& -\bigl(2\alpha -\sigma ^{2}\bigr)y^{2}+2 \frac{\beta \gamma ^{\gamma }}{ \delta ^{\gamma }e^{\gamma }}y\leq \frac{\beta ^{2}\gamma ^{2\gamma }}{(2 \alpha -\sigma ^{2})\delta ^{2\gamma }e^{2\gamma }}, \end{aligned}$$
(2.2)

where \(K=\min \{\frac{\beta ^{2}\gamma ^{2\gamma }}{(2\alpha -\sigma ^{2})\delta ^{2\gamma }e^{2\gamma }},\frac{\beta \gamma ^{\gamma }}{ \delta ^{\gamma }e^{\gamma }}\}\).

Proof

It is easy to analyze the property of the quadratic function, so we omit the proof. □

Lemma 2.2

If \(\alpha >\frac{\sigma ^{2}}{2}\), then for any given initial condition (1.2), (1.3) has a unique solution \(y(t)\) on \([0,+\infty )\) and \(y(t)\) is positive almost surely for \(t\geq 0\).

Proof

Because the constant coefficients of the equations are locally Lipschitz continuous, there is a unique max local solution \(y(t)\) on \([-\tau , \tau _{e})\) for initial condition (1.2), where \(\tau _{e}\) is explosion time. Firstly, we prove \(y(t)>0\) on \([0, \tau _{e}]\) almost surely. We will deal with it stage by stage. For \(t\in [0, \tau ]\), model (1.3) with initial condition (1.2) becomes the following linear stochastic differential equations:

$$ \textstyle\begin{cases} dy(t)=[-\alpha y(t)+b_{1}(t)]\,dt+\sigma y(t)\,dB(t), \\ y_{0}=\varphi (0)>0, \end{cases} $$
(2.3)

where \(b_{1}(t)=\beta \varphi ^{\gamma }(t-\tau )e^{-\delta \varphi (t- \tau )}\geq 0\) a.s., \(t\in [0,\tau ]\). It is easy to see that (2.3) has the explicit solution \(y(t)=e^{-(\alpha -\frac{\sigma ^{2}}{2})t+ \sigma B(t)}[y(0)+\int _{0}^{t}e^{(\alpha -\frac{\sigma ^{2}}{2})s- \sigma B(s)}b_{1}(s)\,ds]>0\) a.s. for \(t\in [0,\tau ]\). Next, on \(t\in [\tau ,2\tau ]\), (1.3) becomes the following linear stochastic differential equation:

$$ \textstyle\begin{cases} dy(t)=[-\alpha y(t)+b_{2}(t)]\,dt+\sigma y(t)\,dB(t), \\ y_{\tau }=y(\tau )>0\quad \mbox{a.s.}, \end{cases} $$
(2.4)

where \(b_{2}(t)=\beta y^{\gamma }(t-\tau )e^{-\delta y(t-\tau )}>0\) a.s., \(t\in [\tau ,2\tau ]\). Also, (2.4) has the explicit solution \(y(t)=e^{-(\alpha -\frac{\sigma ^{2}}{2})(t-\tau )+\sigma (B(t)-B( \tau ))}[y(\tau )+\int _{\tau }^{t}e^{(\alpha -\frac{\sigma ^{2}}{2})s- \sigma B(s)}b_{2}(s)\,ds]>0\) a.s. for \(t\in [\tau ,2\tau ]\). This process can be repeated to demonstrate that for any integer \(m\geq 1\), \(y(t)>0\) on \([m\tau , (m+1)\tau ]\) a.s. Hence, model (1.3) with initial condition (1.2) has the unique solution \(y(t)>0\) almost surely for \(t\in [0, \tau _{e}]\).

In order to prove this solution is global, it is sufficient to show \(\tau _{e}=\infty \) a.s. Let \(k_{0}>0\) be sufficiently large such that \(\max_{-\tau \leq t\leq 0}|y(t)|< k_{0}\). For every integer \(k\geq k_{0}\), define the stopping time

$$ \tau _{k}=\inf \bigl\{ t\in [0, \tau _{e}): y(t)\geq k \bigr\} , $$

where \(\inf \phi =\infty \) (ϕ is the empty set). It is obvious that \(\tau _{k}\) is increasing as \(k\rightarrow \infty \). Set \(\tau _{\infty }=\lim_{k\rightarrow \infty }\tau _{k}\), where \(\tau _{\infty }\leq \tau _{e}\) a.s. If we can show that \(\tau _{\infty }=\infty \) a.s., then \(\tau _{e}=\infty \) a.s.

Define a \(C^{2}\)-function \(V(y)=y^{2}\). Let \(k\geq k_{0}\) and \(T>0\) be arbitrary. It follows from the Itô formula that, for \(0\leq t\leq \tau _{k}\wedge T\),

$$ dV\bigl(y(t)\bigr)=LV\bigl(y(t),y(t-\tau )\bigr)\,dt+2\sigma V\bigl(y(t)\bigr) \,dB(t), $$
(2.5)

where \(LV:R\times R\rightarrow R\) is defined by \(LV(x_{1},x_{2})=-(2 \alpha -\sigma ^{2})x_{1}^{2}+2\beta x_{1}x_{2}^{\gamma }e^{-\delta x _{2}}\). Using (2.2) and noting the fact that \(\sup_{x\in R^{+}}x ^{\gamma }e^{-x}=\frac{\gamma ^{\gamma }}{e^{\gamma }}\), we can show that

$$ LV\bigl(y(t),y(t-\tau )\bigr)\leq -\bigl(2\alpha -\sigma ^{2} \bigr)y^{2}(t)+2\frac{\beta \gamma ^{\gamma }}{\delta ^{\gamma }e^{\gamma }} \bigl\vert y(t) \bigr\vert \leq \frac{\beta ^{2}\gamma ^{2\gamma }}{(2\alpha -\sigma ^{2})\delta ^{2\gamma }e^{2 \gamma }}. $$
(2.6)

In view of (2.6), we obtain from (2.5) that

$$ dV\bigl(y(t)\bigr)\leq \frac{\beta ^{2}\gamma ^{2\gamma }}{(2\alpha -\sigma ^{2}) \delta ^{2\gamma }e^{2\gamma }}\,dt+2\sigma V\bigl(y(t)\bigr) \,dB(t). $$
(2.7)

For any \(t_{1}\in [0,T]\), integrating both sides of (2.7) from 0 to \(\tau _{k}\wedge t_{1}\) yields

$$ V\bigl(y(\tau _{k}\wedge t_{1})\bigr)\leq V\bigl(y(0) \bigr)+ \int _{0}^{\tau _{k}\wedge t_{1}} \frac{\beta ^{2}\gamma ^{2\gamma }}{(2\alpha -\sigma ^{2})\delta ^{2 \gamma }e^{2\gamma }}\,dt+ \int _{0}^{\tau _{k}\wedge t_{1}} 2\sigma V\bigl(y(t)\bigr)\,dB(t). $$

This implies

$$ EV\bigl(y(\tau _{k}\wedge t_{1})\bigr)\leq V\bigl(y(0) \bigr)+E \int _{0}^{\tau _{k}\wedge t _{1}} \frac{\beta ^{2}\gamma ^{2\gamma }}{(2\alpha -\sigma ^{2}) \delta ^{2\gamma }e^{2\gamma }}\,dt\leq \widetilde{K}, $$
(2.8)

where \(\widetilde{K}= V(y(0))+ \frac{T\beta ^{2}\gamma ^{2\gamma }}{(2 \alpha -\sigma ^{2})\delta ^{2\gamma }e^{2\gamma }}\). Specially, \(EV(y(\tau _{k}\wedge T))\leq \widetilde{K}\) for all \(k\geq k_{0}\).

It is clear that \(V(y(\tau _{k},\omega ))\geq k^{2}\) for every \(\omega \in \{\tau _{k}< T\}\). Then we obtain from (2.8) that

$$ \widetilde{K}\geq EV\bigl(y(\tau _{k}\wedge T)\bigr)\geq E \bigl[I_{\{\tau _{k}< T\}}( \omega )V\bigl(y(\tau _{k},\omega )\bigr) \bigr]\geq P{\{\tau _{k}< T\}}k^{2}, $$

where \(I_{\{\tau _{k}< T\}}\) is the indicator function of \(\{\tau _{k}< T \}\). Letting \(k\rightarrow \infty \) gives \(\lim_{k\rightarrow \infty }P\{\tau _{k}\leq T\}=0\), so \(P\{ \tau _{\infty }\leq T\}=0\). Because \(T>0\) is arbitrary, we obtain \(P\{\tau _{\infty }< \infty \}=0\). Hence \(P\{\tau _{\infty }= \infty \}=1\) is proved and the proof of Lemma 2.2 is completed. □

Remark 2.1

It is amusing to find from Lemma 2.2 that the local existence of positive solution of (1.3) with (1.2) is independent of noise intensities, but the global existence of positive solution is no longer, which is verified by (2.2).

3 Main results

In this section we present a criterion for the ultimate boundedness in mean of model (1.3), which is an important property in the stochastic population model.

Theorem 3.1

Let \(\alpha >\frac{\sigma ^{2}}{2}\) hold and \(y(t)\) be the global solution of (1.3) for any given initial value (1.2). Then \(y(t)\) is positive almost surely on \(t\geq 0\) and it has the properties that

$$ \limsup_{t\rightarrow \infty }Ey(t)\leq \frac{\beta \gamma ^{\gamma }}{\alpha \delta ^{\gamma }e^{\gamma }} $$
(3.1)

and

$$ \limsup_{t\rightarrow \infty }\frac{1}{t} \int _{0}^{t}Ey^{2}(s)\,ds \leq \frac{4\beta ^{2}\gamma ^{2\gamma }}{(2\alpha -\sigma ^{2})^{2} \delta ^{2\gamma } e^{2\gamma }} . $$
(3.2)

In particular, (1.3) is ultimately bounded in mean.

Proof

In view of Lemma 2.2, it is easy to see that \(y(t)>0\) on \(t\geq 0\) almost surely. Again using (1.1) and the formula \(\sup_{x\in R^{+}}x^{\gamma }e^{-x}=\frac{\gamma ^{\gamma }}{e ^{\gamma }}\), we have

$$ dy(t)\leq \biggl(-\alpha y(t)+\frac{\beta \gamma ^{\gamma }}{\delta ^{\gamma }e^{\gamma }}\biggr)\,dt+\sigma y(t) \,dB(t). $$
(3.3)

This, with the help of the Itô formula, implies that

$$ d\bigl[e^{\alpha t}y(t)\bigr]=e^{\alpha t}\bigl[\alpha y(t) \,dt+dy(t)\bigr]\leq \frac{ \beta \gamma ^{\gamma }}{\delta ^{\gamma }e^{\gamma }}e^{\alpha t}\,dt+ \sigma e^{\alpha t}y(t)\,dB(t). $$
(3.4)

So

$$ e^{\alpha t}Ey(t)\leq y(0)+ \int _{0}^{t}\frac{\beta \gamma ^{\gamma }}{ \delta ^{\gamma }e^{\gamma }}e^{\alpha s} \,ds=y(0)+\frac{\beta \gamma ^{\gamma }}{\alpha \delta ^{\gamma }e^{\gamma }}\bigl(e^{\alpha t}-1\bigr). $$

This yields \(\limsup_{t\rightarrow \infty }Ey(t)\leq \frac{ \beta \gamma ^{\gamma }}{\alpha \delta ^{\gamma }e^{\gamma }}\). To show the other assertion (3.2), we derive from (2.5) and (2.6) that

$$\begin{aligned} d\bigl[y^{2}(t)\bigr] = & \bigl[-\bigl(2\alpha -\sigma ^{2}\bigr) y^{2}(t)+2\beta y(t)y^{ \gamma }(t-\tau )e^{-\delta y(t-\tau )}\bigr]\,dt+2\sigma y^{2}(t)\,dB(t) \\ \leq &\biggl[-\bigl(2\alpha -\sigma ^{2}\bigr) y^{2}(t)+2 \frac{\beta \gamma ^{\gamma }}{ \delta ^{\gamma }e^{\gamma }} \bigl\vert y(t) \bigr\vert \biggr]\,dt+2\sigma y^{2}(t)\,dB(t). \end{aligned}$$

This implies

$$ 0\leq Ey^{2}(t)\leq y^{2}(0)+E\biggl[ \int _{0}^{t}\biggl(-\bigl(2\alpha -\sigma ^{2}\bigr) y ^{2}(s)+2\frac{\beta \gamma ^{\gamma }}{\delta ^{\gamma }e^{\gamma }} \bigl\vert y(s) \bigr\vert \biggr)\,ds\biggr]. $$
(3.5)

Noting \(-(\alpha -\frac{\sigma ^{2}}{2}) y^{2}(s)+2\frac{\beta \gamma ^{\gamma }}{\delta ^{\gamma }e^{\gamma }}|y(s)|\leq \frac{2\beta ^{2}\gamma ^{2\gamma }}{(2\alpha -\sigma ^{2})\delta ^{2\gamma } e^{2 \gamma }}\), we obtain from (3.5) that

$$ \biggl(\alpha -\frac{\sigma ^{2}}{2}\biggr) \int _{0}^{t}Ey^{2}(s)\,ds\leq y^{2}(0)+\frac{2 \beta ^{2}\gamma ^{2\gamma }}{(2\alpha -\sigma ^{2})\delta ^{2\gamma } e ^{2\gamma }}t, $$

which suggests that

$$ \limsup_{t\rightarrow \infty }\frac{1}{t} \int _{0}^{t}Ey^{2}(s)\,ds \leq \frac{4\beta ^{2}\gamma ^{2\gamma }}{(2\alpha -\sigma ^{2})^{2} \delta ^{2\gamma } e^{2\gamma }} . $$

So the proof is now completed. □

Theorem 3.2

Let \(\alpha >\frac{\sigma ^{2}}{2}\) hold. Then the sample Lyapunov exponent of the solution of (1.3) with (1.2) should not be greater than \(\frac{K}{2}\), that is,

$$ \limsup_{t\rightarrow \infty }\frac{1}{t}\ln y(t)\leq \frac{K}{2}, \quad \textit{a.s.} $$
(3.6)

Proof

Using the Itô formula and the fact \(\sup_{x\in R^{+}}x^{\gamma }e^{-x}=\frac{\gamma ^{\gamma }}{e ^{\gamma }}\) once more, we obtain from (1.3) and (2.1) that

$$\begin{aligned} \ln \bigl(1+y^{2}(t)\bigr) = & \ln \bigl(1+y^{2}(0) \bigr)+ \int _{0}^{t} \frac{1}{1+y^{2}(s)}\bigl[- \bigl(2\alpha -\sigma ^{2}\bigr)y^{2}(s) \\ &{}+2\beta y(s)y^{\gamma }(s-\tau )e^{-\delta y(s-\tau )}\bigr]\,ds-2 \int _{0} ^{t}\frac{\sigma ^{2} y^{4}(s)}{(1+y^{2}(s))^{2}}\,ds+M(t) \\ \leq &\ln \bigl(1+y^{2}(0)\bigr)+ \int _{0}^{t}\frac{1}{1+y^{2}(s)}\biggl[- \bigl(2\alpha - \sigma ^{2}\bigr)y^{2}(s) \\ &{}+2\frac{\beta \gamma ^{\gamma }}{\delta ^{\gamma }e^{\gamma }}y(s)\biggr]\,ds-2 \int _{0}^{t}\frac{\sigma ^{2} y^{4}(s)}{(1+y^{2}(s))^{2}}\,ds+M(t) \\ \leq &\ln \bigl(1+y^{2}(0)\bigr)+Kt-2 \int _{0}^{t}\frac{\sigma ^{2} y^{4}(s)}{(1+y ^{2}(s))^{2}}\,ds+M(t), \end{aligned}$$
(3.7)

where \(M(t)=2\int _{0}^{t}\frac{\sigma y^{2}(s)}{1+y^{2}(s)}\,dB(s)\). For every \(n\geq 0\), application of the known exponential martingale inequality (Theorem 1.7.4 of [20]) yields

$$ P\biggl\{ \sup_{0\leq t\leq n}\biggl[M(t)-2 \int _{0}^{t}\frac{\sigma ^{2} y ^{4}(s)}{(1+y^{2}(s))^{2}}\,ds\biggr]>2 \ln n \biggr\} \leq \frac{1}{n^{2}}. $$

Using the Borel–Cantelli lemma, one sees that for almost all \(\omega \in \varOmega \) there are random integers \(n_{0}=n_{0}(\omega ) \geq 1\) such that

$$ \sup_{0\leq t\leq n}\biggl[M(t)-2 \int _{0}^{t}\frac{\sigma ^{2} y^{4}(s)}{(1+y ^{2}(s))^{2}}\,ds\biggr] \leq 2\ln n \quad \text{if } n\geq n_{0}. $$

That is,

$$ M(t)\leq 2 \int _{0}^{t}\frac{\sigma ^{2} y^{4}(s)}{(1+y^{2}(s))^{2}}\,ds+2 \ln n $$
(3.8)

for all \(0\leq t\leq n\), \(n\geq n_{0}\) almost surely. Then (3.7), together with (3.8), implies that

$$ \ln \bigl(1+y^{2}(t)\bigr)\leq \ln \bigl(1+y^{2}(0) \bigr)+Kt+2\ln n $$

for all \(0\leq t\leq n\), \(n\geq n_{0}\) almost surely. Hence, for almost all \(\omega \in \varOmega \), if \(n\geq n_{0}\), \(n-1\leq t\leq n\), we get

$$ \frac{1}{t}\ln \bigl(1+y^{2}(t)\bigr)\leq \frac{1}{n-1}\bigl[\ln \bigl(1+y^{2}(0)\bigr)+Kn+2 \ln n \bigr]. $$

This implies

$$\begin{aligned} \limsup_{t\rightarrow \infty }\frac{1}{t}\ln y(t) \leq & \limsup _{t\rightarrow \infty }\frac{1}{2t}\ln \bigl(1+y^{2}(t) \bigr) \\ \leq & \limsup_{n\rightarrow \infty }\frac{1}{2(n-1)}\bigl[\ln \bigl(1+x ^{2}(0)\bigr)+Kn+2\ln n\bigr]=\frac{K}{2} \quad \mbox{a.s.} \end{aligned}$$

The proof is over. □

Remark 3.1

One can surprisingly find that the condition \(\alpha >\frac{\sigma ^{2}}{2}\) depends on noise intensity but statement (3.1) does no more. In other words, the ultimate boundedness in mean of (1.3) will fix under small noises. Namely, the property of this boundedness is robust when the environmental noise is small.

4 An example and its numerical simulations

In this section, we provide a test example with numerical simulations to illustrate the main results.

Example 4.1

Consider the following stochastic delay differential neoclassical growth model:

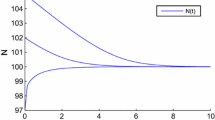
$$ dy(t)=\bigl[-0.0011y(t)+0.02y^{2}(t-1)e^{- y(t-1)}\bigr] \,dt+0.0447y(t)\,dB(t). $$
(4.1)

Obviously, \(\alpha =0.0011\), \(\gamma =2\), \(\beta =0.02\), \(\delta = \tau =1\), \(\sigma =0.0447\), and \(\alpha \geq \frac{\sigma ^{2}}{2}\) hold. In view of Theorems 3.1 and 3.2, we conclude that the solution of system (4.1) satisfies \(\limsup_{t\rightarrow \infty }Ey(t)\leq \frac{80}{11e ^{2}}\), \(\limsup_{t\rightarrow \infty }\frac{1}{t}\int _{0}^{t}Ey ^{2}(s)\,ds\leq \frac{640{,}000}{e^{4}}\), and \(\limsup_{t\rightarrow \infty }\frac{1}{t}\ln y(t)\leq \frac{2}{25e ^{2}}\), a.s. Based on Milstein’s numerical method [21], one can verify this fact in numerical simulations of Fig. 1.

Figure 1
figure 1

Numerical solutions of (4.1) for the initial value 0.1, 0.2, 0.3

Full size image

5 Conclusions

In this paper, we consider the delay differential neoclassical growth model under a stochastic perturbation. This perturbation is of the white noise type that is directly proportional to the model state. Moreover, we deduce the simple sufficient condition \(\alpha > \frac{\sigma ^{2}}{2}\) that guarantees the global positive solution of (1.3) exists uniquely, and we estimate its ultimate boundedness and sample Lyapunov exponent. In particular, all results of [22] are the special situations of this paper with \(\gamma =1\). It is easy to see that if environmental noises are sufficiently large such that the condition \(\alpha >\frac{\sigma ^{2}}{2}\) does not hold, then Lemma 2.2, Theorems 3.1 and 3.2 are invalid. The future work consists of two parts. One is to find conditions weaker than \(\alpha >\frac{\sigma ^{2}}{2}\) such that all the results of this paper still hold. The other is to study deeply dynamic behaviors of the addressed model, such as persistence, extinction, and so on.