Mixed $H_{\infty }/$passive exponential function projective synchronization of delayed neural networks with hybrid coupling based on pinning sampled-data control

Abstract

This paper presents the problem of mixed $H_{\infty }$/passive exponential function projective synchronization of delayed neural networks with constant discrete and distributed delay couplings under pinning sampled-data control scheme. The aim of this work is to focus on designing of pinning sampled-data controller with an explicit expression by which the stable synchronization error system is achieved and a mixed $H_{\infty }$/passive performance level is also reached. Particularly, the control method is designed to determine a set of pinned nodes with fixed coupling matrices and strength values, and to select randomly pinning nodes. To handle the Lyapunov functional, we apply some new techniques and then derive some sufficient conditions for the desired controller existence. Furthermore, numerical examples are given to illustrate the effectiveness of the proposed theoretical results.

1 Introduction

In the recent decades, neural networks (NNs) have been extensively investigated and widely applied in various research fields, for instance, optimization problem, pattern recognition, static image processing, associative memory, and signal processing [1,2,3,4]. In many engineering applications, time delay is one of the typical characteristics in the processing of neurons and plays an important role in causing the poor performance and instability or leading to some dynamic behaviors such as chaos, instability, divergence, and others [5,6,7,8,9]. Therefore, time-delay NNs have received considerable attention in many fields of application.

In the research on stability of neural networks, exponential stability is a more desired property than asymptotic stability because it provides faster convergence rate to the equilibrium point and gives information about the decay rates of the networks. Hence, it is especially important, when the exponential stability property guarantees that, whatever transformation happens, the network stability to store rapidly the activity pattern is left invariant by self-organization [10, 11].

Amongst all kinds of NN behaviors, synchronization is a significant and attractive phenomenon, and it has been studied in various fields of science and engineering [12,13,14]. The synchronization in the network is categorized into two types namely inner and outer synchronization. For inner synchronization, it is a collective behavior within the network and most of the researchers have focused on this type [15, 16]. For outer synchronization, it is a collective behavior between two or more networks [17,18,19].

Furthermore, function projective synchronization (FPS), a generalization of projective synchronization (PS), is one of the synchronization techniques, where two identical (or different) chaotic systems can synchronize up to a scaling function matrix with different initial values. The technique has been widely studied to get a faster chemical rate with its proportional property. Apparently, the unpredictability of the scaling function in FPS can additionally improve the rate of chemical reaction. Recently, many researchers have focused on the exponential stability on function projective synchronization of neural networks [20,21,22].

Passivity theory is an excellent way to determine the stability of a dynamical system. It uses only the general characteristics of the input–output dynamics to present solutions for the proof of absolute stability. Passivity theory formed a fundamental aspect of control systems and electrical networks, in fact its roots can be traced in circuit theory. Recently, a lot of research has been conducted in relation to designing a passive filter for different kinds of systems, for example time-varying uncertain systems, nonlinear systems and switched systems [10, 11, 23]. On the other hand, the problem of $H_{\infty }$ control has been many discussed for neural networks with time delay because the $H_{\infty }$ controller design looks to reduce of the effects of external inputs and minimizes the frequency response peak of the system. Recently, [24] was published. For these reasons, lately the passive control problem and $H_{\infty }$ control problem came to be solved in a unified framework. Then the mixed $H_{\infty }$ and passive filtering problem for the continuous-time singular system has been investigated [25,26,27]. The deterministic input is presented with bounded energy through the $H_{\infty }$ setting together with the passivity theory [27, 28]. As stated above, a lot of research has been conducted in this area. However, relatively little research has been conducted into the problem of mixed $H_{\infty }$ and passive filtering design in discrete-time domain. Consequently, this paper attempts to highlight the benefits of the mixed $H_{\infty }$ and passive filters for discrete-time impulse NCS with the plant being a Markovian jump system.

Nowadays, continuous-time control, for instance, feedback control, adaptive control, has been mainly used for synchronization analysis. The main point in implementing such continuous-time controllers is that the control input must be continuous, which we cannot always ensure in real-time situations. Moreover, due to advanced digital technology in measurement, the continuous-time controllers could be represented discrete-time controllers to achieve more stability, performance, and precision. So, plentiful research in sampled-data control theory has been conducted. By using a sampled-data controller, the sum of transferred information is dramatically decreased and bandwidth usage is consistent. It renders the control more reliable and handy in real world problems. In [29], one studied dissipative sampled-data control of uncertain nonlinear systems with time-varying delays, and so on [30,31,32,33,34]. Meanwhile, pinning control has been introduced to deal with the problem of large number of controllers added to large size of neural network structure [35,36,37,38,39]. In [40], pinning stochastic sampled-data control for exponential synchronization of directed complex dynamical networks with sampled-data communications has been addressed. The problem of exponential $H_{\infty }$ synchronization of Lur’e complex dynamical networks using pinning sampled-data control has been investigated in [41]. However, a pinning sampled-data control technique has not yet been implemented for NNs with inertia and reaction–diffusion terms. These motivate us to further study this in the present work.

As discussed above, this is the first time that mixed $H_{\infty }$/passive exponential function projective synchronization (EFPS) of delayed NNs with hybrid coupling based on pinning sampled-data control has been studied. Therefore, as a first attempt, this paper is meant to address this problem and the main contributions are summarized now:

• To solve the synchronization control problem for NNs, we introduce a simple actual mixed $H_{\infty }$/passive performance index and we make a comparison with a single $H_{\infty }$ design.

• We deal with the EFPS problem for NNs, which is both discrete and distributed time-varying delays consider in hybrid asymmetric coupling, is different from the time-delay case in [25, 28].

• For our control method, the EFPS is carefully studied via mixed nonlinear and pinning sample-data controls, which is different from previous work [34, 40, 41].

Based on constructing the Lyapunov–Karsovskii functional, the parameter update law and the method of handling Jensen’s and Cauchy inequalities, some novel sufficient conditions for the existence of the EFPS of NNs with mixed time-varying delays are achieved. Finally, numerical examples are given to present the benefit of using pinning sample-data controls.

The rest of the paper is organized as follows. Section 2 provides some mathematical preliminaries and a network model. Section 3 presents the EFPS of NNs with hybrid coupling based on pinning sampled-data control. Some numerical examples with theoretical results and conclusions are given in Sects. 4 and 5, respectively.

2 Problem formulation and preliminaries

Notations: The notations used throughout this work are as follows: $\mathcal{R}^{n}$ denotes the n-dimensional space; A matrix A is symmetric if $A=A^{T}$ where the superscript T stands for transpose matrix; $\lambda _{\max }(A)$ and $\lambda _{\min }(A)$ stand for the maximum and the minimum eigenvalues of matrix A, respectively. $z_{i}$ denotes the unit column vector having one element on its ith row and zeros elsewhere; $\mathcal{C}([a,b],\mathcal{R}^{n})$ denotes the set of continuous functions mapping the interval $[a,b]$ to $\mathcal{R}^{n}$; $\mathcal{L}_{2}[0,\infty )$ denotes the space of functions $\phi : \mathcal{R}^{+} \rightarrow \mathcal{R}^{n}$ with the norm $\|\phi \|_{\mathcal{L}_{2}} = [\int _{0}^{\infty }|\phi ( \theta )|^{2} \,d\theta ]^{\frac{1}{2}}$; For $z\in \mathcal{R} ^{n}$, the norm of z is defined by $\|z\| = [\sum_{i=1}^{n} |z _{i}|^{2} ]^{1/2}$; $\Vert z(t+\epsilon ) \Vert _{\mathrm{cl}}=\max \{ \sup_{ - \max \{ {\tau _{1}},{\tau _{2}},h\} \le \epsilon \le 0} { \Vert {z(t + \epsilon )} \Vert ^{2}}, \sup_{ - \max \{ {\tau _{1}},{\tau _{2}},h\} \le \epsilon \le 0} \Vert \dot{z}(t + \epsilon ) \Vert ^{2}\}$; $I_{N}$ denotes an N-dimensional identity matrix; the symbol ∗ denotes the symmetric block in a symmetric matrix. The symbol ⊗ denotes the Kronecker product.

Delayed NNs containing N identical nodes with hybrid couplings are given as follows:

$$\begin{aligned} \textstyle\begin{cases} \dot{x_{i}}(t)= -D x_{i}(t) +Af(x_{i}(t)) +Bf(x_{i}(t-\tau _{1}(t))) +C \int _{t-\tau _{2}(t)}^{t} f(x_{i}(\theta ))\,d\theta \\ \hphantom{\dot{x_{i}}(t)= } {}+c_{1}\sum_{j=1}^{N}g^{(1)}_{ij}L_{1}x_{j}(t) +c_{2}\sum_{j=1}^{N}g^{(2)}_{ij}L_{2}x_{j}(t-\tau _{1}(t)) \\ \hphantom{\dot{x_{i}}(t)= } {}+c_{3}\sum_{j=1}^{N}g^{(3)}_{ij}L_{3}\int _{t-\tau _{2}(t)}^{t} x _{j}(\theta )\,d\theta +u_{i}(t)+\omega _{i}(t), \\ y_{i}(t)=Jx_{i}(t), \quad i=1,2,\ldots , N, \end{cases}\displaystyle \end{aligned}$$

(1)

where $x_{i}(t)\in \mathcal{R}^{n}$ and $u_{i}(t)\in \mathcal{R}^{n}$ are the state variable and the control input of the node i, respectively. $y_{i}(t)\in \mathcal{R}^{l}$ are the outputs, $D=\operatorname{diag}(d_{1}, d_{2}, \ldots , d_{n})>0$ denotes the rate with which the cell i resets its potential to the resting state when being isolated from other cells and inputs. A, B and C are connection weight matrices. $\tau _{1}(t)$ and $\tau _{2}(t)$ are the time-varying delays. $f(x_{i} (\cdot )) = (f_{1}(x_{i1}(\cdot )),f_{2}(x_{i2}( \cdot )),\ldots ,f_{n}(x_{in}(\cdot ))]^{T}$ denotes the neuron activation function vector, the positive constants $c_{1}$, $c_{2}$ and $c_{3}$ are the strengths for the constant coupling and delayed couplings, respectively, $\omega _{i}(t)$ is the system’s external disturbance, which belongs to $\mathcal{L}[0, \infty )$, J is a known matrix with appropriate dimension, $L_{1}, L_{2}, L_{3} \in \mathcal{R}^{n\times n}$ are inner-coupling matrices with constant elements and $L_{1}$, $L_{2}$, $L_{3}$ are assumed as positive diagonal matrices, $G^{(q)}=(g^{(q)}_{ij})_{N\times N}$ ($q=1,2,3$) are the outer-coupling matrices and satisfy the following conditions:

$$\begin{aligned} \textstyle\begin{cases} g^{(q)}_{ij}\geq 0, & i\neq j, q=1,2,3, \\ g^{(q)}_{ii}=-{\sum_{j=1,j\neq i}^{N}} g^{(q)}_{ij}, & i,j=1,2,\ldots ,N, q=1,2,3. \end{cases}\displaystyle \end{aligned}$$

(2)

The following assumptions are made throughout this paper.

Assumption 1

The discrete delay $\tau _{1}(t)$ and distributed delay $\tau _{2}(t)$ satisfy the conditions $0\leq \tau _{1}(t)\leq \tau _{1}$, $\dot{\tau } _{1}(t)<\bar{\tau }_{1}$, and $0\leq \tau _{2}(t)\leq \tau _{2}$.

Assumption 2

The activation functions $f_{i}(\cdot )$, $i=1,2,\ldots ,n$, satisfy the Lipschitzian condition with the Lipschitz constants $\lambda _{i}>0$:

$$\begin{aligned} \bigl\Vert f_{i}\bigl(x(\theta )\bigr)-f_{i}\bigl( \alpha (t)y(\theta )\bigr) \bigr\Vert \leq & \lambda _{i} \bigl\Vert x(\theta )-\alpha (t)y(\theta ) \bigr\Vert , \end{aligned}$$

where Λ is positive constant matrix and $\varLambda = \operatorname{diag}\{\lambda _{i}, i=1,2,\ldots ,n\}$.

The isolated node of network (1) is given by the following delayed neural network:

$$\begin{aligned} \textstyle\begin{cases} \dot{s}(t)= -Ds(t) +Af(s(t)) +Bf(s(t-\tau _{1}(t))) +C \int _{t-\tau _{2}(t)}^{t} f(s(\theta ))\,d\theta , \\ y_{s}(t)=Js(t), \end{cases}\displaystyle \end{aligned}$$

(3)

where $s(t)=(s_{1}(t),s_{2}(t),\ldots ,s_{n}(t))^{T}\in \mathcal{R} ^{n}$ and the parameters D, A, B and C and the nonlinear functions $f (\cdot )$ have the same definitions as in (1).

The network (1) is said to achieve FPS if there exists a continuously differentiable positive function $\alpha (t)>0$ such that

$$ \lim_{t\rightarrow \infty } \bigl\Vert z_{i}(t) \bigr\Vert = \lim_{t\rightarrow \infty } \bigl\Vert x _{i}(t)-\alpha (t)s(t) \bigr\Vert , \quad i=1,2,\ldots ,N, $$

where $\|\cdot\|$ stands for the Euclidean vector norm and $s(t)\in \mathcal{R}^{n}$ can be an equilibrium point. Let $z_{i}(t)=x_{i}(t)- \alpha (t)s(t)$, be the synchronization error. Then, by substituting it into (1), it is easy to get the following:

$$\begin{aligned} \textstyle\begin{cases} \dot{z}_{i}(t) =\dot{x}_{i}(t)-\dot{\alpha }(t)s(t)-\alpha (t)\dot{s}(t) \\ \hphantom{\dot{z}_{i}(t)} = -Dz_{i}(t) +A[f(x_{i}(t))-\alpha (t)f(s(t))] +B[f(x_{i}(t-\tau _{1}(t))) \\ \hphantom{\dot{z}_{i}(t)=}{} -\alpha (t)f(s(t-\tau _{1}(t)))] +C\int _{t-\tau _{2}(t)}^{t}[f(x_{i}( \theta ))-\alpha (t)f(s(\theta ))] \,d\theta \\ \hphantom{\dot{z}_{i}(t)=}{} +c_{1}\sum_{j=1}^{N}g^{(1)}_{ij}L_{1}z_{j}(t) +c_{2}\sum_{j=1}^{N}g^{(2)}_{ij}L_{2}z_{j}(t-\tau _{1}(t)) \\ \hphantom{\dot{z}_{i}(t)=}{} +c_{3}\sum_{j=1}^{N}g^{(3)}_{ij}L_{3}\int _{t-\tau _{2}(t)}^{t} z _{j}(\theta )\,d\theta -\dot{\alpha }(t)s(t)+u_{i}(t)+\omega _{i}(t), \\ \hat{y}_{i}(t)=Jz_{i}(t), \end{cases}\displaystyle \end{aligned}$$

(4)

where $\hat{y}_{i}(t)=y_{i}(t)-y_{s}(t)$.

Remark 1

If the scaling function $\alpha (t)$ is a function of the time t, then the NNs will realize FPS. The FPS includes many kinds of synchronization. If $\alpha (t)=\alpha$ or $\alpha (t)=1$, then the synchronization will be reduced to the projective synchronization [17, 18, 26] or common synchronization, [36, 37], respectively. Therefore, the FPS is more general.

Regarding to the pinning sampled-data control scheme, without loss of generality, the first l nodes are chosen and pinned with sampled-data control $u_{i}(t)$, expressed in the following form:

$$\begin{aligned} u_{i}(t)=u_{i1}(t)+u_{i2}(t), \quad i=1,2, \ldots,N, \end{aligned}$$

(5)

where

$$\begin{aligned}& u_{i1}(t) =\dot{\alpha }(t)s(t) -A\bigl[f\bigl(\alpha (t)s(t) \bigr)-\alpha (t)f\bigl(s(t)\bigr)\bigr]\\& \hphantom{u_{i1}(t) =}{} -B\bigl[f\bigl(\alpha (t)s\bigl(t-\tau _{1}(t)\bigr)\bigr) -\alpha (t)f\bigl(s\bigl(t-\tau _{1}(t)\bigr)\bigr)\bigr]\\& \hphantom{u_{i1}(t) =}{} -C \int _{t-\tau _{2}(t)}^{t}\bigl[f\bigl(\alpha (t)s(\theta ) \bigr)-\alpha (t)f\bigl(s(\theta )\bigr)\bigr]\,d\theta , \\& \quad i=1,2,\ldots , N, \\& u_{i2}(t) = \textstyle\begin{cases} K_{i} z_{i}(t_{k}), & t_{k}\leq t\leq t_{k+1} , i=1,2,\ldots , l, \\ 0 , & i=l+1,l+2,\ldots , N, \end{cases}\displaystyle \end{aligned}$$

where $K_{i}$ is a set of the sampled-data feedback controller gain matrices to be designed, for every $i = 1, 2,\ldots ,N$, $z_{i}(t_{k})$ is discrete measurement of $z_{i}(t)$ at the sampling interval $t_{k}$. Denote the updating instant time of the zero-order-hold (ZOH) by $t_{k}$; satisfying

$$\begin{aligned} & 0=t_{0}< t_{1} < \cdots < t_{k} < \lim _{k\rightarrow +\infty }t_{k}=+ \infty , \\ & t_{k+1}-t_{k} = h_{k} \leq h, \quad \forall k \geq 0, \end{aligned}$$

where $h>0$ represents the largest sampling interval.

By substituting (5) into (4), it can be derived that

$$\begin{aligned} \textstyle\begin{cases} \dot{z}_{i}(t)= -Dz_{i}(t) +A\widetilde{f}(z_{i}(t)) +B\widetilde{f}(z _{i}(t-\tau _{1}(t))) +C\int _{t-\tau _{2}(t)}^{t}\widetilde{f}(z_{i}( \theta )) \,d\theta \\ \hphantom{\dot{z}_{i}(t)=}{} +c_{1}\sum_{j=1}^{N}g^{(1)}_{ij}L_{1}z_{j}(t) +c_{2}\sum_{j=1}^{N}g^{(2)}_{ij}L_{2}z_{j}(t-\tau _{1}(t))+\omega _{i}(t) \\ \hphantom{\dot{z}_{i}(t)=}{} +c_{3}\sum_{j=1}^{N}g^{(3)}_{ij}L_{3}\int _{t-\tau _{2}(t)}^{t} z _{j}(\theta )\,d\theta +K_{i} z_{i}(t-h(t)), \quad i=1,2,3,\ldots ,l, \\ \dot{z}_{i}(t)= -Dz_{i}(t) +A\widetilde{f}(z_{i}(t)) +B\widetilde{f}(z _{i}(t-\tau _{1}(t))) +C\int _{t-\tau _{2}(t)}^{t} \widetilde{f}(z_{i}( \theta )) \,d\theta \\ \hphantom{\dot{z}_{i}(t)=}{} +c_{1}\sum_{j=1}^{N}g^{(1)}_{ij}L_{1}z_{j}(t) +c_{2}\sum_{j=1}^{N}g^{(2)}_{ij}L_{2}z_{j}(t-\tau _{1}(t))+\omega _{i}(t) \\ \hphantom{\dot{z}_{i}(t)=}{} +c_{3}\sum_{j=1}^{N}g^{(3)}_{ij}L_{3}\int _{t-\tau _{2}(t)}^{t} z _{j}(\theta )\,d\theta , \quad i=l+1,l+2,l+3,\ldots ,N, \end{cases}\displaystyle \end{aligned}$$

(6)

where $h(t)=t-t_{k}$ satisfies $0\leq h(t)\leq h$, and

$$\begin{aligned}& \widetilde{f}\bigl(z_{i}(t)\bigr) =f\bigl(x_{i}(t) \bigr)-f\bigl(\alpha (t)s(t)\bigr), \\& \widetilde{f}\bigl(z_{i}\bigl(t-\tau _{1}(t)\bigr) \bigr) =f\bigl(x_{i}\bigl(t-\tau _{1}(t)\bigr)\bigr)-f \bigl( \alpha (t)s\bigl(t-\tau _{1}(t)\bigr)\bigr), \\& \widetilde{f}\bigl(z_{i}(\theta )\bigr) =f\bigl(x_{i}( \theta )\bigr)-f\bigl(\alpha (t)s( \theta )\bigr). \end{aligned}$$

The initial condition of (6) is defined by

$$\begin{aligned} z_{i}(\theta )=\phi _{i}(\theta ), \quad -\bar{\theta }\leq \theta \leq 0, \end{aligned}$$

(7)

where $\bar{\theta }={\mathrm{max}}\{\tau _{1}, \tau _{2}, h\}$ and $\phi _{i}(\theta )\in \mathcal{C}([-\bar{\theta }, 0],\mathcal{R}^{n})$, $i=1,2, \ldots ,N$.

Let us define

$$\begin{aligned}& K = \operatorname{diag}\{ \underbrace{{K_{1}},{K_{2}}, \ldots,{K_{l}}}_{l \text{ times}},\underbrace{{0_{n}}, \ldots,{0_{n}}}_{N - l\text{ times}}\}, \\& z(t) = \begin{bmatrix} z_{1}(t) \\ z_{2}(t) \\ \vdots \\ z_{N}(t) \end{bmatrix}, \qquad \bar{f} \bigl(z(\cdot )\bigr) = \begin{bmatrix} \widetilde{f}(z_{1}(\cdot )) \\ \widetilde{f}(z_{2}(\cdot )) \\ \vdots \\ \widetilde{f}(z_{N}(\cdot )) \end{bmatrix} , \qquad \omega (t) = \begin{bmatrix} \omega _{1}(t) \\ \omega _{2}(t) \\ \vdots \\ \omega _{N}(t) \end{bmatrix}. \end{aligned}$$

Then, with the Kronecker product, we can reformulate the system (6) as follows:

$$\begin{aligned} \textstyle\begin{cases} \dot{z}(t)= -(I_{N}\otimes D) z(t) +(I_{N}\otimes A)\bar{f}(z(t)) +(I _{N}\otimes B)\bar{f}(z(t-\tau _{1}(t))) \\ \hphantom{\dot{z}(t)=}{} +(I_{N}\otimes C)\int _{t-\tau _{2}(t)}^{t} \bar{f}(z(\theta ))\, d \theta +c_{1}(G^{(1)}\otimes L_{1})z(t) \\ \hphantom{\dot{z}(t)=}{} +c_{2}(G^{(2)}\otimes L_{2})z(t-\tau _{1}(t)) +c_{3}(G^{(3)}\otimes L _{3})\int _{t-\tau _{2}(t)}^{t} z(\theta )\,d\theta \\ \hphantom{\dot{z}(t)=}{} +K z(t-h(t))+\omega (t), \\ \widetilde{y}(t)= J z(t). \end{cases}\displaystyle \end{aligned}$$

(8)

The following definitions and lemmas are introduced to serve for the proof of the main results.

Definition 2.1

([33])

The network (1) with $\omega (t)=0$ is an exponential function projective synchronization (EFPS), if there exist two constants $\mu >0$ and $\varpi >0$ such that

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert ^{2} \leq \mu e^{-\varpi t} \bigl\Vert z( \epsilon ) \bigr\Vert _{\mathrm{cl}}. \end{aligned}$$

Definition 2.2

([34])

For given scalar $\sigma \in [0, 1]$, the error system (8) is EFPS and meets a predefined $H_{\infty }$/passive performance index γ, if the following two conditions can be guaranteed simultaneously:

• (i) the error system (8) is EFPS in view of Definition 2.1;

• (ii) under the zero original condition, there exists a scalar $\gamma >0$ such that the following inequality is satisfied:

  $$\begin{aligned} \int _{0}^{\mathcal{T}_{p}} \bigl[-\sigma \widetilde{y}^{T}(t) \widetilde{y}(t) +2(1-\sigma )\gamma \widetilde{y}^{T}(t)\omega (t) \bigr] \,dt \geq -\gamma ^{2} \int _{0}^{\mathcal{T}_{p}} \bigl[\omega ^{T}(t) \omega (t) \bigr] \,dt, \end{aligned}$$

  (9)

  for any $\mathcal{T}_{p}\geq 0$ and any non-zero $\omega (t)\in \mathcal{L}_{2}[0, \infty )$.

Lemma 2.3

([6], Cauchy inequality)

For any symmetric positive definite matrix $N\in M^{n\times n}$ and $x,y\in \mathcal{R}^{n}$ we have

$$ \pm 2x^{T}y \leq x^{T}Nx+y^{T}N^{-1}y. $$

Lemma 2.4

([6]). For any constant symmetric matrix $M\in \mathcal{R}^{m\times m}$, $M=M^{T}>0$, $b>0$, vector function $z : [0,b]\rightarrow \mathcal{R}^{m}$ such that the integrations concerned are well defined, one has

$$\begin{aligned} \biggl( \int _{0}^{b}z^{T}(s)\,ds \biggr)^{T}M \biggl( \int _{0}^{b}z(s)\,ds \biggr) \leq & b \int _{0}^{b}z^{T}(s)Mz(s)\,ds. \end{aligned}$$

Lemma 2.5

([9])

For a positive definite matrix $S>0$ and any continuously differentiable function $x:[a,b]\to {\mathcal{R}^{n}}$ the following inequalities hold:

$$\begin{aligned}& \int _{a}^{b} \dot{z}^{T}(s) S \dot{z}(s) \,ds \geq \frac{1}{b-a} \varXi _{1}^{T}S {\varXi _{1}}+ \frac{3}{b - a}\varXi _{2}^{T}S {\varXi _{2}} + \frac{5}{b-a}\varXi _{3}^{T}S {\varXi _{3}}, \\& \int _{a}^{b} \int _{\theta }^{b} \dot{z}^{T}(s) S \dot{z}(s) \,ds \,d \theta \geq 2\varXi _{4}^{T}S {\varXi _{4}}+ 4\varXi _{5}^{T}S {\varXi _{5}} + 6\varXi _{6}^{T}S {\varXi _{6}}, \end{aligned}$$

where

$$\begin{aligned}& {\varXi _{1}} = z(b) - z(a), \\& {\varXi _{2}} = z(b) + z(a) - \frac{2}{{b - a}} \int _{a}^{b} {z(s)\,ds} , \\& {\varXi _{3}} = z(b) - z(a) + \frac{6}{{b - a}} \int _{a}^{b} {z(s)\,ds} - \frac{{12}}{{{{(b-a)}^{2}}}} \int _{a}^{b} { \int _{\theta }^{b} {z(s)\,ds \,d\theta }}, \\& {\varXi _{4}} = z(b) - \frac{1}{{b - a}} \int _{a}^{b} {z(s)\,ds} , \\& {\varXi _{5}} = z(b) + \frac{2}{{b - a}} \int _{a}^{b} z(s)\,ds - \frac{6}{ {{{(b - a)}^{2}}}} \int _{a}^{b} { \int _{\theta }^{b} {z(s)\,ds \,d\theta } } , \\& {\varXi _{6}} = z(b) - \frac{3}{{b - a}} \int _{a}^{b} {z(s)\,ds} + \frac{ {24}}{{{{(b - a)}^{2}}}} \int _{a}^{b} { \int _{\theta }^{b} {z(s)\,ds\,d \theta } } \\& \hphantom{{\varXi _{6}} = }{}- \frac{{60}}{{{{(b - a)}^{3}}}} \int _{a}^{b} { \int _{\theta }^{b} { \int _{s}^{b} {z(\lambda )\,d\lambda \,ds \,d\theta } } } . \end{aligned}$$

Lemma 2.6

([6], Schur complement lemma)

Given constant symmetric matrices X, Y, Z with appropriate dimensions satisfying $X=X^{T}$, $Y=Y ^{T}>0$, one has $X+Z^{T}Y^{-1}Z<0$ if and only if

$$ \begin{pmatrix} X&Z^{T} \\ Z&-Y \end{pmatrix} < 0 \quad \textit{or} \quad \begin{pmatrix} -Y&Z \\ Z^{T}&X \end{pmatrix} < 0. $$

Remark 2

The condition in Definition 2.2 includes $H_{\infty }$ performance index γ and passivity performance index γ. If $\sigma =1$, then the condition will reduce to the $H_{\infty }$ performance index γ and if $\sigma =0$, then the condition will reduce to the passivity performance index γ. The condition corresponds to mixed $H_{\infty }$ and passivity performance index γ for σ in $(0,1)$.

3 Main results

In this section, we present a control scheme to synchronize the NNs (1) to the homogeneous trajectory (3). Then we will give some sufficient conditions in the EFPS of NNs with mixed time-varying delays and hybrid coupling. To simplify the representation, we introduce some notations as follows:

$$\begin{aligned} \chi (t) =& \biggl[ z^{T}(t), \int _{t-\tau _{1}}^{t} z^{T}(s) \,ds, \int _{t-\tau _{1}}^{t} \int _{\theta }^{t} z^{T}(s)\,ds \,d\theta , \int _{t-\tau _{1}}^{t} \int _{\theta }^{t} \int _{s}^{t} z^{T}(\lambda )\,d\lambda \,ds \,d\theta \biggr]^{T}, \\ \eta (t) =& \biggl[ z^{T}(t), z^{T}\bigl(t-\tau _{1}(t)\bigr), z^{T}(t-\tau _{1}), z^{T}\bigl(t-h(t)\bigr), z^{T}(t-h), \dot{z}(t), \\ & \int _{t-\tau _{1}}^{t} z^{T}(s)\,ds, \int _{t-\tau _{1}}^{t} \int _{\theta }^{t} z^{T}(s) \,ds \,d\theta , \int _{t-\tau _{1}}^{t} \int _{\theta }^{t} \int _{s}^{t} z^{T}(\lambda ) \,d\lambda \,ds \,d\theta , \\ & \int _{t-h}^{t} z^{T}(s)\,ds, \int _{t-h}^{t} \int _{\theta }^{t} z^{T}(s) \,ds \,d\theta , \int _{t-h}^{t} \int _{\theta }^{t} \int _{s}^{t} z^{T}(\lambda ) \,d\lambda \,ds \,d\theta , \\ & \int _{t-\tau _{2}(t)}^{t} z^{T}(s) \,ds, \omega ^{T}(t) \biggr]^{T}, \end{aligned}$$

where $z_{i}\in \mathcal{R}^{n\times 14n}$ is defined as $z_{i}=[0_{n \times (i-1)n}, I_{n}, 0_{n\times (14-i)n}]$ for $i=1,2,\ldots,14$.

Theorem 3.1

Given constants $\tau _{1}$, $\tau _{2}$, $\bar{\tau }_{1}$, h, γ and $\sigma \in [0, 1]$, if real positive matrices $P\in \mathcal{R}^{4n \times 4n}$, $Q_{0}$, $Q_{i}$, $S_{0}$ $S_{i},R_{i}\in \mathcal{R}^{n \times n}$ ($i = 1,2,3$), positive constants $\varepsilon _{i}$ $(i = 1,2,\ldots,6)$, and real matrices ${T_{1}}$, ${T_{2}}$ with appropriate dimensions, such that

$$\begin{aligned} \varUpsilon = \begin{bmatrix} \varUpsilon _{11} &\varUpsilon _{12} &\varUpsilon _{13} &\varUpsilon _{14} &\varUpsilon _{15} &\varUpsilon _{16} &\varUpsilon _{17} \\ *& - {\varepsilon _{1}}I&0&0&0&0&0 \\ *&*& - {\varepsilon _{2}}I&0&0&0&0 \\ *&*&*& - {\varepsilon _{3}}I&0&0&0 \\ *&*&*&*& - {\varepsilon _{4}}I&0&0 \\ *&*&*&*&*& - {\varepsilon _{5}}I&0 \\ *&*&*&*&*&*& - {\varepsilon _{6}}I \end{bmatrix} < 0, \end{aligned}$$

(10)

where

$$\begin{aligned} \textstyle\begin{cases} \varUpsilon _{11}=\sum_{i=1}^{8} \varPi _{i}, \qquad \varUpsilon _{12}=I_{N}\otimes T_{1}A,\qquad \varUpsilon _{13}=I_{N}\otimes T_{1}B, \qquad \varUpsilon _{14}=I_{N}\otimes T_{1}C, \\ \varUpsilon _{15}=I_{N}\otimes T_{2}A,\qquad \varUpsilon _{16}=I_{N}\otimes T_{2}B, \qquad \varUpsilon _{17}=I_{N}\otimes T_{2}C, \\ \varPi _{1}=\varTheta _{1}^{T}P\varTheta _{2}+\varTheta _{2}^{T}P\varTheta _{1} -\varTheta _{3}^{T}S_{1}\varTheta _{3}-\varTheta _{4}^{T}S_{1}\varTheta _{4} +z_{1}^{T}S_{0}z _{1}-z_{5}^{T}S_{0}z_{5}, \\ \varPi _{2}=z_{1}^{T}(Q_{0}+Q_{2})z_{1} +z_{1}^{T}\varLambda ^{T}(Q_{1}+Q_{3}) \varLambda z_{1} -z_{3}^{T}Q_{0}z_{3}-(1-\bar{\tau }_{1})z_{2}^{T}Q_{2}z _{2} \\ \hphantom{\varPi _{2}=}{} -z_{3}^{T}(\varLambda ^{T} Q_{1}\varLambda )z_{3} -(1-\bar{\tau }_{1})z_{2} ^{T}(\varLambda ^{T} Q_{3} \varLambda )z_{2}, \\ \varPi _{3}=\tau _{2}^{2}z_{1}^{T}(\varLambda ^{T}R_{1}\varLambda )z_{1}-z_{13} ^{T}(\varLambda ^{T}R_{1}\varLambda )z_{13}, \\ \varPi _{4}=h^{2}z_{6}^{T}(S_{2}+0.5R_{2})z_{6} -\varTheta _{5}^{T} S_{2} \varTheta _{5}-3\varTheta _{6}^{T}S_{2}\varTheta _{6} -5\varTheta _{7}^{T}S_{2}\varTheta _{7} \\ \hphantom{\varPi _{4}=}{} -2\varTheta _{11}^{T}R_{2}\varTheta _{11} -4\varTheta _{12}^{T}R_{2}\varTheta _{12} -6 \varTheta _{13}^{T}R_{2}\varTheta _{13}, \\ \varPi _{5}=\tau _{1}^{2}z_{6}^{T}(S_{3}+0.5R_{3})z_{6} -\varTheta _{8}^{T} S _{3}\varTheta _{8}-3\varTheta _{9}^{T}S_{3}\varTheta _{9} -5\varTheta _{10}^{T}S_{3} \varTheta _{10} \\ \hphantom{\varPi _{5}=}{} -2\varTheta _{14}^{T}R_{3}\varTheta _{14} -4\varTheta _{15}^{T}R_{3}\varTheta _{15} -6 \varTheta _{16}^{T}R_{3}\varTheta _{16}, \\ \varPi _{6}=z_{1}^{T}T_{1} \mathcal{C}_{0} +\mathcal{C}_{0}^{T}T_{1}^{T}z _{1} +z_{6}^{T}T_{2}\mathcal{C}_{0}+\mathcal{C}_{0}^{T}T_{2}^{T}z_{6} +z_{1}^{T}T_{1}Kz_{4} +z_{4}^{T}K^{T}T_{1}^{T}z_{1} \\ \hphantom{\varPi _{6}=}{} +z_{6}^{T}T_{2}Kz_{4} +z_{4}^{T}K^{T}T_{2}^{T}z_{6} +z_{1}^{T}T_{1}z _{14} +z_{14}^{T}T_{1}^{T}z_{1} -z_{1}^{T}T_{1}z_{6} -z_{6}^{T}T_{1} ^{T}z_{1} \\ \hphantom{\varPi _{6}=}{} +z_{6}^{T}T_{2}z_{14}+z_{14}^{T}T_{2}^{T}z_{6} -z_{6}^{T}T_{2}z_{6}-z _{6}^{T}T_{2}^{T}z_{6}, \\ \varPi _{7} =(\varepsilon _{1}+\varepsilon _{4})z_{1}^{T}(I_{N}\otimes \varLambda ^{T}\varLambda )z_{1} +(\varepsilon _{2}+\varepsilon _{5})z_{2}^{T}(I _{N}\otimes \varLambda ^{T}\varLambda )z_{2} \\ \hphantom{\varPi _{7}=}{} +(\varepsilon _{3}+\varepsilon _{6})z_{13}^{T}(I_{N}\otimes \varLambda ^{T} \varLambda )z_{13}, \\ \varPi _{8} =\sigma (Jz_{1})^{T}(Jz_{1}) -(1-\sigma )\gamma (Jz_{1})^{T}z _{14} -(1-\sigma )\gamma z_{14}^{T}(Jz_{1}) - \gamma ^{2}z_{14}^{T}z _{14}, \\ \mathcal{C}_{0}=[c_{1}(G^{(1)}\otimes L_{1})-(I_{N}\otimes D)]z_{1} +c _{2}(G^{(2)}\otimes L_{2})z_{2} +c_{3}(G^{(3)}\otimes L_{3})z_{13}, \end{cases}\displaystyle \end{aligned}$$

(11)

with

$$\begin{aligned}& \varTheta _{1} =\bigl[z_{1}^{T} ,z_{7}^{T} ,z_{8}^{T} ,z_{9}^{T}\bigr]^{T},\qquad \varTheta _{2}=\bigl[z_{6}^{T}, z_{1}^{T} -z_{3}^{T}, \tau _{1}z_{1}^{T} - z_{7}^{T}, 0.5\tau _{1}^{2}z_{1}^{T}-z_{8}^{T} \bigr]^{T}, \\& \varTheta _{3}=z_{1}-z_{4}, \qquad \varTheta _{4}=z_{4}-z_{5}, \qquad \varTheta _{5}=z_{1}-z_{5}, \\& \varTheta _{6}=z_{1}+z_{5}- \frac{2}{h}{z_{10}}, \qquad \varTheta _{7}=z_{1}-z_{5}+ \frac{6}{h}{z_{10}}-\frac{12}{h^{2}}z_{11}, \qquad \varTheta _{8}=z_{1}-z_{3}, \\& \varTheta _{9}=z_{1}+z_{3}- \frac{2}{\tau _{1}}z_{7}, \qquad \varTheta _{10}=z_{1}-z_{3}+ \frac{6}{\tau _{1}}z_{7}-\frac{12}{\tau _{1} ^{2}}z_{8}, \qquad \varTheta _{11}=z_{1}-\frac{1}{h}z_{5}, \\& \varTheta _{12}=z_{1}+\frac{2}{h}z_{5}- \frac{6}{h^{2}}z_{10}, \qquad \varTheta _{13}=z_{1}- \frac{3}{h}z_{5}+\frac{24}{h^{2}}z_{10} - \frac{60}{h ^{3}}z_{11},\qquad \varTheta _{14}=z_{1}- \frac{1}{\tau _{1}}z_{7}, \\& \varTheta _{15}=z_{1}+\frac{2}{\tau _{1}}z_{7}- \frac{6}{\tau _{1}^{2}}z_{8}, \qquad \varTheta _{16}=z_{1}- \frac{3}{\tau _{1}}z_{7}+\frac{24}{\tau _{1}^{2}}z _{8}- \frac{60}{\tau _{1}^{3}}z_{9}, \end{aligned}$$

then the error system (8) is EFPS and meets a predefined $\mathcal{H}_{\infty }$/passive performance index γ.

Proof

We consider a candidate Lyapunov–Krasovskii functional:

$$\begin{aligned} V(t)=\sum_{k=1}^{5} V_{k}(t), \end{aligned}$$

(12)

where

$$\begin{aligned} V_{1}(t) =&\chi ^{T}(t)P\chi (t) + \int _{t-h}^{t}z^{T}(s)S_{0}z(s)\,ds + \int _{t-h}^{t} \int _{\theta }^{t} \dot{z}^{T}(s)S_{1} \dot{z}(s) \,ds \,d\theta , \\ V_{2}(t) =& \int _{t-\tau _{1}}^{t} \bigl[z^{T}(s)Q_{0}z(s) + f^{T}\bigl(z(s)\bigr)Q _{1}f\bigl(z(s)\bigr) \bigr]\,ds \\ &{}+ \int _{t-\tau _{1}(t)}^{t} \bigl[z^{T}(s)Q_{2}z(s) + f^{T}\bigl(z(s)\bigr)Q_{3}f\bigl(z(s)\bigr) \bigr]\,ds, \\ V_{3}(t) =& \tau _{2} \int _{t-\tau _{2}}^{t} \int _{\theta }^{t}f^{T}\bigl(z(s)\bigr)R _{1} f\bigl(z(s)\bigr)\,ds \,d\theta , \\ V_{4}(t) =&h \int _{t-h}^{t} \int _{\theta }^{t} \dot{z}^{T}(s)S_{2} \dot{z}(s) \,ds \,d\theta + \int _{t-h}^{t} \int _{\theta }^{t} \int _{s} ^{t}\dot{z}^{T}(\lambda )R_{2} \dot{z}(\lambda ) \,d\lambda \,ds\,d \theta , \\ V_{5}(t) =&\tau _{1} \int _{t-\tau _{1}}^{t} \int _{\theta }^{t} \dot{z}^{T}(s)S_{3} \dot{z}(s) \,ds \,d\theta + \int _{t-\tau _{1}}^{t} \int _{\theta }^{t} \int _{s}^{t}\dot{z}^{T}(\lambda )R_{3} \dot{z}( \lambda ) \,d\lambda \,ds \,d\theta . \end{aligned}$$

The time derivatives of $V(t)$ along the trajectories of the error system (8) can be calculated as

$$\begin{aligned} \dot{V}_{1}(t) =&2\dot{\chi }^{T}(t)P \chi (t) +z^{T}(t)S_{0}z(t)-z ^{T}(t-h)S_{0}z(t-h) +h\dot{z}^{T}(t)S_{1} \dot{z}(t) \\ &{}-h \int _{t-h}^{t}\dot{z}^{T}(s)S_{1} \dot{z}(s) \,ds, \end{aligned}$$

(13)

$$\begin{aligned} \dot{V}_{2}(t) \leq & z^{T}(t) (Q_{0}+Q_{2})z(t)+ f^{T}\bigl(z(t)\bigr) (Q_{1}+Q _{3})f \bigl(z(t)\bigr) -z^{T}(t-\tau _{1})Q_{0}z(t- \tau _{1}) \\ &{}-f^{T}\bigl(z(t-\tau _{1})\bigr)Q_{1}f \bigl(z(t-\tau _{1})\bigr) -(1-\bar{\tau }_{1})z ^{T}\bigl(t-\tau _{1}(t)\bigr)Q_{2}z\bigl(t- \tau _{1}(t)\bigr) \\ &{}-(1-\bar{\tau }_{1})f^{T}\bigl(z\bigl(t-\tau _{1}(t)\bigr)\bigr)Q_{3}f^{T}\bigl(z \bigl(t-\tau _{1}(t)\bigr)\bigr) \\ \leq & z^{T}(t) (Q_{0}+Q_{2})z(t)+ z(t) \varLambda ^{T}(Q_{1}+Q_{3})\varLambda z(t) -z^{T}(t-\tau _{1})Q_{0}z(t-\tau _{1}) \\ &{}-z(t-\tau _{1}) \bigl(\varLambda ^{T}Q_{1} \varLambda \bigr)z(t-\tau _{1}) -(1-\bar{ \tau }_{1})z^{T} \bigl(t-\tau _{1}(t)\bigr)Q_{2}z\bigl(t-\tau _{1}(t)\bigr) \\ &{}-(1-\bar{\tau }_{1})z\bigl(t-\tau _{1}(t)\bigr) \bigl(\varLambda ^{T}Q_{3}\varLambda \bigr) z\bigl(t- \tau _{1}(t)\bigr) \\ =& \eta ^{T}(t) \varPi _{2} \eta (t), \end{aligned}$$

(14)

$$\begin{aligned} \dot{V}_{3}(t) =& \tau _{2}^{2} f^{T}(z(t)R_{1}f\bigl(z(t)\bigr) -\tau _{2} \int _{t-\tau _{2}}^{t}f^{T}\bigl(z(s) \bigr)R_{1}f\bigl(z(s)\bigr)\,ds \\ \leq & \tau _{2}^{2} z(t) \varLambda ^{T}R_{1} \varLambda z(t) -\tau _{2} \int _{t-\tau _{2}}^{t}f^{T}\bigl(z(s) \bigr)R_{1}f\bigl(z(s)\bigr)\,ds, \end{aligned}$$

(15)

$$\begin{aligned} \dot{V}_{4}(t) =&h^{2}\dot{z}^{T}(t) (S_{2}+0.5R_{2}) \dot{z}(t) -h \int _{t-h}^{t}\dot{z}^{T}(s)S_{2} \dot{z}(s) \,ds \\ &{}- \int _{t-h}^{t} \int _{\theta }^{t}\dot{z}^{T}(s)R_{2} \dot{z}(s)\,ds\,d \theta , \end{aligned}$$

(16)

$$\begin{aligned} \dot{V}_{5}(t) =&\tau _{1}^{2} \dot{z}^{T}(t) (S_{3}+0.5R_{3}) \dot{z}(t) - \tau _{1} \int _{t-\tau _{1}}^{t}\dot{z}^{T}(s)S_{3} \dot{z}(s) \,ds \\ &{}- \int _{t-\tau _{1}}^{t} \int _{\theta }^{t}\dot{z}^{T}(s)R_{3} \dot{z}(s)\,ds\,d \theta , \end{aligned}$$

(17)

where $\varPi _{2}$ is defined in (11). Applying Lemma 2.4 and Lemma 2.5, it can be shown that

$$\begin{aligned} &{-}h \int _{t-h}^{t}\dot{z}^{T}(s)S_{1} \dot{z}(s) \,ds \\ & \quad =-h \int _{t-h(t)}^{t}\dot{z}^{T}(s)S_{1} \dot{z}(s) \,ds -h \int _{t-h} ^{t-h(t)}\dot{z}^{T}(s)S_{1} \dot{z}(s) \,ds \\ & \quad \leq - \bigl[z(t)-z\bigl(t-h(t)\bigr) \bigr]^{T} S_{1} \bigl[z(t)-z\bigl(t-h(t)\bigr) \bigr] \\ & \qquad {}- \bigl[z\bigl(t-h(t)\bigr)-z(t-h) \bigr]^{T} S_{1} \bigl[z\bigl(t-h(t)\bigr)-z(t-h) \bigr], \end{aligned}$$

(18)

$$\begin{aligned} &{-}\tau _{2} \int _{t-\tau _{2}}^{t}f^{T}\bigl(z(s) \bigr)R_{1}f\bigl(z(s)\bigr)\,ds \\ & \quad \leq -\tau _{2} \int _{t-\tau _{2}(t)}^{t} f^{T}\bigl(z(s) \bigr)R_{1}f\bigl(z(s)\bigr)\,ds \\ & \quad \leq - \int _{t-\tau _{2}(t)}^{t}f^{T}\bigl(z(s)\bigr)\,ds R_{1} \int _{t-\tau _{2}(t)} ^{t} f\bigl(z(s)\bigr)\,ds \\ & \quad \leq - \int _{t-\tau _{2}(t)}^{t}z^{T}(s)\,ds \bigl( \varLambda ^{T}R_{1} \varLambda \bigr) \int _{t-\tau _{2}(t)}^{t} z(s)\,ds, \end{aligned}$$

(19)

$$\begin{aligned} &{-}h \int _{t-h}^{t}\dot{z}^{T}(s)S_{2} \dot{z}(s) \,ds \leq -\varTheta _{5} ^{T} S_{2} \varTheta _{5}-3\varTheta _{6}^{T}S_{2} \varTheta _{6} -5\varTheta _{7}^{T}S _{2}\varTheta _{7}, \end{aligned}$$

(20)

$$\begin{aligned} &{-} \int _{t-h}^{t} \int _{\theta }^{t}\dot{z}^{T}(s)R_{2} \dot{z}(s)\,ds\,d \theta \\ & \quad \leq -2\varTheta _{11}^{T}R_{2}\varTheta _{11} -4\varTheta _{12}^{T}R_{2} \varTheta _{12}-6\varTheta _{13}^{T}R_{2} \varTheta _{13}, \end{aligned}$$

(21)

$$\begin{aligned} &{-}\tau _{1} \int _{t-\tau _{1}}^{t}\dot{z}^{T}(s)S_{3} \dot{z}(s) \,ds \leq -\varTheta _{8}^{T} S_{3} \varTheta _{8}-3\varTheta _{9}^{T}S_{3} \varTheta _{9} -5 \varTheta _{10}^{T}S_{3} \varTheta _{10}, \end{aligned}$$

(22)

$$\begin{aligned} &{-} \int _{t-\tau _{1}}^{t} \int _{\theta }^{t}\dot{z}^{T}(s)R_{3} \dot{z}(s)\,ds\,d \theta \\ & \quad \leq -2\varTheta _{14}^{T}R_{3}\varTheta _{14} -4\varTheta _{15}^{T}R_{3} \varTheta _{15}-6\varTheta _{16}^{T}R_{3} \varTheta _{16}. \end{aligned}$$

(23)

From (13)–(23), we obtain

$$\begin{aligned} \dot{V}_{1}(t)+\dot{V}_{3}(t)+ \dot{V}_{4}(t)+\dot{V}_{5}(t)= \eta ^{T}(t) [ \varPi _{1}+\varPi _{3}+\varPi _{4}+\varPi _{5} ] \eta (t), \end{aligned}$$

(24)

where $\varPi _{i}$, $i = 1,3,4,5$, are defined in (11).

Based on the error system (8), given any matrices $T_{1}$ and $T_{2}$ with appropriate dimensions, it is true that

$$\begin{aligned} 0= {}& 2 \bigl[z^{T}(t)T_{1}+\dot{z}^{T}(t)T_{2} \bigr] \biggl[-(I_{N}\otimes D) z(t)+(I_{N}\otimes A) \bar{f}\bigl(z(t)\bigr)+(I_{N}\otimes B) \\ &{}\times \bar{f}\bigl(z\bigl(t-\tau _{1}(t)\bigr)\bigr) +(I_{N}\otimes C) \int _{t-\tau _{2}(t)} ^{t}\bar{f}\bigl(z(\theta )\bigr)\,d \theta +c_{1}\bigl(G^{(1)}\otimes L_{1} \bigr)z(t) \\ &{}+c_{2}\bigl(G^{(2)}\otimes L_{2}\bigr)z \bigl(t-\tau _{1}(t)\bigr) +c_{3}\bigl(G^{(3)} \otimes L_{3}\bigr) \int _{t-\tau _{2}(t)}^{t}z(\theta )\,d\theta +K z\bigl(t-h(t) \bigr) \\ &{}+\omega (t)-\dot{z}(t) \biggr]. \end{aligned}$$

(25)

Applying Lemma 2.3 and Lemma 2.4, we have

$$\begin{aligned} &z^{T}(t) (I_{N}\otimes T_{1}A)\bar{f} \bigl(z(t)\bigr) \\ & \quad \leq \frac{1}{2\varepsilon _{1}}z^{T}(t) \bigl(I_{N} \otimes T_{1}AA^{T}T _{1}^{T} \bigr)z(t) +\frac{\varepsilon _{1}}{2}\bar{f}^{T}\bigl(z(t)\bigr) (I_{N} \otimes I_{n})\bar{f}\bigl(z(t)\bigr) \\ & \quad \leq \frac{1}{2\varepsilon _{1}}z^{T}(t) \bigl(I_{N} \otimes T_{1}AA^{T}T _{1}^{T} \bigr)z(t) +\frac{\varepsilon _{1}}{2}z^{T}(t) \bigl(I_{N} \otimes \varLambda ^{T}\varLambda \bigr)z(t) \\ & \quad =\frac{1}{2}z^{T}(t) (I_{N}\otimes T_{1}A) \varepsilon _{1}^{-1} \bigl(I _{N}\otimes A^{T}T_{1}^{T} \bigr)z(t) +\frac{\varepsilon _{1}}{2}z^{T}(t) \bigl(I _{N} \otimes \varLambda ^{T}\varLambda \bigr)z(t), \end{aligned}$$

(26)

$$\begin{aligned} &z^{T}(t) (I_{N}\otimes T_{1}B)\bar{f} \bigl(z\bigl(t-\tau _{1}(t)\bigr)\bigr) \\ & \quad \leq \frac{1}{2\varepsilon _{2}}z^{T}(t) \bigl(I_{N} \otimes T_{1}BB^{T}T _{1}^{T} \bigr)z(t) \\ & \qquad {}+\frac{\varepsilon _{2}}{2}\bar{f}^{T}\bigl(\bigl(t-\tau _{1}(t)\bigr)\bigr) (I_{N}\otimes I_{n}) \bar{f}\bigl(z\bigl(t-\tau _{1}(t)\bigr)\bigr) \\ & \quad \leq \frac{1}{2\varepsilon _{2}}z^{T}(t) \bigl(I_{N} \otimes T_{1}BB^{T}T _{1}^{T} \bigr)z(t) \\ & \qquad{} +\frac{\varepsilon _{2}}{2}z^{T}\bigl(t-\tau _{1}(t) \bigr) \bigl(I_{N}\otimes \varLambda ^{T}\varLambda \bigr)z \bigl(t-\tau _{1}(t)\bigr) \\ & \quad =\frac{1}{2}z^{T}(t) (I_{N}\otimes T_{1}B)\varepsilon _{2}^{-1}\bigl(I _{N}\otimes B^{T}T_{1}^{T} \bigr)z(t) \\ & \qquad {}+\frac{\varepsilon _{2}}{2}z^{T}\bigl(t-\tau _{1}(t) \bigr) \bigl(I_{N}\otimes \varLambda ^{T}\varLambda \bigr)z \bigl(t-\tau _{1}(t)\bigr), \end{aligned}$$

(27)

$$\begin{aligned} &z^{T}(t) (I_{N}\otimes T_{1}C) \int _{t-\tau _{2}(t)}^{t}\bar{f}\bigl(z( \theta )\bigr)\,d \theta \\ & \quad \leq \frac{1}{2\varepsilon _{3}}z^{T}(t) \bigl(I_{N} \otimes T_{1}CC^{T}T _{1}^{T} \bigr)z(t) \\ & \qquad {}+\frac{\varepsilon _{3}}{2} \biggl( \int _{t-\tau _{2}(t)}^{t}\bar{f}^{T}\bigl(z( \theta )\bigr)\,d\theta \biggr)^{T}(I_{N}\otimes I_{n}) \biggl( \int _{t-\tau _{2}(t)} ^{t}\bar{f}\bigl(z(\theta )\bigr)\,d \theta \biggr) \\ & \quad \leq \frac{1}{2\varepsilon _{3}}z^{T}(t) \bigl(I_{N} \otimes T_{1}CC^{T}T _{1}^{T} \bigr)z(t) \\ & \qquad{} +\frac{\varepsilon _{3}}{2} \biggl( \int _{t-\tau _{2}(t)}^{t}z^{T}(\theta )d \theta \biggr)^{T}\bigl(I_{N}\otimes \varLambda ^{T} \varLambda \bigr) \biggl( \int _{t-\tau _{2}(t)}^{t}z(\theta )\,d\theta \biggr) \\ & \quad =\frac{1}{2}z^{T}(t) (I_{N}\otimes T_{1}C) \varepsilon _{3}^{-1} \bigl(I _{N}\otimes C^{T}T_{1}^{T} \bigr)z(t) \\ & \qquad{} +\frac{\varepsilon _{3}}{2} \biggl( \int _{t-\tau _{2}(t)}^{t}z^{T}(\theta )d \theta \biggr)^{T}\bigl(I_{N}\otimes \varLambda ^{T} \varLambda \bigr) \biggl( \int _{t-\tau _{2}(t)}^{t}z(\theta )\,d\theta \biggr), \end{aligned}$$

(28)

$$\begin{aligned} &\dot{z}^{T}(t) (I_{N}\otimes T_{2}A) \bar{f}\bigl(z(t)\bigr) \\ & \quad \leq \frac{1}{2\varepsilon _{4}}\dot{z}^{T}(t) \bigl(I_{N}\otimes T_{2}AA ^{T}T_{2}^{T} \bigr)\dot{z}(t) +\frac{\varepsilon _{4}}{2}\bar{f}^{T}\bigl(z(t)\bigr) (I _{N}\otimes I_{n})\bar{f}\bigl(z(t)\bigr) \\ & \quad \leq \frac{1}{2\varepsilon _{4}}\dot{z}^{T}(t) \bigl(I_{N}\otimes T_{2}AA ^{T}T_{2}^{T} \bigr)\dot{z}(t) +\frac{\varepsilon _{4}}{2}z^{T}(t) \bigl(I_{N} \otimes \varLambda ^{T}\varLambda \bigr)z(t) \\ & \quad =\frac{1}{2}\dot{z}^{T}(t) (I_{N} \otimes T_{2}A)\varepsilon _{4}^{-1} \bigl(I _{N}\otimes A^{T}T_{2}^{T}\bigr) \dot{z}(t) +\frac{\varepsilon _{4}}{2}z^{T}(t) \bigl(I _{N} \otimes \varLambda ^{T}\varLambda \bigr)z(t), \end{aligned}$$

(29)

$$\begin{aligned} &\dot{z}^{T}(t) (I_{N}\otimes T_{2}B) \bar{f}\bigl(z\bigl(t-\tau _{1}(t)\bigr)\bigr) \\ & \quad \leq \frac{1}{2\varepsilon _{5}}\dot{z}^{T}(t) \bigl(I_{N}\otimes T_{2}BB ^{T}T_{2}^{T} \bigr)\dot{z}(t) \\ & \qquad {}+\frac{\varepsilon _{5}}{2}\bar{f}^{T}\bigl(\bigl(t-\tau _{1}(t)\bigr)\bigr) (I_{N}\otimes I_{n}) \bar{f}\bigl(z\bigl(t-\tau _{1}(t)\bigr)\bigr) \\ & \quad \leq \frac{1}{2\varepsilon _{5}}\dot{z}^{T}(t) \bigl(I_{N}\otimes T_{2}BB ^{T}T_{2}^{T} \bigr)\dot{z}(t) \\ & \qquad{} +\frac{\varepsilon _{5}}{2}z^{T}\bigl(t-\tau _{1}(t) \bigr) \bigl(I_{N}\otimes \varLambda ^{T}\varLambda \bigr)z \bigl(t-\tau _{1}(t)\bigr) \\ & \quad =\frac{1}{2}\dot{z}^{T}(t) (I_{N} \otimes T_{2}B) \varepsilon _{5}^{-1} \bigl(I_{N}\otimes B^{T}T_{2}^{T} \bigr)\dot{z}(t) \\ & \qquad{} +\frac{\varepsilon _{5}}{2}z^{T}\bigl(t-\tau _{1}(t) \bigr) \bigl(I_{N}\otimes \varLambda ^{T}\varLambda \bigr)z \bigl(t-\tau _{1}(t)\bigr), \end{aligned}$$

(30)

$$\begin{aligned} &\dot{z}^{T}(t) (I_{N}\otimes T_{2}C) \int _{t-\tau _{2}(t)}^{t}\bar{f}\bigl(z( \theta )\bigr)\,d \theta \\ & \quad \leq \frac{1}{2\varepsilon _{6}}\dot{z}^{T}(t) \bigl(I_{N}\otimes T_{2}CC ^{T}T_{2}^{T} \bigr)\dot{z}(t) \\ & \qquad{} +\frac{\varepsilon _{6}}{2} \biggl( \int _{t-\tau _{2}(t)}^{t}\bar{f}^{T}\bigl(z( \theta )\bigr) \,d\theta \biggr)^{T}(I_{N}\otimes I_{n}) \biggl( \int _{t-\tau _{2}(t)}^{t}\bar{f}\bigl(z(\theta )\bigr) \,d \theta \biggr) \\ & \quad \leq \frac{1}{2\varepsilon _{6}}\dot{z}^{T}(t) \bigl(I_{N}\otimes T_{2}CC ^{T}T_{2}^{T} \bigr)\dot{z}(t) \\ & \qquad{} +\frac{\varepsilon _{6}}{2} \biggl( \int _{t-\tau _{2}(t)}^{t}z^{T}(\theta ) \,d\theta \biggr)^{T} \bigl(I_{N}\otimes \varLambda ^{T} \varLambda \bigr) \biggl( \int _{t-\tau _{2}(t)}^{t}z(\theta ) \,d\theta \biggr) \\ & \quad =\frac{1}{2}\dot{z}^{T}(t) (I_{N} \otimes T_{2}C) \varepsilon _{6}^{-1} \bigl(I_{N}\otimes C^{T}T_{2}^{T} \bigr)\dot{z}(t) \\ & \qquad{} +\frac{\varepsilon _{6}}{2} \biggl( \int _{t-\tau _{2}(t)}^{t}z^{T}(\theta )\,d \theta \biggr)^{T} \bigl(I_{N}\otimes \varLambda ^{T} \varLambda \bigr) \biggl( \int _{t-\tau _{2}(t)}^{t}z(\theta )\,d\theta \biggr). \end{aligned}$$

(31)

Then, from (14), (24) and (25)–(31), we obtain

$$\begin{aligned} \dot{V}(t)\le {}& \eta ^{T}(t) \Biggl\{ \sum _{i=1}^{7}\varPi _{i} +z^{T}(t) \bigl[(I_{N}\otimes T_{1}A) \varepsilon _{1}^{-1} \bigl(I_{N}\otimes A^{T}T _{1}^{T}\bigr) \\ &{}+(I_{N}\otimes T_{1}B) \varepsilon _{2}^{-1} \bigl(I_{N}\otimes B^{T}T _{1}^{T}\bigr) +(I_{N} \otimes T_{1}C) \varepsilon _{3}^{-1} \bigl(I_{N}\otimes C ^{T}T_{1}^{T} \bigr) \bigr] z(t) \\ &{}+\dot{z}^{T}(t) \bigl[(I_{N}\otimes T_{2}A)\varepsilon _{4}^{-1} \bigl(I _{N}\otimes A^{T}T_{2}^{T}\bigr) +(I_{N}\otimes T_{2}B) \varepsilon _{5} ^{-1} \bigl(I_{N}\otimes B^{T}T_{2}^{T} \bigr) \\ &{}+(I_{N}\otimes T_{2}C) \varepsilon _{6}^{-1} \bigl(I_{N}\otimes C^{T}T _{2}^{T}\bigr) \bigr] \dot{z}(t) { \Biggr\} } \eta (t), \end{aligned}$$

(32)

where $\varPi _{6}$ and $\varPi _{7}$ are defined in (11). Applying the Schur complement of Lemma 2.6, and defining $\varOmega (t) = \sigma \widetilde{y}^{T}(t)\widetilde{y}(t) -2(1-\sigma )\gamma \widetilde{y}^{T}(t)\omega (t) -\gamma ^{2} \omega ^{T}(t)\omega (t)$, we have

$$\begin{aligned} \dot{V}(t)+\varOmega (t) \le &\eta ^{T}(t) \varUpsilon \eta (t), \end{aligned}$$

where ϒ is defined in (10). If we have $\varUpsilon <0$, then

$$\begin{aligned} \dot{V}(t) +\varOmega (t) < 0. \end{aligned}$$

(33)

Thus, under the zero original condition, it can be inferred that for any $\mathcal{T}_{p}$

$$\begin{aligned} \int _{0}^{\mathcal{T}_{p}} \varOmega (t) \,dt \leq & \int _{0}^{ \mathcal{T}_{p}} \bigl[ \varOmega (t)+ \dot{V}(t) \bigr] \,dt < 0, \end{aligned}$$

which indicates that

$$\begin{aligned} \int _{0}^{\mathcal{T}_{p}} \bigl[ \sigma \widetilde{y}^{T}(t) \widetilde{y}(t) -2(1-\sigma )\gamma \widetilde{y}^{T}(t)\omega (t) \bigr] \,dt \leq & \gamma ^{2} \int _{0}^{\mathcal{T}_{p}} \omega ^{T}(t) \omega (t) \,dt. \end{aligned}$$

In this case, the condition (9) is ensured for any non-zero $\omega (t)\in \mathcal{L}_{2}[0,\infty )$. If $\omega (t)=0$, in view of (33), there exists a scalar δ such that

$$\begin{aligned} \dot{V}(t) < -\delta \bigl\Vert z(t) \bigr\Vert ^{2}. \end{aligned}$$

(34)

We are now ready to deal with the EFPS of error system (8). Consider the Lyapunov–Krasovskii functional $e^{2\alpha t}V(t)$, where α is a constant. By (34), we have

$$\begin{aligned} \frac{d}{\,dt} e^{2\alpha t}V(t) = e^{2\alpha t}\dot{V}(t)+2\alpha e ^{2\alpha t}V(t) \leq e^{2\alpha t} [-\delta +2\alpha \mathcal{M} ] \bigl\Vert z(t+\epsilon ) \bigr\Vert _{\mathrm{cl}}, \end{aligned}$$

(35)

where

$$\begin{aligned} \mathcal{M}= {}& \bigl(1+\tau _{1}+\tau _{1}^{2}+ \tau _{1}^{3}\bigr)\lambda _{\max }(P) +h \lambda _{\max }(S_{0}) +h^{2}\lambda _{\max }(S_{1}) \\ &{}+\tau _{1}\lambda _{\max }\bigl(Q_{0}+ \varLambda ^{T}Q_{1}\varLambda +Q_{2}+ \varLambda ^{T}Q_{3}\varLambda \bigr) +\tau _{2}\lambda _{\max }\bigl(\varLambda ^{T}R_{1} \varLambda \bigr) \\ &{}+h^{3}\lambda _{\max }(S_{2}+R_{2}) +\tau _{1}^{3}\lambda _{\max }(S _{3}+R_{3}). \end{aligned}$$

From now on, we take α to be a constant satisfying $\alpha \leq \frac{\delta }{2\mathcal{M}}$, and then obtain from (35)

$$\begin{aligned} \frac{d}{dt} e^{2\alpha t} V(t) \leq 0, \end{aligned}$$

(36)

which, together with (12) and (36), implies that

$$\begin{aligned} e^{2\alpha t} V(t) \leq V(0)= \sum_{i=1}^{5} V_{i}(0) \leq \mathcal{M} \bigl\Vert z(\epsilon ) \bigr\Vert _{\mathrm{cl}}, \end{aligned}$$

(37)

and therefore

$$\begin{aligned} V(t) \leq \mathcal{M} e^{-2\alpha t} \bigl\Vert z(\epsilon ) \bigr\Vert _{\mathrm{cl}}. \end{aligned}$$

Noticing $\lambda _{\min } (P) \Vert z(t) \Vert ^{2} \leq V(t)$, we obtain

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert ^{2} \leq \frac{\mathcal{M}}{\lambda _{\min } (P)} e ^{-2\alpha t} \bigl\Vert z(\epsilon ) \bigr\Vert _{\mathrm{cl}}. \end{aligned}$$

(38)

Letting $\mu =\frac{\mathcal{M}}{\lambda _{\min } (P)}$ and $\varpi =2\alpha$, we can rewrite (38) as

$$\begin{aligned} \bigl\Vert z(t) \bigr\Vert ^{2} \leq \mu e^{-\varpi t} \bigl\Vert z(\epsilon ) \bigr\Vert _{\mathrm{cl}}. \end{aligned}$$

Hence, the error system (8) is EFPS. Thus, according to Definition 2.2, the error system (8) is an EFPS with a mixed $H_{\infty }$ and passivity performance index γ. The proof is completed. □

Based on Theorem 3.1, the pinning sampled-data controller design, ensuring the EFPS of delayed NNs (1), is explained.

Theorem 3.2

Given constants $\tau _{1}$, $\tau _{2}$, $\bar{\tau }_{1}$, h, γ and $\sigma \in [0, 1]$, if real positive matrices $P\in \mathcal{R}^{4n \times 4n}$, $Q_{0}$, $Q_{i}$, $S_{0}$ $S_{i},R_{i}\in \mathcal{R}^{n \times n}$ ($i = 1,2,3$), positive constants $\varepsilon _{i}$, $i = 1,2,\ldots,6$, and real matrices Y, Z with appropriate dimensions, such that

$$\begin{aligned} \tilde{\varUpsilon }= \begin{bmatrix} \tilde{\varUpsilon }_{11} &\tilde{\varUpsilon }_{12} &\tilde{\varUpsilon }_{13} &\tilde{\varUpsilon }_{14} &\tilde{\varUpsilon }_{15} &\tilde{\varUpsilon } _{16} &\tilde{\varUpsilon }_{17} \\ *& - {\varepsilon _{1}}I&0&0&0&0&0 \\ *&*& - {\varepsilon _{2}}I&0&0&0&0 \\ *&*&*& - {\varepsilon _{3}}I&0&0&0 \\ *&*&*&*& - {\varepsilon _{4}}I&0&0 \\ *&*&*&*&*& - {\varepsilon _{5}}I&0 \\ *&*&*&*&*&*& - {\varepsilon _{6}}I \end{bmatrix} < 0, \end{aligned}$$

(39)

where

$$\begin{aligned} \textstyle\begin{cases} \tilde{\varUpsilon }_{11}=\sum_{i=1}^{8} \tilde{\varPi }_{i}, \\ \tilde{\varUpsilon }_{12}=I_{N}\otimes \beta _{1} YA, \qquad \tilde{\varUpsilon }_{13}=I_{N}\otimes \beta _{1} YB, \qquad \tilde{\varUpsilon }_{14}=I_{N}\otimes \beta _{1} YC, \\ \tilde{\varUpsilon }_{15}=I_{N}\otimes \beta _{2} YA, \qquad \tilde{\varUpsilon }_{16}=I_{N}\otimes \beta _{2} YB, \qquad \tilde{\varUpsilon }_{17}=I_{N}\otimes \beta _{2} YC, \\ \varPi _{1}=\varTheta _{1}^{T}P\varTheta _{2}+\varTheta _{2}^{T}P\varTheta _{1} -\varTheta _{3}^{T}S_{1}\varTheta _{3}-\varTheta _{4}^{T}S_{1}\varTheta _{4} +z_{1}^{T}S_{0}z _{1}-z_{5}^{T}S_{0}z_{5}, \\ \varPi _{2}=z_{1}^{T}(Q_{0}+Q_{2})z_{1} +z_{1}^{T}\varLambda ^{T}(Q_{1}+Q_{3}) \varLambda z_{1} -z_{3}^{T}Q_{0}z_{3}-(1-\bar{\tau }_{1})z_{2}^{T}Q_{2}z _{2} \\ \hphantom{\varPi _{2}=}{} -z_{3}^{T}(\varLambda ^{T} Q_{1}\varLambda )z_{3} -(1-\bar{\tau }_{1})z_{2} ^{T}(\varLambda ^{T} Q_{3} \varLambda )z_{2}, \\ \varPi _{3}=\tau _{2}^{2}z_{1}^{T}(\varLambda ^{T}R_{1}\varLambda )z_{1}-z_{13} ^{T}(\varLambda ^{T}R_{1}\varLambda )z_{13}, \\ \varPi _{4}=h^{2}z_{6}^{T}(S_{2}+0.5R_{2})z_{6} -\varTheta _{5}^{T} S_{2} \varTheta _{5}-3\varTheta _{6}^{T}S_{2}\varTheta _{6} -5\varTheta _{7}^{T}S_{2}\varTheta _{7} \\ \hphantom{\varPi _{4}=}{} -2\varTheta _{11}^{T}R_{2}\varTheta _{11} -4\varTheta _{12}^{T}R_{2}\varTheta _{12} - 6\varTheta _{13}^{T}R_{2}\varTheta _{13}, \\ \varPi _{5}=\tau _{1}^{2}z_{6}^{T}(S_{3}+0.5R_{3})z_{6} -\varTheta _{8}^{T} S _{3}\varTheta _{8}-3\varTheta _{9}^{T}S_{3}\varTheta _{9} -5\varTheta _{10}^{T}S_{3} \varTheta _{10} \\ \hphantom{\varPi _{5}=}{} -2\varTheta _{14}^{T}R_{3}\varTheta _{14} -4\varTheta _{15}^{T}R_{3}\varTheta _{15} -6 \varTheta _{16}^{T}R_{3}\varTheta _{16}, \\ \tilde{\varPi }_{6}=\beta _{1}z_{1}^{T}Y \mathcal{C}_{0} +\beta _{1} \mathcal{C}_{0}^{T}Y^{T}z_{1} +\beta _{2}z_{6}^{T}Y\mathcal{C}_{0} + \beta _{2}\mathcal{C}_{0}^{T}Y^{T}z_{6} +\beta _{1}z_{1}^{T}Zz_{4} \\ \hphantom{\varPi _{6}=}{} +\beta _{1}z_{4}^{T}Z^{T}z_{1} +\beta _{2}z_{6}^{T}Zz_{4} +\beta _{2}z _{4}^{T}Z^{T}z_{6} +\beta _{1}z_{1}^{T}Yz_{14} +\beta _{1}z_{14}^{T}Y ^{T}z_{1} \\ \hphantom{\varPi _{6}=}{} -\beta _{1}z_{1}^{T}Yz_{6} -\beta _{1}z_{6}^{T}Y^{T}z_{1} +\beta _{2}z _{6}^{T}Yz_{14} +\beta _{2}z_{14}^{T}Y^{T}z_{6} -\beta _{2}z_{6}^{T}Yz _{6} \\ \hphantom{\varPi _{6}=}{} -\beta _{2}z_{6}^{T}Y^{T}z_{6}, \\ \varPi _{7}=(\varepsilon _{1}+\varepsilon _{4})z_{1}^{T}(I_{N}\otimes \varLambda ^{T}\varLambda )z_{1} +(\varepsilon _{2}+\varepsilon _{5})z_{2}^{T}(I _{N}\otimes \varLambda ^{T}\varLambda )z_{2} \\ \hphantom{\varPi _{7}=}{} +(\varepsilon _{3}+\varepsilon _{6})z_{13}^{T}(I_{N}\otimes \varLambda ^{T} \varLambda )z_{13}, \\ \varPi _{8} =\sigma (Jz_{1})^{T}(Jz_{1}) -(1-\sigma )\gamma (Jz_{1})^{T}z _{14} -(1-\sigma )\gamma z_{14}^{T}(Jz_{1}) - \gamma ^{2}z_{14}^{T}z _{14}, \\ \mathcal{C}_{0}=[c_{1}(G^{(1)}\otimes L_{1}) -(I_{N}\otimes D)]z_{1} +c _{2}(G^{(2)}\otimes L_{2})z_{2} +c_{3}(G^{(3)}\otimes L_{3})z_{13}, \end{cases}\displaystyle \end{aligned}$$

(40)

with

$$\begin{aligned}& \varTheta _{1}=\bigl[z_{1}^{T} ,z_{7}^{T} ,z_{8}^{T} ,z_{9}^{T}\bigr]^{T},\qquad \varTheta _{2}=\bigl[z_{6}^{T}, z_{1}^{T} -z_{3}^{T}, \tau _{1}z_{1}^{T} - z_{7}^{T}, 0.5\tau _{1}^{2}z_{1}^{T}-z_{8}^{T} \bigr]^{T}, \\& \varTheta _{3}=z_{1}-z_{4}, \qquad \varTheta _{4}=z_{4}-z_{5}, \qquad \varTheta _{5}=z_{1}-z_{5}, \\& \varTheta _{6}=z_{1}+z_{5}- \frac{2}{h}{z_{10}}, \qquad \varTheta _{7}=z_{1}-z_{5}+ \frac{6}{h}{z_{10}}-\frac{12}{h^{2}}z_{11}, \\& \varTheta _{8}=z_{1}-z_{3},\qquad \varTheta _{9}=z_{1}+z_{3}- \frac{2}{\tau _{1}}z_{7}, \\& \varTheta _{10}=z_{1}-z_{3}+ \frac{6}{\tau _{1}}z_{7}-\frac{12}{\tau _{1} ^{2}}z_{8}, \qquad \varTheta _{11}=z_{1}-\frac{1}{h}z_{5}, \\& \varTheta _{12}=z_{1}+\frac{2}{h}z_{5}- \frac{6}{h^{2}}z_{10}, \qquad \varTheta _{13}=z_{1}- \frac{3}{h}z_{5}+\frac{24}{h^{2}}z_{10} - \frac{60}{h ^{3}}z_{11},\qquad \varTheta _{14}=z_{1}- \frac{1}{\tau _{1}}z_{7}, \\& \varTheta _{15}=z_{1}+\frac{2}{\tau _{1}}z_{7}- \frac{6}{\tau _{1}^{2}}z_{8}, \qquad \varTheta _{16}=z_{1}- \frac{3}{\tau _{1}}z_{7}+\frac{24}{\tau _{1}^{2}}z _{8}- \frac{60}{\tau _{1}^{3}}z_{9}, \end{aligned}$$

then the synchronization error system (8) is exponentially stable and meets a predefined $\mathcal{H}_{\infty }$/passive performance index γ. Meanwhile, the designed controller gains are given as follows:

$$\begin{aligned} K=Y^{-1}Z. \end{aligned}$$

Proof

Denote

$$\begin{aligned} T_{1}=\beta _{1} Y, \qquad T_{2}=\beta _{2} Y, \end{aligned}$$

(41)

then the LMIs (39) can be achieved. This completes the proof. □

Remark 3

In Theorem 3.2, we investigate the EFPS of NNs via mixed control. $u_{i1}(t)$ is a nonlinear control (not pinning sampled-data control). Based on the principle of EFPS, $u_{i1}(t)$ needs to be applied for every node. And, based on the principle of pinning sampled-data control, $u_{i2}(t)$ is a pinning sampled-data control meant to apply for the first l nodes $0 \leq i \leq l$.

Remark 4

The advantage of this paper is that this is the first time hybrid couplings are addressed containing constant, discrete and distributed delay couplings considered in the problem of exponential function projective synchronization of delayed neural networks including with mixed $H_{\infty }$ and passivity. So, our conditions are more general than [33, 34] where these couplings are not considered. Hence, we can see that their conditions cannot be applied to our examples.

Remark 5

A challenging problem of this work that is this is the first time the control problem and the passive control problem of exponential function projective synchronization for neural networks with hybrid coupling based on appropriate pinning sampled-data control are studied. The Lyapunov–Krasovskii functional $V(t)$ in (12) has effectively been applied to the entire information on three kinds of time-varying delays. Moreover, some novel double and triple integral functional terms are constructed, for which Wirtinger-based integral inequalities have been employed to give much tighter upper bound on Lyapunov–Krasovskii functional’s derivative and reduce the conservatism effectively.

4 Numerical examples

Several numerical examples are given to present the feasibility of the proposed method and the effectiveness of the above theoretical results.

Example 4.1

Consider the isolated node with both discrete and distributed delays:

$$\begin{aligned} \textstyle\begin{cases} \begin{bmatrix} \dot{s}_{1}(t) \\ \dot{s}_{2}(t) \end{bmatrix} = {-} \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} \begin{bmatrix} s_{1}(t) \\ s_{2}(t) \end{bmatrix} + \begin{bmatrix} 2.0& - 0.1 \\ - 5.0&1.5 \end{bmatrix} \begin{bmatrix} f(s_{1}(t)) \\ f(s_{2}(t)) \end{bmatrix} \\ \hphantom{ \begin{bmatrix} \dot{s}_{1}(t) \\ \dot{s}_{2}(t) \end{bmatrix} =}{} + \begin{bmatrix} -1.5&-0.1 \\ -0.2&-1.0 \end{bmatrix} \begin{bmatrix} f(s_{1}(t-1)) \\ f(s_{2}(t-1)) \end{bmatrix} \\ \hphantom{ \begin{bmatrix} \dot{s}_{1}(t) \\ \dot{s}_{2}(t) \end{bmatrix} =}{} + \begin{bmatrix} 0.6 &0.15 \\ -1.8&-0.12 \end{bmatrix} \begin{bmatrix} \int _{t -\tau _{2}(t)}^{t} f(s_{1}(\theta ))\,d\theta \\ \int _{t -\tau _{2}(t)}^{t} f(s_{2}(\theta ))\,d\theta \end{bmatrix}, \end{cases}\displaystyle \end{aligned}$$

(42)

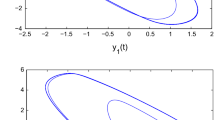
where $f(s_{i})=\tanh (s_{i}(t))$, $(i=1,2)$, $\tau _{1}(t)=\frac{{{1}}}{ {1+e^{-t}}}$ and $\tau _{2}(t)=0.25\sin ^{2}(t)$. Then the trajectory of the isolated node (42) with initial conditions $s_{1}(r)=0.4 \cos (t)$, $s_{2}(r)=0.6\cos (t)$, $\forall r\in [-1, 0]$ is shown in Fig. 1. For mixed $H_{\infty }/$passive EFPS of delayed NNs (1), choosing the time-varying scaling function $\alpha (t)=0.6+0.25\sin (\frac{0.5 \pi }{15}t)$, the coupling strength $c_{1}=0.5$, $c_{2}=0.5$, $c_{3}=0.5$, and the inner-coupling matrices are given by

$$\begin{aligned} L_{1}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\qquad L_{2}= \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix},\qquad L_{3}= \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix}. \end{aligned}$$

We consider the directed NNs as shown in Fig. 2. From Fig. 2, the outer-coupling matrices are described by

$$\begin{aligned} G^{(1)} =& \begin{bmatrix} -1 & 0& 1& 0& 0& 0& 0 \\ 1 &-1& 0& 0& 0& 0& 0 \\ 0 & 0&-1& 1& 0& 0& 0 \\ 1 & 1& 0&-2& 0& 0& 0 \\ 0 & 1& 0& 1&-2& 0& 0 \\ 0 & 0& 1& 1& 0&-3& 1 \\ 0 & 0& 0& 1& 1& 0&-2 \end{bmatrix}, \\ G^{(2)} =& \begin{bmatrix} -1 & 0& 0& 0& 0& 1& 0 \\ 1 &-1& 0& 0& 0& 0& 0 \\ 1 & 0&-2& 1& 0& 0& 0 \\ 1 & 1& 0&-3& 1& 0& 0 \\ 0 & 1& 0& 0&-1& 0& 0 \\ 0 & 0& 1& 1& 0&-3& 1 \\ 0 & 0& 0& 1& 1& 0&-2 \end{bmatrix}, \\ G^{(3)} =& \begin{bmatrix} -1 & 0& 0& 1& 0& 0& 0 \\ 1 &-1& 0& 0& 0& 0& 0 \\ 0 & 1&-1& 0& 0& 0& 0 \\ 0 & 1& 1&-3& 1& 0& 0 \\ 0 & 1& 1& 1&-3& 0& 0 \\ 0 & 0& 0& 0& 0& -1&1 \\ 0 & 0& 0& 0& 1& 0&-1 \end{bmatrix}. \end{aligned}$$

As presented in Fig. 2, according to the pinned-node selection, nodes 1, 3, 4, 5, and 6 are chosen as controller. By applying our Theorem 3.2, the relation among the parameters h, σ, and γ, are shown in Table 1. Moreover, the histogram referring to the obtained relation is also plotted in Fig. 3. Table 2 gives the maximum allowable sampling period of h for different values of ϖ. Thus, if we set $\varpi =0.3$ and $h=0.5$, then the gain matrices of the designed controllers will be obtained as follows:

$$\begin{aligned}& K_{1}= \begin{bmatrix} -1.3426 & -0.4325 \\ -0.5346 & -1.6532 \end{bmatrix}, \qquad K_{3}= \begin{bmatrix} -0.9362 & -0.5792 \\ -0.6378 & -0.8462 \end{bmatrix}, \\ & K_{4}= \begin{bmatrix} -1.1431 & -0.3214 \\ -0.4391 & -0.7896 \end{bmatrix}, \qquad K_{5}= \begin{bmatrix} -1.9403 & -0.9432 \\ -0.8451 & -1.2056 \end{bmatrix}, \\ & K_{6}= \begin{bmatrix} -1.4232 & -0.2142 \\ -0.1674 & -2.0543 \end{bmatrix}, \qquad K_{2} =K_{7} = \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}. \end{aligned}$$

Furthermore, the EFPS of chaotic behaviour for the isolated node $\alpha (t)s(t)$ (42) and network $x_{i}(t)$ (1) with the time-varying scaling function $\alpha (t)$ is given in Fig. 4. Figure 5 shows the state trajectories of the isolated node $\alpha (t)s(t)$ (42) and network $x_{i}(t)$ (1). Figure 6 shows the EFPS errors between the states of the isolated node $\alpha (t)s(t)$ (42) and network $x_{i}(t)$ (1) where $z_{ij}(t)=x_{ij}(t)-\alpha _{j}(t)s _{j}(t)$ for $i = 1,2,\ldots ,7, j = 1,2$ without pinning sampled-data control (5). Figure 7 shows the EFPS errors between the states of the isolated node $\alpha (t)s(t)$ (42) and network $x_{i}(t)$ (1) where $z_{ij}(t)=x_{ij}(t)- \alpha _{j}(t)s_{j}(t)$ for $i = 1,2,\ldots ,7, j = 1,2$ with pinning sampled-data control (5).

Figure 1

The trajectory of the isolated node (42)

Figure 2

Simple directed neural networks with seven nodes

Figure 3

Relation among h, σ, and γ

Figure 4

The trajectory of the isolated node (42) and network (1) with the time-varying scaling function

Figure 5

The state trajectory of the isolated node $\alpha (t)s(t)$ (42) and network $x_{i}(t)$ (1)

Figure 6

The EFPS error between isolate node $\alpha (t)s(t)$ (42) and network $x_{i}(t)$ (1) without sample-data pinning control (5)

Figure 7

The EFPS error between isolate node $\alpha (t)s(t)$ (42) and network $x_{i}(t)$ (1) with sample-data pinning control (5)

Table 1 Minimum allowable values of γ for mixed $H_{\infty }$ and passivity analysis satisfied with different values of h and σ

Table 2 Maximum allowable sampling period of h in Example 4.1

Example 4.2

Consider the isolated node with both discrete and distributed delays:

$$\begin{aligned} \textstyle\begin{cases} \begin{bmatrix} \dot{s}_{1}(t) \\ \dot{s}_{2}(t) \end{bmatrix} = {-} \begin{bmatrix} 1&0 \\ 0&1 \end{bmatrix} \begin{bmatrix} s_{1}(t) \\ s_{2}(t) \end{bmatrix} + \begin{bmatrix} 1.8& - 0.15 \\ - 5.1&3.5 \end{bmatrix} \begin{bmatrix} f(s_{1}(t)) \\ f(s_{2}(t)) \end{bmatrix} \\ \hphantom{ \begin{bmatrix} \dot{s}_{1}(t) \\ \dot{s}_{2}(t) \end{bmatrix} =}{} + \begin{bmatrix} - 1.7& - 0.12 \\ - 0.24& - 1.5 \end{bmatrix} \begin{bmatrix} f(s_{1}(t-1)) \\ f(s_{2}(t-1)) \end{bmatrix} \\ \hphantom{ \begin{bmatrix} \dot{s}_{1}(t) \\ \dot{s}_{2}(t) \end{bmatrix} =}{}+ \begin{bmatrix} 0.6 & 0.15 \\ - 2& - 0.1 \end{bmatrix} \begin{bmatrix} \int _{t -\tau _{2}(t)}^{t} f(s_{1}(\theta ))\,d\theta \\ \int _{t -\tau _{2}(t)}^{t} f(s_{2}(\theta ))\,d\theta \end{bmatrix}, \end{cases}\displaystyle \end{aligned}$$

(43)

where $f(s_{i})=\tanh (s_{i}(t))$, $(i=1,2)$, $\tau _{1}(t)=\frac{{{1}}}{ {1+e^{-t}}}$ and $\tau _{2}(t)=1.2\sin ^{2}(t)$. Then the trajectory of the isolated node (43) with initial conditions $s_{1}(r)=0.5 \cos (t)$, $s_{2}(r)=0.1\cos (t)$, $\forall r\in [-1.2, 0]$ is shown in Fig. 8. Choosing the time-varying scaling function $\alpha (t)=0.65+0.2\sin (\frac{ \pi }{15}t)$, the coupling strength $c_{1}=0.1$, $c_{2}=0.1$, $c_{3}=0.1$, and the inner-coupling matrices are given by

$$\begin{aligned} L_{1}= \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix},\qquad L_{2}= \begin{bmatrix} 0.1 & 0 \\ 0 & 0.1 \end{bmatrix},\qquad L_{3}= \begin{bmatrix} 0.1 & 0 \\ 0 & 0.1 \end{bmatrix}. \end{aligned}$$

We consider the undirected NNs as shown in Fig. 9, and the outer-coupling matrices are described by

$$\begin{aligned} &G^{(1)}= \begin{bmatrix} -2 & 0& 0& 1& 0& 1 \\ 0 &-3 & 0& 1& 1& 1 \\ 0 & 0&-3 & 1& 1& 1 \\ 1 & 1& 1&-4 & 1& 0 \\ 0 & 1& 1& 1&-3 & 0 \\ 1 & 1& 1& 0& 0& -3 \end{bmatrix}, \\ &G^{(2)}= \begin{bmatrix} -2 & 1& 1& 0& 0& 0 \\ 1 &-2& 1& 0& 0& 0 \\ 1 & 1&-5& 1& 1& 1 \\ 0 & 0& 1&-3& 1& 1 \\ 0 & 0& 1& 1&-3& 1 \\ 0 & 0& 1& 1& 1& -3 \end{bmatrix}, \\ &G^{(3)}= \begin{bmatrix} -2 & 1& 0& 0& 0& 1 \\ 1 &-3& 1& 0& 0& 1 \\ 0 & 1&-2& 1& 0& 0 \\ 0 & 0& 1&-3& 1& 1 \\ 0 & 0& 0& 1&-2& 1 \\ 1 & 1& 0& 1& 1& -4 \end{bmatrix}. \end{aligned}$$

As presented in Fig. 9, according to the pinned-node selection, nodes 3, 4, and 6 are chosen as controller. Table 3 gives the maximum allowable sampling period of h for different values of ϖ. Thus, if we set $\varpi =0.3$ and $h=0.5$, then the gain matrices of the designed controllers will be obtained. Thus, if we set $\varpi =0.5$ and $h=0.7$, then the gain matrices of the designed controllers will be obtained as follows:

$$\begin{aligned} &K_{3}= \begin{bmatrix} -3.2051 & -1.3624 \\ -2.3479 & -2.7312 \end{bmatrix}, \qquad K_{4}= \begin{bmatrix} -1.3465 & -0.1384 \\ -0.2478 & -0.7543 \end{bmatrix}, \\ &K_{6}= \begin{bmatrix} -2.4312 & -1.0065 \\ -0.9431 & -1.457 \end{bmatrix}, \qquad K_{1}=K_{2}=K_{5}= \begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}. \end{aligned}$$

Furthermore, the EFPS of chaotic behaviour for the isolated node $\alpha (t)s(t)$ (43) and network $x_{i}(t)$ (1) with $\alpha (t)$ is given Fig. 10. Figure 11 shows the state trajectories of the isolated node $\alpha (t)s(t)$ (43) and network $x_{i}(t)$ (1). Figure 12 shows the EFPS errors between the states of the isolated node $\alpha (t)s(t)$ (43) and network $x_{i}(t)$ (1) where $z_{ij}(t)=x_{ij}(t)-\alpha _{j}(t)s_{j}(t)$ for $i = 1,2,\ldots ,6, j = 1,2$ without pinning sampled-data control (5). Figure 13 shows the EFPS errors between the states of the isolated node $\alpha (t)s(t)$ (43) and network $x_{i}(t)$ (1) where $z_{ij}(t)=x_{ij}(t)-\alpha _{j}(t)s _{j}(t)$ for $i = 1,2,\ldots ,6, j = 1,2$ with pinning sampled-data control (5).

Figure 8

The trajectory of the isolated node (43)

Figure 9

Simple undirected neural networks with six nodes

Figure 10

The trajectory of the isolated node (43) and network (1) with the time-varying scaling function

Figure 11

The state trajectory of the isolated node $\alpha (t)s(t)$ (43) and network $x_{i}(t)$ (1)

Figure 12

The EFPS error between the isolate node $\alpha (t)s(t)$ (43) and network $x_{i}(t)$ (1) without sample-data pinning control (5)

Figure 13

The EFPS error between the isolate node $\alpha (t)s(t)$ (43) and network $x_{i}(t)$ (1) with sample-data pinning control (5)

Table 3 Maximum allowable sampling period of h in Example 4.2

Remark 6

The networks in both examples of our study and the ones in the literature [21, 32, 39] are different. In [21], the FPS of the network is achieved under pinning feedback controller design but the concerned network is still undirected. In [39], the conditions for pinning synchronization are suitable for directed network. In this paper, the pinning synchronization suitable for both directed and undirected networks. So, the considered networks are more general.

Remark 7

Accordingly, it is worthwhile to focus on sampled-data control and it has caused much attention recently [30,31,32,33,34]. In the sampled-data implementation, an important issue is to reduce the data transmission load when using a sampled-data controller to realize the stability, since the computation and communication resources are limited often. However, it is interesting to extend this method to NN systems with even-triggered sampling control in which the control packet can be lost due to several factors, for instance, communication interference, congestion or the transmission event is not triggered and the controller is not updated except when its magnitude reaches the prescribed threshold. Hence, it is necessary to design an event-triggered sampling control for NNs system, which can effectively save the communication bandwidth by only sending a necessary sampling signal through the network; see [42, 43]. Nevertheless, considering the sampled-data controller and the digital form controller, which uses only the sampled information of the system at its instants, the important benefits in using a sampled-data controller are low-cost consumption, reliability, easy installation and being handy in real world problems.

5 Conclusions

In this paper, mixed $H_{\infty }$/passive EFPS of NNs with time-varying delays and hybrid coupling are investigated. We have applied the using of nonlinear and pinning sampled-data controls. Some sufficient conditions were derived to guarantee the EFPS by using of the Lyapunov–Krasovskii function method. In order to manipulate the scaling functions, the drive system and response systems could be synchronized up to the desired scaling functions based on the pinning sampled-data control technique. Furthermore, numerical examples are given to illustrate the effectiveness of the proposed theoretical results in this paper as well.