1 Introduction

Owing to rapid growth in developments of micro-fluidic devices used for various industrial applications such as biofluidic systems using in precision medicine, micro-electric-mechanical system (MEMS), perpetual motion machine, semi-conductor manufacturing equipment, microscale heat exchangers and so on. As micro-fluidic device has characteristic length between 1 μm and 1 mm, the flow behaviour in the microchannel has a non-continuum effect. In the literature, a number of experimental and/or mathematical investigations deal with slip flow and/or heat transfer through microchannels, but the microflow phenomenon is not well understood due to contradictions related to drag effect and transition from laminar to turbulent flow. Due to the difficulty in experiments in this area, continuing effort to resolve these problems mathematically is important. Slip flow phenomenon in microducts has traditionally been studied analytically and numerically [7,8,9, 13, 17,18,19,20]. The governing equations of the slip flow in microducts include the classical Navier–Stokes equations. Based on the assumption of incompressible Newtonian fluid with constant properties, negligible body forces and hydrodynamically fully developed steady state flow, the Navier–Stokes equations reduce to the Poisson equation

$$ \biggl(\frac{\partial ^{2} u}{\partial x^{2}} + \frac{\partial ^{2} u}{ \partial y^{2}} \biggr) = f $$
(1)

subject to Navier’s slip boundary condition

$$ u = -\beta \frac{\partial u}{\partial n}, $$
(2)

or the second-order slip boundary condition

$$ u =- \beta _{v} \lambda \frac{\partial u}{\partial n} + - \beta _{v} \lambda ^{2} \frac{\partial ^{2} u}{\partial n^{2}}, $$
(3)

where β is the slip parameter, \(\beta _{v} = \frac{2-\sigma _{v}}{\sigma _{v}}\) depending on the tangential momentum accommodation coefficient (\(\sigma _{v}\)), λ denotes the molecular mean flow path and n is unit outward normal vector to the boundary.

Wang [18] analysed the slip flow in super-elliptic ducts governed by the Poisson equation (1) with \(f=-1\) subject to Navier’s slip condition. The Ritz method was applied for the solution of the problem. The results indicate that the average velocity increases and the friction factor-Reynolds number product decreases as the slip parameter increases with parameters being fixed. Duan and Muzychka [9] and Das and Tahmouresi [8] described the gaseous slip flow in elliptic microchannel using equation (1) with \(f=\frac{1}{\mu }\frac{\partial p}{\partial z}\) under the first-order slip boundary condition. The method of separation of variables [9] and integral transforms incorporating the Aftken transformation [8] were applied to obtain analytical solutions in elliptic cylinder coordinates. The computed results of friction factor and Reynolds number product were reported. Maurer et al. [13] proposed a second-order slip law in microchannels for helium and nitrogen. An experimental model of gas flow in a shallow microchannel with rectangular cross section was used to study the second-order effects. The experimental results were compared with theoretical expectations. The upper limit of the slip flow regime in terms of the averaged Knudsen number is predicted for two gases. As various problems in micro-fluidic devices involve slip flow with a relationship between temperature and volumetric flow rate [5, 10], understanding the relationship between fluid flow and temperature is important in most micro-fluidic systems. Various projects [2, 3, 11, 12, 15, 16, 21] have been carried out to study the steady slip-flow heat transfer process in microchannels using the classical Navier–Stokes equations and the energy equation. Under the assumption of the fully developed slip-flow heat transfer, the governing equations reduce to

$$ \mu \biggl(\frac{\partial ^{2} u}{\partial x^{2}} + \frac{\partial ^{2} u}{\partial y^{2}} \biggr) = \frac{\partial p}{\partial z} $$
(4)

and

$$ k \biggl(\frac{\partial ^{2} T}{\partial x^{2}} + \frac{\partial ^{2} T}{ \partial y^{2}} \biggr) = F. $$
(5)

Yu and Ameel [21] studied analytically the slip flow and heat transfer of gas in rectangular microchannels with velocity slip and temperature jump conditions at the gas-surface interface. A modified generalised integral transform method was applied for the solution of the problem. Spiga and Vocale [15] described the slip flow with constant heat flux (q) in elliptic microchannels with cross section area (A) by the Poisson equation (1) and energy equations (4) in which the force term is defined by \(F=\frac{q}{A}\frac{u}{\bar{u}}\). To the best of authors’ knowledge, little work has been done to study the unsteady slip flow and heat transfer driven by oscillating pressure gradient in microchannels of elliptic cross section.

This paper is to study transient oscillating pressure-driven slip flow and heat transfer in elliptic microchannels. The model is subject to the Navier slip and convective heat flow conditions at the boundary. Constant heat flux is assumed in the microchannel. Semi-analytical solutions of velocity and temperature fields will be obtained by the Ritz method.

2 Governing equations

This paper concerns a thermal fluid flow inside an elliptical tube with the uniform external temperature. The classical Navier–Stokes and energy equations are

$$\begin{aligned} &\mu \biggl( \frac{\partial ^{2} u}{\partial x^{2}}+\frac{\partial ^{2} u}{ \partial y^{2}}+ \frac{\partial ^{2} u}{\partial z^{2}} \biggr) - \rho \frac{\partial u}{\partial t} = \frac{\partial p}{\partial z}, \end{aligned}$$
(6)
$$\begin{aligned} &k \biggl( \frac{\partial ^{2} T}{\partial x^{2}}+\frac{\partial ^{2} T}{ \partial y^{2}} + \frac{\partial ^{2} T}{\partial z^{2}} \biggr) - \rho c_{p} \biggl( \frac{\partial T}{\partial t} + u \frac{\partial T}{ \partial z} \biggr) = q_{p} \end{aligned}$$
(7)

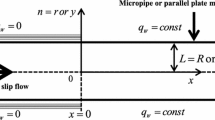
subject to the initial condition \(T = T_{0}\) at \(x=y=z=t=0\) and the boundary conditions on the tube wall

$$ u+\beta \frac{\partial u}{\partial \mathbf{n}} = 0, \qquad h_{\infty }(T-T_{\infty }) - k\frac{\partial T}{\partial \mathbf{n}} = 0, $$
(8)

where u and T represent respectively the flow speed and temperature of fluid, \(\mu, \rho, k\) and \(c_{p}\) denote respectively viscosity, density, thermal conductivity and specific heat of the fluid, \(h_{\infty }\) represents the convective heat transfer coefficient, \(T_{\infty }\) is the tube outer temperature which is assumed to be uniform and \(q_{p}\) is heat flux.

In this study, we assume no swirling flow but the effect of pressure variation on heat flux [4] is considered

$$ \frac{\partial u}{\partial z} = 0, \qquad q_{p} = \frac{q}{\bar{p}} \biggl( \frac{\partial p}{\partial t} + u \frac{ \partial p}{\partial z} \biggr), $$
(9)

where q and p̄ are respectively a heat flux parameter and the average pressure.

We also assume that the flow of fluid along the elliptical tube with uniform shape is driven by the oscillating pressure gradient with frequency ω at time t, i.e.

$$ \frac{\partial p}{\partial z} = p_{0} e^{i \omega t}. $$
(10)

Thus, equations (6) and (7), by using equations (9) and (10), become

$$\begin{aligned} & \mu \biggl( \frac{\partial ^{2} u}{\partial x^{2}}+\frac{\partial ^{2} u}{ \partial y^{2}} \biggr) - \rho \frac{\partial u}{\partial t} = p _{0} e^{i \omega t}, \end{aligned}$$
(11)
$$\begin{aligned} & k \biggl( \frac{\partial ^{2} T}{\partial x^{2}}+\frac{\partial ^{2} T}{ \partial y^{2}}+ \frac{\partial ^{2} T}{\partial z^{2}} \biggr) - \rho c _{p} \biggl( \frac{\partial T}{\partial t} + u \frac{\partial T}{ \partial z} \biggr) = \frac{q}{\bar{p}} ( i \omega z + u ) p_{0} e^{i \omega t}. \end{aligned}$$
(12)

We now find the velocity and temperature fields in the form of

$$ u = v(x,y) e^{i \omega t},\qquad T = h(x,y) \bigl( T_{\infty }+ ( T_{0} - T_{\infty }) e^{-\frac{ \alpha z}{\bar{u}}-\lambda t} \bigr), $$
(13)

where ū is average velocity, \(\alpha = \frac{4 h_{\infty }}{ \rho c_{p} D_{h}}\) and \(\lambda =\sqrt{\frac{h_{\infty } A}{c_{p}}}\) in which A is the area of cross section and \(D_{h}\) is a hydraulic diameter determined by [14]

$$ D_{h}=\frac{4ab(64-16E^{2})}{(a+b)(64-3E^{4})} \quad\text{for } E=\frac{a-b}{a+b}. $$
(14)

We now obtain, from equation (13) and denoting \(\gamma = \frac{ \rho c_{p}}{k}\), the boundary value problem (BVP):

$$\begin{aligned} & \biggl( \frac{\partial ^{2} v}{\partial x^{2}}+\frac{\partial ^{2} v}{ \partial y^{2}} \biggr) - \frac{i \omega \rho }{\mu } v - \frac{p_{0}}{ \mu } = 0, \end{aligned}$$
(15)
$$\begin{aligned} & \biggl( \frac{\partial ^{2} h}{\partial x^{2}}+\frac{\partial ^{2} h}{ \partial y^{2}} \biggr) - g(x,y,z,t) h - f(x,y,z,t) = 0 \end{aligned}$$
(16)

with

$$\begin{aligned} &g(x,y,z,t) = \frac{ ( \gamma \lambda + \gamma \alpha \frac{u}{ \bar{u}} + (\frac{\alpha }{\bar{u}} )^{2} )( T_{ \infty } - T_{0})e^{-(\frac{\alpha }{\bar{u}}z+\lambda t)}}{T_{\infty } +(T_{0}-T_{\infty })e^{-(\frac{\alpha }{\bar{u}}z+\lambda t)}}, \\ &f(x,y,z,t) = \frac{q}{k \bar{p}} \biggl(\frac{ ( i \omega z+ u ) p_{0} e^{i \omega t}}{T_{\infty } +(T_{0}-T_{\infty })e^{-(\frac{ \alpha }{\bar{u}}z+\lambda t)}} \biggr) \end{aligned}$$

subject to the boundary conditions

$$ v+\beta \frac{\partial v}{\partial \mathbf{n}} = 0,\qquad h_{\infty }h + k \frac{\partial h}{\partial \mathbf{n}} = \frac{h _{\infty }T_{\infty }}{T_{\infty } +(T_{0}-T_{\infty })e^{-(\frac{ \alpha }{\bar{u}}z+\lambda t)}}, $$
(17)

which can be solved in elliptical coordinates (see details in our paper [7]).

Here, we solve the above BVP in rectangular coordinates by considering the quadratic minimisation problem to find \(w \in K \subset H^{1}( \varOmega )\) where \(H^{1}(\varOmega )\) is a Hilbert space such that

$$ \min J = \frac{1}{2} a(w,w) - F, $$
(18)

where \(a(w,w)\) is a bilinear form and F is a linear form and the vector space K is convex. Our BVP (15)–(17) is thus equivalent to the following system of equations:

$$\begin{aligned} &I_{v} = \frac{1}{\beta } \int _{\partial \varOmega } v^{2} \,ds + \int _{\varOmega } \biggl( \frac{\partial v}{\partial x} \biggr)^{2} + \biggl( \frac{\partial v}{\partial y} \biggr)^{2} + \frac{i \omega \rho v^{2}}{\mu } + 2 p_{0} v \,d\varOmega = 0, \end{aligned}$$
(19)
$$\begin{aligned} & I_{h} =\frac{h_{\infty }}{k} \int _{\partial \varOmega } h^{2} - \frac{T _{\infty }h}{T_{\infty } +(T_{0}-T_{\infty })e^{-(\frac{\alpha }{ \bar{u}}z+\lambda t)}} \,ds \\ &\phantom{I_{h} =}{}+ \int _{\varOmega } \biggl( \frac{\partial h}{\partial x} \biggr)^{2} + \biggl( \frac{\partial h}{\partial y} \biggr)^{2} + g(x,y,z,t) h^{2} + 2 f(x,y,z,t) h \,d\varOmega = 0. \end{aligned}$$
(20)

For an instant time \(t=t_{n}\) and a fixed \(z=z_{n}\) value, we have \(f_{n} = f(x,y,z_{n},t_{n})\) and \(g_{n} = g(x,y,z_{n},t_{n})\) and obtain the solutions \(v(x,y)\) and \(h(x,y)\) of the above system (19)–(20) by using the Ritz method.

Let \(v(x,y)\) and \(h(x,y)\) be defined by

$$\begin{aligned} & v =v(x,y) = \sum_{i=1}^{N} c_{i}\phi _{i}(x,y),\qquad h = h(x,y) = 1+\sum _{i=1}^{N} d_{i}\varphi _{i}(x,y), \\ &\phi _{i} =\bigl\{ 1,x^{2},y^{2},x^{4},x^{2}y^{2},y^{4},x^{6},x^{2}y^{4},x ^{4}y^{2},y^{6},\ldots \bigr\} , \\ &\varphi _{i} =\bigl\{ xy,x^{2},y^{2},x^{4},x^{2}y^{2},y^{4},x^{6},x^{2}y ^{4},x^{4}y^{2},y^{6},\ldots \bigr\} . \end{aligned}$$
(21)

Substituting equation (21)1 into equation (19) and setting \(\frac{\partial I_{V}}{\partial c_{i}}=0\ (i=1,\ldots, N)\), after some derivation, we obtain the following linear system of equations:

$$ \sum_{j=1}^{N} c_{j} ( K_{ij} + B_{ij} ) = C_{i},\quad i=1,\ldots, N, $$
(22)

with

$$\begin{aligned} &K_{ij} = \int _{\varOmega } \phi _{ix}\phi _{jx}+ \phi _{iy}\phi _{jy}+\frac{i \omega \rho }{\mu }\phi _{i} \phi _{j} \,d\varOmega, \\ &B_{ij} =\frac{1}{\beta } \int _{\partial \varOmega } \phi _{i} \phi _{j} \,ds,\qquad C_{i} = \frac{2 p_{0}}{\mu } \int _{\varOmega } \phi _{i} \,d\varOmega. \end{aligned}$$

By solving system (22) for unknowns \(c_{j}\), and then using equation (6)1, the velocity can be obtained by

$$ u(x,y,t) = \Re \Biggl( e^{i \omega t} \sum _{j=1}^{N} c_{j} \phi _{j}(x,y) \Biggr). $$
(23)

We now consider the temperature field. We substitute equation (21)2 into equation (20) and set \(\frac{\partial I_{h}}{ \partial d_{i}}=0\ (i=1,\ldots, N)\). Then we obtain the linear system of equations

$$ \sum_{j=1}^{N} \,d_{j} \bigl( A_{ij} + B_{ij}' \bigr) = D_{i},\quad i=1,\ldots, N, $$
(24)

with

$$\begin{aligned} \begin{aligned} &A_{ij} = \int _{\varOmega } \varphi _{ix}\varphi _{jx}+ \varphi _{iy}\varphi _{jy}+g_{n} \varphi _{i} \varphi _{j} \,d\varOmega,\qquad B_{ij}' = \frac{h_{\infty }}{k} \int _{\partial \varOmega } \varphi _{i} \varphi _{j} \,ds, \\ &D_{i} = \frac{h_{\infty }}{k} \biggl(\frac{T_{\infty }}{T_{\infty } +(T _{0}-T_{\infty })e^{-(\frac{\alpha }{\bar{u}}z_{n}+\lambda t_{n})}} \biggr) \int _{\partial \varOmega } \varphi _{i} \,ds + 2 \int _{\varOmega }f_{n} \varphi _{i} \,d \varOmega. \end{aligned} \end{aligned}$$
(25)

By solving system (24) for unknowns \(d_{j}\) and using equation (21)2, the temperature T can be determined by

$$ T = \Biggl(1+\Re \sum_{j=1}^{N} \,d_{j} \varphi _{j}(x,y) \Biggr) \bigl( T _{\infty }+ ( T_{0} - T_{\infty }) e^{-(\frac{\alpha }{\bar{u}}z_{n} + \lambda t_{n})} \bigr). $$
(26)

3 Numerical example

In this study, we assume that the elliptic microchannel is a small artery surrounded by body tissue which allows the maximum temperature of 42°C, and the temperature in the middle of the artery at the initial state \(t=0\) s is set to the body temperature of 37°C. To study the slip flow and heat transfer in a microchannel of elliptic cross section with semi-major axis of length a and semi-minor axis of length b, we use the model parameters as shown in Table 1. For the slip flow control, we set the pressure gradient as \(dp/dz = -5ie^{i\omega t}\) for \(\omega =1.55\). Figure 1 shows variations of the pressure profile over time.

Figure 1
figure 1

Oscillating pressure gradient

Full size image
Table 1 Model parameters. Fluid properties at 37°C [1, 6]
Full size table

The velocity and temperature are computed using the first 10-term approximations of the series in equations (22) and (24), respectively. To demonstrate the oscillatory pressure-driven flow under the wall-slip condition, we plot the axial velocity in the microchannel with aspect ratio of 3/4 (\(a=0.1\) cm, \(b=0.075\) cm) and slip length of 0.05 at the first full wave cycle. Figure 2 shows the U-shaped curves of the axial velocities along the major and minor axes. It is noted from Fig. 2(a) that the velocity decreases as t increases when \(dp/dz > 0\), while it increases as t increases when \(dp/dz < 0\). In addition, when \(dp/dz\) approaches zero at \(t=2\) s on the left and \(t=4\) s on the right, the velocity pattern is similar but the fluid moves in the opposite direction.

Figure 2
figure 2

Oscillating flow of fluid. Axial velocity in the 1st full wave cycle for \(a=0.1\) cm, \(b=0.075\) cm and slip length of 0.01

Full size image

To analyse the effect of oscillating flow under the slip condition on the temperature, we use an aspect ratio of 3/4 (\(a=0.1\) cm, \(b=0.075\) cm) and a slip length of 0.05 to plot the temperature and its contour at \(t=121\) s when \(dp/dz>0\), and at \(t=123\) s when \(dp/dz<0\) in the 30th full wave cycle as shown in Fig. 3. It indicates that the oscillating flow gives a significant change in the pattern of temperature distribution on the elliptic cross section.

Figure 3
figure 3

Temperature distribution. Temperature distribution on the cross section \(z=1\) cm in a full wave cycle at time \(t=121\) s when \(\frac{dp}{dz} > 0\), and at \(t=123\) s when \(\frac{dp}{dz} < 0 \) for semi-axes lengths of \(a=0.1\) cm, \(b=0.075\) cm and slip length of 0.05

Full size image

To investigate the effect of slip length on the temperature distribution, we consider the problem in the elliptic microchannel with an aspect ratio of 3/4 (\(a=0.1\) cm, \(b=0.075\) cm). The temperature and its contour are plotted at \(t=123\) s when \(dp/dz<0\) in the 30th full wave cycle. Figure 4 shows the effect of slip length on temperature distribution. It illustrates that the higher the slip length is, the lower the temperature will be in the channel. The slip-length values of 0.05, 0.1 and 0.5 give the maximum temperature of 40.025, 39.30 and 38.95°C, respectively.

Figure 4
figure 4

Temperature distribution. Temperature distribution on the cross section \(z=5\) cm in a full wave cycle at time \(t=123\) s obtained from the model with various slip lengths of \(0.05, 0.1, 0.5\) and semi-axes lengths of \(a=0.1\) cm and \(b=0.075\) cm

Full size image

The effect of aspect ratio \(b/a\) on the temperature distribution is also analysed by setting a constant slip length of 0.1 and choosing three values of the aspect ratio \(b/a=\) 3/4, 1/2 and 1/3 for a fixed value of \(a= 0.1\) cm. The temperature and its contour at \(t=123\) s when \(dp/dz < 0\) in the 30th full wave cycle are presented in Fig. 5. The results indicate that the aspect ratio of the elliptic microchannel has an effect on the temperature distribution. The aspect ratios of 3/4, 1/2 and 1/3 give the maximum temperature of 39.30, 39.55 and 40.40°C, respectively. The patterns of temperature distribution in microchannels with different aspect ratio are different as shown in Fig. 5.

Figure 5
figure 5

Temperature distribution. Temperature distribution on the cross section \(z=5\) cm in a full wave cycle at time \(t=123\) s obtained from the model with three aspect ratios of \(b/a = 3/4, 1/2\) and \(1/3\) for slip length of 0.1 and the semi-major axis of \(a=0.1\) cm

Full size image

4 Conclusion

This paper presents a mathematical model and its semi-analytical solution for the oscillating pressure-driven flow and heat transfer through an elliptic microchannel under the slip condition using the Ritz method. The results show that the characteristics of the oscillating flow of fluid and heat transfer in microchannels depends on the slip length and the aspect ratio of the microchannel. The results of this research may help in the optimisation of certain bioengineering systems.