1 Introduction

The technology of mixing techniques has developed in industrial applications of static mixer. In the early 1950s, a static mixer or turbulator was used in the heat transfer process and its patent was issued on September 16, 1958 to Lynn [1]. In 1970, the static mixer was used in many industrial processes. The first example is helical static mixer which is commonly used in a tube as described in [2]. Another example of static mixers is multi-elements type (see the French patent [3]). Over the past few decades, a new geometry of static mixer was designed and used in various process of petrochemical applications [4,5,6]. Two mixing devices which are commonly applied in the mixing operations are Kenics mixer and static mixer. Static or motionless mixers are the efficient mixing devices. Comparing to the Kenics mixer, the static mixers consume lower energy but require higher cost to reduce a higher pressure drop. In terms of mixing efficiency, the static mixer has a better performance.

A number of researchers have proposed new designs of static mixers to enhance mixing performance with the minimum pressure drop. The design of the static mixers is based on the number of mixer elements, blade layers and blade shapes. One of the challenging problems is the blade design in a pipe. In order to get the best mixing possible and less pressure drop, several research groups have developed and designed a new static mixer geometry for higher mixing performance using computational simulation. The mixing process of granular material in static mixer has been studied for many years ago. Early researches have focused mainly on experimental and analytical approaches. To understand the complex phenomena in the static mixer, many experiments have been performed to investigate the behaviors of granular mixing in static mixer [7, 8]. In 2003, Thakur et al. [9] summarized more details in the field of improving performance and applications of static mixers in industrial processes. Many research groups have compared the mixing result of different types of blade design used in the static mixers. Their reports showed that the static mixer gives a high mixing performance compared with the other devices but has higher cost due to a higher pressure drop. The designs of static mixer geometries to enhance the mixing efficiency with low cost are a big challenging problem. In 2003, Galaktionov et al. [10] investigated the performance of the Kenics mixers with two different blade geometries based on its twist direction and its angle to find its optimal design. Their result showed that the Kenics static mixer with a simple geometry gives a high performance. A powerful design tool was provided for optimizing mixers. In 2011, Theron et al. [11] compared mixing performance of different static mixers including SMXTM, SMVTM, and SMXPlusTM. The pressure drop produced by both solid flow and liquid–solid flow was used to investigate the mixing performance. Meijer et al. [12] compared various static mixers including the Kenics mixer, Low-Low-Pressure Drop (LLPD), the Ross Low-Pressure Drop (LPD), the standard Sulzer SMX, and the new design series of the SMX in terms of compactness and low-pressure drop. Their result showed that the new series SMX(n) gives higher compactness, and Kenics mixer generates a lowest pressure drop.

According to recent studies, discrete element method (DEM) is a common method for studying the particulate flow of the granular materials. In mixing industrial processes, granular movement refers to solid–liquid phase flow in the mixer. A few researches have been achieved to demonstrate the flow behavior of solid–liquid flow in the mixing systems. In order to describe the two-phase flow, the finite element method (FEM) was applied to the basis of constructing a simulation [13,14,15,16]. In 1979, Cundall and Strack [17] proposed the soft-sphere method to study a granular flow simulation. Their method is based on the linear spring given by the magnitude of the normal force between two particles and a dashpot model given by the sum of spring force and damping force. In this method, small deformations are used to calculate elastic, plastic and frictional forces between particles. The particle movement is described by Newton’s laws of motion which is importance in modeling quasi-static systems. In 2012, Bridgwater et al. [18] demonstrated flow patterns of 10,000–250,000 particles under the effect of particle size, equipment size, and internal geometry. The result was simulated by using the couple of mathematical modelings including finite element and discrete element. A literature review in the past two decades of particle simulation using discrete element method and finite element method was presented by Zhu et al. [19]. They classified the previous work into three main parts including particle packing, particle flow, and a couple of particle–fluid flow. The investigation was focused on the effect of particle–fluid, particle–particle and particle–wall interaction. Jovanovic et al. [20] proposed the mixture model based on DEM and CFD approaches to the study of the behavior of particulate-laden flow in the Komax static mixer and Ross mixer. Pezo et al. [21] investigated the behavior of fluid flow and granular flow in revolving Komax static mixer by using a couple DEM-CFD model.

In this paper, a finite element–discrete element coupled approach is used for numerical simulation. Section 2 will focus on a mathematical modeling for describing the two-phase flow with fluid–solid interaction in the static mixer. The effects of static mixer with different blade designs on the efficiency of mixing performance are discussed in Sect. 3. Finally, the conclusion is given in Sect. 4.

2 Governing equation

To study air flow in static mixers containing stationary blades, air is assumed to a laminar flow because it creates a small pressure loss in a pipe. This paper studies the air–particle flow in a cylindrical static mixers with six patterns of blade geometries including four 180∘ twisted blades (TTTT), four 90∘ elliptical blades (EEEE) and other four designs from the combination of the two twisted blades and the two elliptical blades, namely TETE, ETET, TEET and ETTE. The quality of mixing performance is determined by the trajectory of suspended particles through the static mixer and magnitude of the pressure drop along the flow path. To achieve this purpose, we initially solve the airflow model ignoring the volume force due to particle movement for the fluid velocity which is used to determine the fluid drag force in the particle model. The solution of the particle flow model is then carried out for the particle trajectories of the granular materials from a coupled air–particle flow model. The pressure drop is finally determined by the difference between absolute pressures at the beginning and the end of pipe cross sections.

2.1 The air flow model

The air flow during the mixing process is described by the continuity equation and the Navier–Stokes equations:

$$\begin{aligned}& \frac{\partial \rho }{\partial t}+\nabla \cdot \rho \mathbf{u} = 0, \end{aligned}$$
(1)
$$\begin{aligned}& \rho \biggl(\frac{\partial \mathbf{u}}{\partial t}+ (\nabla \cdot \mathbf{u} ) \mathbf{u} \biggr) = \nabla \cdot \bigl[-p \textit{I}+\mu \bigl(\nabla \mathbf{u}+ (\nabla \mathbf{u} ) ^{\mathbf{T}} \bigr) \bigr]+\mathbf{F}, \end{aligned}$$
(2)

where u and p represent the velocity vector and pressure of fluid, F is volume force, ρ and μ denote the fluid density and its viscosity, respectively. The partial differential Eqs. (1) and (2) are subject to the following boundary conditions.

Inlet condition: The inlet velocity is set to be constant velocity, i.e.,

$$ \mathbf{u} = - u_{0}\mathbf{n}. $$
(3)

Outlet condition: A pressure outlet and no shear viscosity are assumed, i.e.,

$$\begin{aligned}& \hat{p}_{0} \leq p_{0}, \end{aligned}$$
(4)
$$\begin{aligned}& \bigl[-p\textbf{I} + \mu \bigl(\nabla \mathbf{u}+ (\nabla \mathbf{u} )^{\mathbf{T}} \bigr) \bigr]\mathbf{n}= -\hat{p} _{0} \mathbf{n}. \end{aligned}$$
(5)

Wall condition: Slip condition is applied, i.e.,

$$\begin{aligned}& \mathbf{u}\cdot \mathbf{n}=0, \end{aligned}$$
(6)
$$\begin{aligned}& \mathbf{K}- (\mathbf{K}\cdot \mathbf{n} )\mathbf{n}= \textbf{0}, \quad \mbox{for } \mathbf{K}= \bigl[\mu \bigl(\nabla \mathbf{u}+ (\nabla \mathbf{u} )^{\mathbf{T}} \bigr) \bigr]\mathbf{n}. \end{aligned}$$
(7)

2.2 The particle flow model

The governing equation of the particle flow is based on Newton’s laws, interaction forces due to the particle–wall, particle–particle interactions and the particle–fluid interaction (the fluid drag force), i.e.,

$$ \frac{d(m_{p} \mathbf{v})}{dt} = \mathbf{F}_{t}, $$
(8)

where \(m_{p}\) denote the particle mass and \(\mathbf{F}_{t}\) is the total contact force acting on particle. The contact force generated by multiplied by a suitable field is defined by

$$ \mathbf{F}_{t} = \chi \cdot \varGamma, $$
(9)

where χ is the susceptibility tensor and Γ is a vector field. The particle velocity is defined by

$$ \mathbf{v} = \frac{d \textbf{q}}{dt}, $$
(10)

where q is the particle position vector.

Wall condition (Bounce): The reflection of particle and the wall appear in the tangent plane. On the normal surface, the incident angle and reflected angle are assumed to be the same and given by

$$ \mathbf{v} = \mathbf{v}_{c} - 2(\mathbf{n} \cdot \mathbf{v}_{c}) \mathbf{n}, $$
(11)

where \(\mathbf{v}_{c}\) is the particle velocity when striking the wall.

The drag force is defined as

$$ \mathbf{F}_{D} = \frac{1}{\tau _{p}}m_{p} (\mathbf{u} - \mathbf{v}) \quad \mbox{for } \tau _{p} = \frac{\rho _{p} d^{2}_{p}}{18\mu }. $$
(12)

Inlet condition: The particles are released with the same speed at the same location (the open top surface), i.e.,

$$ \textbf{q} = \textbf{q}_{0}; \qquad \mathbf{v} = - \mathbf{v}_{0}\mathbf{n}. $$
(13)

Outlet (Freeze) condition: The particle velocity is assumed to equal the particle velocity when striking the outlet. The particle position and particle velocity are the same at all time steps \(t > t_{c}\). The velocity and energy distributions are recovered by this condition:

$$ \mathbf{v} = \mathbf{v}_{c}. $$
(14)

3 Numerical example

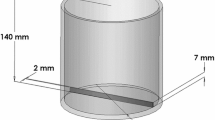
In the previous section, we present the mathematical model for analysing the effect of blade geometry on the mixing performance. Two types of stationary blades proposed by Galaktionov in [10] including 180∘ twisted blade as shown in Fig. 1(a) and 90∘ elliptical blade as shown in Fig. 1(b) are chosen in this study. We investigate the quality of mixing performance using six blade-pattern static mixers of circular cross section with the radius of 2.5 cm and the length of 50 cm. Six blade geometries are the four twisted blade (TTTT), the four elliptical blade (EEEE) and the combination of the two twisted blade and the two elliptical blade (TETE, ETET, TEET and ETTE) as shown in Fig. 2(a)–(f).

Figure 1
figure 1

Two geometries of blade design. (a) A 180∘ twisted blade; (b) a 90∘ elliptical blade

Full size image
Figure 2
figure 2

The cylindrical static mixer with six different blade geometries. (a) TTTT; (b) EEEE; (c) TETE; (d) ETET; (e) TEET; (f) ETTE

Full size image

The parameter values for calculation of the velocity field and pressure field are presented in Table 1. In this study, we concentrate on the mixing performance between two sets of particles and distinguish them with different colors. The binary colored particles are assumed to have a spherical shape with the same diameter of 0.001 cm. For granular mixing visualization in the static mixer, the number of particle per release is 3000 particles. Figure 3(a) presents seven investigated cross sections inside the four twisted blade mixer. Figure 3(b) indicates the distribution of particle positions at the initial time \(t=0\) s on the open top surface at which the same colored particles occupy in a semi-circle area.

Figure 3
figure 3

Investigated cross sections and initial position of binary colored particles. Seven investigated cross sections (a) and distribution of the binary colored particle positions on the inlet where the red particles occupy the half region \(x<0\) of the circular cross section and the blue particles are in the another region \(x>0\)

Full size image
Table 1 Model parameters
Full size table

Numerical solution of the air flow and the particle flow in the static mixer with six different blade geometries was simulated based on the FEM-DEM coupled method using COMSOL Multiphysics. The simulation starts when all binary colored particles are released from the open top (\(z=50\) cm) into the static mixer.

The air velocity as shown in Fig. 4(a)–(f) represents the trend of particle movement when falling in a pipe. The motion group of particle is divided by centrifugal force that is created by the flow passing the stationary blade in a pipe. Figure 5(a)–(f) shows Poincaré plots which are used to visualize the motion of particles mixing in the static mixer. The first cross section of the Poincaré plot represents particles at initial time \(t=0\mbox{ s}\). The mixing process starts when the particle begins to flow following the air flow field. The mixing quality increases along the flow path in pipe. However, at the bottom part of the mixer, Fig. 6(a)–(f) displays a mixture of red and blue particles which are not mixed completely.

Figure 4
figure 4

Air velocity. Surface plot of the air velocity at the seven cross sections for six different blade geometries. (a) TTTT; (b) EEEE; (c) TETE; (d) ETET; (e) TEET; (f) ETTE

Full size image
Figure 5
figure 5

Distribution of all particles on all investigated cross sections for six different blade geometries. (a) TTTT; (b) EEEE; (c) TETE; (d) ETET; (e) TEET; (f) ETTE

Full size image
Figure 6
figure 6

Distribution of all particles on the last cross section at \(z=0\) for six different blade geometries. (a) TTTT; (b) EEEE; (c) TETE; (d) ETET; (e) TEET; (f) ETTE

Full size image

In the mixing process of the pharmaceutical industry, the relative standard deviation (RSD) value is used to evaluate the mixing quality for experimental results or the numerical simulation results. For the previous study [20,21,22,23], the RSD is used to calculate the mixing quality for the static mixers with different geometry, defined as

$$ \mathrm{RSD}=\frac{\sigma }{\overline{x}}\times 100\%,\qquad \sigma = \sqrt{\frac{ \sum_{i=1}^{M} (x_{i}-\overline{x} )^{2}}{M-1}}, $$
(15)

where M is the total number of samples, \(x_{i}\) the density ratio of sample i and x̅ the average density ratio of all samples. The previous study showed that the small RSD is higher mixing quality than the big RSD.

The values of RSD is presented in Table 2. The TEET, TETE, TTTT, ETET, ETTE and EEEE patterns of the mixer geometry give the RSD values of 20.32%, 26.98%, 37.6%, 40.59%, 42.39% and 42.54%, respectively. As the lower values indicate the better mixing performance, the TEET design is the best design compared with others in terms of mixing quality.

Table 2 Value of RSD at the bottom part of the mixer
Full size table

The contour of pressure field obtained from the difference models on seven cross sections \((z=50, 45, 35, 25, 15, 5, 0\mbox{ cm})\) as shown in Figs. 7–12. We now compare the pressure drop obtained from the model with six different blade designs. Table 3 presents the pressure differences between the absolute pressure at the beginning cross section of the pipe (\(z=45\)) and the last cross sections (\(z=5\)). The results indicate that the TTTT design generates the lowest pressure drop whereas the ETTE design induces the highest pressure drop.

Figure 7
figure 7

Contour of pressure field obtained from the model TTTT at seven different cross sections. (a) \(z=50\); (b) \(z=45\); (c) \(z=35\); (d) \(z=25\); (e) \(z=15\); (f) \(z=5\); (g) \(z=0\)

Full size image
Figure 8
figure 8

Contour of pressure field obtained from the model EEEE at seven different cross sections. (a) \(z=50\); (b) \(z=45\); (c) \(z=35\); (d) \(z=25\); (e) \(z=15\); (f) \(z=5\); (g) \(z=0\)

Full size image
Figure 9
figure 9

Contour of pressure field obtained from the model TETE at seven different cross sections. (a) \(z=50\); (b) \(z=45\); (c) \(z=35\); (d) \(z=25\); (e) \(z=15\); (f) \(z=5\); (g) \(z=0\)

Full size image
Figure 10
figure 10

Contour of pressure field obtained from the model ETET at seven different cross sections. (a) \(z=50\); (b) \(z=45\); (c) \(z=35\); (d) \(z=25\); (e) \(z=15\); (f) \(z=5\); (g) \(z=0\)

Full size image
Figure 11
figure 11

Contour of pressure field obtained from the model TEET at seven different cross sections. (a) \(z=50\); (b) \(z=45\); (c) \(z=35\); (d) \(z=25\); (e) \(z=15\); (f) \(z=5\); (g) \(z=0\)

Full size image
Figure 12
figure 12

Contour of pressure field obtained from the model ETTE at seven different cross sections. (a) \(z=50\); (b) \(z=45\); (c) \(z=35\); (d) \(z=25\); (e) \(z=15\); (f) \(z=5\); (g) \(z=0\)

Full size image
Table 3 Pressure drop: the difference between absolute pressure at the beginning cross-section of the pipe and last cross-sections
Full size table

4 Conclusion

For optimization of mixing quality, numerical simulation based on a couple DEM-FEM model are used to investigate the motion of particles and air flow in static mixer with six different blade geometries. The air velocity and the pressure field are calculated by the FEM method. In the DEM, Newton’s laws of motion are used to solve the interaction of particle and particle and the interaction of particle and mixer wall. At the bottom of static mixer, particle positions are used to estimate the quality of the mixing process by using the relative standard deviation. According to the results, the mixing quality is significantly higher and the pressure drop is incontrovertibly lower for TTTT than other designs. We conclude that the TEET geometry can contribute the best quality of the mixing and can significantly reduce the cost of the mixing process.