Structure-preserving stochastic Runge–Kutta–Nyström methods for nonlinear second-order stochastic differential equations with multiplicative noise

Abstract

A class of stochastic Runge–Kutta–Nyström (SRKN) methods for the strong approximation of second-order stochastic differential equations (SDEs) are proposed. The conditions for strong convergence global order 1.0 are given. The symplectic conditions for a given SRKN method to solve second-order stochastic Hamiltonian systems with multiplicative noise are derived. Meanwhile, this paper also proves that the stochastic symplectic Runge–Kutta–Nyström (SSRKN) methods conserve the quadratic invariants of underlying SDEs. Some low-stage SSRKN methods with strong global order 1.0 are obtained by using the order and symplectic conditions. Then the methods are applied to three numerical experiments to verify our theoretical analysis and show the efficiency of the SSRKN methods over long-time simulation.

1 Introduction

Stochastic differential equations (SDEs) have been widely used in many fields such as biology, economics, physics and finance (see, e.g., [1,2,3]) when modeling dynamical phenomenon with random perturbation. Generally, it is difficult to find explicit solutions of SDEs analytically, so the construction of efficient numerical methods is of great significance. Many effective and reliable numerical methods have been designed for SDEs in recent years, for example [4,5,6,7,8,9,10,11,12,13,14].

For some SDEs with specific properties, most general numerical methods may be inappropriate, especially in the case of preservation of geometric structures over long time for the stochastic Hamiltonian systems

$$ \textstyle\begin{cases} dp=- (\frac{\partial H(p,q)}{\partial q} )^{\mathrm{T}}\,dt- (\frac{\partial \widetilde{H}(p,q)}{\partial q} )^{ \mathrm{T}}\circ dB(t),&t\in [0,T], \\ dq= (\frac{\partial H(p,q)}{\partial p} )^{\mathrm{T}}\,dt+ (\frac{\partial \widetilde{H}(p,q)}{\partial p} )^{ \mathrm{T}}\circ dB(t),&t\in [0,T], \\ p(0)=p_{0}\in \mathbb{R}^{d}, \\ q(0)=q_{0}\in \mathbb{R}^{d}, \end{cases} $$

(1.1)

which are given in the Stratonovich sense, where $H(p,q)$ and $\widetilde{H}(p,q)$ are two sufficiently smooth functions, $B(t)$ is a standard one-dimensional Brownian motion defined on the complete probability space $(\varOmega,\mathcal{F},\mathbb{P})$ with a filtration $\{\mathcal{F}_{t}\}_{t\in [0,T]}$ satisfying the usual conditions. The solution of (1.1) is a phase flow almost surely. A good study of its properties can be found in [15]. Consider the differential two-form

$$ \omega ^{2}=dp\wedge dq=dp^{1}\wedge dq^{1}+dp^{2}\wedge dq^{2}+\cdots +dp^{d} \wedge dq^{d}. $$

(1.2)

It turns out that the phase flows of (1.1) preserve the symplectic structure [16], i.e.,

$$ dp(t)\wedge dq(t)=dp_{0}\wedge dq_{0},\quad \forall t\in [0,T]. $$

(1.3)

Motivated by this, it is natural to search for numerical methods that inherit this property. A numerical method with approximation $( P_{ n}, Q_{ n})$ is symplectic provided

$$ dP_{n+1}\wedge dQ_{n+1}=dP_{n}\wedge dQ_{n}. $$

(1.4)

Second-order stochastic Hamiltonian systems driven by Gaussian noises are significant in scientific applications [17], which can describe the classical Hamiltonian systems perturbed by random forces. In [18], the authors construct stochastic symplectic Runge–Kutta methods of mean-square order 2.0 for second-order stochastic Hamiltonian systems with additive noise by means of colored rooted tree theory. Much work has been done on designing stochastic symplectic Runge–Kutta methods and stochastic symplectic partitioned Runge–Kutta methods to solve stochastic Hamiltonian systems in recent years [19, 20], which could be viewed as a stochastic generalization of the deterministic Runge–Kutta methods. Considering the importance of deterministic Runge–Kutta–Nyström (RKN) methods in solving second-order ordinary differential equations, this paper focuses on the extension of RKN methods to d-dimensional second-order SDEs with multiplicative noise

$$ \textstyle\begin{cases} \ddot{y}(t)-f(y(t))-g(y(t))\circ \xi (t)=0,\quad t\in [0,T], \\ y(0)=y_{0}\in \mathbb{R}^{d}, \qquad\dot{y}(0)=z_{0}\in \mathbb{R}^{d}, \end{cases} $$

(1.5)

where $\xi (t)$ is a scalar white noise process. Here $f(y), g(y): \mathbb{R}^{d}\mapsto \mathbb{R}^{d}$ are both Borel measurable. Throughout this work, we use the usual notation “∘” to interpret (1.5) in the Stratonovich sense.

The remainder of this paper is organized as follows. Section 2 discusses the order conditions of stochastic Runge–Kutta–Nyström (SRKN) methods. In Sect. 3, the SRKN methods are applied to solve second-order stochastic Hamiltonian systems with multiplicative noise and symplectic conditions of the SRKN methods are discussed. Section 4 is devoted to discussing the conservation of quadratic invariants of the underlying SDEs under the SRKN discretization. In Sect. 5, as an application of the main results, some low-stage stochastic symplectic Runge–Kutta–Nyström (SSRKN) methods with strong global order 1.0 are constructed. Finally, numerical experiments are presented in Sect. 6.

2 The SRKN methods and their order conditions

The second-order SDE (1.5) describes the position of a particle subject to deterministic forcing $f(y)$ and random forcing $\xi (t)$ [21]. By introducing a new variable $z(t)=\dot{y}(t)$, (1.5) can be written as a pair of first-order Stratonovich type SDEs for $y(t)$ and $z(t)$, the position and velocity variables:

$$ \textstyle\begin{cases} dy(t)=z(t)\,dt,\quad t\in [0,T], \\ dz(t)=f(y(t))\,dt+g(y(t))\circ dB(t),\quad t\in [0,T], \\ y(0)=y_{0}\in \mathbb{R}^{d}, \qquad z(0)=z_{0}\in \mathbb{R}^{d}. \end{cases} $$

(2.1)

Given a step size $h>0$, a stochastic partitioned Runge–Kutta method [20] is applied to compute the approximation $(Y_{n},Z_{n}) \approx (y(t_{n}),z(t_{n}))$ of (2.1), where $t_{n}=nh$, by setting $(Y_{0},Z_{0})=(y_{0},z_{0})$ and forming

$$\begin{aligned} &y_{i}=Y_{n}+h\sum_{j=1} ^{s}\bar{a}_{ij}z_{j},\quad i=1, 2, \ldots, s, \\ &z_{i}=Z_{n}+h\sum_{j=1} ^{s}\hat{a}_{ij}f(y_{j})+J_{n} \sum _{j=1} ^{s}\hat{b}_{ij}g(y_{j}),\quad i=1, 2, \ldots, s, \\ &Y_{n+1}=Y_{n}+h\sum_{i=1} ^{s}\bar{\alpha }_{i}z_{i}, \\ &Z_{n+1}=Z_{n}+h\sum_{i=1} ^{s}\tilde{\alpha }_{i}f(y_{i})+J _{n} \sum_{i=1} ^{s}\tilde{\beta }_{i}g(y_{i}), \end{aligned}$$

where $J_{n}=B(t_{n+1})-B(t_{n})$ are independent $N(0,h)$-distributed Gaussian random variables. Inserting the formula for $z_{i}$ into the others, we get

$$\begin{aligned} &y_{i}=Y_{n}+h\sum_{j=1} ^{s}\bar{a}_{ij}Z_{n}+h^{2} \sum _{j,k=1} ^{s}\bar{a}_{ij} \hat{a}_{jk}f(y_{k})+J_{n}h \sum _{j,k=1} ^{s}\bar{a}_{ij}\hat{b}_{jk}g(y_{k}),\quad i=1, 2, \ldots, s, \\ &Y_{n+1}=Y_{n}+h \sum_{i=1} ^{s}\bar{\alpha }_{i}Z_{n}+h^{2}\sum _{i,j=1} ^{s}\bar{\alpha }_{i} \hat{a}_{ij}f(y_{j}) +J _{n}h\sum _{i,j=1} ^{s}\bar{\alpha }_{i} \hat{b}_{ij}g(y _{j}), \\ &Z_{n+1}=Z_{n}+h\sum_{i=1} ^{s}\tilde{\alpha }_{i}f(y_{i})+J _{n} \sum_{i=1} ^{s}\tilde{\beta }_{i}g(y_{i}). \end{aligned}$$

Then we obtain the following definition:

$$\begin{aligned} \gamma _{i}= \sum_{j=1} ^{s} \bar{a}_{ij},\qquad a_{ij}= \sum_{k=1} ^{s}\bar{a}_{ik}\hat{a}_{kj},\qquad b_{ij}= \sum_{k=1} ^{s}\bar{a}_{ik} \hat{b}_{kj}, \\ \sum_{i=1} ^{s}\bar{\alpha }_{i}=1,\qquad \alpha _{i}= \sum_{j=1} ^{s}\bar{\alpha }_{j}\hat{a}_{ji},\qquad \beta _{i}= \sum_{j=1} ^{s}\bar{\alpha }_{j}\hat{b}_{ji}. \end{aligned}$$

Definition 2.1

Let $\gamma _{i}$, $a_{ij}$, $b_{ij}$, $\alpha _{i}$, $\beta _{i}$, $\tilde{\alpha }_{i}$ and $\tilde{\beta }_{i}$ be real coefficients, $i, j=1, 2, \ldots, s$. A SRKN method for solving (2.1) is given by

$$\begin{aligned} &y_{i}=Y_{n}+h\gamma _{i}Z_{n}+h^{2} \sum _{j=1} ^{s}a_{ij}f(y_{j}) +J_{n}h\sum_{j=1} ^{s}b_{ij}g(y_{j}),\quad i=1, 2, \ldots, s, \end{aligned}$$

(2.2)

$$\begin{aligned} & Y_{n+1}=Y_{n}+hZ_{n}+h^{2} \sum_{i=1} ^{s}\alpha _{i}f(y_{i}) +J_{n}h\sum_{i=1} ^{s}\beta _{i}g(y_{i}), \end{aligned}$$

(2.3)

$$\begin{aligned} & Z_{n+1}=Z_{n}+h \sum _{i=1} ^{s}\tilde{\alpha }_{i}f(y_{i})+J_{n} \sum_{i=1} ^{s}\tilde{\beta }_{i}g(y_{i}). \end{aligned}$$

(2.4)

It is convenient to display the coefficients occurring in (2.2)–(2.4) in the following form, known as a Butcher tableau:

$$ \textstyle\begin{array} {l@{\quad}|@{\quad}l@{\quad}l} \gamma & A &B \\ \hline & \alpha ^{T} & \beta ^{T} \\ \hline & \tilde{\alpha }^{T} & \tilde{\beta }^{T} \end{array} $$

(2.5)

where

$$\begin{array}{rl}& A=\left(\begin{array}{ccc}{a}_{11}& \cdots & a_{1s}\\ a_{21}& \cdots & a_{2s}\\ \cdots & \cdots & \cdots \\ a_{s1}& \cdots & a_{ss}\end{array}\right),B=\left(\begin{array}{ccc}{b}_{11}& \cdots & b_{1s}\\ b_{21}& \cdots & b_{2s}\\ \cdots & \cdots & \cdots \\ b_{s1}& \cdots & b_{ss}\end{array}\right),\\ & {\gamma }^T=({\gamma }_1,\dots ,{\gamma }_s),{\alpha }^T=({\alpha }_1,\dots ,{\alpha }_s),{\tilde{\alpha }}^T=({\tilde{\alpha }}_1,\dots ,{\tilde{\alpha }}_s),\\ & {\beta }^T=({\beta }_1,\dots ,{\beta }_s),{\tilde{\beta }}^T=({\tilde{\beta }}_1,\dots ,{\tilde{\beta }}_s).\end{array}$$

To check the order conditions of the SRKN methods (2.2)–(2.4), one has to compare the expansion of the one-step solutions generated by the SRKN methods with the Stratonovich–Taylor expansion of the exact solution to Eq. (2.1). For simplicity of notations, we focus on $d=1$ and the extension to multi-dimensional case ($d>1$) is a similar work.

By Taylor expansion, one shows

$$\begin{aligned} f(y_{i})={}&f(Y_{n})+f'(Y_{n}) \Biggl[ h\gamma _{i}Z_{n}+h^{2} \sum _{j=1} ^{s}a_{ij}f(y_{j}) +J_{n}h\sum_{j=1} ^{s}b_{ij}g(y_{j}) \Biggr]+\cdots \\ ={}&f(Y_{n})+h\gamma _{i}f'(Y_{n})Z_{n}+h^{2} \sum_{j=1} ^{s}a_{ij}f'(Y_{n})f(Y_{n}) \\ &{} +J_{n}h \sum_{j=1} ^{s}b_{ij}f'(Y_{n})g(Y_{n})+ \cdots \end{aligned}$$

(2.6)

and

$$\begin{aligned} g(y_{i})={}&g(Y_{n})+g'(Y_{n}) \Biggl[ h\gamma _{i}Z_{n}+h^{2} \sum _{j=1} ^{s}a_{ij}f(y_{j}) +J_{n}h\sum_{j=1} ^{s}b_{ij}g(y_{j}) \Biggr]+\cdots \\ ={}&g(Y_{n})+h\gamma _{i}g'(Y_{n})Z_{n}+h^{2} \sum_{j=1} ^{s}a_{ij}g'(Y_{n})f(Y_{n}) \\ &{} +J_{n}h \sum_{j=1} ^{s}b_{ij}g'(Y_{n})g(Y_{n})+ \cdots. \end{aligned}$$

(2.7)

Substituting (2.6) and (2.7) into (2.3) and (2.4) yields

$$\begin{aligned} Y_{n+1}&=Y_{n}+hZ_{n}+h^{2} \sum_{i=1} ^{s}\alpha _{i}f(y_{i}) +J_{n}h\sum_{i=1} ^{s}\beta _{i}g(y_{i}) \\ &=Y_{n}+hZ_{n}+h^{2} \sum _{i=1} ^{s}\alpha _{i}f(Y_{n})+J_{n}h \sum_{i=1} ^{s}\beta _{i}g(Y_{n})+ \cdots \\ &=Y_{n}+hZ_{n}+R_{1} \end{aligned}$$

(2.8)

and

$$\begin{aligned} Z_{n+1}&=Z_{n}+h \sum _{i=1} ^{s}\tilde{\alpha }_{i}f(y_{i})+J_{n} \sum_{i=1} ^{s}\tilde{\beta }_{i}g(y_{i}) \\ &=Z_{n}+h \sum_{i=1} ^{s}\tilde{ \alpha }_{i}f(Y_{n}) +J_{n} \sum _{i=1} ^{s}\tilde{\beta }_{i}g(Y_{n}) +J_{n}h \sum_{i=1} ^{s}\tilde{ \beta }_{i}\gamma _{i}g'(Y_{n})Z _{n}+\cdots \\ &=Z_{n}+h \sum_{i=1} ^{s}\tilde{ \alpha }_{i}f(Y_{n}) +J_{n} \sum _{i=1} ^{s}\tilde{\beta }_{i}g(Y_{n})+R_{2}, \end{aligned}$$

(2.9)

where $R_{1}$ and $R_{2}$ is the remainder terms to (2.8) and (2.9), respectively, and $|\mathbb{E}R_{1}|=O(h^{2})$, $\mathbb{E}|R_{1}|^{2}=O(h^{3})$, $|\mathbb{E}R_{2}|=O(h^{2})$, $\mathbb{E}|R_{2}|^{2}=O(h^{3})$.

Assuming $(y(t_{n}),z(t_{n}))=(Y_{n},Z_{n})$ and using the Stratonovich–Taylor expansion, we derive

$$ y(t_{n+1})=Y_{n}+hZ_{n}+R_{3}, $$

(2.10)

where

$$\begin{aligned} R_{3}= f(Y_{n}) \int _{t_{n}}^{t_{n+1}} \int _{t_{n}}^{s}\,d\tau \,ds +g(Y _{n}) \int _{t_{n}}^{t_{n+1}} \int _{t_{n}}^{s}\circ \,dB(\tau ) \,ds+\cdots \end{aligned}$$

with $|\mathbb{E}R_{3}|=O(h^{2})$ and $\mathbb{E}|R_{3}|^{2}=O(h^{3})$.

Similar to the proof of (2.10), we conclude that

$$ z(t_{n+1})=Z_{n}+hf(Y_{n})+J_{n}g(Y_{n})+R_{4} $$

(2.11)

with $|\mathbb{E}R_{4}|=O(h^{2})$ and $\mathbb{E}|R_{4}|^{2}=O(h^{3})$.

As an application of Theorem 1.1 in [22], together with (2.8), (2.9), (2.10) and (2.11), we can easily establish the following theorem.

Theorem 2.2

Assume that the necessary coefficients of Stratonovich–Taylor expansion of (2.1) are globally Lipschitz and satisfy the linear growth condition, and

$$ \sum_{i=1} ^{s} \tilde{\alpha }_{i}=1,\qquad \sum_{i=1} ^{s}\tilde{\beta }_{i}=1. $$

(2.12)

Then the SRKN methods (2.2)–(2.4) converge to the true solution of (2.1) with the strong global order 1.0.

3 Symplectic conditions of the SRKN methods

In this section, we assume that there exist two sufficiently smooth real-valued functions $V(y)$ and $\widetilde{H}(y)$ such that $\partial V(y)/\partial y=f(y)$ and $\partial \widetilde{H}(y)/\partial y=-g(y)$. Then (2.1) is a stochastic Hamiltonian system determined by two sufficiently smooth real-valued functions $H(y,z)=z^{\mathrm{T}}z/2-V(y)$ and $\widetilde{H}(y)$ over the phase space $\mathbb{R}^{2d}$. Here, $y_{0}$, $z_{0}$, y, z, $( \partial H(y,z)/\partial y )^{\mathrm{T}}$, $(\partial H(y,z)/ \partial z )^{\mathrm{T}}$, $(\partial \widetilde{H}(y)/\partial y )^{\mathrm{T}}$ are d-dimensional column vectors with components $y^{i}_{0}$, $z^{i}_{0}$, $y^{i}$, $z^{i}$, $\partial H(y,z)/\partial y^{i}$, $\partial H(y,z)/\partial z^{i}$, $\partial \widetilde{H}(y)/ \partial y^{i}$, $i=1, 2, \ldots, d$. Let $T=+\infty$. It is shown that the phase flows of (2.1) possess the property of preserving symplectic structure, i.e.,

$$ dy(t)\wedge dz(t)=dy_{0}\wedge dz_{0},\quad \forall t\geq 0. $$

So it is natural to require that the SRKN method (2.2)–(2.4) inherits this property

$$ dY_{n+1}\wedge dZ_{n+1}=dY_{n}\wedge dZ_{n},\quad \forall n\geq 0. $$

Now we discuss the symplectic property of the SRKN method (2.2)–(2.4).

Theorem 3.1

Assume that the coefficients $\gamma _{i}$, $a_{ij}$, $b_{ij}$, $\alpha _{i}$, $\beta _{i}$, $\tilde{\alpha }_{i}$ and $\tilde{\beta } _{i}$ of (2.2)–(2.4) satisfy the conditions

$$\begin{aligned} \begin{aligned}& \alpha _{i}=\tilde{\alpha }_{i}(1-\gamma _{i}),\quad i=1, 2, \ldots, s, \\ &\beta _{i}=\tilde{\beta }_{i}(1-\gamma _{i}),\quad i=1, 2, \ldots, s, \\ &\tilde{\alpha }_{i}(\alpha _{j}-a_{ij})=\tilde{ \alpha }_{j}(\alpha _{i}-a _{ji}),\quad i, j=1, 2, \ldots, s, \\ &\tilde{\beta }_{i}(\alpha _{j}-a_{ij})=\tilde{ \alpha }_{j}(\beta _{i}-b _{ji}),\quad i, j=1, 2, \ldots, s, \\ &\tilde{\beta }_{i}(\beta _{j}-b_{ij})=\tilde{ \beta }_{j}(\beta _{i}-b _{ji}),\quad i, j=1, 2, \ldots, s. \end{aligned} \end{aligned}$$

(3.1)

Then the SRKN method (2.2)–(2.4) is symplectic when applied to solve stochastic Hamiltonian systems (2.1) with $H(y,z)$ and $\widetilde{H}(y)$.

Proof

Introduce the temporary notations $f_{i}=f(y_{i})$, $g_{i}=g(y_{i})$. Differentiating (2.3) and (2.4), we obtain

$$ \begin{aligned}& dY_{n+1}=dY_{n}+h \,dZ_{n}+h^{2}\sum_{i=1}^{s} \alpha _{i}\,df_{i}+J _{n}h\sum _{i=1}^{s}\beta _{i}\,dg_{i}, \\ &dZ_{n+1}=dZ_{n}+h\sum_{i=1}^{s} \tilde{\alpha }_{i}\,df_{i}+J _{n}\sum _{i=1}^{s}\tilde{\beta }_{i} \,dg_{i}. \end{aligned} $$

(3.2)

Then, by a straightforward computation, we have

$$\begin{aligned} &dY_{n+1}\wedge dZ_{n+1} \\ &\quad=dY_{n}\wedge dZ_{n}+h\sum_{i=1}^{s} \tilde{\alpha }_{i}\,dY_{n}\wedge df_{i}+J_{n} \sum_{i=1}^{s} \tilde{\beta }_{i} \,dY_{n}\wedge dg_{i} \\ &\qquad{}+h^{2}\sum_{i=1}^{s}\tilde{ \alpha }_{i}\,dZ_{n}\wedge df_{i}+J _{n}h\sum_{i=1}^{s}\tilde{\beta }_{i}\,dZ_{n}\wedge dg_{i} \\ &\qquad{}+h^{2}\sum_{i=1}^{s}\alpha _{i}\,df_{i}\wedge dZ_{n}+h^{3} \sum _{i,j=1}^{s}\alpha _{i}\tilde{\alpha }_{j}\,df_{i}\wedge df _{j} \\ &\qquad{}+J_{n}h^{2}\sum_{i,j=1}^{s} \alpha _{i}\tilde{\beta }_{j}\,df_{i} \wedge dg_{j}+J_{n}h\sum_{i=1}^{s} \beta _{i}\,dg_{i}\wedge dZ_{n} \\ &\qquad{}+J_{n}h^{2}\sum_{i,j=1}^{s} \beta _{i}\tilde{\alpha }_{j}\,dg_{i} \wedge df_{j}+J_{n}^{2}h\sum _{i,j=1}^{s}\beta _{i} \tilde{\beta }_{j}\,dg_{i}\wedge dg_{j}. \end{aligned}$$

(3.3)

For $i=1, 2, \ldots, s$, differentiating (2.2), we know

$$ dY_{n}=dy_{i}-h\gamma _{i}\,dZ_{n}-h^{2} \sum _{j=1} ^{s}a_{ij}\,df_{j}-J_{n}h \sum_{j=1} ^{s}b_{ij} \,dg_{j}. $$

(3.4)

Note that for any $i=1, 2, \ldots, s$

$$\begin{aligned} \begin{aligned} dY_{n}\wedge df_{i}={}&dy_{i} \wedge df_{i}-h\gamma _{i}\,dZ_{n}\wedge df _{i}-h^{2}\sum_{j=1}^{s}a_{ij} \,df_{j}\wedge df_{i} \\ &{}-J_{n}h\sum_{j=1}^{s}b_{ij} \,dg_{j}\wedge df_{i}, \\ dY_{n}\wedge dg_{i}={}&dy_{i}\wedge dg_{i}-h\gamma _{i}\,dZ_{n}\wedge dg _{i}-h^{2}\sum_{j=1}^{s}a_{ij} \,df_{j}\wedge dg_{i} \\ &{}-J_{n}h\sum_{j=1}^{s}b_{ij} \,dg_{j}\wedge dg_{i}. \end{aligned} \end{aligned}$$

(3.5)

Substituting (3.5) into (3.3) yields

$$\begin{aligned} &dY_{n+1}\wedge dZ_{n+1} \\ &\quad =dY_{n}\wedge dZ_{n}+h\sum_{i=1}^{s} \tilde{\alpha }_{i}\Biggl(dy _{i}\wedge df_{i}-h \gamma _{i}\,dZ_{n}\wedge df_{i}-h^{2} \sum_{j=1} ^{s}a_{ij} \,df_{j}\wedge df_{i} \\ &\qquad{}-J_{n}h\sum_{j=1}^{s}b_{ij} \,dg_{j}\wedge df_{i}\Biggr) +J_{n}\sum _{i=1}^{s}\tilde{\beta }_{i} \Biggl(dy_{i}\wedge dg_{i}-h\gamma _{i}\,dZ _{n}\wedge dg_{i} \\ &\qquad{}-h^{2}\sum_{j=1}^{s}a_{ij} \,df_{j}\wedge dg_{i}-J_{n}h\sum _{j=1}^{s}b_{ij}\,dg_{j}\wedge dg_{i}\Biggr)+h^{2}\sum_{i=1} ^{s}\tilde{\alpha }_{i}\,dZ_{n}\wedge df_{i} \\ &\qquad{}+J_{n}h\sum_{i=1}^{s}\tilde{ \beta }_{i}\,dZ_{n}\wedge dg_{i}+h ^{2} \sum_{i=1}^{s}\alpha _{i} \,df_{i}\wedge dZ_{n}+h^{3}\sum _{i,j=1}^{s}\alpha _{i}\tilde{\alpha }_{j}\,df_{i}\wedge df_{j} \\ &\qquad{} +J_{n}h^{2}\sum_{i,j=1}^{s} \alpha _{i}\tilde{\beta }_{j}\,df _{i}\wedge dg_{j}+J_{n}h\sum_{i=1}^{s} \beta _{i}\,dg_{i}\wedge dZ _{n}+J_{n}h^{2} \sum_{i,j=1}^{s}\beta _{i}\tilde{ \alpha }_{j}\,dg _{i}\wedge df_{j} \\ &\qquad{} +J_{n}^{2}h\sum_{i,j=1}^{s} \beta _{i}\tilde{\beta }_{j}\,dg_{i} \wedge dg_{j} \\ &\quad= dY_{n}\wedge dZ_{n}+h\sum_{i=1}^{s} \tilde{\alpha }_{i}\,dy _{i}\wedge df_{i}+J_{n} \sum_{i=1}^{s}\tilde{\beta }_{i} \,dy_{i} \wedge dg_{i} \\ &\qquad{}+h^{2}\sum_{i=1}^{s}(\tilde{ \alpha }_{i}-\tilde{\alpha }_{i} \gamma _{i}- \alpha _{i})\,dZ_{n}\wedge df_{i} +J_{n}h\sum_{i=1} ^{s}(\tilde{ \beta }_{i}-\tilde{\beta }_{i}\gamma _{i}-\beta _{i})\,dZ_{n} \wedge dg_{i} \\ &\qquad{}+J_{n}h^{2}\sum_{i.j=1}^{s} \bigl(\tilde{\alpha }_{j}(\beta _{i}-b _{ji})- \tilde{\beta }_{i}(\alpha _{j}-a_{ij})\bigr) \,dg_{i}\wedge df_{j} \\ &\qquad{} +h^{3}\sum_{i< j}\bigl(\tilde{\alpha }_{j}(\alpha _{i}-a_{ji})- \tilde{\alpha }_{i}(\alpha _{j}-a_{ij})\bigr) \,df_{i}\wedge df_{j} \\ &\qquad{}+J_{n}^{2}h\sum_{i< j}^{s} \bigl(\tilde{\beta }_{j}(\beta _{i}-b_{ji})- \tilde{\beta }_{i}(\beta _{j}-b_{ij})\bigr) \,dg_{i}\wedge dg_{j}. \end{aligned}$$

(3.6)

By virtue of the sufficiently smooth property of $H(y,z)$, we have

$$ \frac{\partial f^{k}_{i}}{\partial y^{j}_{i}}-\frac{\partial f^{j} _{i}}{\partial y^{k}_{i}}=0, \qquad\frac{\partial g^{k}_{i}}{\partial y ^{j}_{i}}-\frac{\partial g^{j}_{i}}{\partial y^{k}_{i}}=0,\quad k, j=1, 2, \ldots, d. $$

It is easy to check that

$$\begin{aligned} dy_{i}\wedge df_{i}&=\sum _{k=1}^{d}\,dy_{i}^{k} \wedge df_{i}^{k}= \sum_{k=1}^{d} \,dy_{i}^{k}\wedge \sum_{j=1}^{d} \frac{ \partial f_{i}^{k}}{\partial y_{i}^{j}}\,dy_{i}^{j} \\ &=\sum_{k,j=1}^{d} \frac{\partial f_{i}^{k}}{\partial y_{i}^{j}} \,dy_{i}^{k}\wedge dy_{i} ^{j}=\sum _{k< j}\frac{\partial f_{i}^{k}}{\partial y_{i}^{j}}\,dy _{i}^{k} \wedge dy_{i}^{j}+\sum_{k>j}^{d} \frac{\partial f_{i} ^{k}}{\partial y_{i}^{j}}\,dy_{i}^{k}\wedge dy_{i}^{j} \\ &=\sum_{k< j}\frac{\partial f_{i}^{k}}{\partial y_{i}^{j}}\,dy _{i}^{k}\wedge dy_{i}^{j}-\sum _{k>j}^{d}\frac{\partial f_{i} ^{k}}{\partial y_{i}^{j}} \,dy_{i}^{j}\wedge dy_{i}^{k} \\ &=\sum_{k< j}\frac{\partial f_{i}^{k}}{\partial y_{i}^{j}}\,dy _{i}^{k}\wedge dy_{i}^{j}-\sum _{j>k}^{d}\frac{\partial f_{i} ^{j}}{\partial y_{i}^{k}} \,dy_{i}^{k}\wedge dy_{i}^{j} \\ &=\sum_{k< j} \biggl(\frac{\partial f_{i}^{k}}{\partial y_{i} ^{j}}- \frac{\partial f_{i}^{j}}{\partial y_{i}^{k}} \biggr)\,dy_{i}^{k} \wedge dy_{i}^{j}=0. \end{aligned}$$

(3.7)

Similar to the proof of (3.7), we can deduce that

$$ dy_{i}\wedge dg_{i}=0. $$

(3.8)

Inserting (3.1), (3.7) and (3.8) into (3.6), we see that

$$ dY_{n+1}\wedge dZ_{n+1}=dY_{n}\wedge dZ_{n}. $$

The proof is completed. □

In Sect. 5, we will give some concrete SRKN methods satisfying condition (3.1) for $s=1, 2$.

Remark 3.2

If the coefficients of (2.2)–(2.4) satisfy

$$ b_{ij}=\beta _{i}=\tilde{\beta }_{i}=0,\quad i, j=1, 2, \ldots, s, $$

then the SRKN methods reduce to a deterministic RKN method, and the symplectic conditions (3.1) reduce to the symplectic conditions for deterministic RKN methods [23],

$$ \alpha _{i}=\tilde{\alpha }_{i}(1-\gamma _{i}),\qquad \tilde{\alpha }_{i}( \alpha _{j}-a_{ij})=\tilde{ \alpha }_{j}(\alpha _{i}-a_{ji}),\quad i, j=1, 2, \ldots, s. $$

4 The preservation of the quadratic invariants

Quadratic invariants often appear in applications, for example, the conservation law of angular momentum in N-body systems. It is natural to search for numerical methods that preserve quadratic invariants. Many numerical experiments show that such numerical methods not only produce an improved qualitative behavior, but also allow for a more accurate long-time numerical simulation in comparison with general-purpose ones. Let $T=+\infty$.

Theorem 4.1

Let D be a $d\times d$ skew-symmetric matrix such that

$$ y^{\mathrm{T}}Df(y)=y^{\mathrm{T}}Dg(y)=0 $$

holds for any $y\in \mathbb{R}^{d}$. Then system (2.1) possess a quadratic invariant $Q(y,z)=y^{\mathrm{T}}Dz$, i.e., $Q(y(t),z(t))=Q(y _{0},z_{0})$.

Proof

By applying the Stratonovich chain rule we have

$$\begin{aligned} \frac{dQ(y(t),z(t))}{dt} &=y^{\mathrm{T}}(t)D\dot{z}(t)+\bigl(Dz(t) \bigr)^{ \mathrm{T}}\dot{y}(t) \\ &=y^{\mathrm{T}}(t)D\bigl(f\bigl(y(t)\bigr)+g\bigl(y(t)\bigr)\circ \dot{B}(t) \bigr)+z(t)^{ \mathrm{T}}D^{\mathrm{T}}z(t) \\ &=y^{\mathrm{T}}(t)Df\bigl(y(t)\bigr)+y^{\mathrm{T}}(t)Dg\bigl(y(t)\bigr)\circ \dot{B}(t)-z(t)^{ \mathrm{T}}Dz(t) \\ &=0. \end{aligned}$$

The proof is complete. □

Theorem 4.2

Let $(Y_{n},Z_{n}) (n=1, 2, \ldots )$ be the numerical solutions to (2.1) produced by the SRKN method (2.2)–(2.4). Assume that the conditions of Theorem 4.1 are satisfied. If the symplectic conditions (3.1) hold, then the SRKN methods preserve the quadratic invariant $Q(y,z)$ of (2.1), i.e., $Q(Y_{n+1},Z _{n+1})=Q(Y_{n},Z_{n})$.

Proof

By straightforward calculation, we obtain

$$\begin{aligned} &Y_{n+1}^{\mathrm{T}}DZ_{n+1} \\ &\quad =\Biggl[Y_{n}+hZ_{n}+h^{2}\sum _{i=1}^{s}\alpha _{i}f(y_{i})+J_{n}h \sum_{i=1}^{s}\beta _{i} g(y_{i})\Biggr]^{\mathrm{T}}D\Biggl[Z_{n}+h\sum _{i=1}^{s}\tilde{\alpha }_{i}f(y_{i}) \\ &\qquad{}+J_{n}\sum_{i=1}^{s}\tilde{ \beta }_{i}g(y_{i})\Biggr] \\ &\quad = Y_{n}^{\mathrm{T}}DZ_{n}+h\sum _{i=1}^{s}\tilde{\alpha }_{i}Y _{n}^{\mathrm{T}}Df(y_{i})+J_{n}\sum _{i=1}^{s}\tilde{\beta } _{i}Y_{n}^{\mathrm{T}}Dg(y_{i}) +hZ_{n}^{\mathrm{T}}DZ_{n} \\ &\qquad{}+h^{2}\sum_{i=1}^{s}\tilde{ \alpha }_{i}Z_{n}^{\mathrm{T}}Df(y _{i})+J_{n}h \sum_{i=1}^{s}\tilde{\beta }_{i}Z_{n}^{\mathrm{T}}Dg(y _{i})+h^{2} \sum_{i=1}^{s}\alpha _{i}f(y_{i})^{\mathrm{T}}DZ_{n} \\ &\qquad{}+h^{3}\sum_{i,j=1}^{s}\alpha _{i}\tilde{\alpha }_{j}f(y_{i})^{ \mathrm{T}}Df(y_{j})+J_{n}h^{2} \sum_{i,j=1}^{s}\alpha _{i} \tilde{ \beta }_{j}f(y_{i})^{\mathrm{T}}Dg(y_{j}) \\ &\qquad{}+J_{n}h\sum_{i=1}^{s}\beta _{i}g(y_{i})^{\mathrm{T}}DZ_{n} +J _{n}h^{2}\sum_{i,j=1}^{s} \beta _{i}\tilde{\alpha }_{j}g(y_{i})^{ \mathrm{T}}Df(y_{j}) \\ &\qquad{}+J_{n}^{2}h\sum_{i,j=1}^{s} \beta _{i}\tilde{\beta }_{j}g(y_{i})^{ \mathrm{T}}Dg(y_{j}). \end{aligned}$$

Inserting (2.2) into the above equation yields

$$\begin{aligned} &Y_{n+1}^{\mathrm{T}}DZ_{n+1} \\ &\quad =Y_{n}^{\mathrm{T}}DZ_{n}+h\sum _{i=1}^{s}\tilde{\alpha }_{i}y _{i}^{\mathrm{T}}Df(y_{i}) -h^{2}\sum _{i=1}^{s}\tilde{\alpha } _{i}\gamma _{i}Z_{n}^{\mathrm{T}}Df(y_{i}) \\ &\qquad{}-h^{3}\sum_{i,j=1}^{s}\tilde{ \alpha }_{i}a_{ij}f(y_{j})^{ \mathrm{T}}Df(y_{i}) -J_{n}h^{2}\sum_{i,j=1}^{s} \tilde{\alpha }_{i}b_{ij}g(y_{j})^{\mathrm{T}}Df(y_{i}) \\ &\qquad{}+J_{n}\sum_{i=1}^{s}\tilde{ \beta }_{i}y_{i}^{\mathrm{T}}Dg(y _{i}) -J_{n}h\sum_{i=1}^{s}\tilde{\beta }_{i}\gamma _{i}Z_{n} ^{\mathrm{T}}Dg(y_{i}) \\ &\qquad{}-J_{n}h^{2}\sum_{i,j=1}^{s} \tilde{\beta }_{i}a_{ij}f(y_{j})^{ \mathrm{T}}Dg(y_{i}) -J_{n}^{2}h\sum_{i,j=1}^{s} \tilde{\beta } _{i}b_{ij}g(y_{j})^{\mathrm{T}}Dg(y_{i})+hZ_{n}^{\mathrm{T}}DZ_{n} \\ &\qquad{}+h^{2}\sum_{i=1}^{s}\tilde{ \alpha }_{i}Z_{n}^{\mathrm{T}}Df(y _{i}) +J_{n}h\sum_{i=1}^{s}\tilde{\beta }_{i}Z_{n}^{\mathrm{T}}Dg(y _{i}) +h^{2}\sum_{i=1}^{s}\alpha _{i}f(y_{i})^{\mathrm{T}}DZ _{n} \\ &\qquad{}+h^{3}\sum_{i,j=1}^{s}\alpha _{i}\tilde{\alpha }_{j}f(y_{i})^{ \mathrm{T}}Df(y_{j}) +J_{n}h^{2}\sum_{i,j=1}^{s} \alpha _{i} \tilde{\beta }_{j}f(y_{i})^{\mathrm{T}}Dg(y_{j}) \\ &\qquad{}+J_{n}h\sum_{i=1}^{s}\beta _{i}g(y_{i})^{\mathrm{T}}DZ_{n} +J _{n}h^{2}\sum_{i,j=1}^{s} \beta _{i}\tilde{\alpha }_{j}g(y_{i})^{ \mathrm{T}}Df(y_{j}) \\ &\qquad{}+J_{n}^{2}h\sum_{i,j=1}^{s} \beta _{i}\tilde{\beta }_{j}g(y_{i})^{ \mathrm{T}}Dg(y_{j}). \end{aligned}$$

By the symplectic conditions (3.1),

$$\begin{aligned} &Y_{n+1}^{T}DZ_{n+1} \\ &\quad=Y_{n}^{\mathrm{T}}DZ_{n}+hZ_{n}^{\mathrm{T}}DZ_{n}+h \sum_{i=1} ^{s}\tilde{\alpha }_{i}y_{i}^{\mathrm{T}}Df(y_{i}) +J_{n}\sum_{i=1}^{s}\tilde{\beta }_{i}y_{i}^{\mathrm{T}}Dg(y_{i}) \\ &\qquad{}+h^{2}\sum_{i=1}^{s}(\tilde{ \alpha }_{i}-\tilde{\alpha }_{i} \gamma _{i}- \alpha _{i})Z_{n}^{\mathrm{T}}Df(y_{i}) \\ &\qquad{}+h^{3}\sum_{i< j}^{s}\bigl[ \tilde{\alpha }_{j}(\alpha _{i}-a_{ji})- \tilde{ \alpha }_{i}(\alpha _{j}-a_{ij}) \bigr]f(y_{i})^{\mathrm{T}}Df(y_{j}) \\ &\qquad{}+J_{n}h\sum_{i=1}^{s}(\tilde{ \beta }_{i}-\tilde{\beta }_{i} \gamma _{i}-\beta _{i})Z_{n}^{\mathrm{T}}Dg(y_{i}) \\ &\qquad{}+J_{n}h^{2}\sum_{i,j=1}^{s} \bigl[\tilde{\alpha }_{j}(\beta _{i}-b _{ji})- \tilde{\beta }_{i}(\alpha _{j}-a_{ij}) \bigr]g(y_{i})^{\mathrm{T}}Df(y _{j}) \\ &\qquad{}+J_{n}^{2}h\sum_{i< j}^{s} \bigl[\tilde{\beta }_{j}(\beta _{i}-b_{ji})- \tilde{\beta }_{i}(\beta _{j}-b_{ij}) \bigr]g(y_{i})^{\mathrm{T}}Dg(y_{j}) \\ &\quad =Y_{n}^{T}DZ_{n} \end{aligned}$$

is derived, which completes the proof. □

5 Some low-stage SSRKN methods

As an application of our main results, both the order conditions (2.12) and symplectic conditions (3.1) are used to construct low-stage SSRKN methods in this section.

5.1 One-stage SSRKN methods

Consider one-stage SRKN methods

$$ \textstyle\begin{array} {l@{\quad}|@{\quad}l@{\quad}l} \gamma _{1} & a_{11} &b_{11} \\ \hline & \alpha _{1} & \beta _{1} \\ \hline & \tilde{\alpha }_{1} & \tilde{\beta }_{1} \end{array}\displaystyle , $$

(5.1)

substituting the coefficients of (5.1) into (2.12) and (3.1), a family of one-stage SSRKN methods with strong global order 1.0 is given by

$$ \textstyle\begin{array} {l@{\quad}|@{\quad}l@{\quad}l} \gamma _{1} & a_{11} &a_{11} \\ \hline & 1-\gamma _{1} & 1-\gamma _{1} \\ \hline & 1 & 1 \end{array}\displaystyle , $$

where $a_{11}$ and $\gamma _{1}$ are free parameters. If we choose $a_{11}=0.5$ and $\gamma _{1}=0.5$, then the above SSRKN method reduces to

$$ \textstyle\begin{array} {l@{\quad}|@{\quad}l@{\quad}l} 0.5 & 0.5 &0.5 \\ \hline & 0.5 & 0.5 \\ \hline & 1 & 1 \end{array}\displaystyle . $$

(5.2)

5.2 Two-stage explicit SSRKN methods

For solving (2.1), a class of two-stage explicit SRKN methods is given by

$$ \textstyle\begin{array} {l@{\quad}|@{\quad}l@{\quad}l@{\quad}l@{\quad}l} \gamma _{1} & 0 &0 & 0 &0 \\ \gamma _{2}& a_{21} &0 & b_{21} &0 \\ \hline & \alpha _{1} &\alpha _{2} & \beta _{1} &\beta _{2} \\ \hline & \tilde{\alpha }_{1} &\tilde{\alpha }_{2} & \tilde{\beta }_{1} &\tilde{\beta }_{2} \end{array}\displaystyle . $$

(5.3)

According to the order conditions (2.12) and Theorem 3.1, a family of two-stage explicit SSRKN methods with strong global order 1.0 is given by

$$ \textstyle\begin{array} {l@{\quad}|@{\quad}l@{\quad}l@{\quad}l@{\quad}l} \gamma _{1} & 0 &0 & 0 &0 \\ \gamma _{2}& \tilde{\alpha }_{1}(\gamma _{2}- \gamma _{1}) &0 & \tilde{\beta }_{1}(\gamma _{2}-\gamma _{1}) &0 \\ \hline & \tilde{\alpha }_{1}(1-\gamma _{1}) &(1-\tilde{ \alpha }_{1}) (1-\gamma _{2}) & \tilde{\beta }_{1}(1-\gamma _{1}) &(1-\tilde{\beta }_{1}) (1- \gamma _{2}) \\ \hline & \tilde{\alpha }_{1} &1-\tilde{\alpha }_{1} & \tilde{\beta }_{1} &1-\tilde{\beta }_{1} \end{array}\displaystyle , $$

(5.4)

where $\gamma _{1}$, $\gamma _{2}$, $\tilde{\alpha }_{1}$ and $\tilde{\beta }_{1}$ are free parameters. If we choose $\gamma _{1}=1/4$, $\gamma _{2}=3/4$, $\tilde{\alpha }_{1}=1/2$ and $\tilde{\beta }_{1}=1/2$, then method (5.4) reduces to

$$ \textstyle\begin{array} {l@{\quad}|@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 1/4 & 0 &0 & 0 &0 \\ 3/4& 1/4 &0 & 1/4 &0 \\ \hline & 3/8 &1/8 & 3/8 &1/8 \\ \hline & 1/2 &1/2 & 1/2 &1/2 \end{array}\displaystyle . $$

(5.5)

6 Numerical experiments

In this section, the superiority of our symplectic integrators is illustrated by some numerical examples. To compare our symplectic integrators with non-symplectic ones, two non-symplectic SRKN methods with strong global order 1.0 are given by

$$ \textstyle\begin{array} {l@{\quad}|@{\quad}l@{\quad}l} 0.5 & 0 &0.5 \\ \hline & 0 & 0.5 \\ \hline & 1 & 1 \end{array} $$

(6.1)

and

$$ \textstyle\begin{array} {l@{\quad}|@{\quad}l@{\quad}l@{\quad}l@{\quad}l} 1/2 & 0 &0 & 0 &0 \\ 1/2& 1/2 &0 & 1/2 &0 \\ \hline & 1/2 &1/2 & 1/2 &1/2 \\ \hline & 1/4 &3/4 & 1/2 &1/2 \end{array}\displaystyle . $$

(6.2)

6.1 Linear stochastic oscillator with additive noise

Here we perform computations for linear stochastic oscillator with additive noise [19], which is defined by $H(y,z)=(y^{2}+z ^{2})/2$ and $\widetilde{H}(y,z)=\sigma y$, where σ is the noise intensity. We also have the following form:

$$ \textstyle\begin{cases} dy(t)=z(t)\,dt,\quad t\in [0,T], \\ dz(t)=-y(t)\,dt-\sigma \,dB(t), \quad t\in [0,T], \\ y(0)=y_{0}\in \mathbb{R},\qquad z(0)=z_{0}\in \mathbb{R}. \end{cases} $$

(6.3)

Since (6.3) is a SDE with additive noise, its Itô and Stratonovich form are identical. We consider it as a SDE of Stratonovich type. In addition, (6.3) possesses linear growth second moment, i.e.,

$$ \mathbb{E} \bigl(y^{2}(t)+z^{2}(t) \bigr)=y_{0}^{2}+z_{0}^{2}+ \sigma ^{2}t. $$

Firstly, the convergence of the numerical methods we proposed will be tested. We simulate them at terminal time $T=1$, with $\sigma =1$, $z_{0}=0$, $y_{0}=1$ in system (6.3). 1000 different discretized Brownian paths over [0,1] will be computed with step size 2⁻¹⁴. For each path, Euler–Maruyama method, method (6.1), method (5.2), method (5.5) are applied with five different step sizes: $h=2^{-2}, 2^{-3}, 2^{-4}, 2^{-5}, 2^{-6}$. To simulate the exact solution of (6.3), we just use the Euler–Maruyama method with $h=2^{-14}$ as the reference solution. We present the sample average errors, i.e.,

$$ \frac{\sum_{i=1}^{1000}\sqrt{ \vert Y_{N}(\omega _{i})-y(T,\omega _{i}) \vert ^{2}+ \vert Z_{N}(\omega _{i})-z(T,\omega _{i}) \vert ^{2}}}{1000} $$

at the terminal time $T=1$ in Table 1. Figure 1 shows the results of Table 1 in a log–log plot.

Figure 1

The convergence rates of Euler–Maruyama method, method (6.1), method (5.2) and method (5.5) for solving (6.3)

Table 1 The endpoint sample average errors with different methods for solving (6.3)

Then we want to check their ability of preserving the linear growth property of the second moment by numerical tests. The second moment $\mathbb{E}(Y^{2}_{n}+Z^{2}_{n})$ of the numerical solution is approximated by taking sample average of 1000 sample trajectories, i.e.,

$$ \frac{\sum_{i=1}^{1000}( \vert Y_{n}(\omega _{i}) \vert ^{2}+ \vert Z_{n}(\omega _{i}) \vert ^{2})}{1000}. $$

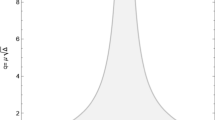
Figure 2 shows the linear growth property of second moment of the numerical solutions produced by the Euler–Maruyama method, method (6.1), method (5.2) and method (5.5) with fixed step size $h=0.1$, $\sigma =1$ and $T=500$, respectively, and the slope of the reference line is 1.

Figure 2

Linear growth property of second moment for Eq. (6.3)

From the point of view of geometry, the symplecticity of the system (6.3) is equivalent to the preservation of the area of the triangle in the phase space along the flow of (6.3), which means $S_{n}=S_{0}$, where $S_{n}$ denotes the area of the triangle at time $t_{n}$, namely, value $S_{n}/S_{0}$ should remain at 1 along the exact flow of (6.3). Let $\sigma =1$ and points for the initial triangle be $(0,0), (1,0), (1,1)$, the Euler–Maruyama method, method (6.1), method (5.2), method (5.5) are applied to solve (6.3) with $h=0.1$ and $T=100$. The evolution of the quantity $S_{n}/S_{0}$ along the numerical solutions is illustrated in Fig. 3. The changes of the triangles along the numerical solutions are displayed in Fig. 4. From Fig. 3 and Fig. 4, it is easy to see that method (5.2) and method (5.5) can preserve the symplecticity of (6.3) exactly, while the Euler–Maruyama method and method (6.1) cannot.

Figure 3

Evolution of the quantity $S_{n}/S_{0}$ along the numerical solutions produced by Euler–Maruyama method, method (6.1), method (5.2) and method (5.5) for Eq. (6.3)

Figure 4

Evolution of the numerical triangles arising from Euler–Maruyama method, method (6.1), method (5.2) and method (5.5) for Eq. (6.3)

6.2 Synchrotron oscillations of particles in storage rings

The second-order stochastic Hamiltonian system defined by $H(p,q)=- \cos (q)+p^{2}/2$ and $\widetilde{H}(p,q)=\sigma \sin (q)$, where σ is the noise intensity, can be written in the following form [20]:

$$ \textstyle\begin{cases} dq(t)=p(t)\,dt, \quad t\in [0,T], \\ dp(t)=-\sin (q(t))\,dt-\sigma \cos (q(t))\circ dB(t),\quad t\in [0,T], \\ p(0)=p_{0}\in \mathbb{R},\qquad q(0)=q_{0}\in \mathbb{R}. \end{cases} $$

(6.4)

System (6.4) is used to simulate synchrotron oscillations of a particle in a storage ring. We consider it as a SDE of Stratonovich type. The phase flow of (6.4) preserves the symplectic structure (1.3). Choose the coefficients of Eq. (6.4) as $\sigma =0.2$, $p_{0}=1$, $q_{0}=1$ and $T=200$. Figure 5 exhibits numerical solutions of a sample phase trajectory of (6.4) simulated by the Euler–Maruyama method, method (6.1), method (5.2) and method (5.5) with fixed step size $h=0.02$, respectively.

Figure 5

Simulation of a sample trajectory of Eq. (6.4)

The plots show the SSRKN methods (5.2) and (5.5) can keep the vibration of the original stochastic system, but other two non-symplectic methods do not have this property.

6.3 Stochastic Kepler problem

In order to test the SSRKN methods of preserving the quadratic invariants of original SDEs, we consider stochastic Kepler problem defined by

$$ H(q_{1},q_{2},p_{1},p_{2})= \frac{1}{2}\bigl(p_{1}^{2}+p_{2}^{2} \bigr)-\frac{1}{\sqrt{q _{1}^{2}+q_{2}^{2}}},\qquad \widetilde{H}(q_{1},q_{2},p_{1},p_{2})=- \frac{1}{\sqrt{q _{1}^{2}+q_{2}^{2}}}, $$

which can be written in the following form:

$$ \textstyle\begin{cases} {d} q_{1}(t) = p_{1}(t) \,dt,\quad t\in [0,T], \\ {d} q_{2}(t)= p_{2}(t) \,dt,\quad t\in [0,T], \\ {d} p_{1}(t)= - \frac{q_{1}(t)}{(q_{1}^{2}(t)+q_{2}^{2}(t))^{3/2}} \,dt-\frac{q _{1}(t)}{(q_{1}^{2}(t)+q_{2}^{2}(t))^{3/2}}\circ \,dB(t),\quad t \in [0,T], \\ {d} p_{2}(t)= - \frac{q_{2}(t)}{(q_{1}^{2}(t)+q_{2}^{2}(t))^{3/2}}\,dt-\frac{q _{2}(t)}{(q_{1}^{2}(t)+q_{2}^{2}(t))^{3/2}}\circ \,dB(t),\quad t \in [0,T], \\ q_{1}(0)=q_{10}\in \mathbb{R}, \qquad q_{2}(0)=q_{20}\in \mathbb{R},\\ p_{1}(0)=p _{10}\in \mathbb{R}, \qquad p_{2}(0)=p_{20}\in \mathbb{R}. \end{cases} $$

(6.5)

According to Theorem 4.1, (6.5) possesses a quadratic invariant

$$ L(q_{1},q_{2},p_{1},p_{2})=p_{2}q_{1}-q_{2}p_{1}. $$

Due to Theorem 4.2, the quadratic invariant will be conserved by the SSRKN methods. So, we use two-stage explicit symplectic method (5.5) and non-symplectic method (6.2) to check the ability of preserving quadratic invariant. As an initial condition we choose

$$ q_{10}=1-e,\qquad q_{20}=0,\qquad p_{10}=0,\qquad p_{20}= \sqrt{\frac{1+e}{1-e}}, $$

where we set $e=0.6$. Consequently, $L_{0}=L(q_{10},q_{20},p_{10},p _{20})=0.8$. Fix the step size $h=0.05$. Figure 6 shows that numerical solution created by method (5.5) preserve the quadratic invariant L of (6.5) exactly, while the non-symplectic method (6.2) does not have this property.

Figure 6

The preservation of the quadratic invariant L of (6.5) with a sample trajectory

All of these numerical experiments demonstrate the superior behavior of our SSRKN methods in long-time simulations compared to some non-symplectic numerical methods.

7 Conclusions

This paper presents the extension of deterministic RKN methods [23] to the stochastic counterpart. For general autonomous d-dimensional second-order SDEs in the Stratonovich sense, a class of SRKN methods is proposed. The order conditions of strong global order 1.0 are obtained. The symplectic conditions of the SRKN methods for solving second-order stochastic Hamiltonian systems with multiplicative noise are given. It is proved that the SSRKN methods can preserve the quadratic invariants of underlying stochastic systems. A class of one-stage SSRKN methods and two-stage explicit SSRKN methods with strong global order 1.0 are constructed based on our main results. Numerical experiments are given to verify the results of our theoretical analysis and show that the methods are valid in a long-time numerical simulation of SDEs.