A high-order numerical scheme using orthogonal spline collocation for solving the two-dimensional fractional reaction–subdiffusion equation

Abstract

In this paper, a high-order numerical scheme is proposed for solving the two-dimensional fractional reaction–subdiffusion equation. The method is based on adopting a third-order weighted and shifted Grünwald difference (WSGD) operator to approximate the time Caputo fractional derivative and applying the orthogonal spline collocation (OSC) method to approximate the spatial derivative. Stability and convergence analysis of the proposed method are rigorously proved. Several numerical examples in one variable and in two space variables are presented to validate our theoretical analysis.

1 Introduction

Fractional equations can be used to describe some physical phenomenon more accurately than the classical integer-order differential equation, one of which fractional reaction–diffusion equations have been researched in recent years in many areas of science and engineering. A fractional reaction–subdiffusion equation can be derived from a continuous time random walk model when the transport is dispersive [1] or a continuous time random walk model with temporal memory and sources [2]. The analytical solutions of such equations are usually difficult to obtain, so seeking numerical solutions becomes more important and emergent. These numerical methods mainly covers compact difference methods [3,4,5], finite element methods [6, 7], spectral methods [8, 9], meshless methods [10, 11], the homotopy analysis method [12], the Legendre operational matrix method [13], and spline collocation methods [14,15,16].

Although there are many studies on numerical methods for one-dimensional fractional partial differential equations, there are few studies on numerical methods for two-dimensional time fractional differential equations, when compared with one-dimensional problems. Huang [17] proposed a numerical algorithm for a two-dimensional fractional reaction subdiffusion equation with $\tau ^{1+\gamma }$ order in time and second order in space. Yu [18] considered a numerical method for the two-dimensional non-linear fractional reaction–subdiffusion equation, which is of second-order temporal accuracy and fourth-order spatial accuracy. In [19], Yang developed novel numerical techniques for the solution of the two-dimensional fractional sub-diffusion equation, which is based on the orthogonal spline collocation method in space and a finite difference method (FDM) in time. Ömer et al. [20] established a wavelet method, based on Haar wavelets and a finite difference scheme for the two-dimensional time fractional reaction–subdiffusion equation. Li [21] proposed a numerical treatment for two-dimensional fractional sub-diffusion equations using the parametric quintic spline. In [22], Dehghan used the dual reciprocity boundary elements method for the numerical solution of two-dimensional linear and nonlinear time-fractional modified anomalous subdiffusion equations and time-fractional convection-diffusion equation. Bhrawy and Zaky applied spectral tau and collocation methods for different kinds of fractional partial differential equations in the multi-dimensional case [23,24,25,26,27].

In this study, we consider the following two-dimensional time fractional reaction–subdiffusion equation:

$$\begin{aligned} _{0}^{C}D^{\alpha }_{t}u(x,y,t) &=K_{\alpha }\Delta u(x,y,t)-C_{\alpha }u(x,y,t)+f(x,y,t),\quad (x,y,t)\in \varOmega \times (0,T] \end{aligned}$$

(1.1)

subject to the initial condition

$$\begin{aligned} u(x,y,0)=\phi (x,y), \quad (x,y)\in \varOmega , \end{aligned}$$

(1.2)

and the boundary condition

$$\begin{aligned} u(x,y,t)=0, \quad (x,y,t)\in \partial \varOmega \times (0,T], \end{aligned}$$

(1.3)

where Δ is Laplace operator, $\varOmega =[0,1]\times [0,1]$ with boundary ∂Ω, $K_{\alpha }>0$ is diffusion coefficient, $C_{\alpha }>0$ is the constant reaction rate, and ${}_{0}^{C}D^{\alpha }_{t}$ denotes the Caputo derivative of order α ($0<\alpha <1$), which reads as follows:

$$\begin{aligned} _{0}^{C}D^{\alpha }_{t}u(x,y,t)= \frac{1}{\varGamma (1-\alpha )} \int _{0} ^{t}{\frac{\partial u(x,y,s)}{\partial s}(t-s)^{-\alpha }} \,ds, \end{aligned}$$

in which $\varGamma (\cdot )$ is the Gamma function.

Recently, Tian et al. [28] proposed second- and third-order approximations for the Riemann–Liouville fractional derivative with order α ($0<\alpha <1$) by using the weighted and shifted Grünwald difference (WSGD) operators. Thereafter, some related discussion problems covering the WSGD idea were addressed by many scholars. Following the idea of the WSGD operator, Wang and Vong [29] used compact finite difference schemes for the modified time sub-diffusion equation with Riemann–Liouville fractional derivative and the temporal Caputo fractional diffusion-wave equation. Ji and Sun [30] applied a third-order approximation for the Caputo fractional derivative and used compact difference scheme to solve fractional sub-diffusion equation. In [31], Liu et al. developed a high-order local discontinuous Galerkin method combined with WSGD approximation for a Caputo time-fractional sub-diffusion equation. In [32], a temporal second-order fully discrete two-grid finite element (FE) scheme is presented to solve nonlinear fractional Cable equation, in which the spatial direction is approximated by two-grid FE method and the integer and fractional derivatives in time are discretized by second-order two-step backward difference method and second-order WSGD operator. In [33], Yang discussed a new numerical approximation for the two-dimensional distributed-order time fractional reaction–diffusion equation, which combines the idea of a WSGD operator with the second order in time direction and the orthogonal spline collocation method in the space direction.

The orthogonal spline collocation (OSC) method has developed into a robust and valuable technique for solving many kinds of partial differential equations [34,35,36,37,38]. The popularity of OSC is due to its simple concept, wide applicability and easy implementation. Comparing with the finite difference method [39] and the Galerkin finite method [40], the OSC method has the following advantages: the calculation of the coefficients in the equation determining the approximate solution is fast since there is no need to calculate the integrals; and it provides approximations to the solution and spatial derivatives. Moreover, the OSC method always leads to the almost block diagonal linear system, which can be solved by the software packages efficiently [41]. Another feature of the OSC method lies in its super-convergence [42].

Inspired and motivated by the work mentioned above, the main purpose of this paper is to propose a high-order OSC approximation method combined with a third-order WSGD operator to solve a two-dimensional fractional reaction–subdiffusion equation, abbreviated WSGD-OSC in forthcoming sections.

The rest of the paper is organized as follows. In Sect. 2, we introduce some notations and preliminaries. In Sect. 3, the fully discrete scheme combined with a WSGD operator with third order and an orthogonal spline collocation scheme is constructed. Stability and convergence analyses of the WSGD-OSC scheme are presented in Sect. 4. Section 5 presents detailed description of the WSGD-OSC scheme. In Sect. 6, numerical experiments are carried out to confirm the convergence analysis. Finally, the conclusion is drawn in Sect. 7.

2 Preliminaries

In this section, we will introduce some notations and basic lemmas. For some positive integers $N_{x}$ and $N_{y}$, $\pi _{x}$ and $\pi _{y}$ are two uniform partitions of $\overline{I}=[0,1]$ which are defined as follows:

$$ \pi _{x}: \quad 0=x_{0}< x_{1}< \cdots < x_{N_{x}}=1, \quad\quad \pi _{y}: \quad 0=y_{0}< y_{1}< \cdots < y_{N_{y}}=1, $$

and $h_{i}^{x}=x_{i}-x_{i-1}$, $I_{i}^{x}=(x_{i-1},x_{i})$, $1\leq i \leq N_{x}$, and $h_{j}^{y}=y_{j}-y_{j-1}$, $I_{j}^{y}=(y_{j-1},y_{j})$, $1 \leq j\leq N_{y}$, $h=\max (\max_{1\leq i \leq N_{x}} h_{i} ^{x},\max_{1\leq j \leq N_{y}} h_{j}^{y})$. Let $M_{r}(\pi _{x})$ and $M_{r}(\pi _{y})$ be the space of piecewise polynomials of degree at most $r\geq 3$, defined by

$$\begin{aligned}& M_{r}(\pi _{x})= \bigl\{ v\in C^{1}[0,1]:v\vert _{I_{i}^{x}}\in P_{r}, 1\leq i \leq N_{x},v(0)=v(1)=0 \bigr\} , \\& M_{r}(\pi _{y})= \bigl\{ v\in C^{1}[0,1]:v\vert _{I_{j}^{y}}\in P_{r}, 1\leq j \leq N_{y},v(0)=v(1)=0 \bigr\} , \end{aligned}$$

where $P_{r}$ denotes the set of polynomial of degree at most r. It is easy to know that the dimension of the spaces $M_{x}(\pi _{x})$ and $M_{y}(\pi _{y})$ are $(r-1)N_{x}:=M_{x}$ and $(r-1)N_{y}:=M_{y}$, respectively.

Let $\pi =\pi _{x}\otimes \pi _{y}$ be a quasi-uniform partition of Ω, and $M_{r}(\pi )=M_{r}(\pi _{x})\otimes M_{r}(\pi _{y})$ with the dimension of $M_{x}\times M_{y}$. Let $\{\lambda _{j}\}_{j=1}^{r-1}$ denote the nodes for the $\{r-1\}$-point Gaussian quadrature rule on the interval I̅ with corresponding weights $\{\omega _{j}\} _{j=1}^{r-1}$. Denote by

$$ \mathcal{G}_{x}= \bigl\{ \xi _{i,l}^{x} \bigr\} _{i,l=1}^{N_{x},r-1} \quad \text{and} \quad \mathcal{G}_{y}= \bigl\{ \xi _{j,m}^{y} \bigr\} _{j,m=1}^{N_{y},r-1} $$

the sets of Gauss points in x and y direction, respectively, where

$$ \xi _{i,l}^{x}=x_{i-1}+h_{i}^{x} \lambda _{l}, \quad\quad \xi _{j,m}^{y}=y_{j-1}+h_{j}^{y} \lambda _{m}, \quad 1\leq l,m\leq r-1. $$

Let $\mathcal{G}=\{\xi =(\xi ^{x},\xi ^{y}):\xi ^{x}\in \mathcal{G}_{x}, \xi _{y}\in \mathcal{G}_{y} \}$. For the functions u and v defined on $\mathcal{G}$, the inner product $\langle u,v\rangle$ and norm $\Vert v\Vert _{M_{r}}$ are, respectively, defined by

$$ \langle u,v\rangle =\sum_{i=1}^{N_{x}}\sum _{j=1}^{N_{y}}h_{i}^{x}h _{j}^{y}\sum_{l=1}^{r-1} \sum_{m=1}^{r-1}\omega _{l}\omega _{m}(uv) (\xi _{i,l},\xi _{j,m}), \quad \Vert v \Vert _{M_{r}}=\langle v,v\rangle ^{\frac{1}{2}}. $$

For m a nonnegative integer, let $H^{m}(\varOmega )$ denote the usual Sobolev space with norm

$$ \Vert v \Vert _{H^{m}}= \Biggl(\sum_{l=0}^{m} \sum_{i+j=l} \biggl\Vert \frac{\partial ^{i+j}v}{\partial x^{i}\partial y^{j}} \biggr\Vert ^{2} \Biggr)^{\frac{1}{2}}, $$

where the norm $\Vert v\Vert$ denotes the usual $L_{2}$ norm, sometimes it is written as $\Vert v\Vert _{H^{0}}$ for convenience. The following important lemmas are required in our forthcoming analysis. First, we introduce the differentiable (resp. twice differentiable) map $W:[0,T]\rightarrow M_{r}(\pi )$ by

$$\begin{aligned} \Delta (u-W)=0 \quad \text{on } \mathcal{G} \times [0,T], \end{aligned}$$

(2.1)

where u is the solution of Eqs. (1.1)–(1.3). Then we have the following estimates for $u-W$ and its time derivatives.

Lemma 2.1

([34])

If $\partial ^{l} u/\partial t^{l} \in H^{r+3-j}$, for all $t\in [0,T]$, $l=0,1,2$, $j=0,1,2$, and W is defined by (2.1), then there exists a constant C such that

$$\begin{aligned} \biggl\Vert \frac{\partial ^{l} (u-W)}{\partial t^{l}} \biggr\Vert _{H^{j}}\leq Ch ^{r+1-j} \biggl\Vert \frac{\partial ^{l} u}{\partial t^{l}} \biggr\Vert _{H^{r+3-j}}. \end{aligned}$$

(2.2)

Lemma 2.2

([34])

If $\partial ^{i} u/\partial t^{i}\in H^{r+3}$, for $t\in [0,T]$, $i=0,1$, then

$$\begin{aligned} \biggl\Vert \frac{\partial ^{l+i} (u-W)}{\partial x^{l_{1}}\partial y^{l _{2}}\partial t^{i}} \biggr\Vert _{M_{r}}\leq Ch^{r+1-l} \biggl\Vert \frac{ \partial ^{i} u}{\partial t^{i}} \biggr\Vert _{H^{r+3}}, \end{aligned}$$

(2.3)

where $0\leq l=l_{1}+l_{2}\leq 4$.

Lemma 2.3

([43])

If $u,v\in M(r,s,\delta )$, then

$$\begin{aligned} \langle -\Delta u,v \rangle =\langle u,-\Delta v\rangle , \end{aligned}$$

(2.4)

and there exists a positive constant C such that

$$\begin{aligned} \langle -\Delta u,u \rangle \geq C \Vert \nabla u \Vert ^{2}\geq 0. \end{aligned}$$

(2.5)

Lemma 2.4

([44])

The norms $\Vert \cdot \Vert _{M_{r}}$ and $\Vert \cdot \Vert$ are equivalent on $M_{r}(\pi )$.

Throughout the paper, we denote $C>0$ a constant which is independent of space–time mesh sizes h and τ. It is not necessarily the same on each occurrence. Besides, the following Young inequality will be used repeatedly:

$$\begin{aligned} de\leq \varepsilon d^{2}+\frac{1}{4\varepsilon }e^{2}, \quad d,e\in \mathcal{R},\varepsilon >0. \end{aligned}$$

(2.6)

3 Construction of the fully discrete orthogonal spline collocation scheme

For the analysis, we need to introduce the Riemann–Liouville fractional derivative and Liouville fractional derivative of order $\alpha (0< \alpha <1)$ for a function $u(t)$, which are defined by

$$\begin{aligned} {_{0}^{RL}}D_{t}^{\alpha }u(t)= \frac{1}{\varGamma (1-\alpha )} \frac{d}{dt} \int _{0}^{t}\frac{u(\tau )}{(t-\tau )^{\alpha }}\,d\tau \end{aligned}$$

(3.1)

and

$$\begin{aligned} {_{-\infty }}D_{t}^{\alpha }u(t)=\frac{1}{\varGamma (1-\alpha )} \frac{d}{dt} \int _{-\infty }^{t}\frac{u(\tau )}{(t-\tau )^{\alpha }}\,d \tau . \end{aligned}$$

(3.2)

Lemma 3.1

([30])

If $f\in C^{(2+m)}(\mathbb{R})$, then $f\in \mathscr{L}^{\alpha +m}(\mathbb{R})$, for any $\alpha \in (0,1)$, where the space is defined as $\mathscr{L}^{\alpha +m}(\mathbb{R})= \{f \vert \int _{-\infty }^{\infty }(1+\Vert \omega \Vert )^{\alpha +m}\Vert \hat{f}(\omega )\Vert \,d\omega <+\infty ,\hat{f} \textit{ is the Fourier transform of } f \}$.

Lemma 3.2

([45])

For any $f\in L_{1}(\mathbb{R})\cap \mathscr{L}^{\alpha +1}( \mathbb{R})$, we define the shifted Grünwald difference operator

$$ A_{\tau ,p}^{(\alpha )}f(t)=\frac{1}{\tau ^{\alpha }}\sum _{k=0}^{ \infty }g_{k}^{(\alpha )}f \bigl(t-(k-p)\tau \bigr), $$

(3.3)

where p is a non-positive and $g_{k}^{(\alpha )}=(-1)^{k}\binom{ \alpha }{k}z^{k}= \frac{\varGamma (k-\alpha )}{\varGamma (-\alpha )\varGamma (k+1)}$. Then

$$ A_{\tau ,p}^{(\alpha )}f(t)={_{-\infty }}D_{t}^{\alpha }f(t)+ \mathscr{O}(\tau ). $$

(3.4)

Lemma 3.3

([28])

Let $f(t)$, ${_{-\infty } {D}_{t}^{\alpha +3}f(t)}$ and its Fourier transform f̂ belong to $L^{1}(\mathbb{R})$. Define the weighted and shifted Grünwald difference operator by

$$ D_{\tau }^{\alpha } f(t)=\rho _{1} A_{\tau ,p}^{(\alpha )}f(t)+\rho _{2} A_{\tau ,q}^{(\alpha )}f(t)+ \rho _{3} A_{\tau ,r}^{(\alpha )}f(t), $$

(3.5)

where

$$\begin{aligned} &\rho _{1}= \frac{12qr-(6q+6r+1)\alpha +3\alpha ^{2}}{12(qr-pq-pr+p^{2})}, \quad\quad \rho _{2}= \frac{12qr-(6q+6r+1)\alpha +3\alpha ^{2}}{12(pr-pq-qr+q^{2})}, \\ &\rho _{3}=\frac{12qq-(6p+6q+1)\alpha +3\alpha ^{2}}{12(pq-pr-pqr+r ^{2})}, \end{aligned}$$

and p, q and r are all integers. Then we have

$$ D_{\tau }^{\alpha } f(t)={_{-\infty } \mathcal{D}_{t}^{\alpha }}f(t)+ \mathscr{O} \bigl(\tau ^{3} \bigr) $$

uniformly for $t\in \mathbb{R}$ as $\tau \rightarrow 0$. We consider the case $p>q>r$ and choose $(p,q,r)=(0,-1-2)$, and we obtain

$$\begin{aligned} &\rho _{1}=\frac{24+17\alpha +3\alpha ^{2}}{24},\quad\quad \rho _{2}=- \frac{11\alpha +3\alpha ^{2}}{12},\quad\quad \rho _{3}=-\frac{5\alpha +3\alpha ^{2}}{24}. \end{aligned}$$

Fixing x, y and defining $u(x,y,t)=f(t)$, $f(t)=0(t<0)$ and noticing that if $f(0)=0$, according to the relationship between the Caputo derivative and the Riemann–Liouville fractional derivative, we have

$$\begin{aligned} _{0}^{C}D_{t}^{\alpha }u(x,y,t_{n}) &={_{0}^{RL}}D_{t}^{\alpha }u(x,y,t _{n})-\frac{u(x,y,0)}{\varGamma (1-\alpha )}t_{n}^{-\alpha } \\ &=\tau ^{-\alpha } \Biggl[\rho _{1}\sum _{k=0}^{n}g_{k}^{(\alpha )}u(x,y,t _{n-k})+\rho _{2}\sum_{k=0}^{n-1}g_{k}^{(\alpha )}u(x,y,t_{n-k-1}) \\ &\quad{} +\rho _{3}\sum_{k=0}^{n-2}g_{k}^{(\alpha )}u(x,y,t_{n-k-2}) \Biggr]+ \mathscr{O} \bigl(\tau ^{3} \bigr) \\ &=\tau ^{-\alpha }\sum_{k=0}^{n}q_{k}^{(\alpha )}u(x,y,t_{n-k})+ \mathscr{O} \bigl(\tau ^{3} \bigr), \end{aligned}$$

(3.6)

where

$$ \textstyle\begin{cases} q_{0}^{(\alpha )} =\rho _{1}g_{0}^{\alpha }, \\ q_{1}^{(\alpha )}=\rho _{1}g_{1}^{\alpha }+\rho _{2}g_{0}^{\alpha }, \\ q_{k}^{(\alpha )}= \rho _{1}g_{k}^{\alpha }+\rho _{2}g_{k-1}^{\alpha }+\rho _{3}g_{k-2}^{ \alpha },\quad k\geq 2. \end{cases} $$

(3.7)

Let $t_{k}=k\tau$, $k=0,1,\ldots,K$, where $\tau =T/K$ is the time step size. We consider discrete-time OSC schemes for solving Eqs. (1.1)–(1.3). The continuous-time OSC scheme to the solution u of (1.1) is a differentiable map $u_{h}:(0,T]\rightarrow M_{r}(\pi )$ such that

$$\begin{aligned} {}_{0}^{C}D^{\alpha }_{\tau }u_{h} \bigl(\xi _{i,k}^{x},\xi _{j,l}^{y},t \bigr) &=K _{\alpha }\Delta u_{h} \bigl(\xi _{i,k}^{x}, \xi _{j,l}^{y},t \bigr)-C_{\alpha }u _{h} \bigl( \xi _{i,k}^{x},\xi _{j,l}^{y},t \bigr) \\ &\quad{} +f_{h} \bigl(\xi _{i,k}^{x},\xi _{j,l}^{y},t \bigr),\quad \bigl(\xi _{i,k}^{x}, \xi _{j,l}^{y},t \bigr) \in \varOmega \times (0,T], \end{aligned}$$

(3.8)

where $f_{h}(\cdot ,\cdot ,t)\in M_{r}(\pi )$ satisfies $\langle f _{h},v\rangle =\langle f ,v\rangle$, $\forall v\in M_{r}(\pi )$. To apply the weighted and shifted Grünwald difference operator to approximate ${}_{0}^{C}D^{\alpha }_{t} u(x,y,t)$, without loss of generality we assume $u(x,y,0)=0$, otherwise, we may consider a transform $u(x,y,0)=u(x,y,0)- \varphi (x,y)$, then ${}_{0}^{C}D^{\alpha }_{t} u(x,y,t)={_{0}^{RL}}D _{t}^{\alpha }u(x,y,t)$. According to Theorem 1 in [28], we can obtain the following estimate of the truncation error.

Lemma 3.4

Suppose $\forall \alpha >0$, and ${_{0}^{RL}}D_{t}^{\alpha +3}u \in L(R)$. We have

$$\begin{aligned} \Biggl\vert {_{0}^{RL}}D_{t}^{\alpha }u(t_{n})- \tau ^{-\alpha }\sum_{k=0}^{n}q _{k}^{(\alpha )}u(t_{n-k}) \Biggr\vert \leq C\tau ^{3} \bigl\Vert \mathscr{F} \bigl[ {_{0}^{RL}}D_{t}^{\alpha +3}u \bigr](\omega ) \bigr\Vert _{L^{1}}, \end{aligned}$$

(3.9)

where $\mathscr{F}$ denotes the Fourier transform symbol.

For the sake of convenience, we use the symbol $D_{\tau }^{\alpha }u(t _{n})=\tau ^{-\alpha }\sum_{k=0}^{n}q_{k}^{(\alpha)}u(x,y,t_{n-k})$ and omit the dependence of $u^{n}(\xi _{i,k}^{x},\xi _{j,l}^{y})$ on $(\xi _{i,k}^{x},\xi _{j,l}^{y})$ in the next equations. By virtue of (3.5) and (3.6), the full-discrete WSGD-OSC scheme for (1.1) consists in finding $\{u_{h}^{n}\}_{n=0}^{K} \subset M_{r}(\pi )$ such that

$$\begin{aligned} D_{\tau }^{\alpha }u_{h}^{n}-K_{\alpha } \Delta u_{h}^{n}+C_{\alpha }u _{h}^{n}=f_{h}^{n},\quad n=0,1,\ldots,K. \end{aligned}$$

(3.10)

4 Stability and convergence analysis of the WSGD-OSC scheme

In this section, we will give the stability and convergence analysis for fully discrete WSGD-OSC scheme (3.10). To this end, we further need the following lemma.

Lemma 4.1

([30])

Let $\{q_{k}^{(\alpha )}\}_{k=0}^{\infty }$ de defined in (3.7). If $\alpha \in (0,\alpha ^{*}]$, then, for any positive integer N and real vector $(v^{0},v^{1},\ldots,v^{N}) \in R^{N+1}$, we have

$$ \sum_{n=0}^{N} \Biggl(\sum _{k=0}^{n}q_{k}^{(\alpha )}v^{n-k} \Biggr)v^{n} \geq 0, $$

where $\alpha ^{*}=0.9569347$.

Theorem 4.1

The fully discrete WSGD-OSC scheme (3.10) is unconditionally stable for sufficiently small $\tau >0$; we have

$$\begin{aligned} C_{\alpha }\tau \sum_{n=0}^{m} \bigl\Vert u_{h}^{n} \bigr\Vert _{M_{r}}^{2} \leq \frac{ \tau }{C_{\alpha }}\sum_{n=0}^{N} \bigl\Vert f_{h}^{n} \bigr\Vert _{M_{r}}^{2},\quad 1\leq m \leq K. \end{aligned}$$

(4.1)

Proof

By using the WSGD operator and making an inner product of (3.10) with $u_{h}^{n}$, we obtain

$$\begin{aligned} \tau ^{-\alpha } \Biggl\langle \sum _{k=0}^{n}q_{k}^{(\alpha)}u_{h}^{n-k},u _{h}^{n} \Biggr\rangle -K_{\alpha } \bigl\langle \Delta u_{h}^{n},u_{h} ^{n} \bigr\rangle +C_{\alpha } \bigl\langle u_{h}^{n},u_{h}^{n} \bigr\rangle = \bigl\langle f_{h}^{n},u_{h}^{n} \bigr\rangle ,\quad n=1,2,\ldots,K. \end{aligned}$$

(4.2)

Note that, from Lemma 2.3, for $v \in M_{r}(\pi )$, there exists a positive constant c such that

$$\begin{aligned} \langle -\Delta v,v \rangle \geq c \Vert \Delta v \Vert ^{2} \geq 0. \end{aligned}$$

(4.3)

Taking (3.10) with $v=u_{h}^{n}$ to the second term on the left hand side (LHS) of (4.2), we have

$$\begin{aligned} -K_{\alpha } \bigl\langle \Delta u_{h}^{n},u_{h}^{n} \bigr\rangle \geq 0. \end{aligned}$$

(4.4)

Summing Eq. (4.2) from $n=0$ to $n=m$ ($0\leq m \leq K$), and then multiplying the resulting equation by 2τ, we obtain

$$\begin{aligned} \begin{aligned}[b] & 2\tau ^{1-\alpha }\sum_{n=0}^{N} \Biggl\langle \sum_{k=0}^{n}q_{\alpha } ^{k}u_{h}^{n-k},u_{h}^{n} \Biggr\rangle -2K_{\alpha }\tau \sum_{n=0} ^{N} \bigl\langle \Delta u_{h}^{n},u_{h}^{n} \bigr\rangle +2C_{\alpha } \tau \sum_{n=0}^{N} \bigl\langle u_{h}^{n},u_{h}^{n} \bigr\rangle \\ &\quad =2 \tau \sum_{n=0}^{N} \bigl\langle f_{h}^{n},u_{h}^{n} \bigr\rangle . \end{aligned} \end{aligned}$$

(4.5)

Taking advantage of the Cauchy–Schwarz inequality to the right hand side (RHS) of (4.5), also using (4.4) and Lemma 4.1, then dropping the first two terms on the LHS of (4.5), we obtain

$$\begin{aligned} 2C_{\alpha }\tau \sum_{n=0}^{m} \bigl\Vert u_{h}^{n} \bigr\Vert _{M_{r}}^{2} \leq \frac{ \tau }{C_{\alpha }}\sum_{n=0}^{m} \bigl\Vert f_{h}^{n} \bigr\Vert _{M_{r}}^{2}+C_{\alpha } \tau \sum_{n=0}^{m} \bigl\Vert u_{h}^{n} \bigr\Vert _{M_{r}}^{2}, \quad 1 \leq m \leq K, \end{aligned}$$

(4.6)

by moving $C_{\alpha }\tau \sum_{n=0}^{m}\Vert u_{h}^{n}\Vert _{M _{r}}^{2}$ to the LHS and combining them, we obtain

$$\begin{aligned} C_{\alpha }\tau \sum_{n=0}^{m} \bigl\Vert u_{h}^{n} \bigr\Vert _{M_{r}}^{2} \leq \frac{ \tau }{C_{\alpha }}\sum_{n=0}^{N} \bigl\Vert f_{h}^{n} \bigr\Vert _{M_{r}}^{2},\quad 1\leq m \leq K. \end{aligned}$$

 □

We get as a result Theorem 4.1.

Theorem 4.2

Suppose u is the exact solution of (1.1)–(1.3), and $u_{h}^{n}(0\leq n \leq K)$ is the solution of the problem (3.10) with $u_{h}^{0}=W^{0}$. If the hypotheses of Lemma 3.4 are satisfied and if $u, {_{0}^{RL}} D_{t}^{\alpha }u\in L^{\infty }(H ^{r+3})$, then there exists a positive constant C, independent of h and τ such that

$$\begin{aligned} \frac{C_{\alpha }}{4}\tau \sum_{n=1}^{N} \bigl\Vert u(t_{n})-u_{h}^{n} \bigr\Vert ^{2} &\leq CTh^{2r+2} \bigl[ \Vert u \Vert _{H^{r+3}}^{2}+ \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha }u \bigr\Vert _{H^{r+3}}^{2} \bigr] \\ &\quad{} +C_{u}T\tau ^{6} \bigl\Vert \mathscr{F} \bigl[{_{0}^{RL}}D_{t}^{\alpha +3}u \bigr]( \omega ) \bigr\Vert _{L^{1}(H^{0})}^{2}, \quad 0\leq N\leq K. \end{aligned}$$

(4.7)

Proof

With W defined in (2.1), we set

$$\begin{aligned} \eta ^{n}=u^{n}-W^{n}, \quad\quad \zeta ^{n}=u_{h}^{n}-W^{n}, \quad 0 \leq n \leq K, \end{aligned}$$

(4.8)

thus we have

$$\begin{aligned} u^{n}-u_{h}^{n}=\eta ^{n}-\zeta ^{n}. \end{aligned}$$

(4.9)

Because the estimate of $\eta ^{n}$ are provided by Lemma 2.1 and 2.2, it is sufficient to bound $\zeta ^{n}$, then we use the triangle inequality to bound $u^{n}-u _{h}^{n}$. Firstly, from (1.1), (2.1), (3.8) and (4.9), then $v\in M_{r}(\pi )$, we obtain

$$\begin{aligned} \bigl\langle { _{0}^{C}}D_{\tau }^{\alpha } \zeta ^{n} , v \bigr\rangle -K_{\alpha } \bigl\langle \Delta \zeta ^{n},v \bigr\rangle +C_{\alpha } \bigl\langle \zeta ^{n},v \bigr\rangle &= \bigl\langle { _{0}^{C}}D_{ \tau }^{\alpha } \eta ^{n}, v \bigr\rangle +C_{\alpha } \bigl\langle \eta ^{n},v \bigr\rangle \\ &\quad{} + \bigl\langle R^{n},v \bigr\rangle , \quad 0 \leq n \leq K, \end{aligned}$$

(4.10)

by using Lemma 3.4

$$\begin{aligned} \bigl\vert R^{n} \bigr\vert \leq c_{u} \Vert \mathscr{F} \bigl[{_{0}^{RL}}D_{t}^{\alpha +3}u \bigr]( \omega )\Vert _{L^{1}}\tau ^{3}. \end{aligned}$$

(4.11)

Taking $v=\zeta ^{n}$ in (4.10), we have

$$\begin{aligned} \begin{aligned}[b] &\tau ^{-\alpha } \Biggl\langle \sum_{k=0}^{n}q_{\alpha }^{k} \zeta ^{n-k}, \zeta ^{n} \Biggr\rangle -K_{\alpha } \bigl\langle \Delta \zeta ^{n},\zeta ^{n} \bigr\rangle +C_{\alpha } \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}}^{2} \\ &\quad = \bigl\langle { _{0}^{C}}D_{t}^{\alpha } \eta ^{n}, \zeta ^{n} \bigr\rangle +C_{\alpha } \bigl\langle \eta ^{n},\zeta ^{n} \bigr\rangle + \bigl\langle R^{n},\zeta ^{n} \bigr\rangle , \quad 0 \leq n \leq K, \end{aligned} \end{aligned}$$

(4.12)

using Lemma 2.2 and the Young inequality, the second term in the RHS of (4.12) can be bounded as

$$\begin{aligned} C_{\alpha } \bigl\langle \eta ^{n},\zeta ^{n} \bigr\rangle &\leq C_{ \alpha } \bigl\Vert \eta ^{n} \bigr\Vert _{M_{r}}\cdot \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}} \\ &\leq C_{\alpha }Ch^{2r+2} \Vert u \Vert _{H^{r+3}}^{2}+\frac{C_{\alpha }}{4} \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}}^{2}. \end{aligned}$$

(4.13)

Applying the Young inequality and (4.11), the last term in (4.12) can be estimated as

$$\begin{aligned} \bigl\langle R^{n},\zeta ^{n} \bigr\rangle &\leq \frac{1}{C_{\alpha }} \bigl\Vert R^{n} \bigr\Vert ^{2}+ \frac{C_{\alpha }}{4} \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}}^{2} \\ &\leq \frac{1}{C_{\alpha }}C_{u}\tau ^{6} \Vert \mathscr{F} \bigl[{_{0}^{RL}}D _{t}^{\alpha +3}u \bigr](\omega )\Vert _{L^{1}(H^{0})}^{2}+ \frac{C_{ \alpha }}{4}\Vert \zeta ^{n}\Vert _{M_{r}}^{2}. \end{aligned}$$

(4.14)

Finally, in order to estimate the first term on the RHS of (4.12), we first define a new elliptic projection W̃ of the exact solution u by $\widetilde{W}:[0,T]\rightarrow M_{r}(\pi )$ by

$$\begin{aligned} \Delta {_{0}^{RL}}D_{t}^{\alpha }u-\Delta \widetilde{W}=0 \quad \text{on } \mathcal{G} \times [0,T], \end{aligned}$$

(4.15)

then, from Theorem 3.4 in [46], it follows that

$$\begin{aligned} \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha }u- \widetilde{W} \bigr\Vert \leq Ch^{r+1} \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha }u \bigr\Vert _{H^{r+3}}, \end{aligned}$$

(4.16)

by introducing ρ defined by

$$\begin{aligned}& -\Delta \rho ={_{0}^{RL}}D_{t}^{\alpha } W- \widetilde{W}, \quad \text{in } \varOmega \times [0,T], \\ & \rho =0, \quad \text{on } \partial \varOmega \times [0,T]. \end{aligned}$$

According to the proof of Lemma 3.5 in [34], and a straightforward modification of the argument given in the proof of Theorem 2.1 of [47], we can obtain

$$\begin{aligned} \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha }W- \widetilde{W} \bigr\Vert \leq Ch^{r+1} \bigl( \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha }u \bigr\Vert _{H^{r+2}}+ \Vert u \Vert _{H^{r+2}} \bigr), \end{aligned}$$

(4.17)

using the triangle inequality and combining (4.16) and (4.17), we can obtain

$$\begin{aligned} \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha }u-{_{0}^{RL}}D_{t}^{\alpha }W \bigr\Vert \leq Ch^{r+1} \bigl( \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha }u \bigr\Vert _{H^{r+3}}+ \Vert u \Vert _{H^{r+2}} \bigr). \end{aligned}$$

(4.18)

Since $D^{\alpha }_{\tau }\eta ^{n}={_{0}^{RL}}D_{t}^{\alpha }\eta ^{n}+\mathscr{O}(\tau ^{3})$, using (4.18), it gives

$$\begin{aligned} & \bigl\langle D^{\alpha }_{\tau }\eta ^{n}, \zeta ^{n} \bigr\rangle \\ &\quad \leq \bigl\Vert D^{\alpha }_{\tau }\eta ^{n} \bigr\Vert _{M_{r}} \cdot \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}} \\ &\quad \leq \frac{1}{C_{\alpha }} \bigl\Vert D^{\alpha }_{\tau }\eta ^{n} \bigr\Vert _{M_{r}} ^{2}+\frac{C_{\alpha }}{4} \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}}^{2} \\ & \quad \leq \frac{1}{C_{\alpha }} \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha } \eta ^{n}+\mathscr{O} \bigl(\tau ^{3} \bigr) \bigr\Vert _{M_{r}}^{2}+\frac{C_{\alpha }}{4} \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}}^{ 2} \\ &\quad \leq \frac{1}{C_{\alpha }} \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha }u^{n}-{_{0}^{RL}}D_{t}^{\alpha }W^{n} \bigr\Vert _{M_{r}}^{2} +C_{u}\tau ^{6}+\frac{C_{\alpha }}{4} \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}}^{2} \\ &\quad \leq \frac{1}{C_{\alpha }} Ch^{2r+2} \bigl( \bigl\Vert {_{0}^{RL}}D_{t} ^{\alpha }u \bigr\Vert _{H^{r+3}}^{2}+ \Vert u \Vert _{H^{r+2}}^{2} \bigr)+C _{u}\tau ^{6}+\frac{C_{\alpha }}{4} \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}}^{2}. \end{aligned}$$

(4.19)

Substituting (4.13)–(4.14) and (4.19) in (4.12), then summing (4.12) from $n=0$ to $n=m (1\leq m\leq K)$, and using Lemma 2.3 and Lemma 4.1, we obtain

$$\begin{aligned} &\frac{C_{\alpha }}{4}\tau \sum_{n=1}^{m} \bigl\Vert \zeta ^{n} \bigr\Vert _{M_{r}}^{2} \\ &\quad \leq \biggl(C_{\alpha }+\frac{1}{C_{\alpha }} \biggr)Ch^{2r+2} \tau \sum_{n=1} ^{m} \bigl( \Vert u \Vert _{H^{r+3}}^{2}+ \bigl\Vert {_{0}^{RL}}D_{t}^{\alpha }u \bigr\Vert _{H^{r+3}}^{2} \bigr) \\ &\quad\quad{} +\frac{1}{C_{\alpha }}C_{u}\tau \sum _{n=1}^{m}\tau ^{6}\Vert \mathscr{F} \bigl[{_{0}^{RL}}D_{t}^{\alpha +3}u \bigr](\omega )\Vert _{L^{1}(H ^{0})}^{2}. \end{aligned}$$

(4.20)

Therefore, using the triangle inequality and Lemmas 2.1–2.2 and 2.4, (4.20) then yields the desired result. □

5 Description of the WSGD-OSC scheme

It can be seen from the fully discrete scheme (3.10) that we need to solve a partial differential equation with two variables at each time level, that is,

$$\begin{aligned} \tau ^{-\alpha }\sum_{k=0}^{n}q_{k}^{(\alpha )}u_{h}^{n-k}-K_{\alpha } \Delta u_{h}^{n}+C_{\alpha }u_{h}^{n}=f_{h}^{n},\quad n=1,\ldots,K. \end{aligned}$$

(5.1)

We denote $\alpha _{0}=\frac{\tau ^{\alpha }}{q_{0}^{(\alpha )}}$, $\beta _{0}=\frac{-1}{q_{0}^{(\alpha )}}$, then the above equation can be rewritten as

$$\begin{aligned} (1+C_{\alpha }\alpha _{0})u_{h}^{n}-K_{\alpha } \alpha _{0}\Delta u_{h} ^{n} =\beta _{0}\sum_{k=1}^{n}q_{k}^{(\alpha )}u_{h}^{n-k}+ \alpha _{0}f _{h}^{n}, \quad n=1,\ldots,K. \end{aligned}$$

(5.2)

For implementing the numerical schemes, we usually first represent $u_{h}^{n}$ by the base functions of $M_{r}(\pi )$, then solve the coefficients of the representation formula. More concretely, letting

$$ M_{r}(\pi _{x})=\operatorname{span}\{\varPhi _{1},\varPhi _{2},\ldots,\varPhi _{M_{x}-1}, \varPhi _{{M_{x}}}\}, \quad\quad M_{r}(\pi _{y})=\operatorname{span}\{ \varPsi _{1},\varPsi _{2},\ldots, \varPsi _{M_{y}-1}, \varPsi _{M_{y}}\}, $$

then

$$ u_{h}^{n}(x,y)=\sum_{j=1}^{M_{y}} \sum_{i=1}^{M_{x}}{\hat{u}^{n}_{i,j}} \varPhi _{i}(x)\varPsi _{j}(y), $$

where $\{{\hat{u}^{n}_{i,j}}\}_{i,j=1}^{M_{x},M_{y}}$ are unknown coefficients to be determined. Setting

$$ \hat{\mathbf{u}}= \bigl[{\hat{u}^{n}_{1,1}},{ \hat{u}^{n}_{1,2}},\ldots, {\hat{u}^{n}_{1,M_{y}}},{ \hat{u}^{n}_{2,1}},{\hat{u}^{n}_{2,2}}, \ldots,{\hat{u}^{n}_{M_{x},M_{y}}} \bigr]^{T} $$

then Eq. (5.1) can be represented in the form of matrix tensor product (Kronecker product)

$$\begin{aligned} \begin{aligned}[b] & \bigl\{ (1+C_{\alpha }\alpha _{0}) \bigl(B^{x}\otimes B^{y} \bigr)+K_{\alpha }\alpha _{0} \bigl(A^{x} \otimes B^{y}+B^{x}\otimes A^{y} \bigr) \bigr\} \hat{ \mathbf{u}}^{n} \\ &\quad = \bigl(B^{x}\otimes B^{y} \bigr)\sum _{k=1}^{n} q_{k}^{(\alpha )} \hat{ \mathbf{u}}^{n-k}+\alpha _{0}\mathbf{F}^{n},\end{aligned} \end{aligned}$$

(5.3)

where

$$\begin{aligned} \begin{aligned} A^{x}= \bigl(a_{i,j}^{x} \bigr)_{i,j=1}^{M_{x}},\quad\quad a_{i,j}^{x}=- \varPhi _{j}^{\prime \prime } \bigl(\xi _{i}^{x} \bigr),\quad\quad B^{x}= \bigl(b_{i,j}^{x} \bigr)_{i,j=1}^{M_{x}},\quad\quad b_{i,j}^{x}= \varPhi _{j} \bigl(\xi _{i}^{x} \bigr), \\ A^{y}= \bigl(a_{i,j}^{y} \bigr)_{i,j=1}^{M_{y}}, \quad\quad a_{i,j}^{y}=-\varPsi _{j}^{\prime \prime } \bigl(\xi _{i}^{y} \bigr),\quad\quad B^{y}= \bigl(b_{i,j}^{y} \bigr)_{i,j=1}^{M_{y}},\quad \quad b_{i,j}^{y}=\varPsi _{j} \bigl(\xi _{i}^{y} \bigr), \end{aligned} \end{aligned}$$

(5.4)

and

$$\begin{aligned} \mathbf{F}^{n}= \bigl[f^{n} \bigl(\xi _{1}^{x}, \xi _{1}^{y} \bigr),f^{n} \bigl(\xi _{1}^{x},\xi _{2}^{y} \bigr), \ldots,f^{n} \bigl(\xi _{1}^{x},\xi _{M_{y}}^{y} \bigr),f^{n} \bigl(\xi _{2} ^{x},\xi _{1}^{y} \bigr),\ldots,f^{n} \bigl(\xi _{M_{x}}^{x},\xi _{M_{y}}^{y} \bigr) \bigr]^{T}. \end{aligned}$$

(5.5)

The matrix $A^{x}$, $B^{x}$, $A^{y}$ and $B^{y}$ are $M_{x}\times M_{y}$ matrices with the sparse structure,

$$\left[\begin{array}{ccccccc}\times & \times & \times & & & & \\ \times & \times & \times & & & & \\ & \times & \times & \times & \times & & \\ & \times & \times & \times & \times & & \\ & & \ddots & \ddots & \ddots & \ddots & \\ & & & & \times & \times & \times \\ & & & & \times & \times & \times \end{array}\right].$$

(5.6)

We implement the WSGD-OSC scheme in the piecewise Hermite cubic spline space $M_{3}(\pi )$.

It is very natural that we choose cubic Hermite polynomials for satisfying the zero boundary condition. In detail, we choose the basis of cubic Hermite polynomial, namely, for $1\leq i \leq N-1$, it follows that

$$ \phi _{i}(x)= \textstyle\begin{cases} \frac{-2(x-x_{i-1})^{3}}{h^{3}}+\frac{3(x-x_{i-1})^{3}}{h^{2}}, & x _{i-1}\leq x \leq x_{i}, \\ \frac{-2(x-x_{i+1})^{3}}{h^{3}}+\frac{3(x-x_{i+1})^{3}}{h^{2}}, & x _{i}\leq x\leq x_{i+1}, \\ 0, & x< x_{i-1} \text{ or } x> x_{i+1}, \end{cases} $$

(5.7)

and

$$ \psi _{i}(x)= \textstyle\begin{cases} \frac{(x-x_{i-1})^{2}(x-x_{i})}{h^{2}}, & x_{i-1}\leq x \leq x_{i}, \\ \frac{(x-x_{i})(x-x_{i+1})^{2}}{h^{2}}, & x_{i}\leq x \leq x_{i+1}, \\ 0, & x< x_{i-1}\text{ or } x> x_{i+1}. \end{cases} $$

(5.8)

Note that functions $\phi _{i}(x)$, $\psi _{i}(x)$ satisfy the zero boundary conditions $\phi _{i}(0)=\phi _{i}(1)=\psi _{i}(0)=\psi _{i}(1)=0$. Renumber the basis functions; let

$$ \{\psi _{0},\phi _{1},\psi _{1},\phi _{2},\ldots,\phi _{N-1},\psi _{N-1}, \psi _{N}\}=\{\varPhi _{1},\varPhi _{2},\varPhi _{3},\ldots,\varPhi _{2N} \}, $$

then

$$ M_{r}(\pi _{x})=\operatorname{span}\{\varPhi _{1},\varPhi _{2},\varPhi _{3},\ldots,\varPhi _{2N} \},\quad\quad M _{r}(\pi _{y})=\operatorname{span}\{ \varPhi _{1},\varPhi _{2},\varPhi _{3},\ldots, \varPhi _{2N} \}. $$

In order to construct the coefficient matrix of Eqs. (5.3), we need to calculate the values of the basis function at the Gauss point and their second derivatives. Through a calculation, we find the formula for the values of the basis function at the Gauss point and the second derivatives. They are defined as follows:

$$\begin{aligned} \begin{aligned} &H_{1}(u_{j})=(1+2u_{j}) (1-u_{j})^{2},\quad\quad H_{2}(u_{j})=u_{j}(1-u_{j})^{2}h _{k},\\ &H_{3}(u_{j})=u_{j}^{2}(3-2u_{j}), \quad\quad H_{4}(u_{j})=u_{j}^{2}(u_{j}-1)h _{k}, \\ &I_{1}(u_{j})=(12u_{j}-6)/h_{k}^{2}, \quad\quad I_{2}(u_{j})=(6u_{j}-4)/h_{k}, \\&I _{3}(u_{j})=(6-12u_{j})/h_{k}^{2}, \quad\quad I_{4}(u_{j})=(6u_{j}-2)/h_{k}, \end{aligned} \end{aligned}$$

(5.9)

where $u_{1}=(3-\sqrt{3})/6$, $u_{2}=(3+\sqrt{3})/6$. With the above descriptions on the basis function, we give an example of the matrix $B^{x}$ and $A^{x}$ in the case of $N_{m}=5$ and $h_{k}=1/N_{m}$. We have

$$B^x=\left[\begin{array}{cccccccccc}{H}_2(u_1)& H_3(u_1)& H_4(u_1)& 0& 0& 0& 0& 0& 0& 0\\ H_2(u_2)& H_3(u_2)& H_4(u_2)& 0& 0& 0& 0& 0& 0& 0\\ 0& H_1(u_1)& H_2(u_1)& H_3(u_1)& H_4(u_1)& 0& 0& 0& 0& 0\\ 0& H_1(u_2)& H_2(u_2)& H_3(u_2)& H_4(u_2)& 0& 0& 0& 0& 0\\ 0& 0& 0& H_1(u_1)& H_2(u_1)& H_3(u_1)& H_4(u_1)& 0& 0& 0\\ 0& 0& 0& H_1(u_2)& H_2(u_2)& H_3(u_2)& H_4(u_2)& 0& 0& 0\\ 0& 0& 0& 0& 0& H_1(u_1)& H_2(u_1)& H_3(u_1)& H_4(u_1)& 0\\ 0& 0& 0& 0& 0& H_1(u_2)& H_2(u_2)& H_3(u_2)& H_4(u_2)& 0\\ 0& 0& 0& 0& 0& 0& 0& H_1(u_1)& H_2(u_1)& H_4(u_1)\\ 0& 0& 0& 0& 0& 0& 0& H_1(u_2)& H_2(u_2)& H_4(u_2)\end{array}\right],$$

(5.10)

$$A^x=\left[\begin{array}{cccccccccc}{I}_2(u_1)& I_3(u_1)& I_4(u_1)& 0& 0& 0& 0& 0& 0& 0\\ I_2(u_2)& I_3(u_2)& I_4(u_2)& 0& 0& 0& 0& 0& 0& 0\\ 0& I_1(u_1)& I_2(u_1)& I_3(u_1)& I_4(u_1)& 0& 0& 0& 0& 0\\ 0& I_1(u_2)& I_2(u_2)& I_3(u_2)& I_4(u_2)& 0& 0& 0& 0& 0\\ 0& 0& 0& I_1(u_1)& I_2(u_1)& I_3(u_1)& I_4(u_1)& 0& 0& 0\\ 0& 0& 0& I_1(u_2)& I_2(u_2)& I_3(u_2)& I_4(u_2)& 0& 0& 0\\ 0& 0& 0& 0& 0& I_1(u_1)& I_2(u_1)& I_3(u_1)& I_4(u_1)& 0\\ 0& 0& 0& 0& 0& I_1(u_2)& I_2(u_2)& I_3(u_2)& I_4(u_2)& 0\\ 0& 0& 0& 0& 0& 0& 0& I_1(u_1)& I_2(u_1)& I_4(u_1)\\ 0& 0& 0& 0& 0& 0& 0& I_1(u_2)& I_2(u_2)& I_4(u_2)\end{array}\right].$$

(5.11)

It is well known from the tensor product calculation results that the WSGD-OSC scheme requires the solution of an almost block diagonal linear system at each time step. This system can be solved efficiently using the software package COLROW [41].

6 Numerical experiments

In this section, several numerical examples are given to illustrate our theoretical analysis. In our implementations, we adopt the space of piecewise Hermite cubic with the standard value and scaled slope basis functions [48] on uniform partitions of I̅ in both the x and y directions with $N_{x}=N_{y}=N$. The forcing term $f(x,y,t)$ is approximated by the piecewise Hermite interpolant projection in the Gauss collocation point. In order to check the accuracy of the proposed method, we present the $L_{\infty }$ and $L_{2}$ errors at $T=1$ and the corresponding rates of convergence defined by

$$ \text{Convergence rate} \approx \frac{\log (e_{m}/e_{m+1})}{\log (h_{m}/h _{m+1})}, $$

where $h=1/N_{m}$ is the time step size with $N=N_{m}$, and $e_{m}$ is the norm of the corresponding error.

Example 1

As the first example, we consider the following one-dimensional fractional reaction–subdiffusion equation:

$$\begin{aligned}& {_{0}^{c}}D^{\alpha }_{t}u(x,t) = \frac{\partial ^{2}u(x,t)}{\partial x ^{2}}-u(x,t)+f(x,t),\quad 0< x< 1,0< t\leq 1, \\& u(x,0) =0,\quad 0\leq x\leq 1, \\& u(0,t) =0,u(1,t)=0,\quad 0\leq t\leq 1, \end{aligned}$$

(6.1)

where $f(x,t)=(\frac{\varGamma (4)}{\varGamma {(4-\alpha )}}t^{3-\alpha }+t ^{3})x^{2}(1-x)^{2}e^{x}-t^{3}e^{x}(2-8x+x^{2}+6x^{3}+x^{4})$. The analytical solution of this equation is $u(x,t)=t^{3}x^{2}(1-x)^{2}e ^{x}$.

Firstly, we take the fixed space $h=1/1000$, which is sufficiently small for the error to be dominated by the time discretization of the method. Table 1 presents the $L_{\infty }$ and $L_{2}$ errors and the corresponding convergence orders of the WSGD-OSC scheme for $\alpha \in (0,1)$. We observe that our scheme generates the temporal accuracy with the order 3. Table 2 shows that our scheme has the accuracy of 4 in spatial direction, where the temporal step size $\tau =1/1000$ is fixed. The numerical solution and the global error for $\alpha =0.5$, $h=1/32$, $\tau =1/32$ are shown in Fig. 1.

Figure 1

Numerical solution (a) and global error (b) for Example 1 with $\alpha =0.5$, $h=1/32$, $\tau =1/32$

Table 1 The $L_{\infty }$, $L_{2}$ errors and temporal convergence orders with $h = 1/1000$ for Example 1

Table 2 The $L_{\infty }$, $L_{2}$ errors and spatial convergence orders with $\tau = 1/1000$ for Example 1

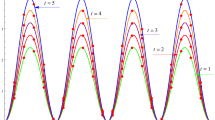
We take Problem 1 as an example to test the effectiveness of the proposed the proposed method for larger final time; the exact solution and the numerical solution are plotted using $h=1/100$, $\tau =1/100$ in Fig. 2 when $\alpha =0.5$, $T=10,50,100$. The corresponding absolute errors are also plotted in Fig. 2. It is clear from Fig. 2 that the numerical solution is highly consistent with the exact solution, which indicates that the proposed method is very effective.

Figure 2

The exact solution and numerical solution at different time ($T=10,50,100$) with $\alpha =0.5$, $h=1/100$, $\tau =1/100$ and corresponding error for Example 1. Dotted line: numerical solution, solid line: exact solution

Example 2

Consider the following two-dimensional fractional reaction–subdiffusion equation:

$$\begin{aligned}& {_{0}^{c}}D^{\alpha }_{t}u(x,y,t)-\Delta u(x,y,t)+u(x,y,t)=f(x,y,t), \\& u(x,y,0)=0,\quad (x,y)\in \varOmega , \\& u(x,y,t)=0,\quad (x,y,t)\in \partial \varOmega \times (0,T], \end{aligned}$$

(6.2)

where $\varOmega =[0,1]\times [0,1]$, $T=1$, $f(x,y,t)= [ \frac{ \varGamma (4)}{\varGamma (4-\alpha )}t^{-\alpha }(1-x)(1-y)-(3x+3y+xy-7) ]t^{3}xye^{x+y}$. The exact solution of the equation is $u(x,y,t)=t^{3}xy(1-x)(1-y)e^{x+y}$.

In order to test the temporal accuracy of the proposed method, we choose $\tau =h$ to avoid contamination of the spatial error. The maximum $L_{\infty }$, $L_{2}$ errors and temporal convergence orders are shown in Table 3. To check the convergence order in space, the time step τ and space step h are chosen such that $\tau ^{3}\approx h ^{4}$ as in [49], and $\alpha =0.1,0.3,0.5,0.7,0.9$. Table 4 lists the maximum $L_{\infty }$, $L_{2}$ errors and spatial convergence orders. The results in Tables 3 and 4 demonstrate the expected convergence rates of order 3 in time and order 4 in space simultaneously. The numerical solution and the global error at $T=1$ with $\alpha =0.7$, $h=1/32$, $\tau =1/32$ are shown in Fig. 3.

Figure 3

Numerical solution (a) and global error (b) for Example 2 with $\alpha =0.7$ at $T=1$ ($h=1/32$, $\tau =1/32$)

Table 3 The $L_{\infty }$, $L_{2}$ errors and temporal convergence orders for Example 2

Table 4 The $L_{\infty }$, $L_{2}$ errors and spatial convergence orders for Example 2

Example 3

Consider the following two-dimensional fractional reaction–subdiffusion equation:

$$\begin{aligned}& {_{0}^{c}}D^{\alpha }_{t}u(x,y,t)-\Delta u(x,y,t)+u(x,y,t)=f(x,y,t), \\& u(x,y,0)=0,\quad (x,y)\in \varOmega , \\& u(x,y,t)=0,\quad (x,y,t)\in \partial \varOmega \times (0,T], \end{aligned}$$

(6.3)

where $\varOmega =[0,1]\times [0,1]$, $T=1$, $f(x,y,t)= (\frac{\varGamma (3+\alpha )}{2}+t^{\alpha } )t^{2}xy(1-x)(1-y)+t^{2+\alpha }2x(1-x)+t ^{2+\alpha }2y(1-y)$. The exact solution of the equation is $u(x,y,t)=t^{2+\alpha }xy(1-x)(1-y)$.

Similar to the selection of parameters in Example 2, Tables 5 and 6 list the maximum $L_{\infty }$, $L_{2}$ errors and convergence orders, respectively. The similar convergence rates in time and space are also obtained. Just as we hope, the convergence order of all numerical results match that of the theoretical analysis. Numerical solution and global error at $T=1$ with $\alpha =0.9$, $h=1/32$, $\tau =1/32$ are shown in Fig. 4.

Figure 4

Numerical solution (a) and global error (b) for Example 3 with $\alpha =0.9$ at $T=1$ ($h=1/32$, $\tau =1/32$)

Table 5 The $L_{\infty }$, $L_{2}$ errors and temporal convergence orders for Example 3

Table 6 The $L_{\infty }$, $L_{2}$ errors and spatial convergence orders for Example 3

Example 4

Finally, we consider the following one-dimensional fractional reaction–subdiffusion equation with Neumann boundary value condition [4]:

$$\begin{aligned}& {_{0}^{c}}D^{\alpha }_{t}u(x,t) = \frac{\partial ^{2}u(x,t)}{\partial x ^{2}}-u(x,t)+f(x,t), \quad 0< x< 1,0< t\leq 1, \\& u(x,0) =0,\quad 0\leq x\leq 1, \\& \frac{\partial {u}(0,t)}{\partial x} =0,\quad\quad \frac{\partial {u}(1,t)}{ \partial x}=0,\quad 0\leq x\leq 1, \end{aligned}$$

(6.4)

where $f(x,t)=\frac{\varGamma (3+\alpha )}{2}t^{2}x^{2}(1-x)^{2}+t^{2+ \alpha }(x^{4}-2x^{3}-11x^{2}+12x-2)$. The analytical solution of this equation is $u(x,t)=t^{2+\alpha }x^{2}(1-x)^{2}$.

To further verify our proposed method, we consider the one-dimensional fractional reaction–subdiffusion equation with Neumann boundary value condition. We take the fixed space step $h=1/1000$ as in [4] to test the convergence rate in time. Table 7 displays the $L_{\infty }$ and $L_{2}$ errors and the corresponding convergence orders in time for some $\alpha \in (0,1)$ and the last four columns present the numerical results obtained in [4]. From Table 7, we find that the proposed method shows better performance than that in [4] for this example, since we adopt a higher-order approximation for the time derivative. In order to investigate the spatial convergence rate, we choose $\tau =1/1000$ and list the $L_{\infty }$ and $L_{2}$ errors and corresponding convergence orders in Table 8. Once again, the expected convergence rates with third-order accuracy in the time direction and fourth-order accuracy in the spatial direction can be seen from two tables. Besides, Fig. 5 shows a comparison of the numerical solution and the exact solution for $\alpha =0.8$ at $t=1$. The numerical solution surface is shown in Fig. 6, and the errors are also displayed in Fig. 7, where $\alpha =0.8$ and $h=\tau =\frac{1}{32}$.

Figure 5

The comparison (a) and absolute error (b) between the numerical solution and the exact solution with $\alpha =0.8$ at $t=1$ ($h=1/32$, $\tau =1/32$)

Figure 6

The global error for Example 4 with $\alpha =0.8$, $h=1/32$, $\tau =1/32$

Figure 7

Exact solution (a) and numerical solution (b) for Example 4 with $\alpha =0.8$, $h=1/32$, $\tau =1/32$

Table 7 The $L_{\infty }$, $L_{2}$ errors and temporal convergence order with $h = 1/1000$ for Example 4

Table 8 The $L_{\infty }$, $L_{2}$ errors and spatial convergence orders with $\tau = 1/1000$ for Example 4

7 Conclusion

In this paper, a discrete orthogonal spline collocation method combining with a third-order approximation for the fractional derivative in time is proposed for solving the two-dimensional fractional reaction–subdiffusion equation. The stability and convergence of the method have been strictly proved. Several numerical examples are given to demonstrate the effectiveness and convergence orders of the proposed method. In future work, we wish to extend the present OSC methods with a third-order convergent alternating direct implicit scheme in the time direction to solve this kind of problems.