1 Introduction

The purpose of this work is to provide the finite difference scheme from an applied point of view. Much more emphasis is put into solution methods rather than to analysis of the theoretical properties of the equations; therefore, in this paper we will try to apply the mean square and mean fourth calculus in order to find the stability condition for the random process solution of the following random problem:

$$ \textstyle\begin{cases} u_{t} + \beta u_{x} = \alpha u_{xx},\quad t \in[0, \infty) , -\infty< x < \infty, \\ u(x,0)= u_{0}(x), \end{cases} $$
(1)

where β is a random variable, α is a constant, t is a time variable, x is the space coordinate and \(u_{t}\), \(u_{x}\) are the partial derivatives with respect to t and x, respectively. Also, \(u_{0}(x)\) is an initial data function which is taken to be deterministic.

Many papers have studied stochastic partial differential equations by using the Brownian motion process [1,2,3] also, with a random potential [3]. In this work we try to develop the convection–diffusion problem from the deterministic case to the random case by dealing with random coefficients. Our model is applied to a membrane containing pores or channels lined with positive fixed charges acting as a barrier between intracellular and extracellular compartments filled with electrolyte solutions. In the pollutants, solute transport from a source through a random medium of air or water is characterized by a parabolic stochastic partial differential equation derived on the principle of conservation of mass; it is known as stochastic advection–diffusion equation (SADE). There are many articles that have studied some stochastic partial differential equations by using finite difference method [4,5,6,7,8]. The motivation in this paper is to prove the consistency and stability by using the relation between the 2-norm and the 4-norm.

The rest of the paper is given as follows: In Sect. 2,we describe the random difference scheme method. In Sect. 3, we prove that our difference scheme is consistent in mean square and mean fourth with the advection–diffusion model, Additionally, in Sect. 4, we will find the stability condition in mean square and mean fourth for the random difference scheme. In Sect. 5, we present some case studies. Finally, in Sect. 6, we give a summary of our contribution.

2 The description of the random finite difference technique

Firstly, for applying the finite difference technique for the approximation solutions of our problem (1), we discretize the space and the time by finite increasing sequences as follows: the grid points for the space are to be taken as \(a = x_{0} < x_{1} < x_{2} < x_{3} < \cdots< x_{k} = b\). Also, the time points are to be taken as \(0 = t_{0} < t_{1} < t_{2} < t_{3} < \cdots< t_{n} = \infty\). Suppose that the grid cells for the space is \(\Delta x = (x_{k} - x_{k-1})\) for \(k \geqslant1\) with time steps \(\Delta t = (t_{n} - t_{n-1})\) for \(t \geqslant1\). Suppose \(u_{k}^{n} = u(k \Delta x ,n \Delta t)\) approximates the exact solution for the problem (1) as, \(u(x,t)\) at the point \((k \Delta x ,n \Delta t)\). To formulate the difference scheme according to the problem (1), we replace the first and second derivative in (1) by difference formulas as follows:

  • The first-order approximation to \(u_{t}\) is

    $$ u_{t}(k\Delta x,n\Delta t) \approx\frac{u_{k}^{n+1} - u_{k}^{n}}{\Delta t}. $$

  • The first-order approximation to \(u_{x}\) is

    $$ u_{x}(k\Delta x,n\Delta t) \approx\frac{u_{k+1}^{n} - u_{k}^{n}}{\Delta x}. $$

  • The second-order approximation to \(u_{xx}\) is

    $$ u_{xx}(k\Delta x,n\Delta t)\approx\frac {u_{k+1}^{n}-2u_{k}^{n}+u_{k-1}^{n}}{(\Delta x)^{2}}; $$

by substituting in (1), we get the random difference scheme

$$ \textstyle\begin{cases} u_{k}^{n+1}=(1 + r \beta\Delta x -2 r \alpha)u_{k}^{n} + (r \alpha- r \beta\Delta x)u_{k+1}^{n} + r \alpha u_{k-1}^{n}, \\ u_{k}^{0} =u_{0}(k\Delta x)=u_{0}(x_{k}) , \\ r=\frac{\Delta t}{(\Delta x)^{2}},\qquad t_{n}=n\Delta t \quad \mbox{and}\quad x_{k}=k\Delta x. \end{cases} $$
(2)

3 Consistency in mean square and mean fourth

For a random finite difference scheme (RFDS) \(L_{k}^{n} u_{k}^{n} = V_{k}^{n}\) that approximates the random partial differential equation (RPDE) \(Lu=V\) to be consistent under the mean square sense at time \(t = (n+1)\Delta t\), for any smooth function \(\varphi=\varphi ( x,t )\), we have in mean square

$$ E \bigl[ \bigl\vert ( L\varphi-G ) _{k}^{n}- \bigl(L_{k}^{n}\varphi (k\Delta x,n\Delta t ) -G_{k}^{n}\bigr) \bigr\vert ^{2} \bigr] \rightarrow0, $$
(3)

as \(\Delta t\rightarrow0\), \(\Delta x\rightarrow0 \) and \((k \Delta x ,n \Delta t) \rightarrow(x,t)\).

Theorem 1

The RFDS (2) defined by (1) is a consistent scheme in mean square area: \(\Delta t \rightarrow0\), \(\Delta x \rightarrow0\) and \((k \Delta x ,n \Delta t) \rightarrow(x,t)\).

Proof

$$\begin{aligned}& \begin{aligned} L(\varphi)_{k}^{n} &= \frac{\varphi(k \Delta x, (n+1) \Delta t)-\varphi (k \Delta x, n\Delta t)}{\Delta t} + \beta\frac{\varphi((k+1) \Delta x, n\Delta t)-\varphi(k \Delta x, n\Delta t)}{\Delta x} \\ &\quad {}- \alpha \int_{n \Delta t}^{(n+1) \Delta t}\varphi_{xx}(k \Delta x,s) \,ds, \end{aligned} \\& \begin{aligned} L_{k}^{n}\varphi(k\Delta x,n\Delta t) &= \frac{\varphi(k \Delta x, (n+1) \Delta t)-\varphi(k \Delta x, n\Delta t)}{\Delta t} \\ &\quad {}+ \beta\frac {\varphi((k+1) \Delta x, n\Delta t)-\varphi(k \Delta x, n\Delta t)}{\Delta x} \\ &\quad {}- \alpha\frac{\varphi((k+1) \Delta x, n \Delta t)-2 \varphi(k \Delta x, n\Delta t) + \varphi((k-1) \Delta x, n\Delta t)}{(\Delta x)^{2}}. \end{aligned} \end{aligned}$$

Then

$$\begin{aligned} E \bigl[ \bigl\vert L ( \varphi )_{k}^{n}-L_{k}^{n} ( \varphi ) \bigr\vert ^{2} \bigr] &= E\biggl[ \biggl\vert \alpha \frac{\varphi((k+1) \Delta x, n \Delta t)-2 \varphi(k \Delta x, n\Delta t) + \varphi((k-1) \Delta x, n\Delta t)}{(\Delta x)^{2}} \\ &\quad {}- \alpha \int_{n \Delta t}^{(n+1) \Delta t}\varphi_{xx}(k \Delta x,s)\,ds \biggr\vert ^{2}\biggr]. \end{aligned}$$

From the Taylor expansion, the second derivative is

$$ \frac{\varphi((k+1) \Delta x, n \Delta t)-2 \varphi(k \Delta x, n\Delta t) + \varphi((k-1) \Delta x, n\Delta t)}{(\Delta x)^{2}} = \frac{\partial^{2} \varphi(k \Delta x, n\Delta t)}{\partial x^{2}} + \mathcal{O} \bigl((\Delta x)^{2} \bigr). $$

Then we have

$$ E \bigl[ \bigl\vert L ( \varphi )_{k}^{n}-L_{k}^{n} ( \varphi ) \bigr\vert ^{2} \bigr] = E\biggl[\biggl\vert \alpha\frac{\partial^{2} \varphi(k \Delta x, n\Delta t)}{\partial x^{2}} + \mathcal{O} \bigl((\Delta x)^{2} \bigr)- \alpha \int_{n \Delta t}^{(n+1) \Delta t}\varphi_{xx}(k \Delta x,s)\,ds \biggr\vert ^{2}\biggr]. $$

As \(\Delta t \rightarrow0\), \(\Delta x \rightarrow 0\) and \((k \Delta x, n\Delta t) \rightarrow(x,t) \),

$$ E \bigl[ \bigl\vert ( L\varphi-G ) _{k}^{n}- \bigl(L_{k}^{n}\varphi (k\Delta x,n\Delta t ) -G_{k}^{n}\bigr) \bigr\vert ^{2} \bigr] \rightarrow0. $$

Thus we have, the RFDS (2) is a mean square consistent as \(\Delta x , \Delta t\rightarrow0\) and \((k \Delta x ,n \Delta t) \rightarrow(x,t)\). □

4 Stability in mean square and mean fourth

The RFDS \(L_{k}^{n} u_{k}^{n} = V_{k}^{n}\) that approximates RPDE \(Lu=V\) is stable in mean square, if, for the constants \(\epsilon>0\), \(\delta>0\), and non-negative constants η, ξ and \(u^{0}\) an initial data, we have

$$ {E} \bigl[ \bigl\vert u^{n+1} \bigr\vert ^{2} \bigr] \leq\eta e^{\xi t}{E} \bigl[ \bigl\vert u^{0} \bigr\vert ^{2} \bigr], $$
(4)

for all, \(t=(n+1)\Delta t \), \(0< \Delta x \leq\epsilon\), \(0< \Delta t \leq\delta\).

Theorem 2

The RFDS (2) defined by (1) under the conditions:

  1. 1.

    \(\Delta t \rightarrow0\), Δx is fixed,

  2. 2.

    β is positive random variable,

  3. 3.

    \(E[\vert\beta\vert^{4}] < \infty\) (fourth-order random variable),

  4. 4.

    \(u^{0}\) is a deterministic initial data,

is to be mean square stable.

Proof

Here

$$\begin{aligned}& u_{k}^{n+1}=(1+r \beta\Delta x-2r\alpha)u_{k}^{n}+(r \alpha-r \beta \Delta x)u_{k+1}^{n}+r \alpha u_{k-1}^{n}, \\& E\bigl[ \bigl\vert u_{k}^{n+1} \bigr\vert ^{2} \bigr]=E\bigl[ \bigl\vert (1+r \beta\Delta x-2r\alpha )u_{k}^{n}+(r \alpha-r \beta\Delta x)u_{k+1}^{n}+r \alpha u_{k-1}^{n} \bigr\vert ^{2}\bigr]. \end{aligned}$$

Also since

$$ E\bigl[ \vert X+Y \vert ^{2}\bigr]\leqslant\bigl[\sqrt{E\bigl( \vert X \vert ^{2}\bigr)}+\sqrt {E\bigl( \vert Y \vert ^{2}\bigr)}\bigr]^{2}, $$

we have

$$\begin{aligned} E\bigl[ \bigl\vert u_{k}^{n+1} \bigr\vert ^{2} \bigr] \leqslant& E\bigl[ \bigl\vert u_{k}^{n} + r \beta ( \Delta x) u_{k}^{n}-2r \alpha u_{k}^{n} \bigr\vert ^{2}\bigr] \\ &{}+ 2E\bigl[ \bigl\vert r \alpha u_{k}^{n} u_{k+1}^{n} - r \beta(\Delta x) u_{k}^{n} u_{k+1}^{n} + 3r^{2} \alpha\beta(\Delta x) u_{k}^{n} u_{k+1}^{n} \\ &{}- r^{2} \beta^{2} (\Delta x)^{2} u_{k}^{n} u_{k+1}^{n} -2 r^{2} \alpha^{2} u_{k}^{n} u_{k+1}^{n} \bigr\vert \bigr] \\ &{}+ 2E\bigl[ \bigl\vert r \alpha u_{k}^{n} u_{k-1}^{n} + r^{2} \alpha\beta(\Delta x) u_{k}^{n} u_{k-1}^{n} - 2 r^{2} \alpha^{2} u_{k}^{n} u_{k-1}^{n} \bigr\vert \bigr] \\ &{}+ 2E\bigl[ \bigl\vert r^{2} \alpha^{2} u_{k+1}^{n} u_{k-1}^{n} - r^{2} \alpha \beta(\Delta x) u_{k+1}^{n} u_{k-1}^{n} \bigr\vert \bigr] \\ &{}+ E\bigl[ \bigl\vert r \alpha u_{k+1}^{n} \bigr\vert ^{2}\bigr] + 2\bigl(E\bigl[ \bigl\vert r \alpha u_{k+1}^{n} \bigr\vert ^{2}\bigr]\bigr)^{1/2}\bigl(E\bigl[ \bigl\vert r \beta(\Delta x) u_{k+1}^{n} \bigr\vert ^{2}\bigr] \bigr)^{1/2} \\ &{}+ E\bigl[ \bigl\vert r \beta(\Delta x) u_{k+1}^{n} \bigr\vert ^{2}\bigr] + E\bigl[ \bigl\vert r \alpha u_{k-1}^{n} \bigr\vert ^{2}\bigr]. \end{aligned}$$

Since

$$ E\bigl[ \vert X+Y+Z \vert \bigr] \leqslant E\bigl[ \vert X \vert \bigr] + E\bigl[ \vert Y \vert \bigr] + E\bigl[ \vert Z \vert \bigr], $$

we have

$$\begin{aligned} E\bigl[ \bigl\vert u_{k}^{n+1} \bigr\vert ^{2} \bigr] \leqslant& E\bigl[ \bigl\vert u_{k}^{n} \bigr\vert ^{2}\bigr] + 2\bigl(E\bigl[ \bigl\vert u_{k}^{n} \bigr\vert ^{2}\bigr]\bigr)^{1/2}\bigl(E\bigl[ \bigl\vert r \beta (\Delta x) u_{k}^{n} - 2 r \alpha u_{k}^{n} \bigr\vert ^{2}\bigr]\bigr)^{1/2} + E\bigl[ \bigl\vert r \beta(\Delta x) u_{k}^{n} \bigr\vert ^{2}\bigr] \\ &{}+ 2 \bigl(E\bigl[ \bigl\vert r \beta(\Delta x) u_{k}^{n} \bigr\vert ^{2}\bigr]\bigr)^{1/2}\bigl(E\bigl[ \bigl\vert 2 r \alpha u_{k}^{n} \bigr\vert ^{2}\bigr] \bigr)^{1/2} + E\bigl[ \bigl\vert 2 r \alpha u_{k}^{n} \bigr\vert ^{2}\bigr] \\ &{}+ 2E\bigl[ \bigl\vert r \alpha u_{k}^{n} u_{k+1}^{n} \bigr\vert \bigr]+ 2E\bigl[ \bigl\vert r \beta(\Delta x) u_{k}^{n} u_{k+1}^{n} \bigr\vert \bigr] + 6E\bigl[ \bigl\vert r^{2} \alpha\beta(\Delta x) u_{k}^{n} u_{k+1}^{n} \bigr\vert \bigr] \\ &{}+ 2E\bigl[ \bigl\vert r^{2} \beta^{2} (\Delta x)^{2} u_{k}^{n} u_{k+1}^{n} \bigr\vert \bigr] + 4E\bigl[ \bigl\vert r^{2} \alpha^{2} u_{k}^{n} u_{k+1}^{n} \bigr\vert \bigr] \\ &{}+ 2E\bigl[ \bigl\vert r \alpha u_{k}^{n} u_{k-1}^{n} \bigr\vert \bigr] + 2E\bigl[ \bigl\vert r^{2} \alpha\beta(\Delta x) u_{k}^{n} u_{k-1}^{n} \bigr\vert \bigr] + 4E\bigl[ \bigl\vert r^{2} \alpha^{2} u_{k}^{n} u_{k-1}^{n} \bigr\vert \bigr] \\ &{}+ 2E\bigl[ \bigl\vert r^{2} \alpha^{2} u_{k+1}^{n} u_{k-1}^{n} \bigr\vert \bigr] + 2E\bigl[ \bigl\vert r^{2} \alpha\beta(\Delta x) u_{k+1}^{n} u_{k-1}^{n} \bigr\vert \bigr] + E\bigl[ \bigl\vert r \alpha u_{k+1}^{n} \bigr\vert ^{2}\bigr] \\ &{}+ 2\bigl(E\bigl[ \bigl\vert r \alpha u_{k+1}^{n} \bigr\vert ^{2}\bigr]\bigr)^{1/2}\bigl(E\bigl[ \bigl\vert r \beta (\Delta x) u_{k+1}^{n} \bigr\vert ^{2}\bigr] \bigr)^{1/2} \\ &{}+ E\bigl[ \bigl\vert r \beta(\Delta x) u_{k+1}^{n} \bigr\vert ^{2}\bigr] + E\bigl[ \bigl\vert r \alpha u_{k-1}^{n} \bigr\vert ^{2}\bigr]. \end{aligned}$$

Since

$$ \Vert X \Vert_{2} = \bigl[E\bigl(X^{2}\bigr) \bigr]^{1/2}\quad \forall X \in L_{2}(\varOmega), $$

we have

$$\begin{aligned} \bigl\Vert u_{k}^{n+1} \bigr\Vert ^{2}_{2} \leqslant& \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{2} + 2 \bigl\Vert u_{k}^{n} \bigr\Vert _{2} \bigl\Vert \bigl(r \beta(\Delta x)- 2 r \alpha\bigr) u_{k}^{n} \bigr\Vert _{2} + \bigl\Vert r \beta(\Delta x)u_{k}^{n} \bigr\Vert ^{2}_{2} \\ &{}+ 2 \bigl\Vert r \beta(\Delta x) u_{k}^{n} \bigr\Vert _{2} \bigl\Vert ( 2 r \alpha) u_{k}^{n} \bigr\Vert _{2}+ \bigl\Vert ( 2 r \alpha) u_{k}^{n} \bigr\Vert ^{2}_{2} + 2 r \alpha \bigl\Vert u_{k}^{n} \bigr\Vert _{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{2} \\ &{}+ 2 r (\Delta x) \Vert \beta \Vert _{2} \bigl\Vert u_{k}^{n} \bigr\Vert _{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{2} + 6 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{2} \bigl\Vert u_{k}^{n} \bigr\Vert _{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{2} \\ &{}+ 2 r^{2} (\Delta x)^{2} \bigl\Vert \beta^{2} \bigr\Vert _{2} \bigl\Vert u_{k}^{n} \bigr\Vert _{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{2} + 4 r^{2} \alpha^{2} \bigl\Vert u_{k}^{n} \bigr\Vert _{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{2} + 2 r \alpha \bigl\Vert u_{k}^{n} \bigr\Vert _{2} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{2} \\ &{}+ 2 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{2} \bigl\Vert u_{k}^{n} \bigr\Vert _{2} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{2} + 4 r^{2} \alpha^{2} \bigl\Vert u_{k}^{n} \bigr\Vert _{2} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{2} \\ &{}+ 2 r^{2} \alpha^{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{2} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{2}+ 2 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{2} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{2} \\ &{}+ r^{2} \alpha^{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert ^{2}_{2} + 2 r^{2} \alpha(\Delta x) \bigl\Vert u_{k+1}^{n} \bigr\Vert _{2} \bigl\Vert \beta u_{k+1}^{n} \bigr\Vert _{2} \\ &{}+ r^{2} (\Delta x)^{2} \bigl\Vert \beta u_{k+1}^{n} \bigr\Vert ^{2}_{2} + r^{2} \alpha^{2} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{2}^{2}. \end{aligned}$$

Since

$$ \Vert XY \Vert_{2} \leqslant\Vert X \Vert_{4}\Vert Y \Vert_{4}\quad \forall X,Y \in L_{4}(\varOmega), $$

we have

$$\begin{aligned} \bigl\Vert u_{k}^{n+1} \bigr\Vert ^{2}_{2} \leqslant& \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + 2 r (\Delta x) \bigl\Vert u_{k}^{n} \bigr\Vert _{4}^{2} \Vert \beta \Vert _{4} + 4 r \alpha \bigl\Vert u_{k}^{n} \bigr\Vert _{4}^{2} + r^{2} (\Delta x)^{2} \Vert \beta \Vert ^{2}_{4} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} \\ &{}+ 4 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + r^{2} \alpha^{2} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + 2 r \alpha \bigl\Vert u_{k}^{n} \bigr\Vert _{4} \bigl\Vert u_{k}^{n+1} \bigr\Vert _{4} \\ &{}+ 2 r (\Delta x) \Vert \beta \Vert _{4} \bigl\Vert u_{k}^{n} \bigr\Vert _{4} \bigl\Vert u_{k}^{n+1} \bigr\Vert _{4}+ 6 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \bigl\Vert u_{k}^{n} \bigr\Vert _{4} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{4} \\ &{}+ 2 r^{2} (\Delta x)^{2} \bigl\Vert \beta ^{2} \bigr\Vert _{4} \bigl\Vert u_{k}^{n} \bigr\Vert _{4} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{4} + 4 r^{2} \alpha^{2} \bigl\Vert u_{k}^{n} \bigr\Vert _{4} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{4} \\ &{}+ 2 r \alpha \bigl\Vert u_{k}^{n} \bigr\Vert _{4} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{4} + 2 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \bigl\Vert u_{k}^{n} \bigr\Vert _{4} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{4} + 4 r^{2} \alpha^{2} \bigl\Vert u_{k}^{n} \bigr\Vert _{4} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{4} \\ &{}+ 2 r^{2} \alpha^{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{4} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{4} + 2 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \bigl\Vert u_{k+1}^{n} \bigr\Vert _{4} \bigl\Vert u_{k-1}^{n} \bigr\Vert _{4} + r^{2} \alpha^{2} \bigl\Vert u_{k+1}^{n} \bigr\Vert ^{2}_{4} \\ &{}+ 2 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \bigl\Vert u_{k+1}^{n} \bigr\Vert ^{2}_{4}+ r^{2} (\Delta x)^{2} \Vert \beta \Vert ^{2}_{4} \bigl\Vert u_{k+1}^{n} \bigr\Vert ^{2}_{4} + r^{2} \alpha^{2} \bigl\Vert u_{k-1}^{n} \bigr\Vert ^{2}_{4}. \end{aligned}$$

Then

$$\begin{aligned} \sup_{k} \bigl\Vert u_{k}^{n+1} \bigr\Vert ^{2}_{2} \leqslant&\sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + 2 r (\Delta x) \Vert \beta \Vert _{4} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert _{4}^{2} + 4 r \alpha\sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert _{4}^{2} \\ &{}+ r^{2} (\Delta x)^{2} \Vert \beta \Vert ^{2}_{4} \sup _{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4}+ 4 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + 4 r^{2} \alpha^{2} \sup _{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} \\ &{}+ 2 r \alpha\sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + 2 r (\Delta x) \Vert \beta \Vert _{4} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4}+ 6 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} \\ &{} + 2 r^{2} (\Delta x)^{2} \bigl\Vert \beta^{2} \bigr\Vert _{4} \sup _{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + 4 r^{2} \alpha^{2} \sup _{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} \\ &{}+ 2 r \alpha\sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + 2 r^{2} \alpha (\Delta x) \Vert \beta \Vert _{4} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4}+ 4 r^{2} \alpha^{2} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} \\ &{}+ 2 r^{2} \alpha^{2} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + 2 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \sup _{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + r^{2} \alpha^{2} \sup _{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} \\ &{}+ 2 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4}+ r^{2} (\Delta x)^{2} \Vert \beta \Vert ^{2}_{4} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} + r^{2} \alpha^{2} \sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4}. \end{aligned}$$

Then

$$\begin{aligned} \sup_{k} \bigl\Vert u_{k}^{n+1} \bigr\Vert ^{2}_{2} \leqslant&\bigl[1 + 8 r \alpha+ 16 r^{2} \alpha^{2} + 4 r (\Delta x) \Vert \beta \Vert _{4} + 4 r^{2} (\Delta x)^{2} \Vert \beta \Vert ^{2}_{4} + 16 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \bigr] \\ &{}\times\sup_{k} \bigl\Vert u_{k}^{n} \bigr\Vert ^{2}_{4} \\ &{}\vdots \\ \leqslant&\bigl[1 + 8 r \alpha+ 16 r^{2} \alpha^{2} + 4 r ( \Delta x) \Vert \beta \Vert _{4} + 4 r^{2} (\Delta x)^{2} \Vert \beta \Vert ^{2}_{4} + 16 r^{2} \alpha(\Delta x) \Vert \beta \Vert _{4} \bigr]^{n+1} \\ &{}\times\sup_{k} \bigl\Vert u_{k}^{0} \bigr\Vert ^{2}_{4}. \end{aligned}$$

Take

$$ 8 r \alpha+ 16 r^{2} \alpha^{2} + 4 r (\Delta x) \Vert\beta \Vert_{4} + 4 r^{2} (\Delta x)^{2} \Vert\beta \Vert^{2}_{4} + 16 r^{2} \alpha (\Delta x) \Vert \beta\Vert_{4} \leqslant\lambda^{2}(\Delta t). $$

Then

$$ \sup_{k} \bigl\Vert u_{k}^{n+1} \bigr\Vert ^{2}_{2} \leqslant\bigl(1 + \lambda^{2} \Delta t\bigr)^{n+1} \sup_{k} \bigl\Vert u_{k}^{0} \bigr\Vert ^{2}_{4}. $$

Since \(u^{0}\) is a deterministic function,

$$ \sup_{k} \bigl\Vert u_{k}^{n+1} \bigr\Vert ^{2}_{2} \leqslant\bigl(1 + \lambda^{2} \Delta t\bigr)^{n+1} \sup_{k} \bigl\Vert u^{0} \bigr\Vert ^{2} $$

and \(\Delta t = \frac{t}{n+1} \), we have

$$ E\bigl[ \bigl\vert u_{k}^{n+1} \bigr\vert ^{2} \bigr] \leqslant\biggl(1 + \frac{\lambda^{2} t}{n+1}\biggr)^{n+1} E\bigl[ \bigl\vert u^{0} \bigr\vert ^{2}\bigr] \leqslant e^{\lambda^{2}t} E\bigl[ \bigl\vert u^{0} \bigr\vert ^{2} \bigr]. $$

Thus, the RFDS (2) satisfies the stability property in a mean square \(\eta=1\), \(\xi=\lambda^{2}\). □

5 Application

The random Cauchy problem for the convection–diffusion equation can be find in a membrane model if the concentration \(u(x,t)\) inside a pore in the membrane is described as the problem in the form

$$ \textstyle\begin{cases} u_{t} + \beta u_{x} = \alpha u_{xx},\quad t\geq0,x\in R, \\ u(x,0)= e^{-x^{2}},\quad x\in R, \end{cases} $$
(5)

where x is the unbounded space coordinate perpendicular to the membrane surfaces, t is the time, α is the diffusion coefficient is a constant and β is the random variable advection velocity.

Now, we can find the exact and approximation solution for this problem and construct a comparison between the expected values of them as in Tables 1–7 and Fig. 1.

Figure 1
figure 1

Expectation of the exact solution and the approximations of expectations using RFDS (7)–(8) at fixed time station \(t=0.2,0.05,0.005,0.000005\)

Full size image
Table 1 \(\beta\sim\operatorname{Binomial} ( 1.0,0.5 )\), \(\alpha=1\)
Full size table
Table 2 \(\beta\sim\operatorname{Beta\ distribution} ( 1.0,2.0 )\), \(\alpha=1\)
Full size table
Table 3 \(\beta\sim\operatorname{Binomial} ( 1.0,0.5 )\), \(\alpha=1\)
Full size table

The exact solution

$$ u(x,t)=\frac{1}{\sqrt{1 + 4 \alpha t}} e^{-\frac{(x - \beta t)^{2}}{1 + 4 \alpha t}}. $$
(6)

The numerical solution

The random finite difference scheme for this problem takes the form

$$\begin{aligned}& u_{k}^{n+1}=(1 + r \beta\Delta x -2 r \alpha)u_{k}^{n} + (r \alpha- r \beta\Delta x)u_{k+1}^{n} + r \alpha u_{k-1}^{n}, \end{aligned}$$
(7)
$$\begin{aligned}& u_{k}^{0} =u_{0}(k\Delta x)=u_{0}(x_{k})=e^{-(k \Delta x)^{2}}, \end{aligned}$$
(8)

since \(r=\frac{\Delta t}{(\Delta x)^{2}}\), \(t_{n}=n\Delta t\) and \(x_{k}=k\Delta x\).

Using the RFDS (7) and (8)

$$\begin{aligned}& \begin{aligned} u_{1}^{1}&=(1 + r \beta\Delta x -2 r \alpha)u_{1}^{0} + (r \alpha- r \beta\Delta x)u_{2}^{0} + r \alpha u_{0}^{0} \\ &=(1 + r \beta\Delta x -2 r \alpha)e^{-(\Delta x)^{2}} + (r \alpha- r \beta\Delta x)e^{-(2 \Delta x)^{2}} + r \alpha, \end{aligned} \\& \begin{aligned} u_{1}^{2}&=(1 + r \beta\Delta x -2 r \alpha)u_{1}^{1} + (r \alpha- r \beta\Delta x)u_{2}^{1} + r \alpha u_{0}^{1}. \\ &= \bigl[(1 + r \beta\Delta x -2 r \alpha)^{2} + 2 r \alpha(r \alpha-r \beta\Delta x) + (r \alpha)^{2}\bigr]e^{-(\Delta x)^{2}} \\ &\quad {}+ 2 \bigl[(r \alpha-r \beta\Delta x) (1 + r \beta\Delta x -2 r \alpha ) \bigr]e^{-(2 \Delta x)^{2}} + (r \alpha-r \beta\Delta x)^{2} e^{-(3 \Delta x)^{2}} \\ &\quad {}+ 2 r \alpha(1 + r \beta\Delta x -2 r \alpha). \end{aligned} \end{aligned}$$

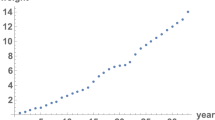
In Fig. 1 we present a comparison at the time instant \(t = 0.2,0.05,0.005\mbox{ and }0.000005\) (time fixed station) of the expectation of the exact solution s.p. and the approximations of the expectations using the random numerical scheme (7)–(8) with different spatial steps and we note that Fig. 1 agrees with our calculations.

Figure 1 indicates that, for fixed expected values of the random variable and Δx and decreasing the step size Δt, we get a more accurate and stable solution to (5).

Also, we can summarize our results from Tables 1–4 that show the convergence between the first moment of the exact stochastic process solution and the numerical stochastic process approximations.

Table 4 \(\beta\sim\operatorname{Beta\ distribution} ( 1.0,2.0 )\), \(\alpha=1\)
Full size table

Additionally, we can confirm the convergence according to \(\lambda ^{2} \) as in Tables 5–7.

Table 5 \(\beta\sim\operatorname{Binomial\ distribution} ( 1.0,0.5 )\), \(\alpha=1\) and \(\Delta x = 0.25\)
Full size table
Table 6 \(\beta\sim\operatorname{Beta\ distribution} ( 1.0,2.0 ) \), \(\alpha=1\) and \(\Delta x = 0.25\)
Full size table
Table 7 \(\beta\sim\operatorname{Exponential} (0.5 ) \), \(\alpha=1\) and \(\Delta x = 0.25\)
Full size table

6 Conclusion

We have presented a consistent and stable RFDS that approximates the stochastic solution of the Cauchy advection–diffusion problem with random variable coefficient under mean square and mean fourth calculus.