Abstract
In this paper, we study a periodic model of hematopoiesis with a time-varying delay. Some new criteria are established to ensure that there are at least two positive periodic solutions by applying Krasnoselskii’s fixed point theorem, which are essentially new and complement some existing ones. Moreover, numerical simulations are performed to substantiate the effectiveness of the theoretical analysis.
Similar content being viewed by others
1 Introduction
In order to describe some physiological control systems in the classic study of population dynamics, Mackey and Glass in [1] initially proposed the following model of hematopoiesis (cell production):
where \(x(t)\) denotes the density of mature cells in blood circulation, a is the rate at which cells are lost from the circulation, the flux \(g(x(t-\tau))=\frac{bx^{m}(t-\tau)}{1+x^{n}(t-\tau)}\) of the cells into the circulation from the stem cell compartment depends on \(x(t-\tau)\) at time \(t-\tau\), and τ is the time delay between the production of immature cells in the bone marrow and their maturation for release in circulating bloodstreams.
In recent years, the model of hematopoiesis has been extensively and intensively studied due to its theoretical and practical significance. A very basic and important dynamics problem is the existence and uniqueness of positive (almost) periodic solutions associated with the study of the following non-autonomous model (1.1) in (almost) periodic environments:
To name a few, when \(m=0\), Liu et al. studied the existence and global attractivity of periodic solution for Eq. (1.2) by using a fixed point theorem in cone and the oscillatory theory. Alzabut et al. in [2] were concerned with the existence and global exponential stability of almost periodic solutions by applying Banach’s contraction mapping principle and Gronwall–Bellman’s inequality. When \(m=1\), Zhou et al. and Wang et al. respectively studied the existence and uniqueness of periodic solution for Eq. (1.2), the methods used therein were mainly based on the exponential dichotomy theory, Mawhin coincidence degree, together with the Lyapunov functional method, see [3, 4]. Wang and Zhang in [5] investigated the existence and uniqueness of almost periodic solution for Eq. (1.2) by establishing a new fixed point theorem in cones free of compactness conditions. For other interesting theoretical results for this model, we refer to [6,7,8,9,10,11,12] and the references therein.
However, it is noteworthy that when \(0< m< n\), the flux function in model (1.2) has stronger nonlinearity than the cases of \(m=0\) or \(m=1\), and thus it may show more complex and rich dynamic behaviors. On the other hand, the aforementioned periodic solution (can be regarded as a special case of almost periodic solution) is unique, as mentioned by May in [13] that a large number of empirical observations shows that many natural communities have a multiplicity of stable states. The multiplicity of periodic solutions is an interesting problem in the qualitative study of delay differential equations, and such an issue of Eq. (1.2) has been seldom considered up to now. Motivated by the above discussions, in this paper we aim to establish some sufficient conditions ensuring that Eq. (1.2) has at least two positive T-periodic solutions. Our approach is based on Krasnoselskii’s fixed point theorem.
The structure of the remaining part of this paper is as follows. In Sect. 2, we present some necessary lemmas. In Sect. 3, some sufficient conditions are established to guarantee that Eq. (1.2) has at least two positive periodic solutions. In Sect. 4, we demonstrate the validity of these theoretical results with numerical simulations. Finally, some conclusions are made and future directions are pointed out in Sect. 5.
2 Preliminaries
In this section, we first introduce some notations and recall well-known Krasnoselskii’s fixed point theorem.
Let \(h\in C(\mathbb{R}, \mathbb{R})\) be a T-periodic function, we denote
On the other hand, let \(g(x)=\frac{x^{m}}{1+x^{n}}\), if \(0< m< n\), we can easily verify that \(g(x)\) increases strictly on \([0, \sqrt[n]{\frac{m}{n-m}} ]\) and decreases on \([ \sqrt[n]{\frac{m}{n-m}}, \infty )\). Thus, there exists a unique \(c_{0}\in (\sqrt[n]{\frac{m}{n-m}}, \infty )\) such that \(g(c_{0})=g (\rho\sqrt[n]{\frac{m}{n-m}} )\), where \(0<\rho<1\).
Definition 2.1
Let X be a Banach space, and let P be a closed, nonempty subset of X. P is a cone if
-
(i)
\(\alpha x+\beta y \in P\) for all \(x, y\in P\) and all \(\alpha , \beta\geq 0\);
-
(ii)
\(x, -x\in P\) imply \(x=0\).
Lemma 2.1
Let X be a Banach space, and let \(P\subset X\) be a cone in X. Assume that \(\varOmega_{1}\), \(\varOmega_{2}\) are open bounded subsets of X with \(0\in\varOmega_{1}\subset\overline{\varOmega}_{1}\subset\varOmega_{2}\), and let
be a completely continuous operator such that either
-
(i)
\(\|\varPhi x\|\leq\|x\|\), \(\forall x\in P\cap\partial \varOmega_{1}\) and \(\|\varPhi x\|\geq\|x\|\), \(\forall x\in P\cap\partial\varOmega_{2}\);
or
-
(ii)
\(\|\varPhi x\|\geq\|x\|\), \(\forall x\in P\cap\partial \varOmega_{1}\) and \(\|\varPhi x\|\leq\|x\|\), \(\forall x\in P\cap\partial\varOmega_{2}\).
Then Φ has a fixed point in \(P\cap(\overline{\varOmega}_{2}\setminus\varOmega_{1})\).
Let
and
Then X is a Banach space equipped with the above norm \(\|\cdot\|\). If \(x(t)\in X\) is a solution of Eq. (1.2), then
Integrating both sides of (2.1) over \([t, t+T]\), we have
where
It is easy to see that, for any \(t\leq s\leq t+T\),
Now, choose the cone defined by
and define an operator \(\varPhi: X\to X\) by
Obviously, to show that Eq. (1.2) has a T-periodic solution, it suffices to prove that Φ has a fixed point on X. To establish the main results, we also make the following assumptions:
-
(H1)
\(a, b, \tau\in C(\mathbb{R}, (0, \infty)) \) are all T-periodic functions;
-
(H2)
\(Nb^{-}Tg(c_{0}) >c_{0}\).
Lemma 2.2
The mapping Φ maps P into P, that is, \(\varPhi P\subset P\).
Proof
For any \(x\in P\), we have from (2.2) and (2.3) that
and
Combining (2.4) with (2.5) gives
Hence, \(\varPhi P\subset P\). The proof is completed. □
Lemma 2.3
\(\varPhi: P\to P\) is completely continuous.
Proof
Denote
First, we show that Φ is continuous. For any \(L > 0\) and \(\varepsilon> 0\), there exists \(\delta> 0\) such that, for \(\varphi, \psi\in X\), \(\|\varphi\|\leq L\), \(\|\psi\|\leq L\), and \(\|\varphi-\psi\|<\delta\) imply
If \(x, y\in X\) with \(\|x\|\leq L\), \(\|y\|\leq L\), and \(\|x-y\|<\delta\), then we have from (2.2), (2.3), and (2.6) that
Thus, Φ is continuous.
Next, we show that Φ is compact. Let \(B > 0\) be any constant, and let \(\mathscr{T}=\{x\in X: \|x\|\leq B\}\) be a bounded set . For any \(x\in\mathscr{T}\), it follows from (2.2) and (2.3) that
Again, from (2.3), we have
which implies that \(\varPhi\mathscr{T}\subset\mathscr{T}\) is a family of uniformly bounded and equi-continuous functions. According to the well-known Ascoli–Arzela theorem, the operator Φ is compact, and so it is completely continuous. The proof is completed. □
3 Main results
We are now in a position to state and prove our main results of this paper.
Theorem 3.1
Let \(0< m< n\) and (H1)–(H2) hold. Then Eq. (1.2) has at least two positive T-periodic solutions.
Proof
By virtue of \(\lim_{x\to 0}\frac{b(t)x^{m}}{1+x^{n}}=\lim_{x\to \infty}\frac{b(t)x^{m}}{1+x^{n}}=0\), for any \(t\in[0, T]\), for any sufficiently small \(\varepsilon>0\) such that \(MT\varepsilon<1\), there exist two constants \(c_{1}\), \(c_{2}\) (\(c_{1}<\sqrt[n]{\frac{m}{n-m}}<c_{0}<c_{2} \)) such that
and
Define
where
If \(x=x(t)\in P\cap\partial\varOmega_{1}\), then \(\|x\|=c_{1}\), and \(x(t)\geq\rho c_{1}\). From (2.2), (2.3), and (3.1), we have
which means that \(\|\varPhi x\|< \|x\|\) for \(x\in P\cap\partial \varOmega_{1}\).
If \(x=x(t)\in P\cap\partial\varOmega_{2}\), then \(\|x\|=\sqrt[n]{\frac{m}{n-m}}\) and \(x(t)\geq\rho \sqrt[n]{\frac{m}{n-m}}\). In view of (2.2)–(2.3), (H2) and the fact that \(\min_{x\in [\rho\sqrt[n]{\frac{m}{n-m}}, \sqrt[n]{\frac{m}{n-m}} ]}g(x)=g(\rho \sqrt[n]{\frac{m}{n-m}})=g(c_{0})\), we have
which implies that \(\|\varPhi x\|>\|x\|\) for \(x\in P\cap\partial \varOmega_{2}\).
If \(x=x(t)\in P\cap\partial\varOmega_{3}\), then \(\|x\|=c_{0}\), and \(x(t)\geq\rho c_{0}>\rho\sqrt[n]{\frac{m}{n-m}}\). Combining (2.2)–(2.3), (H2), and the fact that \(\min_{x\in [\rho c_{0}, c_{0}]}g(x)=g(c_{0})\) produces
and hence \(\|\varPhi x\|>\|x\|\) for \(x\in P\cap\partial\varOmega_{3}\).
If \(x=x(t)\in P\cap\partial\varOmega_{4}\), then \(\|x\|=c_{3}\), and \(x(t)\geq\rho c_{3}\). Due to (2.2) and (2.3), we obtain
and so \(\|\varPhi x\|<\|x\|\) for \(x\in P\cap\partial\varOmega_{4}\), where \(\varLambda_{1}=\{s|s\in[t, t+T], 0\leq x(s-\tau(s))\leq c_{2} \}\) and \(\varLambda_{2}=\{s|s\in[t, t+T], c_{2}< x(s-\tau(s))\leq c_{3} \}\).
Obviously, \(\varOmega_{i}\) (\(i=1,2,3,4\)) are open bounded subsets of X with \(0\in\varOmega_{1}\subset\overline{\varOmega}_{1}\subset\varOmega_{2} \subset\overline{\varOmega}_{2}\subset\varOmega_{3}\subset \overline{\varOmega}_{3}\subset\overline{\varOmega}_{4}\). Since \(\varPhi(P)\subset P\) and Φ is a completely continuous operator on X, we conclude from Lemma 2.1 that Φ has one fixed point \(x_{1}\in P\cap(\overline{\varOmega}_{2}\setminus\varOmega_{1})\) and another fixed point \(x_{2}\in P\cap(\overline{\varOmega}_{4}\setminus\varOmega_{3})\), that is, \(x_{i}(t)=(\varPhi x_{i})(t)\), \(i=1,2\), and \(x_{1}(t)\geq\rho c_{1}>0\) and \(x_{2}(t)\geq\rho c_{0}>0\), i.e., \(x_{1}(t)\) and \(x_{2}(t)\) are two positive T-periodic solutions of Eq. (1.2). The proof is completed. □
Remark 3.1
The method in this paper can be used to study the model of hematopoiesis with periodic coefficients and infinite distributed delay as follows:
where the delay kernel \(p: (0, \infty)\to(0, \infty)\) is assumed to be integrable and normalized such that \(\int_{0}^{\infty}p(s)\,ds=1\). Then the following statements can be obtained immediately.
Theorem 3.2
Let \(0< m< n\) and (H2) hold. Then Eq. (3.3) has at least two positive T-periodic solutions.
4 A numerical example
In this section, we give a numerical example with simulations to illustrate the feasibility of our main results.
Example 4.1
Consider the following 2π-periodic model of hematopoiesis with a time-varying delay:
Here, \(a(t)=0.4+0.2\cos t\), \(b(t)=280+\sin t\), \(\tau(t)=\cos t\), \(m=1\), \(n=2\). It is easy to see that \(N=\frac{1}{e^{0.8\pi}-1}\), \(M=\frac{e^{0.8\pi}}{e^{0.8\pi}-1}\), and so \(\rho=\frac{N}{M}=e^{-0.8\pi}\approx0.081\), \(c_{0}\approx12.345\). A straightforward calculation shows that
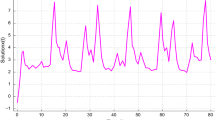
Thus we have verified all the assumptions of Theorem 3.1 and hence Eq. (4.1) has at least two positive 2π-periodic solutions, see Fig. 1.
Equation (4.1) has two 2π-periodic solutions
Remark 4.1
In recent years, by using the continuation theorem, the existence of multiple periodic solutions of delayed population models has widely been studied (see [16, 17] and the references therein), and the multiplicity is heavily dependent on the harvesting term. It is readily seen that our methods are quite different from the previous works and the considered model is without the harvesting term. On the other hand, to the best of authors’ knowledge, there is no research work concerning the multiplicity of periodic solutions of Eq. (1.2). Therefore, the results established in this paper are essentially new and complement some existing ones.
5 Conclusion
In this paper, we have studied the multiplicity of periodic solutions for a delayed model of hematopoiesis, a new set of criteria ensuring the existence of at least two periodic solutions have been derived. The effectiveness of the theoretical results has been demonstrated by a numerical example.
It is known that almost periodic problem is a hot research topic in science [18, 19] and engineering [20, 21]. However, it would be more difficult to find the sufficient condition for the multiplicity of almost periodic solutions than the periodic case since the compact condition fails the almost periodic function family, and then Krasnoselskii’s fixed point theorem controlled by compact conditions cannot be used to solve the existence of almost periodic solutions. Therefore, interesting problems of the existence and stability of multiple almost periodic solutions for the kinds of models described by delay differential equations are still open, and we leave them as our future research work.
References
Mackey, M.C., Glass, L.: Oscillations and chaos in physiological control systems. Science 197, 287–289 (1977)
Alzabut, J.O., Nieto, J.J., Stamov, G.T.: Existence and exponential stability of positive almost periodic solutions for a model of hematopoiesis. Bound. Value Probl. 2009, Article ID 127510 (2009)
Wu, X.M., Li, J.W., Zhou, H.Q.: A necessary and sufficient condition for the existence of positive periodic solutions of a model of hematopoiesis. Comput. Math. Appl. 54, 840–849 (2007)
Zhang, H., Yang, M., Wang, L.: Existence and exponential convergence of the positive almost periodic solution for a model of hematopoiesis. Appl. Math. Lett. 26, 38–42 (2013)
Wang, X., Zhang, H.: A new approach to the existence, nonexistence and uniqueness of positive almost periodic solution for a model of hematopoiesis. Nonlinear Anal., Real World Appl. 11, 60–66 (2010)
Saker, S.H.: Oscillation and global attractivity in hematopoiesis model with periodic coefficients. Appl. Math. Comput. 142, 477–494 (2003)
Liu, B.: New results on the positive almost periodic solutions for a model of hematopoiesis. Nonlinear Anal., Real World Appl. 17, 252–264 (2014)
Ding, H.S., Liu, Q.L., Nieto, J.J.: Existence of positive almost periodic solutions to a class of hematopoiesis model. Appl. Math. Model. 40, 3289–3297 (2016)
Anh, T.T., Nhung, T.V.: On the existence and exponential attractivity of a unique positive almost periodic solution to an impulsive hematopoiesis model with delays. Acta Math. Vietnam. 41, 337–354 (2016)
Diagana, T., Zhou, H.: Existence of positive almost periodic solutions to the hematopoiesis model. Appl. Math. Comput. 274, 644–648 (2016)
Jiang, A.: Pseudo almost periodic solutions for a model of hematopoiesis with an oscillating circulation loss rate. Math. Methods Appl. Sci. 39, 3215–3225 (2016)
Tan, Y., Zhang, M.: Global exponential stability of periodic solutions in a nonsmooth model of hematopoiesis with time-varying delays. Math. Methods Appl. Sci. 40, 5986–5995 (2017)
May, R.: Thresholds and breakpoints in ecosystems with a multiplicity of stable states. Nature 269, 471–477 (1977)
Krasnoselskii, M.A.: Positive Solutions of Operator Equations. Noordhoff, Groningen (1964)
Tang, X., Zou, X.: On positive periodic solutions of Lotka–Volterra competition systems with deviating arguments. Proc. Am. Math. Soc. 134, 2967–2974 (2006)
Chen, Y.: Multiple periodic solutions of delayed predator–prey systems with type IV functional responses. Nonlinear Anal., Real World Appl. 5, 45–53 (2004)
Fang, H.: Existence of eight positive periodic solutions for a food-limited two-species cooperative patch system with harvesting terms. Commun. Nonlinear Sci. Numer. Simul. 18, 1857–1869 (2013)
Fink, A.: Almost Periodic Differential Equations. Springer, Berlin (1974)
Xu, C., Liao, M., Pang, Y.: Existence and convergence dynamics of pseudo almost periodic solutions for Nicholson’s blowflies model with time-varying delays and a harvesting term. Acta Appl. Math. 146, 95–112 (2016)
Stamov, G., Stamova, I.: Almost periodic solutions for impulsive neural networks with delay. Appl. Math. Model. 31, 1263–1270 (2007)
Xu, C., Li, P., Pang, Y.: Exponential stability of almost periodic solutions for memristor-based neural networks with distributed leakage delays. Neural Comput. 28, 2726–2756 (2016)
Acknowledgements
The authors would like to thank the anonymous reviewers and the editor for their constructive comments. This revised form was finished when the first author was visiting Prof. Xianhua Tang at Central South University, and he would like to thank the staff in the School of Mathematics and Statistics for their help and the university for its excellent facilities and support during his stay.
Funding
This work was jointly supported by the National Natural Science Foundation of China (11701007, 61572035), Natural Science Foundation of Anhui Province (1808085QA01), Key Program of University Natural Science Research Fund of Anhui Province (KJ2017A088), China Postdoctoral Science Foundation (2018M640579), Key Program of Scientific Research Fund for Young Teachers of AUST (QN201605), Open Fund of Hunan Provincial Key Laboratory of Mathematical Modeling and Analysis in Engineering (2018MMAEZD17), and the Student’s Platform for Innovation and Entrepreneurship Training Program (201810361096).
Author information
Authors and Affiliations
Contributions
All authors contributed equally to this manuscript. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they do not have any competing interests in this manuscript.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Duan, L., Chen, S., Xiao, H. et al. On multi-periodicity in a delayed model of hematopoiesis. Adv Differ Equ 2019, 14 (2019). https://doi.org/10.1186/s13662-019-1949-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-1949-z