Error estimates of a semi-discrete LDG method for the system of damped acoustic wave equation

Abstract

We consider a system of acoustic wave equation possessing lower-order perturbation terms in a bounded domain in $\mathbb{R}^{2}$. In this paper, we show the system is well-posed and stable with energy decays introducing a local discontinuous Galerkin (LDG) method. Also, we study an a priori $L^{2}$-norm error estimate for the semi-discretized LDG method for the system under additional regularity assumptions. Further, numerical tests are presented to support the theoretical analysis.

1 Introduction

Many phenomena of wave-type propagation with exponential decay of its amplitude can be modeled by a hyperbolic system of damped wave equations. For example, damped linear hyperbolic systems are introduced to model the propagation of pressure waves in a network of pipes or the vibrations of a network of strings [11], an electric transmission lines for time-dependent evolution of voltage and current on networks [13], networks of general elastic multi-structures [21], the simulation of electronic circuits [15], and several types of transmission lines [17, 18, 24] by the telegrapher’s equations. Most perfectly matched layers (PMLs) also appear as a hyperbolic system with a zeroth-order perturbation for the intentional purpose of exponential decay of wave propagation in boundary layers [3, 6, 16, 22]. In spite of many applications of damped wave systems, less attention has been paid to its numerical and theoretical studies, in contrast to damped wave systems which have been popularly researched [1, 10, 12, 14, 19, 23, and the references therein] by recently developed numerical methods such as the discontinuous Galerkin (DG) methods.

In this paper, introducing a general formula of damped linear hyperbolic systems, we show the well-posedness of the system and present a local discontinuous Galerkin (LDG) method with its stability and a priori error estimates. A LDG method, which is developed as a DG method for several advantages, satisfies certain properties of numerical fluxes using jump and average functions on all edges of grid elements in order to have locally conservative, stable, and also high-order accurate method [2, 4, 8, 9]. The stability of the LDG method is shown by the decay of the energy norm constructing proper numerical fluxes on the edges of grid elements. Applying the broken Sobolev norm and seminorm in the error equation obtained by the semi-discretized scheme of LDG method, we estimate a priori $L^{2}$-norm error estimates of the numerical solutions by using the bound of solution on the edges of grid elements, the approximation properties of $L^{2}$-projections, and the dual property of ∇ and $-\nabla\cdot$.

The paper is organized as follows: In Sect. 2.1, we introduce a general formula for damped hyperbolic systems of the wave equation and recall couple existence theorems to show the well-posedness. We develop the LDG method for the system using numerical flux on interfaces of grid elements with discontinuity stabilization parameters in Sect. 2.2. Section 3 presents an error estimate of the system based on the broken Sobolev norm and seminorm with the approximation properties of projections. We provide numerical experiments to support theoretical results with various different parameters and coefficients in Sect. 4. Finally, Sect. 5 contains our conclusion and further discussions.

2 LDG method for a system

2.1 A system of damped wave equation

In this subsection, we introduce a general formula of the first-order linear hyperbolic system of the acoustic wave equation equipped with additional lower-order damping terms and show the well-posedness of the system.

The model problem we are dealing with is as follows: We provide two damping terms in both solutions of the system of the two-dimensional acoustic wave equation. Let $\sigma_{p}$ and $\sigma_{\vec{q}}$ be the damping functions in $L^{\infty}(\varOmega)$, $\varOmega\subset\mathbb{R}^{2}$ defined by

$$ 0 =\sigma_{*}\leq\sigma_{p}({x}),\qquad \sigma_{\vec{q}}({x}) \leq{{\sigma}}^{*}< \infty,\quad x\in\varOmega. $$

Then, we have the following system of damped wave equations defined in $\varOmega\times I$, $I=(0,T]$ for some $T>0$:

$$ \begin{aligned} &\frac{1}{c^{2}({x})}p_{t}({x},t) +\frac{1}{c^{2}({x})}\sigma_{p}({x}) p({x},t)+\nabla\cdot\vec{ {q}}({x},t) = 0 \quad\text{in } {\varOmega}\times I, \\ &\vec{ {q}}_{t}({x},t)+\sigma_{\vec{q}}({x}) \vec{ {q}}({x},t)+ \nabla p({x},t) = \vec{0 }\quad \text{in } {\varOmega} \times I \end{aligned} $$

(2.1)

with the initial condition $( p, \vec{ {q}}) ({x},0) = ( f,\vec{0})$ and the zero Dirichlet boundary condition $p({x},\cdot)=0$ on ∂Ω. Let ${\varOmega}\subset\mathbb{R}^{2}$ be a bounded Lipschitz domain including a sub-domain $\varOmega_{0}$, that is, $\operatorname{supp}(f)\subseteq \varOmega_{0}\subseteq\varOmega$. Here the initial conditions are given by $p_{0}=f \in H^{1}_{0}( {\varOmega})$ and $\vec{ {q} }_{0}=\vec{ {0} }$ and we assume that $c({x}) \in C^{1}( {\varOmega} )$ is bounded below by $c_{*}$ and above by $c^{*}$, that is,

$$ 0< c_{*}\leq c({x}) \leq c^{*} < \infty\quad \text{in } {\varOmega}. $$

(2.2)

Before we show well-posedness of the system, let us denote $V_{m}$ and $\mathcal{M}$ are a Hilbert space with scalar-product $(\cdot,\cdot)_{m}$ and the corresponding Riesz map from $V_{m}$ onto the dual $V_{m}'$, respectively, that is,

$$ \mathcal{M} u ( v )=(u,v)_{m} \quad \forall u, v \in V_{m}. $$

We use the following theorem to show the existence of a solution $(p, {\vec{q}})$ of (2.1).

Theorem 2.1

([27])

Let D be a subspace of $V_{m}$ and assume a linear map $L:D\rightarrow V_{m}'$ is monotone and $\mathcal{M}+{L}: D\rightarrow V_{m}'$ is surjective. Then, for every $g\in C^{1} ([0,\infty);V_{m}')$ and $u_{0} \in D$, there is a unique $u\in C^{1}([0,\infty); V_{m})$ such that $u(0)=u_{0}$ and

$$ \mathcal{M} u'(t) +Lu(t)=g(t),\quad t \geq0. $$

We apply Theorem 2.1 to obtain the well-posedness of the system (2.1).

Theorem 2.2

For every $(p_{0},\vec{ {q}} _{0}) \in H^{1}_{0} ( {\varOmega}) \times {H}_{\mathrm{div}}( {\varOmega})$, there exists a unique solution $(p,\vec{ {q}} )$ of (2.1) such that $(p,\vec{ {q}} ) \in C^{1}(\bar{I};L^{2}( {\varOmega})\times{H}^{2}( {\varOmega})) \cap C(\bar{I}; H^{1}_{0}( {\varOmega}) \times{H}_{\mathrm{div}} ( {\varOmega}) )$ satisfying the initial condition $(p(0),\vec{ {q}} (0))=(p_{0},\vec{ {q}} _{0})$, where ${H}_{\mathrm{div}}(\varOmega): =\{{\vec{v}} \in \mathbb{L}^{2}( {\varOmega}) :\nabla\cdot{\vec{v}} \in L^{2}(\varOmega) \}$ and $\mathbb{L}^{2}( {\varOmega }):=[ L^{2}(\varOmega)]^{2}$.

Proof

Let $V_{m}:=H_{m}(\varOmega)\times\mathbb{L}^{2}( {\varOmega})$, where $H_{m}(\varOmega)=\frac{1}{c^{2}}L^{2}(\varOmega)$ with ${c^{-2}}$-weighted $L^{2}$-inner product, that is,

$$ (p,r)_{m}= (p,r)_{c^{-2}} = \int_{ {\varOmega}} \frac{1}{c^{2}}p({x})r({x})\,d{x} $$

and let $D:=H^{1}_{0}( {\varOmega})\times{H}_{\mathrm{div}} (\varOmega)$. Then it can easily be checked that $\frac{1}{c^{2}}L^{2}( {\varOmega}) \cong L^{2}( {\varOmega})$. Let us define $\mathcal{M}:V_{m} \rightarrow V_{m}'$ and $L:D \rightarrow V_{m}'$ and by

$$ \begin{aligned} &\mathcal{M} (p,\vec{q})^{T} \bigl((r, \vec{v})^{T} \bigr)=(p,r)_{c^{-2}}+(\vec{q},\vec{v})\quad\forall( p, \vec{q} )^{T}\in V_{m}, (r,\vec{v} )^{T} \in V_{m}, \\ &L (p,\vec{q} )^{T} \bigl((r,\vec{v})^{T} \bigr)=( \sigma_{p} p,r)_{c^{-2}}+(\sigma_{\vec{q}}\vec{q},\vec{v})+( \nabla p,\vec{v})+(\nabla\cdot\vec{q},r),\\ &\quad\forall(p,\vec{q} )^{T}\in D, (r,\vec{v} )^{T} \in V_{m}, \end{aligned} $$

where $(\cdot,\cdot)$ is the $L^{2}$-inner product. One can check that L is monotone by the definition and $\mathcal {M}+L$ is surjective from the elliptic form (see [20] for details). □

In the following subsection, we present a LDG method for the system (2.1) of the damped wave equation.

2.2 LDG method of the system (2.1)

We assume that shape-regular meshes $\mathcal{T}_{h}$ partition the domain Ω into disjoint elements $\{K\}$ such that $\bar{ {\varOmega}} =\bigcup_{K\in\mathcal{T}_{h}} \bar{K}$. Thus, if $K \in\mathcal{T}_{h}$, then K is a simplex and the measure of K is denoted by $\operatorname{meas}(K)$. It will always be assumed that $\operatorname{meas}(K)\neq0$. The diameters of K and that of the largest ball included in K are denoted by $h_{K}$ and $\rho_{K}$, respectively. The ratio of these two quantities is denoted by $\varphi_{K}$ and let us denote

$$ \varphi_{K}=\frac{h_{K}}{\rho_{K}},\qquad h_{K}=\operatorname{diam}(K),\qquad \rho _{K}=\sup\bigl\{ r: B_{r}= \bigl\{ x: \vert x -a \vert \leq r \bigr\} \subset K, a \in K \bigr\} . $$

Then it is noted that $\varphi_{K}>1$ and the parameter h refers to $h:=\max_{K\in\mathcal{T}_{h}} h_{K}$. We also assume that the local mesh sizes are of bounded variation; that is, there is a positive constant κ depending only on the shape-regularity of the mesh such that

$$ \kappa h_{K} \leq h_{K'}\leq\kappa^{-1}h_{K} $$

for all neighboring elements K and $K'$. From each adjacent element $K^{+}$ and $K^{-}$ in $\mathcal{T}_{h}$, we denote the set of all faces by $\mathcal{E}$ which consists of both $\mathcal{E}^{I}$ the set of all interior faces of $\partial K^{+} \cap\partial K^{-} \in \mathcal{E}(K^{+})\cup\mathcal{E}(K^{-})$ and $\mathcal{E}^{B}$ the set of all boundary faces of $\partial K \cap\partial{\varOmega}$, that is, $\mathcal{E}=\mathcal{E}^{I}\cup\mathcal{E}^{B}$, where $\mathcal{E}(K)$ is denoted by the set of all edges of the element K. For the error estimation, we define the discontinuity stabilization parameters $\boldsymbol {\alpha}_{11}, \boldsymbol {\alpha}_{12}, \boldsymbol {\alpha}_{22}$ on each $e\in\mathcal{E}$ by

$$ \mathtt{C}_{11}=\boldsymbol {\alpha}_{11} \mathtt{h}^{\alpha},\qquad \mathtt{C}_{22}=\boldsymbol {\alpha}_{22} \mathtt{h}^{\alpha},\qquad \vec{\mathtt{C}}_{22}= [\boldsymbol { \alpha}_{12}\ \boldsymbol {\alpha}_{12} ]^{T}, $$

(2.3)

where the parameters $\boldsymbol {\alpha}_{ij}\ (i,j=1,2)$ independent of local mesh size and the function $\mathtt{h}\in L^{\infty}(\mathcal{E})$ is given by

$$\mathtt{h}= \textstyle\begin{cases} \min\{h_{K^{+}}, h_{K^{-}} \},& e=\partial K^{+} \cap\partial K^{-}, e\in\mathcal{E}^{I}, \\ h_{K}, & e=\partial K \cap\partial\varOmega, e\in\mathcal{E}^{B}. \end{cases} $$

The accuracy of the method relies on the choice of α and we assume $\alpha=0$ in this study. For a piecewise smooth scalar-valued function p, define the trace operators on all faces. Let $e \in\mathcal{E}^{I}$ be an interior face shared by elements $K^{+}$ and $K^{-}$; let $\vec{\mathbf{n}}^{\pm}$ by the unit outward normal vectors on the boundaries $\partial K^{\pm}$, respectively. Denote by $p^{\pm}$ the trace of p taken from within $K^{\pm}$ and define the jump and average of p at $x\in e$ by

$$\begin{aligned} \{\hspace{-2pt}\{p \}\hspace{-2pt}\}:= \frac{1}{2} \bigl(p^{+} + p^{-} \bigr)\quad \text{and}\quad [\hspace{-2pt}[ p]\hspace{-2pt}]:= p^{+}\vec{\mathbf{n}}^{+} + p^{-} \vec {\mathbf{n}}^{-}. \end{aligned}$$

(2.4)

Let $\{\!\{p\}\!\}:=p$ and $[\![p]\!]:= p\vec {\mathbf{n}}$, where $\vec{\mathbf{n}}$ is the unit outward normal vector on ∂Ω in all boundary faces $e \in\mathcal{E}^{B}$. For a vector-valued function q⃗, we set

$$ \{\hspace{-2pt}\{{\vec{q}} \}\hspace{-2pt}\}:=\frac{1}{2} \bigl(\vec{q}^{ +} + {\vec{q}}^{-} \bigr) \quad\text{and}\quad [\hspace{-2pt}[{\vec{q}}]\hspace{-2pt}]:= \vec {q}^{ +}\cdot\vec{\boldsymbol{n}}^{+} + \vec{q}^{ -}\cdot\vec{ \boldsymbol{n}}^{-}. $$

In a similar way, we set $\{\!\{{\vec{q}} \}\!\}:={\vec{q}}$ and $[\![{\vec{q}} ]\!]:= {\vec{q}} \cdot \vec{\boldsymbol{n}}$ in all boundary faces $e \in\mathcal{E}^{B}$. Notice that the jump $[\![p]\!]$ of the scalar function p is a vector parallel to $\vec{\boldsymbol{n}}$ and that $[\![{\vec {q}}]\!]$ is the jump of the normal component of the vector function q⃗, which is a scalar quantity. We also note that there is a trace identity for a scalar-valued function p and a vector-valued function q⃗ with continuous normal components across a face $e\in\mathcal{E}^{I}$; by applying the definitions directly one has

$$ p^{+} \bigl(\vec{q}^{ +} \cdot\vec{\boldsymbol{n}}^{+} \bigr)+p^{-} \bigl( \vec{q}^{ -}\cdot\vec{\boldsymbol{n}}^{-} \bigr)= [\hspace{-2pt}[p]\hspace{-2pt}] \cdot\{\hspace{-2pt}\{{\vec{q}} \}\hspace{-2pt}\}+ \{\hspace{-2pt}\{p\}\hspace{-2pt}\} [\hspace{-2pt}[{\vec{q}}]\hspace{-2pt}]. $$

(2.5)

For a given partition $\mathcal{T}_{h}$ such as triangulation of Ω and an approximation order ${k} \geq1$, we seek an approximate (continuous or possibly discontinuous) solution $(p^{h},{\vec{q}}^{ h})$ in the finite element space

$$ \mathcal{P}^{h}(\varOmega) \times\mathcal{Q}^{h}(\varOmega) = \bigcup_{K \in \mathcal{T}_{h}} \mathcal{P}^{h} (K)\times \mathcal{Q}^{h}(K), $$

where

$$ \mathcal{P}^{h} (K)\times\mathcal{Q}^{h}(K):= \bigl\{ \bigl(p^{h},{\vec{q}}^{ h} \bigr)\in L^{2}(\varOmega) \times\mathbb{L}^{2}(\varOmega): \bigl(p^{h},{ \vec{q}}^{ h} \bigr)|_{K} \in\mathbb{P}^{k}(K) \times\bigl[\mathbb{P}^{k'}(K) \bigr]^{2} \bigr\} $$

and $\mathbb{P}^{k}(K)$ and $\mathbb{P}^{k'}(K)$ are the space of polynomials of total degree at most k and $k'$ on K, respectively. This approximation is said to be non-conformal since $\mathcal{P}^{h}( {\varOmega}) \not\subset H^{1}_{0}( {\varOmega})$; it is said to be conformal otherwise, e.g., continuous Galerkin methods.

Next, following [8], we define LDG methods for the system (2.1) considering only the spatial discretization of this equation as above. First, we assume that $(p^{h},{\vec{q}}^{ h}): I \rightarrow\mathcal{P}^{h}( {\varOmega })\times \mathcal{Q}^{h}( {\varOmega})$ is absolutely continuous. A LDG numerical method is obtained as follows. We discretize the domain Ω, then seek a discontinuous approximate solution $(p^{h},{\vec{q}}^{ h})$ on the element K taken in the space $\mathcal{P}^{h}(K)\times\mathcal{Q}^{h}(K)$ and determined by requiring that

$$ \begin{aligned} & \int_{K}\frac{1}{c^{2}}p^{h}_{t}r^{h} \,dx+ \int_{K}\frac{\sigma _{p}}{c^{2}}p^{h}r^{h} \,dx- \int_{K} {\vec{q}}^{h}\cdot\nabla_{h} r^{h} \,dx+ \int_{\partial K} \bigl(\hat{\vec{q}}^{h}\cdot\vec{ \mathbf{n}} \bigr)r^{h} \,ds=0, \\ & \int_{K} {\vec{q}}^{ h}_{t}\cdot \vec{v}^{ h}\,dx+ \int_{K}\sigma_{\vec {q}} {\vec{q}}^{ h}\cdot{ \vec{v}}^{ h} \,dx- \int_{K}p^{h}\nabla_{h}\cdot{ \vec{v}}^{h}{ h}\,dx+ \int_{\partial K}\hat{p} ^{h} \bigl({\vec{v}}^{ h} \cdot\vec{\mathbf{n}} \bigr) \,ds=0 \end{aligned} $$

(2.6)

for all $(r^{h},{\vec{v}}^{ h})\in\mathcal{P}^{h}(K)\times\mathcal {Q}^{h}(K)$, where $\nabla_{h}$ and $\nabla_{h} \cdot$ are the functions whose restriction to each element $K\in\mathcal{T}_{h}$ are equal to ∇ and ∇⋅, respectively. To complete the definition of the DG method, it remains to define the two numerical traces, $\hat {p}^{ h}$ and $\hat{\vec{q}}^{ h}$. We first begin by finding a stability result for the solution in the original system (2.1). To do that, we multiply the first and second equation of the system (2.1) by p and q⃗, respectively, and integrate over ${\varOmega}\times{I}$ to obtain

$$ \begin{aligned}& \frac{1}{2} \int_{ {\varOmega}}\frac{1}{c^{2}} \bigl\vert {p}(\cdot,T) \bigr\vert ^{2}\,dx+ \int_{0}^{T} \int_{ {\varOmega}}\frac{\sigma_{p}}{c^{2}} \vert{p} \vert^{2} \,dx\,dt+ \int_{0}^{T} \int_{ {\varOmega}}{p}\nabla\cdot{\vec{q}} \,dx\,dt \\ &\quad = \frac {1}{2} \int_{ {\varOmega}}\frac{1}{c^{2}} \bigl\vert {p}(\cdot,0) \bigr\vert ^{2}\,dx, \\ &\frac{1}{2} \int_{ {\varOmega}} \bigl\vert {\vec{q}}(\cdot,T) \bigr\vert ^{2}\,dx+ \int_{0}^{T} \int_{ {\varOmega}}\sigma_{\vec{q}} \vert{\vec{q}} \vert ^{2} \,dx \,dt+ \int_{0}^{T} \int_{ {\varOmega}} \nabla p \cdot{\vec{q}} \,dx\,dt = \frac{1}{2} \int_{ {\varOmega }} \bigl\vert {\vec{q}} (\cdot,0) \bigr\vert ^{2}\,dx. \end{aligned} $$

Adding these two equations, we have

$$\begin{aligned} &\frac{1}{2} \int_{ {\varOmega}} \biggl(\frac{1}{c^{2}} \bigl\vert p(\cdot,T) \bigr\vert ^{2}+ \bigl\vert {\vec{q}} (\cdot,T) \bigr\vert ^{2} \biggr)\,dx+ \int_{0}^{T} \int_{ {\varOmega}} \biggl(\frac{\sigma_{p}}{c^{2}} \vert p \vert ^{2}+\sigma_{\vec{q}} \vert{\vec{q}} \vert^{2} \biggr)\,dx\,dt \\ &\quad =\frac{1}{2} \int_{ {\varOmega}} \biggl(\frac{1}{c^{2}} \bigl\vert p(\cdot,0) \bigr\vert ^{2}+ \bigl\vert {\vec{q}} (\cdot,0) \bigr\vert ^{2} \biggr) \,dx. \end{aligned}$$

We note that a stability result immediately follows from this equation.

Next, we imitate this procedure for the LDG method under consideration. We begin by taking $r^{h}=p^{h}$ and ${\vec{v}}^{ h}={\vec {q}}^{ h}$ in the first and second equation in (2.6), respectively, defining the LDG method, adding over the elements $K\in \mathcal{T}_{h}$, and summing the two equations together to get

$$\begin{aligned} &\frac{1}{2} \int_{ {\varOmega}} \biggl(\frac{1}{c^{2}} \bigl\vert p^{h}(\cdot,T) \bigr\vert ^{2}+ \bigl\vert { \vec{q}}^{ h} (\cdot,T) \bigr\vert ^{2} \biggr)\,dx+ \int_{0}^{T} \int_{ {\varOmega}} \biggl(\frac{\sigma_{p}}{c^{2}} \bigl\vert p^{h} \bigr\vert ^{2}+\sigma_{\vec{q}} \bigl\vert {\vec{q}}^{ h} \bigr\vert ^{2} \biggr)\,dx\,dt \\ &\qquad{}+ \int_{0}^{T}\varTheta_{h}(t)\,dt \\ &\quad =\frac{1}{2} \int_{ {\varOmega}} \bigl( \bigl\vert p^{h}(\cdot,0) \bigr\vert ^{2}+ \bigl\vert {\vec{q}}^{ h}(\cdot,0) \bigr\vert ^{2} \bigr)\,dx, \end{aligned}$$

where

$$ \varTheta_{h}(t):=\sum_{K\in\mathcal{T}_{h}} \int_{\partial K} \bigl( p^{h}\hat{\vec{q}}^{ h} \cdot\vec{\mathbf{n}}+ \bigl(\hat{p}^{h}-p^{h} \bigr){\vec {q}}^{ h}\cdot\vec{\mathbf{n}} \bigr) \,ds. $$

Now, we can define consistent numerical traces $\hat{p}^{h}$ and $\hat {\vec{q}}^{ h}$ that provide the quantity $\varTheta_{h}(t)$ non-negative. Dropping the argument t, we obtain

$$ \varTheta_{h} =\sum_{e\in\mathcal{E}^{I}} \int_{e} \bigl( \bigl[ \hspace{-2pt}\bigl[ p^{h} \bigr]\hspace{-2pt}\bigr] \cdot\bigl(\hat{\vec{q}}^{ h}- \bigl\{ \hspace{-2pt}\bigl\{ {\vec{q}}^{ h} \bigr\} \hspace{-2pt}\bigr\} \bigr)+ \bigl[ \hspace{-2pt}\bigl[\vec{q}^{ h} \bigr]\hspace{-2pt}\bigr] \bigl( \hat{p}^{h}- \bigl\{ \hspace{-2pt}\bigl\{ p^{h} \bigr\} \hspace{-2pt}\bigr\} \bigr) \bigr)\,ds+\partial\varUpsilon_{h}(t), $$

where $\partial\varUpsilon_{h}(t):=\int_{\partial{\varOmega}} ( p^{h}(\hat {\vec{q}}^{ h}-{\vec{q}}^{ h})\cdot\vec{\mathbf{n}}+\hat {p}^{h}{\vec {q}}^{ h}\cdot\vec{\mathbf{n}} ) \,ds$. To get non-negative $\varTheta_{h}$ on $\mathcal{E} ^{I}$, that is, inside the domain Ω, it is enough to take that

$$ \hat{p}^{h}= \bigl\{ \hspace{-2pt}\bigl\{ {p^{h}} \bigr\} \hspace{-2pt} \bigr\} +\mathtt{C}_{22} \bigl[ \hspace{-2pt}\bigl[{{\vec{q}}^{ h}} \bigr]\hspace{-2pt}\bigr]-\vec{ \mathtt{C}}_{12}\cdot\bigl[ \hspace{-2pt}\bigl[{p^{h}} \bigr]\hspace{-2pt}\bigr], \qquad \hat{\vec{q}}^{ h}= \bigl\{ \hspace{-2pt}\bigl\{ {\vec{q}}^{ h} \bigr\} \hspace{-2pt}\bigr\} +\mathtt{C}_{11} \bigl[ \hspace{-2pt}\bigl[p^{h} \bigr]\hspace{-2pt}\bigr]+\vec{\mathtt{C}}_{12} \bigl[ \hspace{-2pt}\bigl[ {{\vec{q}}^{ h}} \bigr]\hspace{-2pt}\bigr] $$

for some positive quantities,

$$\begin{aligned} \mathtt{C}_{11}>0,\qquad \mathtt{C}_{22}>0,\qquad \mathtt{C}^{1}_{12}>0,\qquad \mathtt{C}^{2}_{12}>0,\qquad \vec{\mathtt{C}}_{12}= \bigl[ {\mathtt{C}}_{12}^{1}\ {\mathtt{C}}_{12}^{2} \bigr]^{T} \end{aligned}$$

and its boundary $\hat{p}^{h}=0$ and $\hat{\vec{q}}^{ h}= {\vec{q}}^{ h} +\mathtt{C}_{11}p^{h}\vec{\mathbf{n}}$ to finally obtain

$$\begin{aligned} \varTheta_{h}=\sum_{e\in\mathcal{E} ^{I}} \int_{e} \bigl( \mathtt{C}_{11} \bigl[ \hspace{-2pt}\bigl[p^{h} \bigr]\hspace{-2pt}\bigr]^{2}+{ \mathtt{C}}_{22} \bigl[ \hspace{-2pt}\bigl[ {\vec{q}}^{ h} \bigr]\hspace{-2pt}\bigr]^{2} \bigr)\,dx + \sum_{e\in\mathcal{E}^{B} } \int_{e} \mathtt{C}_{11} \bigl(p^{h} \bigr)^{2} \,ds \geq0. \end{aligned}$$

Note that the vector parameter $\vec{\mathtt{C}}_{12}$ does not have any stabilizing effect; it is not necessary for stability, but could be used to enhance the accuracy of the method (for details, see [9]). Note that the zero Dirichlet boundary condition is imposed weakly through the definition of the numerical trace. Applying the numerical flux $\hat{p}^{h}$ and $\hat{\vec{q}}^{ h}$, we have the LDG system

$$\begin{aligned} &\sum_{K\in\mathcal{T}_{h} } \int_{K} \biggl( \frac{1}{c^{2}} \bigl(p^{h}_{t}+{ \sigma_{p}}p^{h} \bigr) {r^{h}}-{ \vec{q}}^{ h} \cdot\nabla r^{h} \biggr) \,dx + \sum _{e \in\mathcal{E}^{I}} \int_{e} \bigl( \bigl\{ \hspace{-2pt}\bigl\{ { \vec{q}}^{ h} \bigr\} \hspace{-2pt}\bigr\} \\ &\quad{}+\mathtt{C}_{11} \bigl[ \hspace{-2pt}\bigl[p^{h} \bigr]\hspace{-2pt}\bigr]+\vec{ \mathtt{C}}_{12} \bigl[ \hspace{-2pt}\bigl[{\vec{q}^{ h}} \bigr]\hspace{-2pt}\bigr] \bigr)\cdot\bigl[ \hspace{-2pt}\bigl[ r^{h} \bigr]\hspace{-2pt}\bigr] \,ds \\ & \quad{}+ \int_{\partial\varOmega} r^{h} {\vec{q}^{ h}}\cdot\vec{ \mathbf{n}} \,ds=0 \end{aligned}$$

and

$$\begin{aligned} &\sum_{K\in\mathcal{T}_{h}} \int_{K} \biggl( {{\vec{q}}^{ h}}_{t}+ \sigma_{\vec{q}}\vec{q}^{ h} - \int_{K}p^{h}\nabla\biggr)\cdot\vec {v}^{h} \,dx\\ &\quad{} +\sum_{e \in\mathcal{E}^{I}} \int_{e} \bigl( \bigl\{ \hspace{-2pt}\bigl\{ {p^{h}} \bigr\} \hspace{-2pt}\bigr\} +\mathtt{C}_{22} \bigl[ \hspace{-2pt}\bigl[\vec{q}^{ h} \bigr]\hspace{-2pt}\bigr]-\vec{ \mathtt{C}}_{12}\cdot\bigl[ \hspace{-2pt}\bigl[{p^{h}} \bigr]\hspace{-2pt}\bigr] \bigr) \bigl[ \hspace{-2pt}\bigl[\vec{v}^{ h} \bigr]\hspace{-2pt}\bigr] \,ds =0 \end{aligned}$$

for all $(r^{h}, \vec{{v}}^{ h})\in\mathcal{P}^{h}(\varOmega)\times \mathcal {Q}^{h}(\varOmega)$, which completes the definition of LDG method.

Remark 2.3

We show that the LDG method is in fact a mixed formulation. To see this, let us begin by noting that the LDG approximate solution $(p^{h},\vec{q}^{ h} )$ can be characterized as the solution of

$$ \biggl(\frac{1}{c^{2}}p^{h}_{t},r^{h} \biggr) + a_{h} \bigl(p^{h},r^{h} \bigr) - {b}'_{h} \bigl(\vec{q}^{ h},r^{h} \bigr) = 0,\qquad \bigl(\vec{q}^{h}_{t},\vec{v}^{h} \bigr) + b_{h} \bigl(p^{h},\vec{v}^{ h} \bigr) + c_{h} \bigl(\vec{q}^{ h},\vec{v}^{ h} \bigr) = 0 $$

(2.7)

for all $(r^{h},\vec{v}^{ h})\in\mathcal{P}^{h}(\varOmega)\times \mathcal {Q}^{h}(\varOmega)$, where

$$ \begin{aligned} &a_{h} \bigl(p^{h},r^{h} \bigr):=\sum_{K \in\mathcal{T}_{h}} \int_{K} \frac{\sigma _{p}}{c^{2}}p^{h}r^{h} \,dx+ \sum_{e \in\mathcal{E}^{I}} \int_{e} \mathtt{C}_{11} \bigl[ \hspace{-2pt}\bigl[p^{h} \bigr]\hspace{-2pt}\bigr]\cdot\bigl[ \hspace{-2pt}\bigl[r^{h} \bigr]\hspace{-2pt}\bigr]\,ds, \\ &{b}_{h} \bigl(p^{h},\vec{{v}}^{ h} \bigr):=-\sum _{K \in\mathcal{T}_{h}} \int_{K} p^{h} \nabla\cdot\vec{v}^{ h} \,dx -\sum_{e \in\mathcal{E}^{I}} \int_{e} \bigl(\vec{\mathtt{C}}_{12} \cdot\bigl[ \hspace{-2pt}\bigl[p ^{h} \bigr]\hspace{-2pt}\bigr]- \bigl\{ \hspace{-2pt}\bigl\{ p^{h} \bigr\} \hspace{-2pt}\bigr\} \bigr) \bigl[ \hspace{-2pt}\bigl[\vec{v}^{ h} \bigr]\hspace{-2pt}\bigr]\,ds, \\ &{b}'_{h} \bigl(\vec{q}^{ h},r^{h} \bigr):=\sum_{K \in\mathcal{T}_{h}} \int_{K}\vec{q}^{ h} \cdot\nabla r^{h} \,dx -\sum_{e \in\mathcal{E}^{I}} \int_{e} \bigl(\vec{\mathtt{C}}_{12} \bigl[ \hspace{-2pt}\bigl[ \vec{q}^{ h} \bigr]\hspace{-2pt}\bigr]+ \bigl\{ \hspace{-2pt}\bigl\{ \vec{q}^{ h} \bigr\} \hspace{-2pt}\bigr\} \bigr) \cdot\bigl[ \hspace{-2pt}\bigl[r^{h} \bigr]\hspace{-2pt}\bigr]\,ds, \\ & c_{h} \bigl(\vec{q}^{ h},\vec{v}^{ h} \bigr):= \sum_{K \in\mathcal{T}_{h}} \int_{K}\sigma_{\vec{q}}\vec{q}^{ h}\cdot \vec{v}^{ h}\,dx+ \sum_{e \in \mathcal{E}^{I}} \int_{e} \mathtt{C}_{22} \bigl[ \hspace{-2pt}\bigl[ \vec{q}^{ h} \bigr]\hspace{-2pt}\bigr] \bigl[ \hspace{-2pt}\bigl[\vec{v}^{ h} \bigr]\hspace{-2pt}\bigr]\,ds. \end{aligned} $$

(2.8)

Remark 2.4

We have the equality by the trace identity (2.5)

$${b}_{h} \bigl(p^{h},\vec{q}^{ h} \bigr)={b}_{h}' \bigl( \vec{q}^{ h}, p^{h} \bigr) \quad\forall\bigl( p^{h}, \vec{q}^{ h} \bigr) \in\mathcal{P}^{h}(\varOmega) \times\mathcal{Q}^{h}( \varOmega). $$

Note that the second terms on the right hand side of the equations in (2.8) correspond to jump and average terms on element boundaries; they vanish when $p,r \in H^{1}_{0}(\varOmega)$ and $\vec{q},\vec{v} \in {H}_{\mathrm{div}}(\varOmega )$. Therefore, the above semi-discrete LDG formulation (2.7) is consistent with the original continuous problem (2.1).

3 A-priori error estimate of LDG method

In order to establish an error estimate, we introduce the following properties. There is an important inequality in the finite element spaces $\mathcal {P}^{h}( {\varOmega})\times\mathcal{Q}^{h}( {\varOmega})$, which allows the $H^{1}$-norm to be bounded above by the $L^{2}$-norm. Such an inequality is called an inverse inequality. Let us introduce the broken Sobolev space of $\mathcal{T}_{h}$ of the domain Ω,

$$H^{s}( \mathcal{T}_{h}):= \bigl\{ p\in L^{2}( { \varOmega}): p|_{K} \in H^{s}(K)\ \forall K\in \mathcal{T}_{h} \bigr\} $$

with the broken Sobolev norm and seminorm, respectively,

$$\Vert p \Vert _{H^{s}( \mathcal{T}_{h})}:= \biggl(\sum_{K\in \mathcal{T}_{h}} \Vert p \Vert _{H^{s}(K) } \biggr)^{\frac{1}{2}}, \qquad \vert p \vert _{H^{s}( \mathcal{T}_{h})}:= \biggl(\sum_{K\in\mathcal {T}_{h}} \vert p \vert_{H^{s}(K) } \biggr)^{\frac{1}{2}}. $$

Then, the following result can be proved.

Lemma 3.1

(Trace theorem)

Let $p \in\mathcal{P}^{h}( {\varOmega})$ with shape-regularity mesh. Then there exists a constant $C_{\mathrm{inv}}>0$ such that

$$\begin{aligned} \Vert p \Vert _{L^{2}(\partial K)} \leq C_{\mathrm{inv}} \bigl( \Vert p \Vert _{L^{2}(K)} \bigl( h_{K}^{-1} \Vert p \Vert _{L^{2}(K)} + \Vert \nabla p \Vert _{L^{2}(K)} \bigr) \bigr)^{\frac{1}{2}}. \end{aligned}$$

Proof

See Lemma A.3 in [26] for the proof and further details. □

We now consider the following semi-discrete DG approximation for the spatial discretization of (2.1): Find $(p^{h},{\vec{q}}^{ h} ): \bar{I} \times\bar{I} \rightarrow\mathcal{P}^{h} ( {\varOmega })\times \mathcal{Q}^{h}( {\varOmega})$ such that

$$ \begin{aligned} & \biggl(\frac{1}{c^{2}} p^{h}_{t},r^{h} \biggr)+a_{h} \bigl(p^{h},r^{h} \bigr)-{b}_{h}' \bigl({\vec{q}}^{ h},r^{h} \bigr) = 0 \quad\forall r^{h} \in\mathcal{P}^{h}( {\varOmega}), t\in I, \\ & \bigl(\vec{q}^{ h}_{t},\vec{v}^{ h} \bigr)+b_{h} \bigl(p^{h},\vec{v}^{ h} \bigr)+c_{h} \bigl(\vec{q}^{ h}, \vec{v}^{ h} \bigr) = 0 \quad \forall{\vec{v}}^{ h} \in\mathcal{Q}^{h}( { \varOmega}), t \in I, \end{aligned} $$

(3.1)

with

$$p^{h}(\cdot, 0)={\varPi}_{h} p_{0},\qquad \vec{q}^{ h}(\cdot,0)=\boldsymbol {\varPi}_{h}\vec{q}_{0},\qquad p^{h}(x,\cdot)=0\quad \forall x \in\partial\varOmega. $$

Here $\varPi_{h}$ and $\boldsymbol {\varPi}_{h}$ denote the $L^{2}$-projections of p and q⃗ in $L^{2}(\varOmega)$ and $\mathbb{L}^{2}(\varOmega)$ onto $\mathcal {P}^{h} (\varOmega)$ and $\mathcal{Q}^{h}(\varOmega)$, respectively, that is, for any $p \in L^{2}(\varOmega), {\vec{q}} \in\mathbb{L}^{2}(\varOmega)$

$$\begin{aligned} \bigl(\varPi_{h} p, r^{h} \bigr) = \bigl(p,r^{h} \bigr) \quad\text{and}\quad \bigl(\boldsymbol {\varPi}_{h} {\vec{q}} , {\vec{v}}^{ h} \bigr)= \bigl( {\vec{q}}, {\vec{v}}^{ h} \bigr) \quad\forall r^{h}\in\mathcal{P}^{h}( {\varOmega}), { \vec{v}}^{ h} \in\mathcal{Q}^{h}( {\varOmega}), \end{aligned}$$

(3.2)

and the discrete forms $a_{h},b_{h}$, and $c_{h}$ are given by (2.8). For the simplicity of notations, we let $\frac{1}{c^{2}}\mathcal{R}_{p}+ \mathcal{A}_{h}: \mathcal{P}^{h}( {\varOmega}) \rightarrow[\mathcal {P}^{h}(\varOmega)]{'}$, $\mathcal{B}_{h}: \mathcal{P}^{h}( {\varOmega}) \rightarrow[\mathcal{Q}^{h}( {\varOmega})]{'}$, and $\mathcal{R}_{\vec{q}}+ \mathcal{C}_{h}:\mathcal{Q}^{h}( {\varOmega}) \rightarrow[\mathcal{Q}^{h}( {\varOmega})]{'}$ given by

$$\begin{aligned} &\frac{1}{c^{2}}\mathcal{R}_{p}p^{h} \bigl(r^{h} \bigr)= \biggl(\frac{1}{c^{2}}p^{h} ,r^{h} \biggr),\qquad \mathcal{R}_{\vec{q}}{\vec{q}}^{ h} \bigl({\vec{v}}^{h} \bigr) = \bigl({\vec{q}}^{ h}, { \vec{v}}^{ h} \bigr), \\ & \mathcal{A}_{h} p^{h} \bigl(r^{h} \bigr) = a_{h} \bigl(p^{h},r^{h} \bigr),\qquad \mathcal{B}_{h} p^{h} \bigl({\vec{v}}^{ h} \bigr) = b_{h} \bigl(p^{h}, {\vec{v}}^{ h} \bigr),\qquad \mathcal{C}_{h} { \vec{q}}^{ h} \bigl({\vec{v}}^{ h} \bigr) = c_{h} \bigl({\vec{q}}^{ h}, {\vec{v}}^{ h} \bigr). \end{aligned}$$

Then it can be seen that the dual operator of $\mathcal{B}_{h}$, $\mathcal {B}'_{h}:\mathcal{Q}^{h} (\varOmega) \rightarrow[\mathcal {P}^{h}(\varOmega )]{'}$ satisfies

$$\begin{aligned} \mathcal{B}'_{h} {\vec{q}}^{ h} \bigl( r^{h} \bigr) = \mathcal{B}_{h} r^{h} \bigl({\vec {q}}^{ h} \bigr) = b_{h}' \bigl( { \vec{q}}^{ h}, r^{h} \bigr), \end{aligned}$$

which follows from the trace identity (2.5).

Lemma 3.2

There is a unique semi-discrete solution $(p^{h},{\vec {q}}^{ h} )$ of (3.1) satisfying

$$\bigl(p^{h},{\vec{q}}^{ h} \bigr) \in C^{1} \bigl(I; \mathcal{P}^{h}( {\varOmega}) \times\mathcal{Q}^{h}( { \varOmega}) \bigr). $$

Proof

Theorem 2.1 is used for the proof. We use the operator notations of (3.1) to obtain

$${\mathcal{M}}_h\left(\begin{array}{c}{p}^h\\ {\overrightarrow{q}}^h\end{array}\right)+L_h\left(\begin{array}{c}{p}^h\\ {\overrightarrow{q}}^h\end{array}\right)=0\text{in }{[{\mathcal{P}}^h(\Omega )\times {\mathcal{Q}}^h(\Omega )]}^{\prime },$$

where

$${\mathcal{M}}_h=\left[\begin{array}{cc}\frac{1}{c^2}{\mathcal{R}}_p& 0\\ 0& {\mathcal{R}}_{\overrightarrow{q}}\end{array}\right],L_h=\left[\begin{array}{cc}{\mathcal{A}}_h& -{\mathcal{B}}_h^{\prime }\\ {\mathcal{B}}_h& {\mathcal{C}}_h\end{array}\right].$$

Then we show that $L_{h}$ is monotone by the definition and the trace identity (2.5),

$$L_h{(p^h,{\overrightarrow{q}}^h)}^T\left({(p^h,{\overrightarrow{q}}^h)}^T\right)=\left(\begin{array}{c}{\mathcal{A}}_h{p}^h-{\mathcal{B}}_h^{\prime }{\overrightarrow{q}}^h\\ {\mathcal{B}}_h{p}^h+{\mathcal{C}}_h{\overrightarrow{q}}^h\end{array}\right)\left(\begin{array}{c}{p}^h\\ {\overrightarrow{q}}^h\end{array}\right)\ge 0.$$

To obtain $\operatorname{Rg}(\mathcal{M}_{h}+{L}_{h})= [\mathcal{P}^{h} ( {\varOmega})\times \mathcal {Q}^{h}( {\varOmega}) ] '$, it is sufficient to show that $\operatorname{Ker} (\mathcal {M}_{h}+{L}_{h})=\{(0, \vec{{0}})\}$. Since

$$\begin{aligned} \mathcal{M}_{h} \bigl( p ^{h}, {\vec{q}} ^{ h} \bigr)^{ T} \bigl( \bigl( p ^{h}, {\vec{q}} ^{ h} \bigr)^{T} \bigr) = \int_{ {\varOmega}} \biggl( \frac{1}{c^{2}} \bigl(p^{h} \bigr) ^{2}+ \bigl({\vec{q}}^{ h} \bigr){^{2}} \biggr)\,dx \geq C \int_{ {\varOmega}} \bigl( \bigl(p^{h} \bigr) ^{2}+ \bigl({\vec{q}}^{ h} \bigr){^{2}} \bigr)\,dx \end{aligned}$$

for some $C=\min\{ \frac{1}{{c^{*}}^{2}},1 \}$, we can have the surjection, which provides the conclusion. □

To estimate of the difference of the semi-discrete LDG solution $(p^{h} ,{\vec{q}}^{ h})$ in (3.1) with analytical solutions $(p ,{\vec{q}})$ in (2.1), we want to extend to a larger space which contains both solutions. In the next section we show the error estimates.

Extension of LDG form. We define the spaces

$$\mathcal{P}(h):= H^{1}_{0}( {\varOmega}) + \mathcal{P}^{h}( {\varOmega}) \quad\text{and}\quad \mathcal{Q}(h):= {H}_{\mathrm{div}}( {\varOmega}) + \mathcal{Q}^{h}( {\varOmega}) $$

with the DG energy norm on $\mathcal{P}(h) \times\mathcal{Q}(h)$,

$$\bigl\Vert (p,\vec{q}) \bigr\Vert _{h}^{2}:= \Vert p \Vert ^{2} _{\mathcal {P}(h)}+ \Vert \vec{q} \Vert ^{2}_{\mathcal{Q}(h)}, $$

where

$$\begin{aligned} \Vert p \Vert _{\mathcal{P}(h) }^{2}&:=\sum _{K\in\mathcal{T}_{h}} \Vert p \Vert _{H^{1}(K)}^{2}+\sum _{e\in\mathcal{E}} \bigl\Vert \mathtt{C}_{11} [\hspace{-2pt}[p]\hspace{-2pt}] \bigr\Vert _{L^{2}(e)}^{2}, \Vert {\vec{q}} \Vert _{\mathcal{Q}(h) }^{2}\\ &:=\sum_{K\in \mathcal{T}_{h}} \Vert {\vec{q}} \Vert _{{H}_{\mathrm{div}}(K) } ^{2}+\sum _{e\in\mathcal{E}} \bigl\Vert \mathtt{C}_{22} [\hspace{-2pt}[{ \vec{q}}]\hspace{-2pt}] \bigr\Vert _{L^{2}(e)}^{2}, \end{aligned}$$

and the norm $\|\vec{ {q}}\|_{{H}_{\mathrm{div}}(K)} ^{2}:=\|\vec{q}\|_{\mathbb{L}^{2} (K) } ^{2}+\|\nabla\cdot{\vec{q}}\|_{{L}^{2}(K) } ^{2}$. For the convenience of notation, let us denote

$$\Vert \cdot \Vert _{0,\mathcal{E}}:=\sum_{e\in\mathcal{E}} \Vert \cdot \Vert _{L^{2}(e)},\qquad \Vert \cdot \Vert _{s,K}:= \Vert \cdot \Vert _{H^{s}(K)},\qquad \Vert \cdot \Vert _{s,\varOmega}:= \Vert \cdot \Vert _{H^{s}(\varOmega)}, $$

and the same as $\mathbb{H}^{s}(K)$ and $\mathbb{H}^{s}(\varOmega)$, respectively. Furthermore, for $1\leq p\leq\infty$ we use the Bochner space $L^{p}(I;\mathcal{P}(h)\times\mathcal{Q}(h))$

$$\begin{aligned} \bigl\Vert ( p, \vec{{q}} ) \bigr\Vert _{ L^{p}(I;\mathcal{P}(h) \times \mathcal{Q}(h)) }:= \textstyle\begin{cases} (\int_{I} \Vert p \Vert ^{p} _{ \mathcal{P}(h)}+ \Vert {\vec {q}} \Vert ^{p} _{ \mathcal {Q}(h)} \,dt )^{1/p} & \text{if } 1\leq p< \infty,\\ \operatorname{ess} \sup_{t\in I} ( \Vert p \Vert _{ \mathcal{P}(h)}+ \Vert {\vec{q}} \Vert _{ \mathcal{Q}(h)}) & \text{if } p=\infty, \end{cases}\displaystyle \end{aligned}$$

and we denote

$$\begin{aligned} & \Vert \cdot \Vert _{\mathscr{L}^{p}_{s, {\varOmega}}}:= \Vert \cdot \Vert _{L^{p}(I;{H}^{s}( {\varOmega}))},\qquad \Vert \cdot \Vert _{\mathscr {L}^{\infty}_{s, {\varOmega}}}:= \Vert \cdot \Vert _{L^{\infty }(I;{H}^{s}( {\varOmega}))}, \\ & \Vert \cdot \Vert _{\mathscr{L}^{p}_{s, \mathcal{E}}}:= \Vert \cdot \Vert _{L^{p}(I;{H}^{s}( \mathcal{E}))}, \qquad \Vert \cdot \Vert _{\mathscr {L}^{\infty}_{s, \mathcal {E}}}:= \Vert \cdot \Vert _{L^{\infty}(I;{H}^{s}(\mathcal{E}))}. \end{aligned}$$

The main result of this section is to establish the $L^{2}( {\varOmega })$-norm error estimate. It also gives a bound in the $L^{2}( {\varOmega })$-norm of the first time derivative.

Theorem 3.3

Let the analytical solution $(p,{\vec{q}} )$ of (2.1) satisfies

$$ ( p, {\vec{q}} ) \in L^{\infty} \bigl( I; H^{1+s} _{0}( {\varOmega})\times\mathbb{H}^{1+s} ( { \varOmega}) \bigr),\qquad ( p_{t}, {\vec{q}}_{t} ) \in L^{1} \bigl( I; H^{s} ( {\varOmega})\times\mathbb {H}^{s} ( {\varOmega}) \bigr) $$

(3.3)

for a regularity exponent $s>\frac{1}{2}$, and let $(p^{h},{\vec{q}}^{ h} )$ be the semi-discrete DG approximation obtained by (3.1). Then we have the estimate for the error $e^{p}=p-p^{h}$ and $e^{\vec {{q}} }=\vec{ {q}}-\vec{ {q}}^{h}$

$$\begin{aligned} &\sup_{t\in I} \bigl( \bigl\Vert e^{p} \bigr\Vert _{0,\varOmega} + \bigl\Vert e^{{\vec{q}}} \bigr\Vert _{0,\varOmega} \bigr) +\sup_{t\in I} \bigl( \bigl\Vert \bigl[ \hspace{-2pt}\bigl[ e^{p} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{0,\mathcal{E}} + \bigl\Vert \bigl[ \hspace{-2pt}\bigl[e^{{\vec{q}}} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{0,\mathcal{E}} \bigr) \\ &\quad\leq C_{0} \bigl( \bigl\Vert e^{p}(0) \bigr\Vert _{0,\varOmega} + \bigl\Vert e^{{\vec {q}}}(0) \bigr\Vert _{0,\varOmega} \bigr) \\ &\qquad{}+C_{p} h^{\min\{s,k+\frac{1}{2}\}} \bigl( \Vert p \Vert _{\mathscr {L}^{\infty}_{1+s,\varOmega}}+ \Vert p_{t} \Vert _{\mathscr {L}^{1}_{s,\varOmega}} \bigr)+ C_{\vec{q}}h^{\min\{ s,k'+\frac {1}{2} \} } \bigl( \Vert {\vec{q}} \Vert _{\mathscr{L}^{\infty }_{1+s,\varOmega}} + \Vert { \vec{q}}_{t} \Vert _{\mathscr {L}^{1}_{s,\varOmega}} \bigr) \end{aligned}$$

with positive constants $C_{0}, C_{p}, C_{\vec{q}}$ depending on the bounds $c_{*}$, $c^{*}$, and $\sigma^{*}$, which are independent of the mesh size h, where k and $k'$ are the order of approximation polynomials $(p^{h}, \vec{q}^{ h})$, respectively.

Remark 3.4

The condition (3.3) implies that $( p, {\vec{q}} )\in C ( \bar{I}; H^{s} ( {\varOmega})\times\mathbb{H}^{s} ( {\varOmega}) )$, thus it is required to have the initial condition $( p_{0}, {\vec{q}}_{0} ) \in H^{s} ( {\varOmega})\times\mathbb{H}^{s} ( {\varOmega})$ and also

$$\begin{aligned} & \bigl\Vert e^{p}(0) \bigr\Vert _{0,\varOmega} =\bigl\| ( {p}- \varPi_{h} p) (0)\bigr\| _{0,\varOmega} \leq C h^{\min\{s,k +1\}} \Vert p \Vert _{s,\varOmega}, \\ & \bigl\Vert e^{{\vec{q}}}(0) \bigr\Vert _{0,\varOmega} =\bigl\| ({{ \vec{q}}}- \boldsymbol {\varPi}_{h} {{\vec{q}}}) (0)\bigr\| _{0,\varOmega} \leq C h^{\min\{s,k'+1 \}} \Vert {{\vec{q}}} \Vert _{s,\varOmega}. \end{aligned}$$

Therefore, Theorem 3.3 implies

$$\begin{aligned} \sup_{t\in I} \bigl( \bigl\Vert e^{p} \bigr\Vert _{0,\varOmega} + \bigl\Vert e^{{\vec{q}}} \bigr\Vert _{0,\varOmega } \bigr) +\sup_{t\in I} \bigl( \bigl\Vert \bigl[ \hspace{-2pt}\bigl[e^{p} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{0,\mathcal{E}} + \bigl\Vert \bigl[ \hspace{-2pt}\bigl[e^{{\vec{q}}} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{0,\mathcal {E}} \bigr) \leq Ch^{\min\{s,k+\frac{1}{2},k'+\frac{1}{2} \}}. \end{aligned}$$

It can be noted that, for smooth solutions, Theorem 3.3 yields the convergence rates in the $L^{2}$-norm:

$$\begin{aligned} \sup_{t\in I} \bigl( \bigl\Vert e^{p} \bigr\Vert _{0, {\varOmega}} + \bigl\Vert e^{{\vec{q}}} \bigr\Vert _{0, {\varOmega}} \bigr) \leq Ch^{\min\{k,k'\}+\frac{1}{2} }. \end{aligned}$$

Following [25], we introduce lifting operators in order to extend the numerical flux to the entire space $\mathcal{P}(h)\times \mathcal{Q}(h)$. We define the lifting operator $\mathcal{L}_{h}^{+} p \in\mathcal{Q}^{h} ( {\varOmega})$ for $p \in\mathcal{P}(h)$ by

$$\begin{aligned} \int_{ {\varOmega}} \mathcal{L}_{h}^{+} p\cdot{ \vec{q}}^{ h} \,dx = \sum_{e\in\mathcal{E} } \int_{e} [\hspace{-2pt}[p ]\hspace{-2pt}] \bigl( \vec{\mathbf {C}}_{12} \bigl[ \hspace{-2pt}\bigl[{ \vec{q}}^{ h} \bigr]\hspace{-2pt}\bigr]+ \bigl\{ \hspace{-2pt}\bigl\{ {\vec{q}}^{ h} \bigr\} \hspace{-2pt}\bigr\} \bigr) \,ds, \quad\forall{ \vec{q}}^{ h} \in\mathcal{Q}^{h}(\varOmega), \end{aligned}$$

(3.4)

and also $\mathcal{L}^{-}_{h} {\vec{q}} \in\mathcal{P}^{h}( {\varOmega })$ for ${\vec{q}} \in\mathcal{Q}(h)$ by

$$\begin{aligned} \int_{ {\varOmega}} \mathcal{L}_{h}^{-}{\vec{q}} p^{h} \,dx = \sum_{e\in \mathcal {E} } \int_{e} [\hspace{-2pt}[{\vec{q}}]\hspace{-2pt}] \cdot\bigl( \vec{\mathbf {C}}_{12} \bigl[ \hspace{-2pt}\bigl[p^{h} \bigr]\hspace{-2pt}\bigr]- \bigl\{ \hspace{-2pt}\bigl\{ p^{h} \bigr\} \hspace{-2pt}\bigr\} \bigr) \,ds,\quad \forall p^{h} \in \mathcal{P}^{h}( {\varOmega}). \end{aligned}$$

(3.5)

It can be seen that by the definition of the $L^{2}$-projection (3.2) we have

$$\begin{aligned} &\int_{\varOmega} \mathcal{L}^{+}_{h} p \cdot\vec{{q} } \,dx = \int_{\varOmega} \mathcal{L}^{+}_{h} p \cdot\boldsymbol { \varPi}_{h} {\vec{q}}\,dx,\\ &\int_{ {\varOmega }} \mathcal{L}^{-}_{h} {\vec{q}} p \,dx = \int_{\varOmega} \mathcal{L}^{-}_{h} {\vec{q}} {{ \varPi}}_{h} p \,dx\quad \forall p \in\mathcal{P}(h), {\vec{q}} \in \mathcal{Q}(h). \end{aligned}$$

We now extend (3.1) using the two lifting functions

$$ \begin{aligned} & \biggl(\frac{1}{c^{2}} p_{t},r \biggr) + \tilde{a}_{h}(p,r) - \tilde{b}'_{h}({\vec {q}},r) = 0\quad \forall r\in\mathcal{P}(h), t\in I, \\ &({\vec{q}}_{t},{\vec{v}}) + \tilde{b}_{h}(p,{\vec{v}}) + \tilde{c}_{h}({\vec{q}},{\vec{v}}) = 0\quad \forall{\vec{q}} \in\mathcal {Q}(h), t\in I, \end{aligned} $$

where the bilinear forms are given by

$$ \begin{aligned} &\tilde{a}_{h}(p,r) = \sum _{K \in\mathcal{T}_{h}} \int_{K} \frac {\sigma _{p}}{c^{2}}pr \,dx + \sum _{e \in\mathcal{E} } \int_{e} \mathtt{C}_{11} [\hspace{-2pt}[p ]\hspace{-2pt}]\cdot [\hspace{-2pt}[r ]\hspace{-2pt}]\,ds,\\ & \tilde{b}_{h}(p,{\vec{v}}) = -\sum _{K \in\mathcal{T}_{h}} \int_{K} p\nabla\cdot\vec{{v} } \,dx - \int_{\varOmega} p \mathcal{L}^{-}_{h} {\vec{v}} \,dx, \\ &\tilde{b}'_{h}(\vec{{q}},r) = \sum _{K \in\mathcal{T}_{h}} \int_{K}\vec{{q} } \cdot\nabla r \,dx - \int_{\varOmega} \vec{{q}} \cdot\mathcal{L}^{+}_{h} r \,dx,\\ &\tilde{c}_{h}(\vec{{q}},\vec{{v}}) = \sum_{K \in\mathcal{T}_{h}} \int_{K}\sigma_{\vec{q}} \vec{{q}}\cdot\vec{{v}} \,dx + \sum_{e \in \mathcal {E}} \int_{e} \mathtt{C}_{22} [\hspace{-2pt}[{q} ]\hspace{-2pt}] [\hspace{-2pt}[{v} ]\hspace{-2pt}]\,ds. \end{aligned} $$

(3.6)

Error equations. To derive the error equations we define for $r\in\mathcal{P}(h)$, $\vec{{v}}\in\mathcal{Q}(h)$ and $p \in{H}^{1}_{0}{( {\varOmega })}$, $\vec{{q}}\in\mathbb{H}^{1}( {\varOmega})$

$$ \begin{aligned} &\mathcal{R}^{p} (p, \vec{{v}} ):= \sum_{e\in\mathcal{E} } \int_{e} [\hspace{-2pt}[\vec{{v}} ]\hspace{-2pt}] \bigl( - \vec{\mathtt {C}}_{12}\cdot[\hspace{-2pt}[ \varPi_{h} p -p ]\hspace{-2pt}]+ \{\hspace{-2pt}\{ \varPi_{h} p -p \}\hspace{-2pt}\} \bigr) \,ds, \\ &\mathcal{R}^{\vec{q}} (\vec{{q}},r):= \sum_{e\in\mathcal{E} } \int_{e} [\hspace{-2pt}[r]\hspace{-2pt}]\cdot\bigl( \vec{\mathtt {C}}_{12} [\hspace{-2pt}[ \boldsymbol { \varPi}_{h} \vec{{q}} - \vec{{q}} ]\hspace{-2pt}]+ \{\hspace{-2pt}\{\boldsymbol {\varPi}_{h} \vec{{q}} -\vec{{q}} \}\hspace{-2pt}\} \bigr) \,ds. \end{aligned} $$

(3.7)

The assumption that $p \in H^{1}_{0}( {\varOmega}), \vec{{q}} \in\mathbb {H}^{1}( {\varOmega})$ ensures that $\mathcal{R}^{p}(p,\vec{{v}}), \mathcal {R}^{\vec{q}} ( \vec{{q}},r)$ are well defined since the trace map of $p, \vec{{q}}$ are uniquely defined on all $e\in\mathcal{E}$. From the definition (2.4) of the jump it directly follows that $\mathcal{R}^{p}(p,\vec{{v}})=0, \mathcal{R}^{\vec{q}} ( \vec{{q}} ,r)=0$ when $r\in H^{1}_{0}( {\varOmega}), \vec{{v}}\in\mathbb{H}^{1} ( {\varOmega})$. Using the definition of the error equations, we have the following property.

Lemma 3.5

Let the analytical solution $(p,\vec{{q}})$ of (2.1) satisfy

$$( p, \vec{{q}} ) \in L^{\infty} \bigl( I; H^{1} _{0}( {\varOmega})\times\mathbb{H}^{1} ( {\varOmega}) \bigr),\qquad ( p_{t}, \vec{{q}}_{t} ) \in L^{1} \bigl( I; L^{2} ( { \varOmega})\times\mathbb{L}^{2} ( {\varOmega}) \bigr). $$

Let $(p^{h},\vec{{q}}^{h})$ be the semi-discrete DG approximation obtained by (3.1). Then the error $e^{p}=p-p^{h}, e^{\vec{{q}}}=\vec{{q}}-\vec{{q}}^{h}$ satisfy

$$ \begin{aligned} & \biggl(\frac{1}{c^{2}}e^{p}_{t},r^{h} \biggr)+\tilde{a}_{h} \bigl(e^{p},r^{h} \bigr)- \tilde{b}_{h}' \bigl(e^{\vec{ {q}}},r^{h} \bigr)=\mathcal{R}^{\vec{q}} \bigl({\vec{ {q}}},r ^{h} \bigr),\quad \forall r^{h}\in\mathcal{P}^{h}( {\varOmega}) \textit{ a.e. in } I, \\ & \bigl(e^{\vec{{q}}}_{t},\vec{v}^{ h} \bigr) + \tilde{b}_{h} \bigl(e^{p},{\vec{v}^{ h}} \bigr)+ \tilde{c}_{h} \bigl(e^{\vec{{q}}},\vec{v}^{ h} \bigr) = \mathcal{R} ^{p} \bigl(p, \vec{v}^{ h} \bigr) ,\quad\forall \vec{v}^{ h} \in\mathcal{Q}^{h}(\varOmega) \textit{ a.e. in } I. \end{aligned} $$

(3.8)

Proof

Let $p^{h}\in\mathcal{P}^{h}(\varOmega)$ and $\vec{v}^{ h} \in \mathcal{Q}^{h}(\varOmega)$. Then we obtain using the discrete formulation in (3.1)

$$\begin{aligned} & \biggl(\frac{1}{c^{2}}e^{p}_{t},r^{h} \biggr)+ \tilde{a}_{h} \bigl(e^{p},r^{h} \bigr)- \tilde{b}_{h}' \bigl(e^{\vec {{q}}},r^{h} \bigr) \\ &\quad = \biggl(\frac{1}{c^{2}}p_{t},r^{h} \biggr)+ \tilde{a}_{h} \bigl(p,r^{h} \bigr)-\tilde{b}_{h}' \bigl({\vec{{q}}},r^{h} \bigr) \quad \text{a.e. in } I, \\ & \bigl(e^{\vec{{q}}}_{t},\vec{v}^{ h} \bigr)+ \tilde{b}_{h} \bigl(e^{p},\vec{v}^{ h} \bigr)+\tilde {c}_{h} \bigl(e^{\vec{{q}}},\vec{v}^{ h} \bigr) \\ &\quad= \bigl({ \vec{{q}}}_{t},\vec{v}^{ h} \bigr)+\tilde{b}_{h} \bigl(p,\vec{v}^{ h} \bigr)+\tilde{c}_{h} \bigl({\vec{{q}}}, \vec{v}^{ h} \bigr) \quad\text{a.e. in } I. \end{aligned}$$

By the definition of $\tilde{b}_{h}$, the property (3.2) of $L^{2}$-projection $\varPi_{h},\boldsymbol {\varPi}_{h}$, and the definitions (3.4), (3.5) of the lifted elements $\mathcal {L}^{+}_{h}$, $\mathcal{L}^{-}_{h}$, we obtain

$$\begin{aligned} &\tilde{b}_{h} \bigl(p,\vec{v}^{ h} \bigr)=- \sum _{K \in\mathcal{T}_{h}} \int_{K} p \nabla\cdot\vec{v}^{ h} \,dx -\sum _{e\in\mathcal{E}} \int_{e} \bigl[ \hspace{-2pt}\bigl[\vec{v}^{ h} \bigr]\hspace{-2pt}\bigr] \bigl( \vec{\mathtt{C}}_{12}\cdot[\hspace{-2pt}[\varPi_{h} p]\hspace{-2pt}]- \{\hspace{-2pt}\{\varPi_{h} p\}\hspace{-2pt}\} \bigr) \,ds, \\ &\tilde{b}_{h}' \bigl({\vec{{q}}},r^{h} \bigr)= \sum_{K \in\mathcal{T}_{h}} \int_{K}\vec{{q}}\cdot\nabla r^{h} \,dx -\sum _{e\in\mathcal{E} } \int_{e} \bigl[ \hspace{-2pt}\bigl[r^{h} \bigr]\hspace{-2pt}\bigr]\cdot \bigl( \vec{\mathtt{C}}_{12} [\hspace{-2pt}[\boldsymbol {\varPi}_{h} \vec {{q}}]\hspace{-2pt}] + \{\hspace{-2pt}\{\boldsymbol {\varPi}_{h} \vec{{q}} \}\hspace{-2pt}\} \bigr) \,ds. \end{aligned}$$

Since $( p_{t}, \vec{{q}} _{t}) \in L^{1} ( I; L^{2} (\varOmega)\times \mathbb{L}^{2} (\varOmega) )$, we have $\nabla\cdot\vec{{q}} \in L^{2}(\varOmega)$ and $\nabla p\in\mathbb{L}^{2}(\varOmega)$ almost everywhere in I, which implies that p and q⃗ have continuous normal components across all interior faces. By integration by parts in element-wise and combination with the trace operators, we obtain

$$\begin{aligned} &\tilde{b}_{h} \bigl(p,\vec{v}^{ h} \bigr)=\sum _{K \in\mathcal{T}_{h}} \int_{K}\nabla p \cdot\vec{v}^{ h} \,dx -\sum _{\mathcal{E}} \int_{e} \bigl[ \hspace{-2pt}\bigl[\vec{v}^{ h} \bigr]\hspace{-2pt}\bigr] \bigl( \{\hspace{-2pt}\{p\}\hspace{-2pt}\}+\vec{\mathtt{C}}_{12} \cdot[\hspace{-2pt}[\varPi _{h} p] \hspace{-2pt}]- \{\hspace{-2pt}\{\varPi_{h} p\}\hspace{-2pt}\} \bigr) \,ds, \\ &\tilde{b}_{h}' \bigl({\vec{{q}}},r^{h} \bigr)=- \sum_{K \in\mathcal{T}_{h}} \int_{K} \nabla\cdot\vec{{q}} r^{h} \,dx +\sum _{\mathcal{E}} \int_{e} \bigl[ \hspace{-2pt}\bigl[r^{h} \bigr]\hspace{-2pt}\bigr]\cdot \bigl( \{\hspace{-2pt}\{\vec{{q}}\}\hspace{-2pt}\} - \vec{\mathtt{C}}_{12} [\hspace{-2pt}[\boldsymbol { \varPi}_{h} \vec{{q}} ] \hspace{-2pt}] - \{\hspace{-2pt}\{\boldsymbol { \varPi}_{h} \vec{{q}} \}\hspace{-2pt}\} \bigr)\,ds. \end{aligned}$$

From the definition of $\mathcal{R}^{\vec{q}}({\vec{{q}}},r^{h})$ and $\mathcal{R}^{p}(p,\vec{v}^{ h})$ in (3.7) we have

$$\begin{aligned} & \biggl(\frac{1}{c^{2}}p_{t},r^{h} \biggr)+ \tilde{a}_{h} \bigl(p,r^{h} \bigr)-\tilde{b}_{h}' \bigl({\vec{{q}}},r^{h} \bigr) = \biggl(\frac{1}{c^{2}}p_{t} + \frac{\sigma_{p}}{c^{2}}p+ \nabla\cdot{\vec{{q}}},r^{h} \biggr) + \mathcal{R}^{\vec{q}} \bigl({\vec{{q}}},r^{h} \bigr), \\ & \bigl({\vec{{q}}}_{t},\vec{v}^{ h} \bigr)+ \tilde{b}_{h} \bigl(p,\vec{v}^{ h} \bigr)+\tilde {c}_{h} \bigl({\vec{{q}}},\vec{v}^{ h} \bigr) = ( { \vec{{q}}}_{t} +\sigma_{\vec{q}} {\vec{{q}}} +\nabla p,{\vec {{v}}}) + \mathcal{R}^{p} \bigl(p,\vec{v}^{ h} \bigr), \end{aligned}$$

and we obtain

$$\begin{aligned} & \biggl(\frac{1}{c^{2}}e^{p}_{t},r^{h} \biggr)+ \tilde{a}_{h} \bigl(e^{p},r^{h} \bigr)- \tilde{b}_{h}' \bigl(e^{\vec {{q}}},r^{h} \bigr) = \mathcal{R}^{\vec{q}} \bigl({\vec{{q}}},r^{h} \bigr), \\ & \bigl(e^{\vec{{q}}}_{t},\vec{v}^{ h} \bigr)+ \tilde{b}_{h} \bigl(e^{p},\vec{v}^{ h} \bigr)+ \tilde{c}_{h} \bigl(e^{\vec{{q}}},\vec{v}^{ h} \bigr)= \mathcal{R}^{p} \bigl(p,\vec{v}^{ h} \bigr), \end{aligned}$$

where we have used the differential equations in (2.1). □

There is also an important relation between $\tilde{b}_{h}$ and $\tilde {b}'_{h}$ from the dual property of ∇ and $-\nabla\cdot$ in the following lemma.

Lemma 3.6

Let the analytical solution $(p,{\vec {q}})$ of (2.1) satisfy

$$( p, {\vec{q}} ) \in L^{\infty} \bigl( I; H^{1} _{0}( \varOmega)\times\mathbb{H}^{1} (\varOmega) \bigr),\qquad ( p_{t}, { \vec{q}}_{t} ) \in L^{1} \bigl( I; L^{2} (\varOmega) \times\mathbb{L}^{2} (\varOmega) \bigr). $$

Let $(p^{h},{\vec{q}}^{ h})$ be the semi-discrete DG approximation obtained by (3.1). Then the following property holds for all $(r^{h}, {\vec{v}}^{h}) \in \mathcal{P}^{h}(\varOmega)\times\mathcal{Q}^{h}(\varOmega)$:

$$\begin{aligned} &{-}\tilde{b}_{h}' \bigl(e^{ {\vec{q}}}, \varPi_{h} p-p^{h} \bigr)+\tilde{b}_{h} \bigl(e^{p}, \boldsymbol {\varPi}_{h} {\vec{q}}- {\vec{q}}^{ h} \bigr)= 0, \\ & {-}\tilde{b}_{h}' \bigl(\vec{v}^{ h} ,r^{h} \bigr) + \tilde{b}_{h} \bigl(r^{h}, \vec{v}^{ h} \bigr) = 0. \end{aligned}$$

Proof

By the definition of $\tilde{b}_{h}'$, the property (3.4) of lifted element, and the property of $L^{2}$-projection, we obtain

$$\begin{aligned} \tilde{b}_{h}' \bigl({ \vec{q}}-\boldsymbol { \varPi}_{h} \vec{q},r^{h} \bigr)&=0. \end{aligned}$$

(3.9)

Here, we have used the definition of $L^{2}$-projection, $\boldsymbol {\varPi}_{h} ({ \vec{q}}-\boldsymbol {\varPi}_{h} \vec{q} )=\boldsymbol {\varPi}_{h} { \vec{q}}-\boldsymbol {\varPi}_{h} \vec {q}=\vec{0}$. In the similar way, $\tilde{b}_{h}( p- {\varPi}_{h} p, \vec{q} ^{h}) =0.$ For $(r^{h},{\vec{v}} ^{h} ) \in\mathcal{P}^{h}(\varOmega) \times \mathcal {Q}^{h}(\varOmega)$, we use definition of $\tilde{b}_{h}'$, element-wise integration by parts, and the trace identity (2.5) to obtain

$$\begin{aligned} \tilde{b}_{h}' \bigl( \vec{v}^{ h} ,r^{h} \bigr)=-\sum_{K \in\mathcal{T}_{h}} \int_{K} \nabla\cdot\vec{v}^{ h} r^{h} \,dx -\sum_{e\in\mathcal{E} } \int_{e} \bigl( \bigl[ \hspace{-2pt}\bigl[r^{h} \bigr]\hspace{-2pt}\bigr] \cdot\vec{\mathtt{C}}_{12} - \bigl\{ \hspace{-2pt}\bigl\{ r^{h} \bigr\} \hspace{-2pt}\bigr\} \bigr) \bigl[ \hspace{-2pt}\bigl[\vec{v}^{ h} \bigr]\hspace{-2pt}\bigr]\,ds, \end{aligned}$$

and from the definition of $\tilde{b}_{h}$,

$$\begin{aligned} \tilde{b}_{h} \bigl( r^{h}, \vec{v}^{ h} \bigr) =- \sum_{K \in\mathcal{T}_{h}} \int_{K} r^{h} \nabla\cdot\vec{v}^{ h} \,dx -\sum_{e\in\mathcal{E} } \int_{e} \bigl( \bigl[ \hspace{-2pt}\bigl[r^{h} \bigr]\hspace{-2pt}\bigr] \cdot\vec{\mathtt{C}}_{12}- \bigl\{ \hspace{-2pt}\bigl\{ r^{h} \bigr\} \hspace{-2pt} \bigr\} \bigr) \bigl[ \hspace{-2pt}\bigl[ \vec{v}^{ h} \bigr]\hspace{-2pt}\bigr]\,ds. \end{aligned}$$

Subtracting $\tilde{b}'_{h}$ from $\tilde{b}_{h}$ we have

$$ -\tilde{b}_{h}' \bigl( \vec{v}^{ h},r^{h} \bigr) +\tilde{b}_{h} \bigl( r^{h}, \vec{v}^{ h} \bigr)=0\quad \forall\bigl(r^{h}, \vec{v}^{ h} \bigr) \in\mathcal{P}^{h}(\varOmega)\times \mathcal{Q}^{h}(\varOmega). $$

(3.10)

Using the definition of error $e^{p}$ and $e^{\vec{q}}$ with the properties (3.9) and (3.10) we obtain

$$\begin{aligned} \tilde{b}_{h}' \bigl(e^{ \vec{q}}, \varPi_{h} p-p^{h} \bigr)-\tilde{b}_{h} \bigl(e^{p}, \boldsymbol { \varPi}_{h} \vec{q}- \vec{q}^{h} \bigr) &=0, \end{aligned}$$

which completes the proof. □

Approximation properties. Let $\varPi_{h}$ and $\boldsymbol {\varPi}_{h}$ denote the $L^{2}$-projections onto $\mathcal {V}^{h}$ and $\mathcal{Q}^{h}$, respectively. We note the following $L^{2}$-projection approximation properties; see [7]. Using the approximation properties in [7], we introduce the following results.

Lemma 3.7

Let $p\in H^{1+s}(\varOmega), s>\frac{1}{2}$. Then the following holds:

$$\begin{aligned} &\bigl\Vert \{\hspace{-2pt}\{\varPi_{h}p-p\}\hspace{-2pt}\} \bigr\Vert _{0,\mathcal{E}} \leq Ch^{\min\{ s,k\} +\frac{1}{2}} \Vert p \Vert _{1+s,\varOmega}, \\ &\bigl\Vert [\hspace{-2pt}[\varPi_{h}p-p]\hspace{-2pt}] \bigr\Vert _{0,\mathcal {E}} \leq Ch^{\min\{ s,k\} +\frac{1}{2}} \Vert p \Vert _{1+s,\varOmega} \end{aligned}$$

with a constant C that is independent of the local mesh size $h_{K}$ and depends only on the shape-regularity of the mesh, the approximation order k, the dimension d, and the regularity exponent s.

Proof

It is directly obtained from the properties in [7] and definition of jump and average on faces of elements K. □

Lemma 3.8

Let $(p,\vec{q})\in H^{1+s}(\varOmega) \times\mathbb{H}^{1+s}(\varOmega)$ with $s>\frac{1}{2}$. Then, the following holds:

• (i) For $( r,\vec{{v}}) \in\mathcal{P}(h) \times \mathcal{Q}(h)$, the forms (3.7) can be bounded by

  $$\begin{aligned} & \bigl\vert \mathcal{R}^{p} (p, \vec{{v}}) \bigr\vert \leq C_{R}^{p} h^{\min\{ s,k \} + \frac{1}{2}} \bigl\Vert {\mathtt{C} ^{\frac{1}{2}}_{22} } [\hspace{-2pt}[\vec{{v}} ]\hspace{-2pt}] \bigr\Vert _{0,\mathcal{E}} \Vert p \Vert _{{1+s},\varOmega}, \\ & \bigl\vert \mathcal{R}^{\vec{q}} (\vec{q},r) \bigr\vert \leq C_{R}^{\vec{q}} h^{\min\{ s,k' \} + \frac{1}{2}} \bigl\Vert \mathtt{C}_{11} ^{\frac {1}{2}} [\hspace{-2pt}[r ]\hspace{-2pt}] \bigr\Vert _{0,\mathcal{E}} \Vert \vec{ {q}} \Vert _{ {1+s},\varOmega}, \end{aligned}$$

  with constants $C_{R}^{p}$ and $C_{R}^{\vec{q}}$ independent of h, which depend only on the stabilization parameters $\boldsymbol {\alpha }_{11}, \boldsymbol {\alpha}_{12}, \boldsymbol {\alpha}_{22}$ given in (2.3), and the constant in the approximation properties in [7].

• (ii) The bilinear forms are estimated by the following:

  $$\begin{aligned} &\tilde{a}_{h} \bigl(e^{p},\varPi_{h} p-p \bigr) \leq C_{a} h^{\min\{s, k\}+\frac{1}{2} } \bigl( h^{\frac{1}{2} } \bigl\Vert e^{p} \bigr\Vert _{0,\varOmega}+ \bigl\Vert \mathtt {C}_{11}^{\frac {1}{2}} \bigl[ \hspace{-2pt}\bigl[e^{p} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{0,\mathcal {E}} \bigr) \Vert p \Vert _{ {1+s},\varOmega}, \\ &\tilde{c}_{h} \bigl(e^{\vec{q}},\boldsymbol {\varPi}_{h} \vec{q}- \vec{q} \bigr) \leq C_{c} h^{\min \{s,k'\}+\frac{1}{2}} \bigl( h^{\frac{1}{2} } \bigl\Vert e^{\vec {q}} \bigr\Vert _{0,\varOmega} + \bigl\Vert \mathtt{C}_{22}^{\frac{1}{2}} \bigl[ \hspace{-2pt}\bigl[e^{\vec {q}} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{0,\mathcal{E}} \bigr) \Vert \vec{q} \Vert _{ {1+s},\varOmega}, \end{aligned}$$

  with constants $C_{a}$ and $C_{c}$ independent of h, which depend only on $\boldsymbol {\alpha}_{11}, \boldsymbol {\alpha}_{22}$, and the constant in the approximation properties in [7].

Proof

(i) To show the first estimate we begin with the definition of $\mathcal{R}^{p}$ in (3.7) and apply the Cauchy–Schwartz inequality and approximation properties in [7] to obtain

$$\begin{aligned} \bigl\vert \mathcal{R}^{p} (p, \vec{{v}} ) \bigr\vert ^{2} \leq{}& \sum_{e \in\mathcal{E} } \int_{e} \bigl\vert {\mathtt{C}^{\frac {1}{2}}_{22} } [\hspace{-2pt}[\vec{{v}} ]\hspace{-2pt}] \bigr\vert ^{2} \,ds \sum _{e \in\mathcal{E} } \int_{e} {\mathtt{C} ^{-1}_{22} } \bigl\vert \bigl( \vec{\mathtt{C}}_{12}\cdot[\hspace{-2pt}[ \varPi_{h} p -p ]\hspace{-2pt}]+ \{\hspace{-2pt}\{ \varPi_{h} p -p \}\hspace{-2pt}\} \bigr) \bigr\vert ^{2} \,ds \\ \leq{}&\alpha_{22} ^{-1} \bigl\Vert {\mathtt{C}^{\frac{1}{2}}_{22} } [\hspace{-2pt}[ \vec{{v}} ]\hspace{-2pt}] \bigr\Vert _{0,\mathcal{E}}^{2} \sum _{K \in \mathcal{T}_{h} } \bigl(1+ \vert\vec{\mathtt{C}}_{12} \vert\bigr) \Vert p - { \varPi}_{h} p \Vert ^{2} _{0,\partial K} \\ \leq{}& { \bigl({C_{R}^{p}} \bigr)}^{2} h^{2\min\{ s,k \}+ 1 } \bigl\Vert {\mathtt{C}^{\frac {1}{2}}_{22} } [\hspace{-2pt}[\vec{{v}} ]\hspace{-2pt}] \bigr\Vert ^{2}_{0,\mathcal{E}} \Vert p \Vert ^{2} _{1+s,\varOmega} \end{aligned}$$

for a positive constant $C_{R}^{p}$ that depends on $\boldsymbol {\alpha}_{12}, \boldsymbol {\alpha}_{22}$. This completes the first estimate. Similarly, we can have the second bound in (i).

(ii) From the definition of $\tilde{a}_{h}$ and $\tilde{c}_{h}$ in (3.6) we apply Hölder’s inequality, the definition of $\alpha _{11}$, the Cauchy–Schwartz inequality, and the approximation properties in [7] to obtain the estimates of (ii) with the same order of h. □

Proof of Theorem 3.3 .

Proof

From Theorem 2.1, we have

$$e^{p} \in C^{0} \bigl(\bar{I};\mathcal{P}(h) \bigr)\cap C^{1} \bigl( \bar{I}; L^{2}( {\varOmega}) \bigr) \quad\text{and}\quad e^{\vec{q} } \in C^{0} \bigl(\bar{I};\mathcal{Q}(h) \bigr)\cap C^{1} \bigl( \bar{I}; \mathbb{L}^{2}( {\varOmega}) \bigr). $$

Since $e^{p}= p- \varPi_{h} p+ \varPi_{h} p-p^{h}$, $e^{\vec{q}} =\vec{q} -\boldsymbol {\varPi }_{h} \vec{q} +\boldsymbol {\varPi}_{h} \vec{q}-\vec{q} ^{h}$, using the error equations (3.8), we have

$$\begin{aligned} &\frac{1}{2} \biggl(\frac{d}{dt} \biggl\Vert \frac{1}{c}e^{p} \biggr\Vert _{0,\varOmega}^{2}+ \frac {d}{dt} \bigl\Vert e^{\vec{q}} \bigr\Vert _{0,\varOmega}^{2} \biggr)\\ &\quad = \biggl( \frac{1}{c^{2}} e_{t}^{p},p-\varPi_{h} p \biggr)- \tilde{a}_{h} \bigl(e^{p},\varPi_{h}p-p^{h} \bigr) + \bigl(e_{t}^{\vec{q}},\boldsymbol {\varPi}_{h} \vec{q} - \vec{q}^{h} \bigr) \\ &\qquad{}-\tilde{c}_{h} \bigl(e^{\vec{q}},\boldsymbol {\varPi}_{h}\vec{q}- \vec{q}^{h} \bigr) +\mathcal{R}^{\vec{q}} \bigl({\vec{q}}, \varPi_{h}p-p^{h} \bigr) +\mathcal{R}^{p} \bigl(p,\boldsymbol { \varPi}_{h}\vec{q}-\vec{q}^{h} \bigr), \end{aligned}$$

by the property in (2.2). Now we fix $\tau\in I$ and integrate over the time interval $(0,\tau)$, which yields

$$\begin{aligned} &\frac{1}{2} \biggl( \biggl\Vert \frac{1}{c}e^{p}(\tau) \biggr\Vert _{0,\varOmega}^{2} + \bigl\Vert e^{\vec{q}}(\tau) \bigr\Vert _{0,\varOmega}^{2} \biggr)+ \int_{0}^{\tau} \bigl( \tilde{a}_{h} \bigl(e^{p},e^{p} \bigr)+\tilde{ c}_{h} \bigl(e^{\vec{q} },e^{\vec{q}} \bigr) \bigr) \,dt \\ &\quad =\frac{1}{2} \biggl( \biggl\Vert \frac{1}{c}e^{p}(0) \biggr\Vert _{0,\varOmega }^{2} + \bigl\Vert e^{\vec {q}}(0) \bigr\Vert _{0,\varOmega}^{2} \biggr) + \int_{0}^{\tau} \biggl( \biggl(\frac{1}{c^{2}}e_{t}^{p},p- \varPi_{h} p \biggr)+ \bigl(e_{t}^{\vec{q}}, \vec{q}-\boldsymbol { \varPi} _{h}\vec{q} \bigr) \biggr)\,dt \\ &\qquad{} + \int_{0}^{\tau} \bigl(\tilde{a}_{h} \bigl(e^{p},p- \varPi_{h} p \bigr) +\tilde{c}_{h} \bigl(e^{\vec{q}}, \vec{q}- \boldsymbol {\varPi}_{h} \vec{q} \bigr) + \mathcal{R}^{p} \bigl(p,\boldsymbol {\varPi}_{h} \vec{q}- \vec{q}^{ h} \bigr) \\ &\qquad{}+\mathcal{R}^{\vec {q}} \bigl({\vec{q}}, \varPi_{h} p-p^{h} \bigr) \bigr) \,dt. \end{aligned}$$

(3.11)

Integration by parts in the first integral on the right hand side and the standard Hölder inequality yield

$$\begin{aligned} &\int_{0}^{\tau} \biggl( \biggl( \frac{1}{c^{2}}e_{t}^{p},p- \varPi_{h} p \biggr)+ \bigl(e_{t}^{\vec {q}}, \vec{q}-\boldsymbol { \varPi} _{h}\vec{q} \bigr) \biggr)\,dt \\ &\quad= \biggl[ \biggl(\frac{1}{c^{2}}e^{p},p-\varPi p \biggr)+ \bigl( e^{\vec{q}},\vec{q}-\boldsymbol {\varPi}_{h} \vec{q} \bigr) \biggr]_{t=0}^{t=\tau} \\ &\qquad{}- \int_{0}^{\tau} \biggl( \biggl(\frac{1}{c^{2}}e^{p},(p- \varPi_{h} p)_{t} \biggr)+ \bigl(e^{\vec {q}}, (\vec{q}- \boldsymbol { \varPi}_{h} \vec{q})_{t} \bigr) \biggr)\,dt \leq T_{1}, \end{aligned}$$

where

$$\begin{aligned} T_{1}:={}& \biggl\Vert \frac{1}{c} e^{p} \biggr\Vert _{\mathscr{L}^{\infty}_{0, {\varOmega}}} \biggl( 2 \biggl\Vert \frac{1}{c}(p- \varPi_{h} p) \biggr\Vert _{\mathscr{L}^{\infty}_{0, {\varOmega}}} + \biggl\Vert \frac{1}{c}(p-\varPi_{h} p)_{t} \biggr\Vert _{\mathscr{L}^{1}_{0, {\varOmega}}} \biggr)\\ &{}+ \bigl\Vert e^{\vec {q}} \bigr\Vert _{\mathscr{L}^{\infty}_{0, {\varOmega}}} \bigl( 2 \Vert \vec{q}-\boldsymbol {\varPi}_{h} \vec {q} \Vert _{\mathscr{L}^{\infty }_{0, {\varOmega}}} + \bigl\Vert (\vec{q}-\boldsymbol {\varPi}_{h} \vec{q})_{t} \bigr\Vert _{\mathscr {L}^{1}_{0, {\varOmega }}} \bigr). \end{aligned}$$

From the definition of $\tilde{a}_{h}$ and $\tilde{c}_{h}$ and the standard Hölder inequality in the second integral on the right hand side in (3.11), we have

$$\begin{aligned} \int_{0}^{\tau} \bigl(\tilde{a}_{h} \bigl(e^{p},p- \varPi_{h} p \bigr) +\tilde{c}_{h} \bigl(e^{\vec{q}}, \vec{q}- \boldsymbol {\varPi}_{h} \vec{q} \bigr) \bigr)\,dt \leq T_{2}, \end{aligned}$$

where

$$\begin{aligned} T_{2}:={}& {\sigma^{*}}T \biggl( \biggl\Vert \frac{1}{c}e^{p} \biggr\Vert _{{\mathscr {L}^{\infty }(0,\varOmega)}} \bigl\Vert c(p- \varPi_{h} p) \bigr\Vert _{\mathscr{L}^{\infty }_{0, {\varOmega}}}\\ &{}+ \bigl\Vert e^{\vec{q}} \bigr\Vert _{\mathscr{L}^{\infty}(0,( {\varOmega}))} \Vert \vec{q}- \boldsymbol {\varPi}_{h} \vec{q} \Vert _{\mathscr{L}^{\infty}_{0, {\varOmega}}} \biggr) \\ &{}+ \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{11} \bigl[ \hspace{-2pt}\bigl[e^{p} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{\mathscr{L}^{1}(0,\mathcal {E})} \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{11} [\hspace{-2pt}[p- \varPi_{h} p]\hspace{-2pt}] \bigr\Vert _{\mathscr {L}^{\infty}(0,\mathcal {E})} \\ &{}+ \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{22} \bigl[ \hspace{-2pt}\bigl[e^{\vec{q}} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{\mathscr {L}^{1}(0,\mathcal{E})} \bigl\Vert \mathtt{C}^{\frac {1}{2}}_{22} [\hspace{-2pt}[ \vec{q}- \boldsymbol {\varPi} _{h}\vec{q}]\hspace{-2pt}] \bigr\Vert _{\mathscr{L}^{\infty}(0,\mathcal{E})}. \end{aligned}$$

Next, we combine $T_{1}$ and $T_{2}$ and rewrite the left hand side (3.11) with the new bounds

$$\begin{aligned} &\frac{1}{2} \biggl( \biggl\Vert \frac{1}{c}e^{p}( \tau) \biggr\Vert _{0,\varOmega }^{2} + \bigl\Vert e^{\vec {q}}(\tau) \bigr\Vert _{0,\varOmega}^{2} \biggr)\\ &\qquad{} + \int_{0}^{\tau} \biggl( \biggl\Vert \frac{\sigma_{p}}{c^{2}} e^{p} \biggr\Vert ^{2}_{0, {\varOmega}} + \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{11} \bigl[ \hspace{-2pt}\bigl[e^{p} \bigr]\hspace{-2pt}\bigr] \bigr\Vert ^{2}_{0,\mathcal{E}} + \bigl\Vert {\sigma_{\vec{q}}} e^{\vec{q}} \bigr\Vert ^{2}_{0, {\varOmega}} + \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{22} \bigl[ \hspace{-2pt}\bigl[e^{\vec{q}} \bigr]\hspace{-2pt}\bigr] \bigr\Vert ^{2}_{0,\mathcal{E}} \biggr) \,dt \\ &\quad \leq\frac{1}{2} \biggl( \biggl\Vert \frac{1}{c}e^{p}(0) \biggr\Vert _{0, {\varOmega }}^{2} + \bigl\Vert e^{\vec {q}}(0) \bigr\Vert _{0, {\varOmega}}^{2} \biggr) \\ &\qquad{}+ \int_{0}^{\tau} \bigl( \bigl\vert \mathcal{R}^{p} \bigl(p,\boldsymbol {\varPi}_{h} \vec{q}-\vec {q}^{ h} \bigr) \bigr\vert + \bigl\vert \mathcal{R}^{\vec{q}} \bigl({\vec{q}},\varPi_{h} p-p^{h} \bigr) \bigr\vert \bigr) \,dt+T_{1} +T_{2}. \end{aligned}$$

Since this inequality holds for any $\tau\in I$, it also holds for the supremum over I, that is,

$$\begin{aligned} &\frac{1}{2}\sup_{t\in I} \biggl( \biggl\Vert \frac{1}{c} e^{p}(t) \biggr\Vert ^{2}_{0, {\varOmega}} + \bigl\Vert e^{\vec{q}}(t) \bigr\Vert ^{2}_{ 0, {\varOmega }} \biggr)\\ &\qquad{} + \biggl\Vert \frac{\sigma_{p}}{c^{2}} e^{p} \biggr\Vert ^{2}_{\mathscr{L}^{1}_{0, {\varOmega}}} + \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{11} \bigl[ \hspace{-2pt}\bigl[e^{p} \bigr]\hspace{-2pt}\bigr] \bigr\Vert ^{2}_{\mathscr {L}^{1}_{0,{\mathcal{E}}}} + \bigl\Vert {\sigma_{\vec{q}}} e^{\vec{q}} \bigr\Vert ^{2}_{\mathscr {L}^{1}_{0, {\varOmega}}} + \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{22} \bigl[ \hspace{-2pt}\bigl[e^{\vec {q}} \bigr]\hspace{-2pt}\bigr] \bigr\Vert ^{2}_{\mathscr{L}^{1}_{0, {\mathcal{E}}}} \\ &\quad \leq\frac{1}{2} \biggl( \biggl\Vert \frac{1}{c}e^{p}(0) \biggr\Vert _{0, {\varOmega }}^{2} + \bigl\Vert e^{\vec {q}}(0) \bigr\Vert _{0, {\varOmega}}^{2} \biggr) \\ &\qquad{}+ \int_{I} \bigl( \bigl\vert \mathcal{R}^{p} \bigl(p, \boldsymbol {\varPi}_{h} \vec{q}-\vec{q}^{ h} \bigr) \bigr\vert + \bigl\vert \mathcal{R}^{\vec{q}} \bigl({\vec{q}},\varPi_{h} p-p^{h} \bigr) \bigr\vert \bigr)\,dt+T_{1}+T_{2}. \end{aligned}$$

Using the geometric–arithmetic mean inequality $|ab|\leq\frac {1}{2\varepsilon} a^{2} + \frac{\varepsilon}{2}b^{2}$ valid for $\varepsilon>0$, $(a+b)^{2}\leq2(a^{2}+b^{2})$, and the approximation results in Lemma 3.7, we obtain

$$\begin{aligned} T_{1}+T_{2}\leq{}& \frac{1}{ \varepsilon} \biggl( \biggl\Vert \frac{1}{c} e^{p} \biggr\Vert _{\mathscr{L}^{\infty }_{0, {\varOmega}}} ^{2} + \bigl\Vert e^{\vec{q}} \bigr\Vert _{\mathscr {L}^{\infty}_{0, {\varOmega }}} ^{2} \biggr) + \frac{1 }{2\varepsilon'} \bigl( \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{11} \bigl[ \hspace{-2pt}\bigl[e^{p} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{\mathscr{L}^{1}_{0, {\mathcal{E}}}} ^{2} + \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{22} \bigl[ \hspace{-2pt}\bigl[e^{\vec{q}} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{\mathscr{L}^{1}_{0, {\mathcal{E}}}}^{2} \bigr) \\ &{}+C\varepsilon h^{2\min\{s,k\} +2} \biggl( \frac{ 1}{2} \sigma^{*} {^{2}}T^{2} {c^{*}}^{2}+ \frac{4}{{c_{*}^{2}} } \biggr) \Vert p \Vert _{\mathscr {L}^{\infty}_{1+s, {\varOmega}}}^{2} \\ &{}+ C\varepsilon h^{2\min\{s,k'\} +2} \biggl( \frac{ 1}{2} \sigma^{*} {^{2}}T^{2} + 4 \biggr) \Vert \vec{q} \Vert _{\mathscr{L}^{\infty}_{1+s, {\varOmega}}}^{2} \\ &{}+C h^{2\min\{s,k\}+1 } \biggl(\frac{\varepsilon'}{2} \Vert p \Vert _{\mathscr{L}^{\infty}_{1+s, {\varOmega}}} ^{2} +{\varepsilon}\frac { 1}{{c_{*}^{2}} } \Vert p_{t} \Vert _{\mathscr{L}^{1}_{s, {\varOmega}}}^{2} \biggr)\\ &{}+Ch^{2\min\{s,k'\}+1 } \biggl( \frac{\varepsilon'}{2} \Vert \vec {q} \Vert _{\mathscr {L}^{\infty}_{1+s, {\varOmega}}} ^{2}+ \varepsilon \Vert \vec{q}_{t} \Vert _{\mathscr {L}^{1}_{s, {\varOmega }}} ^{2} \biggr). \end{aligned}$$

Using the approximation properties in [7] and Lemma 3.8 we can also bound the error equations

$$\begin{aligned} \int_{I} \bigl\vert \mathcal{R}^{p} \bigl(p,\boldsymbol { \varPi} \vec{q}-\vec{q}^{ h} \bigr) \bigr\vert \,dt \leq{}& \frac{1}{2\varepsilon'} \bigl( \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{22} \bigl[ \hspace{-2pt}\bigl[e^{\vec{q}} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{\mathscr {L}^{1}_{0, \mathcal{E}}}^{2} + \alpha_{22} h^{2\min\{ s,k' \}+1 } \Vert \vec{q} \Vert _{\mathscr{L}^{\infty }_{1+s, \varOmega}}^{2} \bigr) \\ &{} + \frac{\varepsilon'}{2} \bigl({C_{R}^{p}} \bigr)^{2} \bigl(1+T^{2} \bigr) h^{2\min\{ s,k \} +1} \Vert p \Vert _{\mathscr{L}^{\infty}_{1+s, {\varOmega}}}^{2} \end{aligned}$$

and

$$\begin{aligned} \int_{I} \bigl| \mathcal{R}^{q} \bigl({\vec{q}}, \varPi_{h} p-p^{h} \bigr)\bigr|\,dt \leq{}& \frac{1}{2\varepsilon'} \bigl( \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{11} \bigl[ \hspace{-2pt}\bigl[e^{p} \bigr]\hspace{-2pt}\bigr] \bigr\Vert _{\mathscr {L}^{1}_{0, \mathcal{E}}}^{2} + \alpha_{11} h^{2\min\{ s,k \}+1 } \Vert p \Vert _{\mathscr {L}^{\infty}_{1+s,\varOmega}}^{2} \bigr) \\ &{} + \frac{\varepsilon'}{2} \bigl({C_{R}^{\vec{q}}} \bigr)^{2} \bigl(1+T^{2} \bigr) h^{2\min\{ s,k' \} +1} \Vert \vec{q} \Vert _{\mathscr{L}^{\infty}_{1+s, {\varOmega}}}^{2}. \end{aligned}$$

Combining the above estimates and $T_{1}, T_{2}$ with $\varepsilon=4$ and $\varepsilon'=2$, we have

$$\begin{aligned} &\frac{1}{4}\sup_{t\in I} \biggl( \biggl\Vert \frac{1}{c}e^{p} \biggr\Vert ^{2}_{0, {\varOmega}} + \bigl\Vert e^{\vec{q}} \bigr\Vert ^{2}_{0,\varOmega } \biggr) +\frac{1}{2} \bigl( \bigl\Vert \mathtt{C}^{\frac{1}{2}}_{11} \bigl[ \hspace{-2pt}\bigl[e^{p} \bigr]\hspace{-2pt}\bigr] \bigr\Vert ^{2}_{\mathscr {L}^{1}_{0, \mathcal{E}}}+ \bigl\Vert \mathtt{C}^{\frac {1}{2}}_{22} \bigl[ \hspace{-2pt}\bigl[e^{\vec{q}} \bigr]\hspace{-2pt}\bigr] \bigr\Vert ^{2}_{\mathscr{L}^{1}_{0, \mathcal{E}}} \bigr)\\ &\quad \leq\frac{1}{2} \biggl( \biggl\Vert \frac {1}{c}e^{p}(0) \biggr\Vert _{0,\varOmega}^{2}+ \bigl\Vert e^{\vec{q}}(0) \bigr\Vert _{0, {\varOmega }}^{2} \biggr) \\ &\qquad{}+C h^{2\min\{s,k+\frac{1}{2}\}} \bigl( \Vert p \Vert _{\mathscr {L}^{\infty }_{{1+s,\varOmega}}}^{2}+ \Vert p_{t} \Vert _{{\mathscr {L}^{1}_{s,\varOmega}}}^{2} \bigr)+C h^{2\min\{ s,k'+\frac{1}{2} \} } \bigl( \Vert \vec{q} \Vert _{{\mathscr {L}^{\infty}_{1+s,\varOmega}}}^{2} + \Vert \vec{q}_{t} \Vert _{{\mathscr {L}^{1}_{s,\varOmega}}}^{2} \bigr) \end{aligned}$$

with a constant that is independent of the mesh size h. Using the bound $\frac{1}{{c^{*}}^{2}}\|e^{p}\|^{2}_{0,\varOmega} \leq\| \frac {1}{c}e^{p}\|^{2}_{0,\varOmega}$, we conclude the proof of Theorem 3.3. □

Remark 3.9

In our LDG method the parameters are independent of mesh size h, which gives higher accuracy of the $L^{2}$-norms of errors in p and q⃗ with $k+\frac{1}{2}$, $k'+\frac{1}{2}$, respectively, for smooth solutions.

Remark 3.10

In this paper, we consider a first-order hyperbolic system of acoustic wave equation in a bounded domain with lower-order damping terms and present a priori error analysis introducing a LDG method for the system. The system (2.1) with the time-dependent damping terms $\sigma_{p}(x,t)$ and $\sigma_{\vec{q}}(x,t)$ can also be considered and the well-posedness with the initial condition $(p_{0},{\vec{q}}_{0})$ in $D(L)$ is obtained from Theorem 4.10, page 245 in [5].

4 Numerical experiments

In this section, we test the model problem to support the theoretical result of the LDG method. We consider rectangular meshes $\mathcal{T}_{h}$ over $\varOmega=[-1,1]^{2}$, consisting of $N^{2}$ uniform cubes with corresponding mesh size $h=2\sqrt {2}/N$ in the numerical experiments. For the time discretization, we employ a one-step Euler scheme with a sufficiently small time step size, which guarantees the numerical stability and also that errors introduced by the time discretization can be neglected in the experiments. The initial condition is given as a two-dimensional Gaussian function

$$f(x,y)=Ae^{-{\rho( x ^{2}+y^{2})}},\quad (x,y)\in\varOmega:=[-1,1]^{2}, $$

where the amplitude coefficient A and the spreading coefficient ρ are taken as $A=1$ and $\rho=9$. As the initial condition is almost zero around the boundary, we consider the homogeneous boundary condition as the Dirichlet boundary condition. The numerical orders of convergence for numerical solutions are measured as follows:

$$\begin{aligned} e_{h}:=\frac{\log( \frac{ \Vert p^{h}-p^{h/2} \Vert _{0,\varOmega}+ \Vert {\vec{q}}^{ h}-{\vec{q}}^{ h/2} \Vert _{0,\varOmega}}{ \Vert p^{h/2}-p^{h/4} \Vert _{0,\varOmega}+ \Vert {\vec{q}}^{ h/2}-{\vec{q}}^{ h/4} \Vert _{0,\varOmega}} )}{\log (2)}, \end{aligned}$$

where $p^{h/n}$ and ${\vec{q}}^{ h/n}$ are numerical solutions corresponding to mesh size $h/n\ (n=1,2,4)$ at the final time $T=1$. In addition, we demonstrate the behavior of the energy for various dampings, which is defined by

$$ E(t):=\frac{1}{2} \int_{ {\varOmega}} \biggl(\frac{1}{c^{2}} \bigl\vert p^{h}(t) \bigr\vert ^{2} + \bigl\vert { \vec{q}}^{ h} (t) \bigr\vert ^{2} \biggr)\,dx. $$

(4.1)

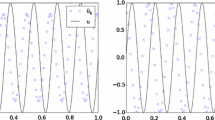
We repeat the tests to obtain convergence order for a sequence of uniformly refined meshes, different damping factors $\sigma_{p}=\sigma _{\vec{q}}=\sigma$ and different coefficients $\mathtt {C}_{11},\mathtt {C}_{22},\vec{\mathtt{C}}_{12}$ with a fixed set $(k,k')$ of the orders of polynomials for $p^{h}$ and $\vec{q}^{ h}$. For the same mesh size h as obtained from $N=11$, we compute the convergence rate $e_{h}$ for different sets of parameters $\vec{\mathtt {C}}_{12}=(1,1)$, $c=1$ and $\vec{\mathtt{C}}_{12}=(1/\sqrt {2},1/\sqrt {2})$, $c=1/2$, respectively. The results are displayed in Tables 1 and 2 for different dampings σ and parameters $\mathtt{C}_{11},\mathtt{C}_{22}$. The figures in the tables show that the method has numerically almost spatial convergence order 1.5 with the bilinear polynomial approximation for different parameters $\mathtt{C}_{11}=\mathtt {C}_{22}=1/5,1/10,1/20$ and dampings $\sigma=1/2,1,2$. This supports the theoretical convergence order shown in Theorem 3.3. Further, we display the energy, defined in (4.1), with the parameters $\mathtt{C}_{11}=\mathtt{C}_{22}=1/5$, $\vec{\mathtt {C}}_{12}=(1/2,1/2)$, $c=1$, $N=31$ for various dampings $\sigma =0,1/2,1,2$ in Fig. 1. The energy decreases exponentially in time when the damping $\sigma>0$ and its decay rate is getting high as σ is increased. Especially, when damping σ and parameters $\mathtt{C}_{jk}\ (j,k=1,2)$ are zero, the energy is almost constant, which shows that the semi-discretized DG method successfully conserves the energy quantity even though it is affected by the temporal discretization errors in fully discretized schemes, which is shown in the case of $\sigma=0$.

Figure 1

Behavior of energy for various dampings

Table 1 Convergence order of the LDG method with $\vec{\mathtt {C}}_{12}=(1, 1)$ and speed $c=1$

Table 2 Convergence order of the LDG method with $\vec{\mathtt {C}}_{12}=(1/\sqrt{2}, 1/\sqrt{2})$ and speed $c=1/2$

5 Conclusion

We introduce a general formula for the system of acoustic damped wave equations in a bounded two-dimensional domain and successfully propose a LDG method for the system. Further, we show the well-posedness of the system and stability using the energy decay property and an a priori error estimate for the semi-discretized LDG method. The theoretical convergence order and the energy behavior of the method are also tested by a numerical experiments with various parameters. We will study the efficient time discretization for the semi-discretized LDG method and analyze its error estimates in a forthcoming work.