1 Introduction

Solving the viscoelastic fluid flow model is a great challenge due to the slow flow and the hyperbolic nature of the constitutive equation [1]. Owing to the complex structure of viscoelastic fluid, it is not solvable similarly to the Navier–Stokes equation. The difficulty arises in performing correct numerical computations due to the hyperbolic character of the constitutive equation, which does not include a dissipative (stabilizing) term for the stress. As a result, a certain technique must be used to discretize the constitutive equation for approximation. It was a great challenge for scientists and researchers to formulate a new mathematical model that can describe the large deformation of the viscoelastic fluid flow. In 1950, James G. Oldroyd was the first to develop a constitutive equation to model the large deformation of the viscoelastic fluids in [2]. By using Oldroyd’s original work many other constitutive equations have been formulated to describe different features of the viscoelastic fluids, for example, the Phan–Thien–Tanner model, the Maxwell model, the Jeffrey model, the Johnson–Segalman model, and so on [3,4,5,6,7].

Over the last decades, significant progress has been made in the development of numerical approximation for the stable and accurate solutions of the viscoelastic flow problems. Currently, the literature on the FE method is burgeoning to approximate the viscoelastic fluid flow model equations by using a variety of alternative stabilization formulations. The most common among them are streamline-upwind Petrov–Galerkin (SUPG) methods [8], discontinuous Galerkin (DG) methods [9], decoupled FE methods [10], multigrid methods [11], variational multiscale methods [12], and so on.

We consider the DG method for the mixed FE approximation of the viscoelastic fluid flow. To the best of our knowledge, Reed and Hill [13] were the first who studied the DG technique. To deal with the hyperbolic nature of the constitutive equation, Lesaint and Raviart [14] analyzed the DG method on the neutron transport equation. Fortin and Fortin [15] first introduced the DG method for the viscoelastic fluid flow. Baranger and Sandri [16] analyzed the stability and error estimates for the steady-state viscoelastic flow by using the DG method. Zhang et al. [17] studied and obtained unconditional error estimate for the viscoelastic fluid flow with the DG method.

The Oseen fluid flow model is the reduced linearized form of the Newtonian fluid described by the Navier–Stokes equation [18]. The nonlinear convective term of the Navier–Stokes equation can be reduced to a linear system by replacing the unknown velocity with a known velocity field. The non-Newtonian fluid flow obeying the Oldroyd-B model is the combination of conservation of momentum equation and constitutive equation. Under the assumption of the creeping flow, the nonlinearity vanishes in the momentum equation of the Oldroyd-B model. So in the viscoelastic fluid flow model, the nonlinearity occurs only in the constitutive equation [19], which can be reduced to a linear form by fixing velocity u with a known velocity field \(\mathbf{b}(x)\). The resulting system of equations can be explicitly described with the parameter space for α, λ, and \({\|\nabla\mathbf{b}\|}_{\infty}\), which guarantee the existence and uniqueness condition for the solution of the continuous problem and its numerical approximation [20,21,22]. To solve the Oseen viscoelastic fluid flow, many methods have been formulated and discussed; the reader can see [23,24,25,26] and the references therein.

We study the mixed FE method to approximate the Oseen viscoelastic fluid flow, which is developed to approximate both scalar (pressure) variables and vector (velocity) variables simultaneously. The mixed FE method in viscoelastic fluid flow [27] introduces two spaces for the approximation of pressure and velocity. These two spaces must satisfy the inf–sup or the Ladyzhenskaya–Babuska–Breezi (LBB) condition for the stability [28, 29]. Here in our interest, during the implementation of the mixed FE method, we prefer to choose lowest equal-order FE triples \(p1-p1-p1_{\mathrm{dg}}\) to approximate the solution of linear velocity, linear pressure, and discontinues stress. We claim that our choice in the sense of FE will be more convenient to approximate the unknowns. However, these elements fail to satisfy the inf–sup condition [30]. The violation of the inf–sup condition often leads to nonphysical pressure oscillation. Therefore, a stabilization term might be introduced. Stabilization methods are often used to overcome the difficulty associated with the stability of the lowest order mixed FE method. The discussion about stabilization of mixed FE methods and the stability term is analyzed briefly in [31]. Moreover, the lowest equal-order FE methods are easily implementable in a scientific computational sense as compared to the higher-order FE. The lowest order FE and stabilization methods have been considered in the Stokes equation [32], the Navier–Stokes equation [33, 34], and the Stokes–Darcy fluid flow model [35]. So far, this method is novel to solve the Oseen viscoelastic fluids with the lowest equal-order FE.

This paper focuses on stabilization of lowest equal-order FE triples for the approximate solution of unknowns in the Oseen viscoelastic fluid flow model with the DG method. The method introduces a stabilized term with respect to the pressure space to get around the inf–sup condition. It has several important aspects; most notably, the new method is free of nonstandard data structures, approximation of higher-order derivatives, and specification of mesh-dependent parameters. Furthermore, the stabilized lowest equal-order method can be cast in the framework of the Oseen viscoelastic fluid flow with all the advantages discussed. The stability and optimal convergence order of the temporal discretized scheme are derived. To show the validation of the theoretical analysis, three numerical tests are executed, which reveal the efficiency of the Oseen viscoelastic fluid flow model.

The rest of the paper is organized as follows. In Sect. 2, we introduce the governing equations for Oseen viscoelastic fluid flow model, the notations, and preliminaries. The variational formulation, spatial discretization, and some well-known lemmas are discussed in Sect. 3. To justify the proposed lowest equal-order FE algorithm, the well-posedness and optimal convergence analysis are derived in Sect. 4. The results of the numerical simulations of three different experiments are illustrated in Sect. 5 to validate the efficiency and accuracy of the stabilization method. Finally, in Sect. 6, we summarize this work by a short conclusion.

2 Model equations

We consider the following two-dimensional (2D) steady-state (Johnson–Segalman) model equations under the influence of applied forces and stress [36, 37]:

$$ \tau+\lambda(\mathbf{u}\cdot\nabla\tau)+\lambda g_{a}( \tau ,\nabla\mathbf{u})-2\alpha D(\mathbf{u})=0, $$
(2.1)

where λ is the Weissenberg number [38]. The term \(g_{a}(\tau,\nabla\mathbf{u})\) is defined as

$$ g_{a}(\tau,\nabla\mathbf{u}) = \frac{1-a}{2}\bigl( \tau(\nabla \mathbf{u})+(\nabla\mathbf{u})^{T}\tau\bigr)- \frac{1+a}{2}\bigl((\nabla \mathbf{u}) \tau+\tau(\nabla\mathbf{u})^{T} \bigr), $$
(2.2)

where \(a\in[-1,1]\) is related to the material parameter. Specifically, the choice of \(a=1\) represents the Oldroyd-B constitutive model, which is the reduced form of the Johnson–Segalman model. The momentum equation under the influence of the force f can be written as

$$ (\mathbf{u}\cdot\nabla)\mathbf{u}-\nabla\cdot\tau_{\mathrm{tot}}=\mathbf{f}, $$

where \(\tau_{\mathrm{tot}}=-pI+\tau_{N}+\tau\) denotes the total stress tensor with the Newtonian and viscoelastic parts \(\tau_{N}\) and τ. The Newtonian part is given by \(\tau_{N}=2(1-\alpha)D(\mathbf{u})\), and the deformation tensor is defined as

$$ D(\mathbf{u}) = \frac{1}{2}\bigl(\nabla\mathbf{u}+(\nabla \mathbf{u})^{T}\bigr). $$

The gradient of u is defined such that \((\nabla\mathbf {u})_{ij}=\frac{\partial\mathbf{u}_{i}}{\partial x_{j}}=\mathbf{u}_{i,j}\). The viscoelastic flow is essential for understanding many problems in non-Newtonian fluid mechanics, especially those related to flow instabilities [36]. The factor (\(1-\alpha\)) represents the part of the total viscosity that is considered Newtonian. Hence \(\alpha\in(0, 1)\) describes the proportion of the total viscosity that is considered to be viscoelastic in nature. For example, if a polymer is immersed within a Newtonian carrier fluid, then α is related to the percentage of polymer in the mix. Based on the full information, the momentum equation reads as

$$ (\mathbf{u}\cdot\nabla)\mathbf{u}- 2(1-\alpha)\nabla\cdot D(\mathbf {u})-\nabla\cdot\tau+\nabla p = \mathbf{f}. $$
(2.3)

Guillopé and Saut [20] proved equation (2.3) for the assumption of creeping flow \((\mathbf{u}\cdot \nabla)\mathbf{u} =0\). So the viscoelastic fluid flow follows as

$$ - 2(1-\alpha)\nabla\cdot D(\mathbf{u})-\nabla\cdot\tau+\nabla p = \mathbf{f}. $$
(2.4)

2.1 Model problem

We consider the steady-state model equations under the open, bounded, and connected domain Ω. For the velocity u, we impose the homogenous Dirichlet boundary condition. In this case, there is no inflow boundary, and thus no boundary condition is required for stress. Hence by summarizing the modeling equations are

$$\begin{aligned}& {\tau}+\lambda(\mathbf{u}\cdot\nabla)\tau+ \lambda g_{a}(\tau ,\nabla \mathbf{u})-2\alpha D(\mathbf{u}) =0\quad \mbox{in } \varOmega, \end{aligned}$$
(2.5)
$$\begin{aligned}& \nabla p-2(1-\alpha)\nabla\cdot D(\mathbf{u})-\nabla\cdot{\tau }=\mathbf{f} \quad \mbox{in } \varOmega, \end{aligned}$$
(2.6)
$$\begin{aligned}& \nabla\cdot\mathbf{u} =0 \quad \mbox{in } \varOmega, \end{aligned}$$
(2.7)
$$\begin{aligned}& \mathbf{u} =0 \quad \mbox{on } \varGamma, \end{aligned}$$
(2.8)

where f denotes the body force, τ is the polymeric stress tensor, u is the velocity vector field, p is the pressure, and λ is the Weissenberg number (defined as the product of the relaxation time and a characteristic strain rate). Assume that p has zero mean value over the domain Ω. The existence and uniqueness of equations (2.5)–(2.8) are discussed in [39, 40].

In the analysis, we consider the Oseen system as a linearization of viscoelastic model equations. For the ease of presentation, we suppose homogeneous Dirichlet boundary conditions with given velocity \(\mathbf{b}(x)\).

Problem \((O)\)

Find the solution of \((\tau,\mathbf{u},p)\) such that

$$\begin{aligned}& \tau+\lambda(\mathbf{b}\cdot\nabla)\tau+\lambda g_{a}( \tau ,\nabla \mathbf{b})-2\alpha D(\mathbf{u}) =0 \quad \mbox{in }\varOmega, \end{aligned}$$
(2.9)
$$\begin{aligned}& \nabla p-2(1-\alpha)\nabla\cdot D(\mathbf{u})-\nabla\cdot\tau =\mathbf{f} \quad \mbox{in } \varOmega, \end{aligned}$$
(2.10)
$$\begin{aligned}& \nabla\cdot\mathbf{u} =0 \quad \mbox{in } \varOmega, \end{aligned}$$
(2.11)
$$\begin{aligned}& \mathbf{u} =\mathbf{0}\quad \mbox{on } \varGamma. \end{aligned}$$
(2.12)

We make the following assumption for \(\mathbf{b}(x)\) [39]: there exists \(M>0\) such that

$$ \mathbf{b}\in H^{1}_{0}(\varOmega),\qquad \nabla\cdot \mathbf{b}=0,\qquad \|\mathbf{b} \|_{\infty}\leq M, \qquad \|\nabla \mathbf{b}\|_{\infty}\leq M < \infty. $$

2.2 Variational formulation

For the mathematical setting, we introduce some basic notations. For \(m\in N\), the norm is associated with the Sobolev space \(W^{m,p}(\varOmega)\) by \(\|\cdot\|_{W^{m,p}}\); the particular case \(W^{m,2}(\varOmega)\) is written as \(H^{m}(\varOmega)\) with the norm \(\|\cdot\|_{m}\) and seminorm \(|\cdot|_{m}\) [41]. The inner product and norm in \(L^{2}(\varOmega)\) are denoted by \((\cdot ,\cdot)\) and \(\|\cdot\|=\|\cdot\|_{\varOmega}\), respectively. The \(L^{p}(\varOmega)\) norm is denoted by \(\|\cdot\|_{L^{p}}\); in the particular cases of \(L^{2}(\varOmega)\) and \(L^{\infty}(\varOmega)\), the norms are denoted by \(\|\cdot\|\) and \(\|\cdot\|_{\infty}\). The function spaces for the velocity u, pressure p, and stress τ are introduced as follows:

$$\begin{aligned}& X: = H_{0}^{1}(\varOmega)^{2}:=\bigl\{ \mathbf{v}\in H^{1}(\varOmega)^{2}: \mathbf {v}=\mathbf{0} \mbox{ on } \varGamma \bigr\} , \\& Q: = L^{2}_{0}(\varOmega)=\biggl\{ q\in L^{2}( \varOmega): \int_{\varOmega}q\, dx=0\biggr\} , \\& S: = \bigl\{ \tau=(\tau_{ij});\tau_{ij}=\tau_{ji}: \tau_{ij}\in L^{2}(\varOmega);i,j=1,2\bigr\} \\& \hphantom{S:={}}{}\cap\bigl\{ \tau=(\tau_{ij}); \mathbf{b}\cdot\nabla \tau\in L^{2}(\varOmega )^{2\times2},\forall \mathbf{b} \in X\bigr\} . \end{aligned}$$

To find the corresponding variational formulation of Problem \((O)\), we take the inner product of stress, velocity, and pressure test functions σ, v, and q, respectively.

Given \(\mathbf{f}\in H^{-1} (\varOmega)\), find \((\tau, \mathbf{u}, p) \in S \times X\times Q\) such that

$$\begin{aligned}& (\tau,\sigma)+\lambda\bigl((\mathbf{b}\cdot\nabla)\tau,\sigma \bigr)+\lambda \bigl( g_{a}(\tau,\nabla\mathbf{b}),\sigma\bigr)-2\alpha\bigl( D( \mathbf {u}),\sigma\bigr) = 0 \quad \forall\sigma\in S, \end{aligned}$$
(2.13)
$$\begin{aligned}& -(p,\nabla\cdot\mathbf{v})+2(1-\alpha) \bigl(D(\mathbf{u}),D(\mathbf {v})\bigr)+ \bigl(\tau,D(\mathbf{v})\bigr) = (\mathbf{f},\mathbf{v}) \quad \forall\mathbf{v} \in X, \end{aligned}$$
(2.14)
$$\begin{aligned}& ({q,\nabla\cdot\mathbf{u}}) = 0 \quad \forall q \in Q. \end{aligned}$$
(2.15)

Note that the velocity and pressure spaces X and Q satisfy the inf–sup (or LBB) condition:

$$\begin{aligned} \sup_{\mathbf{v}\in X } \frac{(q,\nabla\cdot\mathbf {v})}{| \mathbf{v}|_{1}} \geq C\| q\|_{0}, \quad \forall q \in Q, \end{aligned}$$

where the constant \(C>0\) is independent of h. For further simplification, we multiply 2α with equations (2.14)–(2.15) and add the resulting equations together with (2.13). Then, we use the bilinear form Ā and B for convenience:

$$\begin{aligned}& \begin{aligned}[b] \bar{A}\bigl((\tau,\mathbf{u},p),(\sigma,\mathbf{v},q)\bigr) &=(\tau,\sigma )+\lambda \bigl( g_{a}(\tau,\nabla\mathbf{b}),\sigma \bigr)-2\alpha\bigl(D(\mathbf {u}),\sigma\bigr) \\ &\quad {}+ 2\alpha\bigl(\tau,D(\mathbf{v})\bigr)+4\alpha(1-\alpha ) \bigl(D( \mathbf {u}),D(\mathbf{v})\bigr) \\ &\quad {}-2\alpha(p,\nabla\cdot\mathbf{v})+2\alpha({q,\nabla \cdot\mathbf{u}}), \end{aligned} \end{aligned}$$
(2.16)
$$\begin{aligned}& \lambda B(\mathbf{b},\tau,\sigma) = \lambda\bigl((\mathbf{b}\cdot \nabla)\tau, \sigma\bigr). \end{aligned}$$
(2.17)

By using the bilinear form \(\bar{A}((\cdot,\cdot,\cdot),(\cdot,\cdot ,\cdot))\) and \(B(\cdot,\cdot,\cdot)\) equations (2.13)–(2.15) can be written as

$$ \bar{A}\bigl((\tau,\mathbf{u},p),(\sigma,\mathbf{v},q)\bigr)+ \lambda B(\mathbf {b},\tau,\sigma)= 2\alpha(\mathbf{f},\mathbf{v}). $$
(2.18)

An equivalent formulation of (2.18) can be written as

$$ \widetilde{\mathscr{L}} \bigl((\tau,\mathbf{u},p),(\sigma,\mathbf {v},q)\bigr)= 2\alpha(\mathbf{f},\mathbf{v}) \quad \forall(\sigma, \mathbf {v},q) \in S\times X\times Q, $$
(2.19)

where

$$ \widetilde{\mathscr{L}}\bigl((\tau,\mathbf{u},p),(\sigma, \mathbf{v},q)\bigr)= \bar{A}\bigl((\tau,\mathbf{u},p),(\sigma,\mathbf{v},q)\bigr)+ \lambda B(\mathbf {b},\tau,\sigma). $$

3 Discontinuous FE approximation

The DG and SUPG methods [42, 43] are commonly used to solve the Oseen viscoelastic fluid flow problems. For discontinuous stress, we use the DG method as an upwinding technique. Let \(T^{h}\) denote a triangulation of Ω such that \(\widetilde{\varOmega}=\{\bigcup K:K\in T^{h}\}\). Assume that there exist positive constants \(r_{1}\), \(r_{2}\) such that

$$ r_{1}h\leq h_{K}\leq r_{2} {\rho_{K}}, $$

where \(h_{{K}}\) is the diameter of the triangle K, \(\rho_{K}\) is the diameter of the greatest ball included in K, and \(h=\max_{K\in T^{h}}h_{K}\). Accordingly, we define discrete subspaces for the FE approximation of equation (2.19):

$$\begin{aligned}& X^{h} := \bigl\{ \mathbf{v}\in X\cap C^{0}(\widetilde{ \varOmega})^{2}; \mathbf {v}_{|K}\in P_{1}(K)^{2} \ \forall K\in T^{h}\bigr\} , \\& Q^{h} := \bigl\{ q\in Q\cap C^{0}(\widetilde{\varOmega}); q_{|K}\in P_{1}(K)\ \forall K\in T^{h}\bigr\} , \\& S^{h} := \bigl\{ \sigma\in S;\sigma_{|K}\in P_{1}(K)^{2\times2}\ \forall K\in T^{h}\bigr\} , \end{aligned}$$

where \(P_{1}(K)\) denotes the space linear polynomial of degree set on \(K \in T^{h}\). Some notations are introduced for approximating the discontinuous stress, which is analyzed elsewhere [17, 37, 44]. We define \(\partial K^{-}(\mathbf{b}) = \{x\in\partial K; \mathbf{b}(x)\cdot \mathbf{n}(x) < 0\}\), where ∂K is the boundary of \(K\in T^{h}\), n is the outward unit normal to ∂K, and

$$\begin{aligned}& \varGamma^{h}= \Bigl\{ \bigcup\partial K : K \in T^{h} \Bigr\} \bigm\backslash \varGamma, \\& \tau^{\pm}\bigl(\mathbf{b}(x)\bigr)=\lim_{\varepsilon\rightarrow0} \tau \bigl(x \pm\varepsilon\mathbf{b}(x)\bigr). \end{aligned}$$

Also, for any \(( \tau,\sigma) \in\prod_{K\in T^{h}}[H^{1}(K)]^{4}\), we define

$$\begin{aligned}& (\tau,\sigma)_{h}=\sum_{K\in T^{h}}(\tau, \sigma)_{K}, \\& \bigl\langle \tau^{\pm},\sigma^{\pm}\bigr\rangle _{h,\mathbf{b}}= \sum_{K\in T^{h}} \int _{\partial K^{-}(\mathbf {b})}\bigl(\tau^{\pm}(\mathbf{b}), \sigma^{\pm}(\mathbf{b})\bigr)|\mathbf {n}\cdot \mathbf{b}|\,ds, \\& \bigl\langle \bigl\langle \tau^{\pm}\bigr\rangle \bigr\rangle _{h,\mathbf {b}}^{2}=\bigl\langle \tau ^{\pm}, \tau^{\pm}\bigr\rangle _{h,\mathbf{b}}, \\& \|\tau\|_{0,\varGamma^{h}}=\biggl(\sum_{K\in T^{h}}| \tau|_{0,\partial K}^{2}\biggr)^{1/2}. \end{aligned}$$

The term \(((\mathbf{b}\cdot\nabla)\tau, \sigma)\) is approximated by means of an operator \(B^{h}\) on \((X^{h}, S^{h}, S^{h})\), which is stated in [36] by

$$\begin{aligned} B^{h}\bigl(\mathbf{b}, \tau^{h},\sigma^{h}\bigr) =& \bigl((\mathbf{b}\cdot\nabla )\tau^{h},\sigma^{h} \bigr)_{h} + (1/2) \bigl(\nabla\cdot\mathbf{b}\tau^{h}, \sigma^{h}\bigr) + \bigl\langle \tau^{h+} -\tau^{h-}, \sigma^{h+}\bigr\rangle _{h,\mathbf {b}}, \\ =& -\bigl((\mathbf{b}\cdot\nabla)\sigma^{h}, \tau^{h} \bigr)_{h} - (1/2) \bigl(\nabla \cdot\mathbf{b} \sigma^{h}, \tau^{h}\bigr) + \bigl\langle \tau^{h-},\sigma^{h-}- \sigma ^{h+}\bigr\rangle _{h,\mathbf{b}}, \\ =& \bigl((\mathbf{b}\cdot\nabla) \tau^{h},\sigma^{h} \bigr)_{h} + \bigl\langle \tau ^{h+}-\tau^{h-}, \sigma^{h+}\bigr\rangle _{h,\mathbf{b}}, \quad \mbox{if } \nabla\cdot \mathbf{b}=0. \end{aligned}$$
(3.1)

Thus

$$ B^{h}\bigl(\mathbf{b}, \tau^{h}, \tau^{h}\bigr) = (1/2)\bigl\langle \bigl\langle \tau^{h+}- \tau^{h-}\bigr\rangle \bigr\rangle ^{2}_{h,\mathbf{b}} \geq0 . $$
(3.2)

Due to the choice of lowest equal-order FE triples, the scheme is not stable in discrete formulation. Hence it needs a stabilization term to circumvent the inf–sup condition. To ensure stabilization, we introduce a symmetric, nontrivial, and bilinear stabilization term that is free of penalizing parameter. It is proposed and applied in [29, 33, 45,46,47,48]:

$$ G\bigl(p^{h},q^{h}\bigr)=\bigl((I-\varPi)p^{h},(I- \varPi)q^{h}\bigr), $$

where \(\varPi:L^{2}{(\varOmega)}\rightarrow\mathbb{R}_{0}\) is the standard \(L^{2}\)-projection into the piecewise constant space \(\mathbb {R}_{0}\) associated with the partition \(T^{h}\), and I is the identity. The projection operator Π has the following properties:

$$ \|\varPi p\|_{0} \leq C\| p \|_{0}, \qquad \| p-\varPi p\|_{0} \leq Ch\| p \|_{1}. $$
(3.3)

Throughout the paper, we use C to denote a generic positive constant whose value may change from place to place, but it remains independent of the mesh size h. To the best of our knowledge, so far, this method has never been presented in the literature on the Oseen viscoelastic fluids. We state some lemmas that result from [29, 32, 34, 35] directly to specify the bounds.

Lemma 3.1

Let \(Q^{h}\) and \(X^{h}\) be the spaces. Then there exist positive constants \(C_{1}\) and \(C_{2}\) such that

$$ \sup_{\mathbf{v}^{h}\in X^{h} } \frac{\int_{\varOmega}p^{h}\nabla \cdot \mathbf{v}^{h} \, d\varOmega}{ \Vert \mathbf{v}^{h} \Vert _{1}} \geq C_{1} \bigl\Vert p^{h} \bigr\Vert _{0}-C_{2} h \bigl\Vert \nabla p^{h} \bigr\Vert _{0} \quad \forall p^{h}\in Q^{h}. $$
(3.4)

Proof

Thanks to [29]. □

Lemma 3.2

There exists a positive nonzero constant C such that

$$ Ch \bigl\Vert \nabla p^{h} \bigr\Vert _{0}\leq \bigl\Vert p^{h}-\varPi p^{h} \bigr\Vert _{0}. $$
(3.5)

Proof

Thanks to [29]. □

Now, the stabilized scheme for the approximation of the Oseen viscoelastic fluid flow problem for the lowest equal-order triples is formed in the discrete way as

Problem \((O_{Dg})\)

Find \((\mathbf{u}^{h},\tau^{h},p^{h})\in (X^{h} \times S^{h}\times Q^{h})\) such that, for all \((\sigma^{h},\mathbf {v}^{h},q^{h}) \in(S^{h} \times X^{h}\times Q^{h})\),

$$ \mathscr{L}\bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(\sigma^{h},\mathbf{v}^{h},q^{h}\bigr) \bigr) =2\alpha{\bigl(\mathbf{f},\mathbf{v}^{h}\bigr) }, $$
(3.6)

and hence

$$\begin{aligned} \mathscr{L}\bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(\sigma^{h},\mathbf {v}^{h},q^{h}\bigr) \bigr) =& \bigl(\tau^{h},\sigma^{h}\bigr)+\lambda \bigl(g_{a}\bigl(\tau^{h},\nabla\mathbf{b}\bigr),\sigma ^{h}\bigr)-2\alpha \bigl(D\bigl(\mathbf{u}^{h}\bigr), \sigma^{h}\bigr) \\ &{} +2\alpha\bigl(\tau^{h},D\bigl(\mathbf{v}^{h}\bigr) \bigr)+4\alpha(1-\alpha ) \bigl(D\bigl(\mathbf{u}^{h}\bigr),D\bigl( \mathbf{v}^{h}\bigr)\bigr) \\ &{} -2\alpha\bigl(p^{h},\nabla\cdot\mathbf{v}^{h}\bigr)+2 \alpha \bigl({q^{h},\nabla\cdot\mathbf{u}^{h}}\bigr) \\ &{} +2\alpha G\bigl(p^{h},q^{h}\bigr)+ \lambda B^{h}\bigl(\mathbf{b},\tau^{h},\sigma^{h} \bigr). \end{aligned}$$
(3.7)

We finish this section with the inverse inequalities and some approximation facts [44]. If \(\tilde{\mathbf{u}}^{h} \in X^{h} \) is defined as the interpolant of u in X, \(\tilde{p}^{h}\in Q^{h}\) is the orthogonal projection of \(p \in Q\), and \(\tilde{\tau}^{h} \in S^{h}\) is the orthogonal projection of τ on \(T^{h}\) in S, then we have:

$$\begin{aligned}& \bigl\Vert {\mathbf{u}}-\tilde{\mathbf{u}}^{h} \bigr\Vert _{0}+ h \bigl\Vert \nabla\bigl({\mathbf{u}}-\tilde{ \mathbf{u}}^{h}\bigr) \bigr\Vert _{0} \leq Ch^{2} \Vert {\mathbf{u}} \Vert _{2}, \end{aligned}$$
(3.8)
$$\begin{aligned}& \bigl\Vert p- \tilde{p}^{h} \bigr\Vert _{0} \leq Ch \Vert p \Vert _{1}, \end{aligned}$$
(3.9)
$$\begin{aligned}& \bigl\Vert \tau-\tilde{\tau}^{h} \bigr\Vert _{0}+h \bigl\Vert \nabla\bigl(\tau -\tilde{\tau}^{h}\bigr) \bigr\Vert _{0} \leq Ch^{2} \Vert \tau \Vert _{2}. \end{aligned}$$
(3.10)

The inverse estimates are defined as [23, 44]

$$\begin{aligned}& \bigl\Vert \nabla\tau^{h} \bigr\Vert _{0,h} \leq Ch^{-1} \bigl\Vert {\tau ^{h}} \bigr\Vert _{0}, \quad \tau^{h}\in S^{h}. \end{aligned}$$
(3.11)
$$\begin{aligned}& \bigl\Vert \tau^{h} \bigr\Vert ^{2}_{0,\varGamma^{h}} \leq C h^{-1/2} \bigl\Vert \tau^{h} \bigr\Vert ^{2}_{0, K}, \quad \tau^{h}\in S^{h}. \end{aligned}$$
(3.12)

4 Existence and uniqueness of Problem \((O_{Dg})\) and error bound

In this section, we analyze the existence and uniqueness of the developed stabilized scheme with the lowest equal-order triples for the FE approximation of the Oseen viscoelastic problem.

Theorem 4.1

Let \(\mathbf{f}\in\mathbf{H}^{-1}(\varOmega)\). If \(1-2\lambda Md >0\). Then there exists a unique solution \((\tau ^{h},\mathbf{u}^{h},p^{h})\in(S^{h}\times X^{h} \times Q^{h})\) of (3.6).

Proof

Equation (3.6) is equivalent to

$$\begin{aligned} &\mathscr{L}\bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(\sigma^{h},\mathbf {v}^{h},q^{h}\bigr) \bigr) \\ &\quad =F\bigl(\sigma^{h},\mathbf{v}^{h},q^{h} \bigr) \quad \forall\bigl(\sigma ^{h},\mathbf {v}^{h},q^{h} \bigr)\in S^{h}\times X^{h} \times Q^{h}, \end{aligned}$$
(4.1)

where \(F: S^{h}\times X^{h}\longrightarrow\mathbb{R} \) is the functional defined by

$$ F\bigl(\sigma^{h},\mathbf{v}^{h},q^{h}\bigr)=2 \alpha\bigl(\mathbf{f},\mathbf{v}^{h}\bigr). $$

By simple calculation the functional F can be bounded as

$$\begin{aligned} \bigl\vert F\bigl(\sigma^{h},\mathbf{v}^{h},q^{h} \bigr) \bigr\vert &\leq2\alpha\|\mathbf{f} \|_{-1} \bigl\Vert \mathbf{v}^{h} \bigr\Vert _{1} \\ & \leq2\alpha\|\mathbf{f} \|_{-1} \bigl|\!\bigl|\!\bigl|\bigl( \sigma^{h}, \mathbf{v}^{h},q^{h} \bigr) \bigr|\!\bigr|\!\bigr|_{(S^{h}\times X^{h}\times Q^{h})}, \end{aligned}$$
(4.2)

where \(|\!|\!|(\sigma^{h}, \mathbf{v}^{h},q^{h})|\!|\!|_{(S^{h}\times X^{h}\times Q^{h})}=(\|\sigma^{h}\|^{2}_{0}+\| \mathbf{v}^{h}\|^{2}_{1}+\| q^{h}\|^{2}_{0})^{\frac{1}{2}}\).

We prove that the bilinear form \(\mathscr{L}((\cdot,\cdot,\cdot ),(\cdot,\cdot,\cdot))\) is continuous in \((S^{h}\times X^{h}\times Q^{h} )\). By using (3.11) we have

$$\begin{aligned} B^{h}\bigl(\mathbf{b}, \tau^{h},\sigma^{h} \bigr)&=\bigl((\mathbf{b}\cdot\nabla )\tau ^{h},\sigma^{h} \bigr)_{h}+\bigl\langle \tau^{h+} -\tau^{h-},\sigma ^{h+}\bigr\rangle _{h,\mathbf{b}} \\ & \leq C \bigl[ \Vert \mathbf{b} \Vert _{\infty } \bigl\Vert \nabla \tau^{h} \bigr\Vert _{0,h} \bigl\Vert \sigma^{h} \bigr\Vert _{0} + \Vert \mathbf{b} \Vert _{\infty} \bigl\Vert \tau^{h} \bigr\Vert _{0,\varGamma^{h}} \bigl\Vert \sigma^{h} \bigr\Vert _{0,\varGamma^{h}} \bigr] \\ & \leq C \bigl[ M \bigl\Vert \nabla\tau^{h} \bigr\Vert _{0} \bigl\Vert \sigma^{h} \bigr\Vert _{0}+ \Vert \mathbf{b} \Vert _{\infty}\bigl(h^{-1/2} \bigl\Vert \tau^{h} \bigr\Vert _{0}\bigr) \bigl(h^{-1/2} \bigl\Vert \sigma^{h} \bigr\Vert _{0}\bigr) \bigr] \\ & \leq C \bigl[ M \bigl(h^{-1} \bigl\Vert \tau^{h} \bigr\Vert _{0}\bigr) \bigl\Vert \sigma^{h} \bigr\Vert _{0}+Mh^{-1} \bigl\Vert \tau ^{h} \bigr\Vert _{0} \bigl\Vert \sigma^{h} \bigr\Vert _{0} \bigr] \\ & \leq CM h^{-1} \bigl\Vert \tau^{h} \bigr\Vert _{0} \bigl\Vert \sigma^{h} \bigr\Vert _{0}. \end{aligned}$$
(4.3)

It is easy to get

$$\begin{aligned} \lambda\bigl(g_{a}\bigl(\tau^{h},\nabla\mathbf{b}\bigr), \sigma^{h}\bigr) &\leq2d\lambda \Vert \nabla\mathbf{b} \Vert _{\infty} \bigl\Vert \tau^{h} \bigr\Vert _{0} \bigl\Vert \sigma^{h} \bigr\Vert _{0} \\ & \leq2dM \lambda \bigl\Vert \tau^{h} \bigr\Vert _{0} \bigl\Vert \sigma^{h} \bigr\Vert _{0}. \end{aligned}$$
(4.4)

By combining all the bounded terms we have

$$\begin{aligned} &{\mathscr{L}}\bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(\sigma^{h},\mathbf {v}^{h},q^{h} \bigr)\bigr) \\ &\quad \leq \bigl\Vert \tau^{h} \bigr\Vert _{0} \bigl\Vert \sigma ^{h} \bigr\Vert _{0}+2Md\lambda \bigl\Vert \tau^{h} \bigr\Vert _{0} \bigl\Vert \sigma^{h} \bigr\Vert _{0} \\ &\qquad {} +2\alpha \bigl\Vert D\bigl(\mathbf{u}^{h}\bigr) \bigr\Vert _{0} \bigl\Vert \sigma^{h} \bigr\Vert _{0}+2\alpha \bigl\Vert \tau ^{h} \bigr\Vert _{0} \bigl\Vert D\bigl(\mathbf{v}^{h}\bigr) \bigr\Vert _{0} \\ &\qquad {} +4\alpha(1-\alpha) \bigl\Vert D\bigl(\mathbf {u}^{h} \bigr) \bigr\Vert _{0} \bigl\Vert D\bigl(\mathbf{v}^{h} \bigr) \bigr\Vert _{0} \\ &\qquad {} +2\alpha d \bigl\Vert q^{h} \bigr\Vert _{0} \bigl\Vert \nabla\mathbf{u}^{h} \bigr\Vert _{0}+2\alpha d \bigl\Vert p^{h} \bigr\Vert _{0} \bigl\Vert \nabla \mathbf{v}^{h} \bigr\Vert _{0} \\ &\qquad {} +2\alpha \bigl\Vert p^{h} \bigr\Vert _{0} \bigl\Vert q^{h} \bigr\Vert _{0} + C M h^{-1} \bigl\Vert \tau^{h} \bigr\Vert _{0} \bigl\Vert \sigma ^{h} \bigr\Vert _{0} \\ &\quad \leq C \bigl|\!\bigl|\!\bigl|\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr) \bigr|\!\bigr|\!\bigr|_{(S^{h}\times X^{h}\times Q^{h})} \bigl|\!\bigl|\!\bigl|\bigl(\sigma^{h}, \mathbf {v}^{h},q^{h}\bigr) \bigr|\!\bigr|\!\bigr|_{(S^{h}\times X^{h}\times Q^{h})}, \end{aligned}$$
(4.5)

which proves the continuity.

To prove the weak coercivity, suppose that there is a positive constant ϒ, independent of h, such that for all \((\tau^{h},\mathbf {u}^{h},p^{h})\in S^{h}\times X^{h}\times Q^{h} \),

$$ \sup_{(\sigma^{h},\mathbf{v}^{h},q^{h})\in S^{h}\times X^{h}\times Q^{h}} \frac{{\mathscr{L}}((\tau^{h},\mathbf{u}^{h},p^{h}),(\sigma ^{h},\mathbf{v}^{h},q^{h} ))}{|\!|\!|(\sigma^{h},\mathbf {v}^{h},q^{h} )|\!|\!|}\geq\varUpsilon \bigl|\!\bigl|\!\bigl|\bigl(\tau ^{h},\mathbf {u}^{h},p^{h} \bigr) \bigr|\!\bigr|\!\bigr|. $$
(4.6)

Firstly, for all \(p^{h}\in Q^{h}\subset Q\), let \(\mathbf{w}\in X \) be such that \((\nabla\cdot\mathbf{w}, p^{h})=\| p^{h}\|^{2}_{0}\) and \(\|\mathbf{w} \|_{1}\leq\varUpsilon\| p^{h}\|_{0}\). Assigning the value in FE approximation for normalization of \(\mathbf {w}^{h}\in X^{h}\) of w [29, 32, 34, 49], assume that

$$ \bigl\Vert \mathbf{w}^{h} \bigr\Vert _{1} \leq\varUpsilon_{0} \bigl\Vert p^{h} \bigr\Vert _{0}. $$
(4.7)

Thanks to [29],

$$ \int_{\varOmega}p^{h}\nabla\cdot\mathbf{w}^{h}\, d \varOmega\geq C_{1} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0}-C_{2} \bigl\Vert (I-\varPi)p^{h} \bigr\Vert _{0} \bigl\Vert p^{h} \bigr\Vert _{0}. $$
(4.8)

By substituting \(\mathbf{v}^{h}=\mathbf{u}^{h}-\xi\mathbf{w}^{h}, q^{h}=p^{h}\), and \(\sigma^{h}=\tau^{h}\) into (4.1) with \(\xi\in \mathbb{R}\) we have

$$\begin{aligned} &{\mathscr{L}}\bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(\tau^{h},\mathbf {u}^{h}-\xi \mathbf{w}^{h},p^{h}\bigr)\bigr) \\ &\quad = {\mathscr{L}}\bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(\tau ^{h},\mathbf{u}^{h},p^{h}\bigr) \bigr) +{\mathscr{L}}\bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(0,-\xi\mathbf{w}^{h},0\bigr)\bigr). \end{aligned}$$
(4.9)

The right-hand side of (4.9) can be bounded in the following way.

First term of (4.9). Thanks to (3.2), (3.7), and (4.4), we have

$$\begin{aligned} &{\mathscr{L}}\bigl(\bigl(\tau^{h}, \mathbf{u}^{h},p^{h} \bigr),\bigl(\tau^{h},\mathbf {u}^{h},p^{h}\bigr) \bigr) \\ &\quad \geq \bigl\Vert \tau^{h} \bigr\Vert ^{2}_{0}+ \lambda \bigl(g_{a}\bigl(\tau ^{h},\nabla\mathbf{b}\bigr), \tau^{h}\bigr)+4\alpha(1-\alpha) \bigl\Vert D\bigl(\mathbf {u}^{h}\bigr) \bigr\Vert ^{2}_{0} \\ &\qquad {} +2\alpha \bigl\Vert (I-\varPi)p^{h} \bigr\Vert ^{2}_{0}+(\lambda /2)\bigl\langle \bigl\langle \tau^{h+}- \tau^{h-}\bigr\rangle \bigr\rangle ^{2}_{h,\mathbf{b}} \\ &\quad \geq \bigl\Vert \tau^{h} \bigr\Vert ^{2}_{0}-2 \lambda Md \bigl\Vert \tau^{h} \bigr\Vert ^{2}_{0}+4 \alpha(1-\alpha) \bigl\Vert D\bigl(\mathbf {u}^{h}\bigr) \bigr\Vert ^{2}_{0} \\ & \qquad {} +2\alpha \bigl\Vert (I-\varPi)p^{h} \bigr\Vert ^{2}_{0}+(\lambda /2)\bigl\langle \bigl\langle \tau^{h+}- \tau^{h-}\bigr\rangle \bigr\rangle ^{2}_{h,\mathbf{b}} \\ &\quad \geq(1-2\lambda Md) \bigl\Vert \tau^{h} \bigr\Vert ^{2}_{0}+4\alpha(1-\alpha) \bigl\Vert D\bigl( \mathbf{u}^{h}\bigr) \bigr\Vert ^{2}_{0} \\ &\qquad {} +2\alpha \bigl\Vert (I-\varPi)p^{h} \bigr\Vert ^{2}_{0}+(\lambda /2)\bigl\langle \bigl\langle \tau^{h+}- \tau^{h-}\bigr\rangle \bigr\rangle ^{2}_{h,\mathbf{b}}. \end{aligned}$$
(4.10)

Second term of (4.9).

$$\begin{aligned} & {\mathscr{L}} \bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(0,-\xi\mathbf{w}^{h},0\bigr)\bigr) \\ &\quad = -4\alpha(1-\alpha) \xi\bigl( D\bigl(\mathbf{u}^{h}\bigr), D \bigl(\mathbf {w}^{h}\bigr)\bigr)-2\alpha\xi\bigl(\tau^{h},D \bigl(\mathbf{w}^{h}\bigr)\bigr) + 2\alpha\xi\bigl(p^{h}, \nabla\cdot\mathbf{w}^{h}\bigr). \end{aligned}$$
(4.11)

To estimate the right-hand side of equation (4.11), using (3.8), (4.7), (4.8), and Young’s inequality, we have

$$\begin{aligned}& \begin{aligned} 4\alpha(1-\alpha) \xi\bigl( D\bigl(\mathbf{u}^{h} \bigr), D\bigl(\mathbf{w}^{h}\bigr)\bigr)& \leq4\alpha(1-\alpha) \xi \bigl\Vert D\bigl(\mathbf{u}^{h}\bigr) \bigr\Vert _{0} \bigl\Vert D\bigl(\mathbf{w}^{h}\bigr) \bigr\Vert _{0} \\ & \leq4\alpha(1-\alpha) \xi \bigl\Vert D\bigl(\mathbf{u}^{h}\bigr) \bigr\Vert _{0} \varUpsilon_{0} \bigl\Vert p^{h} \bigr\Vert _{0} \\ & \leq\frac{4\alpha(1-\alpha)^{2} \xi\varUpsilon ^{2}_{0}}{C_{1}} \bigl\Vert D\bigl(\mathbf{u}^{h}\bigr) \bigr\Vert ^{2}_{0}+ 4\alpha\xi C_{1} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0}, \end{aligned} \\& \begin{aligned} 2\alpha\xi\bigl(\tau^{h},D\bigl(\mathbf{w}^{h} \bigr)\bigr)& \leq2\alpha\xi \bigl\Vert \tau ^{h} \bigr\Vert _{0} \bigl\Vert D\bigl(\mathbf{w}^{h}\bigr) \bigr\Vert _{0} \\ & \leq2\alpha\xi\varUpsilon_{0} \bigl\Vert \tau^{h} \bigr\Vert _{0} \bigl\Vert p^{h} \bigr\Vert _{0} \\ & \leq2\alpha\xi\varUpsilon^{2}_{0}\frac{1}{C_{1}} \bigl\Vert \tau ^{h} \bigr\Vert ^{2}_{0}+{2 C_{1}\alpha\xi} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} 2\alpha\xi\bigl(p^{h},\nabla\cdot w^{h}\bigr)&\geq 2\alpha \xi\bigl(C_{1} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0}-C_{2} \bigl\Vert (I-\varPi)p^{h} \bigr\Vert _{0} \bigl\Vert p^{h} \bigr\Vert _{0}\bigr) \\ & \geq2\alpha\xi C_{1} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0}-2\alpha \xi C_{2} \bigl\Vert (I- \varPi)p^{h} \bigr\Vert _{0} \bigl\Vert p^{h} \bigr\Vert _{0} \\ & \geq2\alpha\xi C_{1} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0}- 2\alpha \xi\frac{C_{2}^{2}}{C_{1}} \bigl\Vert (I- \varPi)p^{h} \bigr\Vert ^{2}_{0}-2\alpha \xi{C_{1}} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0}. \end{aligned}$$

Substituting all the bounds into (4.11), we obtain

$$\begin{aligned} &{\mathscr{L}}\bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(0,-\xi\mathbf{w}^{h},0\bigr)\bigr) \\ &\quad \geq- 2\alpha\xi\varUpsilon^{2}_{0}\frac{1}{ {C_{1}}} \bigl\Vert \tau^{h} \bigr\Vert ^{2}_{0} - \frac{4\alpha(1-\alpha)^{2} \xi\varUpsilon^{2}_{0}}{C_{1}} \bigl\Vert D\bigl(\mathbf {u}^{h}\bigr) \bigr\Vert ^{2}_{0} \\ & \qquad {} + 4\alpha\xi C_{1} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0}- 2\alpha\xi\frac{C_{2}^{2}}{C_{1}} \bigl\Vert (I-\varPi)p^{h} \bigr\Vert ^{2}_{0}. \end{aligned}$$
(4.12)

As a result, combining the bounded terms (4.10)–(4.12), it is easy to see that

$$\begin{aligned} &{\mathscr{L}} \bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(\tau^{h},\mathbf {u}-\xi \mathbf{w}^{h},p^{h} \bigr)\bigr) \\ &\quad \geq\biggl(1-2 \lambda Md- 2\alpha\xi\varUpsilon^{2}_{0} \frac {1}{ {C_{1}}}\biggr) \bigl\Vert \tau^{h} \bigr\Vert ^{2}_{0} \\ &\qquad {} +\biggl( 4\alpha(1-\alpha) -\frac{4\alpha(1-\alpha)^{2} \xi\varUpsilon^{2}_{0}}{C_{1}}\biggr) \bigl\Vert D \bigl(\mathbf{u}^{h}\bigr) \bigr\Vert ^{2}_{0} \\ &\qquad {} + 4\alpha\xi C_{1} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0} +2\alpha\biggl( 1- \xi\frac{C_{2}^{2}}{C_{1}} \biggr) \bigl\Vert (I-\varPi)p^{h} \bigr\Vert ^{2}_{0} \\ &\quad \geq C_{3} \bigl\Vert \tau^{h} \bigr\Vert ^{2}_{0}+C_{4} \bigl\Vert D\bigl( \mathbf{u}^{h}\bigr) \bigr\Vert ^{2}_{0}+ C_{5} \bigl\Vert p^{h} \bigr\Vert ^{2}_{0} \\ &\quad \geq C^{*} \bigl|\!\bigl|\!\bigl|\bigl(\tau^{h}, \mathbf{u}^{h},p^{h}\bigr) \bigr|\!\bigr|\!\bigr|^{2}_{S^{h}\times X^{h}\times Q^{h}}. \end{aligned}$$
(4.13)

From equation (4.7) we have

$$\begin{aligned} & \bigl\Vert \tau^{h} \bigr\Vert _{0}+ \bigl\Vert \mathbf{u}-\xi\mathbf{w}^{h} \bigr\Vert _{1}+ \bigl\Vert p^{h} \bigr\Vert _{0} \\ &\quad \leq \bigl\Vert \tau^{h} \bigr\Vert _{0}+ \Vert \mathbf {u} \Vert _{1} +\xi \bigl\Vert \mathbf{w}^{h} \bigr\Vert _{0}+ \bigl\Vert p^{h} \bigr\Vert _{0} \\ &\quad \leq \bigl\Vert \tau^{h} \bigr\Vert _{0}+ \Vert \mathbf {u} \Vert _{1} +\xi\varUpsilon_{0} \bigl\Vert p^{h} \bigr\Vert _{0}+ \bigl\Vert p^{h} \bigr\Vert _{0} \\ &\quad \leq C\bigl( \bigl\Vert \tau^{h} \bigr\Vert _{0}+ \Vert \mathbf{u} \Vert _{1} + \bigl\Vert p^{h} \bigr\Vert _{0}\bigr). \end{aligned}$$
(4.14)

Then it is easy to see that

$$\begin{aligned} &{\mathscr{L}} \bigl(\bigl(\tau^{h},\mathbf{u}^{h},p^{h} \bigr),\bigl(\tau^{h},\mathbf {u}-\xi\mathbf{w}^{h},p^{h} \bigr)\bigr) \\ &\quad \geq C^{**} \bigl|\!\bigl|\!\bigl|\bigl(\tau^{h}, \mathbf{u}^{h},p^{h}\bigr) \bigr|\!\bigr|\!\bigr|\bigl|\!\bigl|\!\bigl|\bigl( \tau^{h},\mathbf{u}^{h}-\xi\mathbf{w}^{h},p^{h} \bigr) \bigr|\!\bigr|\!\bigr|, \end{aligned}$$
(4.15)

which completes the proof of coercivity. □

Theorem 4.2

If \(1-2\lambda Md>0\), \((\tau^{h},\mathbf{u}^{h},p^{h})\in(S^{h}\times X^{h} \times Q^{h})\) satisfies equation (3.6), and \((\tau,\mathbf{u} ,p )\in(S \times X \times Q)\) satisfies (2.19), then we have the estimate

$$ \bigl\Vert \tau-\tau^{h} \bigr\Vert _{0}+ \bigl\Vert \mathbf{u}-\mathbf {u}^{h} \bigr\Vert _{1} + \bigl\Vert p-p^{h} \bigr\Vert _{0}\leq Ch. $$
(4.16)

Proof

Subtracting equation (3.6) from equation (2.19), for all \((\sigma^{h},\mathbf{v}^{h},q^{h})\in(S^{h}\times X^{h}\times Q^{h})\), we have

$$ {\mathscr{L}}\bigl(\bigl(\tau-\tau^{h},\mathbf{u}- \mathbf {u}^{h},p-p^{h}\bigr),\bigl(\sigma ^{h}, \mathbf{v}^{h},q^{h}\bigr)\bigr)= 2\alpha G \bigl(p,q^{h}\bigr). $$
(4.17)

By adding and subtracting the projection terms \((\tilde{\tau}^{h},\tilde {\mathbf{u}}^{h},\tilde{p}^{h})\) we get

$$\begin{aligned} &{\mathscr{L}}\bigl(\bigl(\tilde{\tau}^{h}-\tau^{h},\tilde{ \mathbf {u}}^{h}-\mathbf {u}^{h},\tilde{p}^{h}-p^{h} \bigr),\bigl(\sigma^{h},\mathbf{v}^{h},q^{h}\bigr) \bigr) \\ &\quad = {\mathscr{L}}\bigl(\bigl(\tilde{\tau}^{h}-\tau,\tilde{\mathbf {u}}^{h}-\mathbf{u},\tilde{p}^{h}-p\bigr),\bigl( \sigma^{h},\mathbf{v}^{h},q^{h}\bigr)\bigr) +2 \alpha G\bigl(p,q^{h}\bigr). \end{aligned}$$
(4.18)

Using the weak coercivity bound (4.6), error orthogonality, and (4.18) we get

$$\begin{aligned} &\varUpsilon \bigl|\!\bigl|\!\bigl|\bigl(\tilde{\tau}^{h}-\tau^{h}, \tilde{\mathbf {u}}^{h}-\mathbf{u}^{h},\tilde{p}^{h}-p^{h}\bigr) \bigr|\!\bigr|\!\bigr|\\ &\quad \leq\sup_{(\sigma^{h},\mathbf{v}^{h},q^{h})\in S^{h}\times X^{h}\times Q^{h}} \frac{{\mathscr{L}}((\tilde{\tau}^{h}-\tau ^{h},\tilde{\mathbf{u}}^{h}-\mathbf{u}^{h},\tilde{p}^{h}-p^{h}),(\sigma ^{h},\mathbf{v}^{h},q^{h}))}{|\!|\!|(\sigma^{h},\mathbf{v}^{h},q^{h})|\!|\!|} \\ &\quad =\sup_{(\sigma^{h},\mathbf{v}^{h},q^{h})\in S^{h}\times X^{h}\times Q^{h}} \frac{{\mathscr{L}}((\tilde{\tau}^{h}-\tau,\tilde {\mathbf {u}}^{h}-\mathbf{u},\tilde{p}^{h}-p),(\sigma^{h},\mathbf {v}^{h},q^{h}))+2\alpha G(p,q^{h})}{|\!|\!|(\sigma^{h},\mathbf{v}^{h},q^{h} )|\!|\!|}. \end{aligned}$$

From (3.3) we have that

$$ 2\alpha G\bigl(p,q^{h}\bigr)\leq C 2\alpha G(p,p)^{1/2} \bigl\Vert q^{h} \bigr\Vert _{0}. $$
(4.19)

From (4.5) we have

$$\begin{aligned} &{\mathscr{L}}\bigl(\bigl(\tilde{\tau}^{h}-\tau,\tilde{ \mathbf{u}}^{h}-\mathbf {u},\tilde{p}^{h}-p\bigr),\bigl(\tilde{\tau}^{h}-\tau^{h},\tilde{\mathbf {u}}^{h}-{ \mathbf{u}}^{h},\tilde{p}^{h}-p^{h}\bigr)\bigr) \\ &\quad \leq C \bigl( \bigl\Vert \tilde{\tau}^{h}-\tau \bigr\Vert _{0}+ \bigl\Vert \tilde{\mathbf{u}}^{h}-{\mathbf{u}} \bigr\Vert _{1}+ \bigl\Vert \tilde{p}^{h} -p \bigr\Vert _{0}+ 2\alpha \bigl\Vert (I-\varPi)p \bigr\Vert _{0}\bigr) \\ &\qquad {}\times \bigl|\!\bigl|\!\bigl|\bigl(\sigma^{h},\mathbf{v}^{h},q^{h} \bigr) \bigr|\!\bigr|\!\bigr|. \end{aligned}$$
(4.20)

As a result,

$$\begin{aligned} &\varUpsilon \bigl|\!\bigl|\!\bigl|\bigl(\tilde{\tau}^{h}-\tau^{h}, \tilde{\mathbf {u}}^{h}-\mathbf{u}^{h},\tilde{p}^{h}-p^{h}\bigr) \bigr|\!\bigr|\!\bigr|\\ &\quad \leq \sup_{(\sigma^{h},\mathbf{v}^{h},q^{h})\in S^{h}\times X^{h}\times Q^{h}}\frac{C( \Vert \tilde{\tau}^{h}-\tau \Vert _{0}+ \Vert \tilde {\mathbf{u}}^{h}-{\mathbf{u}} \Vert _{1}+ \Vert \tilde{p}^{h} -p \Vert _{0}+ 2\alpha \Vert (I-\varPi)p \Vert _{0})|\!|\!|(\sigma^{h},\mathbf{v}^{h},q^{h})|\!|\!|}{|\!|\!|(\sigma ^{h},\mathbf {v}^{h},q^{h})|\!|\!|} \\ &\quad \leq\frac{C }{\varUpsilon}\bigl( \bigl\Vert \tilde{\tau}^{h}-\tau \bigr\Vert _{0}+ \bigl\Vert \tilde{\mathbf{u}}^{h}-{ \mathbf{u}} \bigr\Vert _{1}+ \bigl\Vert \tilde{p}^{h} -p \bigr\Vert _{0}+ \bigl\Vert (I-\varPi)p \bigr\Vert _{0} \bigr). \end{aligned}$$

To end the proof, we use the triangle inequality to obtain (4.16) □

5 Numerical tests

This section illustrates the numerical simulation results in support of the proposed stabilized lowest equal-order FE scheme and its theoretical analysis performed in Theorem 4.2 for the Oseen viscoelastic fluid flow model. For numerical evaluation, we design and examine three different experiments, that is, a nonphysical example with an exact solution, a viscoelastic cavity flow problem, and a benchmark 4-to-1 contraction channel flow [27]. In the analytical solution test, we demonstrate the optimal convergence order by assuming an exact solution. The second experiment elucidates the viscoelastic cavity flow to show the characteristics of the pressure contour and its behavior. The flow speed, behavior of the contours, streamlines patterns, and the pressure oscillation are examined by the 4-to-1 contraction channel flow. To show the distinguishing features of the new stabilized model, we compare newly formulated method for the lowest equal-order FE triples \(p1-p1-p1_{\mathrm{dg}}\) with the standard MINI element triples \(p1b-p1-p1_{\mathrm{dg}}\). All numerical tests are performed by using public domain software Freefem++ [50]. The figures and graphs are drawn by using Tecplot and MATLAB, respectively.

5.1 Analytical solution test

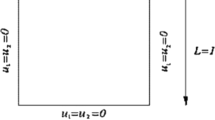
The theoretical convergence rates are verified by considering fluid flow across a unit square with known solution. To test the numerical stability of the new stabilized method, we considered the lowest equal-order FE triples \(p1-p1-p1_{\mathrm{dg}}\) for velocity, pressure, and stress. Different authors used this experimental pattern for the Stokes and Navier–Stokes equations [11, 44, 51].

In this example, the known function \(\mathbf{b}(x)\) is chosen to be the exact solution of the velocity u. Moreover, the true solution of the problem for velocity \(\mathbf{u}=(u_{1}, u_{2})\), pressure p, and polymeric stress τ is given by

{ u = ( − 10 ( x 4 − 2 x 3 + x 2 ) ( 2 y 3 − 3 y 2 + y ) 10 ( 2 x 3 − 3 x 2 + x ) ( y 4 − 2 y 3 + y 2 ) ) , p = − 10.0 ( 2 x − 1 ) ( 2 y − 1 ) , τ = 2 α D ( u ) .

The right-hand sides and initial and boundary conditions are derived by model Problem \((O)\) with parameters \(a=0\), \(\lambda=5.0\), and \(\alpha=0.5\).

In Tables 1–3, we illustrate the distinguished feature of the lowest equal-order FE method for the Oseen viscoelastic fluid flow model by comparing the results with the standard FE \(p1b-p1-p1_{\mathrm{dg}}\) triples. We listed the \(H^{1}\)-norm error for velocity, \(L^{2}\)-norm error for pressure, and \(L^{2}\)-norm error for stress with varying spacing \(h=1/8, 1/16, 1/32, 1/64\). Table 1 represents the computations of the errors for the standard FE with \(p1b-p1-p1_{\mathrm{dg}}\) triples. Table 2 demonstrates the results for the approximation of the Oseen viscoelastic fluid model by FE \(p1-p1-p1_{\mathrm{dg}}\) triples without stabilization term. Table 3 shows the error obtained from the approximate values with stabilization term by using FE \(p1-p1-p1_{\mathrm{dg}}\) triples.

Table 1 The illustration of the error for the Oseen viscoelastic fluid flow with standard FE \(p1b-p1-p1_{\mathrm{dg}}\) triples
Full size table
Table 2 The illustration of the error for the Oseen viscoelastic fluid flow without stabilization term for the FE \(p1-p1-p1_{\mathrm{dg}}\) triples
Full size table
Table 3 The illustration of the error for the Oseen viscoelastic fluid flow with stabilization term for the FE \(p1-p1-p1_{\mathrm{dg}}\) triples
Full size table

To verify the desirable feature of the method, we compare the convergence orders in Fig. 1 for the three methods by using the log–log plots of the data listed in Tables 1–3. The experiment shows that, for all three methods, the order of convergence of velocity and stress is optimal as h decreases. From Tables 1–3 and Fig. 1 we can observe that the velocity \(H^{1}\)-norm error and stress \(L^{2}\)-norm error obtain an optimal convergence order, whereas the pressure \(L^{2}\)-norm error is affected without stabilization term. The accuracy of the convergence order of the pressure is ensured by adding a stabilization term, which is illustrated in Table 3. This experimental test concludes that the technique we have adopted can be applied successfully for the Oseen viscoelastic fluid flow model.

Figure 1
figure 1

The illustration of the order of convergence. (a) \(H^{1}\)-norm error for velocity; (b) \(L^{2}\)-norm error for pressure; (c) \(L^{2}\)-norm error for stress

Full size image

5.2 The viscoelastic cavity flow

In this test, we apply the stabilization method in the famous problem for testing numerical validity is known as the “lid-driven cavity.” The aforementioned problem is chosen because some standard data are available for comparison. Cavity flows has been used in many test cases for testing the incompressible fluid dynamics algorithm for the Stokes flow [52]. To investigate the pressure oscillation, we perform the viscoelastic cavity flow experiment for standard FE \(p1b-p1-p1_{\mathrm{dg}}\) triples, FE \(p1-p1-p1_{\mathrm{dg}}\) triples without stabilization, and FE \(p1-p1-p1_{\mathrm{dg}}\) triples with stabilization. Moreover, we compare the pressure lines of lowest equal-order triples with standard FE methods.

The fluid is enclosed in a unit square domain with the boundary condition for velocity \(\mathbf{u}=(1,0)\) on the upper boundary and the homogeneous Dirichlet condition on the remaining boundaries. The parameters value are chosen as follows: \(a=0\), \(\lambda=5.0\), \(\mathbf{f}=0\), and \(\alpha=0.5\). In this numerical formulation, \(\mathbf{b}(x)\) denotes a known vector function used to linearize the nonlinear viscoelastic fluid flow model into reduced Oseen model equations. We output the data by computing the velocity vector field \(\mathbf {u}=(u_{1},u_{2}) \) for there different FE triples known as \(p1b-p1-p1_{\mathrm{dg}}\) standard or MINI elements, \(p1-p1-p1_{\mathrm{dg}}\) without stabilization, and \(p1-p1-p1_{\mathrm{dg}}\) with stabilization. Furthermore, the computed solution \(\mathbf{u}=(u_{1},u_{2}) \) is used as the known solution \(\mathbf{b}(x)=(b_{1},b_{2})\) to reduce the nonlinear term as linear. The resulting effect makes the viscoelastic fluid flow model as the Oseen fluid flow model.

Figure 2(a) represents a standard method for the approximation of the mixed FE triples \(p1b-p1-p1_{\mathrm{dg}}\), where the pressure lines on the top corners are regular. For comparison of the lowest equal order, we present the numerical result in Fig. 2(b) without addition of a stabilization term. It can be seen that the pressure is poorly oscillated and obtain irregular shape. It is easy to observe that after adding a stabilization term in Fig. 2(c), the pressure lines are appeared in similar precision with Fig. 2(a). Based on this experiment, it is clear that the stabilization term ensures the stability of the scheme for the lowest equal-order triples to the approximation of the Oseen viscoelastic fluid flow model.

Figure 2
figure 2

The pressure lines for the Oseen viscoelastic cavity flow. (a) Standard FE \(p1b-p1-p1_{\mathrm{dg}}\) triples; (b) FE \(p1-p1-p1_{\mathrm{dg}}\) triples without stabilization term; (c) FE \(p1-p1-p1_{\mathrm{dg}}\) triples with stabilization term

Full size image

5.3 The 4-to-1 contraction channel flow

The third example is the well-known benchmark problem for viscoelastic fluid flow “4-to-1 contraction channel flow problem,” which has enormous application in polymeric liquid industries. The 4-to-1 channel flow has been extensively used to show the convergence, stability, behavior of the streamlines of the contraction channel, and the behavior of pressure [10, 24, 53]. The domain of this problem is constructed in such a way that the channel lengths are sufficiently long for a fully developed Poiseuille flow at both inflow and outflow boundaries. Similar to our experiment, the diagram of the flow geometry is demonstrated in Fig. 3. The computations are performed on a uniformly refined version of the mesh shown in Fig. 4 with \(\triangle x_{\mathrm{min}}= 0.0625\) and \(\triangle y_{\mathrm{min}}= 0.015625\), with \(\varGamma_{\mathrm{in}}=\{ (x,y):x=0,0\leqslant y\leqslant1\}\) and \(\varGamma_{\mathrm{out}}=\{(x,y):x=8,0\leqslant y\leqslant0.25\}\). For the velocity inflow in the boundary and velocity outflow in the boundary, it is declared by

$$\begin{aligned}& u_{1}=\frac{1}{32}\bigl(1-y^{2}\bigr),\qquad u_{2}=0\quad \mbox{on } \varGamma_{\mathrm{in}}, \\& u_{1}=2\biggl(\frac{1}{16}-y^{2}\biggr),\qquad u_{2}=0 \quad \mbox{on } \varGamma_{\mathrm{out}}. \end{aligned}$$

For stress, on \(\varGamma_{\mbox{in}}\),

$$\begin{aligned}& \sigma_{11}=\frac{-\alpha\lambda(a+1)(-y/16)^{2}}{(a^{2}-1)\lambda^{2} (-y/16)^{2}-1}, \\& \sigma_{12}=\sigma_{21}=\frac{-\alpha(-y/16)}{(a^{2}-1)\lambda^{2} (-y/16)^{2}-1}, \\& \sigma_{22}=\frac{-\alpha\lambda(a-1)(-y/16)^{2}}{(a^{2}-1)\lambda^{2} (-y/16)^{2}-1}. \end{aligned}$$

Symmetry conditions for the velocity on the solid walls of the concentration are imposed at the bottom of the computational domain. No-slip boundary condition is assumed in the other boundaries of the contraction channel. Besides, the physical parameters α, λ, and a are sequentially chosen 1, \(8/9\), 0.7, and 1. Furthermore, we compute \(b_{1}\) and \(b_{2}\) by following the procedure similar to that mentioned in Sect. 5.2. This formulation have three cases in this section, namely, \(p1b-p1-p1\) standard, \(p1-p1-p1_{\mathrm{dg}}\) without stabilization, and \(p1-p1-p1_{\mathrm{dg}}\) with stabilization. For all cases, we use the solution of \(u_{1}\) and \(u_{2}\) as the known solution of \(b_{1}\) and \(b_{2}\) to compute the approximate solution.

Figure 3
figure 3

The 4-to-1 contraction domain with sample contraction mesh

Full size image
Figure 4
figure 4

Streamlines and magnitudes of the velocity u. (a) Standard FE \(p1b-p1-p1_{\mathrm{dg}}\) triples; (b) FE \(p1-p1-p1_{\mathrm{dg}}\) triples without stabilization term; (c) FE \(p1-p1-p1_{\mathrm{dg}}\) triples with stabilization term

Full size image

Figure 4(a) illustrates the streamlines and flow speed of the standard FE triples \(p1b-p1-p1_{\mathrm{dg}}\). Figure 4(b) shows the streamlines without stabilization term for the FE triples \(p1-p1-p1_{\mathrm{dg}}\), and Fig. 4(c) presents the streamlines with stabilization term for the FE \(p1-p1-p1_{\mathrm{dg}}\) triples. We can observe that without the addition of the stabilization term as shown in Fig. 4(b), the approximate value of the streamlines and vortex for the FE \(p1-p1-p1_{\mathrm{dg}}\) triples is different and shows some irregularities. However, Fig. 4(a) and Fig. 4(c) appear similar in manner. The behavior of the streamlines and vortex confirm the theoretical results for the approximation of the Oseen viscoelastic fluid flow with the lowest equal-order FE triples.

In Fig. 5(a), we plot the pressure contours with standard Galerkin FE known as \(p1b-p1-p1_{\mathrm{dg}}\). To check the validity of the stabilization term, we plot the data without adding stabilization term in Fig. 5(b). We can clearly observe that the contours of this plot attain an irregular shape and so-called pressure oscillation. On the other hand, we display the results of the contour with stabilization term in Fig. 5(c), which is assumed as a stable scheme. Furthermore, the contour displayed in Fig. 5(b) without stabilization term is different from the rest of the figures. These results also affirm the theoretical analysis for the pressure stabilization under the lowest equal-order FE triples for the approximation of the Oseen viscoelastic fluid flow.

Figure 5
figure 5

The pressure contours for pressure field p. (a) Standard FE \(p1b-p1-p1_{\mathrm{dg}}\) triples; (b) FE \(p1-p1-p1_{\mathrm{dg}}\) triples without stabilization term; (c) FE \(p1-p1-p1_{\mathrm{dg}}\) triples with stabilization term

Full size image

6 Conclusion and future work

In this contribution, a stabilized method for lowest equal-order finite elements (FE) triples \(p1-p1-p1_{\mathrm{dg}}\) for the Oseen viscoelastic fluid flow is presented. In the standard Galerkin finite element method, the inf–sup (or LBB) condition is substantial while we circumvent the difficulty for the FE triples \(p1-p1-p1_{\mathrm{dg}}\) by adding a stabilization term essentially in the Oseen viscoelastic fluid flow model. This technique is new for the lowest equal-order FE triples for the reduced linearized viscoelastic fluid flow model. We proposed a stabilized FE algorithm and derived the well-posedness of the scheme. The desired error estimate is proved, and the optimal convergence order is obtained. In support of the given method, three numerical tests have been successfully implemented. In the analytical solution test, we demonstrate the optimal convergence order for lowest equal order. The second experiment elucidates the viscoelastic cavity flow to show the characteristics of the pressure contour and its behavior. The flow speed, behavior of the contours, streamlines patterns, and the pressure oscillation are examined by the “4-to-1 contraction channel flow.” This method can be extended to the streamline-upwind Petrov–Galerkin (SUPG) method for approximation of the Oseen viscoelastic fluid flow in the future studies.