The delta-shock wave for the two variables of a class of Temple system

Abstract

We investigate the Riemann problem for one-dimensional Temple class, obtain the Riemann solutions containing delta-shock wave, and discover that each variable of this system contains the Dirac delta function in different region. By the interaction of the delta-shock wave with the elementary waves we present the generalized Riemann problem for this system and construct the global solutions. By studying the limits of the solutions as perturbed parameter ε approaches zero we observe that the Riemann solutions are stable for such perturbations of the initial data.

1 Introduction

In this paper, we are concerned with the conservation laws

$$ \textstyle\begin{cases} \partial_{t} u+\partial_{x}(u^{2} v)=0,\\ \partial_{t} v+\partial_{x}(uv^{2})=0, \end{cases} $$

(1.1)

where $u\geq0$ and $v\geq0$. By introducing the function $\phi (u,v)=uv$ system (1.1) can be derived directly from the Temple system

$$ \textstyle\begin{cases} \partial_{t} u+\partial_{x}(u\phi(u,v))=0,\\ \partial_{t} v+\partial_{x}(v\phi(u,v))=0. \end{cases} $$

(1.2)

System (1.2) plays a key role in many engineering applications such as the enhanced oil recovery [33] and the theory of elasticity [11]. If $\phi(u,v)=\phi(uv)$, then this system can also be seen as a symmetric Keyfitz–Kranzer system [11, 27]; also see [15]. In this case, we can see the corresponding Riemann problem introduced by Shen [27]. For the Temple system, its chock curves coincide with rarefaction wave curves in the phase plane [33, 34]. For the related results on Temple systems, we refer to [1, 2] and the references therein.

Many studies of system (1.2) have been delivered from various aspects. Tan, Zhang, and Zheng [32] studied a reduced one-dimensional system and established the corresponding Riemann solutions. Moreover, they obtained the existence, uniqueness, and stability of delta-shock waves. In fact, setting $\phi (u,v)=u$, we can obtain the reduced system in [32]. Recently, the nonlinear chromatography

$$ \textstyle\begin{cases} \partial_{t} u+\partial_{x} (u+\frac{u}{1-u+v})=0,\\ \partial_{t} v+\partial_{x} (v+\frac{v}{1-u+v})=0, \end{cases} $$

(1.3)

has been extensively studied by many researchers [5, 8, 38, 39]. By the change of the coordinates and letting $a_{1}=a_{2}$, system (1.3) can be derived from the nonlinear chromatography system in [16, 17]. In addition, system (1.3) can also be obtained by setting $\phi(u,v)=1+\frac{1}{1-u+v}$ in (1.2); see [35, 40]. There is an important phenomenon that the delta-shock-type solutions occur in two component for these systems.

The delta-shock wave is a kind of nonclassical nonlinear waves in which at least one state variable becomes a singular measure; see [4, 6, 7, 9, 10, 12–14, 19–29, 31, 32, 37, 40] and the references therein.

The motivation for studying system (1.1) comes from the fact that the delta-shock-type solutions occur in two components. Moreover, Yang and Zhang [38, 39] assumed that $\phi(u,v)=\phi(au+bv)$ is a given smooth function satisfying $a^{2}+b^{2}\neq0$ or $\phi(u,v)=\phi(\alpha u,\alpha v)$, $\alpha>0$, and constructed the corresponding Riemann solutions.

Based on these two aspects, we first consider the Riemann problem for system (1.1) with the initial data

$$ (u,v) (x,0)= \textstyle\begin{cases} (u_{-},v_{-}),& x< 0,\\ (u_{+},v_{+}),& x>0, \end{cases} $$

(1.4)

where $u_{\pm}\geq0$ and $v_{\pm}\geq0$ are some constants. With the help of the characteristic analysis, we discover that there exists the delta-shock-type solution for (1.1) and (1.4). Different from the nonlinear chromatography system, there does not exist a delta-shock-type solution for both two components $(u,v)$ in the plane, that is,

• (1) when $u_{-}>0$, $v_{-}>0$ and $u_{+}=0$, $v_{+}>0$, there exists a delta-shock wave for the component v;

• (2) when $u_{-}>0$, $v_{-}>0$ and $u_{+}>0$, $v_{+}=0$, there exists a delta-shock wave for the component u.

Moreover, to investigate the stability of the Riemann solution, we consider the initial value problem with three pieces of constant states

$$ (u,v) (x,0)= \textstyle\begin{cases} (u_{-},v_{-}),& x < 0, \\ (u_{m},v_{m}),& 0 < x < \varepsilon, \\ (u_{+},v_{+}),& x > \varepsilon, \end{cases} $$

(1.5)

where $u_{i}\geq0$, $v_{i}\geq0$, $i=\pm$, m, and $\varepsilon> 0$ is arbitrarily small. The data (1.5) is a perturbation of the Riemann initial data (1.4). By discussing the interactions of δ-shock and elementary waves, we demonstrate whether the Riemann solutions of (1.1) and (1.4) are the limits of the solutions of (1.1) and (1.5) as $\varepsilon\rightarrow0$; see also [18, 28, 36] and the references therein. In addition, we refer the readers to the monograph of Chang and Hsiao [3] or [30] for the work on interactions of elementary waves and the stability of the Riemann solutions.

The organization of this paper is as follows. In Sect. 2, the Riemann solutions to system (1.1) are constructed, and the existence of the nonclassical solutions, δ-shock waves, is analyzed. In Sect. 3, we consider the initial value problem with three pieces of constant states. The global solutions are constructed. Moreover, we obtain that the solutions of the perturbed initial value problem converge to the corresponding Riemann solutions as ε approaches zero. Finally, we present the conclusions.

2 Solutions to the Riemann problem

In this section, we discuss Riemann solutions of (1.1) with initial data (1.4).

By calculation we can obtain that the eigenvalues of (1.1) are

$$ \lambda_{1}=uv\quad\mbox{and}\quad \lambda_{2}=3uv $$

(2.1)

with the corresponding right-eigenvectors

$$ r_{1}=(u,-v)^{T} \quad\mbox{and}\quad r_{2}=(u,v)^{T}. $$

(2.2)

It is easy to see that $\nabla\lambda_{1}\cdot r_{1}=0$ and $\nabla \lambda_{2}\cdot r_{2}\neq0$, where ∇ denotes the gradient with respect to $(u,v)$. Hence $\lambda_{1}$ is linearly degenerate, $\lambda_{2}$ is genuinely nonlinear, and system (1.1) is nonstrictly hyperbolic for $uv=0$. It is easy to obtain that the Riemann invariants of system (1.1) can be taken as

$$ w=uv,\qquad z=v/u. $$

(2.3)

Since equations (1.1) and the Riemann data are invariant under uniform stretching of coordinates

$$ (x,t)\longrightarrow(\kappa x,\kappa t),\quad\kappa\mbox{ is constant}, $$

we consider the self-similar solutions of (1.1) and (1.4)

$$ (u,v) (x,t)=(u,v) (\xi),\quad\xi=x/t. $$

Then the Riemann problem becomes a boundary value problem of ordinary differential equations

$$ \textstyle\begin{cases} -\xi u_{\xi}+(u^{2}v)_{\xi}=0,\\ -\xi v_{\xi}+(uv^{2})_{\xi}=0, \end{cases} $$

(2.4)

with

$$ (u,v) (\pm\infty)=(u_{\pm},v_{\pm}). $$

For smooth solutions, equations (2.4) can be rewritten as

$$ \begin{pmatrix} 2uv-\xi& u^{2} \\ v^{2} & 2uv-\xi \end{pmatrix} \begin{pmatrix} u\\ v \end{pmatrix} _{\xi}=0. $$

(2.5)

It follows from (2.5) that, besides the constant solution, it provides a continuous solution of (2.5) of the form $(u,v)(\xi)$.

Given a left state $(u_{-},v_{-})$, the possible states which can be connected to $(u_{-},v_{-})$ on the right by a rarefaction wave lie on a curve given as follows:

$$ R(u_{-},v_{-}): \quad \textstyle\begin{cases} \xi=\lambda_{2}=3uv,\\ \frac{v}{u}=\frac{v_{-}}{u_{-}},\\ v>v_{-},\qquad u>u_{-}. \end{cases} $$

(2.6)

For a bounded discontinuous solutions, the Rankine–Hugoniot conditions

$$ \textstyle\begin{cases} -\sigma[u]+[u^{2}v]=0,\\ -\sigma[v]+[uv^{2}]=0, \end{cases} $$

(2.7)

hold, where and in what follows, we use the notation $[h]=h_{+}-h_{-}$ with $h_{-}$ and $h_{+}$ the values of a function h on the left- and right-hand sides of the discontinuity curve, respectively, and σ is the velocity of the discontinuity. So, we obtain from (2.7) that

$$ (u_{+}v_{+}-u_{-}v_{-}) (u_{+}v_{-}-u_{-}v_{+})=0, $$

(2.8)

which gives $(u_{+}v_{-}-u_{-}v_{+})=0$ or $(u_{+}v_{+}-u_{-}v_{-})=0$. Thus, for a left state $(u_{-},v_{-})$, $(u_{+}v_{-}-u_{-}v_{+})=0$, and the Lax entropy conditions imply that the possible states can be connected to $(u_{-},v_{-})$ on the right by a shock wave satisfying

$$ S(u_{-},v_{-}):\quad \textstyle\begin{cases} \sigma=\frac{v_{-}}{u_{-}}(u^{2}+u u_{-}+u_{-}^{2}),\\ \frac{v}{u}=\frac{v_{-}}{u_{-}},\\ v< v_{-},\qquad u< u_{-}. \end{cases} $$

(2.9)

For this system (1.1), we can see that the shock wave curves coincide with the rarefaction wave curves.

If $(u_{+}v_{+}-u_{-}v_{-})=0$, then $u_{+}v_{+}=u_{-}v_{-}$. Since the first characteristic $\lambda_{1}=uv$ is linearly degenerate, this means that it is a contact discontinuity. Then the possible states that can be connected to $(u_{-},v_{-})$ on the right by a contact discontinuity lie on the curve

$$ J:\quad uv=u_{-}v_{-}. $$

(2.10)

To seek the Riemann solutions based on the value of the left state $(u_{-},v_{-})$, we divide the phase plane $I=\{(u,v): u\geq0, v\geq0\}$ into three parts: $\mathcal{A}=\{u>0 \mbox{ and } v>0\}$, $\mathcal {B}=\{u=0, v\neq0\}\cup\{v=0,u\neq0\}$, and $\mathcal{C}=\{u=0, v=0\}$.

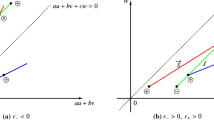
Case 1: $(u_{-},v_{-})\in\mathcal{A}$. In this case, we draw three curves (2.6), (2.9), and (2.10) from the point $(u_{-},v_{-})$ by R, S, and J, respectively. Obviously, the curve J has asymptotes $u=0$ and $v=0$. So, we divide the phase plane into six domains: $\mbox{I} \cup\mbox{II} \cup\mbox{III} \cup\mbox{IV} \cup \mathcal{B} \cup\mathcal{C}$; see Fig. 1. Hence we divide this case to four subcases as follows.

Figure 1

Elementary waves for case 1

Case 1.1: $(u_{+},v_{+})\in \mbox{I or II}$. The Riemann solutions can be described as

$$ (u_{-},v_{-})+J+(u_{*},v_{*})+R+(u_{+},v_{+}), $$

(2.11)

where and in what follows, “+” means “followed by”, denotes the state $(u_{-},v_{-})$, and the state $(u_{*},v_{*})$ is determined by

$$ \textstyle\begin{cases} u_{*}v_{*}=u_{-}v_{-},\\ \frac{v_{*}}{u_{*}}=\frac{v_{+}}{u_{+}}, \end{cases} $$

(2.12)

which gives

$$ u_{*}=\sqrt{\frac{u_{+}u_{-}v_{-}}{v_{+}}},\qquad v_{*}= \sqrt{\frac{v_{+}u_{-}v_{-}}{u_{+}}}. $$

(2.13)

Moreover, the rarefaction wave R can be expressed as follows:

$$\begin{aligned} R:\quad \textstyle\begin{cases} \xi=\lambda_{2}=3uv,\\ \frac{v}{u}=\frac{v_{+}}{u_{+}},\\ u_{*}\leq u\leq u_{+},\qquad v_{*}\leq v\leq v_{+}. \end{cases}\displaystyle \end{aligned}$$

(2.14)

Case 1.2: $(u_{+},v_{+})\in$ III or IV. We can obtain that the corresponding Riemann solutions are

$$ (u_{-},v_{-})+J+(u_{*},v_{*})+S+(u_{+},v_{+}), $$

(2.15)

where the intermediate state $(u_{*},v_{*})$ is described by (2.13), and the shock wave S is expressed as follows:

$$ S:\quad \textstyle\begin{cases} \sigma=\frac{v_{*}}{u_{*}}(u_{+}^{2}+u_{+} u_{*}+u_{*}^{2}),\\ \frac{v_{+}}{u_{+}}=\frac{v_{*}}{u_{*}},\\ v_{+}< v_{*},\qquad u_{+}< u_{*}. \end{cases} $$

(2.16)

Case 1.3: $(u_{+},v_{+})=(0,0)\in\mathcal{C}$. The Riemann solutions are

$$ (u_{-},v_{-})+S+(u_{+},v_{+}), $$

(2.17)

where the speed of the shock wave S is

$$ \sigma=u_{-}v_{-}. $$

(2.18)

Case 1.4:. $(u_{+},v_{+})\in\mathcal{B}$. In this case, we can see that

$$ \lambda_{2}^{+}=\lambda_{1}^{+}=0< \lambda_{1}^{-}=u_{-}v_{-}< \lambda_{2}^{-}=3 u_{-}v_{-}, $$

(2.19)

which implies that the solutions cannot be constructed as before. Hence the Riemann solutions containing a weighted δ-measure supported on a line should be constructed to establish the existence.

To define the measure solutions, we introduce the following definitions.

Definition 2.1

A pair of $(u,v)$ constitutes a solution of (1.1) in the sense of distributions if

$$ \textstyle\begin{cases} \int_{0}^{+\infty}\int_{-\infty}^{+\infty} \{\varphi_{t}+(uv)\varphi_{x}\}u \,dx \,dt=0,\\ \int_{0}^{+\infty}\int_{-\infty}^{+\infty} \{\varphi_{t}+(uv)\varphi_{x}\}v \,dx \,dt=0, \end{cases} $$

(2.20)

for all test functions $\varphi(t,x)\in C_{0}^{\infty}(R_{+}\times R)$.

Definition 2.2

A two-dimensional weighted δ-measure $\omega(s)\delta_{\Gamma }$ supported on a smooth curve $\Gamma=\{(t(s),x(s)): a< s< b\}$ is defined by

$$ \bigl\langle \omega(s)\delta_{\Gamma},\varphi\bigl(t(s),x(s)\bigr)\bigr\rangle = \int_{a}^{b} \omega(s)\varphi\bigl(t(s),x(s)\bigr)\,ds $$

(2.21)

for all test functions $\varphi(t,x)\in C_{0}^{\infty}(R\times R)$.

Definition 2.3

A pair of $(u,v)$ is called a delta-shock wave solution of (1.1) if it is represented in the form

$$ (u,v) (t,x)= \textstyle\begin{cases} (u_{-},v_{-}),& x< x(t),\\ (u_{\delta},\omega(t)\delta(x-x(t))),& x=x(t),\\ (0,v_{+}),& x>x(t), \end{cases} $$

(2.22)

or

$$ (u,v) (t,x)= \textstyle\begin{cases} (u_{-},v_{-}),& x< x(t),\\ (\omega(t)\delta(x-x(t)),v_{\delta}),& x=x(t),\\ (u_{+},0),& x>x(t), \end{cases} $$

(2.23)

and satisfies Definition 2.1, where $(u_{l},v_{l})$, $(u_{r},v_{r})$ are piecewise smooth bounded solutions of (1.1), $\omega (t)\in C^{1}[0,+\infty)$, $\delta(\cdot)$ is the standard Dirac measure supported on the curve $x=x(t)$, and $\omega(t)$ is the weight of the delta-shock wave on the state variable u or v.

Now, we consider the case $(u_{-},v_{-})\in\mathcal{A}$ and $(0,v_{+})\in \mathcal{B}$. Similarly, we also describe the other case $(u_{-},v_{-})\in \mathcal{A}$ and $(u_{+},0)\in\mathcal{B}$.

Following [4, 5, 22, 27, 38, 39], we claim that (2.22) is a delta-shock wave solution of (1.1) in the sense of distributions if it satisfies the following generalized Rankine–Hugoniot condition:

$$ \textstyle\begin{cases} \frac{dx}{dt}=\sigma_{\delta},\\ \sigma_{\delta}[u]=[u^{2}v],\\ \frac{d\omega(t)}{dt}=\sigma_{\delta}[v]-[uv^{2}], \end{cases} $$

(2.24)

with

$$ \sigma_{\delta}=u_{-}v_{-},\qquad\omega(t)=u_{-}v_{-}v_{+} t. $$

(2.25)

In addition to the generalized Rankine–Hugoniot condition, the discontinuity must satisfy the delta-shock wave entropy condition (2.19), which means that all the characteristic lines on both sides of the discontinuity are not outcoming.

Case 2. $(u_{-},v_{-})\in\mathcal{B}$. Here, we only consider the case $(u_{-},v_{-})\in\mathcal{B}$ and $u_{-}=0$. As for the other case $(u_{-},v_{-})\in\mathcal{B}$ and $v_{-}=0$, we can obtain the same results and omit the details. We divide this case into two subcases; see Fig. 2.

Figure 2

Elementary waves for case 2

Case 2.1. $(u_{+},v_{+})\in\mathcal{B}\cup\mathcal{C}$. The corresponding Riemann solutions are expressed by

$$ (u_{-},v_{-})+J+(u_{+},v_{+}), $$

(2.26)

where the speed of the contact discontinuity $\sigma_{J}=0$; see Fig. 3.

Figure 3

Solutions for case 2.1

Case 2.2. $(u_{+},v_{+})\in\mathcal{A}$. The Riemann solutions are constructed as

$$ (u_{-},v_{-})+J+(0,0)+R+(u_{+},v_{+}), $$

(2.27)

where the speed of J vanishes. The J and R are formed as a composite wave; see Fig. 4.

Figure 4

Solutions for case 2.2

So, we complete the construction of the Riemann solutions to system (1.1).

3 Interactions of δ-shock wave with elementary waves

In this section, we consider problem (1.1) and (1.5). We divide this into four cases.

Case 1. -shock. This case can be divided into two subcases.

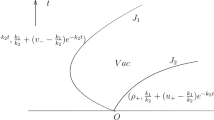
Case 1.1. $(u_{-},v_{-})\in\mathcal{B}$, $(u_{+},v_{+})\in\mathcal {B}$, $(u_{m},v_{m})\in\mathcal{A}$, and $u_{-}=u_{+}=0$ (or $v_{-}=v_{+}=0$); see Fig. 5.

Figure 5

Case 1.1. -shock

A composite wave emitting from the point O consists of a contact discontinuity and a rarefaction wave. The Riemann solution is a delta-shock wave $\delta {S_{1}}$, whose speed is $\sigma_{\delta}=u_{m} v_{m}$.

As for the characteristic line OB of rarefaction wave R, we have $\lambda=\frac{dx}{dt}=3 u_{m} v_{m}$. The rarefaction wave R will overtake the delta shock at some finite time. The intersection point $B(x,t)$ is determined by

$$ \textstyle\begin{cases} \frac{x}{t}=3u_{m} v_{m}, \\ \frac{x-\varepsilon}{t}=u_{m} v_{m}, \end{cases} $$

(3.1)

which implies

$$ (x_{B},t_{B})=\biggl(\frac{3 \varepsilon}{2}, \frac{\varepsilon}{2u_{m} v_{m}}\biggr). $$

(3.2)

After the time $t_{B}$, the δ-shock interacts with the rarefaction wave R and changes into another new δ-shock (denoted by $\delta{S_{2}}$), which is calculated by

$$ \textstyle\begin{cases} \frac{x}{t}=3 u v, \\ \frac{v}{u}=\frac{v_{m}}{u_{m}},\quad0< u\leq u_{m}, 0< v\leq v_{m},\\ \frac{dx}{dt}=\sigma_{\delta}=u v,\\ x \vert_{t_{B}}=x_{B}. \end{cases} $$

(3.3)

From (3.3) we obtain

$$ x=x_{B}\biggl(\frac{t}{t_{B}}\biggr)^{\frac{1}{3}}, \qquad \sigma_{\delta}=\frac{v_{m}}{u_{m}}u^{2},\quad0< u\leq u_{m}, $$

(3.4)

from which we have

$$ \lim_{u\rightarrow0}\sigma_{\delta}=0 $$

(3.5)

and conclude that the delta shock $\delta{S_{2}}$ has the straight line $\frac{dx}{dt}=0$ as its asymptote, which gives that the delta shock cannot penetrate the rarefaction wave R. For large time, that is, as $t\rightarrow\infty$, the solution can be expressed as

$$ (u_{-},v_{-})+J+(0,0)+R+\delta{S_{2}}+(u_{+},v_{+}). $$

As $\varepsilon\rightarrow0$, we can see that the limit of solution (1.1) and (1.5) is the corresponding Riemann solution in this case.

Case 1.2. $(u_{-},v_{-})\in\mathcal{A}$, $(u_{m},v_{m})\in\mathcal {A}$, $(u_{+},v_{+})\in\mathcal{B}$, and $u_{+}=0$ (or $v_{+}=0$). In addition, we assume that $u_{-} v_{-}< u_{m} v_{m}$; see Fig. 6.

Figure 6

Case 1.2:

By case 1.1 we can see that the $\delta_{AB}$-shock will be overtaken by the rarefaction R and the intersection point $(x_{B},t_{B})$ can be given by (3.2). After the time $t_{B}$, the δ-shock begins to interact with the rarefaction wave R, and the δ-shock can be determined by (3.3). Unlike case 1.1, the δ-shock will penetrate the R at finite time.

In fact, when the δ-shock interacts with the R, its speed is $\sigma_{\delta}=\frac{dx}{dt}=uv$. With the help of (3.3), we have $\frac{d^{2}x}{dt^{2}}<0$, which means that $\sigma_{\delta}$ decelerates in the penetration. In addition, we also have , which implies that the δ-shock can penetrate R at some point $C(x_{C},t_{C})$.

From the first equation of (3.3) we have

$$ \frac{x_{C}}{t_{C}}=3 u_{i} v_{i}. $$

Combining this equation and (3.4), we have

$$ x_{C}=\sqrt{\frac{x_{B}^{3}}{3 u_{i} v_{i} t_{B}}},\qquad t_{C}=\sqrt{\frac {x_{B}^{3}}{(3 u_{i} v_{i})^{3} t_{B}}}. $$

(3.6)

Meantime, a new Riemann problem is formed, and the Riemann solution is a $\delta_{{CD}}$-shock with speed $\sigma_{\delta}=u_{i} v_{i}$. It is easy to see that the $\delta _{{CD}}$-shock is parallel to the contact discontinuity J; see Fig. 6.

Letting $\varepsilon\rightarrow0$, the limit of the solution (1.1) and (1.5) is the corresponding Riemann solution.

Case 2. δ-shock . In this case, $(u_{-},v_{-})\in\mathcal{A}$, $(u_{+},v_{+})\in\mathcal{A}$, and $(u_{m},v_{m})\in\mathcal{B}$. We divide this case into two subcases.

Case 2.1. $u_{-} v_{-}< u_{+} v_{+}$; see Fig. 7.

Figure 7

Case 2.1:

The speed of the $\delta_{{OB}}$-shock is $\sigma_{\delta}=u_{-} v_{-}$ and that of the contact discontinuity $J_{{AB}}$ is $\lambda_{1}=0< u_{-} v_{-}$. Obviously, the δ-shock overtakes J at some point $B(x_{B},t_{B})$, which satisfies

$$ \textstyle\begin{cases} x=\varepsilon,\\ \frac{x}{t}=u_{-} v_{-}. \end{cases} $$

(3.7)

Thus we have

$$ x_{{B}}=\varepsilon,\qquad t_{{B}}= \frac{\varepsilon}{u_{-} v_{-}}. $$

(3.8)

After the point B, the δ-shock entropy condition (2.19) is not satisfied, a contact discontinuity BC and a shock wave $\widehat{BD}$ emit from the point B. The contact discontinuity BC is $J_{{BC}}: x-x_{{B}}=u_{-} v_{-} (t-t_{{B}})$ and $t>t_{{B}}$. The shock $S_{{\widehat{BD}}}$ will cross the rarefaction wave R with varying speed of propagation during the penetration, which means that the shock $S_{{\widehat{BD}}}$ is no longer a straight line. Moreover, the shock wave $S_{{\widehat{BD}}}$ is determined by

$$ \textstyle\begin{cases} \frac{dx}{dt}=\sigma_{ S}=\frac{v_{i}}{u_{i}}(u^{2}+u u_{i}+u_{i}^{2}),\\ x \vert_{t_{B}}=x_{{B}},\\ \frac{x-\varepsilon}{t}=3 u v,\\ \frac{v}{u}=\frac{v_{i}}{u_{i}}=\frac{v_{+}}{u_{+}},\quad0< u\leq u_{i}, 0< v\leq v_{i}. \end{cases} $$

(3.9)

Obviously, during the penetration, we have $\frac{du}{dt}>0$, which implies $\frac{d^{2} x}{dt^{2}}>0$. Thus, the shock wave curve $S_{{\widehat{BD}}}$ is concave in the $(x,t)$-plane, as shown in Fig. 7.

From the last two equations of (3.9) we have

$$ \frac{x-\varepsilon}{t}=3 u^{2}\frac{v_{i}}{u_{i}}, $$

which, combined with the first equation of (3.9), gives

$$ \frac{dt}{t}=\frac{6 u}{(u^{2}+u u_{i}+u_{i}^{2})-3 u^{2}} \,du. $$

(3.10)

Integrating (3.10) over $[0,u_{i}]$ gives

$$ \ln\frac{t}{t_{B}}= \int_{0}^{u_{i}}\frac{6 u}{(u^{2}+u u_{i}+u_{i}^{2})-3 u^{2}} \,du, $$

(3.11)

which implies that $t\rightarrow\infty$ as $u\rightarrow u_{i}$. So, the shock wave $S_{{\widehat{BD}}}$ cannot penetrate the rarefaction wave R and has the straight line $\frac{dx}{dt}=3 u_{i} v_{i}$ as its asymptote.

Moreover, we can obtain that as $\varepsilon\rightarrow0$, the limit of the solution (1.1) and (1.5) is the corresponding Riemann solution.

Case 2.2. $u_{-} v_{-}>u_{+} v_{+}$; see Fig. 8.

Figure 8

Case 2.2:

Unlike case 2.1, the shock wave $S_{{\widehat{BDE}}}$ can penetrate the rarefaction wave at finite time. In fact, integrating (3.10) over $[0,u_{+}]$ yields

$$ \ln\frac{t}{t_{B}}= \int_{0}^{u_{ +}}\frac{6 u}{(u^{2}+u u_{i}+u_{i}^{2})-3 u^{2}} \,du, $$

(3.12)

where $u_{+}< u_{i}$. We obtain from (3.12) that, at some time $t_{{D}}$, the shock wave $S_{{\widehat{BDE}}}$ penetrate R, where

$$ t_{D}=t_{B} \exp\biggl( \int_{0}^{u_{ +}}\frac{6 u}{(u^{2}+u u_{i}+u_{i}^{2})-3 u^{2}} \,du\biggr). $$

(3.13)

The shock wave $S_{{\widehat{BD}}}$ is given by (3.9), where $0< u\leq u_{+}< u_{i}$ and $0< v\leq v_{+}< v_{i}$. At the point D, a straight shock $S_{{DE}}$ emits with speed $\sigma_{S}=\frac{v_{+}}{u_{+}}(u_{+} ^{2}+u_{i} u_{+}+u_{i}^{2})$.

Thus, for large time, the solutions can be described as

$$ (u_{-},v_{-})+J+(u_{i},v_{i})+S+(u_{+},v_{+}). $$

Moreover, as $\varepsilon\rightarrow0$, the limit of the solution (1.1) and (1.5) is the corresponding Riemann solution.

Case 3. -shock. In this case, we have $(u_{-},v_{-})\in\mathcal{A}$, $(u_{m},v_{m})\in\mathcal {A}$, $(u_{+},v_{+})\in\mathcal{B}$, and $u_{-}v_{-}>u_{m} v_{m}$; see Fig. 9. Here, we assume that $u_{+}=0$ and also obtain the same results for the case $v_{+}=0$.

Figure 9

Case 2.3:

The propagation speed of the shock $S_{{OB}}$ is $\sigma_{\delta }=\frac{v_{m}}{u_{m}}(u_{m}^{2}+u_{m} u_{i}+u_{i}^{2})$, which is greater than that of the delta-shock wave $\delta_{{AB}}$, $\sigma_{\delta}=u_{m} v_{m}$, where $(u_{i},v_{i})$ may be calculated by (2.12), that is,

$$ \textstyle\begin{cases} u_{i}v_{i}=u_{-}v_{-},\\ \frac{v_{i}}{u_{i}}=\frac{v_{m}}{u_{m}}. \end{cases} $$

(3.14)

Then S intersects with the δ-shock at a point $B(x_{B},t_{B})$, which is calculated by

$$ \textstyle\begin{cases} x=\frac{v_{m}}{u_{m}}(u_{m}^{2}+u_{m} u_{i}+u_{i}^{2}) t,\\ x-\varepsilon=u_{m} v_{m} t. \end{cases} $$

(3.15)

A direct calculation leads to

$$ x_{B}=\frac{u_{m}^{2}+u_{m} u_{i}+u_{i}^{2}}{u_{i}(u_{m}+u_{i})}\varepsilon,\qquad t_{B}=\frac{u_{m}}{u_{i}v_{m}(u_{m}+u_{i})}\varepsilon. $$

(3.16)

At the point B, a new delta-shock wave $\delta_{{BD}}$ occurs, the propagation speed of which is $\sigma_{\delta}=u_{i} v_{i}$. Meantime, the speed of the contact discontinuity $J_{{OC}}$ is $\sigma_{J}=u_{i} v_{i}=u_{-}v_{-}$, which leads to that it is parallel to the $\delta_{{BD}}$-shock.

As $t\rightarrow\infty$, the time-asymptotic solution can be described as

$$ (u_{-},v_{-})+J+(u_{i},v_{i})+\delta\mbox{-shock}+(u_{+},v_{+}). $$

As $\varepsilon\rightarrow0$, the intermediate state $(u_{i},v_{i})$ disappears, whereas $\delta_{{BD}}$-shock and $J_{{OC}}$ unify into one delta-shock wave since $\delta_{{BD}}$-shock and $J_{{OC}}$ propagate with the same speed $u_{-}v_{-}$. So the solution tends to the corresponding Riemann solution as $\varepsilon\rightarrow0$.

Case 4. . In this case, we have $(u_{-},v_{-})\in\mathcal{A}$, $(u_{m},v_{m})\in \mathcal{B}$, and $(u_{+},v_{+})\in\mathcal{B}$. We can check that the propagating speed of the $\delta_{{OB}}$-shock $\sigma_{\delta}=u--v_{-}$ is greater than that of the contact discontinuity $J_{{AB}}$, $\sigma_{J}=0$, which implies that $\delta _{{S_{1}}}$ will overtake the $J_{{AB}}$ at some point $B(x_{{B}},t_{{B}})$, which is expressed by (3.8). They interact with each other and yield a new delta-shock wave $\delta _{S_{2}}$ with the propagating speed $\sigma_{\delta}=u_{i} v_{i}$; see Fig. 10.

Figure 10

Case 2.4:

So far, we have finished the discussion on the interactions of the δ-shock and the elementary waves, and the global solutions for the perturbed initial value problem (1.1) and (1.5) have been constructed. We summarize our results in the following:

Theorem 3.1

The limit of the perturbed Riemann solution of (1.1) and (1.5) is exactly the corresponding Riemann solution of (1.1) and (1.4). The Riemann solution of (1.1) and (1.4) is stable and admissible with respect to such small perturbations of the initial data.

4 Conclusions

In this paper, we discuss the delta-shock waves of a class of symmetric nonstrictly hyperbolic conservation law equations in which each variable may contain the Dirac delta function in different regions. This enriches the content of the Temple system. Furthermore, we discuss the interaction of elementary waves, involving the composite wave, which is different from the corresponding contents in [35, 36, 38–40]. In the future, we will focus ourselves on the corresponding two-dimensional equations and the related content.