1 Introduction

In various branches of mathematical and physical sciences, nonlinear evolution equations have been the subject of concentrated study to understand the physical phenomena of nonlinear sciences. Among the possible solutions to NLEEs, certain particular form solutions may depend only on a single combination of the variables such as soliton solutions. A soliton is defined as a self-reinforcing solitary wave in the form of a wave packet or a pulse that always maintains its shape while it travels at steady speed. Solitons occur as the solutions of an extensive class of weakly nonlinear dispersive partial differential equations for describing physical structures. The soliton solutions are usually obtained by means of the inverse scattering transform [1] and their constancy to the integrability of the field equations. Analytical solutions of nonlinear PDEs play a significant rule to perfect understanding qualitative features and physical interpretation of numerous phenomena. Analytical solutions of nonlinear PDEs symbolically and graphically demonstrate unraveling the mechanisms of many nonlinear complex phenomena such as absence or multiplicity of steady states under different necessary conditions, the existence of peaking regimes, a spatial localization of transfer processes, and many others.

Several methods have been constructed for finding exact traveling wave solutions of nonlinear PDEs in the form of soliton, solitary wave, and elliptic function solutions such as Hirota’s bilinear method [2], Jacobi elliptic function method [3], semiinverse variational principle [4], Darboux transformation [5, 6], expansion method [7, 8], extended direct algebraic method [9, 10], auxiliary method [11], sine–cosine method [12], the Kudryashov method [13], and extended simple equation method [14]. The study of solutions, structures, interaction, and further properties of solitons and solitary wave solutions gained much consideration [15–43].

In this work, we have employed novel \((\frac{G'}{G})\) expansion method on the three important models for constructing exact and solitary wave solutions of the nonlinear Ablowitz–Kaup–Newell–Segur water wave equation, which is used as a reduction for some nonlinear evolution equations, \((2 + 1)\)-dimensional Boussinesq dynamical wave equation, which explains the gravity of wave propagation on the surface of the water and also describes the collision of oblique waves transformation movement in different aspects, and \((3+1)\)-dimensional Yu–Toda–Sasa–Fukuyama wave equation, which is used for investigation of the dynamics of solutions and nonlinear waves in fluid dynamics, plasma physics, weakly dispersive media, and many others. Our new constructed solutions are helpful in exploring nonlinear wave phenomena in physical problems, and the results involve long and classified computations.

The paper is organized as follows. The chief steps of the description method are specified in Sect. 2. In Sect. 3, we apply the present method to our three selective models for constructing exact and solitary wave solutions. Discussions of the results are given in Sect. 4. Lastly, a summary of the work is given in Sect. 5.

2 Description of the method

We consider a nonlinear partial differential equation of the form

$$ R ( u, u_{x}, u_{y}, u_{t}, u_{xx}, u_{yy}, u_{tt},\ldots ) =0, $$
(1)

where R is a polynomial function of \(u(x,y,t)\) and its partial derivatives, in which the highest order derivatives and nonlinear terms are involved. The main steps of our method are as follows.

Step 1. The traveling wave transformations can be deduced as

$$ u(x,y,t)= U(\zeta ),\quad \zeta = x +y+ \omega t. $$
(2)

Utilizing this transformation in Eq. (1), we have the ODE of the form

$$ S \bigl( U, U', U'', U''',\ldots \bigr) =0, $$
(3)

where S is a polynomial of \(U(\zeta )\) and its derivatives with respect to ζ.

Step 2. Let us assume that the solution of Eq. (3) has the form

$$ V(\zeta )= A_{0}+\sum^{m}_{i=1}A_{i} \biggl( \frac{G'}{G} \biggr) ^{i},\qquad A_{m}\neq 0, $$
(4)

where \(A_{i}\) (\(i = 0,1,2,\ldots,m\)) are arbitrary constants to be determined latter, and m is a positive integer, which can be calculated by applying the homogeneous balance principle to Eq. (3).

Let \(G( \zeta )\) satisfy the second-order LODE

$$ G''+\lambda_{1} G'+\lambda_{2} G=0, $$
(5)

where \(\lambda_{1}\) and \(\lambda_{2}\) are arbitrary constants.

Step 3. Substituting Eq. (4) along with Eq. (5) into Eq. (3) and collecting the coefficients at \(( \frac{G'}{G} ) ^{i}\) and then equating the coefficients to zero, we acquire a system of algebraic equations, which can be solved by Mathematica, and consider the following solution cases:

Case 1. When \(\lambda_{1}^{2}-4\lambda_{2}>0\),

$$ \biggl( \frac{G'}{G} \biggr) = \frac{\sqrt{\lambda_{1}^{2}-4\lambda_{2}}}{2} \biggl( \frac{B_{1}\sinh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda_{2}})\zeta +B_{2}\cosh ( \frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda_{2}})\zeta }{B_{1}\cosh ( \frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda_{2}})\zeta +B_{2}\sinh ( \frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda_{2}})\zeta } \biggr) -\frac{ \lambda_{1}}{2}. $$
(6)

Case 2. When \(\lambda_{1}^{2}-4\lambda_{2}<0\),

$$ \biggl( \frac{G'}{G} \biggr) = \frac{\sqrt{4\lambda_{2}-\lambda_{1}^{2}}}{2} \biggl( \frac{-B_{1} \sin (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta +B_{2} \cos (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta }{B_{1} \cos (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta +B_{2} \sin (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta } \biggr) -\frac{ \lambda_{1}}{2}. $$
(7)

Case 3. When \(\lambda_{1}^{2}-4\lambda_{2}=0\),

$$ \biggl( \frac{G'}{G} \biggr) =\frac{B_{2}}{B_{1}+B_{2}\zeta }- \frac{ \lambda_{1}}{2}. $$
(8)

Step 4. Substituting all solutions of Eq. (5) into Eq. (3), we obtain the required solutions of Eq. (1).

3 Applications of description method

3.1 Fourth-order nonlinear Ablowitz–Kaup–Newell–Segur water equation

In this section, we apply our method to the well-known AKNS equation [44] of the general form

$$ 4u_{xt}+u_{xxxt}+8u_{x}u_{xy}+ 4u_{xx}u_{y}-\gamma u_{xx} =0. $$
(9)

This equation includes some nonlinear evolution equations such as sine-Gordon, nonlinear Schrödinger, KdV, and other equations having numerous application in physical science.

The traveling wave transformations can be reduced to the form

$$ u(x,y,t)=U(\zeta ) , \quad \zeta =x+y+\omega t, $$
(10)

where ω is an arbitrary constant to be determined latter. Applying this transformation to Eq. (10) and integrating, we arrive at the ordinary differential equation

$$ (4\omega -\gamma )U^{\prime}+6U^{\prime {2}} +\omega U^{'''}=0. $$
(11)

Applying the homogeneous balance principle between \(U^{\prime 2}\) and \(U^{\prime\prime\prime} \) in Eq. (11), we get \(m=1\). We assume that solution of Eq. (11) is of the form

$$ U(\zeta )=A_{0}+A_{1} \biggl( \frac{G'}{G} \biggr) . $$
(12)

Substituting Eq. (12) along with Eq. (5) into Eq. (11), we get algebraic equations in parameters \(A_{0}\), \(A _{1}\), and ω. This system of equations can be solved with the help of Mathematica:

$$ A_{1}= \biggl( \frac{\gamma }{\lambda_{1} ^{2}-4\lambda_{2} +4} \biggr) , \qquad A_{0}=A_{0}, \qquad \omega = \biggl( \frac{\beta }{6+\lambda_{1} ^{2}-4 \lambda_{2} -2} \biggr) . $$
(13)

Substituting Eq. (13) into Eq. (12), we obtain the exact traveling solution

$$ U(\zeta )=A_{0}+ \biggl( \frac{\gamma }{\lambda_{1} ^{2}-4\lambda_{2} +4} \biggr) \biggl( \frac{G'}{G} \biggr) . $$
(14)

Now we discuss three different cases regarding the solution (14).

Case 1. When \(\lambda_{1}^{2}-4\lambda_{2}>0\), substituting Eq. (6) into Eq. (14), we get the following solution of Eq. (9):

$$\begin{aligned} &U_{1}(\zeta ) \\ &\quad =A_{0}+ \biggl(\frac{\gamma }{\lambda_{1} ^{2}-4 \lambda_{2} +4} \biggr) \\ &\quad \quad {}\times \biggl( \frac{\sqrt{\lambda_{1}^{2}-4\lambda_{2}}}{2} \biggl( \frac{B_{1}\sinh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda _{2}})\zeta +B_{2}\cosh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda _{2}})\zeta }{B_{1}\cosh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda _{2}})\zeta +B_{2}\sinh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda _{2}})\zeta } \biggr) -\frac{\lambda_{1}}{2} \biggr) . \end{aligned}$$
(15)

Case 2. When \(\lambda_{1}^{2}-4\lambda_{2}<0\), substituting Eq. (7) into Eq. (14), we get the following solution of Eq. (9):

$$\begin{aligned} &U_{2}(\zeta ) \\ &\quad =A_{0}+ \biggl(\frac{\gamma }{\lambda_{1} ^{2}-4 \lambda_{2} +4} \biggr) \\ &\quad \quad {}\times \biggl( \frac{\sqrt{4\lambda_{2}-\lambda_{1}^{2}}}{2} \biggl( \frac{-B_{1} \sin (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta +B_{2} \cos (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta }{B_{1} \cos (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta +B_{2} \sin (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta } \biggr) -\frac{ \lambda_{1}}{2} \biggr) . \end{aligned}$$
(16)

Case 3. When \(\lambda_{1}^{2}-4\lambda_{2}=0\), substituting Eq. (9) into Eq. (14), we get the following solution of Eq. (9):

$$ U_{3}(\zeta )=A_{0}+ \biggl( \frac{\gamma }{\lambda_{1} ^{2}-4 \lambda _{2} +4} \biggr) \biggl( \frac{B_{2}}{B_{1}+B_{2}\zeta }-\frac{\lambda _{1}}{2} \biggr) . $$
(17)

3.2 \((2+1)\)-D Boussinesq dynamical equation

The general form of the \((2+1)\)-dimensional Boussinesq dynamical equation [45] is the following;

$$ u_{tt}-u_{xx}-\beta \bigl(u^{2} \bigr)_{xx}-u_{yy}-u_{xxxx}=o,\quad \beta \neq 0. $$
(18)

The extreme merit of this equation is that it is used to describe the gravity waves propagation on the water surface and also clarifies the collision of oblique wave transformation.

The traveling wave transformations for Eq. (18) can be deduced as

$$ u(x,y,t)=U(\zeta ) ,\quad \zeta =x+y+k t. $$
(19)

Using these transformations to Eq. (18), we obtain the ordinary differential equation

$$ 2\beta U^{\prime 2}+2\beta U U^{\prime\prime}+\bigl(2-k^{2}\bigr)U^{\prime\prime}+U^{\prime\prime\prime\prime}=0. $$
(20)

Here, applying the homogeneous balance principle to Eq. (20), we get \(m=2\). We suppose that the solution of Eq. (20) is of the form

$$ U(\zeta )=A_{0}+A_{1} \biggl( \frac{G'}{G} \biggr) +A_{2} \biggl( \frac{G'}{G} \biggr) ^{2}. $$
(21)

Substituting Eq. (21) along with Eq. (5) into Eq. (20), we obtain numerous algebraic equations in parameters \(A_{0}\), \(A_{1}\), \(A _{2}\), and k. These equations can be solved with the help of Mathematica:

$$ A_{0}= \frac{-\lambda_{1} ^{2}-8\lambda_{2} +k ^{2}-2}{2 \beta },\qquad A_{1}= - \frac{6 \lambda_{1} }{\beta },\qquad A_{2}= -\frac{6}{\beta }. $$
(22)

Substituting Eq. (22) into Eq. (21), we obtain the exact traveling solution

$$\begin{aligned} U(\zeta )= \frac{-\lambda_{1} ^{2}-8\lambda_{2} +k ^{2}-2}{2 \beta } -\frac{6 \lambda_{1} }{\beta } \biggl( \frac{G'}{G} \biggr) -\frac{6}{ \beta } \biggl( \frac{G'}{G} \biggr) ^{2}. \end{aligned}$$
(23)

Now we discuss three different cases regarding solution (23).

Case 1. When \(\lambda_{1}^{2}-4\lambda_{2}>0\), substituting Eq. (6) into Eq. (23), we obtain the following solution of Eq. (18):

$$\begin{aligned} U_{4}(\zeta )&= \frac{-\lambda_{1} ^{2}-8 \lambda_{2} +k ^{2}-2}{2\beta } \\ &\quad {}- \frac{6 \lambda_{1} }{\beta } \biggl( \frac{\sqrt{\lambda_{1} ^{2}-4\lambda_{2}}}{2} \biggl( \frac{B_{1}\sinh (\frac{1}{2}\sqrt{ \lambda_{1}^{2}-4\lambda_{2}})\zeta +B_{2}\cosh (\frac{1}{2}\sqrt{ \lambda_{1}^{2}-4\lambda_{2}})\zeta }{B_{1}\cosh (\frac{1}{2}\sqrt{ \lambda_{1}^{2}-4\lambda_{2}})\zeta +B_{2}\sinh (\frac{1}{2}\sqrt{ \lambda_{1}^{2}-4\lambda_{2}})\zeta } \biggr) - \frac{\lambda_{1}}{2} \biggr) \\ &\quad {}-\frac{6}{\beta } \biggl( \frac{\sqrt{\lambda_{1}^{2}-4\lambda_{2}}}{2} \biggl( \frac{B_{1}\sinh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda _{2}})\zeta +B_{2}\cosh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda _{2}})\zeta }{B_{1}\cosh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda _{2}})\zeta +B_{2}\sinh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4\lambda _{2}})\zeta } \biggr) -\frac{\lambda_{1}}{2} \biggr) ^{2}, \\ &\quad \beta \neq 0. \end{aligned}$$
(24)

Case 2. When \(\lambda_{1}^{2}-4\lambda_{2}<0\), substituting Eq. (7) into Eq. (23), we obtain the following solution of Eq. (18):

$$\begin{aligned} U_{5}(\zeta )&= \frac{-\lambda_{1} ^{2}-8 \lambda_{2} +k ^{2}-2}{2\beta } \\ &\quad {}-\frac{6 \lambda_{1} }{\beta } \biggl( \frac{\sqrt{4\lambda _{2}-\lambda_{1}^{2}}}{2} \biggl( \frac{-B_{1}\sin (\frac{1}{2}\sqrt{4 \lambda_{2}-\lambda_{1}^{2}})\zeta +B_{2}\cos (\frac{1}{2}\sqrt{4 \lambda_{2}-\lambda_{1}^{2}})\zeta }{B_{1}\cos (\frac{1}{2}\sqrt{4 \lambda_{2}-\lambda_{1}^{2}})\zeta +B_{2}\sin (\frac{1}{2}\sqrt{4 \lambda_{2}-\lambda_{1}^{2}})\zeta } \biggr) - \frac{\lambda_{1}}{2} \biggr) \\ &\quad {}-\frac{6}{\beta } \biggl( \frac{\sqrt{4\lambda_{2}-\lambda_{1}^{2}}}{2} \biggl( \frac{-B_{1} \sin (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta +B_{2} \cos (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta }{B_{1} \cos (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta +B_{2} \sin (\frac{1}{2}\sqrt{4\lambda_{2}-\lambda_{1}^{2}})\zeta } \biggr) -\frac{\lambda_{1}}{2} \biggr) ^{2}, \\ &\quad {}\beta \neq 0. \end{aligned}$$
(25)

Case 3. When \(\lambda_{1}^{2}-4\lambda_{2}=0\), substituting Eq. (8) into Eq. (23), we obtain the following solution of Eq. (18):

$$\begin{aligned} &U_{6}(\zeta )\frac{-\lambda_{1} ^{2}-8 \lambda_{2} +k ^{2}-2}{2 \beta } -\frac{6 \lambda_{1} }{\beta }\biggl( \frac{B_{2}}{B_{1}+B_{2} \zeta }-\frac{\lambda_{1}}{2} \biggr) \\ &\quad {}-\frac{6}{\beta } \biggl( \frac{B _{2}}{B_{1}+B_{2}\zeta }-\frac{\lambda_{1}}{2} \biggr) ^{2},\quad \beta \neq 0. \end{aligned}$$
(26)

3.3 \((3+1)\)-Dimensional Yu–Toda–Sasa–Fukuyama equation

The general form of the \((3+1)\)-dimensional Yu–Toda–Sasa–Fukuyama equation [46] is

$$ -4u_{xt}+u_{xxxz}+4u_{x}u_{xz}+2u_{z}u_{xx}+3u_{yy}=0. $$
(27)

The advantage of this equation is that it is used for investigation of the dynamics of solutions and nonlinear waves in fluid dynamics, plasma physics, and weakly dispersive media.

The traveling wave transformations for the Yu–Toda–Sasa–Fukuyama equation can be deduced as

$$ u(x,y,z,t)=U(\zeta ) ,\quad \zeta =x+y+z-\eta t. $$
(28)

Using these transformations in Eq. (27) and integrating, we obtain the ordinary differential equation

$$ U^{\prime \prime \prime}+3 U^{\prime 2}+(4\eta +3)U^{\prime}=0. $$
(29)

We assume that the solution of Eq. (29) has the form (12). Substituting Eq. (12) along Eq. (5) into Eq. (29), we obtain a series of algebraic equations in parameters \(A _{0}\), \(A_{1}\), and η. This class of algebraic equations can be solved, We have:

$$ A_{1}= 2,\qquad A_{0}=A_{0}, \qquad \eta = \frac{1}{4} \bigl( -\lambda_{1} ^{2}+4 \lambda_{2} -3 \bigr) . $$
(30)

Substituting Eq. (30) into Eq. (12), we obtain the exact traveling wave solution

$$ U(\zeta )=A_{0}+ 2 \biggl( \frac{G'}{G} \biggr) . $$
(31)

Now we discuss three different cases regarding solution (31).

Case 1. When \(\lambda_{1}^{2}-4\lambda_{2}>0\), substituting Eq. (6) into Eq. (31), we obtain the following solution of Eq. (27):

$$\begin{aligned} &U_{7}(\zeta ) \\ &\quad =A_{0} \\ &\quad \quad {}+2 \biggl( \frac{\sqrt{\lambda_{1}^{2}-4\lambda _{2}}}{2} \biggl( \frac{B_{1}\sinh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4 \lambda_{2}})\zeta +B_{2}\cosh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4 \lambda_{2}})\zeta }{B_{1}\cosh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4 \lambda_{2}})\zeta +B_{2}\sinh (\frac{1}{2}\sqrt{\lambda_{1}^{2}-4 \lambda_{2}})\zeta } \biggr) -\frac{\lambda_{1}}{2} \biggr). \end{aligned}$$
(32)

Case 2. When \(\lambda_{1}^{2}-4\lambda_{2}<0\), substituting Eq. (7) into Eq. (31), we obtain the following solution of Eq. (27):

$$\begin{aligned} &U_{8}(\zeta ) \\ &\quad =A_{0} \\ &\quad \quad {}+2 \biggl( \frac{\sqrt{4\lambda_{2}-\lambda_{1} ^{2}}}{2} \biggl( \frac{-B_{1}\sin (\frac{1}{2}\sqrt{4\lambda_{2}- \lambda_{1}^{2}})\zeta +B_{2}\cos (\frac{1}{2}\sqrt{4\lambda_{2}- \lambda_{1}^{2}})\zeta }{B_{1}\cos (\frac{1}{2}\sqrt{4\lambda_{2}- \lambda_{1}^{2}})\zeta +B_{2}\sin (\frac{1}{2}\sqrt{4\lambda_{2}- \lambda_{1}^{2}})\zeta } \biggr) -\frac{\lambda_{1}}{2} \biggr) . \end{aligned}$$
(33)

Case 3. When \(\lambda_{1}^{2}-4\lambda_{2}=0\), substituting Eq. (8) into Eq. (31), we obtain the following solution of Eq. (27):

$$ U_{9}(\zeta )=A_{0}+2 \biggl( \frac{B_{2}}{B_{1}+B_{2}\zeta }-\frac{ \lambda_{1}}{2} \biggr) . $$
(34)

4 Discussion of the results

In this section, we show a good comparison between our results and those obtained by other researchers in different papers by different techniques.

  • By choosing different values of \(A_{i}\) (\(i=1,2\)), Eq. (12) and Eq. (21) have numerous types of particular solutions in the form of trigonometric functions, hyperbolic functions, and rational functions.

However, some of our constructed solutions are likely similar to the following:

  • The solutions of (21) and (22) in [46] are likely similar to our solutions (17) and (34), respectively.

  • The solution of (3.39) and solution of (3.34) in [47] are also likely similar to our solutions (24) and (25), respectively.

  • The solution of (3.12) in [48] is also likely similar to our solution (34).

All our derived solutions are novel and have not been formulated before in any literature and helpful for solving nonlinear problems in mathematics and physics.

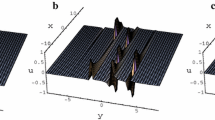
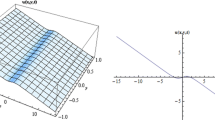
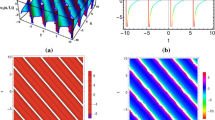
In Fig. 1: Kink solitary waves of solution (15) at (a) and dark solitary waves of solution (16) at (b) are plotted by taking the following values of parameters: \(A_{0}=1.5\), \(\lambda =4\), \(\mu =0.2\), \(\beta =-5\), \(B_{1}=4\), \(B_{2}=2 \) and \(A_{0}=1.5\), \(\lambda =1\), \(\mu =1\), \(\beta =1\), \(B_{1}=-1\), \(B_{2}=-2\), respectively.

Figure 1
figure 1

The 3D surfaces of Eq. (9) for solution (15) at (a) and solution (16) at (b) are plotted by assigning different values to the parameters under the constrain conditions

Full size image

In Fig. 2: Solitary wave of solution (17) at (a) and dark solitary wave of solution (24) at (b) are schemed by choosing the following values of parameters: \(A_{0}=1.5\), \(\lambda =2\), \(\mu =1\), \(\beta =-1\), \(B _{1}=-0.2\), \(B_{2}=2 \) and \(A_{0}=1.5\), \(\lambda =4\), \(\mu =0.2\), \(\alpha =-1\), \(B_{1}=-4\), \(B_{2}=-1\), \(\omega =-1 \), respectively.

Figure 2
figure 2

The 3D surfaces of Eq. (9) for solution (17) at (a) and of Eq. (18) for solution (24) at (b) are plotted by passing on with different values of the parameters under constrain conditions on the solutions

Full size image

In Fig. 3: Solitary wave solution (25) at (a) and bright solitary wave solution (26) at (b) are plotted by choosing the following values of parameters: \(A_{0}=1.5\), \(\lambda =1\), \(\mu =1\), \(\alpha =-3\), \(B_{1}=1\), \(B _{2}=2\), \(\omega =1 \) and \(A_{0}=1.5\), \(\lambda =2\), \(\mu =1\), \(\alpha =1\), \(B_{1}=2\), \(B_{2}=2\), \(\omega =1 \), respectively.

Figure 3
figure 3

The 3D surfaces of Eq. (18) for the solution (25) at (a) and for solution (26) at (b) by assigning different values to the parameters

Full size image

In Fig. 4: Kink solitary wave solution (32) at (a) and periodic solitary wave solution (33) at (b) are plotted from the following values of parameters: \(A_{0}=1.5\), \(\lambda =4\), \(\mu =0.2\), \(B_{1}=-4 \), \(B _{2}=-1\) and \(A_{0}=-1.5\), \(\lambda =-1\), \(\mu =1\), \(B_{1}=-1\), \(B _{2}=-1\), respectively.

Figure 4
figure 4

The 3D surfaces of Eq. (27) for solution (32) at (a) and for solution (33) at (b) are plotted under the necessary constrain conditions on the parameter values

Full size image

The movement of different kinds of solitary waves and comparison of our results with those of other researchers illustrate that our method is more efficient and powerful tool to solve nonlinear wave problems in nonlinear sciences.

5 Conclusion

In this paper, we have investigated exact and solitary wave solutions of three important models: the fourth-order nonlinear Ablowitz–Kaup–Newell–Segur equation, the \((2 + 1)\)-dimensional Boussinesq dynamical equation, and the \((3+1)\)-dimensional Yu–Toda–Sasa–Fukuyama equation by successfully applying the algorithm of the \((G'/G)\) expansion method. These solutions help us to appreciate the complex physical phenomena and have crucial importance in applied sciences. The extreme merit of our method is that all calculations are very simple and straightforward, which gives more general solutions than other existing methods, and the reduction in the size of computational work and consistency gives its wider applicability.