Desired clustering of genetic regulatory networks with mixed delays

Abstract

In this study, we propose two techniques for clustering genetic regulatory networks with mixed delays. Laws for identifying coupling parameters are designed, and the Lyapunov theorem and Lipschitz condition are employed to achieve the desired stability and to identify the coupling parameters. Using our proposed methods, the value of a cluster or the sum of clusters can approach the expected values. Numerical examples verify the feasibility and effectiveness of this method.

1 Introduction

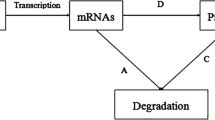
After the double helix structure of DNA was discovered by Watson and Crick in 1953, we entered a new era of molecular biology, and many subsequent studies have shown that physiological functions are controlled by biological networks instead of several molecules and genes. Biological networks include metabolic networks, protein interaction networks, and genetic regulatory networks (GRNs), where the latter are significant for studies of the interactions between mRNA and proteins at the molecular level. GRNs have been elucidated increasingly in the last 30 years due to great progress in genome sequencing and gene recognition, thereby attracting considerable attention from researchers in the areas of biology, computer science, physics, and mathematics; and thus GRNs is a focus of interdisciplinary research. Various models have been proposed to describe the transcription and translation of DNA, e.g., Boolean networks [1–3] and differential equation models [4–12], where the latter can depict the continuous dynamic behavior of mRNA and protein.

Time delays are ubiquitous in biology [13], physics [14], chemistry [15], optics [16], and complex networks [17, 18]. Thus, time delays need to be considered in GRNs because of the finite speeds of the slow processes of transcription, translation, and translocation [7–10, 12]. Furthermore, inappropriate considerations of time delays can lead to incorrect predictions of the behavior of GRNs.

Stability is essential for the design or control of GRNs because it ensures that an organism can robustly regulate its functions even if the state of the organism moves away from the equilibrium points. Zhang et al. used the improved integral inequality to conduct stability analysis for a GRN with interval time-varying delays [19]. Wang et al. performed exponential convergence analysis for an uncertain GRN with time-varying delays [20]. Zhang et al. established globally asymptotic stability criteria for a GRN with time-varying discrete and unbounded distributed delays [21]. Liu and Wu analyzed the global asymptotical stability of a GRN with time-varying delays via a convex combination method [22].

These previous studies considered the stability of GRNs but not clustering phenomena. In general, cells can communicate with neighboring cells via quorum sensing because the genetic signals transmitted from genes can support different physiological functions [23]. Therefore, clustering is a common phenomenon in interacting populations, and clustering is an important aspect of biological control [24]. Recently, some studies have investigated the clustering of GRNs, such as how the influence of coupling or noise can generate cluster patterns in an ensemble of cellular oscillators [25], how individual GRNs are divided into different clusters by cluster synchronization [23, 24, 26], and how temporal control is introduced to cluster mammalian signaling modules [27]. In this study, we investigate the desired clustering of GRNs where clusters of GRNs could have different features according to two proposed strategies. In particular, we impose no limitations on the number of nodes in each cluster, the division of the clusters of GRNs, and the time delay for feedback regulation. Comparing with the previous research of GRNs, we not only analyze the stability of GRNs, but also make the concentrations of protein and mRNA approach the desired values through our tactics. Linear matrix inequality (LMI) method is often used to obtain the stability criteria for GRNs, but the computation of LMI is complex. In this paper, stability criterion is given by a Lyapunov function.

The real genetic regulatory network is over complex, and the number of nodes is huge. Since “network motifs” [28, 29] were proposed by Alon et al. in 2002, few node genetic regulatory networks have become research hotspots. It is hoped that the real genetic regulatory network can be understood gradually by the research of such network motifs. In 2000, Elowitz et al. used three transcriptional repressor systems to build a synthetic oscillating network in Escherichia coli [30]. Gardner et al. used two transcriptional repressors to construct a synthetic toggle switch genetic regulatory network in Escherichia coli also in 2000 [31]. Therefore, 7 or 20 genes with clustering as numerical examples in Sect. 4 are significant.

2 Model of GRNs

GRNs with mixed delays [12] are described by Eq. (1):

$$\begin{aligned} \textstyle\begin{cases} \dot{m}_{i} ( t ) = -a_{i} m_{i} ( t ) + \sum_{j=1}^{N} \omega_{ij} (t) f_{j} ( p_{j} ( t-\tau(t) ) ) + l_{i} (t),\\ \dot{p}_{i} ( t ) = -c_{i} p_{i} ( t ) + d_{i} m_{i} ( t-\sigma ( t ) ),\quad i\in \{ 1,2,\ldots,n \}, \end{cases}\displaystyle \end{aligned}$$

(1)

where $m ( t ) =[m_{1} ( t ) \cdots m_{n} (t)]\in R^{n}$ and $p ( t ) =[p_{1} ( t ) \cdots p_{n} (t)]\in R^{n}$ are the concentrations of mRNA and protein for node i at the time t, respectively, the parameters $a_{i}$ and $\mathrm{c}_{i}$ are the degradation rates of the mRNA and protein, and $d_{i}$ is the translation rate. The feedback regulation delays $\tau ( t )$, $\sigma(t)$ are both positive, and $f_{i} (x)$ is the Hill form regulatory function, which represents the feedback regulation of the protein on transcription, and it is described by Eq. (2):

$$ f_{j} ( x ) = \frac{( \frac{x}{v_{j}} )^{H_{j}}}{1+( \frac{x}{v_{j}} )^{H_{j}}}, $$

(2)

where $H_{i}$ is the Hill coefficient, $v_{j}$ is a positive constant, and we propose that $f_{j} ( x )$ is positive. $l_{i} (t)= \sum_{j\in I_{i}} \alpha_{ij} (t)$ and $I_{i}$ is the set of all j, which is a repressor of gene i. The coupling matrix $W = \omega_{ij} \in R^{n\times n}$ is described as follows:

$$ \omega_{ij} (t)= \textstyle\begin{cases} \alpha_{ij} ( t )& \text{if } j \text{ is an activator of gene } i, \\ 0& \text{if there is no link from node } j \text{ to } i,\\ -\alpha_{ij} ( t )& \text{if } j \text{ is an repressor of gene } i. \end{cases} $$

(3)

As shown in Fig. 1, we assume that there are M clusters in the GRNs (1) ($M\geq1$), which are denoted by $C_{1}, C_{2}, \ldots, C_{m}$, where $C_{k} =\{ q_{k-1} +1, q_{k-1} +2,\ldots, q_{k} \}$, with $k=1,2,\ldots,m, q_{0} =0$, and $q_{m} =N$.

Figure 1

Cluster of GRNs where $q_{k} - q_{k-1}$ represents the number of nodes in the kth cluster and $\{ q_{k-1} +1,\ldots, q_{k-1} + \gamma,\ldots, q_{k} \}$ represents the index set of all the nodes in the kth cluster. We find that $m_{i} = m_{q_{k-1} +\gamma}$, when the index of the ith gene is the γth gene in the kth cluster

Let $\overline{m}_{k} ( t ) =( m_{q_{k-1} +1}, m_{q_{k-1} +2},\ldots, m_{q_{k}} )$, $\overline{p}_{k} ( t ) =( p_{q_{k-1} +1}, p_{q_{k-1} +2},\ldots, p_{q_{k}})$.

Definition 1

$X(t) \in R^{n}$ will approach the desired values $\hat{X} \in R^{n}$ if $\lim_{t\rightarrow\infty} \vert X(t )- \hat{X} \vert =0$.

3 Desired clustering of GRNs

In this section, the GRNs (1) are clustered using two techniques.

3.1 Method 1

In this method, the concentrations of mRNA and protein within a cluster have the same desired values $\hat{{m}}_{{k}}$ and $\hat{{p}}_{{k}}$, and the desired values of the nodes vary in different clusters.

Theorem 1

The desired clustering of GRNs with mixed delays will be achieved when the law for identifying the coupling parameters $\omega_{ij}$, $a_{i}$, $c_{i} \beta_{i}$ ($i \in \{ q_{k-1} +1, q_{k-1} +2,\ldots, q_{k} \}, j \in \{ 1,\ldots,N \}$) and $\hat{{p}}_{{k}}$ is taken as follows, respectively:

$$\begin{aligned} &\dot{{\omega}}_{{ij}} ({t} )=\alpha \bigl( \hat{{m}}_{{k}} ({t} )- m_{{i}} \bigr) , \end{aligned}$$

(4)

$$\begin{aligned} &a_{i} +\delta- \varepsilon_{i} >0, \end{aligned}$$

(5)

$$\begin{aligned} &c_{i} >0, \end{aligned}$$

(6)

$$\begin{aligned} &\beta_{i} = \frac{a_{i} \hat{m}_{k}}{ \sum_{j=1}^{n} \hat{\omega}_{ij}}>0, \end{aligned}$$

(7)

$$\begin{aligned} &\hat{p}_{k}=\lim_{t\rightarrow\infty} {\theta}_{k} m_{i} \bigl( t-\sigma ( t ) \bigr), \end{aligned}$$

(8)

where the real numbers δ and $\varepsilon_{i}$ are positive; the estimated identification of the uncertain adjustment parameters $\omega_{ij}$ is $\hat{{\omega}}_{{ij}}$ and α is an adjustment parameter; ${\theta}_{{k}}= d_{k} / c_{k}$ is a scale factor that represents the proportional relationship between $\hat{{p}}_{{k}}$ and $\hat{{m}}_{{k}}$, $c_{k} = c_{q_{k-1} +1} =\cdots= c_{{q}_{{k}}}$, and $d_{k} = d_{q_{k-1} +1} =\cdots= d_{{q}_{{k}}}$.

Proof

For $i \in C_{k}$, the error between $m_{i}$ and $\hat{{m}}_{{k}}$ and the error between $p_{i}$ and $p_{i} ( t-\sigma ( t ) )$ are defined by Eq. (9).

$$ \textstyle\begin{cases} e_{1i} ( t ) = m_{i} (t)- \hat{{m}}_{{k}},\\ e_{2i} ( t ) = p_{i} ( t )- \hat{{p}}_{{k}}. \end{cases} $$

(9)

We establish the Lyapunov function as follows.

$$\begin{aligned} V(t)={}& \frac{1}{2} \Biggl( \sum_{i=1}^{N} e_{1i}^{\mathrm{T}} ( t ) e_{1i} ( t ) + \sum _{i=1}^{N} e_{2i}^{\mathrm{T}} ( t ) e_{2i} ( t ) + \frac{\beta_{i}}{\alpha} \sum_{i=1}^{N} \sum_{j=1}^{N} \bigl( \hat{{ \omega}}_{{ij}}- \omega_{ij} (t) \bigr)^{\mathrm{T}} \bigl( \hat{{\omega}}_{{ij}}- \omega_{ij} (t) \bigr) \Biggr) \\ ={}& \frac{1}{2} \sum_{k=1}^{M} \sum _{i= q_{k-1} +1}^{q_{k}} \Biggl( e_{1 i}^{\mathrm{T}} ( t ) e_{1i} ( t ) + e_{2 i}^{\mathrm{T}} ( t ) e_{2i} ( t ) \\ &{} + \frac{\beta_{i}}{ \alpha} \sum_{j=1}^{N} \bigl( \hat{{\omega}}_{ij}- \omega_{ij} (t) \bigr)^{\mathrm{T}} \bigl( \hat{{\omega}}_{ij}- \omega_{ij} (t) \bigr) \Biggr). \end{aligned}$$

(10)

The derivative form of $V(t)$ can be described as follows:

$$\begin{aligned} \dot{V} ( t ) = {}&\sum_{k=1}^{M} \sum _{i= q_{k-1} +1}^{q_{k}} \Biggl[ e_{1 i}^{\mathrm{T}} ( t ) \Biggl( - a_{i} m_{i} ( t ) + \sum _{j=1}^{N} \omega_{ij} f_{j} \bigl( p_{j} \bigl( t-\tau(t) \bigr) \bigr) + l_{i} (t) + \beta_{i} \sum_{j=1}^{N} ( \hat{{ \omega}}_{i{j}}- \omega_{ij} ) \Biggr) \\ &{}+ e_{2 i}^{\mathrm{T}} ( t ) \bigl( - c_{i} p_{i} ( t ) + d_{i} m_{i} \bigl( t-\sigma ( t ) \bigr) \bigr) \Biggr] \\ = {}&\sum_{k=1}^{M} \sum _{i= l_{k-1} +1}^{q_{k}} \Biggl[ e_{1 i}^{\mathrm{T}} ( t ) ( - (a_{i} +\delta)m_{i} ( t ) + (a_{i} + \delta) \hat{m}_{k} + F_{i} \bigl( m_{i} (t) \bigr)- H_{i} ( \hat{m}_{k} ) \\ &{} + \beta_{i} \sum_{j=1}^{N} \hat{{\omega}}_{i{j}} - a_{i} \hat{m}_{k} + e_{2 i}^{\mathrm{T}} ( t ) \bigl( - c_{i} p_{i} ( t ) + c_{i} \hat{{p}}_{{k}} +d_{i} m_{i} \bigl( t-\sigma ( t ) \bigr) - c_{i} \hat{{p}}_{{k}} \bigr) \Biggr], \end{aligned}$$

(11)

where

$$\begin{aligned} &F_{i} =\delta^{m}_{i}{(t)}+ \sum_{j=1}^{N} \omega_{ij} \bigl[ f_{j} \bigl( p_{j} \bigl( t-\tau(t) \bigr) \bigr) - \beta_{i} \bigr] + l_{i} ( t ), \end{aligned}$$

(12)

$$\begin{aligned} &H_{i} ( \hat{m}_{k} ) = (a_{i} +\delta) \hat{m}_{k}. \end{aligned}$$

(13)

For the real number $\varepsilon_{i} > 0$, the following relationship is obtained using the Lipschitz condition:

$$ \bigl\Vert F_{i} \bigl({m}_{i} ( t ) \bigr) - H_{i} ( \hat{m}_{k} ) \bigr\Vert \leq \varepsilon_{i} \bigl\Vert {m}_{i} ( t ) - \hat{{m}}_{{k}} \bigr\Vert , $$

(14)

and Eq. (10) can be simplified as follows:

$$\begin{aligned} \dot{V} ( t ) \leq{}& \sum_{k=1}^{M} \sum_{i= q_{k-1} +1}^{q_{k}} \Biggl\{ ( \varepsilon_{i} - a_{i} -\delta) e_{1i}^{\mathrm{T}} ( t ) e_{1i} (t)+e_{1i}^{\mathrm{T}} ( t ) \Biggl( \beta_{i} \sum_{j=1}^{N} \hat{{ \omega}}_{ij} - a_{i} \hat{m}_{k} \Biggr) - c_{i} e_{2i}^{\mathrm{T}} ( t ) e_{2i} ( t ) \\ &{}+ e_{2i}^{\mathrm{T}} ( t ) \bigl[ d_{i} m_{i} \bigl( t-\sigma ( t ) \bigr) - c_{i} \hat{{p}}_{{k}} \bigr] \Biggr\} . \end{aligned}$$

(15)

The following inequation is obtained while Eq. (7) is substituted into Eq. (15):

$$\begin{aligned} \dot{V} ( t ) \leq{}& \sum_{k=1}^{M} \sum _{i= q_{k-1} +1}^{q_{k}} \bigl\{ ( \varepsilon_{i} - a_{i} -\delta ) e_{1i}^{\mathrm{T}} ( t ) e_{1i} ( t ) - c_{i} e_{2i}^{\mathrm{T}} ( t ) e_{2i} ( t ) \\ &{} + e_{2i}^{\mathrm{T}} ( t ) \bigl[ d_{i} m_{i} \bigl( t-\sigma ( t ) \bigr) - c_{i} \hat{{p}}_{{k}} \bigr] \bigr\} . \end{aligned}$$

(16)

Clearly, when (5), (6), (8) are satisfied, we find that $\lim_{t\rightarrow\infty} \dot{V} ( t ) \leq0$. According to stability theory and Definition 1, $m_{i} ( t ) \in \overline{m}_{k} ( t )$ and $p_{i} ( t ) \in \overline{p}_{k} ( t )$ will approach the desired values, where $\hat{{p}}_{{k}}= \lim_{{t\rightarrow\infty}} {\theta}_{{k}} m_{i} ( t-\sigma ( t ) )= \theta_{{k}} \hat{m}_{k}\ ( i \in \{ q_{k-1} +1, q_{k-1} +2,\ldots, q_{k} \} )$. □

3.2 Method 2

In this method, the GRNs is clustered by summing, which means that the sums of $\overline{m}_{k} (t)$ and $\overline{p}_{k} (t)$ have the desired values $\hat{{S}}_{{1k}}$ and $\hat{{S}}_{{2k}}$, respectively, and the desired values of the sum of the various clusters are different. The sums of the mRNAs and proteins in the kth cluster are defined as follows:

$$\begin{aligned} &S_{1k} (t)= \sum_{i= q_{k-1} +1}^{q_{k}} m_{i} ( t ), \end{aligned}$$

(17)

$$\begin{aligned} &S_{2k} (t)= \sum_{i= q_{k-1} +1}^{q_{k}} p_{i} ( t ). \end{aligned}$$

(18)

The error between $S_{1k} ( t )$ and $\hat{S}_{1k}$ and the error between $S_{2k} ({t} )$ and $\hat{{S}}_{{2k}}$ are defined as follows:

$$\begin{aligned} &{E}_{{1k}} ({t} ) = S_{1k} ({t} ) - \hat{S}_{1k}, \end{aligned}$$

(19)

$$\begin{aligned} &{E}_{{2k}} ({t} )= S_{2k} ({t} ) - \hat{{S}}_{{2k}}. \end{aligned}$$

(20)

Theorem 2

The desired cluster of GRNs with mixed delays will be achieved when the law for identifying the coupling parameters $\omega_{ij}$, $a_{i}$, $c_{i}$, $\beta_{i}$ $( i \in \{ q_{k-1} +1, q_{k-1} +2,\ldots, q_{k} \},j \in \{ 1,\ldots,N \} )$, and $\hat{{S}}_{{2k}}$ is taken as follows, respectively:

$$\begin{aligned} &\dot{{\omega}}_{{ij}} ({t} ) = {\alpha} \bigl( \hat{S}_{1k} - S_{1k} ({t} ) \bigr) \end{aligned}$$

(21)

$$\begin{aligned} &a_{k} +\xi- \mu_{k} >0 \end{aligned}$$

(22)

$$\begin{aligned} &c_{k} >0 \end{aligned}$$

(23)

$$\begin{aligned} &\beta_{k} = \frac{a_{k} \hat{S}_{1k}}{ \sum_{i= q_{k-1} +1}^{q_{k}} \sum_{j=1}^{N} \hat{\omega}_{ij}}>0 \end{aligned}$$

(24)

$$\begin{aligned} &\hat{{S}}_{{2k}}= \lim_{{t\rightarrow\infty}} {\vartheta}_{{k}} S_{1k} \bigl( t-\sigma ( t ) \bigr), \end{aligned}$$

(25)

where the real numbers ξ and $\mu_{k}$ are positive; ${\vartheta}_{{k}}= d_{k} / c_{k}$ is a scale factor that represents the proportional relationship between $\hat{{S}}_{{2k}}$ and $\hat{S}_{1k}$; $a_{k} = a_{q_{k-1} +1} =\cdots= a_{{q}_{{k}}}$, $c_{k} = c_{q_{k-1} +1} =\cdots= c_{{q}_{{k}}}$, and $d_{k} = d_{q_{k-1} +1} =\cdots= d_{{q}_{{k}}}$.

Proof

The Lyapunov function is established as follows:

$$\begin{aligned} V ( t ) ={}& \frac{1}{2} \Biggl( \sum_{k=1}^{M} E_{1k}^{\mathrm{T}} ( t ) E_{1k} ( t ) + \sum _{k=1}^{M} E_{2k}^{\mathrm{T}} ( t ) E_{2k} ( t ) \\ &{} + \frac{\beta_{k}}{\alpha} \sum_{k=1}^{M} \sum_{i= q_{k-1}}^{q_{k}} \sum _{j=1}^{N} ( \hat{{\omega}}_{{ij}}- \omega_{ij} )^{\mathrm{T}} ( \hat{{\omega}}_{{ij}}- \omega_{ij} ) \Biggr). \end{aligned}$$

(26)

The derivative form of $V(t)$ can be described as follows:

$$\begin{aligned} \dot{V} ( t ) ={}& \sum_{k=1}^{M} E_{1k}^{\mathrm{T}} ( t ) \dot{E}_{1k} ( t ) + \sum _{k=1}^{M} E_{2k}^{\mathrm{T}} ( t ) \dot{E}_{2k} ( t ) - \frac{\beta_{k}}{\alpha} \sum _{k=1}^{M} \sum_{i= q_{k-1}}^{q_{k}} \sum_{j=1}^{N} ( \hat{{\omega}}_{{ij}}- \omega_{ij} )^{\mathrm{T}} \dot{\omega}_{ij} \\ ={}& \sum_{k=1}^{M} \Biggl( E_{1k}^{\mathrm{T}} ( t ) \sum_{i= q_{k-1} +1}^{q_{k}} \dot{m}_{i\gamma} ( t ) + E_{2k}^{\mathrm{T}} ( t ) \sum _{i= q_{k-1} +1}^{q_{k}} \dot{p}_{i} ( t ) + \beta_{k} E_{1k}^{\mathrm{T}} ( t ) \sum _{i= q_{k-1} +1}^{q_{k}} \sum_{j=1}^{N} ( \hat{{\omega}}_{ij}- \omega_{ij} ) \Biggr) \\ = {}& \sum_{k=1}^{M} \Biggl\{ E_{1k}^{\mathrm{T}} ( t ) \Biggl[ \sum_{i= q_{k-1} +1}^{q_{k}} \Biggl( - a_{i} m_{i} ( t ) + \sum _{j=1}^{N} \omega_{ij} f_{j} \bigl( p_{j} \bigl( t-\tau(t) \bigr) \bigr) + l_{i} (t) \\ &{}+ \beta_{k} \sum_{j=1}^{N} ( \hat{{ \omega}}_{ij}- \omega_{ij} ) \Biggr)\Biggr] \\ &{} +E_{2k}^{\mathrm{T}} ( t ) \sum_{i= q_{k-1} +1}^{q_{k}} \bigl[ - c_{i} p_{i} ( t ) + d_{i} m_{i} \bigl( t-\sigma ( t ) \bigr) \bigr] \Biggr\} . \end{aligned}$$

(27)

When $a_{k} = a_{q_{k-1} +1} =\cdots= a_{{q}_{{k}}}$, $c_{k} = c_{q_{k-1} +1} =\cdots= c_{{q}_{{k}}}$, and $d_{k} = d_{q_{k-1} +1} =\cdots= d_{{q}_{{k}}}$, Eq. (27) is simplified as follows:

$$\begin{aligned} \dot{V} ( t ) ={}& \sum_{k=1}^{M} \Biggl\{ E_{1k}^{\mathrm{T}} ( t ) \Biggl[ - a_{k} S_{1k} ( t ) + \sum_{i= q_{k-1} +1}^{q_{k}} \Biggl( \sum _{j=1}^{N} \omega_{ij} \bigl( f_{j} \bigl( p_{j} \bigl( t-\tau(t) \bigr) \bigr) - \beta_{k} \bigr) + l_{i} (t) \\ &{}+ \beta_{k} \sum _{j=1}^{N} \hat{{\omega}}_{ij} \Biggr) \Biggr] \\ &{}+ E_{2k}^{\mathrm{T}} ( t ) \bigl[ - c_{k} S_{2k} ( t ) + d_{k} S_{1k} \bigl( t-\sigma ( t ) \bigr) \bigr]\Biggr\} \\ ={}& \sum_{k=1}^{M} \Biggl\{ E_{1k}^{\mathrm{T}} ( t ) \Biggl[ - (a_{k} + \xi)S_{1k} ( t ) + (a_{k} +\xi) \hat{S}_{1k} + \Lambda_{k} ( S_{1k} )- \Psi_{k} ( \hat{S}_{1k} ) \\ &{}+ \beta_{k} \sum_{i= q_{k-1} +1}^{q_{k}} \sum_{j=1}^{N} \hat{{\omega}}_{ij} - a_{k} \hat{S}_{1k} \Biggr] \\ &{} + E_{2k}^{\mathrm{T}} ( t ) \bigl[ - c_{k} S_{2k} ( t ) + c_{k} \hat{{S}}_{{2k}} + d_{k} S_{1k} \bigl( t-\sigma ( t ) \bigr) - c_{k} \hat{{S}}_{{2k}} \bigr] \Biggr\} , \end{aligned}$$

(28)

where

$$\begin{aligned} &\Lambda_{k} \bigl({S}_{{1k}} ( t ) \bigr) = \xi{S}_{{1k}} ({t} )+ \sum_{i= q_{k-1} +1}^{q_{k}} \Biggl( \sum_{j=1}^{N} \omega_{ij} \bigl( f_{j} \bigl( p_{j} \bigl( t-\tau ( t ) \bigr) \bigr) - \beta_{k} \bigr) + l_{i} ( t ) \Biggr), \end{aligned}$$

(29)

$$\begin{aligned} &\Psi_{k} ( \hat{S}_{1k} ) = (a_{k} +\xi) \hat{S}_{1k}. \end{aligned}$$

(30)

For the real number $\mu_{k} > 0$, the following relationship can be obtained using the Lipschitz condition:

$$ \bigl\Vert \Lambda_{k} \bigl({S}_{{1k}} ( t ) \bigr) - \Psi_{k} ( \hat{S}_{1k} ) \bigr\Vert \leq \mu_{k} \bigl\Vert \Lambda_{{1k}} ( t ) - \hat{S}_{1k} \bigr\Vert , $$

(31)

and Eq. (28) can be simplified as follows:

$$\begin{aligned} \dot{V} ( t ) \leq{}& \sum_{k=1}^{M} \Biggl\{ ( \mu_{k} - a_{k} -\xi) E_{1k}^{\mathrm{T}} ( t ) E_{1k} +E_{1k}^{\mathrm{T}} ( t ) \Biggl[ \beta_{k} \sum_{i= q_{k-1} +1}^{q_{k}} \sum _{j=1}^{N} \hat{\omega}_{ij} f_{j} \bigl( p_{j} \bigl( t-\tau(t) \bigr) \bigr) - a_{k} \hat{S}_{1k} \Biggr] \\ &{}- c_{k} E_{2k}^{\mathrm{T}} ( t ) E_{2k} + E_{2k}^{\mathrm{T}} ( t ) \bigl[ d_{k} S_{1k} \bigl( t-\sigma ( t ) \bigr) - c_{k} \hat{{S}}_{{2k}} \bigr] \Biggr\} . \end{aligned}$$

(32)

The following inequation is obtained while Eq. (24) is substituted into Eq. (32):

$$\begin{aligned} \dot{V} ( t ) \leq \sum_{k=1}^{M} \bigl\{ ( \mu_{k} - a_{k} -\xi ) E_{1k}^{\mathrm{T}} ( t ) - c_{k} E_{2k}^{\mathrm{T}} ( t ) E_{2k} + E_{2k}^{\mathrm{T}} ( t ) \bigl[ d_{k} S_{1k} \bigl( t-\sigma ( t ) \bigr) - c_{k} \hat{{S}}_{{2k}} \bigr] \bigr\} . \end{aligned}$$

(33)

Based on (22), (23), (25), one can deduce $\lim_{t\rightarrow\infty} \dot{V} ( t ) \leq0$. According to stability theory and Definition 1, ${S}_{{1k}}{(t)}$ and ${S}_{{2k}}{(t)}$ will approach the desired values, where $\hat{{S}}_{{2k}}= \lim_{{t\rightarrow\infty}} {\vartheta}_{{k}} S_{1k} ( t-\sigma ( t ) )= \vartheta_{{k}} \hat{S}_{1k}$. □

4 Numerical simulation

Example 1

In the numerical simulation of Example 1, the number of the nodes is fixed as $n =7$; the parameters are fixed as $a_{i} =2$ ($i =1,\ldots,7$), $c_{k} =1$, and $d_{k} = c_{k} \hat{p}_{k} / \hat{m}_{k} \ ( k =1,\ldots, M)$; and the adjustment parameter ${\alpha=0.5}$.

We assume that there are two clusters in the GRNs, $M =2$, where

$$\begin{aligned} & \begin{pmatrix} \overline{m}_{1}\\ \overline{p}_{1} \end{pmatrix} = \left \{ \begin{pmatrix} {m_{1} (t)}\\ {p_{1} (t)} \end{pmatrix}, \begin{pmatrix} {m_{2} (t)}\\ {p_{2} (t)} \end{pmatrix}, \begin{pmatrix} {m_{3} (t)}\\ {p_{3} (t)} \end{pmatrix} \right \}, \\ & \begin{pmatrix} \overline{m}_{2}\\ \overline{p}_{2} \end{pmatrix} = \left \{ \begin{pmatrix}{m_{4} (t)}\\ {p_{4} (t)} \end{pmatrix}, \begin{pmatrix} {m_{5} (t)} \\{p_{5} (t)} \end{pmatrix}, \begin{pmatrix} {m_{6} (t)} \\{p_{6} (t)} \end{pmatrix}, \begin{pmatrix} {m_{7} (t)}\\ {p_{7} (t)} \end{pmatrix} \right \}, \\ & \begin{pmatrix} \hat{m}_{1}\\ \hat{p}_{1} \end{pmatrix} = \begin{pmatrix} 1.5\\ 3 \end{pmatrix} , \begin{pmatrix} \hat{m}_{2}\\ \hat{p}_{2} \end{pmatrix} = \begin{pmatrix} 3\\ 6 \end{pmatrix} . \end{aligned}$$

The temporal evolution of $m_{i} \ ( i =1,\ldots,7)$ and $p_{i}$ is shown in Fig. 2. Figure 2 clearly indicates that the concentrations of $m_{i}$ and $p_{i}$ at equilibrium approach the desired values. In addition, $m_{i}, p_{i}\ ( i =1,2,3)$ belong to the first cluster and the concentration of $m_{i}$, $p_{i} \ ( i =4,5,6,7)$ belongs to the second cluster.

Figure 2

Time trajectories of $m_{i} (t)$ and $p_{i} (t)$, ($i =1,\ldots,7$), and identification process for the uncertain parameter $\omega_{1j} \ ( j =1,\ldots,7)$

According to Figs. 2 and 3, the curves for identifying $\omega_{ij} \ (i=1,2,\ldots,7;j=1,2,\ldots,7)$ gradually tend toward the fixed values as follows:

$$\hat{W} = \begin{pmatrix} 1.28& 0.48& -0.71& 0.28& - 0.41& 0.48& 0.58\\ -1.98& 1.31& 0.21& 0.02& - 0.28& -0.28& 1.41\\ 1.51& 0.01& 0.01& 0.31& 1.01& 0.31& -0.28\\ 1.21& 1.01& 1.01& -0.68& 1.01& 1.41& 0.71\\ 0.56& 3.01& 0.31& 0.61& 0.81& 0.51& 0.61\\ 1.64& 0.64& 2.14& 0.71& 0.64& -0.45& 0.64\\ 2.31 & 0.71& 0.31 & 1.01& 0.31& 1.01 & 0.71 \end{pmatrix}, $$

where Ŵ is the identification estimates for the uncertain coupling matrix W;

$$\begin{aligned} &\beta_{1} = \frac{a_{1} \hat{m}_{1}}{\sum_{j=1}^{7} \hat{\omega}_{1j}} =1.50,\qquad \beta_{2} = \frac{a_{2} \hat{m}_{1}}{\sum_{j=1}^{7} \hat{\omega}_{2j}} =6.82, \\ & \beta_{3} = \frac{a_{3} \hat{m}_{1}}{ \sum_{j=1}^{7} \hat{\omega}_{3j}} =1.03,\qquad \beta_{4} = \frac{a_{4} \hat{m}_{2}}{\sum_{j=1}^{7} \hat{\omega}_{4j}} =1.05, \\ &\beta_{5} = \frac{a_{5} \hat{m}_{2}}{\sum_{j=1}^{7} \hat{\omega}_{5j}} =0.94,\qquad \beta_{6} = \frac{a_{6} \hat{m}_{2}}{\sum_{j=1}^{7} \hat{\omega}_{6j}} =1.00,\qquad \beta_{7} = \frac{a_{7} \hat{m}_{2}}{ \sum_{j=1}^{7} \hat{\omega}_{7j}} =0.93. \end{aligned}$$

Figure 3

Identification process for the uncertain parameters $\omega_{ij} \ ( i =2,\ldots,7; j =1,\ldots,7)$

Clearly, the value of $\beta_{i}$, ($i =1,\ldots,7$) is positive, and thus inequation (7) is satisfied.

Furthermore, when we expand the number of nodes of GRNs to 20 and assume that there are three clusters in the GRNs, where $a_{i} =3\ ( i =1,\ldots,20)$, $c_{k} =1$, $d_{k} = c_{k} \hat{p}_{k} / \hat{m}_{k} \ ( k =1,\ldots, M )$; $M =3$; $\alpha=0.3$;

$$\begin{aligned} & \begin{pmatrix} \overline{m}_{1}\\ \overline{p}_{1} \end{pmatrix} = \left \{ \begin{pmatrix} {m_{1} (t)} \\{p_{1} (t)} \end{pmatrix}, \ldots, \begin{pmatrix}{m_{10} (t)}\\{p_{10} (t)} \end{pmatrix} \right \},\qquad \begin{pmatrix} \overline{m}_{2}\\ \overline{p}_{2} \end{pmatrix} = \left \{ \begin{pmatrix}{m_{11} (t)}\\ {p_{11} (t)} \end{pmatrix}, \ldots , \begin{pmatrix} {m_{15} (t)}\\ {p_{15} (t)} \end{pmatrix} \right \}, \\ & \begin{pmatrix} \overline{m}_{3}\\ \overline{p}_{3} \end{pmatrix} = \left \{ \begin{pmatrix} {m_{16} (t)} \\{p_{16} (t)} \end{pmatrix}, \ldots, \begin{pmatrix} {m_{20} (t)}\\ {p_{20} (t)} \end{pmatrix} \right \}, \\ & \begin{pmatrix} \hat{m}_{1}\\ \hat{p}_{1} \end{pmatrix} = \begin{pmatrix} 1\\ 2 \end{pmatrix} , \begin{pmatrix} \hat{m}_{2}\\ \hat{p}_{2} \end{pmatrix} = \begin{pmatrix} 2\\ 4 \end{pmatrix}, \begin{pmatrix} \hat{m}_{3}\\ \hat{p}_{3} \end{pmatrix} = \begin{pmatrix} 3.5\\ 7 \end{pmatrix} \end{aligned}$$

The temporal evolution of $m_{i} \ ( i =1,\ldots,7)$ and $p_{i}$ is shown in Fig. 4. According to Fig. 4, $m_{i} (t)$ and $p_{i} (t)$ reach equilibrium at the desired values and the concentrations of $m_{i}$ and $p_{i} \ ( i =1,\ldots,10)$ belong to the first cluster, the concentrations of $m_{i}$ and $p_{i} \ ( i =11,\ldots,15)$ belong to the second cluster, and the concentrations of $m_{i}, p_{i} \ ( i =16,\ldots,20)$ approach the third cluster.

Figure 4

State trajectories of $m_{i} (t)$ and $p_{i} (t) \ ( i =1,2,\ldots,20)$

According to Fig. 5, the curves for identifying $\omega_{ij} \ (i=1,2,\ldots,20;j=1,2,\ldots,20)$ gradually tend to the fixed values. Based on Fig. 6, inequation (7) is satisfied.

Figure 5

Identification process for adjustment parameter $\omega_{ij}$, ($i =1,\ldots,20; j =1,\ldots,20$)

Figure 6

Value of $\beta_{i}$, ($i =1,\ldots,20$)

Example 2

In the numerical simulation of Example 2, the number of the nodes is fixed as $n =7$, and it is assumed that there are two clusters in the GRNs, where $a_{i} =2\ ( i =1,\ldots,7)$, $c_{k} =2$, $d_{k} = c_{k} \hat{S}_{2k} / \hat{S}_{1k} \ ( k =1,\ldots, M )$; $M =2$; $\alpha=0.5$.

$$\begin{aligned} & \begin{pmatrix} \overline{m}_{1}\\ \overline{p}_{1} \end{pmatrix} = \left \{ \begin{pmatrix} {m_{1} (t)}\\ {p_{1} (t)} \end{pmatrix}, \begin{pmatrix} {m_{2} (t)}\\ {p_{2} (t)} \end{pmatrix}, \begin{pmatrix} {m_{3} (t)} \\{p_{3} (t)} \end{pmatrix} \right \},\\ & \begin{pmatrix} \overline{m}_{2}\\ \overline{p}_{2} \end{pmatrix} = \left \{ \begin{pmatrix} {m_{4} (t)} \\ {p_{4} (t)} \end{pmatrix}, \begin{pmatrix} {m_{5} (t)}\\ {p_{5} (t)} \end{pmatrix}, \begin{pmatrix}{m_{6} (t)}\\ {p_{6} (t)} \end{pmatrix}, \begin{pmatrix} {m_{7} (t)}\\ {p_{7} (t)} \end{pmatrix} \right \}; \end{aligned}$$

where $S_{11} = m_{1} ( t ) + m_{2} ( t ) + m_{3} (t)$ and $S_{12} = m_{4}(t)+ m_{5} ( t ) + m_{6} ( t ) + m_{7} (t)$; $S_{21} = p_{1} ( t ) + p_{2} ( t ) + p_{3} (t)$ and $S_{22} = p_{4}(t)+ p_{5} ( t ) + p_{6} ( t ) + p_{7} (t)$ and the desired values of $S_{11}$, $S_{12}$, $S_{21}$, $S_{22}$ are fixed at $\hat{S}_{11} =30$, $\hat{S}_{12} =10$, $\hat{S}_{21} =15$, $\hat{S}_{22} =5$, respectively.

The temporal evolution of $m_{i} \ ( i =1,\ldots,7)$ and $p_{i}$ are shown in Fig. 7, respectively. Figure 8(c) clearly indicates that the values of $S_{1k}$ and $S_{2k}\ ( k =1,2 )$ approach those of $\hat{S}_{1k}$ and $\hat{S}_{2k}$. It is important to note that the GRNs are divided into two clusters, where the concentrations of $m_{i}$, $p_{i} \ ( i =1,2,3)$ belong to the first cluster and the concentrations of $m_{i}$, $p_{i} \ ( i =4,5,6,7)$ belong to the second cluster.

Figure 7

State trajectory of $m_{i} (t) \ ( i =1,2,\ldots,7)$, and identification process for the uncertain parameter $\omega_{1j} \ ( j =1,\ldots,7)$

Figure 8

(a), (b): Identification process for the adjustment parameter $\omega_{ij} \ ( i, j =2,\ldots,7)$; (c): state trajectories of $S_{1k} (t)$ and $S_{2k} (t) \ ( k =1,2)$

According to Figs. 7 and 8(a)–(b), the curves for identifying $\omega_{ij} \ (i=1,2,\ldots,7;j=1,2,\ldots,7)$ gradually tend toward the fixed values as follows:

$$\hat{W} = \begin{pmatrix} 4.56& 3.76& 2.56& 3.56& 2.86& 3.76& 3.86\\ 1.86& 5.16& 4.06& 3.86& 3.56& 3.56& 5.26\\ 5.06& 3.56& 3.56& 3.86& 4.56& 3.86& 3.26\\ 0.63& 0.43& 0.43& -1.27& 0.43& 0.83& 0.12\\ 0.68& 3.13& 0.43& 0.73& 0.93& 0.63& 0.72\\ 1.63& 0.63& 2.13& 0.73& 0.63& -0.47& 0.63\\ 2.43 & 0.83& 0.43& 1.13& 0.43& 1.13& 0.83 \end{pmatrix}, $$

where Ŵ is the identification estimates for the uncertain coupling matrix W.

$$\beta_{1} = \frac{a_{1} \hat{S}_{11}}{\sum_{i=1}^{3} \sum_{j=1}^{7} \hat{\omega}_{ij}} =0.75,\qquad \beta_{2} = \frac{a_{2} \hat{S}_{12}}{ \sum_{i=4}^{7} \sum_{j=1}^{7} \hat{\omega}_{ij}} =0.91. $$

Clearly, the value of $\beta_{k}$ ($k =1,2$) is positive, and thus inequation (24) is satisfied.

Furthermore, when we expand the number of nodes of GRNs to 20 and assume that there are three clusters in the GRNs, where $a_{i} =3\ ( i =1,\ldots,20)$, $c_{k} =0.5$, $d_{k} = c_{k} \hat{S}_{2k} / \hat{S}_{1k} \ ( k =1,\ldots, M )$; $M =3$; ${\alpha=0.2}$,

$$\begin{aligned} & \begin{pmatrix} \overline{m}_{1}\\ \overline{p}_{1} \end{pmatrix} = \left \{ \begin{pmatrix}{m_{1} ( t )}\\ {p_{1} ( t )} \end{pmatrix}, \ldots, \begin{pmatrix} {m_{10} ( t )}\\ {p_{10} ( t )} \end{pmatrix} \right \},\\ & \begin{pmatrix} \overline{m}_{2}\\ \overline{p}_{2} \end{pmatrix} = \left \{ \begin{pmatrix} {m_{11} ( t )} \\{p_{11} ( t )} \end{pmatrix}, \ldots, \begin{pmatrix} {m_{15} ( t )}\\ {p_{15} ( t )} \end{pmatrix} \right \},\\ & \begin{pmatrix} \overline{m}_{3}\\ \overline{p}_{3} \end{pmatrix} = \left \{ \begin{pmatrix}{m_{16} ( t )}\\ {p_{16} ( t )} \end{pmatrix}, \ldots, \begin{pmatrix} {m_{20} ( t )}\\ {p_{20} ( t )} \end{pmatrix} \right \}, \end{aligned}$$

such that $S_{11} = \sum_{i=1}^{10} m_{i} ( t ), S_{12} = \sum_{i=11}^{15} m_{i} ( t ), S_{13} = \sum_{i=16}^{20} m_{i} ( t ); S_{21} = \sum_{i=1}^{10} p_{i} ( t ), S_{22} = \sum_{i=11}^{15} p_{i} ( t ), S_{23} = \sum_{i=16}^{20} p_{i} ( t )$.

The desired values of $S_{11}$, $S_{12}$, $S_{13}$, $S_{21}$, $S_{22}$, $S_{23}$ are fixed at $\hat{S}_{11} =15$, $\hat{S}_{12} =20$, $\hat{S}_{13} =30$, $\hat{S}_{21} =30$, $\hat{S}_{22} =40$, $\hat{S}_{23} =60$, respectively.

The temporal evolution of $m_{i}$ and $p_{i}$ ($i =1,\ldots,20$) is shown in Fig. 9. According to Fig. 10, the values of $S_{1k}$ and $S_{2k} \ ( k =1,2,3)$ clearly approach those of $\hat{S}_{1k}$ and $\hat{S}_{2k}$. It is important to note that the GRNs are divided into three clusters, where the concentrations of $m_{i}$, $p_{i} \ ( i =1,\ldots,10)$ belong to the first cluster, the concentrations of $m_{i}$, $p_{i} \ ( i =11,\ldots,15)$ belong to the second cluster, and the concentrations of $m_{i}$, $p_{i} \ ( i =16,\ldots,20)$ belong to the third cluster.

Figure 9

State trajectories of $m_{i} (t)$ and $p_{i} (t) \ ( i =1,2,\ldots,20)$

Figure 10

State trajectories of $S_{1k} (t)$ and $S_{2k} (t) \ ( k =1,2,3)$

According to Fig. 11, the curves for identifying $\omega_{ij} \ (i=1,2,\ldots,20;j=1,2,\ldots,20)$ gradually tend toward the fixed values.

$$\begin{aligned} &\beta_{1} = \frac{a_{1} \hat{S}_{11}}{\sum_{i=1}^{10} \sum_{j=1}^{7} \hat{\omega}_{ij}} =1.47,\qquad \beta_{2} = \frac{a_{2} \hat{S}_{12}}{ \sum_{i=11}^{15} \sum_{j=1}^{7} \hat{\omega}_{ij}} =0.95,\\ & \beta_{3} = \frac{a_{3} \hat{S}_{13}}{\sum_{i=16}^{20} \sum_{j=1}^{7} \hat{\omega}_{ij}} =0.95. \end{aligned}$$

Figure 11

Identification process for the uncertain parameter $\omega_{ij}$, ($i =1,\ldots,20; j =1,\ldots,20$)

Clearly, the value of $\beta_{k}$ ($k =1,2,3$) is positive, and thus inequation (24) is satisfied.

5 Conclusions

In this study, we investigated desired clusters of GRNs with fixed time lags based on the Lyapunov theorem and Lipschitz condition. GRNs can be clustered using the two proposed strategies. In the first method, the concentrations of mRNAs in the same cluster approach the unique desired value. In the second method, the sums of clusters tend toward the desired value. Numerical examples were provided to demonstrate the effectiveness of the proposed clustering techniques. The results showed that the number of possible clusters in the GRNs does not affect the targeted stability of the cluster. In addition, not limiting the number of nodes in each cluster enhances the practicality and flexibility of these methods.