Abstract
In this paper, the numerical stability of a partial differential equation with piecewise constant arguments is considered. Firstly, the θ-methods are applied to approximate the original equation. Secondly, the numerical asymptotic stability conditions are given when the mesh ratio and the corresponding parameter satisfy certain conditions. Thirdly, the conditions under which the numerical stability region contains the analytic stability region are also established. Finally, some numerical examples are given to demonstrate the theoretical results.
Similar content being viewed by others
1 Introduction
Recently, differential equations with piecewise constant arguments (EPCA) have received much attention from a number of investigators [1–5] in such various fields as population dynamics, physics, mechanical systems, control science and economics. The theory of EPCA was initiated in 1983 and 1984 with the contributions of Cooke and Wiener [6], Shah and Wiener [7], Wiener [8], and it has been developed by many authors [9–13]. In 1993, Wiener, pioneer of EPCAs, recollects in the book [14] the investigation of EPCA until that moment. Later, continuous efforts have been made devoted to considering various properties of EPCA [15–18].
Generally speaking, in many cases analytic solutions of EPCA are hard to achieve and we are forced to use numerical methods to approximate them. Nevertheless, compared with the qualitative investigation of EPCA, the numerical study of EPCA is very late and rare. The original work for this field should be attributed to Liu et al. [19]. We think that it is the key step toward solving EPCA by numerical methods. Next, several results about the convergence, the stability and the dissipativity of numerical solutions for EPCA have been reported [20–24]. However, all of them are based on ordinary differential equations (ODEs). To the best of the author’s knowledge, only few results were presented in the case of numerical treatment of partial differential equations with piecewise constant arguments (PEPCA) [25, 26]. In these two articles, the authors investigated the numerical stability of θ-methods and Galerkin methods for a simple PEPCA, respectively. In contrast to [25, 26], in the present paper we study a more complicated model and analyze the numerical stability.
In this paper, we consider the following initial boundary value problem (IBVP):
where \(a,b,c \in\mathbb{R}\) and \(a\neq0\), \(u: \Omega=[0,1] \times [0,\infty)\rightarrow\mathbb{R}\), \(v: [0,1]\rightarrow\mathbb{R}\), \([\cdot]\) signifies the greatest integer function.
For the sake of the coming discussion, we derive the following stability conditions of (1) by using the similar method in [27, 28].
Lemma 1
If the following conditions are satisfied:
where
then the zero solution of the equation in (1) is asymptotically stable.
2 The stability of the numerical solution
In this section, we consider the numerical asymptotic stability of θ-methods for (1).
2.1 The difference equation
Let \(\Delta t>0\) and \(\Delta x>0\) be time and spatial stepsizes, respectively. We also assume that Δt satisfies \(\Delta t=1/m\), where \(m \geq1\) is an integer, and Δx satisfies \(\Delta x=1/p\) for \(p\in\mathbb{N}\). Define the mesh points
and
Applying the θ-methods to (1), we have
where \(u_{i}^{n}\), \(u^{h}(x_{i},2[(t_{n}+1)/2])\) and \(u^{h}(x_{i},[t_{n}])\) are approximations to \(u(x_{i},t_{n})\), \(u(x_{i},2[(t_{n}+1)/2])\) and \(u(x_{i},[t_{n}])\), respectively.
Denote \(n=km+l\), \(k=0,1,2,\ldots\) , \(l=0,1,\ldots, m-1\), by the same technique in [29], we can define \(u^{h}(x_{i},[t_{n}+\eta h])\triangleq u_{i}^{km}\), \(u^{h}(x_{i},2[(2k-1+lh+\eta h+1)/2])\triangleq u_{i}^{2km}\) and \(u^{h}(x_{i},2[(2k+lh+\eta h+1)/2])\triangleq u_{i}^{2km}\), where \(\eta\in[0,1]\). So the equation in (3) reduces to the following two recurrence relations:
when k is even and
when k is odd.
Basically, in each interval \([n,n+1)\), the equation in (1) can be seen as an original PDE, so the θ-methods for (1) are convergent of \(O(\Delta t+\Delta x^{2})\) if \(\theta\neq 1/2\), of \(O(\Delta t^{2}+\Delta x^{2})\) if \(\theta= 1/2\). A more detailed analysis on the convergence of the θ-methods can be found in [30, 31].
Let \(r=\Delta t/\Delta x^{2}\), so (4) and (5) become
and
respectively. Moreover, let \(i=1,2,\ldots,p-1\), (6) and (7) yield
and
respectively, where \(\omega=1-2a^{2}(1-\theta)r\).
Introducing \(\mathbf{u}^{n}=(u_{1}^{n},u_{2}^{n},\ldots,u_{p-1}^{n})^{T}\), \(n=0,1,2,\ldots \) , \(\mathbf{v}(x)=(v(x_{1}),v(x_{2}),\ldots,v(x_{p-1}))^{T}\) and the \((p-1)\times(p-1)\) triple-diagonal matrix \(\mathbf{F}=\mathsf {diag}(-1,2,-1)\), then (3) becomes
when k is even, and
when k is odd.
2.2 Stability analysis
From (8), we obtain
where
By (9), we also obtain
where
Iteration of (10) gives
in the same way, from (11) we have
Thus we get
So
Let \(l=m-1\) in (15) gives
Hence we have \(\mathbf{u}^{(2j+1)m}=\mathbf{M}\mathbf{u}^{(2j-1)m}\), where
Therefore
where \(\mathbf{u}^{1}=\mathbf{N}\mathbf{u}^{0}\), \(\mathbf{N}=\mathbf {R}^{m}+(\mathbf{R}^{m}-\mathbf{I})(\mathbf{R}-\mathbf{I})^{-1}\mathbf {S}\) and \(l=0,1,\ldots,m-1\).
Lemma 2
If the coefficients a, b and c satisfy
and
then the zero solution of the equation in (3) is asymptotically stable, where
Proof
From (16) and [25], we know that the largest eigenvalue (in modulus) of the matrix M is
where β is defined in (19). The zero solution of the equation in (3) is asymptotically stable if and only if \(|\lambda_{\mathbf{M}}|<1\). So (17) and (18) are got. □
Theorem 1
Under the conditions of Lemma 2, if the conditions
and
are satisfied, where \(c\neq a^{2}/(\beta^{m}-1)\), \(a\neq0\), then the zero solution of the equation in (3) is asymptotically stable.
Proof
If \(a\neq0\), (17) and (18) are equivalent to
and
After some derivations we can get (20) and (21). The proof is completed. □
Definition 1
The set of all points \((a,b,c)\) which satisfies (2) is called an asymptotic stability region denoted by H.
Definition 2
The set of all points \((a,b,c)\) at which the θ-methods for (1) which satisfies (20) is asymptotically stable is called an asymptotic stability region denoted by S.
For convenience, we divide the region H into three parts:
In the similar way, we denote
It is easy to see that \(H=H_{0}\cup H_{1}\cup H_{2}\), \(S=S_{0}\cup S_{1}\cup S_{2}\), \(H_{i}\cap H_{j}=\Phi\), \(S_{i}\cap S_{j}=\Phi\) and \(H_{i}\cap S_{j}=\Phi\), \(i \neq j\), \(i,j=0,1,2\).
Theorem 2
Under the constraints
and
if the following conditions are satisfied:
\(r\neq1/(a^{2} \lambda_{\mathbf{F}} (1-\theta))\) and
for m is even, and
for m odd, then \(H_{1}\subseteq S_{1}\).
Proof
By the definition of \(H_{1}\) we know that (2) is satisfied when (22) and (23) hold. In the same way, according to the definition of \(S_{1}\) we know that (20) is satisfied when (22) and (23) hold and \(0<\beta ^{m}<1\), where β is defined in (19), then we can get \(H_{1}\subseteq S_{1}\). Therefore, (24) and (25) can be obtained from \(0<\beta^{m}<1\). The proof is completed. □
Theorem 3
Under the constraints
and
if the following conditions are satisfied:
\(r\neq1/(a^{2} \lambda_{\mathbf{F}} (1-\theta))\) and
for m even, and
for m odd, then \(H_{2}\subseteq S_{2}\).
Proof
Similar to the proof of Theorem 2, we can omit it. □
Theorem 4
Under the constraints
and
if the following conditions are satisfied:
\(r\neq1/(a^{2} \lambda_{\mathbf{F}} (1-\theta))\) and
for m even, and
for m odd, then \(H_{0}\subseteq S_{0}\).
Proof
Follows directly from the proof of Theorem 2. □
Remark 1
If \(\theta=1\), then the corresponding fully implicit finite difference scheme is asymptotically stable unconditionally.
3 Numerical experiments
To demonstrate our theoretical result, some numerical examples are adopted in this section. Consider the following two problems:
In Tables 1–4 we list the absolute errors \(\operatorname{AE}(1/m,1/p)\), \(\operatorname{AE}(1/4m,1/2p)\) and \(\operatorname{AE}(1/2m, 1/2p)\) at \(x=1/2\), \(t=1\) of the θ-methods for (31) and (32), the ratio of \(\operatorname{AE}(1/m,1/p)\) over \(\operatorname{AE}(1/4m,1/2p)\) in Tables 1, 3 and the ratio of \(\operatorname{AE}(1/m,1/p)\) over \(\operatorname{AE}(1/2m,1/2p)\) in Tables 2, 4. We can see from these tables that the numerical methods conserve their orders of convergence.
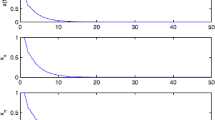
In Figures 1–4, we draw the numerical solutions of the θ-methods. It is easy to see that the numerical solutions are asymptotically stable. In Figures 5 and 6, we draw the error figures for the numerical solutions with \(\theta=1\). It can be seen that the numerical method is of high accuracy.
The numerical solution of (31) with \(\theta= 0\), \(m = 6400\), \(p = 20\) and \(r = 1/16\)
The numerical solution of (31) with \(\theta= 0.5\), \(m = 128\), \(p = 16\) and \(r = 2\)
The numerical solution of (32) with \(\theta= 0\), \(m = 6400\), \(p = 20\) and \(r = 1/16\)
The numerical solution of (32) with \(\theta= 0.5\), \(m = 128\), \(p = 16\) and \(r = 2\)
Errors of (31) with \(\theta= 1\), \(m = 1024\), \(p = 32\) and \(r = 1\)
Errors of (32) with \(\theta= 1\), \(m = 1024\), \(p = 32\) and \(r = 1\)
References
Cavalli, F., Naimzada, A.: A multiscale time model with piecewise constant argument for a boundedly rational monopolist. J. Differ. Equ. Appl. 22, 1480–1489 (2016)
Dai, L., Fan, L.: Analytical and numerical approaches to characteristics of linear and nonlinear vibratory systems under piecewise discontinuous disturbances. Commun. Nonlinear Sci. Numer. Simul. 9, 417–429 (2004)
Dai, L., Singh, M.C.: On oscillatory motion of spring-mass systems subjected to piecewise constant forces. J. Sound Vib. 173, 217–232 (1994)
Gurcan, F., Bozkurt, F.: Global stability in a population model with piecewise constant arguments. J. Math. Anal. Appl. 360, 334–342 (2009)
Wiener, J., Lakshmikantham, V.: A damped oscillator with piecewise constant time delay. Nonlinear Stud. 1, 78–84 (2000)
Cooke, K.L., Wiener, J.: Retarded differential equations with piecewise constant delays. J. Math. Anal. Appl. 99, 265–297 (1984)
Shah, S.M., Wiener, J.: Advanced differential equations with piecewise constant argument deviations. Int. J. Math. Math. Sci. 6, 671–703 (1983)
Wiener, J.: Differential equations with piecewise constant delays. In: Lakshmikantham, V. (ed.) Trends in the Theory and Practice of Nonlinear Differential Equations, pp. 547–580. Dekker, New York (1983)
Akhmet, M.U., Arugǎslan, D., Yılmaz, E.: Stability in cellular neural networks with a piecewise constant argument. J. Comput. Appl. Math. 233, 2365–2373 (2010)
Bereketoglu, H., Seyhan, G., Ogun, A.: Advanced impulsive differential equations with piecewise constant arguments. Math. Model. Anal. 15, 175–187 (2010)
Karakoc, F.: Asymptotic behaviour of a population model with piecewise constant argument. Appl. Math. Lett. 70, 7–13 (2017)
Muroya, Y.: New contractivity condition in a population model with piecewise constant arguments. J. Math. Anal. Appl. 346, 65–81 (2008)
Pinto, M.: Asymptotic equivalence of nonlinear and quasi linear differential equations with piecewise constant arguments. Math. Comput. Model. 49, 1750–1758 (2009)
Wiener, J.: Generalized Solutions of Functional Differential Equations. World Scientific, Singapore (1993)
Berezansky, L., Braverman, E.: Stability conditions for scalar delay differential equations with a non-delay term. Appl. Math. Comput. 250, 157–164 (2015)
Dimbour, W.: Almost automorphic solutions for differential equations with piecewise constant argument in a Banach space. Nonlinear Anal. 74, 2351–2357 (2011)
El Raheem, Z.F., Salman, S.M.: On a discretization process of fractional-order logistic differential equation. J. Egypt. Math. Soc. 22, 407–412 (2014)
Muminov, M.I.: On the method of finding periodic solutions of second-order neutral differential equations with piecewise constant arguments. Adv. Differ. Equ. 2017, 336 (2017)
Liu, M.Z., Song, M.H., Yang, Z.W.: Stability of Runge–Kutta methods in the numerical solution of equation \(u'(t)=au(t)+a_{0}u([t])\). J. Comput. Appl. Math. 166, 361–370 (2004)
Li, C., Zhang, C.J.: Block boundary value methods applied to functional differential equations with piecewise continuous arguments. Appl. Numer. Math. 115, 214–224 (2017)
Milosevic, M.: The Euler–Maruyama approximation of solutions to stochastic differential equations with piecewise constant arguments. J. Comput. Appl. Math. 298, 1–12 (2016)
Song, M.H., Liu, X.: The improved linear multistep methods for differential equations with piecewise continuous arguments. Appl. Math. Comput. 217, 4002–4009 (2010)
Wang, W.S., Li, S.F.: Dissipativity of Runge–Kutta methods for neutral delay differential equations with piecewise constant delay. Appl. Math. Lett. 21, 983–991 (2008)
Zhang, G.L.: Stability of Runge–Kutta methods for linear impulsive delay differential equations with piecewise constant arguments. J. Comput. Appl. Math. 297, 41–50 (2016)
Liang, H., Liu, M.Z., Lv, W.J.: Stability of θ-schemes in the numerical solution of a partial differential equation with piecewise continuous arguments. Appl. Math. Lett. 23, 198–206 (2010)
Liang, H., Shi, D.Y., Lv, W.J.: Convergence and asymptotic stability of Galerkin methods for a partial differential equation with piecewise constant argument. Appl. Math. Comput. 217, 854–860 (2010)
Wang, Q., Wen, J.C.: Analytical and numerical stability of partial differential equations with piecewise constant arguments. Numer. Methods Partial Differ. Equ. 30, 1–16 (2014)
Wiener, J., Debnath, L.: A wave equation with discontinuous time delay. Int. J. Math. Math. Sci. 15, 781–788 (1992)
Song, M.H., Liu, M.Z.: Numerical stability and oscillations of the Runge–Kutta methods for the differential equations with piecewise continuous arguments of alternately retarded and advanced type. J. Inequal. Appl. 2012, 290 (2012)
Blanco-Cocom, L., Àvila-Vales, E.: Convergence and stability analysis of the θ-method for delayed diffusion mathematical models. Appl. Math. Comput. 231, 16–25 (2014)
Zhang, Q.F., Chen, M.Z., Xu, Y.H., Xu, D.H.: Compact θ-method for the generalized delay diffusion equation. Appl. Math. Comput. 316, 357–369 (2018)
Acknowledgements
The author is grateful to the reviewers for their careful reading and useful comments. This work is supported by the National Natural Science Foundation of China (No. 11201084) and Natural Science Foundation of Guangdong Province (No. 2017A030313031).
Author information
Authors and Affiliations
Contributions
The author read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The author declares that he has no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, Q. Stability of numerical solution for partial differential equations with piecewise constant arguments. Adv Differ Equ 2018, 71 (2018). https://doi.org/10.1186/s13662-018-1514-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-018-1514-1