1 Introduction

In nature, the anomalous diffusion phenomena occur in multiple scientific fields including physical chemistry, bioscience and engineering technology [1–4]. When many researchers attempt to describe or characterize these phenomena by the conventional integer-order differential equations, the theoretical analyses are not in good agreement with the real observations [4]. With the development of fractional calculus theory (FCT), the scientists discovered that the fractional differential equations (FDEs) have great advantages in solving many anomalous physical phenomena [5–8]. Kumar et al. [9] proposed a time-fractional modified Kawahara equation based on the Caputo-Fabrizio operator and discussed a fractional model of convective radial fins with the aid of the Homotopy analysis transform method numerically [10]. Singh et al. [11] analyzed the El Nino-Southern Oscillation model via the iterative method and fixed point theorem, as well as a nonlinear fractional dynamical model of interpersonal and romantic relationships through the q-homotopy analysis Sumudu transform method [12]. Especially, the anomalous behaviors involving the diffusion problem, heat transfer, creep phenomena, fluid flow process, oscillating circuits and the convection dispersion have been the research hot spots (see [13–18]). For instance, Metzler and Klafter presented the kinetic diffusion equations based on the fractional derivative (FD) in [19]. Yang et al. proposed the rheological models with the aid of FD in [20]. Ren et al. solved the time-fractional convection dispersion equations in [21]. However, the methods for obtaining the analytic solutions of those FDEs are still lacking due to the complexity of FCT (see [22, 23]).

The Mittag-Leffler function (MLF) and its extended forms, which are closely related to the FCT, seem to provide us with new ideas in describing some anomalous phenomena and solving the FDEs [24, 25]. Based on the MLFs, many fractional differential operators (FDOs) have been suggested (see [18, 25–31]). For example, Caputo and Fabrizio [30] defined a new fractional derivative without singular kernel. Atangana et al. used the MLF to replace the exponent function in the integral kernel of the above definition and obtained its new form in [18]. Giusti et al. suggested the Prabhakar-like fractional derivative in [31]. A family of general FDOs based on the extensions of the classical MLFs (Gösta Mittag-Leffler, Wiman and Prabhakar functions) were proposed in [25, 28]. In fact, there are close relationships among these FDOs. As analyzed in [9] by Kumar, the Caputo-Fabrizio operator is much more efficient than the classical Caputo derivative. For Atangana’s suggestion to the new fractional derivative with one-parameter MLF, it is an extended version of the Caputo-Fabrizio operator [18]. Similarly, the Prabhakar-like fractional derivative can return to the Caputo-Fabrizio operator and the new FDOs defined by Yang when the parameters take the particular values (see [25, 28, 31]). These FDOs involving the MLFs in the integral kernel have been applied to model many physical phenomena, such as the anomalous relaxation, heat-transfer problems, viscoelastic problems, Euler-Lagrange equation and the boundary value problem, extensively (see [18, 28–36]). Especially, the new general FDOs with the aid of Laplace transform (LT) of the MLFs may be provided to describe different anomalous physical phenomena (see [28]). Inspired by this, this paper aims to model the anomalous diffusion problems by the new general FDOs and to obtain the analytic solution.

The remainder of this paper is structured as follows. In Section 2, the definitions of several MLFs, the new Liouville-Caputo general FDO with the extension of Wiman function, as well as the LT of the Wiman and Prabhakar MLFs with power-law functions, are reviewed. In Section 3, an anomalous diffusion model (ADM) based on the above general FDO is proposed, and its analytic solution is also given. In addition, the ADMs with different parameters are analyzed graphically. Finally, the conclusions are summarized in Section 4.

2 The MLF and a new general FDO

2.1 The MLF and LTs of its generations

In recent decades, owing to the successful applications of MLFs in multiple fields involving applied sciences and pure mathematics, they have received wide attention. Correspondingly, a variety of the extensions or generalizations of the MLF have been suggested. Here, we review them as follows.

Let \(\mathbb{C}\), \(\mathbb{ R}\) and \(\mathbb{N}\) be the sets of complex numbers, real numbers and positive integers, respectively.

Definition 1

The MLF proposed by Gösta Magnus Mittag-Leffler in 1903 [24, 26, 28] is given by

$$ E_{\vartheta}( \chi )=\sum_{\lambda =0}^{\infty}{\frac{\chi ^{\lambda}}{\Gamma ( {\vartheta \lambda +1} )}} , $$
(1)

where ϑ, \(\chi \in \mathbb{C}\), \(\operatorname{Re} \vartheta >0\), \(\lambda \in \mathbb{ N}\), and \(\Gamma ( \cdot )\) denotes the Gamma function.

Definition 2

The first extended form to the MLF, suggested by Wiman in 1905 [24, 28], is defined as

$$ E_{\vartheta ,\varpi } ( \chi )=\sum_{\lambda =0}^{\infty}{\frac{\chi ^{\lambda}}{\Gamma ( {\vartheta \lambda +\varpi } )}} , $$
(2)

where ϑ, ϖ, \(\chi \in \mathbb{C}\), \(\operatorname{Re}\vartheta >0\) and \(\lambda \in \mathbb{ N}\).

Definition 3

The extension of the MLF containing three parameters, proposed by Prabhakar in 1971 [24, 27, 28], is described as

$$ E_{\vartheta ,\varpi }^{\tau}( \chi )=\sum _{\lambda =0}^{\infty}{\frac{ ( \tau )_{\lambda}}{\Gamma ( {\lambda +1} )\Gamma ( {\vartheta \lambda +\varpi } )}\chi ^{\lambda}} , $$
(3)

where ϑ, ϖ, χ, \(\tau \in \mathbb{C}\), Reϑ, \(\tau >0\), \(\lambda \in \mathbb{ N}\), and the Pochhammer symbol is

$$ ( \tau )_{\lambda}=\tau ( {\tau +1} )\cdots(\tau +\lambda -1)=\textstyle\begin{cases} 1,&\lambda \mbox{=}0, \\ \frac{\Gamma ( {\tau +\lambda } )}{\Gamma ( \tau )},&\lambda \ge 1. \end{cases} $$
(4)

Definition 4

The new extended forms to the MLFs of Wiman and Prabhakar types are defined as follows [28]:

$$ E_{\vartheta ,\varpi +\theta } ( \chi )=\sum_{\lambda =0}^{\infty}{\frac{\chi ^{\lambda}}{\Gamma ( {\vartheta \lambda +\varpi +\theta } )}} $$
(5)

and

$$ E_{\vartheta ,\varpi +\theta }^{\tau}( \chi )=\sum _{\lambda =0}^{\infty}{\frac{ ( \tau )_{\lambda}}{\Gamma ( {\lambda +1} )\Gamma ( {\vartheta \lambda +\varpi +\theta } )}\chi ^{\lambda}} , $$
(6)

where ϑ, ϖ, χ, \(\tau \in \mathbb{C}\), Reϑ, \(\tau >0\) and \(\lambda \in \mathbb{ N}\).

Definition 5

The LT of a real function \(\phi ( x )\), \(x>0\), is defined as [37, 38]

$$ F ( \xi )=L \bigl[ {\phi ( x )} \bigr]= \int_{0}^{\infty}{\phi ( x )e^{-\xi x}\,dx} ,\quad \xi >0, $$
(7)

where L is the LT operator.

According to the literature [28], the LTs of the new extensions of Wiman and Prabhakar functions with power-law functions are listed in Table 1.

Table 1 The LT of the new extensions of Wiman and Prabhakar functions with the power-law functions [ 28 ]
Full size table

2.2 The new Liouville-Caputo general FDO with the extension of Wiman function

Definition 6

Let \(0<\vartheta <1\) and ϑ, ϖ, \(\theta \in \mathbb{ R}\). The new Liouville-Caputo general FDO with the extension of Wiman function is defined as [28]

$$ \bigl( {{ }_{0}^{LC} {\mathrm{D}}_{\chi}^{ ( \vartheta )} \Omega } \bigr) ( \chi )= \int_{0}^{\gamma}{ \bigl[ { ( {\gamma -\chi } )^{\varpi +\theta -1}E_{\vartheta ,\varpi +\theta } \bigl( { ( {\gamma -\chi } )^{\vartheta}} \bigr)} \bigr]\Omega ^{ ( 1 )} ( \chi )\,d\chi }, $$
(8)

where

$$\Omega ^{ ( 1 )} ( \chi )=\frac{d\Omega ( \chi )}{d\chi}. $$

The LT of Eq. (8) is given as follows [28, 38, 39]:

$$ F ( \xi )=\xi ^{- ( {\varpi +\theta } )} \bigl( {1-\xi ^{-\vartheta }} \bigr)^{-1}\times \bigl[ {\xi L \bigl[ {\Omega ( \chi )} \bigr]-\Omega ( 0 )} \bigr]. $$
(9)

Remark

According to the literature [31], there is

$$\lim_{\eta \to 0} \chi^{\varpi +\theta -1}E_{\vartheta ,\varpi+\theta } \bigl({\eta} { \chi ^{\vartheta}} \bigr)=\frac{\chi^{\varpi +\theta -1}}{\Gamma ( {\varpi+\theta } )}, $$

which is the integral kernel of the Liouville-Caputo FDO. It indicates that the Liouville-Caputo fractional derivative is a special case of the general Liouville-Caputo fractional-order derivative of Wiman type.

3 Analyses of the ADM

3.1 Analytic solution of the ADM

Applying the new Liouville-Caputo general FDO with the extension of Wiman function equation (8), we can obtain a new anomalous diffusion model as follows:

$$ \bigl( {{ }_{0}^{LC} {\mathrm{D}}_{\chi}^{ ( \vartheta )} u} \bigr) ( {x,\chi } )=\varepsilon \frac{\partial ^{2}u ( {x,\chi } )}{\partial x^{2}},\quad x, \chi >0, $$
(10)

where ε is a real constant reflecting the magnitudes of the diffusion capacity.

The initial value condition of the above anomalous diffusion equation is

$$ u ( {x,0} )=0, $$
(11)

and the boundary value conditions are

$$ \textstyle\begin{cases} u ( {0,\chi } )=c, \\ u ( {\infty ,\chi } )=B, \end{cases} $$
(12)

where c is a real constant and B is a bounded real number.

From Eqs. (8) and (9), performing LT of Eq. (10) with respect to γ, we can obtain

$$ \xi ^{- ( {\varpi +\theta } )} \bigl( {1-\xi ^{-\vartheta }} \bigr)^{-1}\times \bigl[ {\xi U(x,\xi )-u ( {x,0} )} \bigr]=\varepsilon U^{ ( 2 )}(x,\xi ). $$
(13)

Meanwhile, the corresponding boundary value conditions via LT become

$$ \textstyle\begin{cases} U(0,\xi )=\frac{c}{\xi }, \\ U ( {\infty ,\xi } )=B. \end{cases} $$
(14)

Substituting Eq. (11) into Eq. (13), we have

$$ MU(x,\xi )=\varepsilon U^{ ( 2 )}(x,\xi ), $$
(15)

where

$$ M=\xi ^{1- ( {\varpi +\theta } )} \bigl( {1-\xi ^{-\vartheta }} \bigr)^{-1}. $$
(16)

Then, applying the eigenvalue method [40], we can obtain the analytic solution of Eq. (15) as follows:

$$ U(x,\xi )=C_{1} e^{\sqrt {\frac{M}{\varepsilon }} x}+C_{2} e^{-\sqrt {\frac{M}{\varepsilon }} x}. $$
(17)

Next, the substitution of Eq. (14) into Eq. (17) results in

$$ \textstyle\begin{cases} C_{1} +C_{2} =\frac{c}{\xi }, \\ C_{1} =0. \end{cases} $$
(18)

Finally, substituting Eq. (18) into Eq. (17), we obtain

$$ U(x,\xi )=\frac{c}{\xi }e^{-\sqrt {\frac{M}{\varepsilon }} x}. $$
(19)

To obtain the series solution of Eq. (8), consider the following Taylor series [41]:

$$ e^{-\sqrt {\frac{M}{\varepsilon }} x}=1- \biggl( {\frac{M}{\varepsilon }} \biggr)^{1 / 2}x+\frac{1}{2}\frac{M}{\varepsilon }x^{2}- \frac{1}{6} \biggl( {\frac{M}{\varepsilon }} \biggr)^{3 / 2}x^{3}+ \frac{1}{24} \biggl( {\frac{M}{\varepsilon }} \biggr)^{2}x^{4}+ \cdots. $$
(20)

Substituting Eqs. (16) and (20) into Eq. (19), we have

$$\begin{aligned} U(x,\xi ) =&\frac{c}{\xi }-\frac{c}{\xi } \biggl( { \frac{\xi ^{1- ( {\varpi +\theta } )} ( {1-\xi ^{-\vartheta }} )^{-1}}{\varepsilon }} \biggr)^{1 / 2}x+\frac{c}{2\xi } \frac{\xi ^{1- ( {\varpi +\theta } )} ( {1-\xi ^{-\vartheta }} )^{-1}}{\varepsilon }x^{2} \\ &{}-\frac{c}{6\xi } \biggl( {\frac{\xi ^{1- ( {\varpi +\theta } )} ( {1-\xi ^{-\vartheta }} )^{-1}}{\varepsilon }} \biggr)^{3 / 2}x^{3}+ \frac{c}{24\xi } \biggl( {\frac{\xi ^{1- ( {\varpi +\theta } )} ( {1-\xi ^{-\vartheta }} )^{-1}}{\varepsilon }} \biggr)^{2}x^{4} +\cdots \\ =&\frac{c}{\xi }-\frac{c}{\sqrt {\varepsilon}}\xi ^{{ ( {-1- ( {\varpi +\theta } )} )} / 2} \bigl( {1-\xi ^{-\vartheta }} \bigr)^{-1 / 2}x \\ &{} +\frac{c}{2\varepsilon }\xi ^{- ( {\varpi +\theta } )} \bigl( {1-\xi ^{-\vartheta }} \bigr)^{-1}x^{2} \\ &{} -\frac{c}{6\varepsilon ^{3 / 2}}\xi ^{{ ( {1-3 ( {\varpi +\theta } )} )} / 2} \bigl( {1-\xi ^{-\vartheta }} \bigr)^{-3/2}x^{3} \\ &{} +\frac{c}{24\varepsilon ^{2}}\xi ^{1-2 ( {\varpi +\theta } )} \bigl( {1-\xi ^{-\vartheta }} \bigr)^{-2}x^{4}+\cdots. \end{aligned}$$
(21)

Finally, using Table 1, we can easily obtain

$$\begin{aligned} u(x,\chi ) =&c-\frac{c}{\sqrt {\varepsilon}}x\chi ^{{ ( {\varpi +\theta -1} )} / 2}E_{\vartheta ,{ ( {1+ ( {\varpi +\theta } )} )} / 2}^{1 / 2} \bigl( {\chi ^{\vartheta}} \bigr) \\ &{} +\frac{c}{2\varepsilon }x^{2}\chi ^{\varpi +\theta -1}E_{\vartheta ,\varpi +\theta } \bigl( {\chi ^{\vartheta}} \bigr) \\ &{}-\frac{c}{6\varepsilon ^{3 / 2}}x^{3}\chi ^{{3 ( {\varpi +\theta -1} )} / 2}E_{\vartheta ,{ ( {3 ( {\varpi +\theta } )-1} )} / 2}^{3 / 2} \bigl( {\chi ^{\vartheta}} \bigr) \\ &{} +\frac{c}{24\varepsilon ^{2}}x^{4}\chi ^{2 ( {\varpi +\theta -1} )}E_{\vartheta ,2 ( {\varpi +\theta } )-1}^{2} \bigl( {\chi ^{\vartheta}} \bigr)+\cdots \\ =&c+\sum_{n=1}^{\infty}{ \biggl[ { \frac{c ( {-x} )^{n}}{n!\varepsilon ^{n / 2}}\chi ^{{n ( {\varpi +\theta -1} )} / 2}E_{\vartheta ,{n ( {\varpi +\theta -1} )} / 2+1}^{n / 2} \bigl( {\chi ^{\vartheta}} \bigr)} \biggr]} . \end{aligned}$$
(22)

3.2 Numerical analyses of the ADM

In this subsection, we illustrate the numerical analyses of the ADM from multiple angles. Firstly, we analyze the convergence of Eq. (22) by discussing the values of n. Secondly, the comparisons between the conventional diffusion and the anomalous diffusion are presented graphically. Next, the characteristics of the anomalous diffusion with the varied fractional orders are represented. Finally, the ADMs with several varied parameters are shown graphically.

The applications of the series solution with the complete terms are not conducive to solving the practical problems. In fact, the series solution may converge to its finite terms. For Eq. (22) with \(\vartheta =0.2\), we compare its results graphically when n takes 1, 2, 3 and 4, respectively. As shown in Figure 1, when n tends to 4, the solution of Eq. (22) is almost consistent with the result with \(n=3\), which indicates that Eq. (22) when \(n=4\) can be treated as the convergence solution. Similarly, when ϑ takes 0.4 and 0.6, Eq. (22) also converges to the result with \(n=4\) (see Figure 2).

Figure 1
figure 1

Numerical solution of the anomalous diffusion equation ( 22 ) as a function of time χ and space x for \(\pmb{c=0.5}\) , \(\pmb{\varepsilon =0.8}\) , \(\pmb{\varpi =0.5}\) , \(\pmb{\theta =0.3}\) , \(\pmb{\vartheta =0.2}\) , \(\pmb{n=4}\) .

Full size image
Figure 2
figure 2

(a) Numerical solution of the anomalous diffusion equation ( 22 ) as a function of time χ and space x for \(\pmb{c=0.5}\) , \(\pmb{\varepsilon =0.8}\) , \(\pmb{\varpi =0.5}\) , \(\pmb{\theta =0.3}\) , \(\pmb{\vartheta =0.4}\) , \(\pmb{n=1,2,3,4}\) , (b) numerical solution of the anomalous diffusion equation ( 22 ) as a function of time χ and space x for \(\pmb{c=0.5}\) , \(\pmb{\varepsilon =0.8}\) , \(\pmb{\varpi =0.5}\) , \(\pmb{\theta =0.3}\) , \(\pmb{\vartheta =0.6}\) , \(\pmb{n=1,2,3,4}\) .

Full size image

In order to illustrate the differences between the conventional diffusion and the anomalous diffusion, we give the exact solution of the conventional diffusion model as follows [39]:

$$ u ( {x,\chi } )=c\times \mathit{erfc} \biggl( {\frac{x}{2\sqrt {\varepsilon \chi } }} \biggr). $$
(23)

Eq. (23) is compared to the results of Eq. (22) with \(\vartheta =0.2\) and 0.4 graphically. As shown in Figure 3, the anomalous diffusion processes present different characteristics from the conventional diffusion. The gradient of anomalous diffusion is smaller than that of the conventional diffusion.

Figure 3
figure 3

Comparisons between conventional diffusion with \(\pmb{c=0.5}\) , \(\pmb{\varepsilon =0.8}\) and anomalous diffusion with \(\pmb{c=0.5}\) , \(\pmb{\varepsilon =0.8}\) , \(\pmb{\varpi =0.5}\) , \(\pmb{\theta =0.3}\) , \(\pmb{\vartheta =0.2, 0.4}\) , \(\pmb{n=4}\) .

Full size image

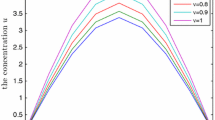
Figure 4 shows the effects of different orders on the anomalous diffusion processes. Clearly, the smaller the orders are, the stronger the diffusion processes are. Under the same conditions, the diffusion concentrations approximately range from 0.45 to 0.4 for \(\vartheta =0.2\), 0.46 to 0.425 for \(\vartheta =0.4\), 0.47 to 0.44 for \(\vartheta =0.6\) and 0.475 to 0.45 for \(\vartheta =0.8\), respectively.

Figure 4
figure 4

Comparisons of anomalous diffusion processes with different fractional orders.

Full size image

Considering the effect of different parameters on the anomalous diffusion processes, we present the diffusion processes with several varied parameters in Figure 5. The values of different parameters are listed in Table 2.

Figure 5
figure 5

Numerical solutions of the anomalous diffusion equation ( 22 ) as a function of time χ and space x with different parameters shown in Table  2 .

Full size image
Table 2 Different parameters for the anomalous diffusion model
Full size table

4 Conclusions

In the current paper, we have solved a new ADM based on a new Liouville-Caputo general FDO with the extension of Wiman function. The analytic series solution was obtained and its convergence was discussed. The results show that the numerical solutions can satisfy the accuracy when \(n=4\), and the new FDO is effective in describing the anomalous diffusion phenomena. In addition, the anomalous diffusion processes exhibit different characteristics from the conventional diffusion, and they are greatly affected by the varied parameters. Specially, the smaller the orders are, the stronger the diffusion processes are.