1 Introduction and statement of model formulation

With the increase in global population and the rapid development of industry and agriculture, water consumption increases sharply. Wastewater containing harmful substances, such as harmful microbes and heavy metal elements, is discharged into lakes, rivers, etc., and the ecological environment is seriously polluted. Water pollution threatens human health and the sustainable development of the whole society. In order to control water pollution, a series of methods of wastewater treatment have been proposed [1]. The methods of wastewater treatment typically involve physical treatment (such as filtering), chemical treatment (such as electrolysis), and biological treatment (such as aerobic/anaerobic method). Biological treatment is to remove harmful microorganisms in wastewater by using the metabolism of organisms such as bacteria, molds, or protozoa. Biological treatment largely depends on the process of adsorption degradation to organic material solids, harmful microbes, etc. [2, 3]. Because of its cost effectiveness, superior performance, and environmental friendliness, biological treatment has been generally employed in wastewater treatment [3, 4].

In the past few years, the flocculation sedimentation method has been widely used in wastewater treatment and collecting microorganisms [5, 6]. Harmful substances in wastewater can be degraded by using flocculants. There are many kinds of flocculants, which mainly include two categories: inorganic flocculants and organic flocculants [7]. Inorganic flocculants mainly include inorganic coagulants and inorganic high molecular flocculants such as iron salt, aluminum salt, etc. [8]. Related studies have shown that inorganic flocculants are likely to cause secondary pollution which has a negative impact on human health [9]. Organic flocculants include synthetic organic polymer flocculants, natural organic high molecular flocculants, and microbial flocculants such as polyacrylamide [4]. With the progress of science and technology, the research and development of different kinds of microbial flocculants have been carried out rapidly.

As a new type of flocculants, microbial flocculants have been widely used in wastewater treatment [3, 10, 11]. Microbial flocculants are mainly divided into three types according to their compositions [12]: (1) microbial cells such as some bacteria; (2) microbial cell extracts such as yeast cell wall glucan; and (3) microbial metabolites. Microbial flocculants have many advantages such as biodegradation, no secondary pollution, non-toxicity, high security, etc. A lot of experimental studies have been carried out on microbial flocculants [13].

In the research of microbial flocculants, flocculant-producing bacteria have received extensive attention. As early as 1935, Butterfield successfully isolated flocculant-producing bacteria from activated sludge. Since 1970s, researchers have isolated a variety of flocculant-producing bacteria from the environment. Kurane and Tomizuka isolated Rhodococcus erythropolis with flocculant activity from nature and first got microbial flocculant NOC-1 [14]. The flocculant has a very good effectiveness on the livestock wastewater treatment, expansion of sludge treatment, and so on.

The chemostat is an important experimental device which has been used extensively in microbial continuous culture and environmental pollution treatment [15–19]. The chemostat can be used to model nutrient consumption and microbial competition [20–27]. In some cases, microorganisms can produce toxins or inhibitors against its competitors. Chao and Levin performed a basic experiment about antibiotic inhibitors [28]. In the evolutive chemostat model, in order to make it more biologically significant, inhibitors or toxins are introduced to competitive models [29–33]. For example, in [29, 33], and [34], the chemostat models with internal and external inhibitors were established, respectively.

The following classic model equipped with toxins produced by microorganism in chemostat is proposed in [32]:

$$ \textstyle\begin{cases} \dot{S}(t) = D (S^{0}-S(t) )-\frac{m_{1}S(t)}{a_{1}+S(t)}\frac{x(t)}{ \gamma_{1}} -\frac{m_{2}S(t)}{a_{2}+S(t)}\frac{y(t)}{\gamma_{2}}, \\ \dot{x}(t) = x(t) [\frac{m_{1}S(t)}{a_{1}+S(t)}-D-\gamma P(t) ], \\ \dot{y}(t) = y(t) [(1-k)\frac{m_{2}S(t)}{a_{2}+S(t)}-D ], \\ \dot{P}(t) = k\frac{m_{2}S(t)y(t)}{a_{2}+S(t)}-DP(t). \end{cases} $$
(1)

In model (1), \(S(t)\), \(x(t)\), \(y(t)\), and \(P(t)\) denote the concentrations of nutrient, toxin-sensitive microorganism, toxin-producing organism, and toxin present at time t, respectively. \(S^{0}\) is the input concentration of nutrient. D is the washout rate. \(m_{i}\) are the maximal growth rates. \(a_{i}\) are the Michaelis-Menten constants. \(\gamma_{i}\) are the yield constants (\(i=1,2\)). k (\(0< k<1\)) is the toxin production rate. In appropriate biological backgrounds, model (1) can be applied to the removal of toxin-sensitive microorganism (considered as harmful microorganism).

In this paper, motivated by microbial flocculants and model (1), we propose a model which may have potential applications of microbial metabolites as flocculants in the control of harmful microorganisms in wastewater treatment.

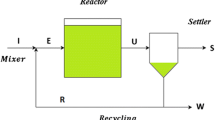
Let \(s(t)\), \(x(t)\), \(y(t)\), and \(p(t)\) denote the concentrations of limiting nutrient, harmful microorganism (such as E. coli), microbial flocculant-producing bacterium (such as Bacillus subtilis), and microbial flocculant at time t, respectively. We need to point out that the microbial flocculant is the metabolic product of the microbial flocculant-producing bacterium. It is assumed that the constant \(s^{0}\) is the input concentration of nutrient, and the constant D is the washout rate of nutrient. Furthermore, from [35], we see that the microbial flocculant-producing bacterium and its metabolic products follow the following relationship:

$$\dot{p}(t)=\alpha \dot{y}(t)+\beta y(t), $$

where α and β are determined by pH value [35]. Further, the metabolic products are the microbial flocculant used to flocculate the harmful microorganism. Therefore, we finally assume that the change rate \(\dot{p}(t)\) is in accordance with the following equation:

$$\dot{p}(t)= \alpha \bigl(c_{1}s(t)y(t)-Dy(t) \bigr)+\beta y(t)-Dp(t)-d_{3}x(t)p(t), $$

where \(c_{1}\) is the nutrient uptake rate of microbial flocculant-producing bacterium. \(d_{3}\) is the consumption rate of the microbial flocculant. In accordance with the biological meanings, it is assumed that \(D\alpha \leq \beta \).

From the above analysis and the discussions in [24, 36], and [37], we have the following model:

$$ \textstyle\begin{cases} \dot{s}(t) = Ds^{0}-Ds(t)-a_{1}s(t)x(t)-a_{2}s(t)y(t), \\ \dot{x}(t) = b_{1}s(t)x(t)-Dx(t)-b_{2}x(t)p(t), \\ \dot{y}(t) = c_{1}s(t)y(t)-Dy(t), \\ \dot{p}(t) =\alpha \bigl(c_{1}s(t)y(t)-Dy(t) \bigr)+\beta y(t)-Dp(t)-d_{3}x(t)p(t), \end{cases} $$
(2)

where \(a_{1}\) and \(a_{2}\) are the nutrient uptake rates of the harmful microorganism and the microbial flocculant-producing bacterium, respectively. \(b_{1}\) and \(c_{1}\) are the growth rates of the harmful microorganism and the microbial flocculant-producing bacterium. \(b_{2}\) is the removing rate of the harmful microorganism by the microbial flocculant. In addition, we assume that \(D>0\) and all other parameters are nonnegative.

If \(\beta -D\alpha =d_{3}=0\), model (2) has a similar structural form to model (1). In [32], model (1) has been completely analyzed by reducing the dimension.

As usual, for the convenience of theoretical analysis, model (2) will be first transformed into a dimensionless form. Let

$$\begin{aligned}& s=s^{0}S,\qquad x=X,\qquad y=Y,\qquad p=P, \qquad t=\frac{\bar{t}}{D},\qquad \bar{a}_{1}= \frac{a _{1}}{D}, \qquad \bar{a}_{2}=\frac{{a}_{2}}{D}, \\& \bar{b}_{1}=\frac{{b}_{1}s^{0}}{D},\qquad \bar{b}_{2}= \frac{{b}_{2}}{D},\qquad \bar{c}_{1}=\frac{c_{1}s^{0}}{D},\qquad \bar{\alpha }= \alpha,\qquad \bar{ \beta }=\frac{{\beta }}{D}, \qquad \bar{d}_{3}= \frac{{d}_{3}}{D}. \end{aligned}$$

Model (2) becomes

$$ \textstyle\begin{cases} \dot{S}(t) = 1 -S(t) -a_{1}S(t)X(t) -a_{2}S(t)Y(t), \\ \dot{X}(t) = b_{1}S(t)X(t) -X(t) -b_{2}X(t)P(t), \\ \dot{Y}(t) = c_{1}S(t)Y(t) -Y(t), \\ \dot{P}(t) = d_{1}c_{1}S(t)Y(t) +d_{2}Y(t) -P(t) -d_{3}X(t)P(t). \end{cases} $$
(3)

In model (3), we still use t, \(a_{i}\), \(b_{i}\), \(c_{1}\), α, β, and \(d_{3}\) to denote t̄, \(\bar{a}_{i}\), \(\bar{b}_{i}\), \(\bar{c}_{1}\), ᾱ, β̄, \(i=1,2\), and \(\bar{d}_{3}\), respectively, and let \(d_{1}=\alpha\), \(d_{2}=\bar{ \beta }-\bar{\alpha }\).

Based on biological meanings, the initial condition of model (3) is given as follows:

$$ S(0)=S_{0}\geq 0,\qquad X(0)=X_{0}\geq 0,\qquad Y(0)=Y_{0}\geq 0,\qquad P(0)=P_{0} \geq 0, $$
(4)

where \(S_{0}\), \(X_{0}\), \(Y_{0}\), and \(P_{0}\) denote the initial concentrations of nutrient, harmful microorganism, microbial flocculant-producing bacterium, and the microbial flocculant, respectively.

The remaining part of this paper is organized as follows. In Section 2, global existence, uniqueness, nonnegativity, and boundedness of the solutions of model (3) with the initial condition (4) are investigated. The existence of the equilibria of model (3) and their stability are considered in Section 3. Finally, some numerical simulations and conclusions are given in Section 4.

2 Global existence, uniqueness, nonnegativity, and boundedness of solutions

In this section, the existence, uniqueness, nonnegativity, and boundedness of the solutions of model (3) with the initial condition (4) are studied.

Theorem 2.1

The solution of model (3) with the initial condition (4) is existent, unique, and nonnegative on \([0,\infty)\) and satisfies \(\limsup_{t\rightarrow +\infty }H(t)\leq N(d_{2}+1)\) and \(\liminf_{t\rightarrow +\infty }S(t)\geq Q_{0}\), where \(H(t)=NS(t)+X(t)+(d _{2}+1)Y(t)+P(t)\),

$$N=\frac{b_{1}}{a_{1}}+\frac{c_{1}(d_{1}+d_{2}+1)}{a_{2}},\qquad Q_{0}=\frac{1}{1+N(d _{2}+1)(a_{1}+a_{2})}. $$

Proof

From local existence and uniqueness theorems of solutions [38], we have that the solution \((S(t), X(t), Y(t), P(t))\) of model (3) with the initial condition (4) is existent and unique on \([0,\delta)\) for some constant \(\delta >0\). Furthermore, it is easy to show that the solution \((S(t), X(t), Y(t), P(t))\) is also nonnegative on \([0,\delta)\).

Next, let us show that the solution \((S(t), X(t), Y(t), P(t))\) can be extended to \([0,+\infty)\). Taking derivative of \(H(t)\), it follows that, for \(t\in [0,\delta)\),

$$ \dot{H}(t)\leq N-\frac{H(t)}{d_{2}+1}. $$
(5)

By applying the well-known comparison principle to (5), we have that \(H(t)\) is bounded on \([0, \delta)\). Accordingly, the solution \((S(t), X(t), Y(t), P(t))\) is bounded on \([0, \delta)\). With the aid of the continuation theorem [38], the solution \((S(t), X(t), Y(t), P(t))\) can be extended to \([0,+\infty)\). Furthermore, we can also get that the solution \((S(t), X(t), Y(t), P(t))\) is nonnegative on \([0,+\infty)\).

From (5), it easily follows that \(\limsup_{t\rightarrow +\infty }H(t) \leq N(d_{2}+1)\). Hence, from the first equation of model (3) and \(\limsup_{t\rightarrow +\infty }(X(t)+Y(t))\leq N(d_{2}+1)\), we easily get that \(\liminf_{t\rightarrow +\infty }S(t)\geq Q_{0}\).

The proof is complete. □

Furthermore, we can easily show the following result.

Corollary 2.1

The set \(G= \{U=(S,X,Y,P)\in \mathbb{R}^{+}_{4}: H=NS+X+(d_{2}+1)Y+P \leq N(d_{2}+1), Q_{0} \leq S \leq 1\} \) attracts all of solutions of model (3) and is positively invariant with respect to model (3).

The subsequent discussion will be confined to the closed set G.

3 The existence of equilibria and their stability analysis

3.1 The existence of equilibria

For the existence of the equilibria of model (3), we have the following results.

  1. (a)

    Model (3) always has the boundary equilibrium \(E_{0}=(S _{0},X_{0},Y_{0},P_{0})=(1,0,0,0)\) without harmful microorganism, microbial flocculant-producing bacterium, and microbial flocculant.

  2. (b)

    If \(b_{1}>1\), then model (3) has the second boundary equilibrium \(E_{1}=(S_{1},X_{1},Y_{1},P_{1})=(\frac{1}{b_{1}},\frac{b _{1}-1}{a_{1}},0,0)\) without microbial flocculant-producing bacterium and microbial flocculant.

  3. (c)

    If \(c_{1}>1\), then model (3) has the third boundary equilibrium that is harmful microorganism free equilibrium \(E_{2}=(S _{2},X_{2},Y_{2},P_{2})=(\frac{1}{c_{1}},0,\frac{c_{1}-1}{a_{2}}, \frac{(d _{1}+d_{2})(c_{1}-1)}{a_{2}})\).

  4. (d)

    If \(b_{1}>c_{1}\) and \(b_{2}c_{1}(d_{1}+d_{2})(c_{1}-1)>a_{2}(b _{1}-c_{1})\), then model (3) has a positive equilibrium \(E^{*}=(S^{*},X^{*},Y^{*},P^{*})\), where

    $$\begin{aligned}& S^{*}=\frac{1}{c_{1}},\qquad X^{*}=\frac{b_{2}c_{1}(c_{1}-1)(d_{1}+d_{2})-a _{2}(b_{1}-c_{1})}{a_{1}b_{2}c_{1}(d_{1}+d_{2})+a_{2}d_{3}(b_{1}-c _{1})}, \\& Y^{*}=\frac{P^{*}(1+d_{3}X^{*})}{d_{1}+d_{2}},\qquad P^{*}=\frac{b_{1}-c _{1}}{b_{2}c_{1}}. \end{aligned}$$

Model (3) has the above three boundary equilibria \(E_{0}\), \(E _{1}\), \(E_{2}\) and the positive equilibrium \(E^{*}\). Figure 1 gives existence regions of the equilibria \(E_{0}\), \(E_{1}\), and \(E_{2}\), and \(E^{*}\). In Figure 1, the curve \(l_{0}\) is determined by \(b_{2}c_{1}(d _{1}+d_{2})(c_{1}-1)=a_{2}(b_{1}-c_{1})\).

Figure 1
figure 1

Existence regions of the equilibria in the \(\pmb{c_{1}}\) - \(\pmb{b_{1}}\) plane.

Full size image

The biological meanings of the conditions for the existence of the equilibria will be given in Remarks 3.1, 3.2, 3.3, and 3.4 in Subsection 3.2.

3.2 Stability of the boundary equilibria

Stability of the boundary equilibrium \(E_{0}\) is given as follows.

Theorem 3.1

If \(b_{1}<1\) and \(c_{1}<1\), then the boundary equilibrium \(E_{0}\) is globally asymptotically stable with respect to G.

Proof

By calculating, the characteristic equation at the boundary equilibrium \(E_{0}\) is given by \((\lambda +1)^{2}(\lambda -b_{1}+1)(\lambda -c _{1}+1)=0\). Clearly, the boundary equilibrium \(E_{0}\) is locally asymptotically stable since \(b_{1}<1\) and \(c_{1}<1\). Thus, we only need to show that \(E_{0}\) is globally attractive.

Define a function \(V_{0}\) as follows:

$$V_{0}=X+Y. $$

\(V_{0}\) is continuous on the set \(G(=\bar{G})\). The derivative of \(V_{0}\) along the solutions of model (3) is given by

$$ \dot{V}_{0}= \bigl(b_{1}S(t)-1-b_{2}P(t) \bigr)X(t)+ \bigl(c_{1}S(t)-1 \bigr)Y(t)\leq (b_{1}-1)X(t)+(c _{1}-1)Y(t)\leq 0 $$
(6)

for \(t\geq 0\). Hence, from (6), we have that \(V_{0}\) is a Lyapunov function of model (3) on G. Define \(E=\{(X,S,Y,P)\vert (X,S,Y,P)\in \bar{G}, \dot{V}_{0}=0\}\). Then we have that

$$E \subset \bigl\{ (X,S,Y,P)\vert (X,S,Y,P) \in \bar{G}, X=0, Y=0 \bigr\} . $$

Let M be the largest set in E which is invariant with respect to model (3). Clearly, M is not empty since \(E_{0} \in M\). From the invariance of M and model (3), we can further show that \(M=\{E_{0} \}\). By the LaSalle invariance principle [38], it follows that \(E_{0}\) is globally attractive.

The proof is completed. □

Remark 3.1

The conditions \(b_{1}<1\) and \(c_{1}<1\) in Theorem 3.1 are equivalent to \(b_{1}s^{0}< D\) and \(c_{1}s^{0}< D\) for model (2). From biological points of view, stability of the boundary equilibrium \({E_{0}}=(1,0,0,0)\) indicates that, for the fixed input concentration of nutrient \(s^{0}\), when both the growth rate of harmful microorganism \(b_{1}\) and microbial flocculant-producing bacterium \(c_{1}\) are smaller comparing with the washout rate D, as the time t goes on, the concentrations of harmful microorganism, microbial flocculant-producing bacterium, and microbial flocculant, \(x(t)\), \(y(t)\), and \(p(t)\), tend to zero, and the concentration of nutrient \(s(t)\) tends to some constant value.

Stability of the boundary equilibrium \(E_{1}\) is given as follows.

Theorem 3.2

If \(b_{1}>1\) and \(c_{1}< b_{1}\), then the boundary equilibrium \(E_{1}\) is locally asymptotically stable. In addition, if \(a_{1}>0\), \(b_{2}>0\), and \(b_{2}c_{1}(d_{1}+d_{2})(b_{1}-1) < a_{2}(b_{1}-c_{1})\), then the boundary equilibrium \(E_{1}\) is globally asymptotically stable with respect to \(G_{1}\), where \(G_{1}=\{(S,X,Y,P)\mid (S,X,Y,P)\in G, X>0\}\).

Proof

By calculating, the characteristic equation of model (3) at the boundary equilibrium \(E_{1}\) is given by \((\lambda +1-\frac{c _{1}}{b_{1}} ) (\lambda +1 +\frac{d_{3}(b_{1}-1)}{a_{1}} )( \lambda +1)(\lambda +b_{1}-1)=0\). Clearly, the boundary equilibrium \(E_{1}\) is locally asymptotically stable since \(b_{1}>1\) and \(c_{1}< b_{1}\). Thus, we only need to show that \(E_{1}\) is globally attractive.

Let \(\partial {G_{1}}=\{(S,X,Y,P)\mid (S,X,Y,P)\in G_{1}, XYP=0\}\). We can easily show that \(G_{1}\) is also positively invariant with respect to model (3). Consider a function \(V_{1}\) as follows: \(V_{1}=S-S_{1}-S_{1}\ln \frac{S}{S_{1}}+\frac{a_{1}}{b_{1}}(X-X_{1}-X _{1}\ln \frac{X}{X_{1}}) +\frac{a_{2}+b_{2}d_{2}(b_{1}-1)}{b_{1}}Y + \frac{b _{2}(b_{1}-1)}{b_{1}}P\). \(V_{1}\) is continuous on the set \(G_{1}\) and satisfies condition (ii) of Definition 1.1 in [39] or Lemma 3.1 in [40] on \(\partial G=G\backslash G_{1}\). The derivative of \({V_{1}}\) along the solutions of model (3) is given by

$$\begin{aligned} \dot{V_{1}} = & (S_{1}+a_{1}S_{1}X_{1}) \biggl(2-\frac{S(t)}{S_{1}}-\frac{S _{1}}{S(t)} \biggr) - \biggl( \frac{a_{1}b_{2}}{b_{1}}+\frac{b_{2}d_{3}(b_{1}-1)}{b _{1}} \biggr)X(t)P(t) \\ &{} + \biggl(\frac{b_{2}c_{1}d_{1}(b_{1}-1)}{b_{1}}+\frac{a _{2}c_{1}+b_{2}c_{1}d_{2}(b_{1}-1)}{b_{1}}-a_{2} \biggr)S(t)Y(t) \\ \leq & 0 \end{aligned}$$

for \(t\geq 0\). Thus, \(V_{1}\) is a Lyapunov function on \(G_{1}\) (see, for example, [39, 40]). Define \(E=\{(S,X,Y,P): (S,X,Y,P) \in \bar{G}, \dot{V}_{1}(S,X,Y,P)=0\}\). It is obvious that \(E \subset \{(S,X,Y,P): (S,X,Y,P)\in \bar{G}, S=S_{1}, XP=0, Y=0\}\). Let M be the largest set in E which is invariant with respect to model (3). Hence, we have that

$$M \subset \bigl\{ (S,X,Y,P): (S,X,Y,P)\in \bar{G}, S=S_{1}, XP=0, Y=0 \bigr\} . $$

From the invariance of M and model (3), we can show that \(M=\{E_{1} \}\). Therefore, it follows from Theorem 1.2 in [39] or Lemma 3.1 in [40] that \(E_{1}\) is globally attractive with respect to \(G_{1}\).

The proof is completed. □

Remark 3.2

The conditions \(c_{1}< b_{1}\) and \(b_{1}>1\) in Theorem 3.2 are equivalent to \(c_{1}< b_{1}\) and \(D< b_{1}s^{0}\) for model (2). From biological points of view, stability of the boundary equilibrium \({E_{1}}= (\frac{1}{b_{1}},\frac{b_{1}-1}{a_{1}},0,0)\) implies that, for the fixed input concentration of nutrient \(s^{0}\), when (i) the growth rate of harmful microorganism \(b_{1}\) is larger comparing with the growth rate of microbial flocculant-producing bacterium \(c_{1}\), and (ii) the growth rate of harmful microorganism \(b_{1}\) is larger comparing with the washout rate D, as the time t goes on, the concentrations of microbial flocculant-producing bacterium and microbial flocculant, \(y(t)\) and \(p(t)\), tend to zero, and the concentrations of nutrient and harmful microorganism, \(s(t)\) and \(x(t)\), tend to some constant values.

Stability of the boundary equilibrium \(E_{2}\) is given as follows.

Theorem 3.3

If \(b_{2}c_{1}(d_{1}+d_{2})(c_{1}-1)> a_{2}(b_{1}-c_{1})\) and \(c_{1}>1\), then the boundary equilibrium \(E_{2}\) is locally asymptotically stable. In addition, if \(a_{1}>0\) and \(c_{1}>b_{1}\), then the boundary equilibrium \(E_{2}\) is globally asymptotically stable with respect to \(G_{2}\), where \(G_{2}=\{(S,X,Y,P)\mid (S,X,Y,P)\in G, Y>0\}\).

Proof

The characteristic equation of model (3) at the boundary equilibrium \(E_{2}\) is given by \((\lambda +1) (\lambda +1-\frac{b_{1}}{c_{1}} +\frac{b_{2}(d_{1}+d_{2})(c_{1}-1)}{a_{2}} )(\lambda +1)(\lambda +c _{1}-1)=0\). Clearly, the boundary equilibrium \(E_{2}\) is locally asymptotically stable since \(c_{1}>1\) and \(b_{2}c_{1}(d_{1}+d_{2})(c _{1}-1)> a_{2}(b_{1}-c_{1})\). Thus, we only need to show that the boundary equilibrium \(E_{2}\) is globally attractive.

Let \(\partial {G_{2}}=\{(S,X,Y,P)\mid (S,X,Y,P)\in G_{2}, XYP=0\}\). We can easily show that \(G_{2}\) is also positively invariant with respect to model (3). Consider a function \(V_{2}\) as follows:

$$V_{2}(S,X,Y,P)=S-S_{2}-S_{2}\ln \frac{S}{S_{2}} +\frac{a_{1}}{b_{1}}X+\frac{a _{2}}{c_{1}} \biggl(Y-Y_{2}-Y_{2} \ln \frac{Y}{Y_{2}} \biggr). $$

It is clear that \(V_{2}\) is continuous on the set \(G_{2}\) and satisfies condition (ii) of Definition 1.1 in [39] or Lemma 3.1 in [40] on \(\partial G=G\backslash G_{2}\). The derivative of \(V_{2}\) along the solutions of model (3) is given by

$$\begin{aligned} \dot{V}_{2} = & (S_{2}+a_{2}S_{2}Y_{2}) \biggl(2-\frac{S(t)}{S_{2}}-\frac{S _{2}}{S(t)} \biggr) +\frac{a_{1}}{b_{1}} \biggl( \frac{b_{1}}{c_{1}}-1-b_{2}P(t) \biggr)X(t) \\ \leq & 2-\frac{S(t)}{S_{2}}-\frac{S_{2}}{S(t)} + \frac{a_{1}}{b_{1}} \biggl( \frac{b_{1}}{c_{1}}-1 \biggr)X(t) \\ \leq & 0 \end{aligned}$$
(7)

for \(t\geq 0\). Thus, \(V_{2}\) is a Lyapunov function on \(G_{2}\) (see, for example, [39, 40]). Define \(E=\{(S,X,Y,P): (S,X,Y,P) \in \bar{G}, \dot{V}_{2}(S,X,Y,P)=0 \}\). It is obvious that \(E \subset \{(S,X,Y,P): (S,X,Y,P)\in \bar{G}, S=S_{2}, X=0\}\). Let M be the largest set in E which is invariant with respect to model (3). Hence, we have that

$$M \subset \bigl\{ (S,X,Y,P): (S,X,Y,P)\in \bar{G}, S=S_{2}, X=0 \bigr\} . $$

From the invariance of M and model (3), we can show that \(M=\{E_{2} \}\). Therefore, it follows from Theorem 1.2 in [39] or Lemma 3.1 in [40] that \(E_{2}\) is globally attractive with respect to \(G_{2}\).

The proof is completed. □

Remark 3.3

The conditions \(b_{2}c_{1}(d_{1}+d_{2})(c_{1}-1) > a_{2}(b_{1}-c_{1})\) and \(c_{1}>1\) in Theorem 3.3 are equivalent to \(b_{2}c_{1} \beta (c_{1}s^{0}-D) > D^{2}a_{2}(b_{1}-c_{1})\) and \(c_{1}s^{0}>D\) for model (2). From biological points of view, stability of the boundary equilibrium \({E_{2}}=(\frac{1}{c_{1}},0, \frac{c_{1}-1}{a_{2}},\frac{(d_{1}+d_{2})(c_{1}-1)}{a_{2}})\) indicates that, for the fixed input concentration of nutrient \(s^{0}\), when (i) the growth rate of microbial flocculant-producing bacterium \(c_{1}\) or the removing rate of microbial flocculant-producing bacterium \(b_{2}\) is larger comparing with the washout rate D, and (ii) the growth rate of harmful microorganism \(b_{1}\) is sufficiently small, as the time t goes on, the concentration of harmful microorganism \(x(t)\) tends to zero (i.e., harmful microorganism can be removed successfully), and the concentrations of nutrient, microbial flocculant-producing bacterium, and microbial flocculant, \(s(t)\), \(y(t)\), and \(p(t)\), tend to some constant values.

3.3 Stability of the positive equilibrium

For stability of the positive equilibrium \(E^{*}\), we have the following result.

Theorem 3.4

If \(b_{1}>c_{1}\) and \(b_{2}c_{1}(d_{1}+d_{2})(c_{1}-1)>a_{2}(b_{1}-c _{1})\), then the positive equilibrium \(E^{*}\) is unstable.

Proof

The characteristic equation of model (3) at the positive equilibrium \(E^{*}\) is given by \(\text{ }F ( \lambda) = \lambda^{4}+A\lambda^{3} +B\lambda^{2}+C\lambda +D=0\), where

$$\begin{aligned}& A= 1+c_{1}+d_{3}X^{*}, \\& B= c_{1}+a_{1}b_{1}S^{*}X^{*}+a_{2}Y^{*}+c_{1}d_{3}X^{*}-b_{2}d _{3}P^{*}X^{*}, \\& C= a_{1}b_{1}S^{*}X^{*}+a_{2}Y^{*}+a_{1}b_{1}d_{3}S^{*}{X^{*}}^{2}-b _{2}c_{1}d_{3}P^{*}X^{*}+a_{2}d_{3}X^{*}Y^{*} \\& \hphantom{C=}{}-a_{1}b_{2}d_{1}X^{*}Y^{*}, \\& D= -a_{1}b_{2}(d_{1}+d_{2})X^{*}Y^{*}-a_{2}b_{2}d_{3}X^{*}Y^{*}P ^{*}. \end{aligned}$$

It is easy to know that the above characteristic equation has at least one positive real root since \(D<0\). Therefore, the positive equilibrium \(E^{*}\) is unstable.

The proof is completed. □

Remark 3.4

Instability of the positive equilibrium \(E^{*}\) in Theorem 3.4 indicates that, under certain conditions, the evolution among nutrient, harmful microorganism, microbial flocculant-producing bacterium, and microbial flocculant may become more complicated. Whether or not harmful microorganism can be removed will depend on the initial state \((S_{0},X_{0},Y_{0},P_{0})\).

4 Numerical simulations and discussions

4.1 Numerical simulations

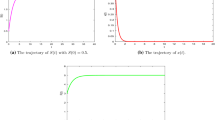
In Section 3, stability of the equilibria of model (3) is analyzed. From Theorem 3.1, we have that the boundary equilibrium \(E_{0}\) is globally asymptotically stable when \(b_{1}<1\) and \(c_{1}<1\), and Figure 2 gives the corresponding numerical simulation. From Theorem 3.2, we have that the boundary equilibrium \(E_{1}\) is locally asymptotically stable when \(c_{1}< b_{1}\) and \(b_{1}>1\), and Figure 3 gives the corresponding numerical simulation. From Theorem 3.3, we have that the boundary equilibrium \(E _{2}\) is locally asymptotically stable when \(b_{2}c_{1}(d_{1}+d_{2})(c _{1}-1) > a_{2}(b_{1}-c_{1})\) and \(c_{1}>1\), and Figure 4 gives the corresponding numerical simulation. From Theorem 3.4, we have that the positive equilibrium \(E^{*}\) is always unstable when it exists, i.e., \(b_{1}>c_{1}\) and \(b_{2}c_{1}(d_{1}+d_{2})(c_{1}-1)>a_{2}(b_{1}-c _{1})\). Furthermore, we have from Theorems 3.2 and 3.3 that, in the existence region of the positive equilibrium \(E ^{*}\), both the boundary equilibrium \(E_{1}\) and the boundary equilibrium \(E_{2}\) are asymptotically stable, i.e., the region is a bistable region. Figure 5 gives the corresponding numerical simulation. The local asymptotic stability regions of all the equilibria are shown in Figure 6, where the curve \(l_{1}\) is determined by \(b_{2}c_{1}(d _{1}+d_{2})(c_{1}-1)=a_{2}(b_{1}-c_{1})\).

Figure 2
figure 2

The boundary equilibrium \(\pmb{E_{0}}\) is asymptotically stable with the parameters \(\pmb{a_{1}=1}\) , \(\pmb{a_{2}=1}\) , \(\pmb{b_{1}=0.9}\) , \(\pmb{b_{2}=1}\) , \(\pmb{c_{1}=0.9}\) , \(\pmb{d_{1}=1}\) , \(\pmb{d_{2}=1}\) and \(\pmb{d_{3}=1}\) .

Full size image
Figure 3
figure 3

The boundary equilibrium \(\pmb{E_{1}}\) is locally asymptotically stable with the parameters \(\pmb{a_{1}=1}\) , \(\pmb{a_{2}=1}\) , \(\pmb{b_{1}=1.5}\) , \(\pmb{b_{2}=1}\) , \(\pmb{c_{1}=0.7}\) , \(\pmb{d_{1}=1}\) , \(\pmb{d_{2}=1 }\) and \(\pmb{d_{3}=1}\) .

Full size image
Figure 4
figure 4

The boundary equilibrium \(\pmb{E_{2}}\) is locally asymptotically stable with the parameters \(\pmb{a_{1}=1}\) , \(\pmb{a_{2}=1}\) , \(\pmb{b_{1}=2}\) , \(\pmb{b_{2}=2}\) , \(\pmb{c_{1}=1.2}\) , \(\pmb{d_{1}=1}\) , \(\pmb{d_{2}=1 }\) and \(\pmb{d_{3}=1}\) .

Full size image
Figure 5
figure 5

The positive equilibrium \(\pmb{E^{*}}\) is unstable, and both the boundary equilibrium \(\pmb{E_{1}}\) and the boundary equilibrium \(\pmb{E_{2}}\) are locally asymptotically stable with the parameters \(\pmb{a_{1}=1}\) , \(\pmb{a_{2}=1}\) , \(\pmb{b_{1}=2}\) , \(\pmb{b_{2}=1}\) , \(\pmb{c_{1}=1.5}\) , \(\pmb{d_{1}=1}\) , \(\pmb{d_{2}=1 }\) and \(\pmb{d_{3}=1}\) .

Full size image
Figure 6
figure 6

The local asymptotic stability regions of the equilibria in the \(\pmb{c_{1}}\) - \(\pmb{b_{1}}\) plane.

Full size image

Furthermore, from Theorems 3.2 and 3.3, we have that, in order to ensure global asymptotic stability of the boundary equilibria \(E_{1}\) and \(E_{2}\), additional conditions \(b_{2}c_{1}(d _{1}+d_{2})(b_{1}-1) < a_{2}(b_{1}-c_{1})\) and \(c_{1}>b_{1}\) are assumed, respectively. The global asymptotic stability regions of the boundary equilibria \(E_{1}\) and \(E_{2}\) are shown in Figures 7 and 8. The curve \(l_{2}\) is determined by \(b_{2}c_{1}(d_{1}+d_{2})(b_{1}-1)=a _{2}(b_{1}-c_{1})\) for \(b_{2}(d_{1}+d_{2})< a_{2}\), and the curve \(l_{3}\) is also determined by \(b_{2}c_{1}(d_{1}+d_{2})(b_{1}-1)=a_{2}(b _{1}-c_{1})\) for \(b_{2}(d_{1}+d_{2})> a_{2}\).

Figure 7
figure 7

The global asymptotic stability regions of the boundary equilibria \(\pmb{E_{1}}\) and \(\pmb{E_{2}}\) ( \(\pmb{b_{2}(d_{1}+d_{2})> a_{2}}\) ) in the \(\pmb{c_{1}}\) - \(\pmb{b_{1}}\) plane.

Full size image
Figure 8
figure 8

The global asymptotic stability regions of the boundary equilibria \(\pmb{E_{1}}\) and \(\pmb{E_{2}}\) ( \(\pmb{b_{2}(d_{1}+d_{2})< a_{2}}\) ) in the \(\pmb{c_{1}}\) - \(\pmb{b_{1}}\) plane.

Full size image

However, the numerical simulations strongly suggest that, in the regions \(D_{1}\) and \(D_{2}\) in Figures 7 and 8, respectively, the boundary equilibrium \(E_{1}\) should also be globally asymptotically stable.

4.2 Discussions

Firstly, it should be pointed out that we cannot get global asymptotic stability of the boundary equilibrium \(E_{1}\) in the regions \(D_{1}\) and \(D_{2}\) in Figures 7 and 8 because of the difficulties in constructing suitable Lyapunov functions.

Secondly, in biology, when model (3) is applied to some wastewater treatment, and the state variable \(x(t)\) represents harmful microorganism to be removed, the local/global asymptotic stability of the boundary equilibrium \(E_{1}=(S_{1},X_{1},Y_{1},P_{1})=\) \((\frac{1}{b_{1}},\frac{b_{1}-1}{a_{1}},0,0)\) in Theorem 3.2 implies that harmful microorganism cannot be removed by using the microbial flocculant because of insufficiency of the growth of microbial flocculant-producing bacterium and microbial flocculant.

On the other hand, the local/global asymptotic stability of the boundary equilibrium \(E_{2}=(S_{2},X_{2},Y_{2},P_{2})=\) \((\frac{1}{c_{1}},0,\frac{c _{1}-1}{a_{2}}, \frac{(d_{1}+d_{2})(c_{1}-1)}{a_{2}})\) in Theorem 3.3 implies that harmful microorganism can be removed successfully by using microbial flocculant under suitable assumptions. Hence, Theorem 3.3 gives some feasible strategy to control harmful microorganism in applications. However, from Theorem 3.4, we have that the positive equilibrium \(E^{*}\) is always unstable if it exists, and there exists a bistable region (i.e., both the boundary equilibrium \(E_{1}\) and the boundary equilibrium \(E_{2}\) are asymptotically stable). Thus, Theorem 3.4 implies that the controlling of harmful microorganism will become more complicated, and the initial value \((S_{0},X_{0},Y_{0},P_{0})\) will play an important role.

Finally, model (2) can be also considered as a class of chemostat competition models. It is well known that the general chemostat competition models have been studied systematically [15] and ‘competitive exclusion principle’ holds in general chemostat competition models [41–44]. The so-called competitive exclusion principle refers to the phenomenon that different species compete in a shortage of resources, making a species excluded or replaced in competition. In 1980, Hansen and Hubbel [43] observed the competitive exclusion principle in the biological chemostat experiments. Some important research shows that, if inhibitors are considered (for example, model (1)), the competition results may be changed [32]. In model (2), microbial flocculant-producing bacterium and microbial flocculant are considered and Theorems 3.2 and 3.3 show similar properties.