Robustness of proper dynamic output feedback for discrete-time singularly perturbed systems

Abstract

In this paper, the dynamic output feedback control problem of discrete-time singularly perturbed systems is considered based on the reduced-order technique. We first show that a proper but not strictly proper dynamic output feedback controller designed for the reduced-order model generally is not a stabilizing compensator for the original system, even though the fast subsystem is stable. To obtain the robustness of the dynamic output feedback controller, an auxiliary system is designed. Based on this, the design of the dynamic output feedback for the reduced-order subsystem is reduced to the simultaneous design of a static output feedback controller for the fast subsystem and a strictly proper dynamic output feedback controller for the auxiliary system, respectively. Based on the obtained results, we confirm that it is possible to generate the robustness for the proposed dynamic output feedback control. Thus, the restriction on the strict properness can be alleviated. Finally, a realistic practical example for the nuclear reactor model is provided to show the effectiveness of the obtained theoretical results.

1 Introduction

The problem of controller design for singularly perturbed systems has attracted the attention of many researchers for many years [1–4]. A common method adopted to deal with such systems is based on the two-time-scale decomposition technique, which can effectively alleviate the ill condition and high dimensionality resulting from the interaction of slow and fast subsystems [1]. Due to the great development of information technique, the design of the feedback controller for discrete-time singularly perturbed systems has been investigated by many studies, and some important results have also been obtained despite being in much fewer numbers than the continuous case [5–15].

In the past years, the linear matrix inequality (LMI) technique has been widely proposed to solve control problems [16]. In contrast to the Riccati approach, the LMIs that arise in a system and control theory can be formulated as convex optimization problems that are amenable to compute a solution and can be solved effectively. Another advantage of the LMI is the ability to add constraints to the parametrical optimization problem provided they are linear with respect to unknowns. Recently, many important results for discrete-time singularly perturbed systems have been obtained by using the LMI technique [17–22]. It is shown in [19] and [20] that an LMI approach has been proposed to solve the $H _{\infty }$ control problems for the discrete-time singularly perturbed systems. However, some inequalities were used in the derivation of solvability conditions, which would lead to some conservatism. For this, references [21] and [22] present new LMI sufficient conditions to improve the results.

On the other hand, it can be seen that most of the above results are based on the state feedback. However, in most practical control systems, not all the state variables are directly measurable. In this case, it is necessary to design an output feedback controller. In general, the output feedback control is addressed by the following ways: static output feedback, observer-based output feedback and dynamic output feedback. Compared with the first two cases, the dynamic output feedback is more effective to improve the closed-loop transient response. However, in exchange, the design of the dynamic output feedback controller is more complex and difficult. Thus, there are few works reported on this topic [23–27]. It is shown in [27] that the dynamic output feedback controller designed for the slow subsystems and the fast subsystems must be strictly proper. Otherwise, a proper dynamic output feedback may destabilize the stable boundary system unless the system has a particular structure. Moreover, only the theoretical results are given in [23–26], how to search an effective approach to solve the gain matrices of the dynamic output feedback controller has not been discussed. Therefore, when revisiting this problem, we find that there is still much room left for improvement, which motivates the present study.

In this paper, we focus on the problem of designing a proper but not strictly proper dynamic output feedback controller for a class of fast sampling discrete-time singularly perturbed systems using the reduced-order model. By constructing an auxiliary system for the slow subsystem, the design of the dynamic output feedback controller for the slow subsystem is reduced to the simultaneous design of the static output feedback controller for the fast subsystem and the strictly proper dynamic output feedback controller for the auxiliary system, respectively. Thus, asymptotic stability of the resulting closed-loop system is guaranteed when the perturbation parameter is sufficiently small. Finally, a realistic practical example for the nuclear reactor model is provided to illustrate the derived results. Compared with the existing results, the developed method in this paper has the following advantages: (1) the proposed method links the reduced technique and the LMI together, which not only alleviates the high dimensionality and ill condition resulting from the interaction of slow and fast dynamics models, but also avoids the regularity restrictions attached to the Riccati-based solutions; (2) the developed results show that the proposed sufficient condition has alleviated the requirement on the strict properness; (3) the presented condition can be easily verified because it only depends on the solution of a linear matrix inequality.

Notation: Throughout this paper the superscripts ‘T’ and ‘−1’ stand for the transpose of a matrix and the inverse of a matrix, respectively; the notation $P > 0$ (or $P \ge 0$) means that P is symmetric and positive definite (or semi-positive definite); $\lambda (A)$ stands for the eigenvalues of the matrix A; I denotes the identity matrix with appropriate dimensions; $\operatorname{Re} ( \cdot )$ denotes the real part of a complex number.

2 Problem formulation

In this paper, we are concerned with the dynamic output feedback problem for the following discrete-time singularly perturbed system:

$$\begin{aligned}& x_{1}(k + 1) = (I + \varepsilon A_{11})x_{1}(k) + \varepsilon A_{12}x _{2}(k) + \varepsilon B_{1}u(k), \end{aligned}$$

(1a)

$$\begin{aligned}& x_{2}(k + 1) = A_{21}x_{1}(k) + A_{22}x_{2}(k) + B_{2}u(k), \end{aligned}$$

(1b)

$$\begin{aligned}& y(k) = C_{1}x_{1}(k) + C_{2}x_{2}(k), \end{aligned}$$

(2)

where $x_{1} \in R^{n_{1}}$ and $x_{2} \in R^{n_{2}}$ ($n_{1} + n _{2} = n$) denote the state vectors of the slow and fast dynamics, respectively; $u \in R^{q}$ is the control input; $y \in R^{p}$ is the output; the small parameter $\varepsilon > 0$ is positive; all matrices in system (1)-(2) are constant matrices with appropriate dimensions. It is shown in [6] that this model can be obtained by the discrete-time analogue for a continuous system under the fast sampling rate.

As a precondition for implementing the two-time-scale technique, we first give the following assumption for system (1)-(2).

Assumption 1

$I - A_{22}$ is invertible.

Noticing the two-time-scale property of (1), the slow and fast subsystems for (1) can be decomposed by the reduced technique in [6]:

$$\begin{aligned}& \dot{x}_{s}(t) = A_{s}x_{s}(t) + B_{s}u_{s}(t), \quad x_{s}(0) = x_{10}, \end{aligned}$$

(3a)

$$\begin{aligned}& y_{s}(t) = C_{s}x_{s}(t) + D_{s}u_{s}(t), \end{aligned}$$

(3b)

$$\begin{aligned}& \bar{x}_{2}(t) = (I - A_{22})^{ - 1} \bigl(A_{21}x_{s}(t) + B_{s}u_{s}(t) \bigr), \end{aligned}$$

(4)

and

$$\begin{aligned}& x_{f}(k + 1) = A_{22}x_{f}(k) + B_{2}u_{f}(k), \quad x_{f}(0) = x_{20} - \bar{x}_{2}(0), \end{aligned}$$

(5a)

$$\begin{aligned}& y_{f}(k) = C_{2}x_{f}(k), \end{aligned}$$

(5b)

where

$$\begin{aligned}& A_{s} = A_{11} + A_{12}(I - A_{22})^{ - 1}A_{21}, \qquad B_{s} = B_{1} + A_{12}(I - A_{22})^{ - 1}B_{2}, \\& C_{s} = C_{1} + C_{2}(I - A_{22})^{ - 1}A_{21}, \qquad D_{s} = C_{2}(I - A_{22})^{ - 1}B_{2}. \end{aligned}$$

Remark 1

This hybrid state arises from the definition of the slow and fast subsystems, where the evolution of continuous-time slow subsystems is justified although there is little else which is surprising in the theory. A more detailed description can be found in [5] and [6].

Since (3) is only an approximate model of system (1), can a dynamic output feedback designed for the reduced-order subsystem stabilize the original full-order system? Next, we will address this problem.

We consider the following dynamic output feedback controller for reduced-order subsystem (3):

$$ \dot{\zeta } (t) = M\zeta (t) + Ny_{s}(t), \qquad u_{s}(t) = G\zeta (t) + Hy_{s}(t), $$

(6)

where $\zeta (t) \in R^{n_{1}}$ is the controller state. M, N, G and H are unknown constant matrices to be determined. Because (3b) has a direct transmission item, it is required that $I - D_{s}H$ is invertible. Thus, this guarantees that $y_{s}$ can be determined uniquely. Submitting this controller to the reduced-order subsystem (3) gives the following closed-loop system:

$$\left(\begin{array}{c}{\dot{x}}_s(t)\\ \dot{\zeta }(t)\end{array}\right)={\mathrm{\Lambda }}_s\left(\begin{array}{c}{x}_s(t)\\ \zeta (t)\end{array}\right),$$

(7)

where

$${\mathrm{\Lambda }}_s=\left(\begin{array}{cc}{A}_s+B_{s}H{(I-D_{s}H)}^{-1}{C}_s& B_{s}G+B_{s}H{(I-D_{s}H)}^{-1}{D}_{s}G\\ N{(I-D_{s}H)}^{-1}{C}_s& M+N{(I-D_{s}H)}^{-1}{D}_{s}G\end{array}\right)\left(\begin{array}{c}{x}_s(t)\\ \zeta (t)\end{array}\right).$$

By applying a discrete version of the dynamic output feedback (6)

$$ u(k) = G\xi (k) + Hy(k), $$

(8)

where $\xi (k) \in R^{n_{1}}$, the controller state is defined by

$$ \xi (k + 1) = (I + \varepsilon M)\xi (k) + \varepsilon Ny(k), $$

(9)

the actual closed-loop system of (1) can be obtained as

$$\left(\begin{array}{c}v(k+1)\\ x_2(k+1)\end{array}\right)=\mathrm{\Gamma }\left(\begin{array}{c}v(k)\\ x_2(k)\end{array}\right)=\left(\begin{array}{cc}I+\epsilon {\mathrm{\Gamma }}_{11}& \epsilon {\mathrm{\Gamma }}_{12}\\ {\mathrm{\Gamma }}_{21}& {\mathrm{\Gamma }}_{22}\end{array}\right)\left(\begin{array}{c}v(k)\\ x_2(k)\end{array}\right),$$

(10)

where

$$\begin{array}{c}v=\left(\begin{array}{c}{x}_1\\ \xi \end{array}\right),{\mathrm{\Gamma }}_{11}=\left(\begin{array}{cc}{A}_{11}+B_{1}H{C}_1& B_{1}G\\ N{C}_1& M\end{array}\right),{\mathrm{\Gamma }}_{12}=\left(\begin{array}{c}{A}_{12}+B_{1}H{C}_2\\ N{C}_2\end{array}\right),\hfill \\ {\mathrm{\Gamma }}_{21}=\left(\begin{array}{cc}{A}_{21}+B_{2}H{C}_1& B_{2}G\end{array}\right),{\mathrm{\Gamma }}_{22}=A_{22}+B_{2}H{C}_2.\hfill \end{array}$$

In order to show the relation between systems (7) and (10), using the nonsingular transformation [8], the slow and fast parts of closed-loop system (10) can be separated by defining

$$\left(\begin{array}{c}\sigma (k)\\ \tau (k)\end{array}\right)=T\left(\begin{array}{c}v(k)\\ x_2(k)\end{array}\right),T=\left(\begin{array}{cc}{I}_{2n_1}+\epsilon HR& \epsilon H\\ R& I_{n_2}\end{array}\right),T^{-1}=\left(\begin{array}{cc}{I}_{2n_1}& -\epsilon H\\ -R& I_{n_2}+\epsilon RH\end{array}\right),$$

where

$$ R = - (I - \Gamma_{22})^{ - 1}\Gamma_{21} + O( \varepsilon ), \qquad H = \Gamma_{12}(I - \Gamma_{22})^{ - 1} + O(\varepsilon ). $$

(11)

This results in

$$\left(\begin{array}{c}\sigma (k+1)\\ \tau (k+1)\end{array}\right)=\left(\begin{array}{cc}I+\epsilon E_s& O\\ O& E_f\end{array}\right)\left(\begin{array}{c}\sigma (k)\\ \tau (k)\end{array}\right),$$

(12)

where

$$\begin{aligned}& E_{s} = \Gamma_{11} - \Gamma_{12}R = \Gamma_{11} + \Gamma_{12}(I - \Gamma_{22})^{ - 1} \Gamma_{21} + O(\varepsilon ), \end{aligned}$$

(13)

$$\begin{aligned}& E_{f} = \Gamma_{22} + \varepsilon R\Gamma_{12} = \Gamma_{22} + O( \varepsilon ) = A_{22} + B_{2}HC_{2} + O(\varepsilon ). \end{aligned}$$

(14)

It can be seen from (11) that the nonsingularity of the matrix $I - \Gamma_{22}$ is needed. Next, let us verify that $I - \Gamma_{22}$ is nonsingular. Use of the identity

$$ (I - A_{22} - B_{2}HC_{2}) (I - \Gamma_{22})^{ - 1} = I $$

yields

$$ (I - \Gamma_{22})^{ - 1} = (I - A_{22})^{ - 1} \bigl[I + B_{2}HC_{2}(I - \Gamma_{22})^{ - 1} \bigr]. $$

(15)

Rearranging (15), we have

$$ (I - A_{22})^{ - 1} = \bigl[I - (I - A_{22})^{ - 1}B_{2}HC_{2} \bigr](I - \Gamma _{22})^{ - 1}, $$

so that

$$ C_{2}(I - A_{22})^{ - 1} = [I - D_{s}H]C_{2}(I - \Gamma_{22})^{ - 1}. $$

(16)

Pre-multiplication of both sides of (16) by $(I - D_{s}H)^{ - 1}$ results in

$$ (I - D_{s}H)^{ - 1}C_{2}(I - A_{22})^{ - 1} = C_{2}(I - \Gamma_{22})^{ - 1}. $$

(17)

Hence, substituting (17) into (15), we have

$$ (I - \Gamma_{22})^{ - 1} = (I - A_{22})^{ - 1} \bigl[I + B_{2}(I - D_{s}H)^{ - 1}C_{2}(I - A_{22})^{ - 1}\bigr]. $$

Thus, (13) is well defined.

Similarly, for $E_{s}$, it can be shown after lengthy manipulation that

$$ E_{s} = \Gamma_{11} + \Gamma_{12}(I - \Gamma_{22})^{ - 1}\Gamma_{21} + O(\varepsilon )= \Lambda_{s} + O(\varepsilon ). $$

(18)

Then the asymptotic stability of closed-loop system (10) requires that the following conditions hold:

$$ (1) \quad \operatorname{Re} \bigl\{ \lambda (E_{s})\bigr\} < 0,\quad \quad (2) \quad \bigl\vert \lambda (E_{f})\bigr\vert < 1. $$

(19)

From inequality (18), it is easy to see that condition (1) can be satisfied if closed-loop system (7) is asymptotically stable. However, condition (2) cannot be generally guaranteed even if the matrix $A_{22}$ is stable, unless one of the following conditions is satisfied:

• i. $\vert \lambda (A_{22})\vert < 1$, $B_{2} = 0$ or $\vert \lambda (A_{22})\vert < 1$, $C_{2} = 0$, i.e., the asymptotically stable fast subsystem is either not directly fed from the input or not directly sensed at the output.

• ii. $\vert \lambda (A_{22})\vert < 1$, $H = 0$, i.e., the output feedback control (8)-(9) does not have a static output feedback.

• iii. ($A_{22}$, $B_{2}$) is controllable and $C_{2}$ is full-rank.

For the first two cases, the results show that the dynamic output feedback designed for the reduced-order system is strictly proper or the system has a particular structure. For the third case, the proposed condition is general; however, only the theoretical result is given, the design of gain matrices has not been discussed in [23–26]. How to design these parameters is very important. Next, we will investigate a non-strictly proper dynamic output feedback controller for system (1)-(2).

3 Main results

Consider the following auxiliary system:

$$ \dot{\tilde{x}}_{s} = \tilde{A}_{s}\tilde{x}_{s} + \tilde{B}_{s} \tilde{u}_{s}, \qquad \tilde{y}_{s} = \tilde{C}_{s}\tilde{x}_{s} + \tilde{D}_{s} \tilde{u} _{s}, $$

(20)

where

$$\begin{aligned}& \tilde{A}_{s} = A_{s} + B_{s}H(I - D_{s}H)^{ - 1}C_{s},\qquad \tilde{B}_{s} = B_{s} + B_{s}H(I - D_{s}H)^{ - 1}D_{s}, \\& \tilde{C}_{s} = (I - D_{s}H)^{ - 1}C_{s}, \qquad \tilde{D}_{s} = (I - D _{s}H)^{ - 1}D_{s}. \end{aligned}$$

It is easy to see that the design of the proper dynamic output feedback controller for reduced-order system (3)-(4) is equivalent to the strictly proper one for auxiliary system (19) with the following form:

$$ \dot{\tilde{\zeta }} (t) = M\tilde{\zeta } (t) + N \tilde{y}_{s}(t), \qquad \tilde{u}_{s}(t) = G\tilde{\zeta } (t), $$

(21)

where M, N and G are defined in (6).

Combining (19) and (20), we can see that the robustness problem considered here is to find some sufficient conditions such that the static output feedback gain matrix H and the strictly proper dynamic output feedback gain matrices M, N and G can assign the desired stable poles to the auxiliary systems and fast subsystem (5)-(6), respectively.

For the static output feedback of fast subsystem (5)-(6), using the pole-assignment technique, the gain matrix H can be designed to place $\min (n_{ 1},p)$ eigenvalues arbitrarily close to their desired locations [10]. In fact, there are a lot of existing works addressing this problem, and various methods have been proposed, e.g., Riccati equation approach, rank-constrained condition, approach based on structural properties, bilinear matrix inequality (BMI) approaches, min-max optimization techniques, and linear matrix inequality approaches [28, 29]. Among them, the LMI approaches are much more efficient in dealing with synthesis problems [30–32], thus many results have also been obtained. In addition, the survey on the development of static output feedback can be found in [33].

For the strictly proper dynamic output feedback design of auxiliary system (20), a sufficient and necessary condition in terms of LMIs is given in the following theorem.

Theorem 1

Consider auxiliary system (20). There exists a strictly proper dynamic output feedback in the form of (21) such that the resulting closed system is asymptotically stable if and only if there exist matrices $X > 0$, $Y > 0$, Φ and Ψ satisfying the following LMIs:

$$\left(\begin{array}{cc}X& I\\ I& Y\end{array}\right)\ge 0,$$

(22)

$$\begin{aligned}& \tilde{A}_{s}^{T}X + X^{T}\tilde{A}_{s} + \Phi \tilde{C}_{s} + \tilde{C}_{s}^{T} \Phi^{T} < 0, \end{aligned}$$

(23)

$$\begin{aligned}& \tilde{A}_{s}Y + Y^{T}\tilde{A}_{s}^{T} - \tilde{B}_{s}\Psi - \Psi ^{T}\tilde{B}_{s}^{T} < 0. \end{aligned}$$

(24)

If (22)-(24) hold, then the dynamic output feedback controller gain matrices in (21) can be chosen as

$$ \begin{gathered} M = \bigl(X - Y^{ - 1}\bigr)^{ - T}\bigl(\tilde{A}_{s}^{T}Y^{ - 1} + X^{T}\tilde{A} _{s} - X^{T}\tilde{B}_{s} \Psi Y^{ - 1} + \Phi \tilde{C}_{s} - \Phi \tilde{D}_{s} \Psi Y^{ - 1}\bigr), \\ N = \bigl(Y^{ - 1} - X\bigr)^{ - T}\Phi , \qquad G = - \Psi Y^{ - 1}. \end{gathered} $$

(25)

Proof

(Sufficiency) When (22)-(24) is satisfied, we first show that there exist matrices X, Y, Φ and Ψ such that $Y^{ - 1} - X$ is nonsingular. In fact, if $Y^{ - 1} - X$ is singular, then we can choose any positive definite matrix X̄ and let $\theta \in (0,1)$ satisfying that θ is not an eigenvalue of $(Y^{ - 1} - X)\bar{X}^{ - 1}$ and is small enough such that X is replaced by $X + \theta \bar{X}$, the inequality in (22)-(24) still holds. Then it is not difficult to see that $X + \theta \bar{X} - Y ^{ - 1}$ is nonsingular. Applying the dynamic output feedback controller with the parameters given in (25), we obtain the following closed-loop system:

$$\left(\begin{array}{c}{\dot{x}}_s(t)\\ \dot{\zeta }(t)\end{array}\right)=\left(\begin{array}{cc}{\tilde{A}}_s& -{\tilde{B}}_s\mathrm{\Psi }{Y}^{-1}\\ {(Y^{-1}-X)}^{-T}\mathrm{\Phi }{\tilde{C}}_s& \mathrm{\Xi }\end{array}\right)\left(\begin{array}{c}{x}_s(t)\\ \zeta (t)\end{array}\right),$$

(26)

where $\Xi = (X - Y^{ - 1})^{ - T}(\tilde{A}_{s}^{T}Y^{ - 1} + X^{T} \tilde{A}_{s} - X^{T}\tilde{B}_{s}\Psi Y^{ - 1} + \Phi \tilde{C}_{s})$. Set

$$P_s=\left(\begin{array}{cc}X& Y^{-1}-X\\ Y^{-1}-X& X-Y^{-1}\end{array}\right).$$

Considering that $X - (Y^{ - 1} - X)(X - Y^{ - 1})^{ - 1}(Y^{ - 1} - X) = X + Y^{ - 1} - X > 0$. According to the Schur complement lemma, one has $P_{s} > 0$. Furthermore, after some algebraic operations, it can be verified

$${\mathrm{\Lambda }}_s^T{P}_s+P_s^T{\mathrm{\Lambda }}_s=\left(\begin{array}{cc}{\mathrm{\Delta }}_{11}& -{\mathrm{\Delta }}_{11}\\ -{\mathrm{\Delta }}_{11}& {\mathrm{\Delta }}_{22}\end{array}\right),$$

where

$$\begin{aligned}& \Delta_{11} = \tilde{A}_{s}^{T}X + X^{T}\tilde{A}_{s} + \Phi \tilde{C}_{s} + \tilde{C}_{s}^{T}\Phi^{T}, \\& \Delta_{22} = \Delta_{11} + \tilde{A}_{s}^{T}Y^{ - 1} + Y^{ - T} \tilde{A}_{s} - Y^{ - T}\bigl( \tilde{B}_{s}\Psi + \Psi^{T}\tilde{B}_{s} ^{T}\bigr)Y^{ - 1}. \end{aligned}$$

Pre- and post-multiplying both sides of (24) with $Y^{ - T}$ and $Y^{ - 1}$, we get

$$ \tilde{A}_{s}^{T}Y^{ - 1} + Y^{ - T} \tilde{A}_{s} - Y^{ - T}\bigl( \tilde{B}_{s}\Psi + \Psi^{T}\tilde{B}_{s}^{T}\bigr)Y^{ - 1} < 0. $$

It follows from (23) that $\Delta_{22} < 0$. Noticing $\Delta_{11} < 0$, $\Delta_{22} - \Delta_{11} < 0$, and using the Schur complement lemma again, we obtain

$$\left(\begin{array}{cc}{\mathrm{\Delta }}_{11}& -{\mathrm{\Delta }}_{11}\\ -{\mathrm{\Delta }}_{11}& {\mathrm{\Delta }}_{22}\end{array}\right)<0.$$

Thus, $\Lambda_{s}^{T}P_{s} + P_{s}^{T}\Lambda_{s} < 0$. That is, closed-loop system (20) is asymptotically stable.

(Necessity) Suppose that there exists a dynamic output feedback controller in (21) such that closed-loop system (20) is asymptotically stable. Then there exists a positive definite matrix $Q_{s} > 0$ such that

$$ \Lambda_{s}^{T}Q_{s} + Q_{s}^{T} \Lambda_{s} < 0. $$

(27)

Denote

$$Q_s=\left(\begin{array}{cc}{Q}_{s1}& Q_{s2}\\ Q_{s3}& Q_{s4}\end{array}\right).$$

Then it is easy to see that $Q_{s1} > 0$, $Q_{s2} > 0$ and $\Pi = Q _{s1} - Q_{s2}Q_{s4}^{ - 1}Q_{s3} > 0$. By the 1-1 block of (27), we have

$$ \tilde{A}_{s}^{T}Q_{s1} + Q_{s1}^{T} \tilde{A}_{s} + Q_{s3}^{T}N \tilde{C}_{s} + \tilde{C}_{s}^{T}N^{T}Q_{s3} < 0. $$

Set $X = Q_{s1}$, $\Phi = Q_{s3}^{T}N$. Then it can be seen that (23) holds. Now, let

$$\mathrm{\Upsilon }=\left(\begin{array}{cc}I& O\\ -Q_{s4}^{-1}{Q}_{s3}& I\end{array}\right).$$

Pre- and post-multiplying (27) by $\Upsilon^{T}$ and ϒ, respectively, we have

$$ \Pi^{T}\tilde{A}_{s} + \tilde{A}_{s}^{T} \Pi - \Pi^{T}\tilde{B}_{s}GQ _{s4}^{ - 1}Q_{s3} - Q_{s3}^{T}Q_{s4}^{ - T}G^{T} \tilde{B}_{s}^{T} \Pi < 0. $$

Set $Y = \Pi^{ - 1}$, $\Psi = GQ_{s4}^{ - 1}Q_{s3}Y$, and pre- and post-multiplying the above inequality by $Y^{T}$ and Y, respectively, one has that (24) holds.

Observe that $X > 0$ and $X - Y^{ - 1} = Q_{s2}Q_{s4}^{ - 1}Q_{s3} \ge 0$. By the Schur complement, we have that (22) is satisfied. This completes the proof. □

Remark 2

Theorem 1 presents a sufficient and necessary condition for the existence of the dynamic output feedback controller of the reduced-order subsystem. Furthermore, a workable way for solving the gain matrices M, N and G is also given. It is worth mentioning that, under this condition, there is no other restriction for the dynamic output feedback controller design, except the system itself.

Remark 3

The proposed method in this paper guarantees that the proper dynamic output feedback controller designed for the reduced-order subsystem is a stabilizing one for the full-order system. In particular, it is not difficult to see that the stability of the limit case (i.e., slow subsystems and fast subsystems) of the resulting closed-loop systems is still preserved as $\varepsilon \to 0$. It is worth pointing out that the singular perturbation approach is not yet fully adopted in many literature works. Instead, the singular system approach is adopted, in which the singular perturbation parameter $\varepsilon > 0$ is viewed as a static scalar. This brings some simplification to system analysis and synthesis. However, the performance of the limit case of the closed-loop systems may not be guaranteed as $\varepsilon \to 0$, and even more, the basic requirement for poles placement cannot be satisfied.

4 A numerical example

Consider a nuclear reactor model whose physical model can be found in [20], which can be described by the following state equations:

$$\begin{aligned}& \dot{x}_{1} = - \lambda x_{1} + \lambda x_{2}, \end{aligned}$$

(28)

$$\begin{aligned}& \dot{x}_{2} = \frac{\beta }{\nu } x_{1} + \frac{\beta }{\nu } x_{2} + \frac{\rho }{\nu }, \end{aligned}$$

(29)

where $x_{1}$ and $x_{2}$ represent the normalized precursors’ concentration and neutron density, respectively. The parameters ρ, λ, β and ν represent the reactivity, precursors’ decay constant, delayed-neutron yield and neutron generation-time, respectively, where $\lambda = 0.001$, $\beta = 0.0064$ and $\nu = 0.08$. By discretizing the model with a sampling period $T = 0.05s$ and a zero-order holder, we can obtain the discrete model with a controlled output considered in the following form:

$$\begin{aligned}& x_{1}(k + 1) = (1 - 0.3417\varepsilon )x_{1}(k) + 0.3417 \varepsilon x _{2}(k) + 9.0021\varepsilon u(k), \end{aligned}$$

(30a)

$$\begin{aligned}& x_{2}(k + 1) = 0.2733x_{1}(k) + 0.7267x_{2}(k) + 42.7983u(k), \end{aligned}$$

(30b)

$$\begin{aligned}& y(k) = 2x_{1}(k) + x_{2}(k). \end{aligned}$$

(31)

From (30)-(31), the slow and fast subsystems are obtained as

$$\begin{aligned}& \dot{x}_{s}(t) = 62.5117u_{s}(t), \end{aligned}$$

(32a)

$$\begin{aligned}& y_{s}(t) = 3x_{s}(t) + 156.5982u_{s}(t) \end{aligned}$$

(32b)

and

$$\begin{aligned}& x_{f}(k + 1) = 0.7267x_{f}(k) + 42.7983u_{f}(k), \end{aligned}$$

(33a)

$$\begin{aligned}& y_{f}(k) = x_{f}(k). \end{aligned}$$

(33b)

We first give the following controller for the slow subsystem:

$$\begin{aligned}& \dot{\zeta } (t) = 0.3\zeta (t) - 0.2y_{s}(t), \\& u_{s}(t) = - 0.008\zeta (t) + 0.05y_{s}(t), \end{aligned}$$

which locates the poles at $\{ - 0.5548 + 2.3812\mathrm{i}, - 0.5548 - 2.3812\mathrm{i} \}$, thus system (32) with the above dynamic output feedback control is stable. When this controller is applied to the full-order system, it results in the following closed-loop system:

$$\left(\begin{array}{c}{x}_1(k+1)\\ \xi (k+1)\\ x_2(k+1)\end{array}\right)=\left(\begin{array}{ccc}1+\epsilon 0.5585& -0.072& 0.7918\\ -0.4& 1+\epsilon 0.3& -0.2\\ 4.5531& -0.3424& 2.8666\end{array}\right)\left(\begin{array}{c}{x}_1(k)\\ \xi (k)\\ x_2(k)\end{array}\right).$$

We find that the closed-loop system is unstable for sufficiently small parameter ε because $\Gamma_{22} = A_{22} + B_{2}HC_{2} = 2.8667 > 1$. In order to guarantee that a non-strictly dynamic output feedback with the gain matrices M, N, G and H designed for reduced-order subsystem (32) can stabilize system (30), the proposed method in this paper is considered.

First, by resorting to Theorem 1 in [32], the static output feedback controller gain matrix for the fast subsystem is obtained as $H = - 0.017$.

Using Theorem 1 with the aid of LMI toolbox, the following solutions for the auxiliary system can be obtained from (22)-(24):

$$\begin{aligned}& X = 5.2782 \times 10^{8},\qquad Y = 5.2782 \times 10^{8}, \\& \Phi = 2.3875 \times 10^{8},\qquad \Psi = - 1.1458 \times 10^{7}. \end{aligned}$$

Thus, one has

$$ M = - 0.1214,\qquad N = - 0.4523,\qquad G = 0.0217. $$

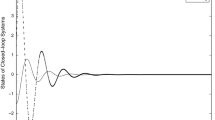
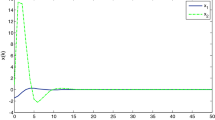
From Theorem 1, we can conclude that the dynamic output feedback controller designed for the reduced-order subsystem stabilizes the original full-order system (30) for a sufficiently small ε. For the small parameter ε, Li et al. in [14] proposed the latest result to compute the upper bound. Applying the method to system (30)-(31), we obtain the exact ε upper bound as $\varepsilon^{*} = 1.1906$. Given the initial condition $( x_{1}(0) \ \xi (0) \ x_{2}(0) )^{T} = ( {-} 1.5 \ {-} 1.5 \ 1.5 )^{T}$, the simulation results for the response of closed-loop system (5) are shown in Figures 1-2, from which it can be seen that the presented proper but not strictly proper dynamic output feedback control scheme can effectively guarantee the stability of the closed-loop system. Thus, the requirement for the strict properness can be alleviated.

Figure 1

The state response of closed-loop system (5) with $\pmb{\varepsilon = 0.1}$ .

Figure 2

The state response of closed-loop system (5) with $\pmb{\varepsilon = 1.18}$ .

5 Conclusion

In this paper, the proper dynamic output feedback controller for the fast sampling discrete-time singularly perturbed system is addressed using the reduced-order model. The design of a proper but not strictly proper dynamic output feedback controller is reduced to the simultaneous design of the static output feedback controller for the fast subsystem and the strictly proper dynamic output feedback controller for the auxiliary system, respectively. Thus, the requirement for the strict properness of the dynamic output feedback controller has been removed successfully. This is the main difference from the existing works. Finally, the given example has illustrated the effectiveness of the obtained method.